3D Simulations of Intracerebral Hemorrhage Detection Using Broadband Microwave Technology
Abstract
1. Introduction
2. Method
2.1. Electromagnetic Modeling and Simulations
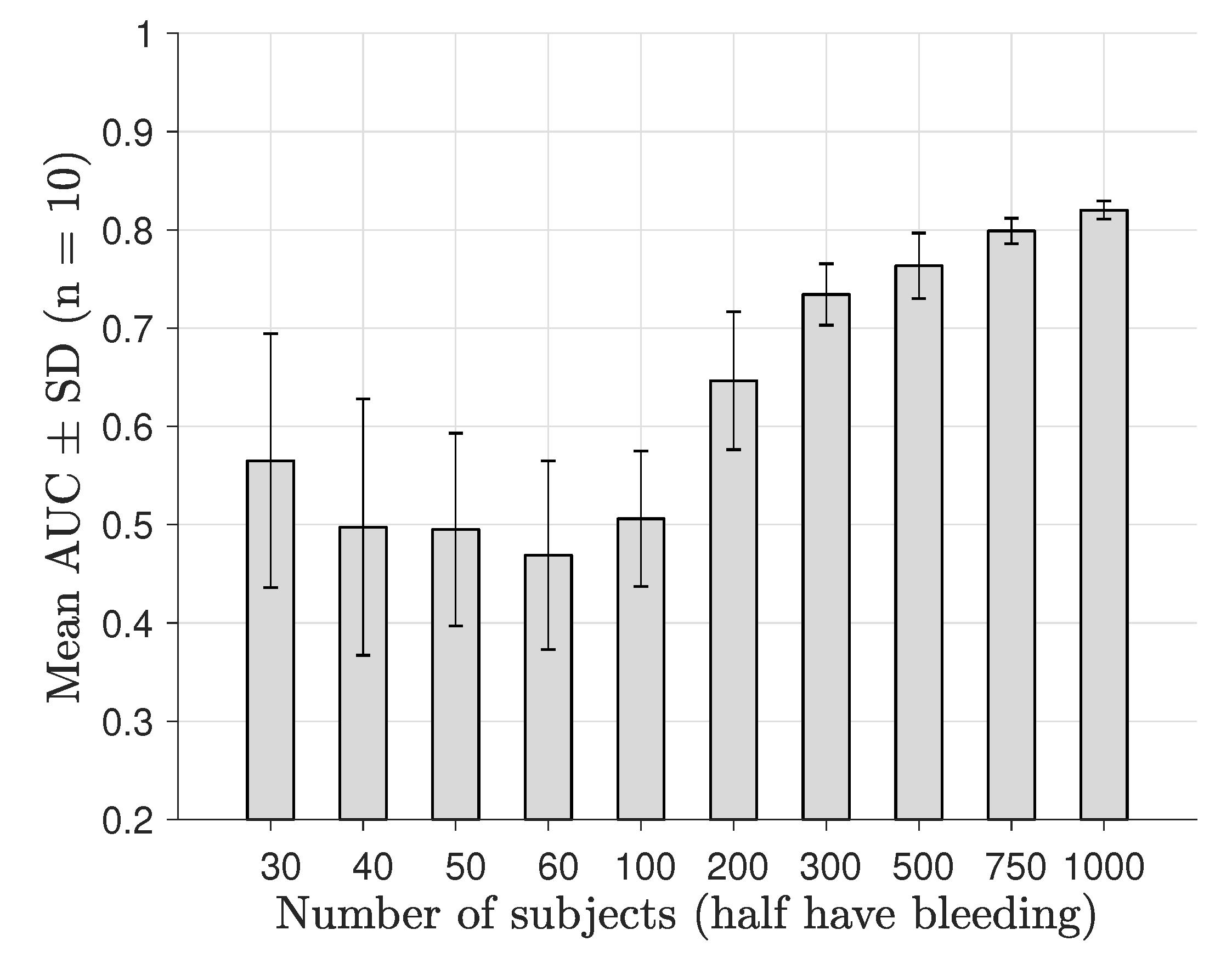
2.2. Classification of Modeled Subjects and Assessment of Diagnostic Performance for Different Numbers of Subjects
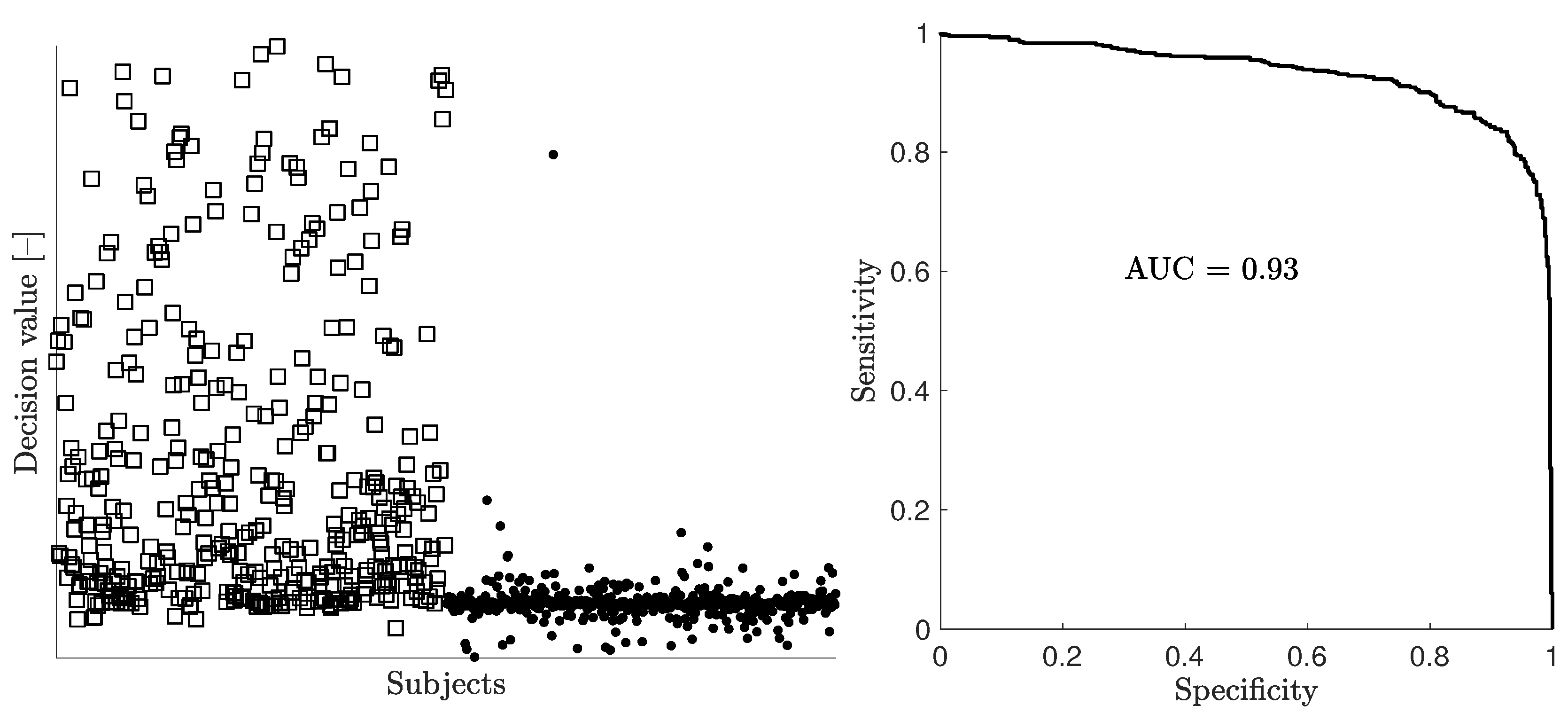
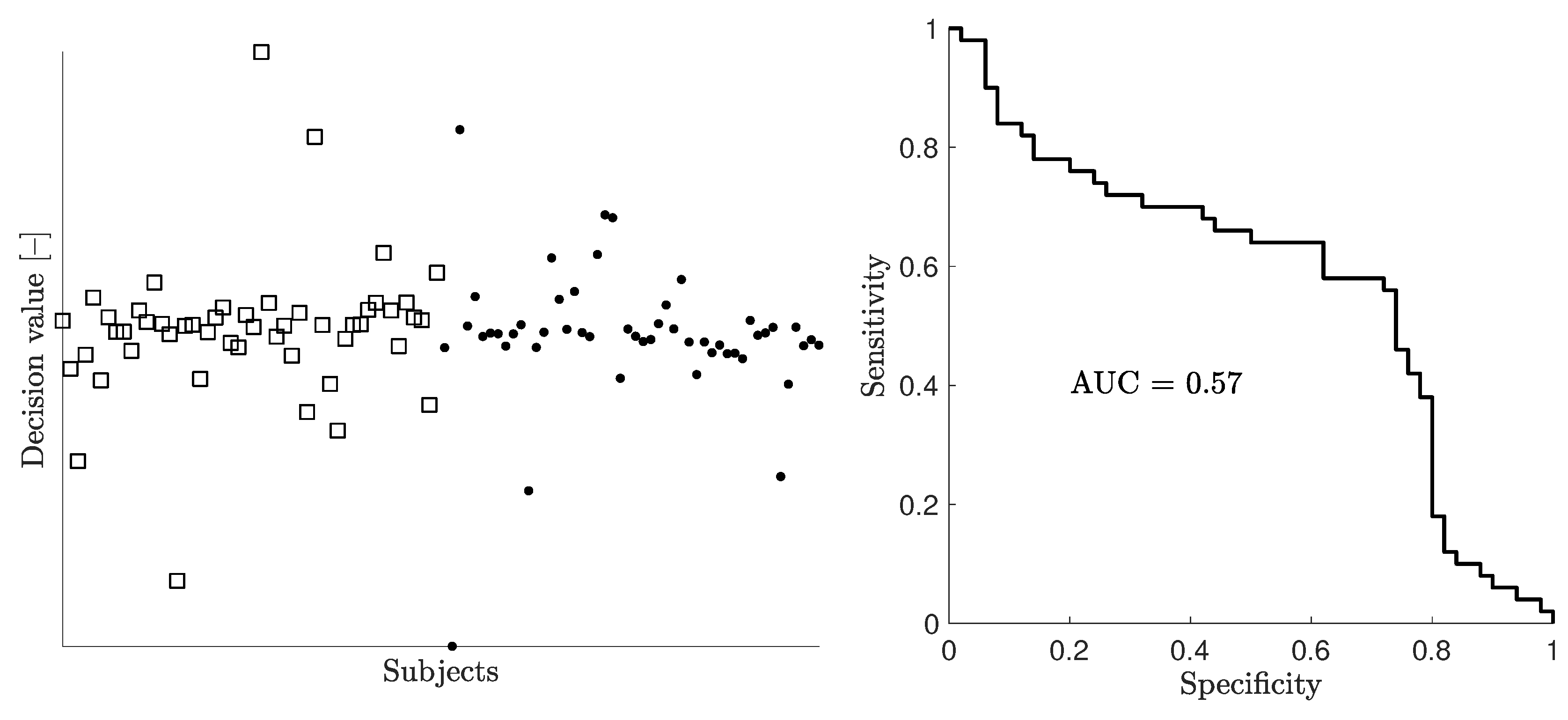
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fhager, A.; Candefjord, S.; Elam, M.; Persson, M. Microwave Diagnostics Ahead: Saving Time and the Lives of Trauma and Stroke Patients. IEEE Microw. Mag. 2018, 19, 78–90. [Google Scholar] [CrossRef]
- Persson, M.; Fhager, A.; Trefna, H.D.; Yu, Y.; McKelvey, T.; Pegenius, G.; Karlsson, J.E.; Elam, M. Microwave-based stroke diagnosis making global pre-hospital thrombolytic treatment possible. IEEE Trans. Biomed. Eng. 2014, 61, 2806–2817. [Google Scholar] [CrossRef] [PubMed]
- Ljungqvist, J.; Candefjord, S.; Persson, M.; Jönsson, L.; Skoglund, T.; Elam, M. Clinical Evaluation of a Microwave-Based Device for Detection of Traumatic Intracranial Hemorrhage. J. Neurotrauma 2017, 34, 2176–2182. [Google Scholar] [CrossRef] [PubMed]
- Semenov, S.; Seiser, B.; Stoegmann, E.; Auff, E. Electromagnetic tomography for brain imaging: From virtual to human brain. In Proceedings of the 2014 IEEE Conference on Antenna Measurements Applications (CAMA), Antibes Juan-les-Pins, France, 16–19 November 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Semenov, S.; Planas, R.; Hopfer, M.; Hamidipour, A.; Vasilenko, A.; Stoegmann, E.; Auff, E. Electromagnetic tomography for brain imaging: Initial assessment for stroke detection. In Proceedings of the 2015 IEEE Biomedical Circuits and Systems Conference (BioCAS), Atlanta, GA, USA, 22–24 October 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Semenov, S.; Hopfer, M.; Planas, R.; Hamidipour, A.; Henriksson, T. Electromagnetic tomography for brain imaging: 3D reconstruction of stroke in a human head phantom. In Proceedings of the 2016 IEEE Conference on Antenna Measurements Applications (CAMA), Syracuse, NY, USA, 23–27 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Hopfer, M.; Planas, R.; Hamidipour, A.; Henriksson, T.; Semenov, S. Electromagnetic Tomography for Detection, Differentiation, and Monitoring of Brain Stroke: A Virtual Data and Human Head Phantom Study. IEEE Antennas Propag. Mag. 2017, 59, 86–97. [Google Scholar] [CrossRef]
- Mobashsher, A.T.; Bialkowski, K.S.; Abbosh, A.M.; Crozier, S. Design and Experimental Evaluation of a Non-Invasive Microwave Head Imaging System for Intracranial Haemorrhage Detection. PLoS ONE 2016, 11, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Mobashsher, A.T.; Mahmoud, A.; Abbosh, A.M. Portable Wideband Microwave Imaging System for Intracranial Hemorrhage Detection Using Improved Back-projection Algorithm with Model of Effective Head Permittivity. Sci. Rep. 2016, 6, 20459. [Google Scholar] [CrossRef] [PubMed]
- Mobashsher, A.T.; Abbosh, A.M. On-site Rapid Diagnosis of Intracranial Hematoma using Portable Multi-slice Microwave Imaging System. Sci. Rep. 2016, 6, 37620. [Google Scholar] [CrossRef] [PubMed]
- Bjelogrlic, M.; Volery, M.; Fuchs, B.; Thiran, J.P.; Mosig, J.R.; Mattes, M. Stratified Spherical Model for Microwave Imaging of the Brain: Analysis and Experimental Validation of Transmitted Power. Microw. Opt. Technol. Lett. 2018, 60, 1042–1048. [Google Scholar] [CrossRef]
- Crocco, L.; Karanasiou, I.; James, M.L.; Conceição, R.C. (Eds.) Emerging Electromagnetic Technologies for Brain Diseases Diagnostics, Monitoring and Therapy; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Conceição, R.C.; Mohr, J.J.; O’Halloran, M. An Introduction to Microwave Imaging for Breast Cancer Detection; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Oliveira, B.L.; Godinho, D.; O’Halloran, M.; Glavin, M.; Jones, E.; Conceição, R.C. Diagnosing Breast Cancer with Microwave Technology: Remaining Challenges and Potential Solutions with Machine Learning. Diagnostics 2018, 8, 36. [Google Scholar] [CrossRef]
- Tournier, P.; Aliferis, I.; Bonazzoli, M.; de Buhan, M.; Darbas, M.; Dolean, V.; Hecht, F.; Jolivet, P.; Kanfoud, I.E.; Migliaccio, C.; et al. Microwave Tomographic Imaging of Cerebrovascular Accidents by Using High-Performance Computing. Parallel Comput. 2019, 85, 88–97. [Google Scholar] [CrossRef]
- Lim, H.B.; Nhung, N.T.T.; Li, E.; Thang, N.D. Confocal Microwave Imaging for Breast Cancer Detection: Delay-Multiply-and-Sum Image Reconstruction Algorithm. IEEE Trans. Biomed. Eng. 2008, 55, 1697–1704. [Google Scholar] [CrossRef] [PubMed]
- Scapaticci, R.; Bucci, O.M.; Catapano, I.; Crocco, L. Differential Microwave Imaging for Brain Stroke Followup. Int. J. Antennas Propag. 2014, 2014, 312528. [Google Scholar] [CrossRef]
- Mahmood, Q.; Li, S.; Fhager, A.; Candefjord, S.; Chodorowski, A.; Mehnert, A.; Persson, M. A Comparative Study of Automated Segmentation Methods for Use in a Microwave Tomography System for Imaging Intracerebral Hemorrhage in Stroke Patients. J. Electromagn. Anal. Appl. 2015, 7, 152–167. [Google Scholar] [CrossRef]
- Grzegorczyk, T.M.; Meaney, P.M.; Kaufman, P.A.; di Florio Alexander, R.M.; Paulsen, K.D. Fast 3-D Tomographic Microwave Imaging for Breast Cancer Detection. IEEE Trans. Med. Imaging 2012, 31, 1584–1592. [Google Scholar] [CrossRef] [PubMed]
- Hosseinzadegan, S.; Fhager, A.; Persson, M.; Meaney, P. Application of Two-Dimensional Discrete Dipole Approximation in Simulating Electric Field of a Microwave Breast Imaging System. IEEE J. Electromagn. RF Microw. Med. Biol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Jordan, M.I.; Mitchell, T.M. Machine Learning: Trends, Perspectives, and Prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Horvitz, E.; Mulligan, D. Data, Privacy, and the Greater Good. Science 2015, 349, 253–255. [Google Scholar] [CrossRef]
- Candefjord, S.; Winges, J.; Yu, Y.; Rylander, T.; McKelvey, T. Microwave technology for localization of traumatic intracranial bleeding—A numerical simulation study. In Proceedings of the 35th Annual International Conference of the IEEE EMBS, Osaka, Japan, 3–7 July 2013; pp. 1948–1951. [Google Scholar]
- Candefjord, S.; Winges, J.; Malik, A.A.; Yu, Y.; Rylander, T.; McKelvey, T.; Fhager, A.; Elam, M.; Persson, M. Microwave technology for detecting traumatic intracranial bleeding: Tests on phantom of subdural hematoma and numerical simulations. Med. Biol. Eng. Comput. 2017, 55, 1177–1188. [Google Scholar] [CrossRef]
- Cocosco, C.; Kwan, R.S.; Collins, D. BrainWeb: Simulated Brain Database. Available online: http://brainweb.bic.mni.mcgill.ca/brainweb (accessed on 20 February 2017).
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef]
- Fhager, A.; Gustafsson, M.; Nordebo, S. Image Reconstruction in Microwave Tomography Using a Dielectric Debye Model. IEEE Trans. Biomed. Eng. 2012, 59, 156–166. [Google Scholar] [CrossRef]
- Andreuccetti, D.; Fossi, R.; Petrucci, C. An Internet Resource for the Calculation of the Dielectric Properties of Body Tissues in the Frequency Range 10 Hz–100 GHz. Available online: http://niremf.ifac.cnr.it/tissprop/ (accessed on 1 August 2018).
- BrainWeb: Simulated Brain Database. Available online: http://www.bic.mni.mcgill.ca/brainweb (accessed on 1 August 2018).
- Tilley, A.R.; Associates, H.D. The Measure of Man and Woman: Human Factors in Design; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Statnikov, A.; Tsamardinos, I.; Dosbayev, Y.; Aliferis, C.F. GEMS: A System for Automated Cancer Diagnosis and Biomarker Discovery from Microarray Gene Expression Data. Int. J. Med. Inform. 2005, 74, 491–503. [Google Scholar] [CrossRef] [PubMed]
- Ambroise, C.; McLachlan, G.J. Selection Bias in Gene Extraction on the Basis of Microarray Gene-Expression Data. Proc. Natl. Acad. Sci. USA 2002, 99, 6562–6566. [Google Scholar] [CrossRef] [PubMed]
- Cawley, G.C.; Talbot, N.L.C. On Over-Fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
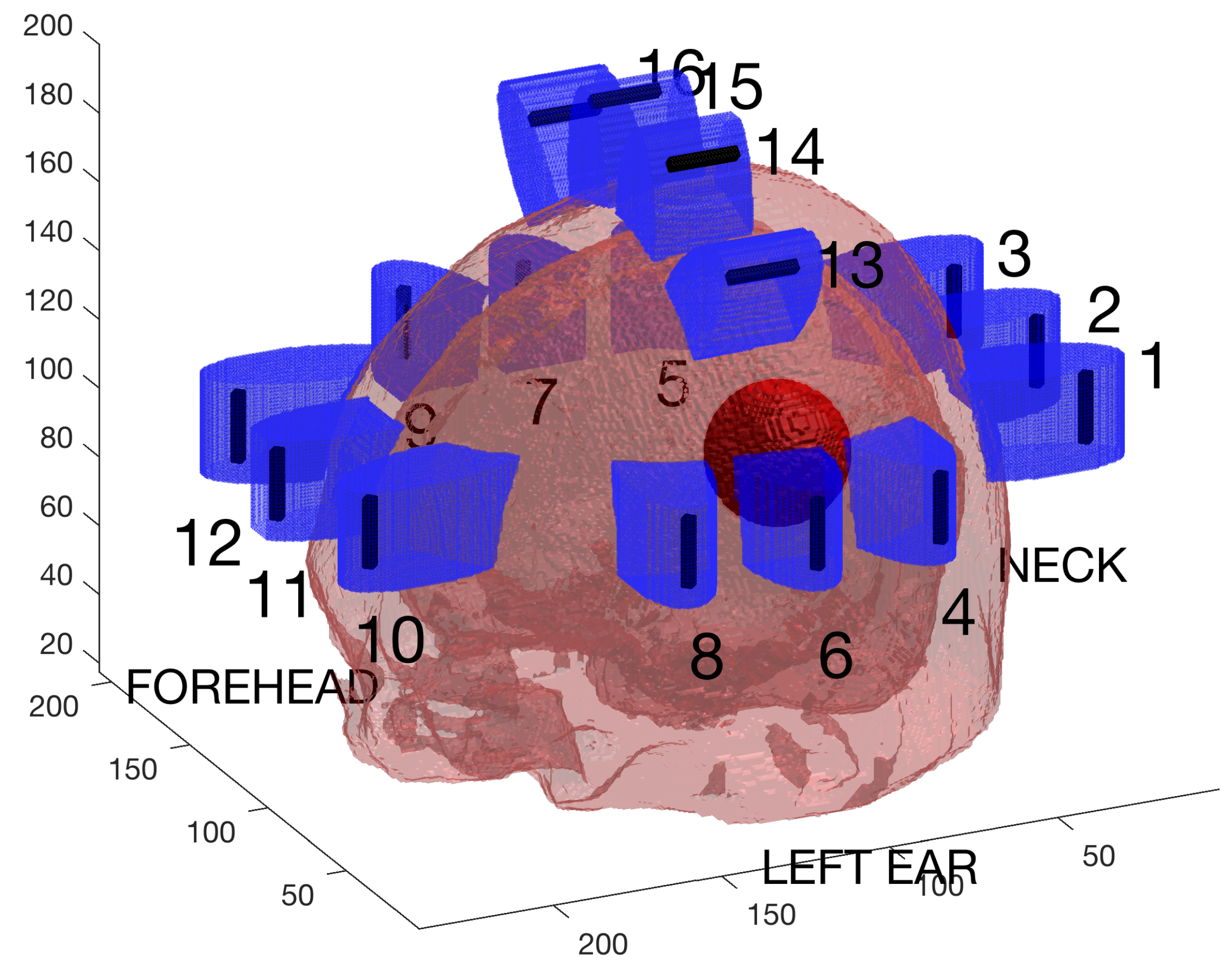
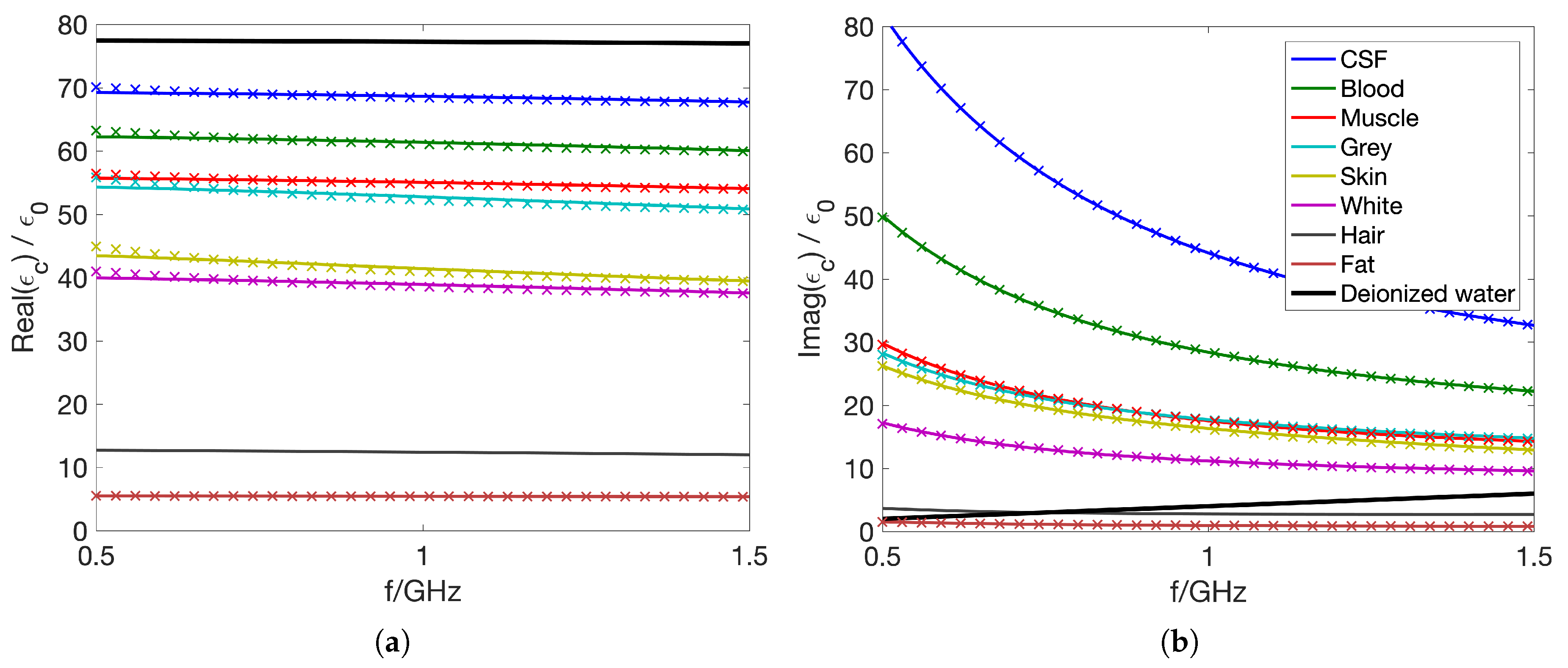
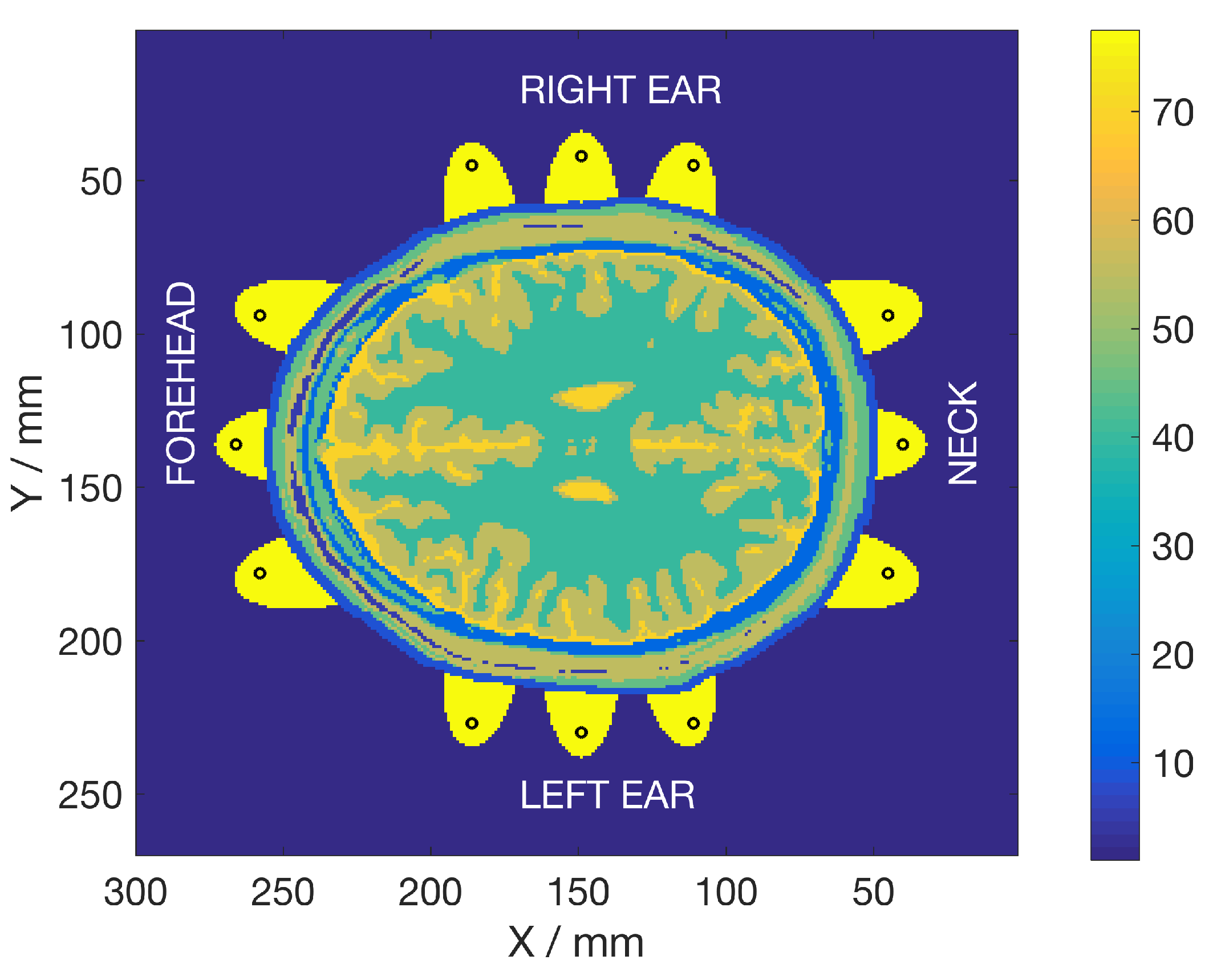
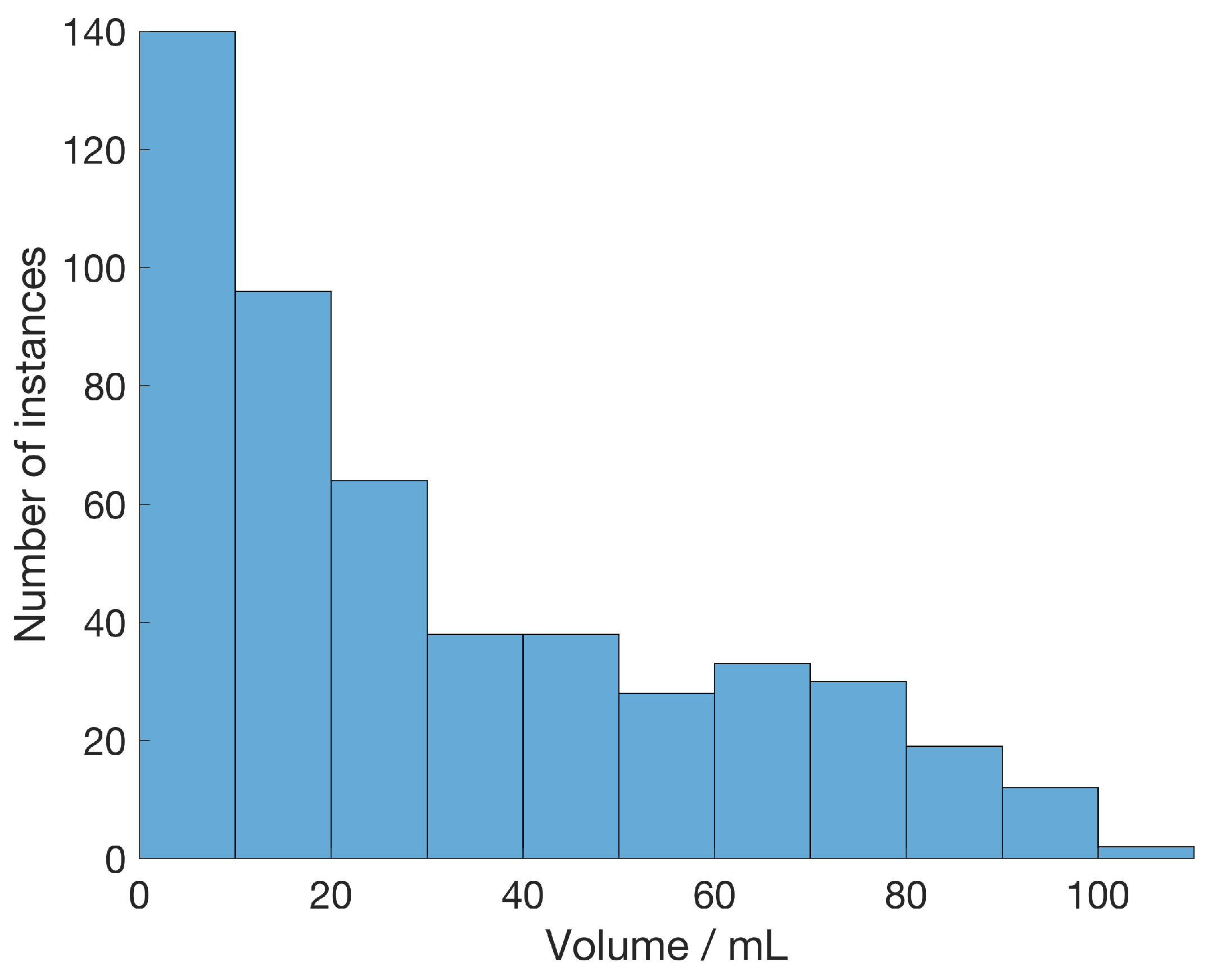

| Male | Female | Computational Model | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Percentiles | 1 | 50 | 99 | 1 | 50 | 99 | 1 | 50 | 99 |
| Ear-Ear | 142 | 155 | 169 | 132 | 145 | 159 | 132 | 150 | 169 |
| Forehead-Neck | 180 | 196 | 214 | 162 | 180 | 198 | 162 | 188 | 214 |
| Top-Below Eye | 112 | 125 | 137 | 109 | 122 | 135 | 109 | 123.5 | 137 |
| N | 30 | 40 | 50 | 60 | 100 | 200 | 300 | 500 | 750 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|
| dB | 0.073 | 0.524 | 0.562 | 0.834 | 0.394 | < | < | < | < | < |
| dB | 0.961 | 0.135 | 0.664 | 0.891 | 0.041 | < | < | < | < | < |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fhager, A.; Candefjord, S.; Elam, M.; Persson, M. 3D Simulations of Intracerebral Hemorrhage Detection Using Broadband Microwave Technology. Sensors 2019, 19, 3482. https://doi.org/10.3390/s19163482
Fhager A, Candefjord S, Elam M, Persson M. 3D Simulations of Intracerebral Hemorrhage Detection Using Broadband Microwave Technology. Sensors. 2019; 19(16):3482. https://doi.org/10.3390/s19163482
Chicago/Turabian StyleFhager, Andreas, Stefan Candefjord, Mikael Elam, and Mikael Persson. 2019. "3D Simulations of Intracerebral Hemorrhage Detection Using Broadband Microwave Technology" Sensors 19, no. 16: 3482. https://doi.org/10.3390/s19163482
APA StyleFhager, A., Candefjord, S., Elam, M., & Persson, M. (2019). 3D Simulations of Intracerebral Hemorrhage Detection Using Broadband Microwave Technology. Sensors, 19(16), 3482. https://doi.org/10.3390/s19163482





