Wireless, Portable Fiber Bragg Grating Interrogation System Employing Optical Edge Filter
Abstract
1. Introduction
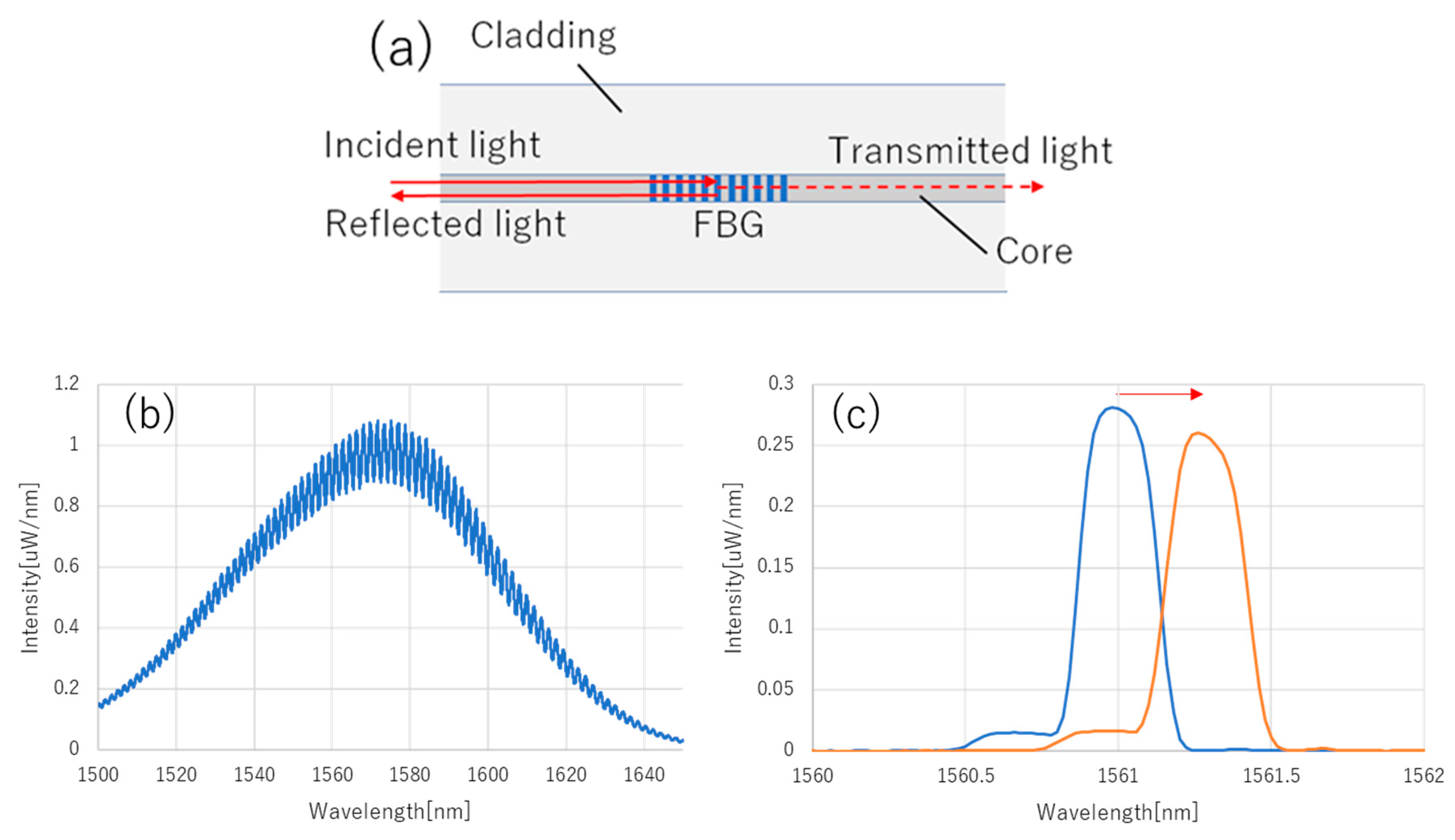
2. Edge Filter-Based FBG Interrogator
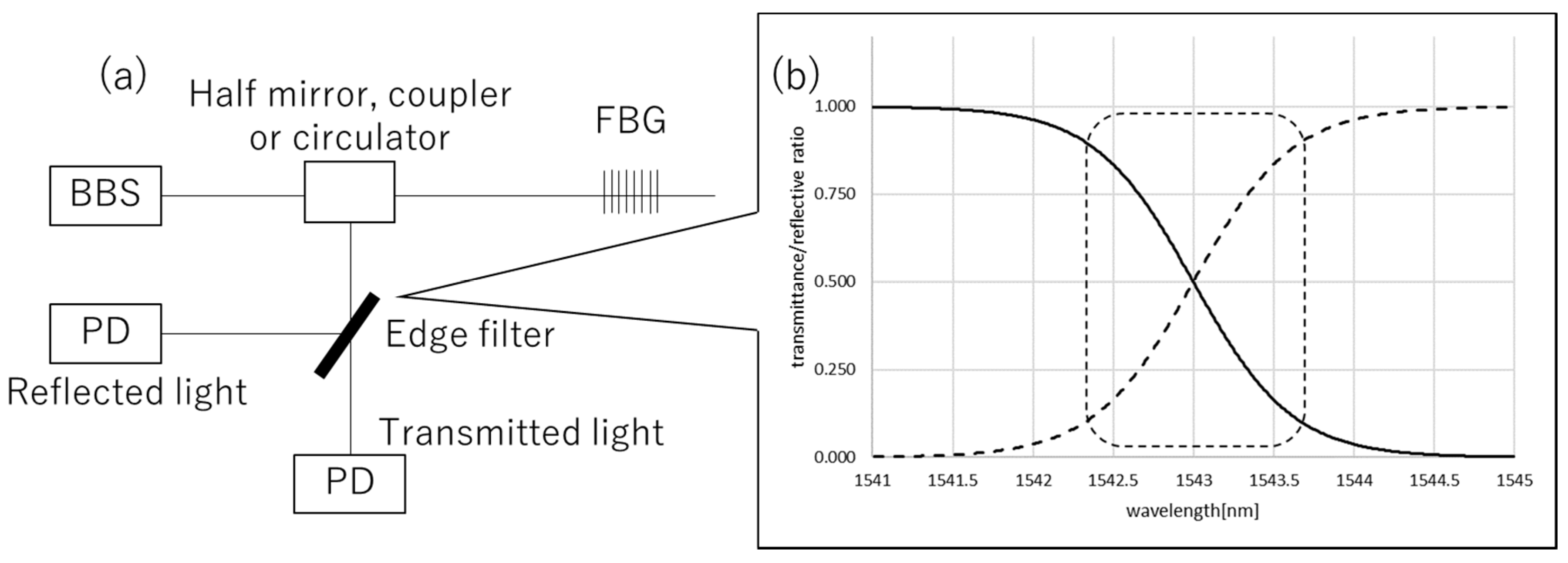
2.1. Principle of Edge Filter-Based FBG Interrogation
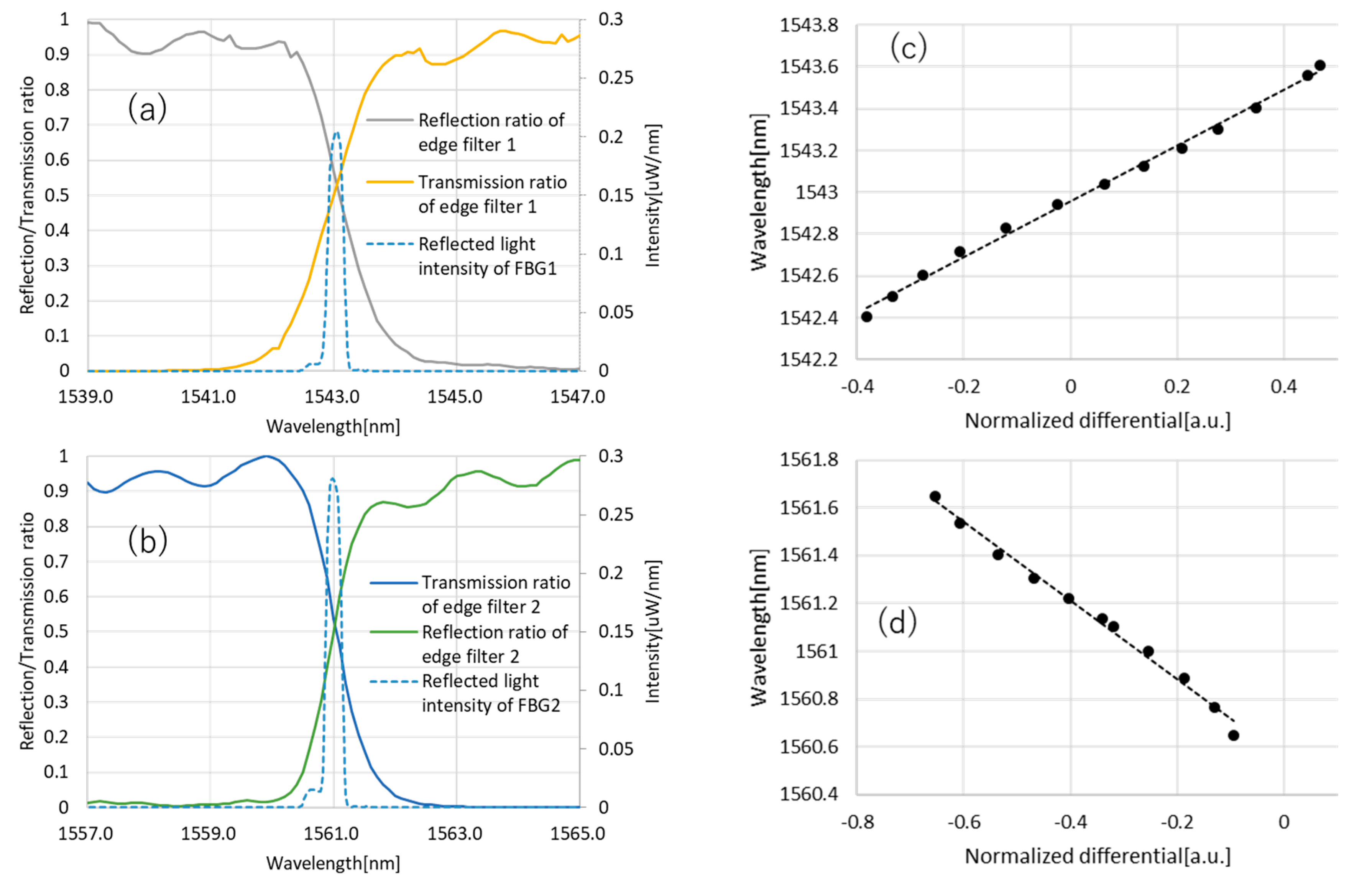
2.2. Characteristics of the Developed FBG Interrogator
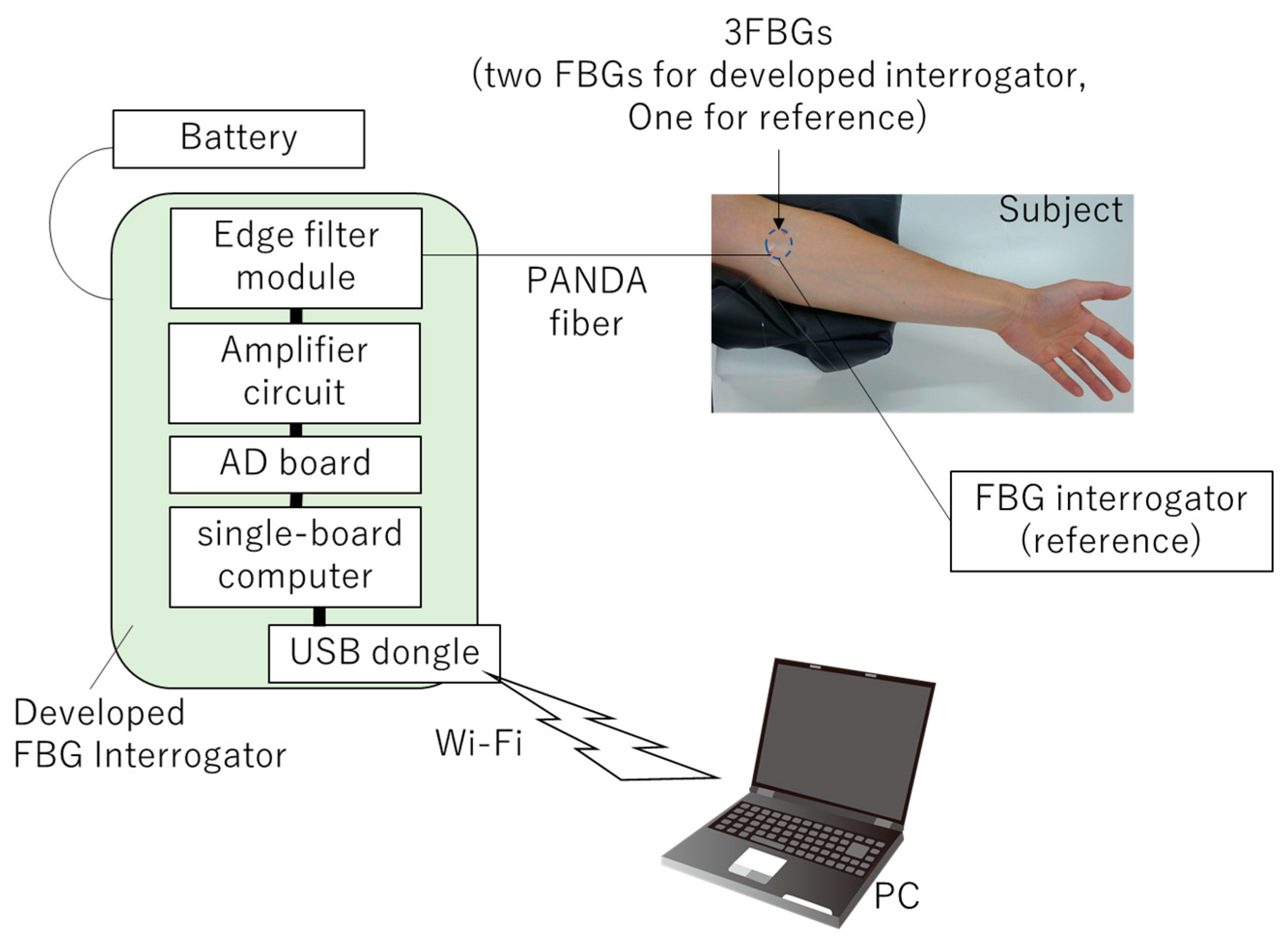
3. Application to Vital Sign Monitoring
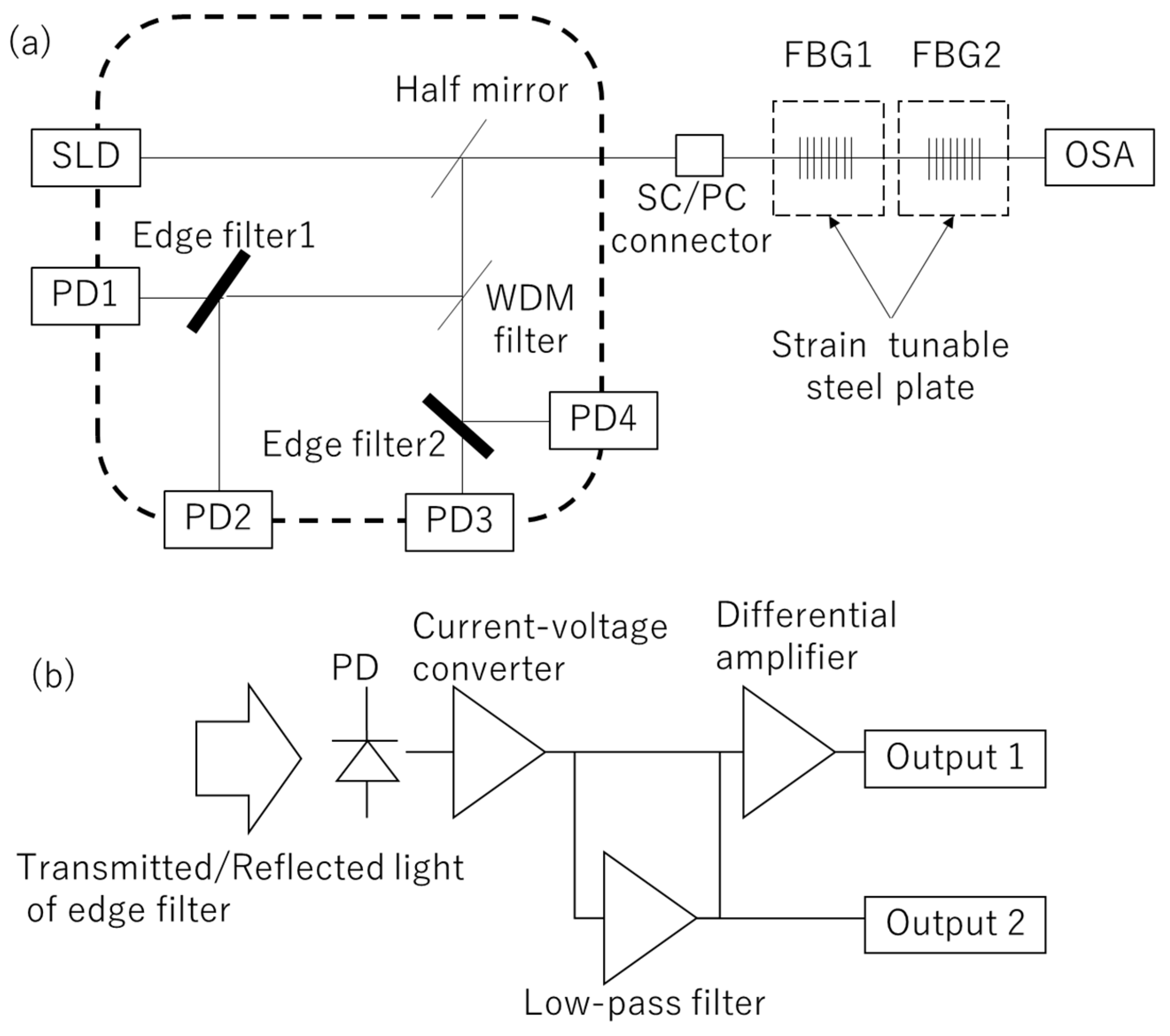
3.1. Principle and Setup
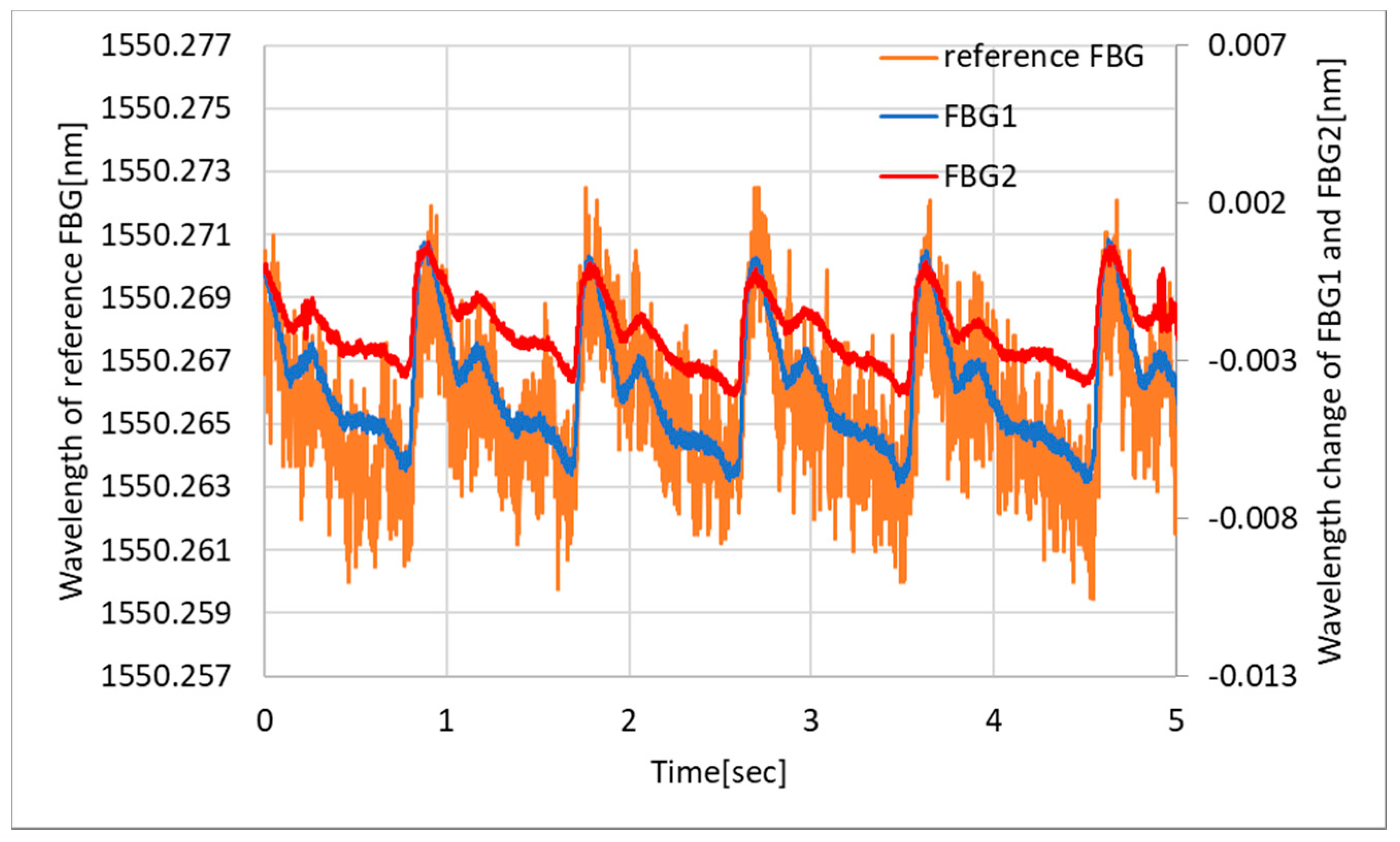
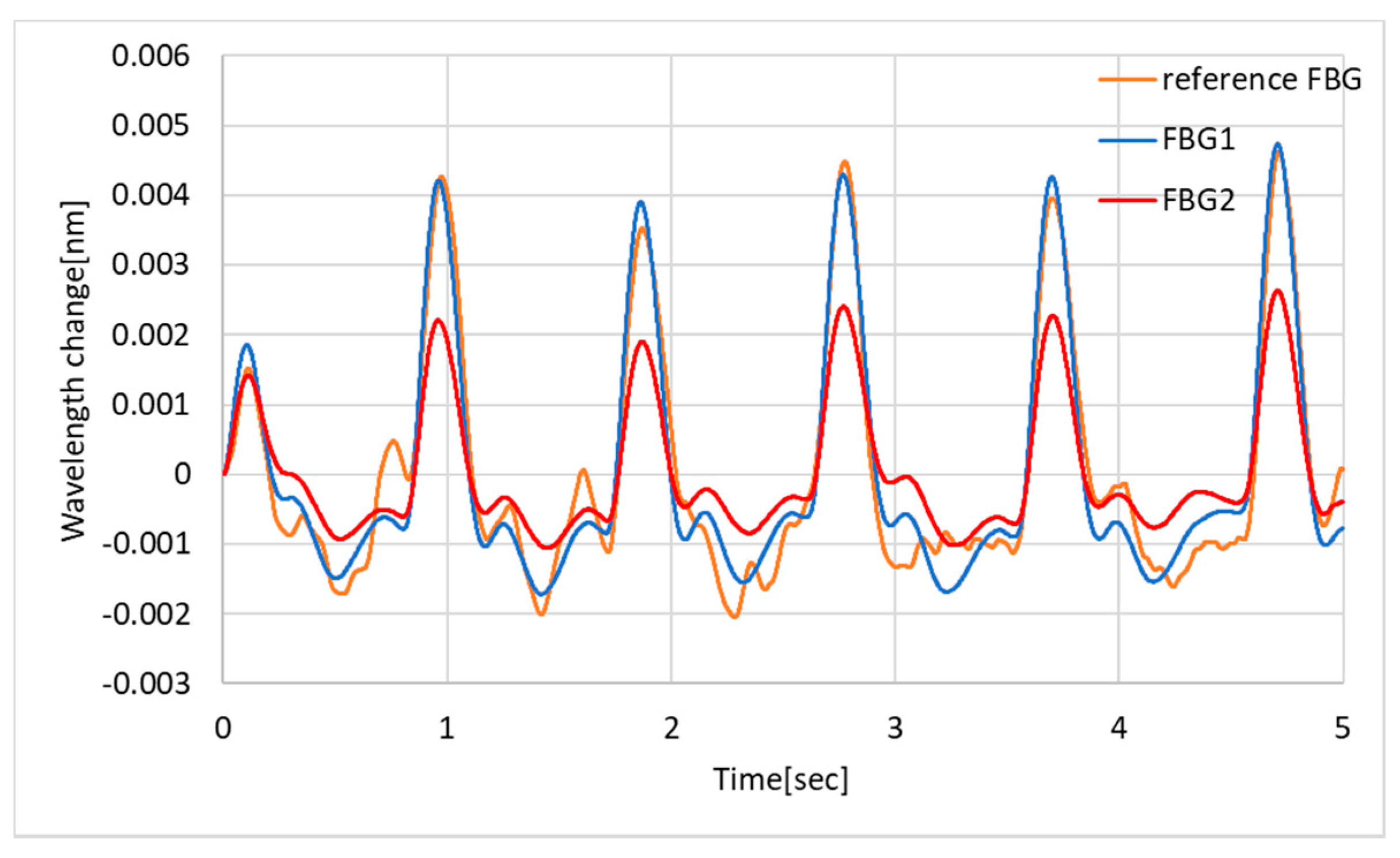
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Galeotti, L.; Scully, C.G. A method to extract realistic artifacts from electrocardiogram recordings for robust algorithm testing. J. Electrocardiol. 2018, 51, S56–S60. [Google Scholar] [CrossRef] [PubMed]
- Sa-Ngasoongsong, A.; Kunthong, J.; Sarangan, V.; Cai, X.; Bukkapatnam, S.T. A low-cost, portable, high-throughput wireless sensor system for phonocardiography applications. Sensors 2012, 12, 10851–10870. [Google Scholar] [CrossRef] [PubMed]
- Warren, K.; Harvey, J.; Chon, K.; Mendelson, Y. Improving pulse rate measurements during random motion using a wearable multichannel reflectance photoplethysmograph. Sensors 2016, 16, 342. [Google Scholar] [CrossRef] [PubMed]
- Wei, P.; Guo, R.; Zhang, J.; Zhang, Y.T. A new wristband wearable sensor using adaptive reduction filter to reduce motion artifact. In Proceedings of the 2008 International Conference on Information Technology and Applications in Biomedicine, Shenzhen, China, 30–31 May 2008; pp. 278–281. [Google Scholar]
- Hill, K.O.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Lightwave Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber grating sensors. J. Lightwave Technol. 1997, 15, 1442–1463. [Google Scholar] [CrossRef]
- Rajan, G. Optical Fiber Sensors: Advanced Techniques and Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Yoshino, T.; Sano, Y.; Ota, D.; Fujita, K.; Ikui, T. Fiber-Bragg-grating based single axial mode Fabry-Perot interferometer and its strain and acceleration sensing applications. J. Lightwave Technol. 2016, 34, 2241–2250. [Google Scholar] [CrossRef]
- Chan, T.H.; Yu, L.; Tam, H.-Y.; Ni, Y.-Q.; Liu, S.Y.; Chung, W.H.; Cheng, L.K. Fiber Bragg grating sensors for structural health monitoring of Tsing Ma bridge: Background and experimental observation. Eng. Struct. 2006, 28, 648–659. [Google Scholar] [CrossRef]
- Majumder, M.; Gangopadhyay, T.K.; Chakraborty, A.K.; Dasgupta, K.; Bhattacharya, D.K. Fibre Bragg gratings in structural health monitoring—Present status and applications. Sens. Actuators A Phys. 2008, 147, 150–164. [Google Scholar] [CrossRef]
- Laffont, G.; Roussel, N.; Rougeault, S.; Boussoir, J.; Maurin, L.; Ferdinand, P. Innovative FBG sensing techniques for the railway industry: Application to overhead contact line monitoring. In Proceedings of the 20th International Conference on Optical Fibre Sensors, International Society for Optics and Photonics, Edinburgh, UK, 5–9 October 2009; Volume 7503, p. 75035K. [Google Scholar]
- Bocciolone, M.; Bucca, G.; Collina, A.; Comolli, L. Pantograph–catenary monitoring by means of fibre Bragg grating sensors: Results from tests in an underground line. Mech. Syst. Signal Process. 2013, 41, 226–238. [Google Scholar] [CrossRef]
- Takahashi, N.; Yoshimura, K.; Takahashi, S.; Imamura, K. Development of an optical fiber hydrophone with fiber Bragg grating. Ultrasonics 2000, 38, 581–585. [Google Scholar] [CrossRef]
- Fisher, N.E.; Webb, D.J.; Pannell, C.N.; Jackson, D.A.; Gavrilov, L.R.; Hand, J.W.; Zhang, L.; Bennion, I. Ultrasonic hydrophone based on short in-fiber Bragg gratings. Appl. Opt. 1998, 37, 8120–8128. [Google Scholar] [CrossRef] [PubMed]
- Koyama, S.; Sakaguchi, A.; Ishizawa, H.; Yasue, K.; Oshiro, H.; Kimura, H. Vital Sign Measurement Using Covered FBG Sensor Embedded into Knitted Fabric for Smart Textile. J. Fiber Sci. Technol. 2017, 73, 300–308. [Google Scholar] [CrossRef]
- Sakaguchi, A.; Kato, M.; Ishizawa, H.; Kimura, H.; Koyama, S. Fabrication of optical fiber embedded knitted fabrics for smart textiles. J. Text. Eng. 2016, 62, 129–134. [Google Scholar] [CrossRef][Green Version]
- Roriz, P.; Carvalho, L.; Frazão, O.; Santos, J.L.; Simões, J.A. From conventional sensors to fibre optic sensors for strain and force measurements in biomechanics applications: A review. J. Biomech. 2014, 47, 1251–1261. [Google Scholar] [CrossRef] [PubMed]
- Gurkan, D.; Starodubov, D.; Yuan, X. Monitoring of the heartbeat sounds using an optical fiber Bragg grating sensor. In Proceedings of the SENSORS, 2005 IEEE, Irvine, CA, USA, 30 October–3 November 2005; p. 4. [Google Scholar]
- Zhang, C.; Miao, C.; Gao, H.; Gan, J.; Li, H.-Q. Research on fiber Bragg grating heart sound sensing and wavelength demodulation method. In Proceedings of the Advanced Sensor Systems and Applications IV, International Society for Optics and Photonics, Beijing, China, 18–20 October 2010; Volume 7853, p. 78531Q. [Google Scholar]
- Allsop, T.; Lloyd, G.; Bhamber, R.S.; Hadzievski, L.; Halliday, M.; Webb, D.J.; Bennion, I. Cardiac-induced localized thoracic motion detected by a fiber optic sensing scheme. J. Biomed. Opt. 2014, 19, 117006. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.F.; Carmo, J.P.; Mendes, P.M.; Correia, J.H. Simultaneous cardiac and respiratory frequency measurement based on a single fiber Bragg grating sensor. Meas. Sci. Technol. 2011, 22, 075801. [Google Scholar] [CrossRef]
- Presti, D.L.; Massaroni, C.; Formica, D.; Saccomandi, P.; Giurazza, F.; Caponero, M.A.; Schena, E. Smart textile based on 12 fiber Bragg gratings array for vital signs monitoring. IEEE Sens. J. 2017, 17, 6037–6043. [Google Scholar] [CrossRef]
- Dziuda, L.; Krej, M.; Skibniewski, F.W. Fiber Bragg grating strain sensor incorporated to monitor patient vital signs during MRI. IEEE Sens. J. 2013, 13, 4986–4991. [Google Scholar] [CrossRef]
- Massaroni, C.; Saccomandi, P.; Formica, D.; Presti, D.L.; Caponero, M.A.; Di Tomaso, G.; Giurazza, F.; Muto, M.; Schena, E. Design and feasibility assessment of a magnetic resonance-compatible smart textile based on fiber Bragg grating sensors for respiratory monitoring. IEEE Sens. J. 2016, 16, 8103–8110. [Google Scholar] [CrossRef]
- Nedoma, J.; Fajkus, M.; Novak, M.; Strbikova, N.; Vasinek, V.; Nazeran, H.; Vanus, J.; Perecar, F.; Martinek, R. Validation of a novel fiber-optic sensor system for monitoring cardiorespiratory activities during mri examinations. Adv. Electr. Electron. Eng. 2017, 15, 536–543. [Google Scholar] [CrossRef]
- Miyauchi, Y.; Koyama, S.; Ishizawa, H. Basic experiment of blood-pressure measurement which uses FBG sensors. In Proceedings of the 2013 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013; pp. 1767–1770. [Google Scholar]
- Katsuragawa, Y.; Ishizawa, H. Non-invasive blood pressure measurement by pulse wave analysis using FBG sensor. In Proceedings of the 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Proceedings, Pisa, Italy, 11–14 May 2015; pp. 511–515. [Google Scholar]
- Koyama, S.; Ishizawa, H.; Fujimoto, K.; Chino, S.; Kobayashi, Y. Influence of individual differences on the calculation method for FBG-type blood pressure sensors. Sensors 2017, 17, 48. [Google Scholar] [CrossRef] [PubMed]
- Haseda, Y.; Ishizawa, H.; Koyama, S.; Ogawa, K.; Fujita, K.; Chino, S.; Fujimoto, K. Fundamental Research of Pulse Wave and Blood Pressure Measurement Using Passive Edged Filter Integrated in Fiber Bragg Grating Measurement System. Proc. IEEE SICE 2018. [Google Scholar]
- Kurasawa, S.; Koyama, S.; Ishizawa, H.; Fujimoto, K.; Chino, S. Verification of Non-Invasive Blood Glucose Measurement Method Based on Pulse Wave Signal Detected by FBG Sensor System. Sensors 2017, 17, 2702. [Google Scholar] [CrossRef]
- Miyauchi, Y.; Ishizawa, H.; Niimura, M. Measurement of Pulse Rate and Respiration Rate Using Fiber Bragg Grating Sensor. Trans. Soc. Instrum. Control Eng. 2013, 49, 1101–1105. [Google Scholar] [CrossRef][Green Version]
- Ogawa, K.; Koyama, S.; Ishizawa, H.; Fujiwara, S.; Fujimoto, K. Simultaneous Measurement of Heart Sound, Pulse Wave and Respiration with Single Fiber Bragg Grating Sensor. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–5. [Google Scholar]
- Yun, S.H.; Richardson, D.J.; Kim, B.Y. Interrogation of fiber grating sensor arrays with a wavelength-swept fiber laser. Opt. Lett. 1998, 23, 843–845. [Google Scholar] [CrossRef]
- Nakazaki, Y.; Yamashita, S. Fast and wide tuning range wavelength-swept fiber laser based on dispersion tuning and its application to dynamic FBG sensing. Opt. Express 2009, 17, 8310–8318. [Google Scholar] [CrossRef] [PubMed]
- Todd, M.D.; Johnson, G.A.; Chang, C.C. Passive, light intensity-independent interferometric method for fibre Bragg grating interrogation. Electron. Lett. 1999, 35, 1970–1971. [Google Scholar] [CrossRef]
- Léguillon, Y.; Tow, K.H.; Besnard, P.; Mugnier, A.; Pureur, D.; Doisy, M. First demonstration of a 12 DFB fiber laser array on a 100 GHz ITU grid, for underwater acoustic sensing application. In Proceedings of the Optical Sensing and Detection II, International Society for Optics and Photonics, Brussels, Belgium, 16–19 April 2012; Volume 8439, p. 84390J. [Google Scholar]
- Davis, M.A.; Kersey, A.D. All-fibre Bragg grating strain-sensor demodulation technique using a wavelength division coupler. Electron. Lett. 1994, 30, 75–77. [Google Scholar] [CrossRef]
- Díaz, C.; Leitão, C.; Marques, C.; Domingues, M.; Alberto, N.; Pontes, M.; Frizera, A.; Ribeiro, M.; André, P.; Antunes, P. Low-cost interrogation technique for dynamic measurements with fbg-based devices. Sensors 2017, 17, 2414. [Google Scholar] [CrossRef]
- Díaz, C.A.; Marques, C.A.; Domingues, M.F.F.; Ribeiro, M.R.; Frizera-Neto, A.; Pontes, M.J.; André, P.S.; Antunes, P.F. A cost-effective edge-filter based FBG interrogator using catastrophic fuse effect micro-cavity interferometers. Measurement 2018, 124, 486–493. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogawa, K.; Koyama, S.; Haseda, Y.; Fujita, K.; Ishizawa, H.; Fujimoto, K. Wireless, Portable Fiber Bragg Grating Interrogation System Employing Optical Edge Filter. Sensors 2019, 19, 3222. https://doi.org/10.3390/s19143222
Ogawa K, Koyama S, Haseda Y, Fujita K, Ishizawa H, Fujimoto K. Wireless, Portable Fiber Bragg Grating Interrogation System Employing Optical Edge Filter. Sensors. 2019; 19(14):3222. https://doi.org/10.3390/s19143222
Chicago/Turabian StyleOgawa, Ken, Shouhei Koyama, Yuuki Haseda, Keiichi Fujita, Hiroaki Ishizawa, and Keisaku Fujimoto. 2019. "Wireless, Portable Fiber Bragg Grating Interrogation System Employing Optical Edge Filter" Sensors 19, no. 14: 3222. https://doi.org/10.3390/s19143222
APA StyleOgawa, K., Koyama, S., Haseda, Y., Fujita, K., Ishizawa, H., & Fujimoto, K. (2019). Wireless, Portable Fiber Bragg Grating Interrogation System Employing Optical Edge Filter. Sensors, 19(14), 3222. https://doi.org/10.3390/s19143222




