Adaptive Noise Reduction for Sound Event Detection Using Subband-Weighted NMF †
Abstract
1. Introduction
- WNMF is applied for audio source separation instead of NMF, which introduces a control on different frequencies and time frames of the input mixture signal. Such a control can help to better emphasize certain important components for distinguishing the target sound events from noise, such as the critical subbands of target sounds, and thus improve the separation quality.
- Noise estimation results from the noise dictionary learning step are exploited in developing both the frequency weights and temporal weights. This produces noise-adapted weights so as to fit the WNMF decomposition to time-varying background noise.
2. NMF and Weighted NMF
2.1. NMF
2.2. Weighted NMF
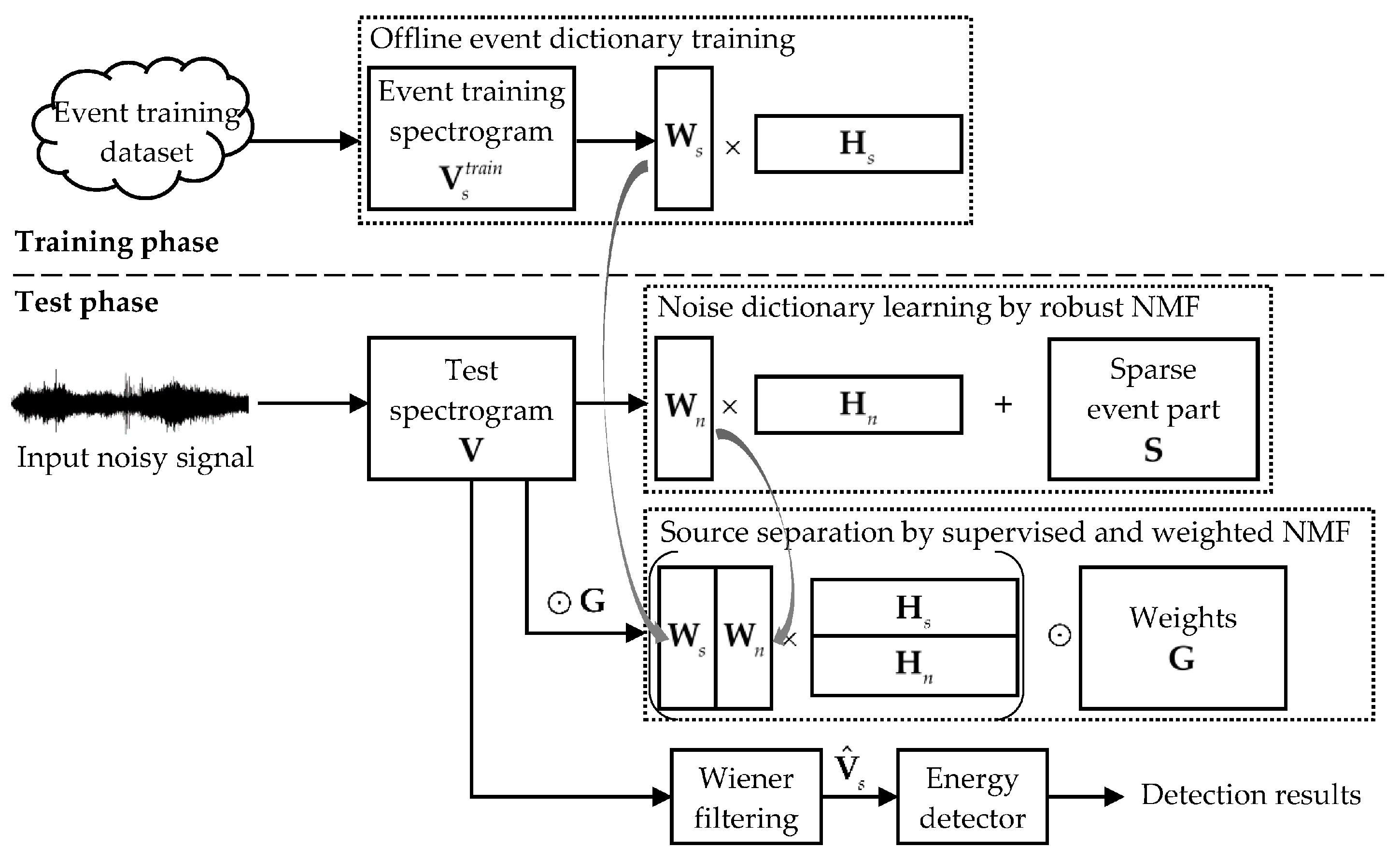
3. Proposed Method
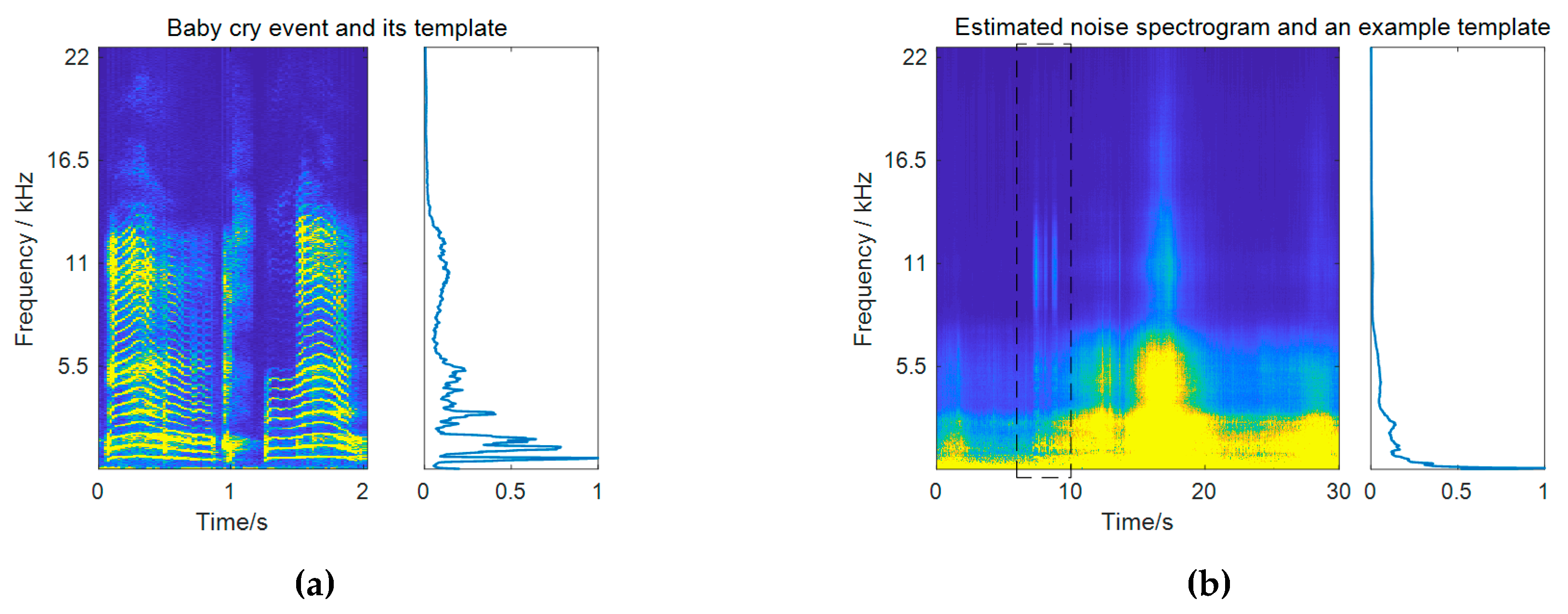
3.1. Noise Dictionary Learning by Robust NMF
| Algorithm 1. Noise dictionary learning by robust NMF | |
| Input: spectrogram of an input signal V, the number of noise bases , sparsity parameter | |
| Output: estimated noise dictionary and spectrogram | |
| 1: | Initialize , , and S with random non-negative values |
| 2: | repeat |
| 3: | update , , and S using Equations (14)–(16) |
| 4: | until convergence |
| 5: | Compute |
3.2. Source Separation by Supervised and Weighted NMF
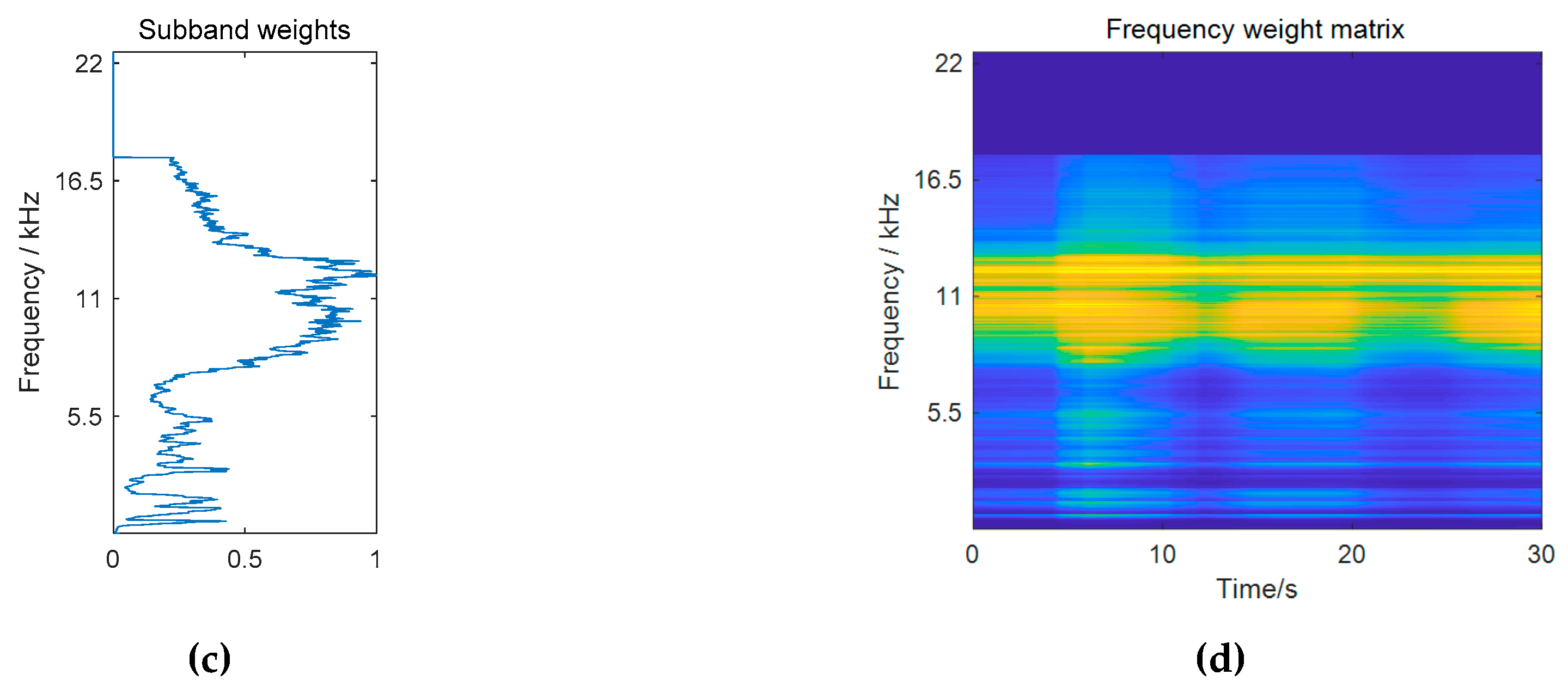
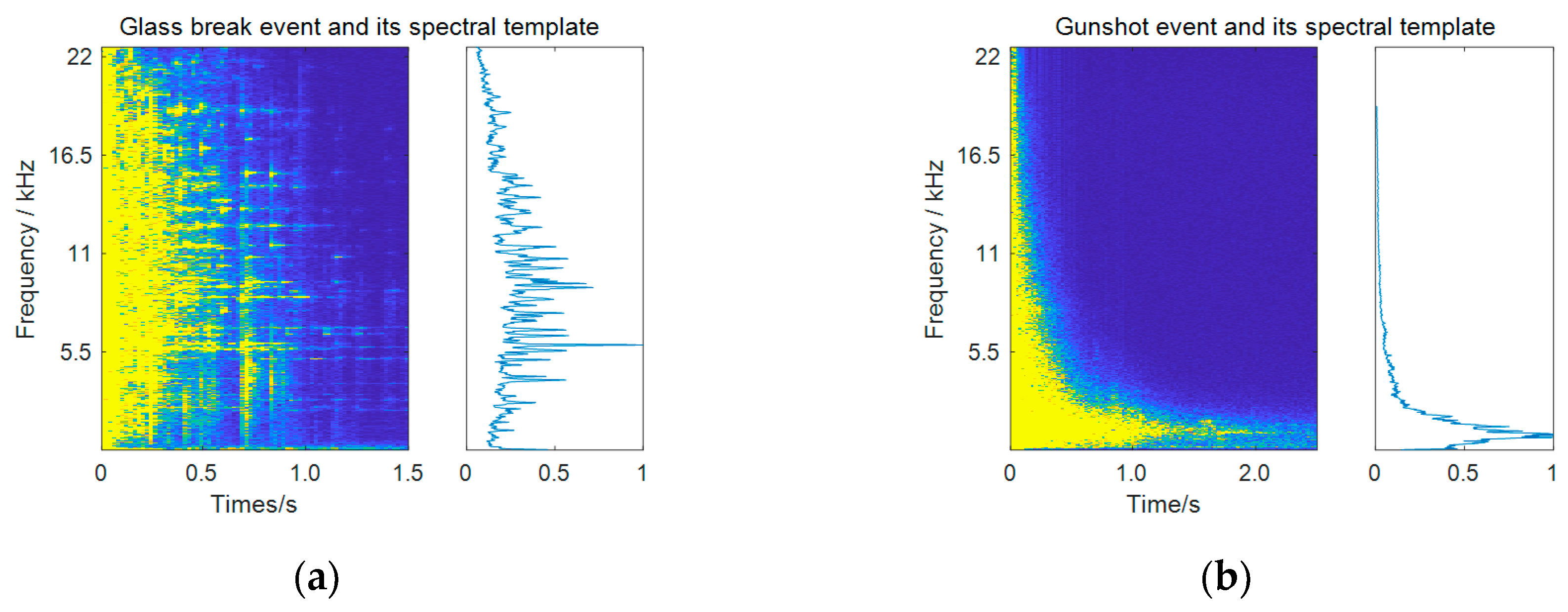
3.2.1. Frequency Weighting Based on Subband Importance
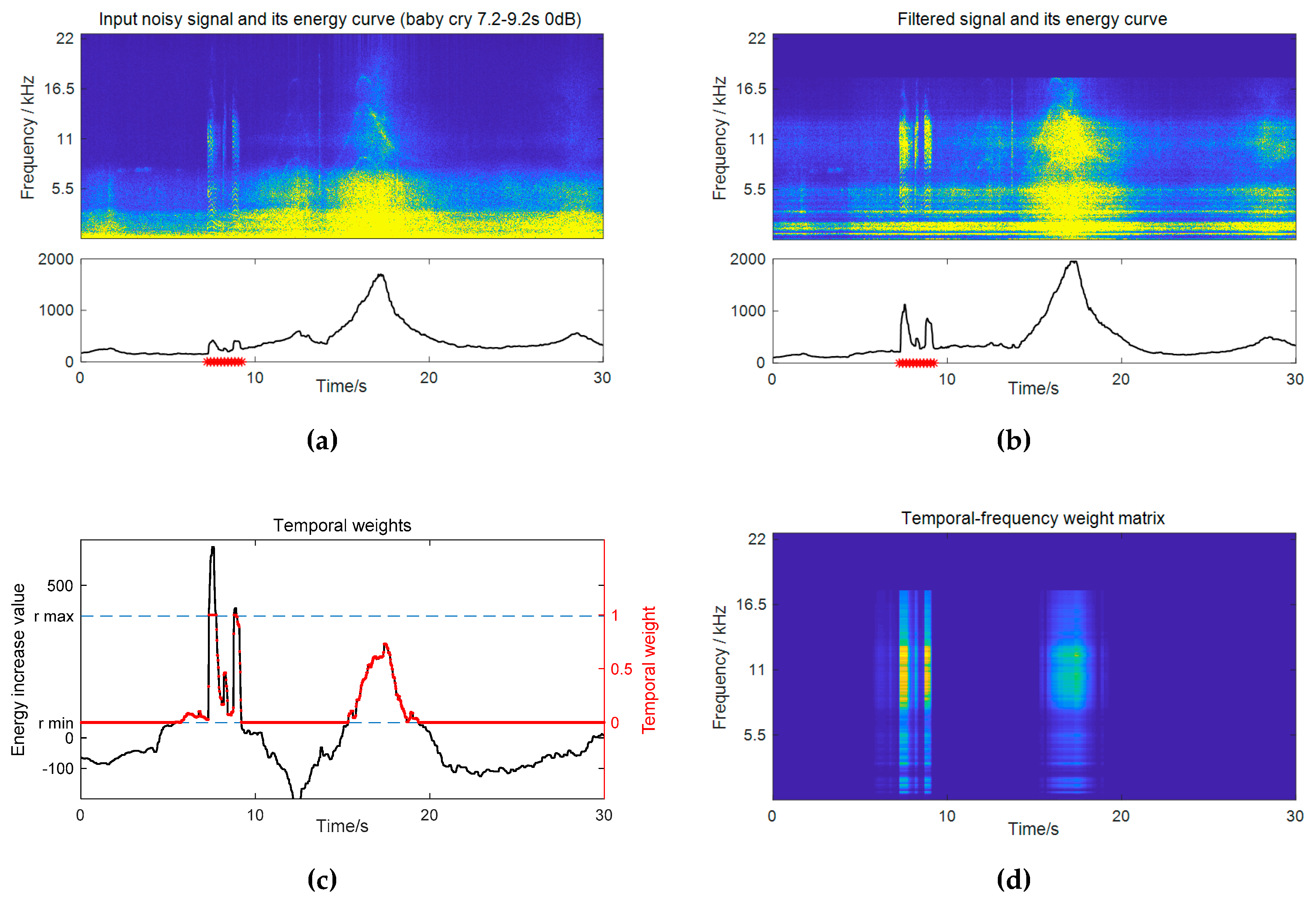
3.2.2. Temporal Weighting Based on Event Presence Probability
3.2.3. Combined Time-Frequency Weighting
| Algorithm 2. Source separation by supervised and weighted NMF | |
| Input: spectrogram of an input noisy signal V, training spectrogram for the target event class and the event dictionary , estimated noise dictionary and spectrogram , parameters , , , and theTypeOfWeighting | |
| Output: activations and | |
| 1: | switch theTypeOfWeighting do |
| 2: | case frequency_weighting |
| 3: | calculate frequency weights using Equations (17)–(19), and set |
| 4: | case temporal_weighting |
| 5: | calculate temporal weights using Equations (17)–(22) , and set |
| 6: | case time_frequency_weighting |
| 7: | calculate time-frequency weights using Equations (17)–(23) , and set |
| 8: | otherwise |
| 9: | |
| 10: | endsw |
| 11: | Initialize and with random non-negative values |
| 12: | repeat |
| 13: | update and using Equation (10) |
| 14: | until convergence |
3.3. Event Detection
4. Experimental Results
4.1. Dataset and Metric
- TP: a detected event whose temporal duration overlaps with that of an event in the reference, under the condition that the output onset is within the range of 500 ms of the actual onset;
- FP: a detected event that has no correspondence to any events in the reference under the onset condition;
- FN: an event in the reference that has no correspondence to any events in the system output under the onset condition.
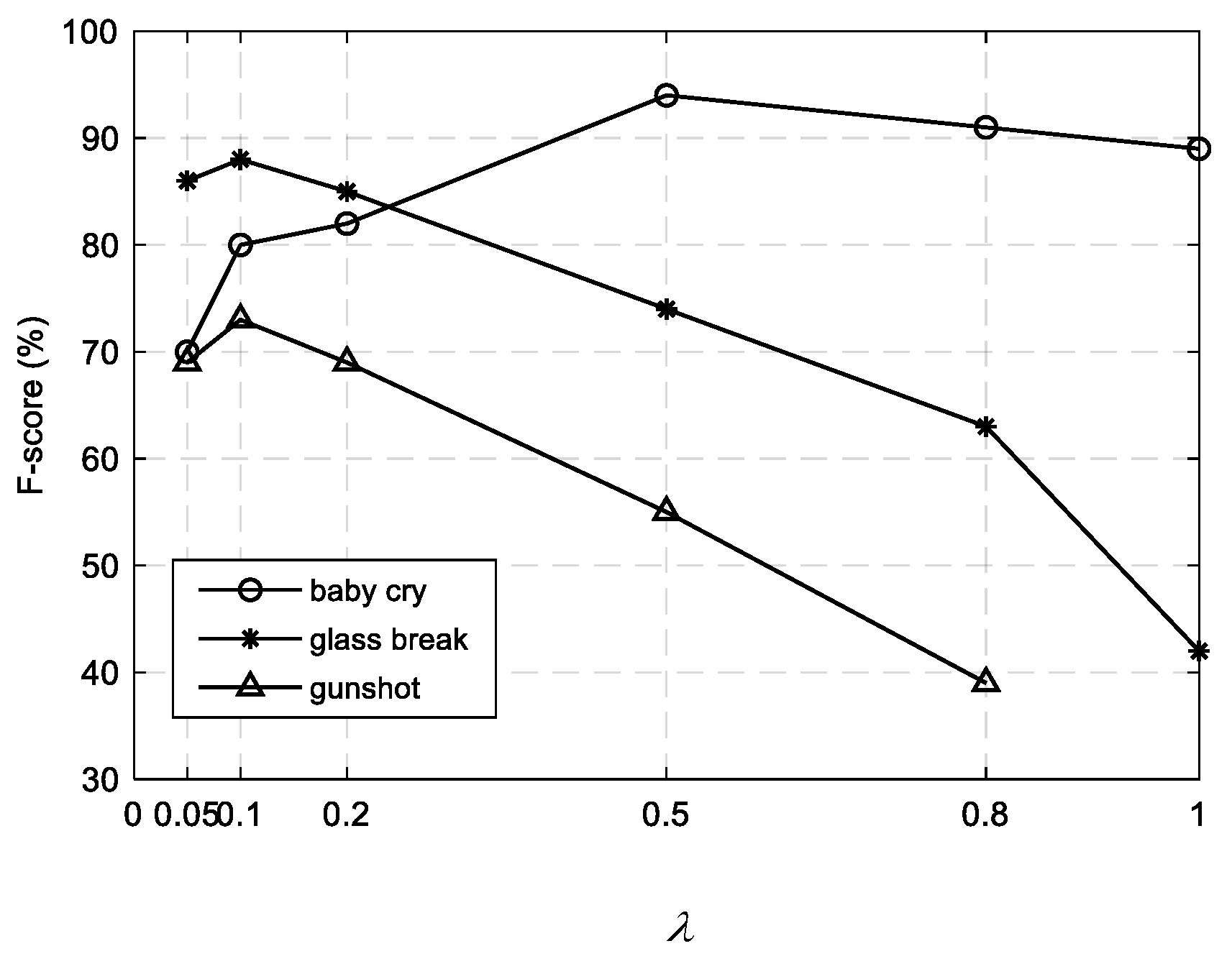
4.2. Parameter Selection
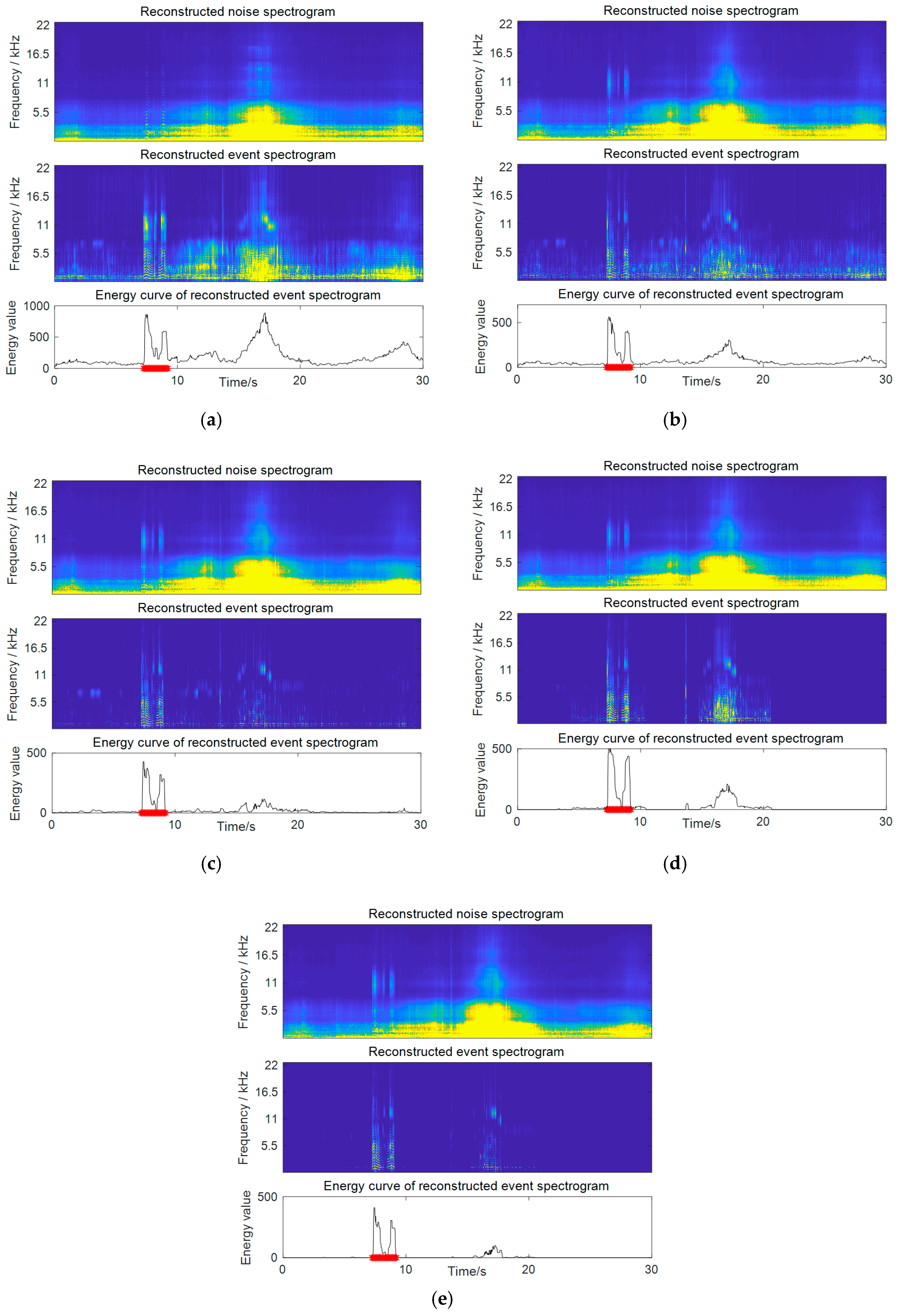
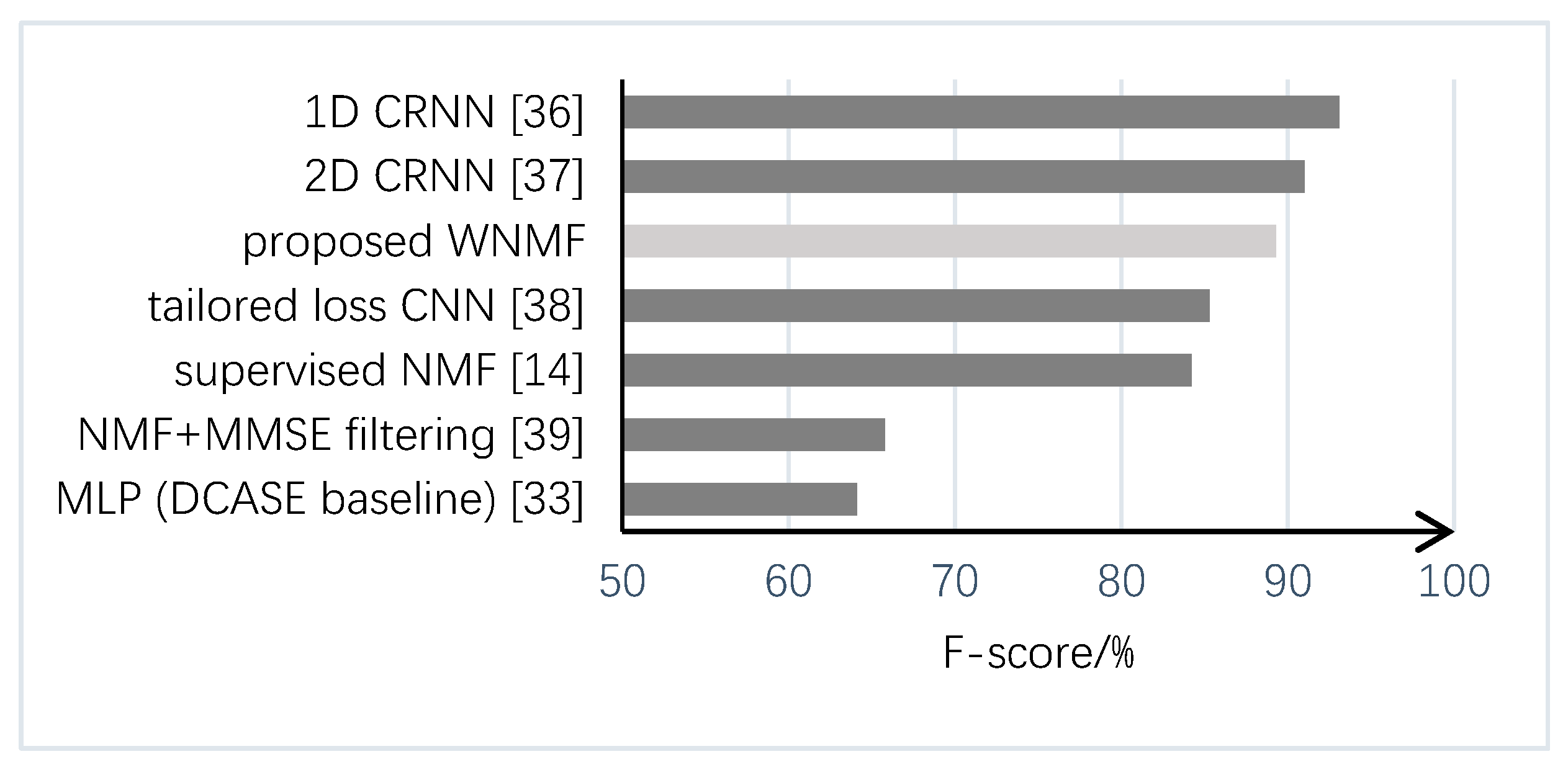
4.3. Detection Results and Comparative Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Crocco, M.; Cristani, M.; Trucco, A.; Murino, V. Audio surveillance: A systematic review. ACM Comput. Surv. 2016, 48, 52. [Google Scholar] [CrossRef]
- Alsina-Pagès, R.M.; Navarro, J.; Alías, F.; Hervás, M. homeSound: Real-time audio event detection based on high performance computing for behaviour and surveillance remote monitoring. Sensors 2017, 17, 854. [Google Scholar] [CrossRef]
- Anwar, M.Z.; Kaleem, Z.; Jamalipour, A. Machine learning inspired sound-based amateur drone detection for public safety applications. IEEE Trans. Veh. Technol. 2019, 68, 2526–2534. [Google Scholar] [CrossRef]
- Du, X.; Lao, F.; Teng, G. A sound source localisation analytical method for monitoring the abnormal night vocalisations of poultry. Sensors 2018, 18, 2906. [Google Scholar] [CrossRef] [PubMed]
- Stowell, D.; Benetos, E.; Gill, L.F. On-bird sound recordings automatic acoustic recognition of activities and contexts. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 1193–1206. [Google Scholar] [CrossRef]
- Sharan, R.V.; Moir, T.J. An overview of applications and advancements in automatic sound recognition. Neurocomputing 2016, 200, 22–34. [Google Scholar] [CrossRef]
- Cakir, E.; Parascandolo, G.; Heittola, T.; Huttunen, H.; Virtanen, T. Convolutional recurrent neural networks for polyphonic sound event detection. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 1291–1303. [Google Scholar] [CrossRef]
- Févotte, C.; Vincent, E.; Ozerov, A. Single-channel audio source separation with NMF: Divergences, constraints and algorithms. In Audio Source Separation; Makino, S., Ed.; Springer: Cham, Switzerland, 2018; pp. 1–24. [Google Scholar]
- Gemmeke, J.; Vuegen, L.; Karsmakers, P.; Vanrumste, B.; Van hamme, H. An exemplar-based NMF approach to audio event detection. In Proceedings of the 2013 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 20–23 October 2013. [Google Scholar]
- Komatsu, T.; Toizumi, T.; Kondo, R.; Yuzo, S. Acoustic event detection method using semi-supervised non-negative matrix factorization with a mixture of local dictionary. In Proceedings of the Detection and Classification of Acoustic Scenes and Events 2016 Workshop (DCASE2016), Budapest, Hungary, 3 September 2016. [Google Scholar]
- Komatsu, T.; Senda, Y.; Kondo, R. Acoustic event detection based on non-negative matrix factorization with mixtures of local dictionaries and activation aggregation. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016. [Google Scholar]
- Kim, M.; Smaragdis, P. Mixtures of local dictionaries for unsupervised speech enhancement. IEEE Signal Process. Lett. 2015, 22, 293–297. [Google Scholar] [CrossRef]
- Kameoka, H.; Higuchi, T.; Tanaka, M.; Li, L. Nonnegative matrix factorization with basis clustering using cepstral distance regularization. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1029–1040. [Google Scholar] [CrossRef]
- Zhou, Q.; Feng, Z. Robust sound event detection through noise estimation and source separation using NMF. In Proceedings of the Detection and Classification of Acoustic Scenes and Events 2017 Workshop (DCASE2017), Munich, Germany, 16–17 November 2017. [Google Scholar]
- Virtanen, T. Monaural sound source separation by non-negative matrix factorization with temporal continuity and sparseness criteria. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 1066–1074. [Google Scholar] [CrossRef]
- Schmidt, M.N.; Larsen, J.; Lyngby, K. Wind noise reduction using non-negative sparse coding. In Proceedings of the 2007 IEEE International Workshop on Machine Learning for Signal Processing, Thessaloniki, Greece, 27–29 August 2007. [Google Scholar]
- Vaz, C.; Ramanarayanan, V.; Narayanan, S. Acoustic denoising using dictionary learning with spectral and temporal regularization. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 967–980. [Google Scholar] [CrossRef] [PubMed]
- Smaragdis, P.; Févotte, C.; Mysore, G.J.; Mohammadiha, N.; Hoffman, M. Static and dynamic source separation using nonnegative factorizations: A unifed view. IEEE Signal Process. Mag. 2014, 31, 66–75. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y. Nonnegative matrix factorization: A comprehensive review. IEEE Trans. Knowl. Data Eng. 2013, 25, 1336–1353. [Google Scholar] [CrossRef]
- Kim, Y.; Choi, S. Weighted nonnegative matrix factorization. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Taipei, Taiwan, 19–24 April 2009. [Google Scholar]
- Guillamet, D.; Vitria, J.; Schiele, B. Introducing a weighted non-negative matrix factorization for image classification. Pattern Recognit. Lett. 2003, 24, 2447–2454. [Google Scholar] [CrossRef]
- Blondel, V.D.; Ho, N.D.; Van Dooren, P. Weighted Nonnegative Matrix Factorization and Face Feature Extraction. Available online: https://pdfs.semanticscholar.org/e20e/98642009f13686a540c193fdbce2d509c3b8.pdf (accessed on 19 July 2019).
- Duong, N.Q.K.; Ozerov, A.; Chevallier, L. Temporal annotation-based audio source separation using weighted nonnegative matrix factorization. In Proceedings of the 2014 IEEE 4th International Conference on Consumer Electronics Berlin (ICCE-Berlin), Berlin, Germany, 7–10 September 2014. [Google Scholar]
- Virtanen, T. Monaural Sound Source Separation by Perceptually Weighted Non-Negative Matrix Factorization; Technical Report; Tampere University of Technology: Tampere, Finland, 2007; Available online: http://www.cs.tut.fi/tuomasv/publications.html (accessed on 5 April 2019).
- Hu, Y.; Zhang, Z.; Zou, X.; Min, G.; Sun, M.; Zheng, Y. Speech enhancement combining NMF weighted by speech presence probability and statistical model. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2015, 98, 2701–2704. [Google Scholar] [CrossRef]
- Feng, Z.; Zhou, Q.; Zhang, J.; Jiang, P.; Yang, X. A target guided subband filter for acoustic event detection in noisy environments using wavelet packets. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 1230–1241. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Z.; Zheng, M.; He, X. Robust non-negative matrix factorization. Front. Electr. Electron. Eng. China 2011, 6, 192–200. [Google Scholar] [CrossRef]
- Sun, M.; Li, Y.; Gemmeke, J.F.; Zhang, X. Speech enhancement under low SNR conditions via noise estimation using sparse and low-rank NMF with K-L divergence. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 1233–1242. [Google Scholar] [CrossRef]
- Chen, Z.; Ellis, D.P.W. Speech enhancement by sparse, low-rank, and dictionary spectrogram decomposition. In Proceedings of the 2013 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 20–23 October 2013. [Google Scholar]
- Mesaros, A.; Heittola, T.; Diment, A.; Elizalde, B.; Shah, A.; Vincent, E.; Raj, B.; Virtanen, T. DCASE 2017 challenge setup: Tasks, datasets and baseline system. In Proceedings of the Detection and Classification of Acoustic Scenes and Events 2017 Workshop (DCASE2017), Munich, Germany, 16–17 November 2017. [Google Scholar]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Févotte, C.; Idier, J. Algorithms for nonnegative matrix factorization with the β-divergence. Neural Comput. 2011, 23, 2421–2456. [Google Scholar] [CrossRef]
- Mao, Y.; Saul, L. Modeling distances in large-scale networks by matrix factorization. In Proceedings of the 2004 ACM SIGCOMM Internet Measurement Conference, Taormina, Italy, 25–27 October 2004. [Google Scholar]
- Mesaros, A.; Heittola, T.; Virtanen, T. Metrics for polyphonic sound event detection. Appl. Sci. 2016, 6, 162. [Google Scholar] [CrossRef]
- DCASE2017. Detection of Rare Sound Events. Available online: http://www.cs.tut.fi/sgn/arg/dcase2017/challenge/task-rare-sound-event-detection-results (accessed on 5 April 2019).
- Lim, H.; Park, J.; Han, Y. Rare sound event detection using 1D convolutional recurrent neural networks. In Proceedings of the Detection and Classification of Acoustic Scenes and Events 2017 Workshop (DCASE2017), Munich, Germany, 16–17 November 2017. [Google Scholar]
- Cakir, E.; Virtanen, T. Convolutional recurrent neural networks for rare sound event detection. In Proceedings of the Detection and Classification of Acoustic Scenes and Events 2017 Workshop (DCASE2017), Munich, Germany, 16–17 November 2017. [Google Scholar]
- Phan, H.; Krawczyk-Becker, M.; Gerkmann, T.; Mertins, A. DNN and CNN with Weighted and Multi-Task Loss Functions for Audio Event Detection. Available online: http://www.cs.tut.fi/sgn/arg/dcase2017/documents/challenge_technical_reports/DCASE2017_Phan_174.pdf (accessed on 19 July 2019).
- Jeon, K.M.; Kim, H.K. Nonnegative Matrix Factorization-Based Source Separation with Online Noise Learning for Detection of Rare Sound Events. Available online: http://www.cs.tut.fi/sgn/arg/dcase2017/documents/challenge_technical_reports/DCASE2017_Jeon_171.pdf (accessed on 19 July 2019).
| Method | Baby Cry | Glass Break | Gunshot | Average | |||||
|---|---|---|---|---|---|---|---|---|---|
| ER | F (%) | ER | F (%) | ER | F (%) | ER | F (%) | ||
| Proposed supervised NMF + | combined weighting | 0.10 | 94.8 | 0.06 | 96.9 | 0.46 | 76.2 | 0.21 | 89.3 |
| frequency weighting | 0.11 | 94.0 | 0.13 | 93.7 | 0.51 | 74.0 | 0.25 | 87.2 | |
| temporal weighting | 0.14 | 92.4 | 0.12 | 94.3 | 0.52 | 73.3 | 0.26 | 86.7 | |
| no weighting [14] | 0.17 | 91.4 | 0.22 | 89.1 | 0.55 | 72.0 | 0.31 | 84.2 | |
| Semi-supervised NMF | 0.29 | 84.9 | 0.36 | 81.3 | 0.65 | 60.7 | 0.43 | 75.6 | |
| Subband filtering [26] | 0.62 | 66.4 | 0.25 | 86.7 | 0.54 | 67.5 | 0.47 | 73.5 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Feng, Z.; Benetos, E. Adaptive Noise Reduction for Sound Event Detection Using Subband-Weighted NMF. Sensors 2019, 19, 3206. https://doi.org/10.3390/s19143206
Zhou Q, Feng Z, Benetos E. Adaptive Noise Reduction for Sound Event Detection Using Subband-Weighted NMF. Sensors. 2019; 19(14):3206. https://doi.org/10.3390/s19143206
Chicago/Turabian StyleZhou, Qing, Zuren Feng, and Emmanouil Benetos. 2019. "Adaptive Noise Reduction for Sound Event Detection Using Subband-Weighted NMF" Sensors 19, no. 14: 3206. https://doi.org/10.3390/s19143206
APA StyleZhou, Q., Feng, Z., & Benetos, E. (2019). Adaptive Noise Reduction for Sound Event Detection Using Subband-Weighted NMF. Sensors, 19(14), 3206. https://doi.org/10.3390/s19143206






