Design and Analysis of a Magnetically Coupled Multi-Frequency Hybrid Energy Harvester
Abstract
1. Introduction
2. Design
3. Modeling
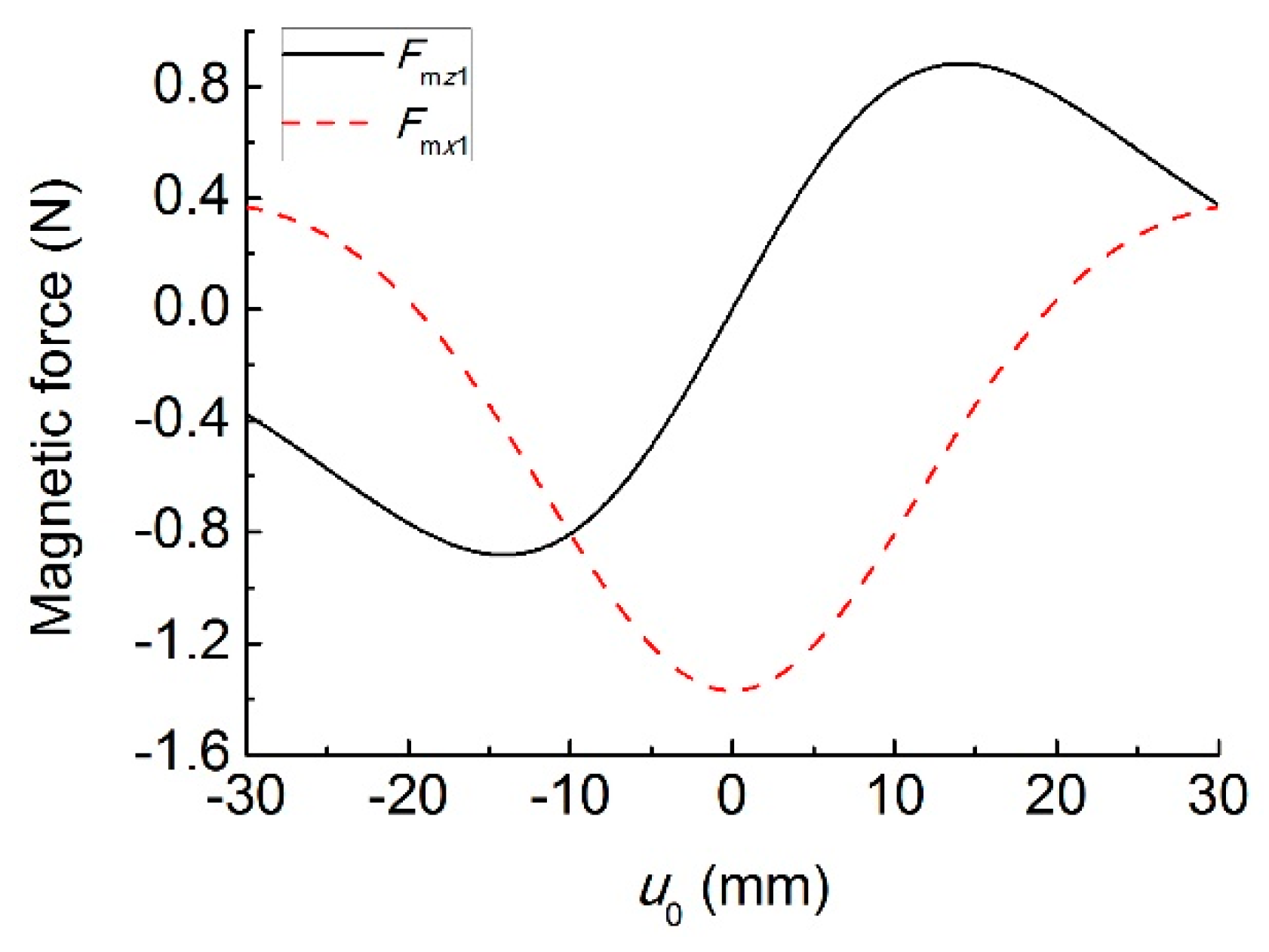
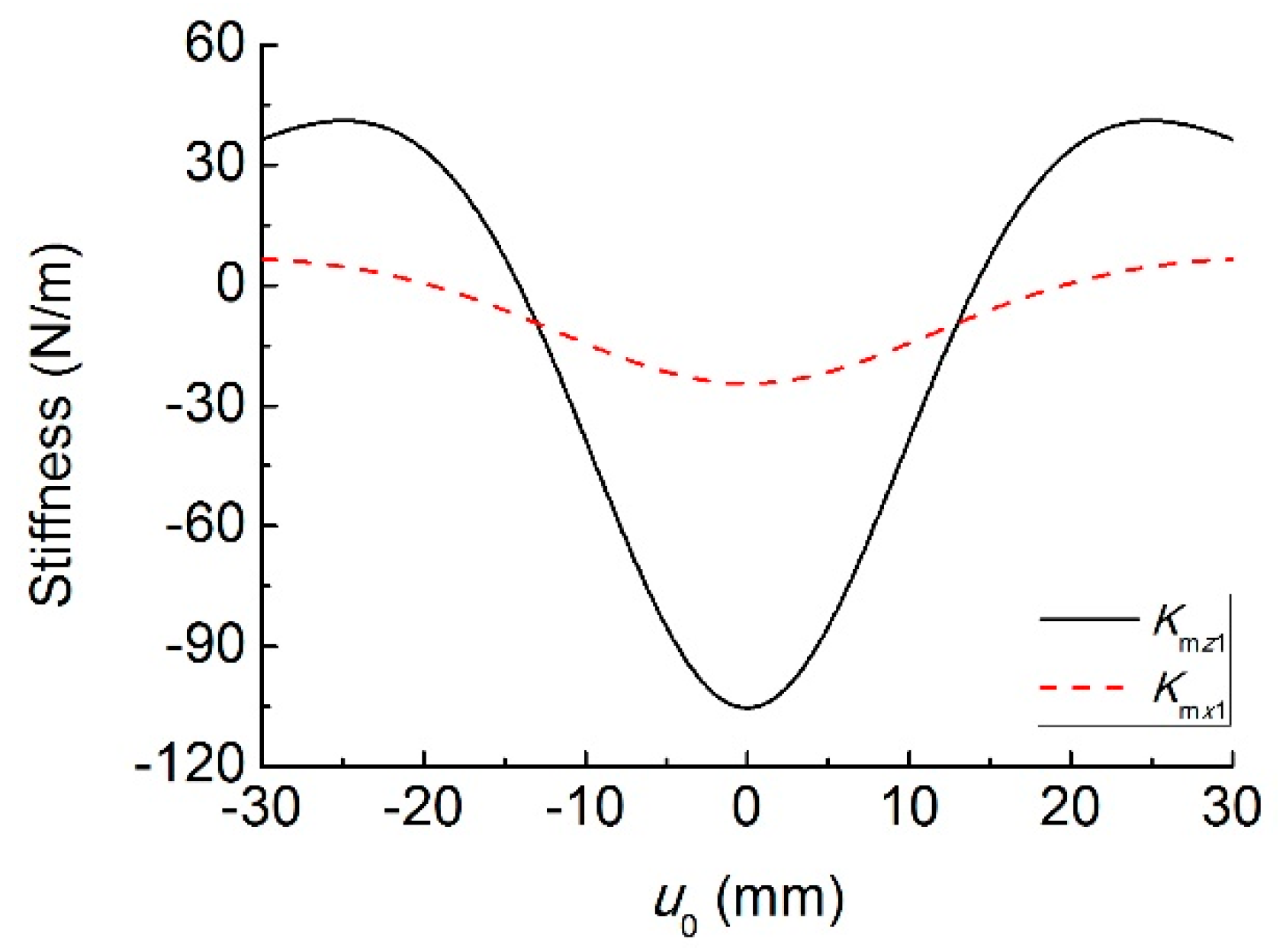
3.1. Magnetic Force
3.2. Electromechanical Coupling Model
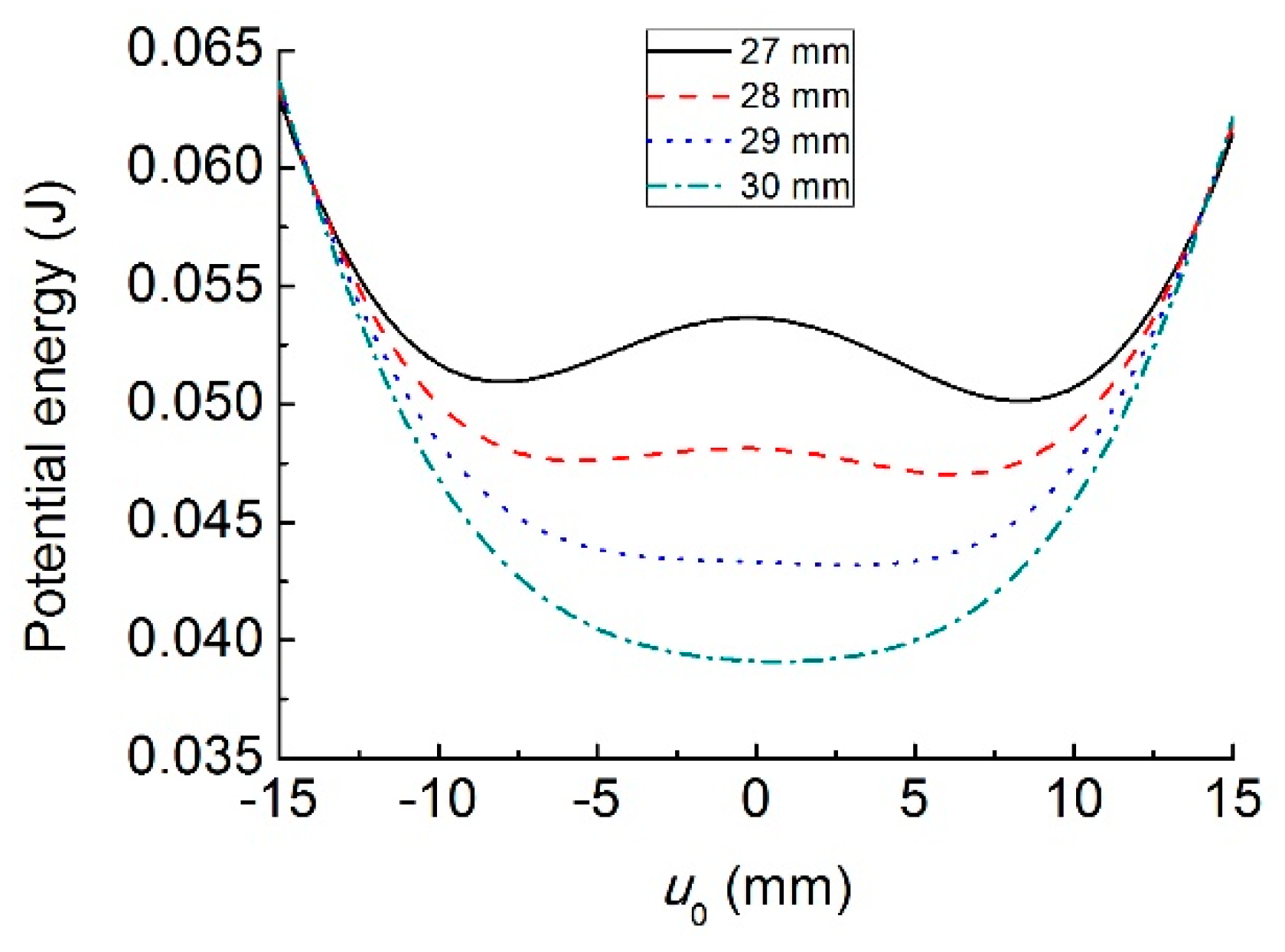
3.3. Magnetic Force and Potential Energy
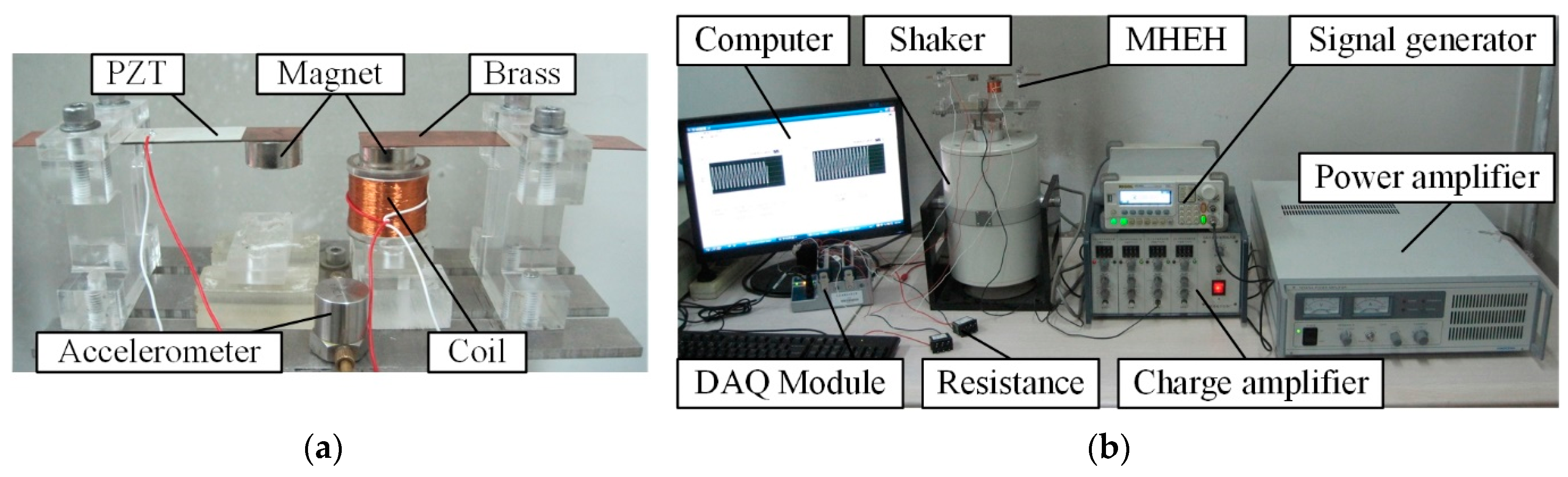
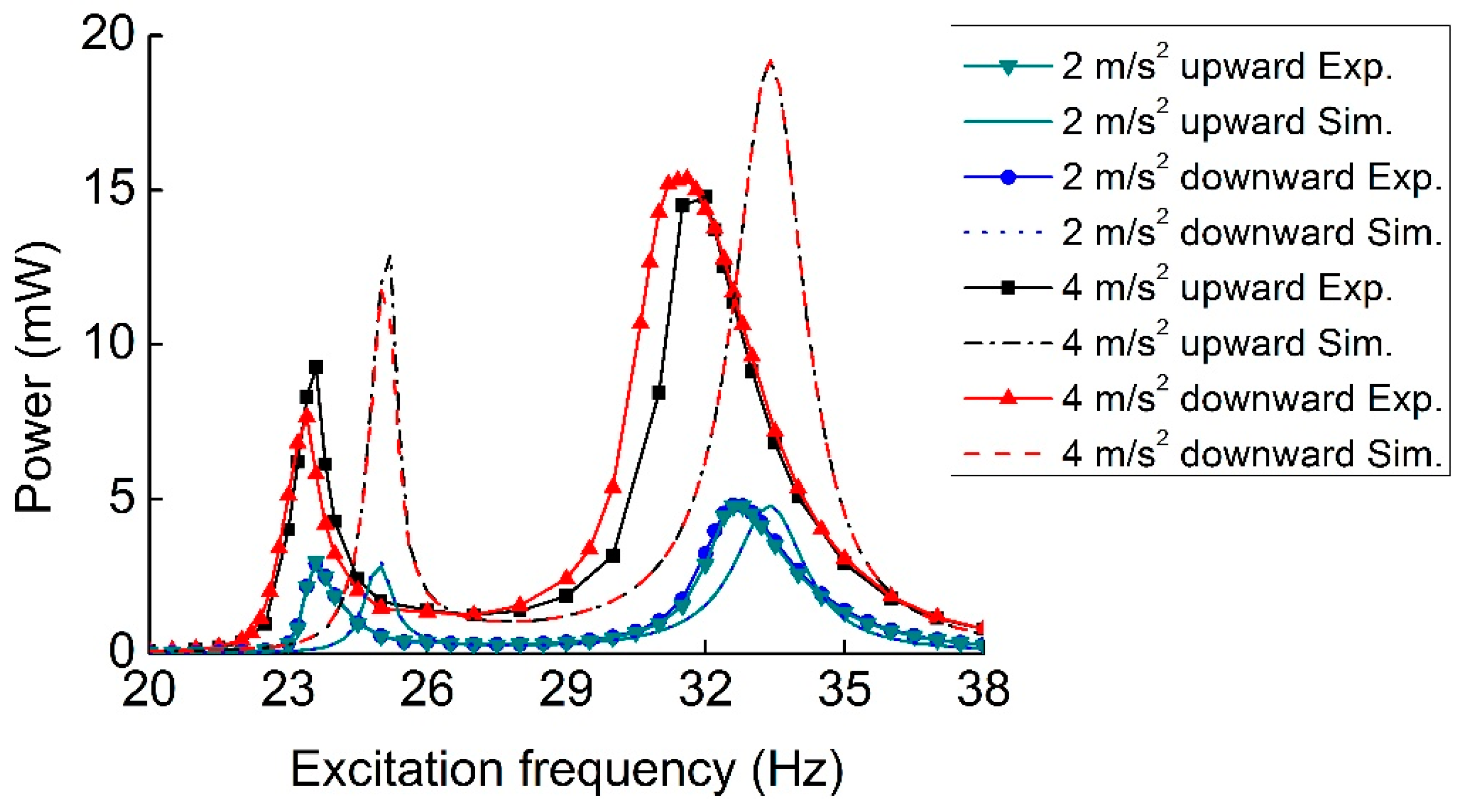
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gafforelli, G.; Corigliano, A.; Xu, R.; Kim, S.G. Experimental verification of a bridge-shaped, nonlinear vibration energy harvester. Appl. Phys. Lett. 2014, 105, 203901. [Google Scholar] [CrossRef]
- Shan, X.; Tian, H.; Chen, D.; Xie, T. A curved panel energy harvester for aeroelastic vibration. Appl. Energy 2019, 249, 58–66. [Google Scholar] [CrossRef]
- Shan, X.; Li, H.; Yang, Y.; Feng, J.; Wang, Y.; Xie, T. Enhancing the performance of an underwater piezoelectric energy harvester based on flow-induced vibration. Energy 2019, 172, 134–140. [Google Scholar] [CrossRef]
- Zhou, M.; Chen, Q.; Xu, Z.; Wang, W. Piezoelectric wind energy harvesting device based on the inverted cantilever beam with leaf-inspired extensions. AIP Adv. 2019, 9, 035213. [Google Scholar] [CrossRef]
- Yan, B.; Wang, K.; Kang, C.X.; Zhang, X.N.; Wu, C.Y. Self-sensing electromagnetic transducer for vibration control of space antenna reflector. IEEE/ASME Trans. Mechatron. 2017, 22, 1944–1951. [Google Scholar] [CrossRef]
- Tao, K.; Tang, L.; Wu, J.; Lye, S.W.; Chang, H.; Miao, J. Investigation of multimodal electret-based mems energy harvester with impact-induced nonlinearity. J. Microelectromech. Syst. 2018, 27, 1–13. [Google Scholar] [CrossRef]
- Yang, Z.; Tan, Y.; Zu, J. A multi-impact frequency up-converted magnetostrictive transducer for harvesting energy from finger tapping. Int. J. Mech. Sci. 2017, 126, 235–241. [Google Scholar] [CrossRef]
- Kok, S.L.; White, N.M.; Harris, N.R. A novel piezoelectric thick-film free-standing cantilever energy harvester. In Proceedings of the Eurosensors: XXII, Dresden, Germany, 7–11 September 2008; pp. 395–399. [Google Scholar]
- Liu, J.; Fang, H.; Xu, Z.; Mao, X.; Shen, X.; Chen, D.; Liao, H.; Cai, B. A mems-based piezoelectric power generator array for vibration energy harvesting. Microelectr. J. 2008, 39, 802–806. [Google Scholar] [CrossRef]
- Lumentut, M.F.; Francis, L.A.; Howard, I.M. Analytical techniques for broadband multielectromechanical piezoelectric bimorph beams with multifrequency power harvesting. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 2555–2568. [Google Scholar] [CrossRef]
- Castagnetti, D. Experimental modal analysis of fractal-inspired multi-frequency structures for piezoelectric energy converters. Smart Mater. Struct. 2012, 21, 094009. [Google Scholar] [CrossRef]
- Yildirim, T.; Zhang, J.; Sun, S.; Alici, G.; Zhang, S.; Li, W. Design of an enhanced wideband energy harvester using a parametrically excited array. J. Sound Vib. 2017, 410, 416–428. [Google Scholar] [CrossRef]
- Yang, B.; Liu, J.; Tang, G.; Luo, J.; Yang, C.; Li, Y. A generator with nonlinear spring oscillator to provide vibrations of multi-frequency. Appl. Phys. Lett. 2011, 99, 223505. [Google Scholar] [CrossRef]
- Li, X.; Yu, K.; Upadrashta, D.; Yang, Y. Multi-branch sandwich piezoelectric energy harvester: Mathematical modeling and validation. Smart Mater. Struct. 2019, 28, 035010. [Google Scholar] [CrossRef]
- Castagnetti, D.; Radi, E. A piezoelectric based energy harvester with dynamic magnification: Modelling, design and experimental assessment. Meccanica 2018, 53, 2725–2742. [Google Scholar] [CrossRef]
- Dhote, S.; Li, H.; Yang, Z. Multi-frequency responses of compliant orthoplanar spring designs for widening the bandwidth of piezoelectric energy harvesters. Int. J. Mech. Sci. 2019, 53, 11–12. [Google Scholar] [CrossRef]
- Zhou, S.; Hobeck, J.D.; Cao, J.; Inman, D.J. Analytical and experimental investigation of flexible longitudinal zigzag structures for enhanced multi-directional energy harvesting. Smart Mater. Struct. 2017, 26, 035008. [Google Scholar] [CrossRef]
- Toyabur, R.M.; Salauddin, M.; Cho, H.; Park, J.Y. A multimodal hybrid energy harvester based on piezoelectric-electromagnetic mechanisms for low-frequency ambient vibrations. Energy Convers. Manag. 2018, 168, 454–466. [Google Scholar] [CrossRef]
- Deng, H.; Du, Y.; Wang, Z.; Ye, J.; Zhang, J.; Ma, M.; Zhong, X. Poly-stable energy harvesting based on synergetic multistable vibration. Commun. Phys. 2019, 2, 21. [Google Scholar] [CrossRef]
- Lan, C.; Tang, L.; Qin, W.; Xiong, L. Magnetically coupled dual-beam energy harvester: Benefit and trade-off. J. Intell. Mater. Syst. Struct. 2017, 29, 1216–1235. [Google Scholar] [CrossRef]
- Fan, K.Q.; Chao, F.B.; Zhang, J.G.; Wang, W.D.; Che, X.H. Design and experimental verification of a bi-directional nonlinear piezoelectric energy harvester. Energy Convers. Manag. 2014, 86, 561–567. [Google Scholar] [CrossRef]
- Kim, P.; Nguyen, M.S.; Kwon, O.; Kim, Y.J.; Yoon, Y.J. Phase-dependent dynamic potential of magnetically coupled two-degree-of-freedom bistable energy harvester. Sci. Rep. 2016, 6, 34411. [Google Scholar] [CrossRef]
- Upadrashta, D.; Yang, Y.; Tang, L. Material strength consideration in the design optimization of nonlinear energy harvester. J. Intell. Mater. Syst. Struct. 2014, 26, 1980–1994. [Google Scholar] [CrossRef]
- Gao, Y.J.; Leng, Y.G.; Fan, S.B.; Lai, Z.H. Performance of bistable piezoelectric cantilever vibration energy harvesters with an elastic support external magnet. Smart Mater. Struct. 2014, 23, 095003. [Google Scholar] [CrossRef]
- Xu, Z.; Shan, X.; Chen, D.; Xie, T. A novel tunable multi-frequency hybrid vibration energy harvester using piezoelectric and electromagnetic conversion mechanisms. Appl. Sci. 2016, 6, 10. [Google Scholar] [CrossRef]
- Al-Ashtari, W.; Hunstig, M.; Hemsel, T.; Sextro, W. Frequency tuning of piezoelectric energy harvesters by magnetic force. Smart Mater. Struct. 2012, 21, 035019. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, W.; Xie, J.; Xu, Z.; Zhou, M.; Yang, H. An impact-based frequency up-converting hybrid vibration energy harvester for low frequency application. Energies 2017, 10, 1761. [Google Scholar] [CrossRef]
- Xu, Z.; Shan, X.; Yang, H.; Wang, W.; Xie, T. Parametric analysis and experimental verification of a hybrid vibration energy harvester combining piezoelectric and electromagnetic mechanisms. Micromachines 2017, 8, 189. [Google Scholar] [CrossRef]
- Mahmoodi, S.N.; Jalili, N.; Daqaq, M.F. Modeling, nonlinear dynamics, and identification of a piezoelectrically actuated microcantilever sensor. IEEE/ASME Trans. Mechatron. 2008, 13, 58–65. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Nayfeh, A.H.; Hajj, M.R. Global nonlinear distributed-parameter model of parametrically excited piezoelectric energy harvesters. Nonlinear Dyn. 2012, 67, 1147–1160. [Google Scholar] [CrossRef]
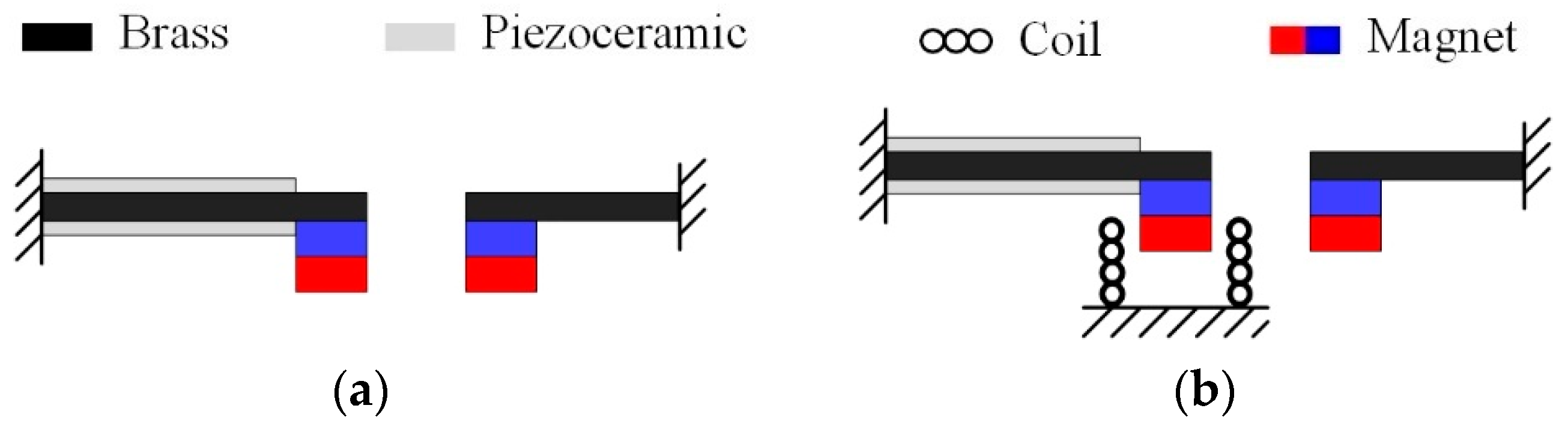
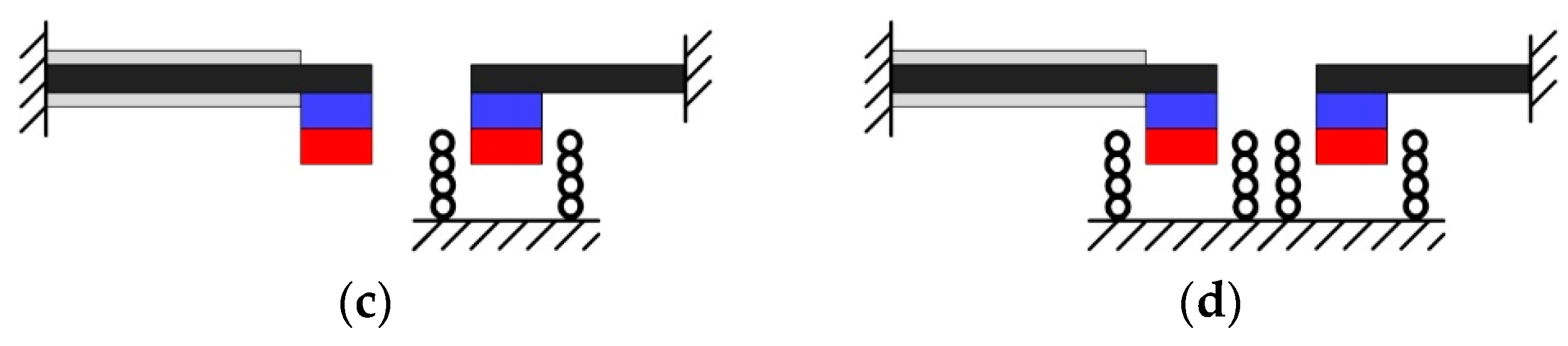
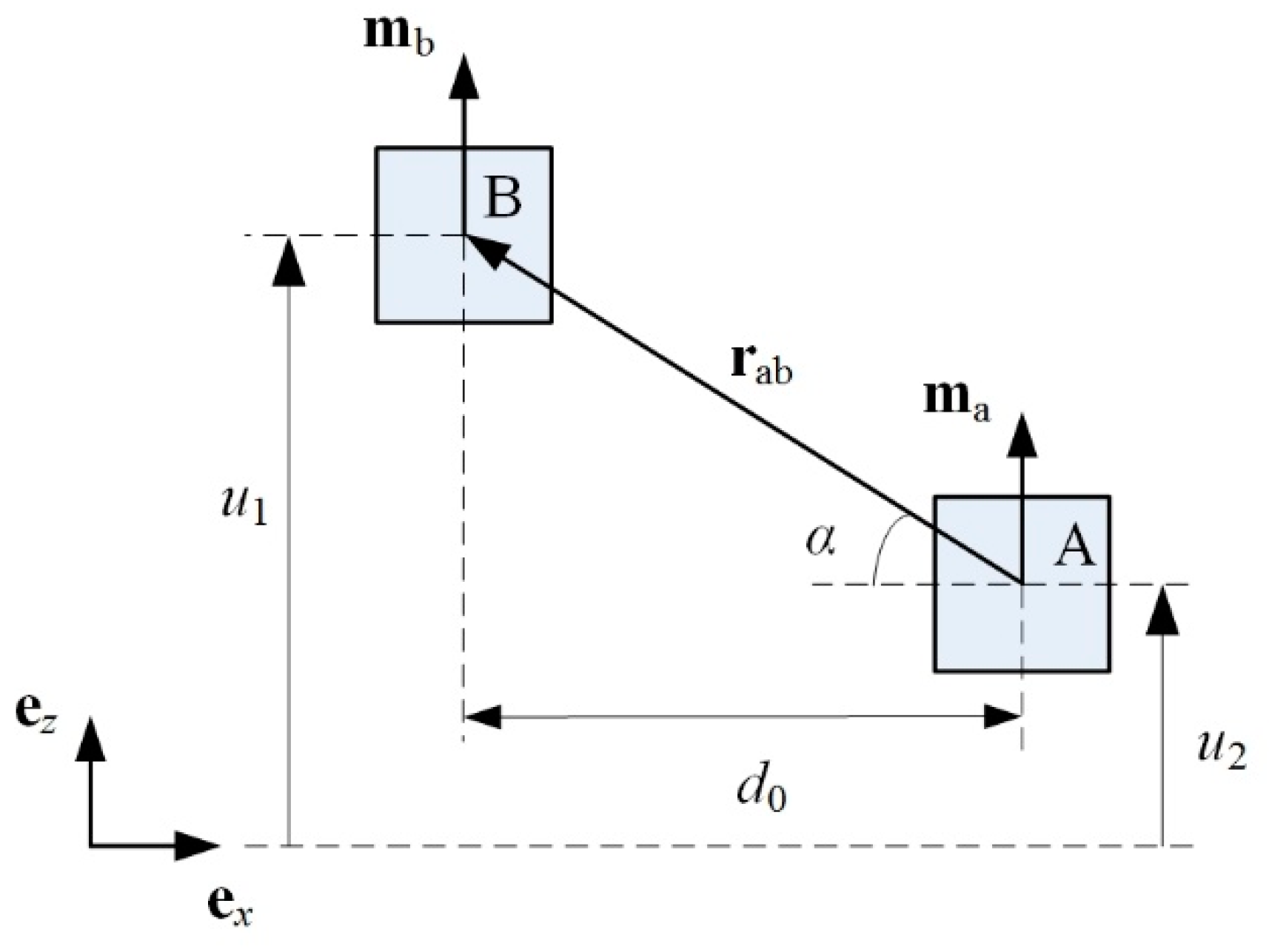
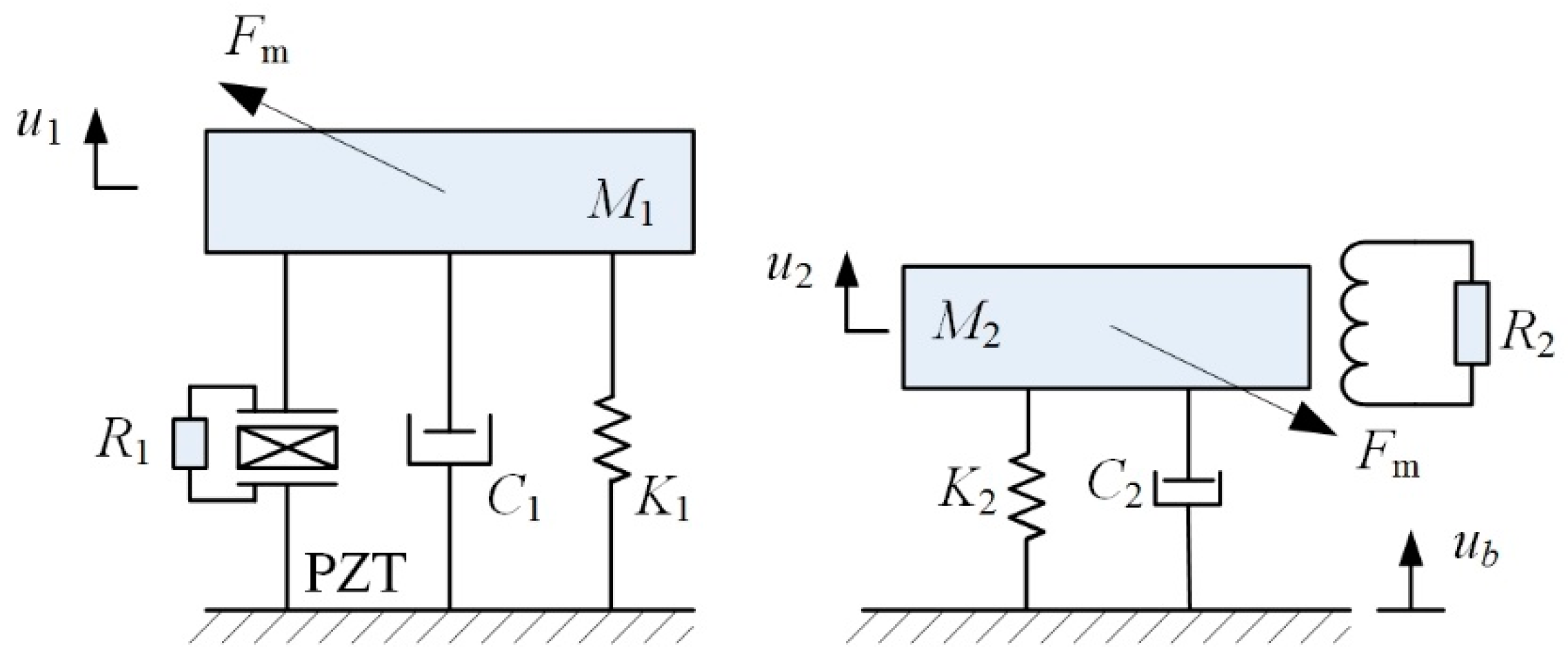
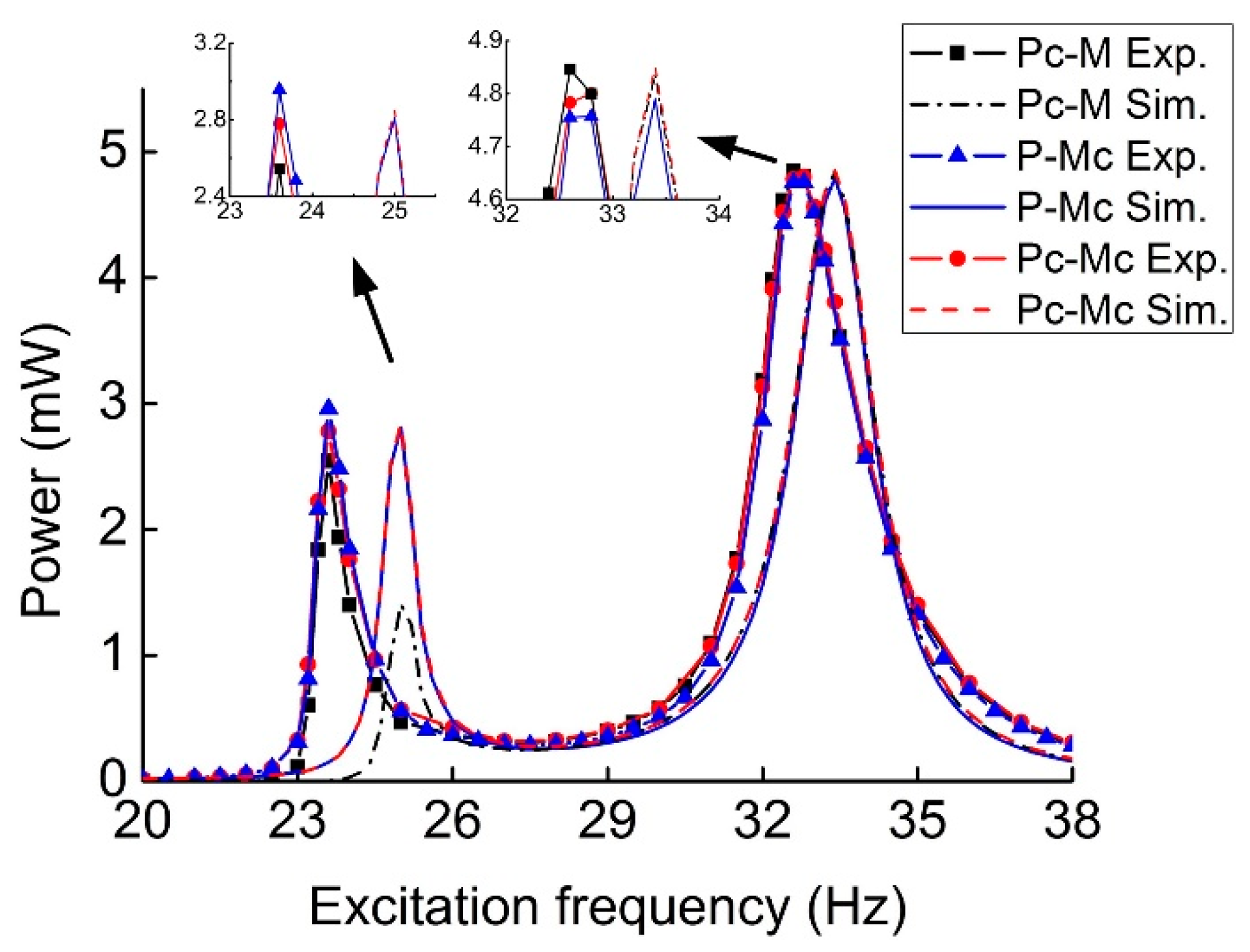
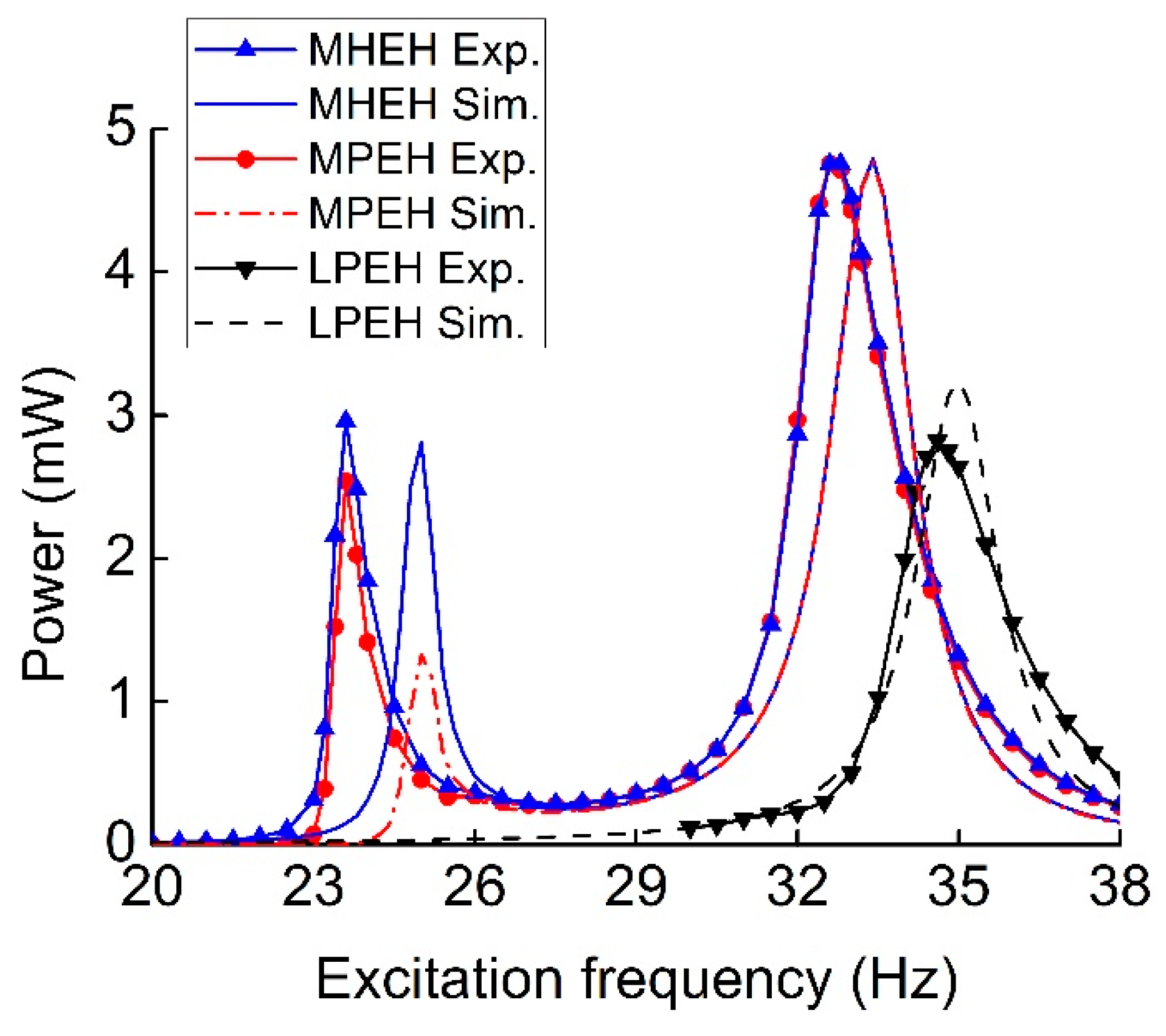
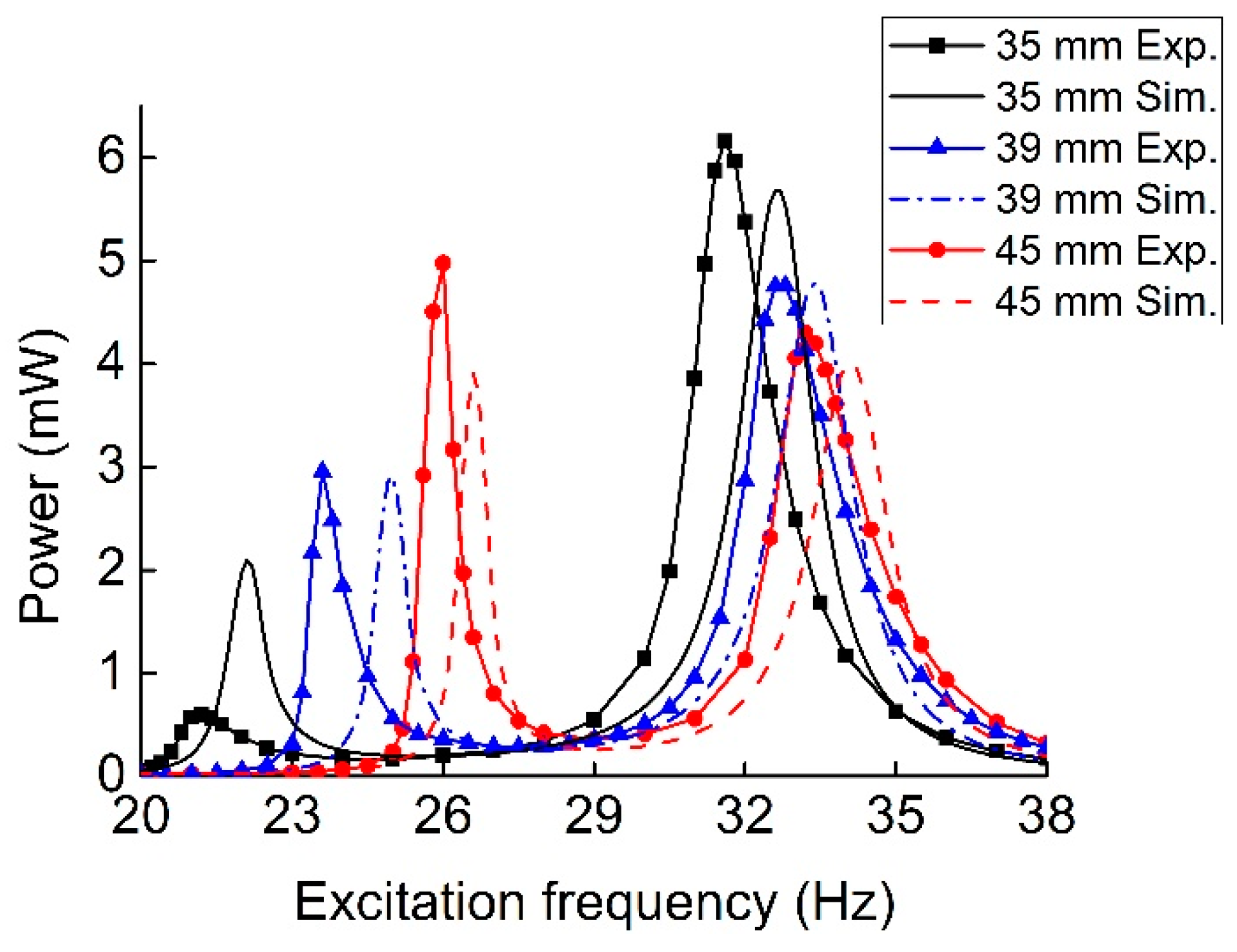
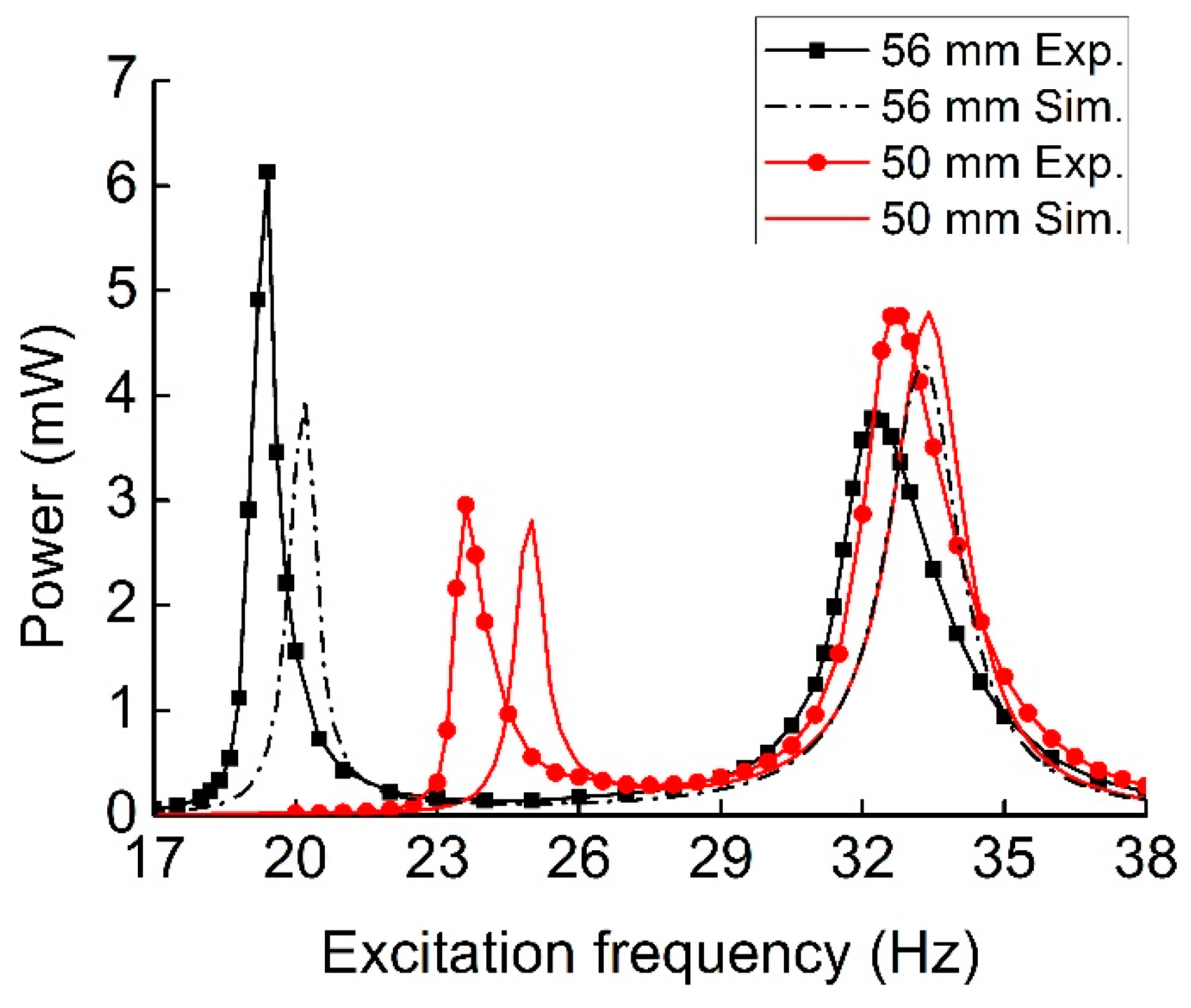
| Parameter | Value |
|---|---|
| Substrate A length × width × thickness (mm3) | 60 × 20 × 0.5 |
| Substrate B length × width × thickness (mm3) | 50 × 20 × 0.54 |
| Substrate density (kg/m3) | 8920 |
| Young’s modulus of substrate (GPa) | 121 |
| Piezoceramic length × width × thickness (mm3) | 40 × 20 × 0.2 |
| Piezoceramic density (kg/m3) | 7386 |
| Young’s modulus of piezoceramic (GPa) | 59.77 |
| Piezoelectric stress constant (C/m2) | −13.74 |
| Dielectric permittivity (nF/m) | 38.62 |
| Magnet radius × height (mm2) | 10 × 10 |
| Residual magnetic flux density (T) | 1.3 |
| Magnet density (kg/m3) | 7500 |
| Coil turns | 2000 |
| Internal resistance of coil A (Ω) | 352 |
| Internal resistance of coil B (Ω) | 360 |
| Ref. | Volume (mm3) | Resonant Frequency f1 (Hz) | Peak Power P1 (mW) | Power Density D1 (mW/mm3) | Resonant Frequency f2 (Hz) | Peak Power P2 (mW) | Power Density D2 (mW/mm3) |
|---|---|---|---|---|---|---|---|
| [23] | 945.84 | 22 | 0.013 | 1.37 × 10−6 | 27.7 | 1.658 | 1.75 × 10−3 |
| [25] | 29895 | 23.2 | 2.12 | 7.09 × 10−5 | 26.8 | 1.57 | 5.25 × 10−5 |
| This paper | 21550 | 23.6 | 2.96 | 1.37 × 10−4 | 32.8 | 4.76 | 2.21 × 10−4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Yang, H.; Zhang, H.; Ci, H.; Zhou, M.; Wang, W.; Meng, A. Design and Analysis of a Magnetically Coupled Multi-Frequency Hybrid Energy Harvester. Sensors 2019, 19, 3203. https://doi.org/10.3390/s19143203
Xu Z, Yang H, Zhang H, Ci H, Zhou M, Wang W, Meng A. Design and Analysis of a Magnetically Coupled Multi-Frequency Hybrid Energy Harvester. Sensors. 2019; 19(14):3203. https://doi.org/10.3390/s19143203
Chicago/Turabian StyleXu, Zhenlong, Hong Yang, Hao Zhang, Huawei Ci, Maoying Zhou, Wen Wang, and Aihua Meng. 2019. "Design and Analysis of a Magnetically Coupled Multi-Frequency Hybrid Energy Harvester" Sensors 19, no. 14: 3203. https://doi.org/10.3390/s19143203
APA StyleXu, Z., Yang, H., Zhang, H., Ci, H., Zhou, M., Wang, W., & Meng, A. (2019). Design and Analysis of a Magnetically Coupled Multi-Frequency Hybrid Energy Harvester. Sensors, 19(14), 3203. https://doi.org/10.3390/s19143203






