Analysis of the Impact of Interpolation Methods of Missing RR-intervals Caused by Motion Artifacts on HRV Features Estimations
Abstract
:1. Introduction
1.1. Paper Contribution
1.2. Related Work
2. Materials and Methods
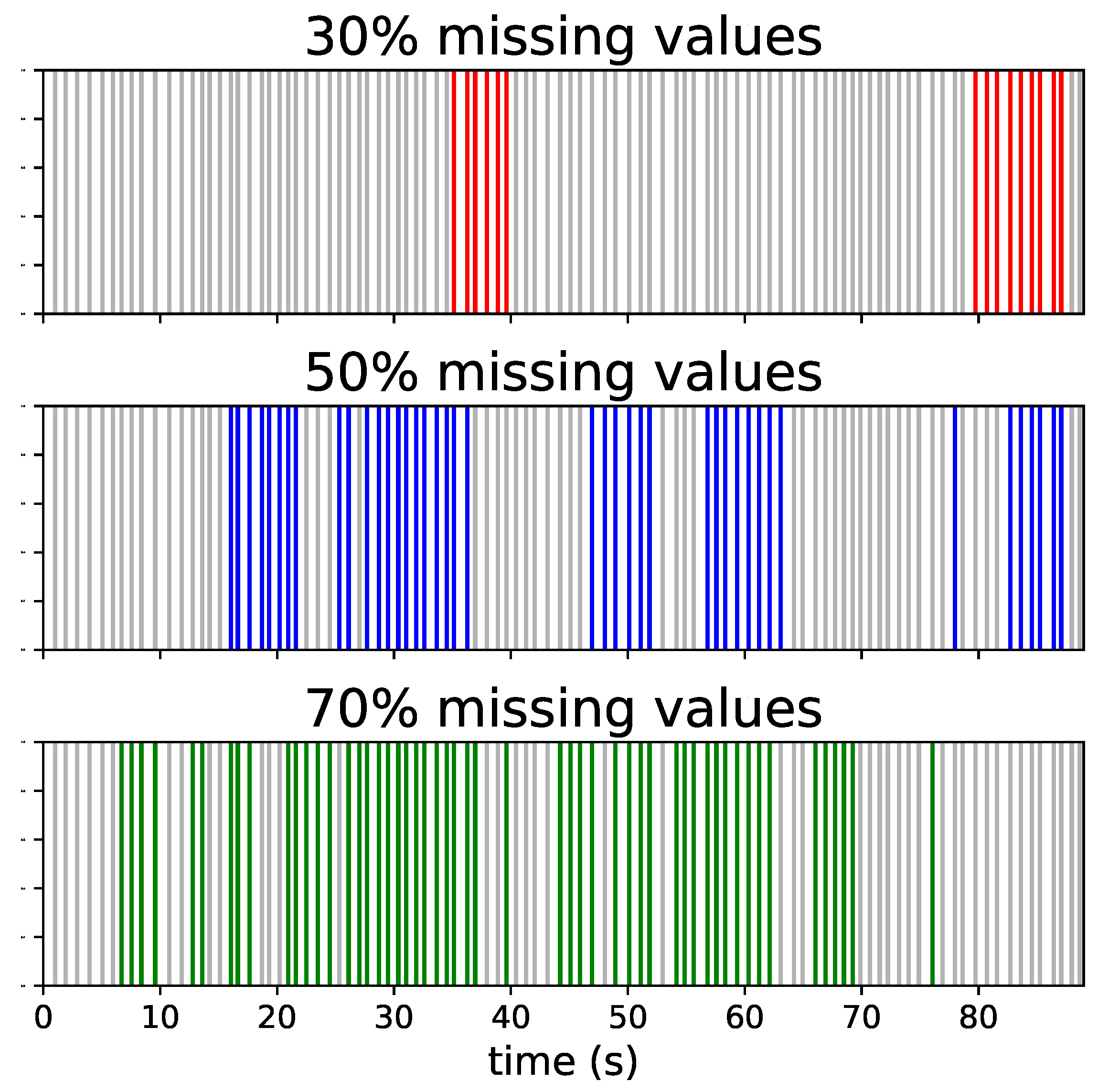
2.1. Dataset
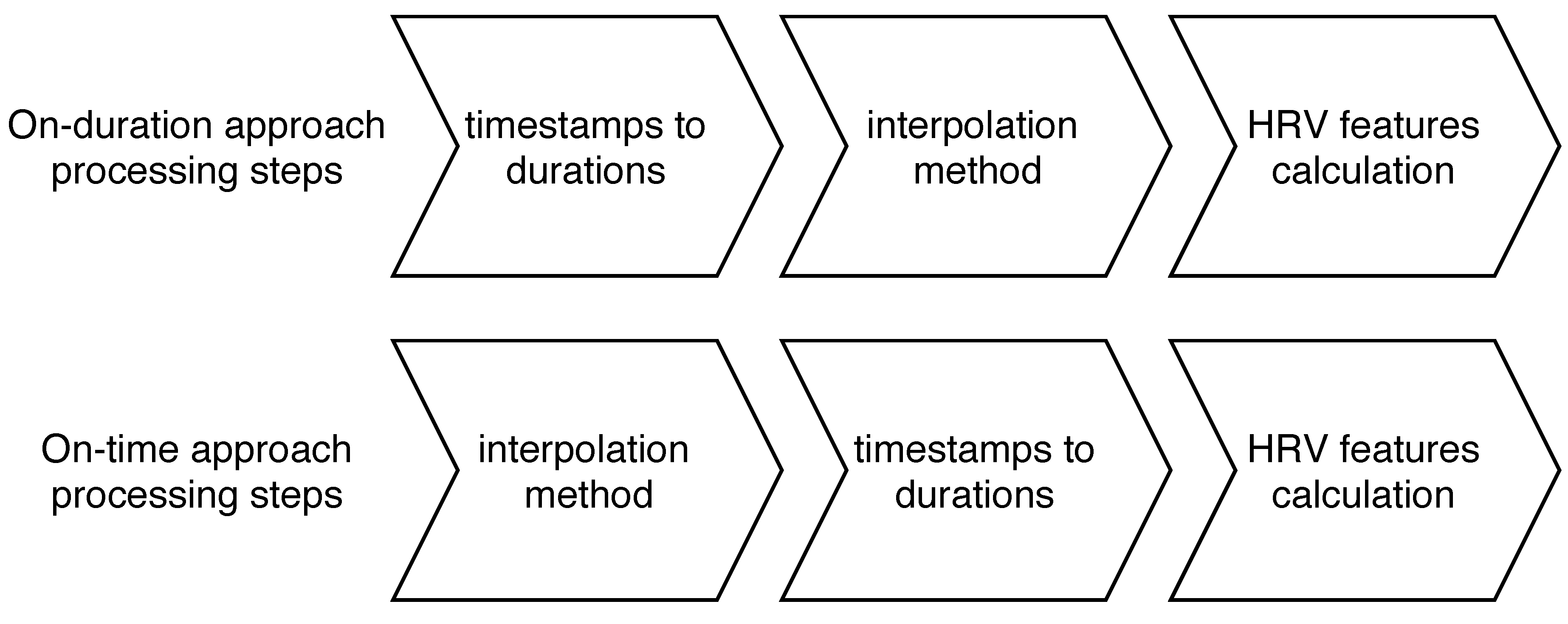
2.2. Missing Values Interpolation
- No interpolation: this approach does not create interpolated values of missing RR-intervals. Differently to the Deletion method that remove missing values merging non-consecutive beats that induce in missing interpretation of HRV features, the no-interpolation method maintains the missing values into the RR-intervals time series.
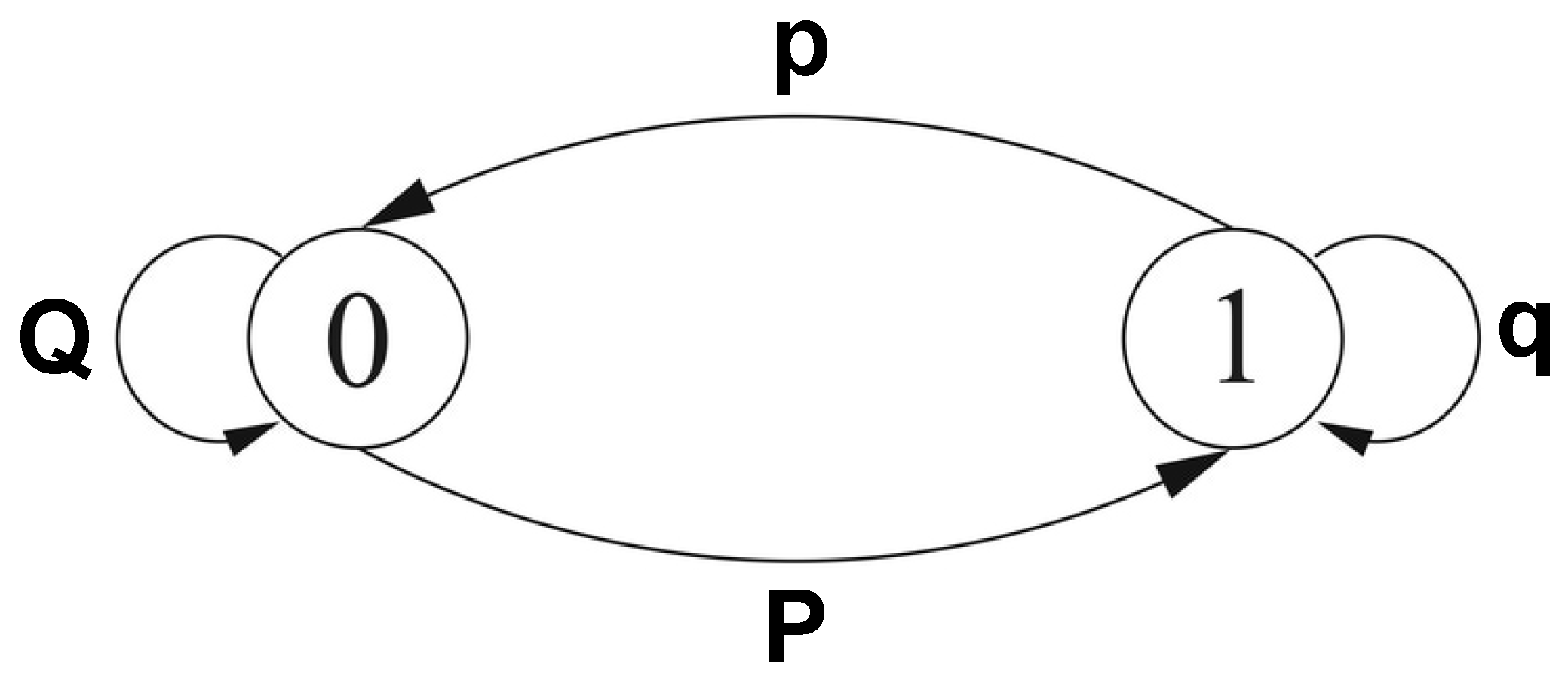
- Nearest neighbor: the nearest neighbor or proximate interpolation is the easiest interpolation method [12]. This interpolation assigns the value of the closest known (existing) neighbor to the missing- value as shows in Equation (6).where a and b are the indexes of and . Interpolated data by this method are discontinuous and it often yields the worst results [13]
- Linear: this method fits a straight line passing through points and [14]. Interpolated data by the linear model are bound between and as showed in Equation (7).Gaunck et al. [14] demonstrated that this method is efficient, and most of the time it is better than non-linear interpolations for predicting missing values in environmental phenomena with constant rates. In addition, they also found that in average this interpolation model underestimated the real values but it strongly depends on the distribution of the data.
- Spline cubic: fitting datapoints using polynomials of degree higher than one leads to problems of oscillation outside the fitted points, known as Runge’s phenomenon [15]. This problem can be avoided by using a spline, a function defined piecewise by polynomials, using datapoints as control points instead of forcing the fitted function to pass through the data points. Cubic spline is a spline composed of piecewise third-order polynomials. By using third degree polynomials is possible to ensure that the resulting curve is smooth [15], avoiding the problem of the straight polynomial interpolation that tends to induce distortions on the edges of the polynomials, given by the fact that, in general, the first and second derivative of the function defined by piecewise polynomials will not be continuous at the edges of polynomials. With cubic spline, it is possible to force the first and second derivatives of consecutive polynomials to be equal, ensuring smoothness of the resulting curve.
2.3. Feature Engineering
- Time domain:
- -
- HR mean: mean values of heart rate (HR) computed as showed in Equation (9).where N is the number of beats and R is the time when the beats happened.
- -
- RMSSD: root mean square of the successive RR-intervals differences (Equation (10)) represents the strength of the autonomic nervous system (specifically the parasympathetic branch) at a given time.where N is the number of beats and R is the time when the beats happened.
- -
- SDNN: standard deviation of RR-intervals (Equation (11)). It reflects the cyclic components responsible for variability in the RR-intervals time series. The SDNN is the “gold standard” for medical stratification of both morbidity and mortality [16].where N is the number of beats and RR is the intervals between two consecutive R and is the mean of RR-intervals in the time series.
- -
- PNN50: the ratio between NN50 (i.e., number of pairs of successive RR intervals that differ by more than 50 ms) and the total number of RR-intervals (Equation (12)).
- Frequency domain:
- -
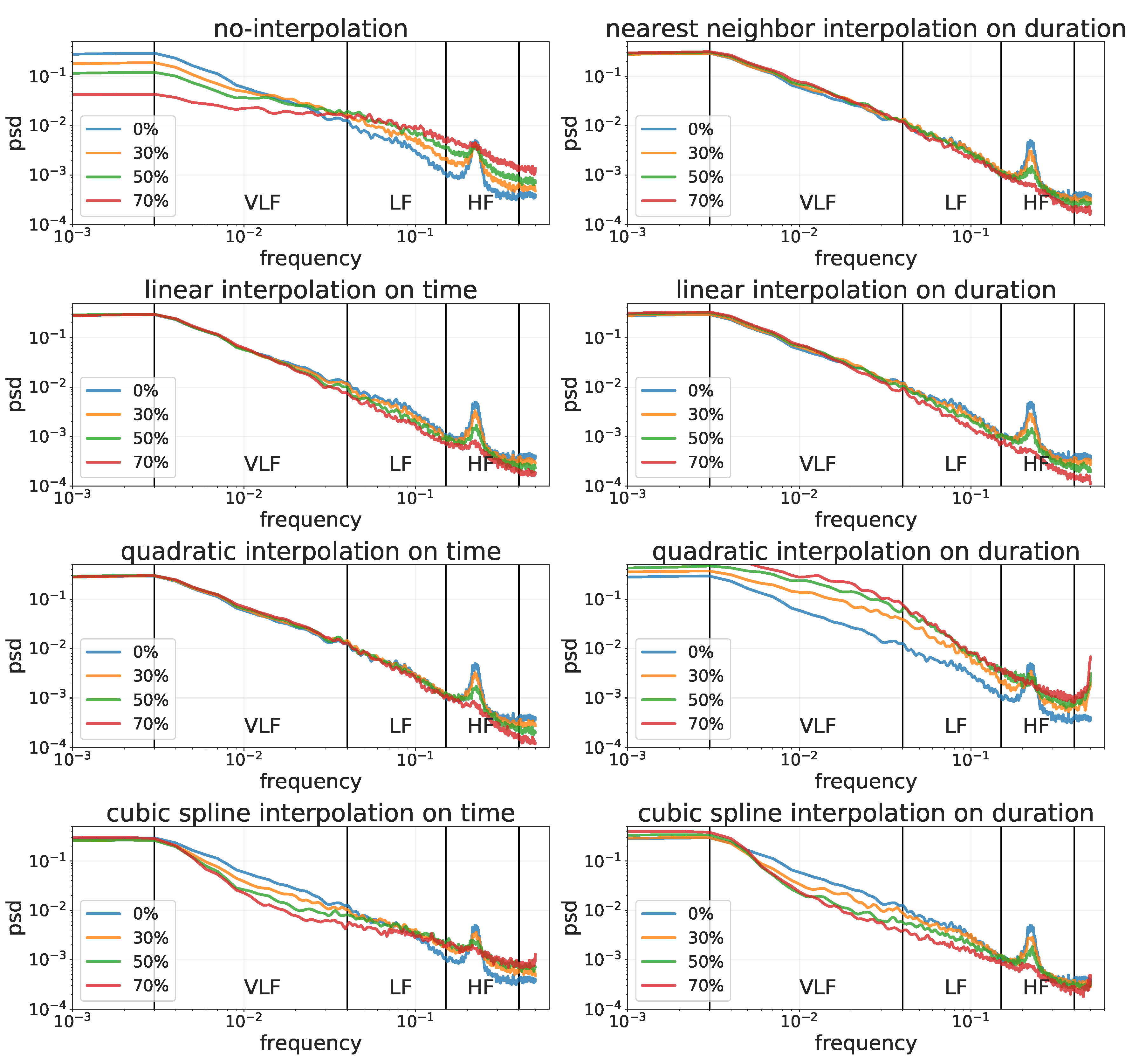
- Power spectral density (PSD): describes the distribution of power into frequency components composing that signal. The Lomb–Scargle periodogram for PSD estimation was found to be the most appropriate method to analyze RR-interval data [5,6]. VLF (power in very-low-frequency ranges, i.e., ≤0.04 Hz), LF (power in low-frequency ranges, i.e., 0.04–0.15 Hz), HF (Power in high-frequency ranges, i.e., 0.15, 0.4 Hz), LF/HF ratio (ratio between LF and HF expressed as ms), and total power (Power in all the frequency ranges, i.e., ≤0.4) were obtained by the sum of the power in the relevant frequency range in the spectrum.
- Non-linear HRV features:
- -
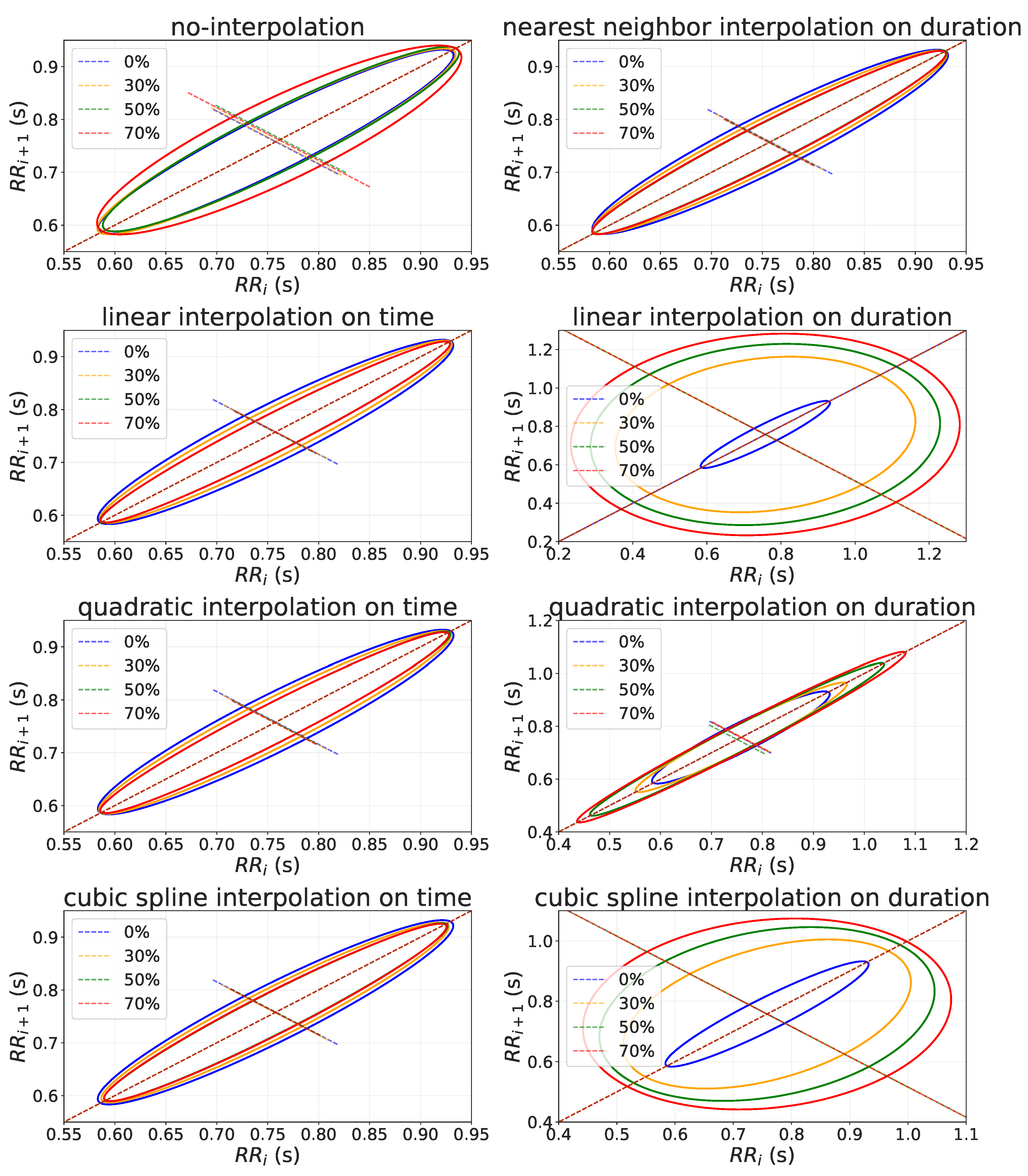
- Poincaré plot: it is a type of recurrence plot used to quantify self-similarity in processes. A Poincaré plot is a graph of RR interval () against the previous one (). From this scatter plot, it is possible to quantitatively analyze the variance of two consecutive RR-intervals by fitting an ellipse to the plotted shape. is the standard deviation of Poincaré plot perpendicular to the line-of-identity, while is the standard deviation of the Poincaré plot along the line-of-identity.
2.4. Success Metrics
3. Results and Discussions
3.1. Results Summary
3.2. HRV Features
3.2.1. Time Domain
3.2.2. Frequency Domain
3.2.3. Non-Linear Domain
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Laborde, S.; Mosley, E.; Thayer, J.F. Heart Rate Variability and Cardiac Vagal Tone in Psychophysiological Research—Recommendations for Experiment Planning, Data Analysis, and Data Reporting. Front. Psychol. 2017, 8, 213. [Google Scholar] [CrossRef] [PubMed]
- Haghi, M.; Thurow, K.; Stoll, R. Wearable Devices in Medical Internet of Things: Scientific Research and Commercially Available Devices. Healthc. Inform. Res. 2017, 23, 4–15. [Google Scholar] [CrossRef] [PubMed]
- Karlsson, M.; Hörnsten, R.; Rydberg, A.; Wiklund, U. Automatic filtering of outliers in RR intervals before analysis of heart rate variability in Holter recordings: A comparison with carefully edited data. Biomed. Eng. 2012, 11, 2. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.K.; Lim, Y.G.; Kim, J.S.; Park, K.S. Effect of missing RR-interval data on heart rate variability analysis in the time domain. Physiol. Meas. 2007, 28, 1485–1494. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.K.; Kim, J.S.; Lim, Y.G.; Park, K.S. The effect of missing RR-interval data on heart rate variability analysis in the frequency domain. Physiol. Meas. 2009, 30, 1039–1050. [Google Scholar] [CrossRef] [PubMed]
- Clifford, G.D.; Tarassenko, L. Quantifying errors in spectral estimates of HRV due to beat replacement and resampling. IEEE Trans. Biomed. Eng. 2005, 52, 630–638. [Google Scholar] [CrossRef] [PubMed]
- Peltola, M.A. Role of editing of R–R intervals in the analysis of heart rate variability. Front. Physiol. 2012, 3, 148. [Google Scholar] [CrossRef] [PubMed]
- Salo, M.; Huikuri, H.; Seppänen, T. Ectopic beats in heart rate variability analysis: Effects of editing on time and frequency domain measures. Ann. Noninvasive Electrocardiol. 2001, 6, 5–17. [Google Scholar] [CrossRef] [PubMed]
- Kamath, M.V.; Fallen, E.L. Correction of the heart rate variability signal for ectopics and missing beats. In Heart Rate Variability; Futura Publishing Company: Armonk, NY, USA, 2001; pp. 75–85. [Google Scholar]
- Normal Sinus Rhythm RR Interval Database, doi:10.13026/C2S881. Available online: https://physionet.org/physiobank/database/nsr2db/ (accessed on 1 June 2019).
- Hideki, I. Essentials of Error-Control Coding Techniques; Academic Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Sibson, R. A brief description of natural neighbor interpolation. In Interpreting Multivariate Data; John Wiley & Sons: Sheffield, UK, 1980; pp. 24–27. ISBN 978-0-471-28039-2. [Google Scholar]
- Lepot, M.; Aubin, J.B.; Clemens, F.H.L.R. Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment. Water 2017, 9, 796. [Google Scholar] [CrossRef]
- Gnauck, A. Interpolation and approximation of water quality time series and process identification. Anal. Bioanal. Chem. 2004, 380, 484–492. [Google Scholar] [CrossRef] [PubMed]
- De Boor, C. A Practical Guide to Splines; Springer: Berlin, Germany, 1978. [Google Scholar]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef] [PubMed]
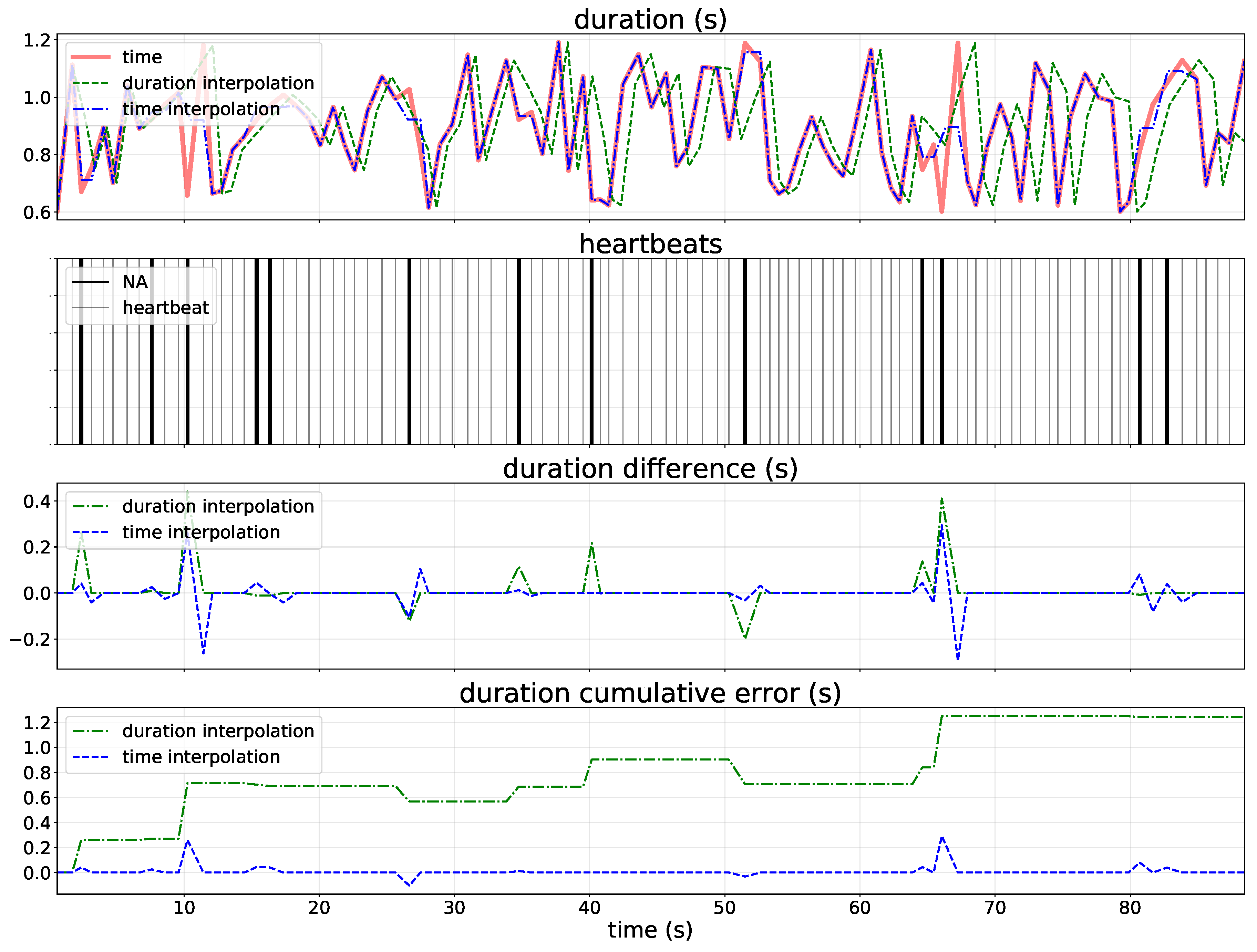
| Window Time (s) | RMSE (s) | RE (%) | ||||
|---|---|---|---|---|---|---|
| Interpolation | Time | Duration | Time | Duration | Time | Duration |
| No-missing values | 90.11 | — | — | |||
| Nearest | — | 91.95 | — | 0.096 | — | 5.11 |
| Linear | 90.11 | 91.83 | 0.075 | 0.090 | 3.70 | 4.86 |
| Quadratic | 90.11 | 92.13 | 0.084 | 0.107 | 4.35 | 5.83 |
| Cubic spline | 90.11 | 92.24 | 0.085 | 0.109 | 3.46 | 6.63 |
| HRV Features | Mean | 95% CI |
|---|---|---|
| IBI (s) | 0.78 | [0.54, 1.11] |
| PNN50 (n) | 8 | [4, 16] |
| RMSSD (s) | 0.039 | [0.017, 0.36] |
| SD1 (s) | 0.027 | [0.012, 0.26] |
| SD2 (s) | 0.077 | [0.040, 0.25] |
| SDNN (s) | 0.059 | [0.017, 0.25] |
| VLF (s) | 0.87 | [0.22, 4.15] |
| LF (s) | 0.477 | [0.12, 5.57] |
| HF (s) | 0.28 | [0.050, 3.024] |
| total power (s) | 1.91 | [0.53, 21.44] |
| LF/HF (s) | 2.9 | [1.2, 10.2] |
| Interpolation | |||||
|---|---|---|---|---|---|
| Missing Values (%) | HRV | How | Method | RE (%) | RMSE |
| 30 | RMSSD (s) | No-interpolation | 14.65 | 0.38 | |
| SDNN (s) | Time | quadratic | 9.42 | 0.34 | |
| PNN50 (n) | No-interpolation | 24.37 | 1.51 | ||
| SD1 (s) | No-interpolation | 14.68 | 0.27 | ||
| SD2 (s) | Time | quadratic | 8.57 | 0.47 | |
| VLF (s) | Time | quadratic | 14.50 | 0.82 | |
| LF (s) | Time | quadratic | 26.87 | 2.01 | |
| HF (s) | Time | quadratic | 32.18 | 4.48 | |
| LF/HF (s) | Time | cubic | 41.39 | 1.73 | |
| total power (s) | Time | quadratic | 17.16 | 6.26 | |
| 50 | RMSSD (ms) | No-interpolation | 23.13 | 0.76 | |
| SDNN (s) | Time | quadratic | 15.47 | 0.41 | |
| PNN50 (n) | No-interpolation | 39.01 | 2.35 | ||
| SD1 (s) | No-interpolation | 23.18 | 0.54 | ||
| SD2 (s) | Time | quadratic | 13.49 | 0.49 | |
| VLF (s) | Time | quadratic | 23.72 | 0.40 | |
| LF (s) | Time | quadratic | 42.42 | 1.12 | |
| HF (s) | Time | quadratic | 52.56 | 2.48 | |
| LF/HF (s) | Time | cubic | 58.07 | 2.26 | |
| total power (s) | Time | quadratic | 27.59 | 3.96 | |
| 70 | RMSSD (s) | No-interpolation | 34.37 | 0.91 | |
| SDNN (s) | Time | quadratic | 22.76 | 0.47 | |
| PNN50 (n) | Time | linear | 63.90 | 3.88 | |
| SD1 (s) | No-interpolation | 34.46 | 0.59 | ||
| SD2 (s) | Time | quadratic | 19.19 | 0.51 | |
| VLF (s) | Time | quadratic | 29.73 | 0.52 | |
| LF (s) | Time | quadratic | 56.41 | 1.45 | |
| HF (s) | Time | quadratic | 72.98 | 3.34 | |
| LF/HF (s) | Time | cubic | 72.07 | 2.80 | |
| total power (s) | Time | quadratic | 72.07 | 5.27 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morelli, D.; Rossi, A.; Cairo, M.; Clifton, D.A. Analysis of the Impact of Interpolation Methods of Missing RR-intervals Caused by Motion Artifacts on HRV Features Estimations. Sensors 2019, 19, 3163. https://doi.org/10.3390/s19143163
Morelli D, Rossi A, Cairo M, Clifton DA. Analysis of the Impact of Interpolation Methods of Missing RR-intervals Caused by Motion Artifacts on HRV Features Estimations. Sensors. 2019; 19(14):3163. https://doi.org/10.3390/s19143163
Chicago/Turabian StyleMorelli, Davide, Alessio Rossi, Massimo Cairo, and David A. Clifton. 2019. "Analysis of the Impact of Interpolation Methods of Missing RR-intervals Caused by Motion Artifacts on HRV Features Estimations" Sensors 19, no. 14: 3163. https://doi.org/10.3390/s19143163
APA StyleMorelli, D., Rossi, A., Cairo, M., & Clifton, D. A. (2019). Analysis of the Impact of Interpolation Methods of Missing RR-intervals Caused by Motion Artifacts on HRV Features Estimations. Sensors, 19(14), 3163. https://doi.org/10.3390/s19143163






