1. Introduction
The Internet of Things (IoT), also known as the Internet of Objects, is a trending concept intended as a network of interconnected smart objects receiving and sending data without human intervention [
1,
2,
3]. The development of applications in IoT is strongly related to the notion of physical location and positions. Therefore, localization technologies will play an important role in the IoT and may become embedded into the infrastructure or into the object. In fact, collected data are reported for a specific IoT application, which requires dedicated data analytic tools to make sense of them and take the appropriate action. Plenty of applications are related to location-based services, which increases the importance of location information. This information can be used for target tracking, surveillance applications, guiding autonomous vehicles, etc. [
4,
5,
6,
7]. Therefore, collected data are meaningless if not combined with the accurate location of the concerned sensor node. The latter can be obtained by using Global Navigation Satellite Systems (GNSS), such as the Global Positioning System (GPS) [
8], which is an efficient outdoor localization system. These solutions cannot be deployed in indoor environments due to the multipath effects caused by obstacles existing between satellites and users, which cause an important degradation of the signals. To overcome this limitation, the idea is to use radio signals for communication between objects. The communication technology is also a challenge in the IoT development, and the choice is closely related to the application. Bluetooth [
9], Ultra-Wide Band (UWB) [
10], Radio Frequency Identification (RFID) [
11], and wireless local area network WiFi [
12] have been widely used in indoor localization. Most proposed indoor localization systems are based on WiFi signals due to the wide use of mobile devices that support this technology. In fact, the other aforementioned communication solutions require specialized infrastructure (wireless radio beacons) to be installed in the indoor environment and extra equipment in the devices. Because the signal characteristics are strongly related to the distance between the transmitter and the receiver, they can be used to perform localization [
13,
14,
15]. Usually, the easy to obtain parameters are the Received Signal Strength Indicator (RSSI) [
16,
17,
18], Channel State Information (CSI) [
19,
20], Angle Of Arrival (AOA) [
14,
21], Time Of Arrival (TOA) [
22], and time difference of arrival [
23]. RSSI does not require specific hardware for time or phase synchronization, and no modification is needed on the device firmware to be able to acquire it. That is why it is the parameter being explored most today.
Based on RSSI signals, existing methods can be essentially classified into fingerprinting-based solutions and ranging-based solutions. The latter is combined with trilateration method and uses geometric properties to estimate the sensor’s location [
24]. In such a solution, the distance to Reference Positions (RPs) is estimated by a propagation model, and at least four RPs are needed to get a 3D position. This requires that the RPs have known positions, which is not easy to obtain in real indoor scenes, this being the major drawback of the trilateration technique. Furthermore, the performance of such a technique depends on the number of RPs and the precision of the propagation model, which depends on the multipath effects. The fingerprinting method overcomes the mentioned drawbacks because it employs a constructed radio map to be compared to RSSI measurements associated with the sensor to localize [
25]. It is a cost-effective solution, and its accuracy is related to the sufficiency of data, where huge RSSI databases are constructed and manipulated to achieve a good localization accuracy. This increases the complexity and the running time of fingerprint-based localization systems, making them not adapted to real-time localization and not able to deal with big sensor networks. Therefore, for a solution that uses a learned model, reducing the online complexity is extremely needed. Recently, promising indoor localization solutions were implemented based on RSSI fingerprinting combined with Machine Learning (ML) methods [
26]. Since data preparation and preprocessing are assured in the offline/training phase, only the prediction task is performed online. Therefore, to find its position, a sensor node interrogates a trained model, which performs the estimated position. Such algorithms shift the computational complexity from the online/prediction process to the model offline/training step. Thus, such solutions based ML are highly recommended in real-time localization applications. This is motivated by the highly-efficient Deep Learning (DL) algorithms, which have been demonstrated to show very good performance in different contexts and applications related to the indoor localization field: LOS/NLOS identification [
19,
27], activity recognition [
28], uncertainty prediction [
29], denoising autoencoders [
30], and localization [
31,
32]. These DL-based methods have been widely introduced into indoor localization, estimating either the location coordinates or other localization information such as room identification [
31], floor identification [
17], region identification [
13,
14,
33], etc. Sound-based localization systems have been proposed in [
13,
14], ensuring a region identification prediction. The sensor data (sound) used require the use of specific hardware (microphones) to be measured. The authors in [
33] detected the region of the sensor node and explored the nodes in the vicinity to estimate the sensor’s location based on RSSI measurements and geometric properties. The mentioned works were not flexible, due to the fact that they needed to place microphones or RPs at the top of each square region formed, which is impractical.
As said before, different localization approaches based on DL methods, like Support Vector Machine (SVM) [
34] and Neural Networks (NN) [
35], have been developed. Different types of NN have been used in the indoor localization context, especially Deep Neural Networks (DNN) and their variants: Multi-Layer Perceptron (MLP) [
29], Recurrent Neural Networks (RNN) [
16], Convolutional Neural Networks (CNN) [
36,
37], etc. The authors in [
38] used a DNN to predict the node location coordinates (latitude and longitude) in a multi-building and multi-floor environment, achieving
m localization error. The approach implemented in [
16] introduced RNN models as the DL method, where RSSI signals were used as input data and GPS coordinates were used as output neurons to train RNN models, in order to generate a model able to predict the location. The MLP introduced in [
29] was applied to predict location uncertainty, while it was applied to RSSI statistics in [
17] to predict the user’s floor. To deal with the constraints of network training and to reduce the number of neural network parameters (weights and biases) to learn and the complexity of traditional NN, Convolutional Neural Networks (CNN) [
36] have been deployed. CNN is a class of deep NN that is widely used. It reduces the complexity of traditional NN and the number of weights to learn by its weight-sharing structure. This means that CNN requires less training parameters and can bring better generalization and robustness. Another reason why we use CNN is to deal with the need for large datasets required by traditional NN, to avoid overfitting problems. Another challenge in implementing positioning systems based on CNNs is that these networks have translational invariance. This feature coincides with the temporal dependency between RSSI fingerprints. Since this NN structure has high invariance in translation, it has been widely used in image processing and classification [
39,
40,
41], achieving a spectacular success in this field. Thus, applying CNN on fingerprint images recently has arisen as an important interest in the localization community.
In [
28], the researchers designed a CNN for a pedestrian activity recognition, which can serve as landmarks for indoor localization. Here, one-dimensional sensor data from accelerometers, magnetometers, gyroscopes, and barometers were considered as network inputs. This work needed specific types of sensors and did not take into consideration the energy consumption problem. In [
13], the authors converted the sound signal collected by a microphone into a spectral map to input it into a CNN model. The authors in [
19] used CNN to determine the NLOS channel classification and ranging error estimation based on UWB CIR data. Here, the CNN models used were fed one-dimensional input CIR images, then, to estimate the position, Least Square (LS) and Weighted Lest Square (WLS) algorithms were used, needing at least four detected access points (APs). Recently, other designed localization systems based on RSSI measurements were proposed. In [
16], a hierarchical classifier employed a combination of smaller CNN models, which worked together to deliver a location prediction. This system took 2D RSSI images, where each image was of size (
),
N was the number of training points, and
K was the number of APs. The authors in [
42] identified the location of a user (building ID and floor ID) by leveraging RSSI obtained from neighboring APs. From a given 1D RSSI fingerprint associated with a training point, a 2D image was made, adding some dummy values (for example: (
), 2D image was constructed from a (
) RSSI fingerprint where 520 is the number of APs, adding nine dummy data). A hierarchical CNN architecture was proposed in [
18] using fingerprint images combining WiFi and magnetic field peculiarities in a single image. The WiFi branch and the magnetic one produced two different predictions. Then, the prediction vectors were combined as the input of a united branch to estimate the user’s location. A framework was implemented in [
38] using CNN to determine the building ID and the floor ID, then a DNN was introduced to estimate the position’s coordinates. In this work, 2D RSSI images were considered where each image corresponded to a specific training point, i.e., an image was formed by RSSI measurements received by a training point from different APs at different instants.
Few existing localization solutions related to localization NN have explored 3D radio images. They have always been used when working on robots’ localization, due to the fact that multiple types of sensors are integrated on a robot (camera, laser, odometer, etc.) [
43,
44,
45,
46]. Therefore, each radio image plane contained data received from a specific sensor. Besides robot localization, 3D radio images can be used in systems exploring different types of data. For instance, the authors in [
18] explored RSSI data accompanied by magnetic and acceleration information. Based on CSI, 3D radio images can be generated as developed in [
20,
47], where one CSI matrix of an antenna was considered as the red, green and blue planes of the image. Therefore, the image was constructed by combining three channels of CSI.
In this paper, we deal with the issue of indoor localization in the context of the IoT as a 3D radio image-fingerprint-based location recognition problem motivated by the outstanding performance of CNN in image classification problems and based on RSSI fingerprints. RSSI measurements can be significantly affected by noise and environmental changes. Different sources of RSSI measurement uncertainty were deeply analyzed in [
48] in order to determine the impact of each disturbing phenomena on the localization accuracy. The authors in [
49] evaluated the effect of different propagation conditions on the localization accuracy in order to predict a satisfying accuracy, performing a linearization process and a Kalman filter. However, this does not impact significantly the accuracy due to the correlated shadowing process. To minimize their temporal variation and fluctuation, during the 2017 IPIN competition explained in [
50], the UMinho Team merged the fingerprints collected in the same position to generate a less noisy fingerprint and potentially improve the localization accuracy. In this paper, we exploit multiple RSSI measurements like the authors in [
51], expecting to remove the noise and improve the localization accuracy. CNN are used taking into account the correlation between different RSSI measurements. We propose to split the studied environment into region “classes” limited in space, and we construct radio images from measured RSSI fingerprints. These radio images are used as our CNN model input data to predict the real-time region index. The main contributions of this paper are summarized as follows.
An advanced cost-effective indoor localization framework inspired by the image classification process is developed using CNN for region recognition on radio tensors based on collected RSSI data.
To the best of our knowledge, this is the first time that radio tensors (used as CNN localization system inputs) have been constructed based on RSSI data alone, without exploring extra information (magnetic information, acceleration, visual data, etc.). This avoids modifications of the existing infrastructure and the increase in the cost of the proposed solution. For this, we propose to use the kurtosis values calculated from measured RSSI. By using the kurtosis, we aim to provide a statistical parameter that will give global information to local filters. This choice is justified later, empirically. Furthermore, the proposed approach is independent of the communication technology because in all of them, the RSSI can be measured.
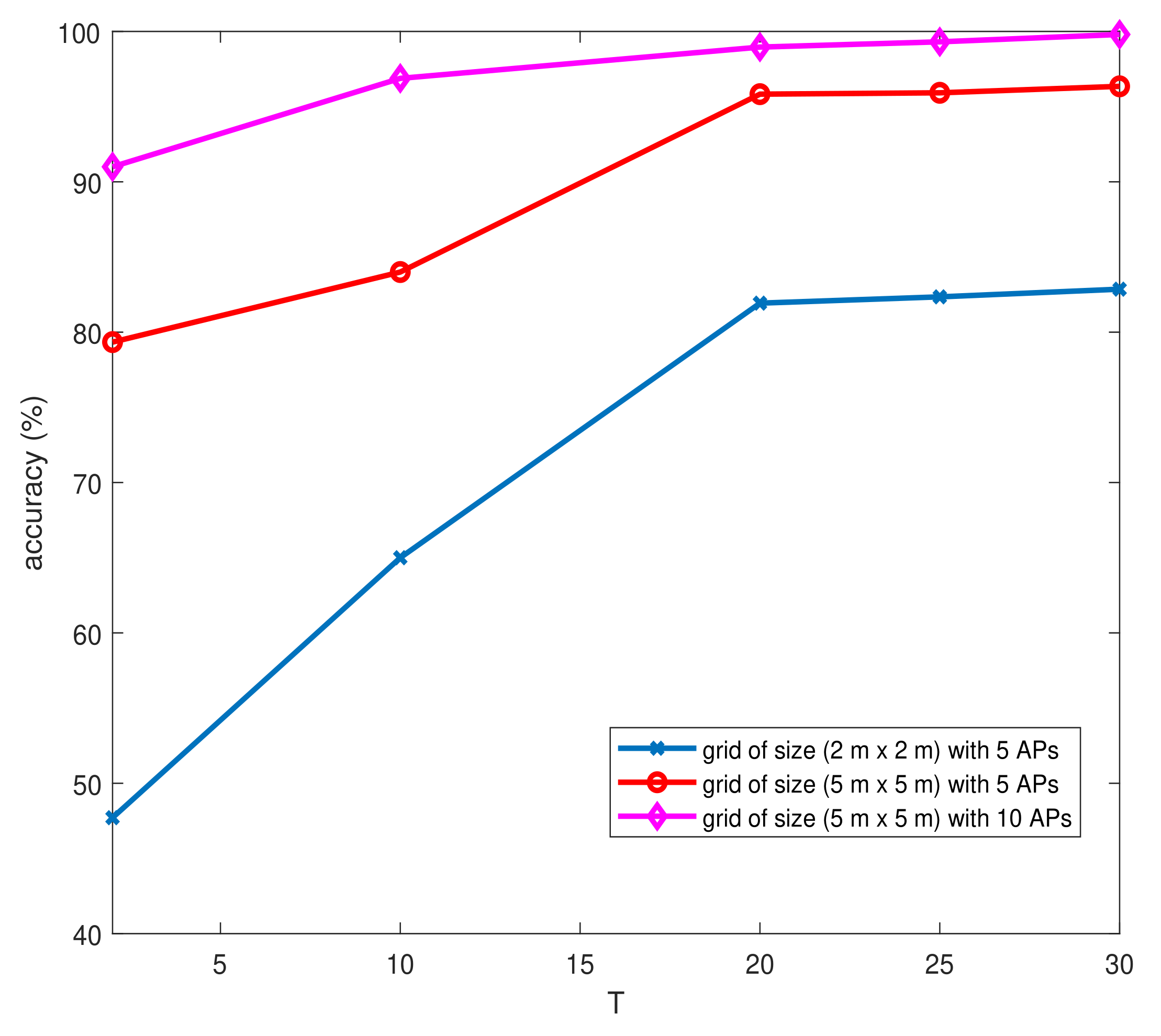
To train CNN models, multiple datasets are used where each dataset corresponds to a specific training point, presenting RSSI values received from different APs during T. The parameter T is varied in order to study its impact on the localization accuracy and choose the best value considering the trade-off between localization accuracy and computational complexity. This is the first time that such an input data structure has been introduced analyzing the impact of T on localization performance.
Our implemented classification network uses radio tensors to predict the index of the region containing the target. For this, our environment can be split into different grid sizes and forms, without the need to add or place APs in specific positions. Thus, we develop a flexible framework that can be applied to any existing indoor environment. As mentioned before, existing approaches based on region recognition are not flexible and require the use of extra hardware.
Simulation results based on a realistic propagation model are presented. Different parameters are empirically justified. Finally, the localization accuracy associated with different indoor localization approaches is compared in order to illustrate the outperformance of the proposed one.
The remainder of this paper is organized as follows: In
Section 2, we present the system model and explain each step of our developed framework based CNN. In
Section 3, the architecture and different aspects of CNN are presented. The obtained results are presented and discussed in
Section 4. Finally, the conclusion is given in
Section 5.
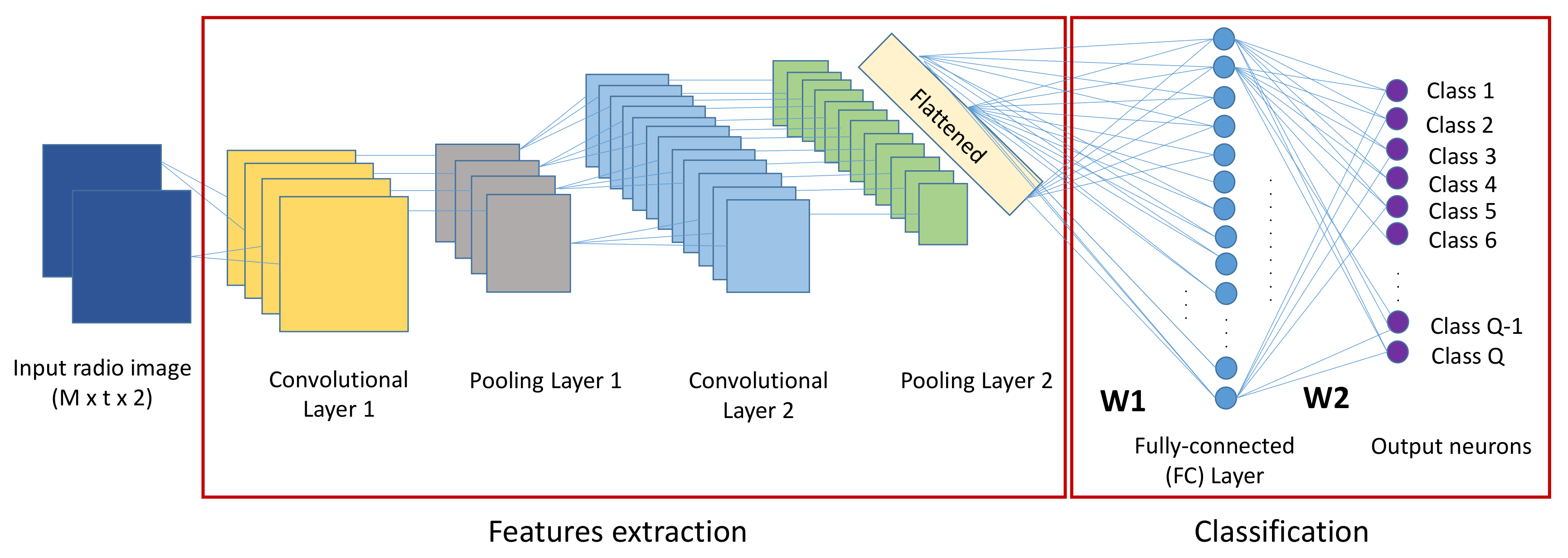
2. System Model of the Proposed CNN-Based Localization Framework
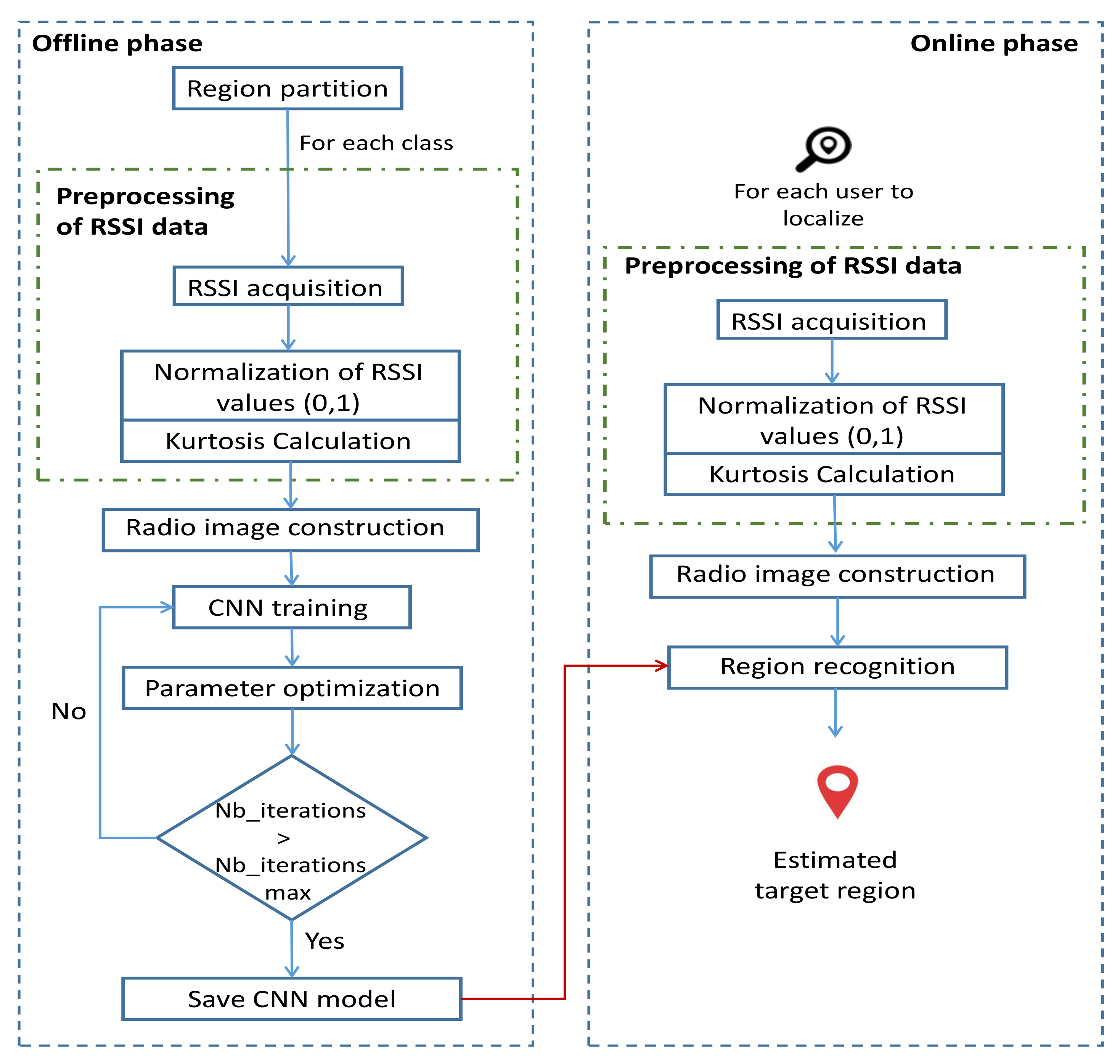
Our system model included two phases (
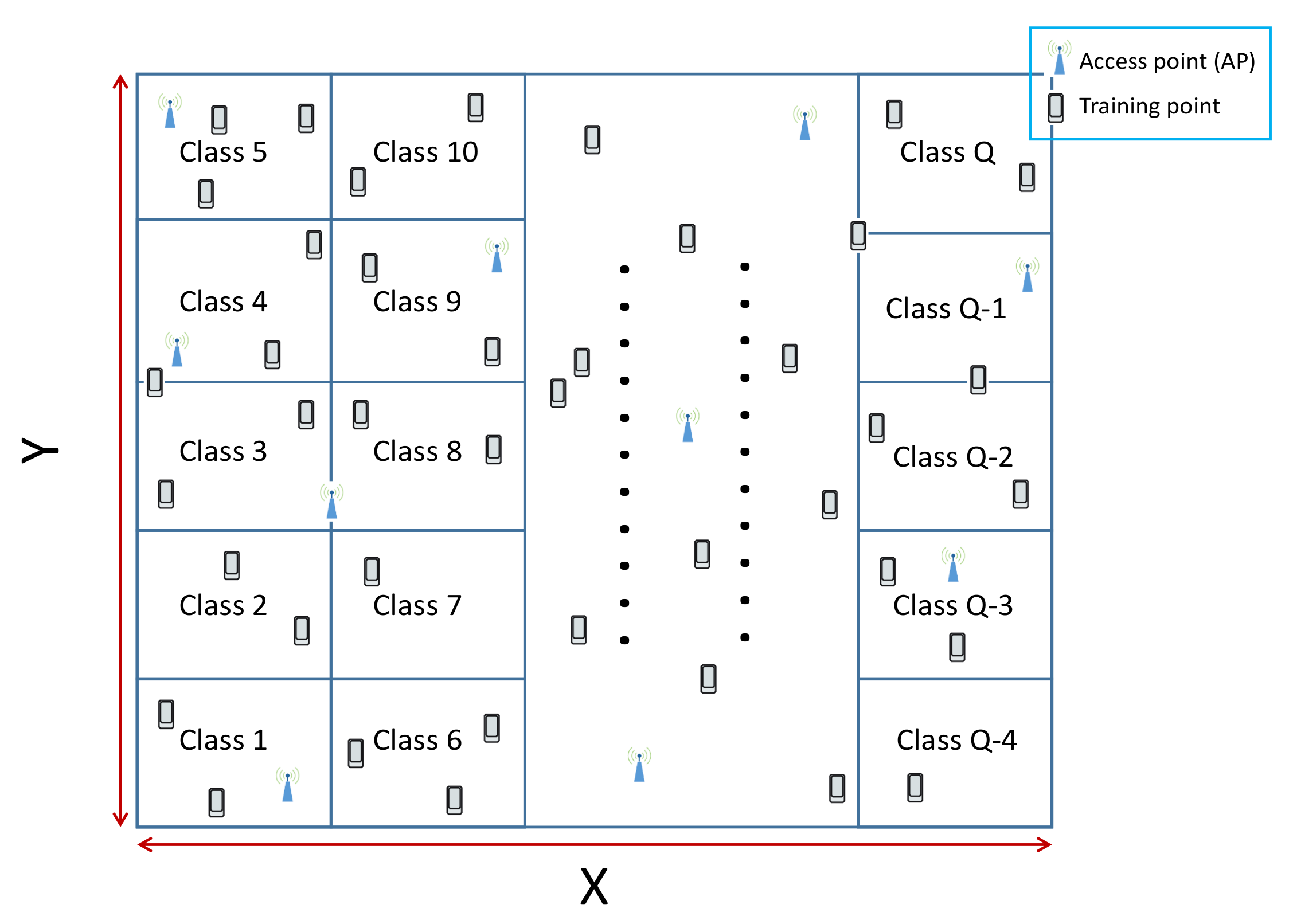
Figure 1): an offline phase including the collection and preprocessing of data to be used as inputs for the localization CNN model and the training of the latter and an online phase introduced to find the position of each sensor node in the studied area using the trained model. First, the studied area was split into different partitions named “classes”, as shown in
Figure 2. Each region was labeled class
q with
, and
Q is the number of classes. We mention that the area of each class is a choice, based on the precision of localization required by the application and the availability of computing resources.
RSSI values received from M deployed APs at different training points (sensor nodes) were measured at different instants. After acquiring RSSI measurements, a normalization process was conducted in order to make all RSSI values be included in [0,1]. RSSI matrix was used as two dimensions (2D) of the radio tensor. Then, a statistic parameter named “kurtosis” was calculated and added in the third dimension (3D) of the radio tensor, leading to the development of two localization frameworks: without and with the kurtosis plane, referred to as CNNLocWoC and CNNLocWC, respectively. After organizing the inputs of CNN, which is a crucial step, many CNN architectures were implemented and tested in order to ensure a satisfying localization accuracy. Finally, a sensor node could be localized efficiently using the considered trained model. In our system, the localization was formalized as a classification problem with Q classes. Each step is explained and described in detail later.
2.1. Preprocessing of RSSI Data
Preprocessing of RSSI data refers to transformations on the input data before they are fed to the CNN model. Different steps and techniques, applied in order to speed up training and to lead to good classification performance, are described in detail (RSSI acquisition, RSSI normalization, and kurtosis calculation).
2.1.1. RSSI Acquisition and Normalization
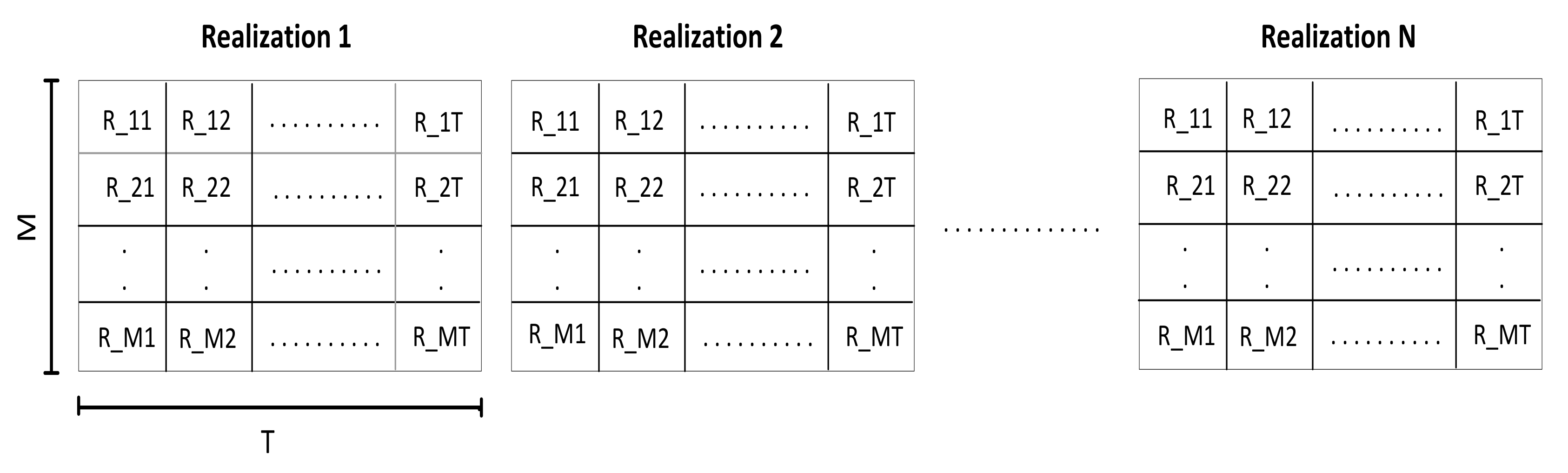
At each training point,
T consecutive RSSI measurements, received from
M APs, were taken.
N RSSI databases, called realizations, were constructed for each training point, as illustrated in
Figure 3; where
N is the number of realizations,
T is the number of RSSI measurements received from each AP, and
M is the number of APs. Therefore, each realization presented RSSI values received from different APs at
T instants. Notice that
N and
T were experimentally adjusted.
The most important factor in deep learning is how much data are available for training and how relevant they are. Furthermore, data are generally required to be normalized, especially when using gradient-based optimization methods, in order to accelerate the learning process and minimize the risk of algorithm divergence [
52,
53].
2.1.2. Kurtosis Calculation
In order to improve the efficiency of our developed framework, we considered using the kurtosis as the third dimension of our tensor, because we wanted to introduce new information to our network. By using the latter, we aimed to provide statistical information calculated from RSSI values that can present useful information (global information of the input image). The kurtosis brings nonlinear information, which can be useful and non-redundant since the operations ensured by a neural network are linear operations. It was defined by Karl Pearson as the fourth moment [
54].
is the RSSI value received from AP
m at instant
t, where
and
. For a specified sensor node, the kurtosis is calculated as follows:
where:
and:
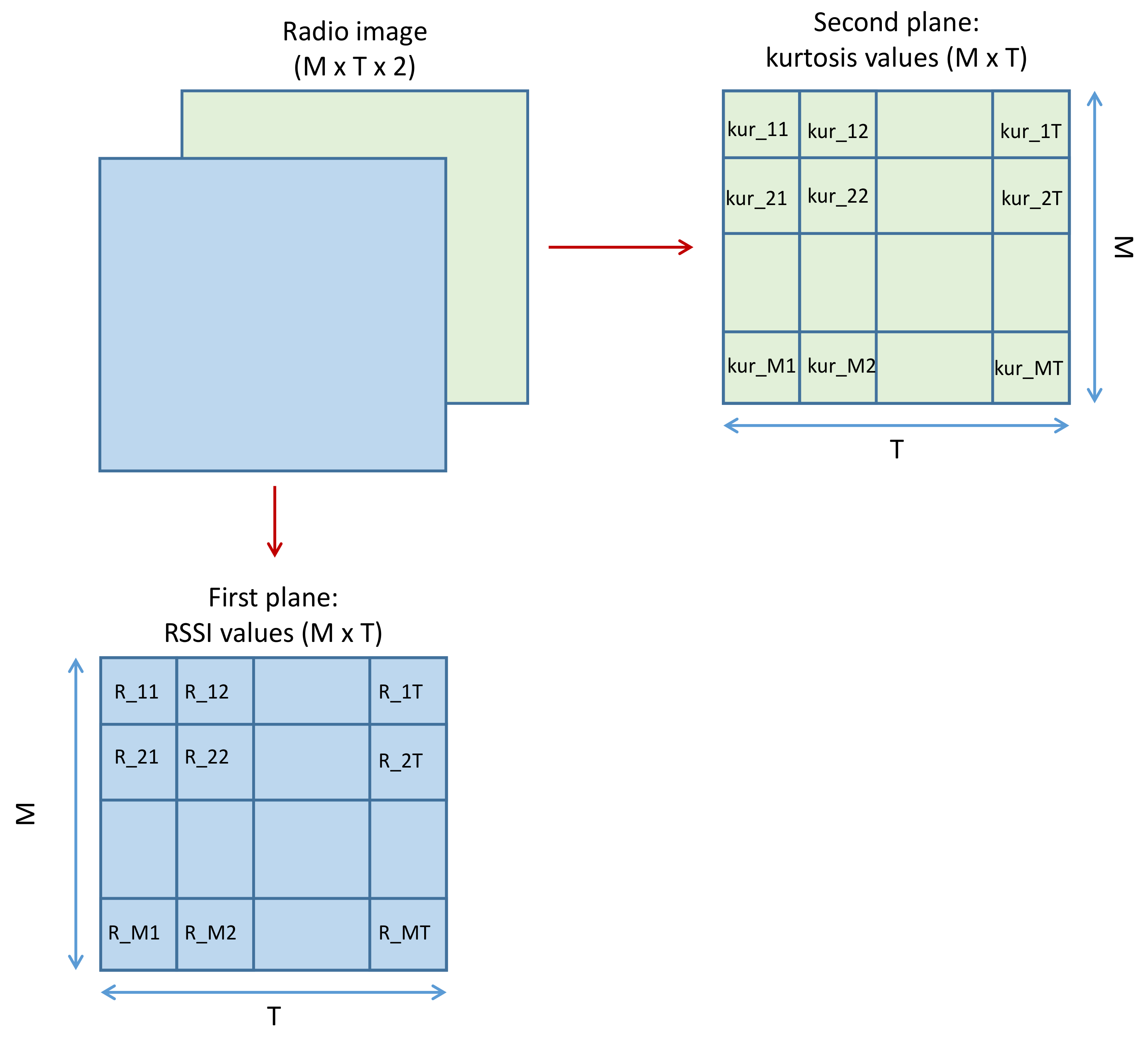
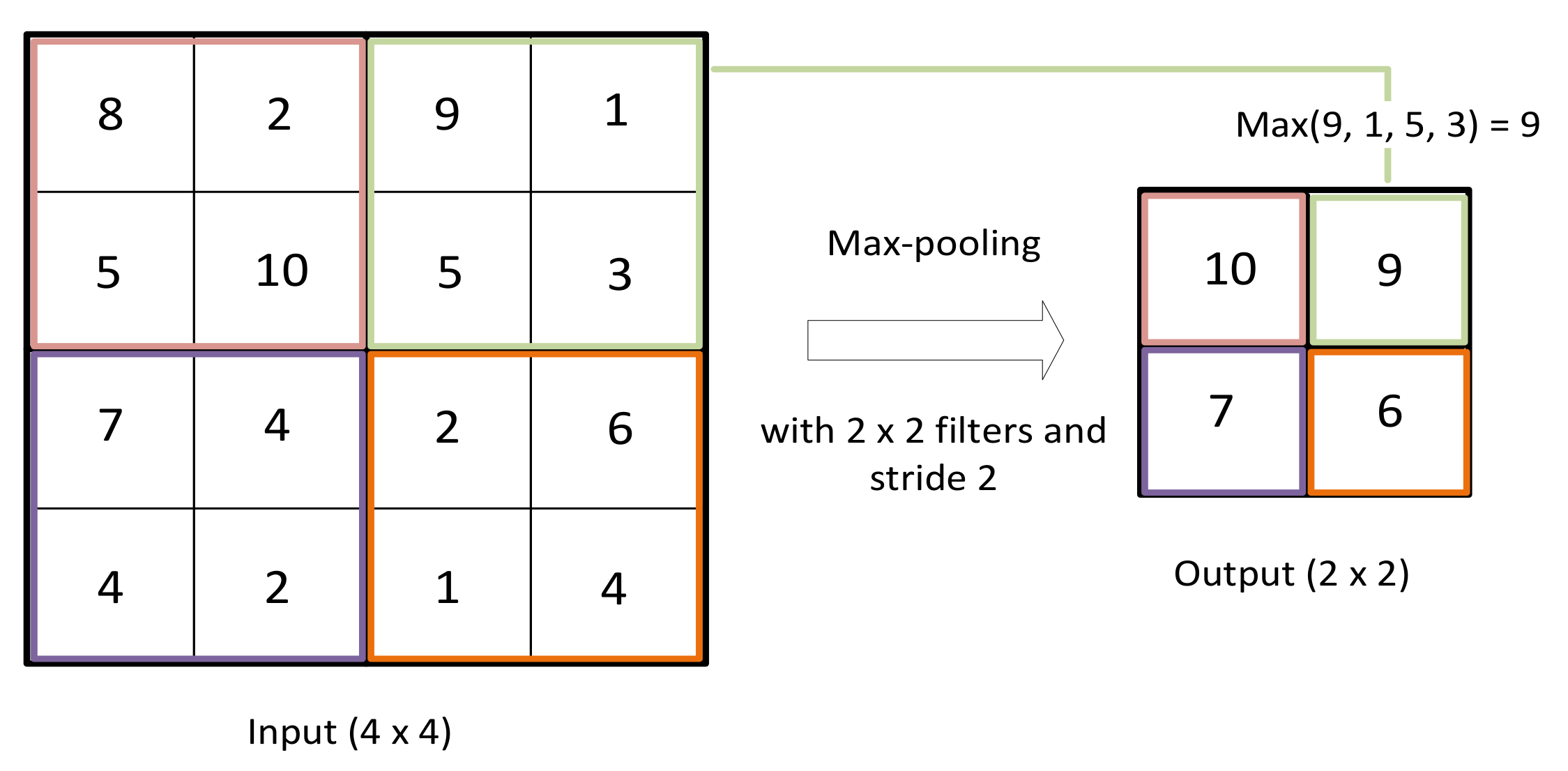
2.2. Radio Image Construction
After collecting RSSI values and calculating the values of kurtosis corresponding to each RSSI database forming a radio tensor, 3D radio images were constructed. As the two first dimensions, we put
T measured RSSI values from
M APs, and we put kurtosis values in the third dimension. Thus, the size of each realization became
(
Figure 4). Constructed radio images needed to be classified and organized, so each image was labeled
q,
. Then,
N realizations of each sensor node should belong to the associated class. Images were organized into
Q folders labeled
, each containing the appropriate radio images.
2.3. Model Training and Target Localization
Training refers to finding the best set of weights that maximize the model’s accuracy. This is related to maximizing the classification score. For this, a backpropagation process associated with an optimization algorithm was used. After training (in the offline phase), our model was able to localize a sensor node accurately in its target area. In the next section, we discuss the CNN architecture, the training process, and some design aspects.
To find a sensor’s position, after acquiring RSSI values and doing the preprocessing of the data, a radio image was constructed having the same dimension and structure of those used for training. This image was fed to the trained model in order to predict the region to which the sensor node belonged. For this, probabilities were assigned to each class, and the sum of these probabilities was equal to one. The predicted class was the one that corresponded to the highest probability.