A Robust Transmission Scheduling Approach for Internet of Things Sensing Service with Energy Harvesting
Abstract
1. Introduction
- We formulate the transmission scheduling problem as a utility optimization problem subject to the energy constraints.
- We introduce a flexible model to describe the harvested energy, which is robust against the inaccuracy of an exact energy model.
- We conduct extensive experiments on real-world data and explore the impacts of the prediction model and various parameters; numerical results demonstrate the robustness of the proposed scheduling approach.
2. Related Work
2.1. Utility Optimization without Prior Knowledge of the Harvested Energy Profile
2.2. Utility Optimization Based on a Known Harvested Energy Profile
2.3. Utility Optimization Assuming the Energy Harvesting Process as a Random Process
3. Robust Transmission Scheduling
3.1. Network Model
3.2. Optimization Formulation
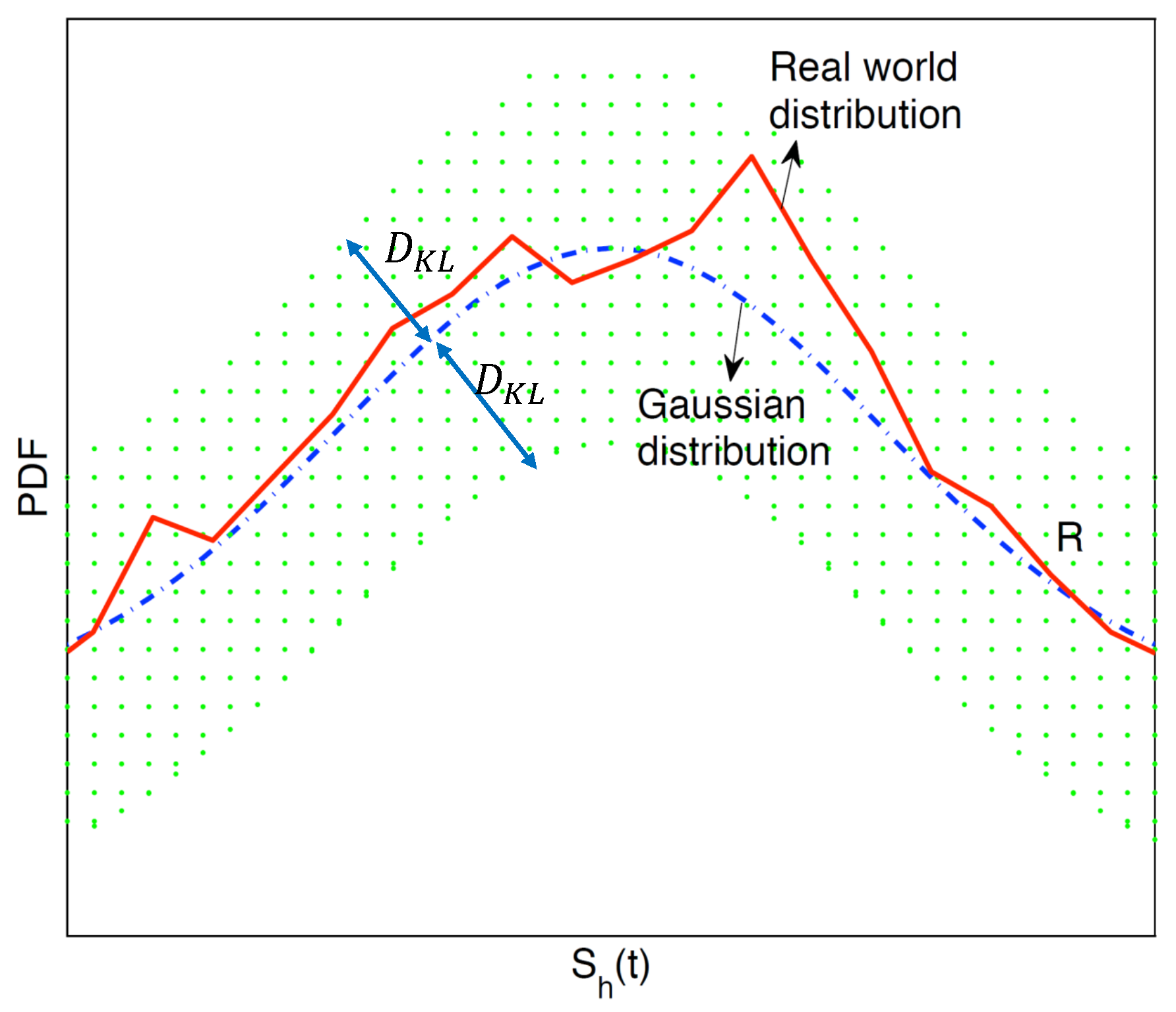
3.3. Handling the Random Variable
3.3.1. Transforming the Constraints
3.3.2. Calculating Threshold
4. Adaptive Transmission Scheduling
| Algorithm 1 UHETS-adaptation |
| Input:, , , Output: Adjusted transmission decision for the remaining slots, i.e., .
|
5. Summary and Discussion
5.1. Working Procedure Summary
| Algorithm 2 Working procedure of UHETS |
| Input: and required by the application, the variance of based on historical data denoted as Output:
|
5.2. Scalability
5.3. Complexity Analysis
6. Evaluation
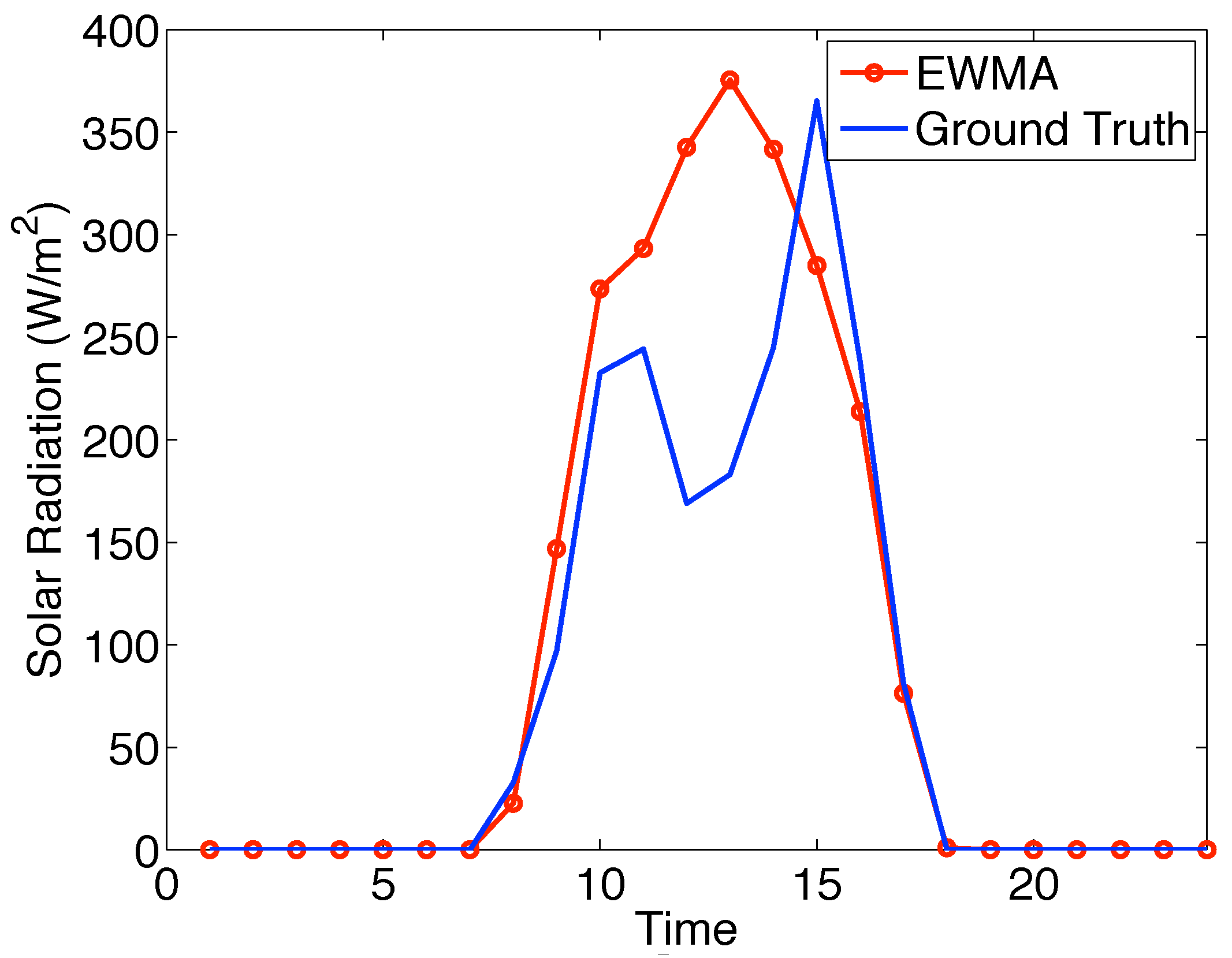
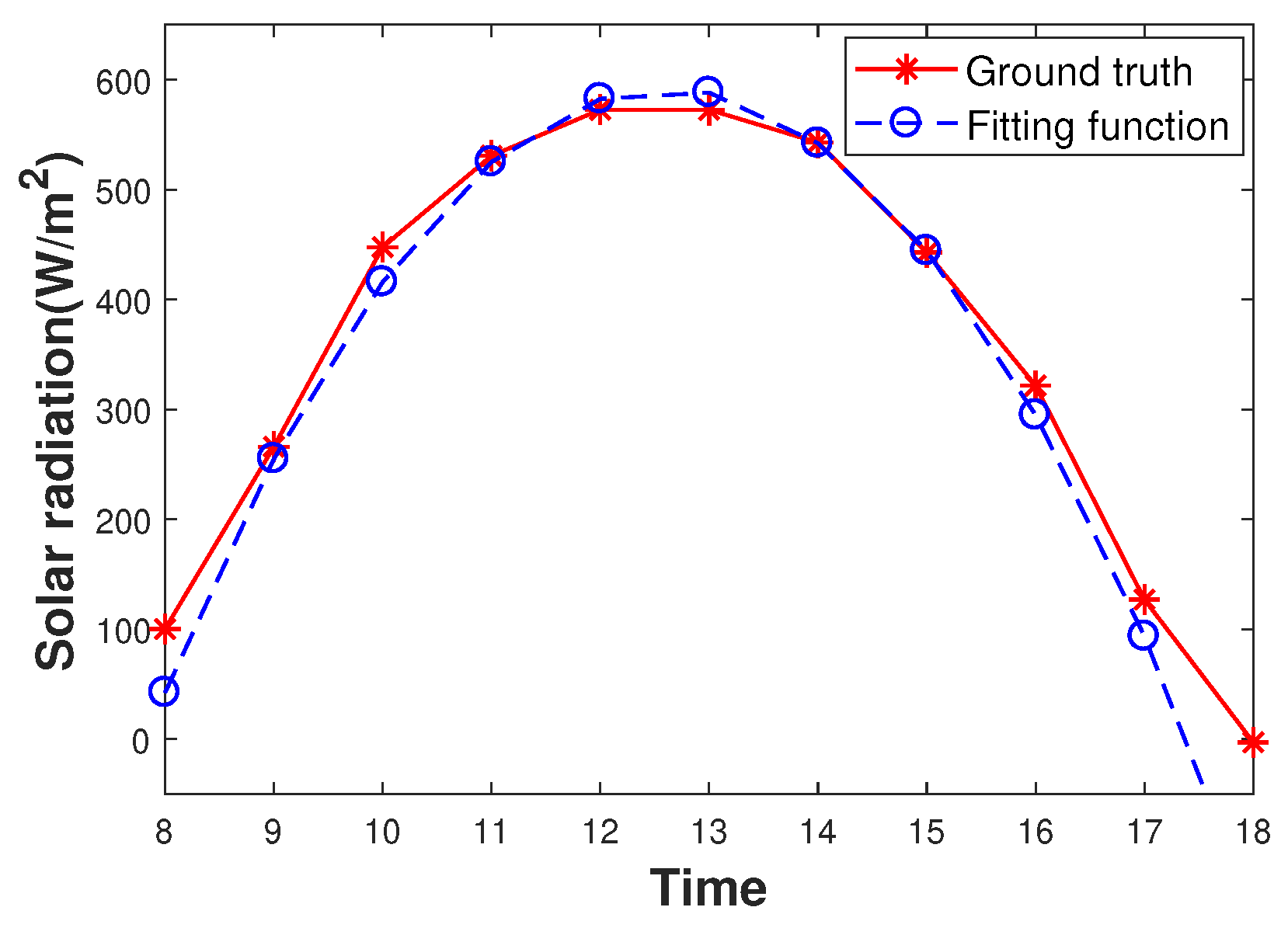
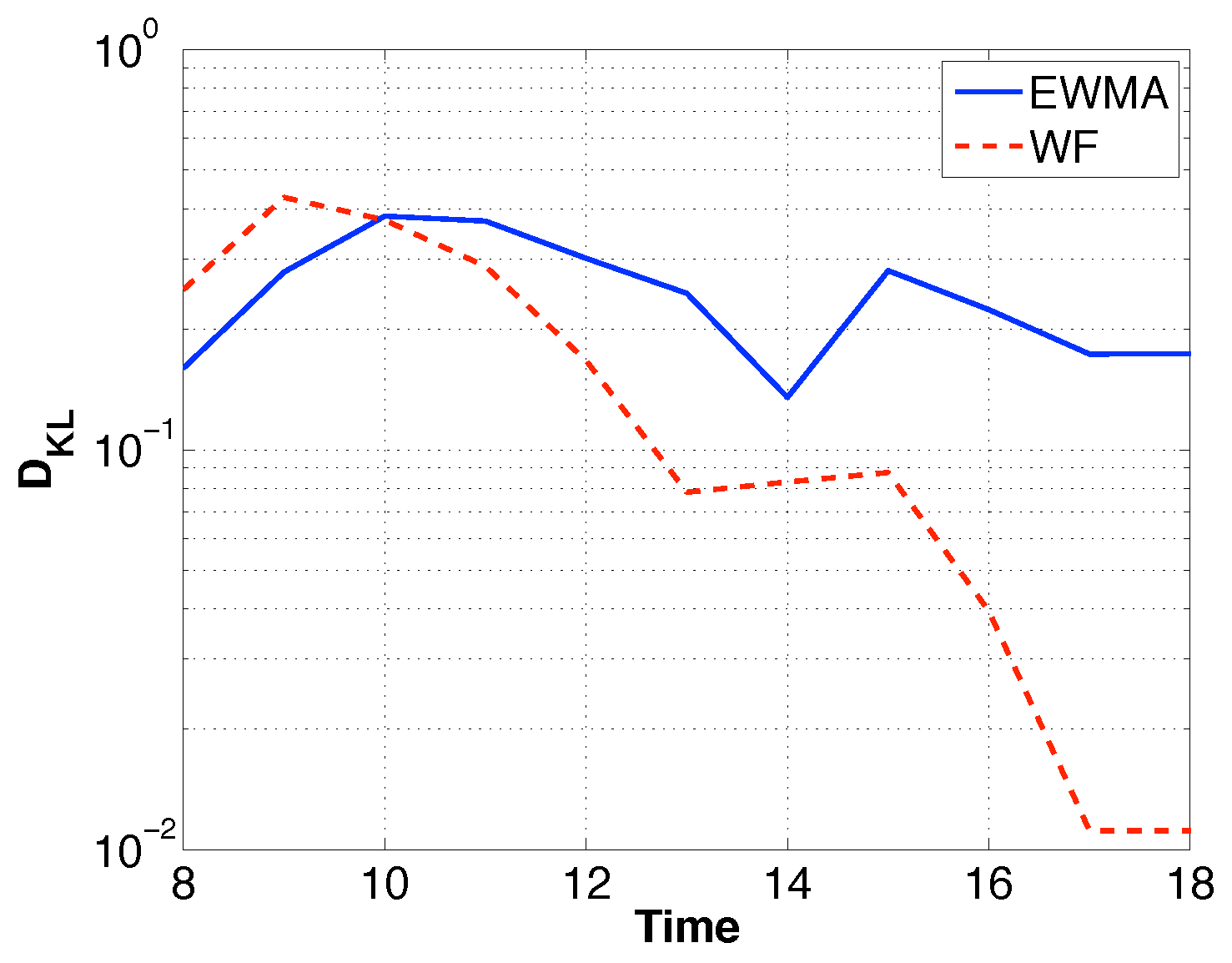
6.1. Prediction Model
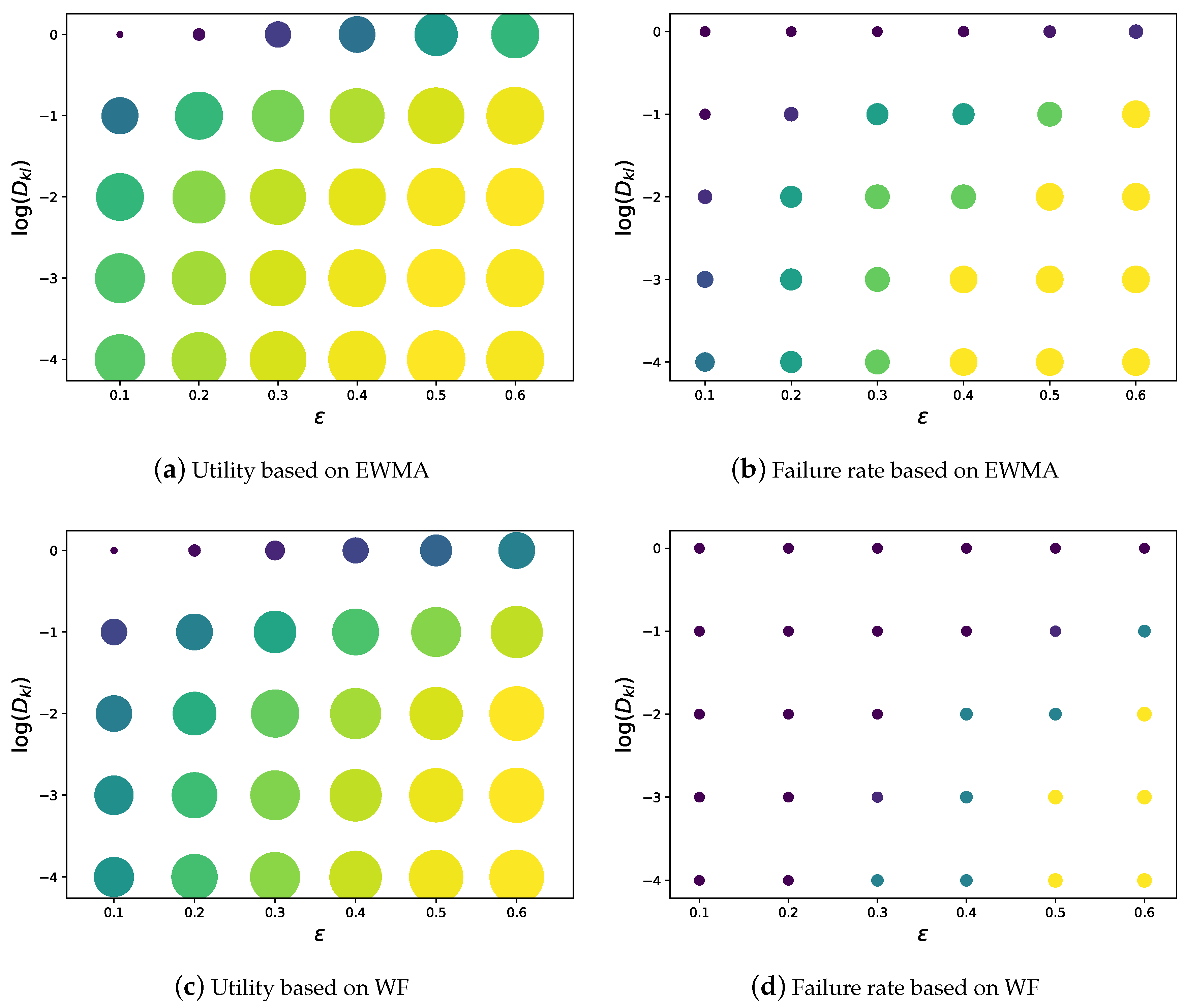
6.2. The Impacts of Parameters
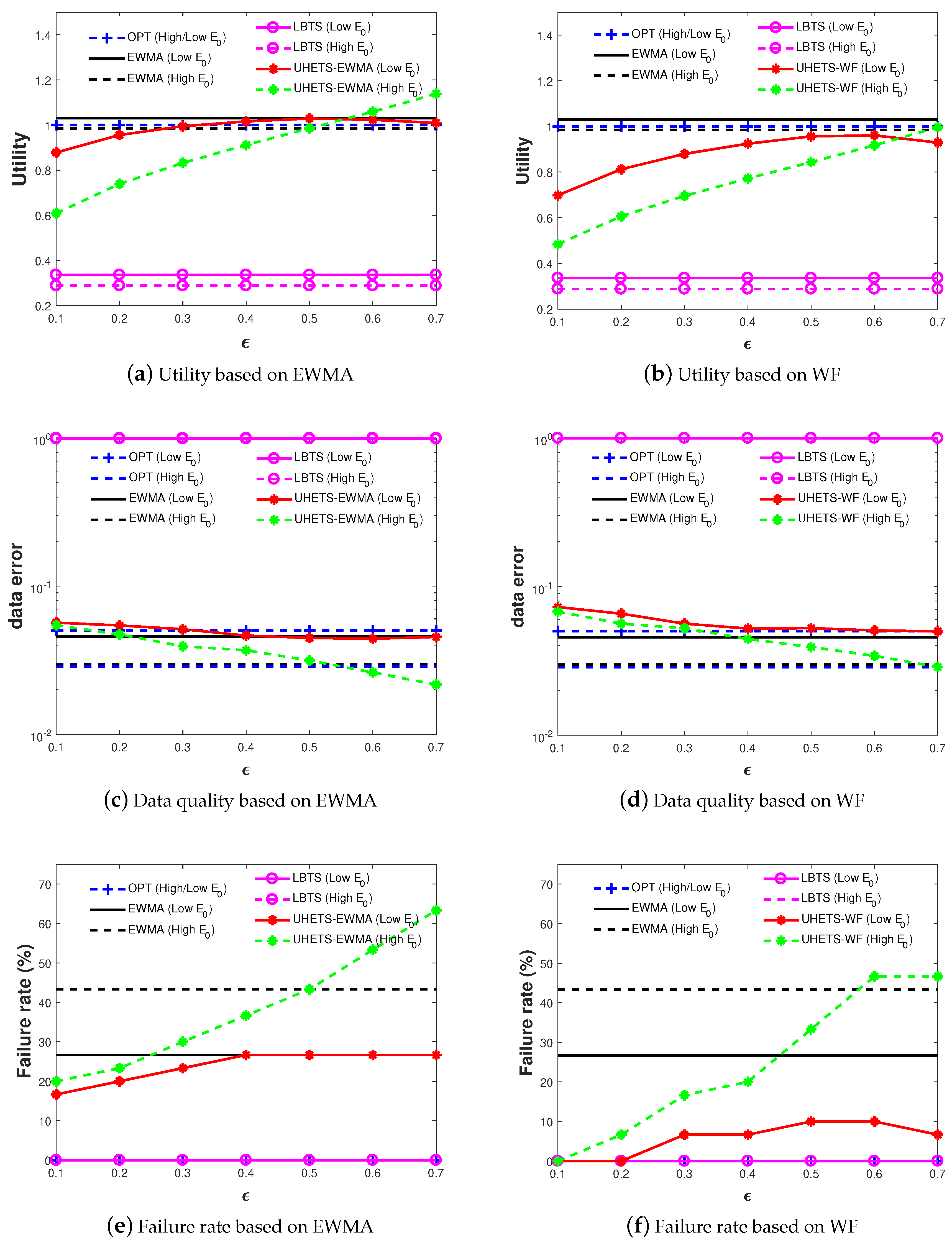
6.3. Performance
6.4. UHETS-Adaptation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| Algorithm A1 The iterative method to calculate |
| Input:, search range , iteration tolerance , . Output:.
|
References
- Kaur, N.; Sood, S.K. An energy-efficient architecture for the Internet of Things (IoT). IEEE Syst. J. 2017, 11, 796–805. [Google Scholar] [CrossRef]
- Kansal, A.; Hsu, J.; Zahedi, S.; Srivastava, M.B. Power management in energy harvesting sensor networks. ACM Trans. Embed. Comput. Syst. 2007, 6, 32. [Google Scholar] [CrossRef]
- Hao, J.; Wang, R.; Zhuang, Y.; Zhang, B. A Flexible Network Utility Optimization Approach for Energy Harvesting Sensor Networks. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, UAE, 9–13 December 2018. [Google Scholar]
- Kar, K.; Krishnamurthy, A.; Jaggi, N. Dynamic node activation in networks of rechargeable sensors. In Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March 2006; Volume 14, pp. 15–26. [Google Scholar]
- Ozel, O.; Ulukus, S. Information-Theoretic Analysis of an Energy Harvesting Communication System. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications Workshops, Instanbul, Turkey, 26–30 September 2010; pp. 330–335. [Google Scholar]
- Ho, C.K.; Zhang, R. Optimal Energy Allocation for Wireless Communications with Energy Harvesting Constraints. IEEE Trans. Signal Process. 2011, 60, 4808–4818. [Google Scholar] [CrossRef]
- Sharma, V.; Mukherji, U.; Joseph, V.; Gupta, S. Optimal Energy Management Policies for Energy Harvesting Sensor Nodes. IEEE Trans. Wirel. Commun. 2010, 9, 1326–1336. [Google Scholar] [CrossRef]
- Tapparello, C.; Simeone, O.; Rossi, M. Dynamic Compression-Transmission for Energy-Harvesting Multihop Networks with Correlated Sources. IEEE/ACM Trans. Netw. 2014, 22, 1729–1741. [Google Scholar] [CrossRef]
- Mao, Z.; Koksal, C.E.; Shroff, N.B. Near Optimal Power and Rate Control of Multi-Hop Sensor Networks with Energy Replenishment: Basic Limitations with Finite Energy and Data Storage. IEEE Trans. Autom. Control 2012, 57, 815–829. [Google Scholar]
- Liu, R.S.; Sinha, P.; Koksal, C.E. Joint Energy Management and Resource Allocation in Rechargeable Sensor Networks. In Proceedings of the IEEE Infocom, San Diego, CA, USA, 14–19 March 2010; pp. 902–910. [Google Scholar]
- Ciuonzo, D.; Aubry, A.; Carotenuto, V. Rician MIMO channel-and jamming-aware decision fusion. IEEE Trans. Signal Process. 2017, 65, 3866–3880. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Rossi, P.S.; Dey, S. Massive MIMO channel-aware decision fusion. IEEE Trans. Signal Process. 2014, 63, 604–619. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Rossi, P.S. Quantizer design for generalized locally optimum detectors in wireless sensor networks. IEEE Wirel. Commun. Lett. 2017, 7, 162–165. [Google Scholar] [CrossRef]
- Vigorito, C.M.; Ganesan, D.; Barto, A.G. Adaptive control of duty cycling in energy-harvesting wireless sensor networks. In Proceedings of the 2007 4th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, San Diego, CA, USA, 18–21 June 2007; pp. 21–30. [Google Scholar]
- Yoon, I.; Kim, H.; Dong, K.N. Adaptive Data Aggregation and Compression to Improve Energy Utilization in Solar-Powered Wireless Sensor Networks. Sensors 2017, 17, 1226. [Google Scholar] [CrossRef]
- Djenouri, D.; Bagaa, M. Energy harvesting aware relay node addition for power-efficient coverage in wireless sensor networks. In Proceedings of the IEEE International Conference on Communications, London, UK, 8–12 June 2015; pp. 86–91. [Google Scholar]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless Information and Power Transfer: Architecture Design and Rate-Energy Tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Multiobjective Resource Allocation for Secure Communication in Cognitive Radio Networks with Wireless Information and Power Transfer. IEEE Trans. Veh. Technol. 2016, 65, 3166–3184. [Google Scholar] [CrossRef]
- Wu, Q.; Tao, M.; Kwan Ng, D.W.; Chen, W.; Schober, R. Energy-Efficient Resource Allocation for Wireless Powered Communication Networks. IEEE Trans. Wirel. Commun. 2016, 15, 2312–2327. [Google Scholar] [CrossRef]
- Ju, H.; Zhang, R. Optimal resource allocation in full-duplex wireless-powered communication network. IEEE Trans. Commun. 2014, 62, 3528–3540. [Google Scholar] [CrossRef]
- Vamvakas, P.; Tsiropoulou, E.E.; Vomvas, M.; Papavassiliou, S. Adaptive power management in wireless powered communication networks: A user- centric approach. In Proceedings of the 2017 IEEE 38th Sarnoff Symposium, Newark, NJ, USA, 18–20 September 2017; pp. 1–6. [Google Scholar]
- Boshkovska, E.; Ng, D.W.K.; Zlatanov, N.; Schober, R. Practical Non-Linear Energy Harvesting Model and Resource Allocation for SWIPT Systems. IEEE Commun. Lett. 2015, 19, 2082–2085. [Google Scholar] [CrossRef]
- Tran, V.; Georges, K.; Trung, T.K. Resource Allocation in SWIPT Networks under a Non-Linear Energy Harvesting Model: Power Efficiency, User Fairness, and Channel Non-Reciprocity. IEEE Trans. Veh. Technol. 2018, 67, 8466–8480. [Google Scholar] [CrossRef]
- Boshkovska, E.; Ng, D.W.K.; Zlatanov, N.; Koelpin, A.; Schober, R. Robust Resource Allocation for MIMO Wireless Powered Communication Networks Based on a Non-Linear EH Model. IEEE Trans. Commun. 2017, 65, 1984–1999. [Google Scholar] [CrossRef]
- Jiang, R.; Xiong, K.; Fan, P.; Zhang, Y.; Zhong, Z. Optimal Design of SWIPT Systems with Multiple Heterogeneous Users under Non-linear Energy Harvesting Model. IEEE Access 2017, 5, 11479–11489. [Google Scholar] [CrossRef]
- Xiong, K.; Wang, B.; Liu, K.J.R. Rate-Energy Region of SWIPT for MIMO Broadcasting Under Nonlinear Energy Harvesting Model. IEEE Trans. Wirel. Commun. 2017, 16, 5147–5161. [Google Scholar] [CrossRef]
- Ponnimbaduge Perera, T.D.; Jayakody, D.N.K.; Sharma, S.K.; Chatzinotas, S.; Li, J. Simultaneous Wireless Information and Power Transfer (SWIPT): Recent Advances and Future Challenges. IEEE Commun. Surv. Tutor. 2018, 20, 264–302. [Google Scholar] [CrossRef]
- Gündüz, D.; Devillers, B. Two-hop communication with energy harvesting. In Proceedings of the 2011 4th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), San Juan, Puerto Rico, 13–16 December 2011; pp. 201–204. [Google Scholar]
- Fan, L.; Chen, S.; Tang, S.; Xiao, H.; Yu, W. Efficient Topology Design in Time-Evolving and Energy-Harvesting Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Mobile Ad-hoc and Sensor Systems, Hangzhou, China, 14–16 October 2013. [Google Scholar]
- Maemoto, D.; Mori, K.; Sanada, K. Adaptive clustering control for energy-harvesting WSNs with non-uniform energy harvesting rate. In Proceedings of the 2017 IEEE Sensors, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Tunc, C.; Akar, N. Markov fluid queue model of an energy harvesting IoT device with adaptive sensing. Perform. Eval. 2017, 111, 1–16. [Google Scholar] [CrossRef]
- Guntupalli, L.; Li, F.Y.; Gidlund, M. Energy Harvesting Powered Packet Transmissions in Duty-Cycled WSNs: A DTMC Analysis. In Proceedings of the IEEE Global Communications Conference, Singapore, 4–8 December 2018. [Google Scholar]
- Gorlatova, M.; Wallwater, A.; Zussman, G. Networking low-power energy harvesting devices: Measurements and algorithms. IEEE Trans. Mob. Comput. 2013, 12, 1853–1865. [Google Scholar] [CrossRef]
- Tarighati, A.; Gross, J.; Jaldén, J. Decentralized hypothesis testing in energy harvesting wireless sensor networks. IEEE Trans. Signal Process. 2017, 65, 4862–4873. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, R.; Cui, S. Throughput Maximization for the Gaussian Relay Channel with Energy Harvesting Constraints. IEEE J. Sel. Areas Commun. 2013, 31, 1469–1479. [Google Scholar] [CrossRef]
- Yadav, A.; Goonewardena, M.; Ajib, W.; Dobre, O.A.; Elbiaze, H. Energy Management for Energy Harvesting Wireless Sensors with Adaptive Retransmission. IEEE Trans. Commun. 2017, 65, 5487–5498. [Google Scholar] [CrossRef]
- Chamanian, S.; Baghaee, S.; Uluşan, H.; Zorlu, Ö.; Uysal-Biyikoglu, E.; Külah, H. Implementation of Energy-Neutral Operation on Vibration Energy Harvesting WSN. IEEE Sens. J. 2019, 19, 3092–3099. [Google Scholar] [CrossRef]
- Cai, J.F.; Cand, S.E.J.; Shen, Z. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J. Optim. 2008, 20, 1956–1982. [Google Scholar] [CrossRef]
- Anastasi, G.; Conti, M.; Francesco, M.D.; Passarella, A. Energy conservation in wireless sensor networks: A survey. Ad Hoc Netw. 2009, 7, 537–568. [Google Scholar] [CrossRef]
- Wang, R.; Wang, P.; Xiao, G. A robust optimization approach for energy generation scheduling in microgrids. Energy Convers. Manag. 2015, 106, 597–607. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Casanova-Mateo, C.; Muñoz-Marí, J.; Camps-Valls, G. Prediction of Daily Global Solar Irradiation Using Temporal Gaussian Processes. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1936–1940. [Google Scholar] [CrossRef]
- Tsiropoulou, E.; Koukas, K.; Papavassiliou, S. A socio-physical and mobility-aware coalition formation mechanism in public safety networks. EAI Endorsed Trans. Future Internet 2018, 4, 154176. [Google Scholar] [CrossRef]
- Lin, C.R.; Gerla, M. Adaptive clustering for mobile wireless networks. IEEE J. Sel. Areas Commun. 1997, 15, 1265–1275. [Google Scholar] [CrossRef]
- Mattingley, J.; Boyd, S. CVXGEN: A code generator for embedded convex optimization. Optim. Eng. 2012, 13, 1–27. [Google Scholar] [CrossRef]
- Nrel: National Renewable Energy Laboratory. Available online: http://www.nrel.gov/midc/nwtc_m2/ (accessed on 25 April 2019).
- Available online: https://www.quectel.com/product/bc95.htm (accessed on 12 February 2019).
- Sharma, N.; Gummeson, J.; Irwin, D.; Shenoy, P. Cloudy Computing: Leveraging Weather Forecasts in Energy Harvesting Sensor Systems. In Proceedings of the 2010 7th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Boston, MA, USA, 21–25 June 2010; pp. 1–9. [Google Scholar]
- Nws: National Oceanic and Atmospheric Administration’s National Weather Service. Available online: https://w2.weather.gov/climate/ (accessed on 26 April 2019).
- SVT. Available online: http://svt.stanford.edu/code.html (accessed on 6 February 2019).
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]


| Symbol | Definition |
|---|---|
| T | Decision period, h in this paper |
| Slot | |
| Duration of a slot, h in this paper | |
| Battery capacity | |
| Initial battery energy | |
| Residual battery energy at slot t | |
| Energy consumption for a single packet | |
| Harvested energy at slot t | |
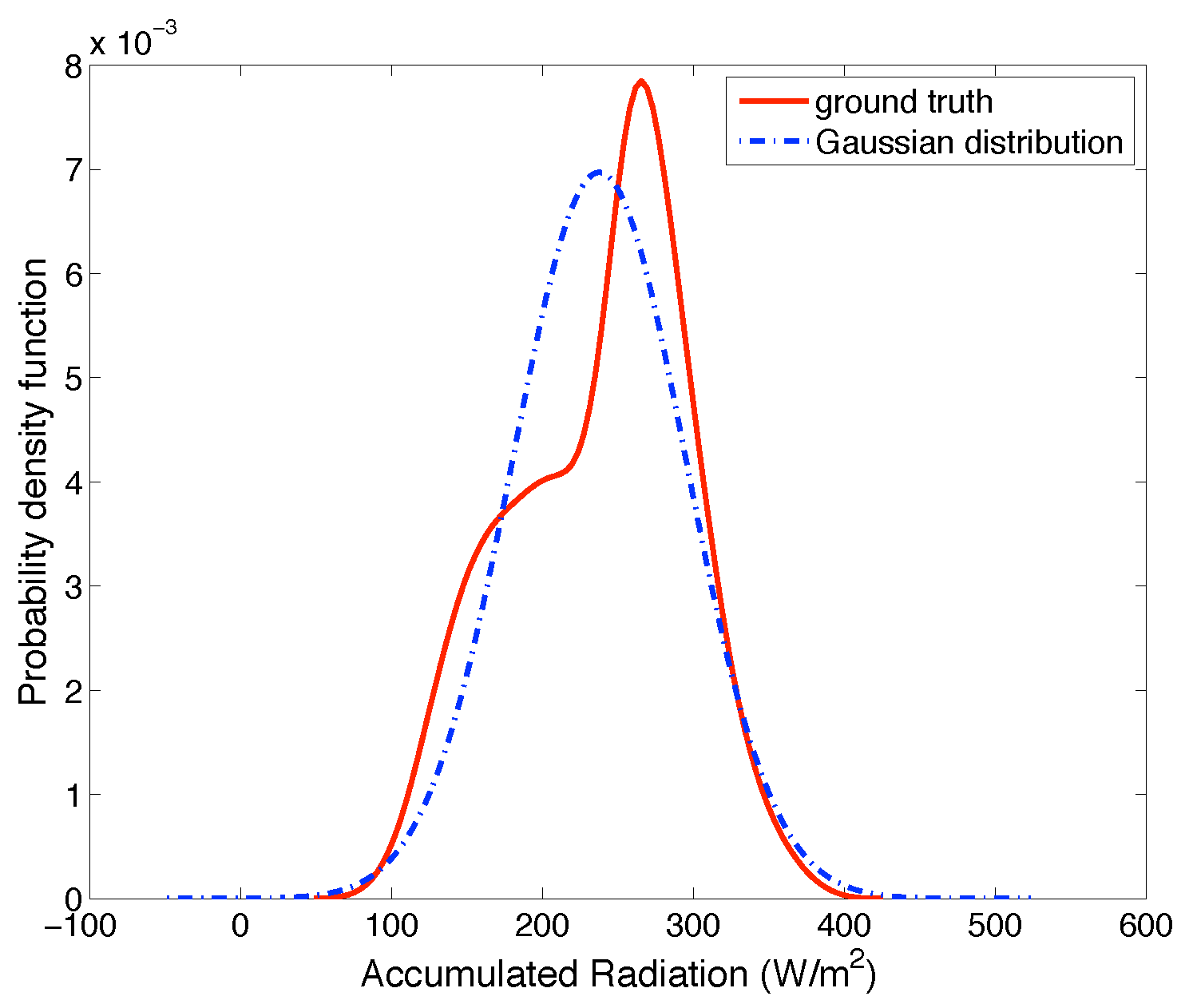
| Real-world distribution | |
| Gaussian distribution | |
| n | The number of high-resolution samples generated at each slot |
| The number of samples transmitted in slot t | |
| Transmission decision |
| a | b | c | |
|---|---|---|---|
| January | −25.88 | 12.61 | 592.21 |
| February | −21.87 | 12.50 | 738.19 |
| March | −23.89 | 12.70 | 818.22 |
| MSE | RSE | |
|---|---|---|
| EWMA | ||
| WF |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, J.; Chen, J.; Wang, R.; Zhuang, Y.; Zhang, B. A Robust Transmission Scheduling Approach for Internet of Things Sensing Service with Energy Harvesting. Sensors 2019, 19, 3090. https://doi.org/10.3390/s19143090
Hao J, Chen J, Wang R, Zhuang Y, Zhang B. A Robust Transmission Scheduling Approach for Internet of Things Sensing Service with Energy Harvesting. Sensors. 2019; 19(14):3090. https://doi.org/10.3390/s19143090
Chicago/Turabian StyleHao, Jie, Jing Chen, Ran Wang, Yi Zhuang, and Baoxian Zhang. 2019. "A Robust Transmission Scheduling Approach for Internet of Things Sensing Service with Energy Harvesting" Sensors 19, no. 14: 3090. https://doi.org/10.3390/s19143090
APA StyleHao, J., Chen, J., Wang, R., Zhuang, Y., & Zhang, B. (2019). A Robust Transmission Scheduling Approach for Internet of Things Sensing Service with Energy Harvesting. Sensors, 19(14), 3090. https://doi.org/10.3390/s19143090





