An Improved Time-Series Model Considering Rheological Parameters for Surface Deformation Monitoring of Soft Clay Subgrade †
Abstract
:1. Introduction
2. Time-Series Modeling Considering Rheological Parameters
2.1. Time-Series Deformation Model
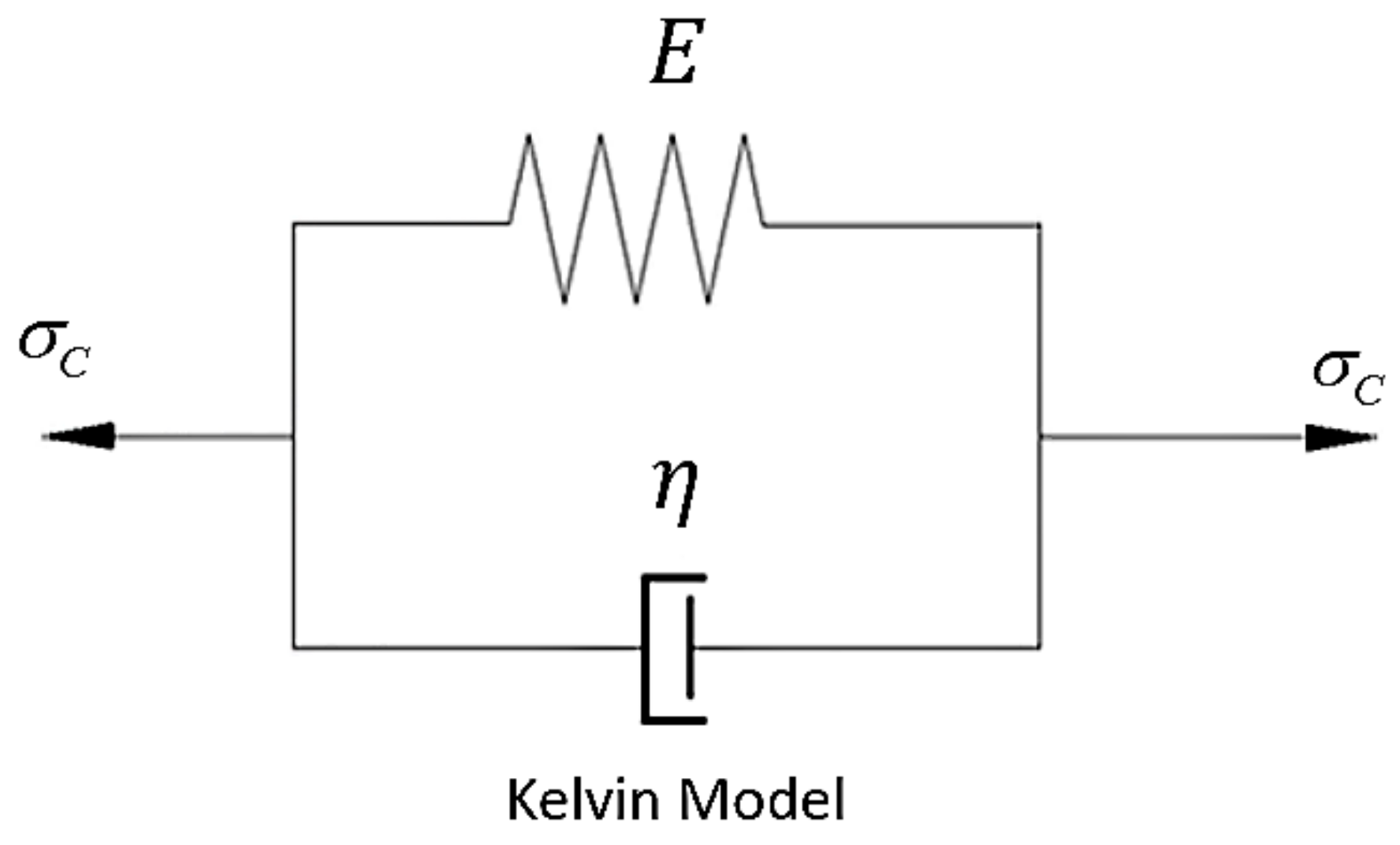
2.2. Rheological Model Based on the Kelvin Model
2.3. Improved Deformation Model Considering Rheological Parameters
2.4. Unknown Parameter Estimation
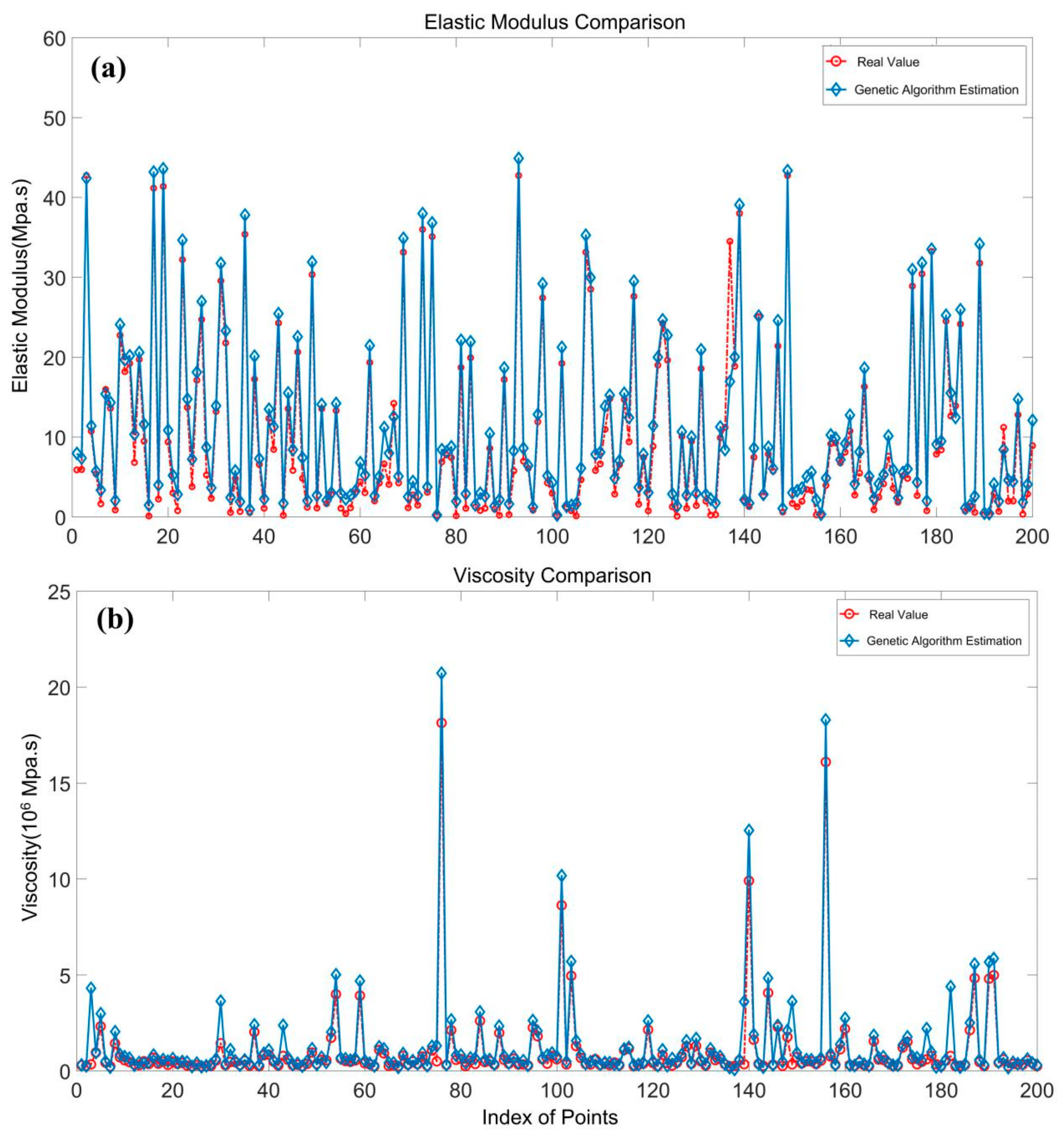
3. Simulated Experiment
4. Real Data Analysis
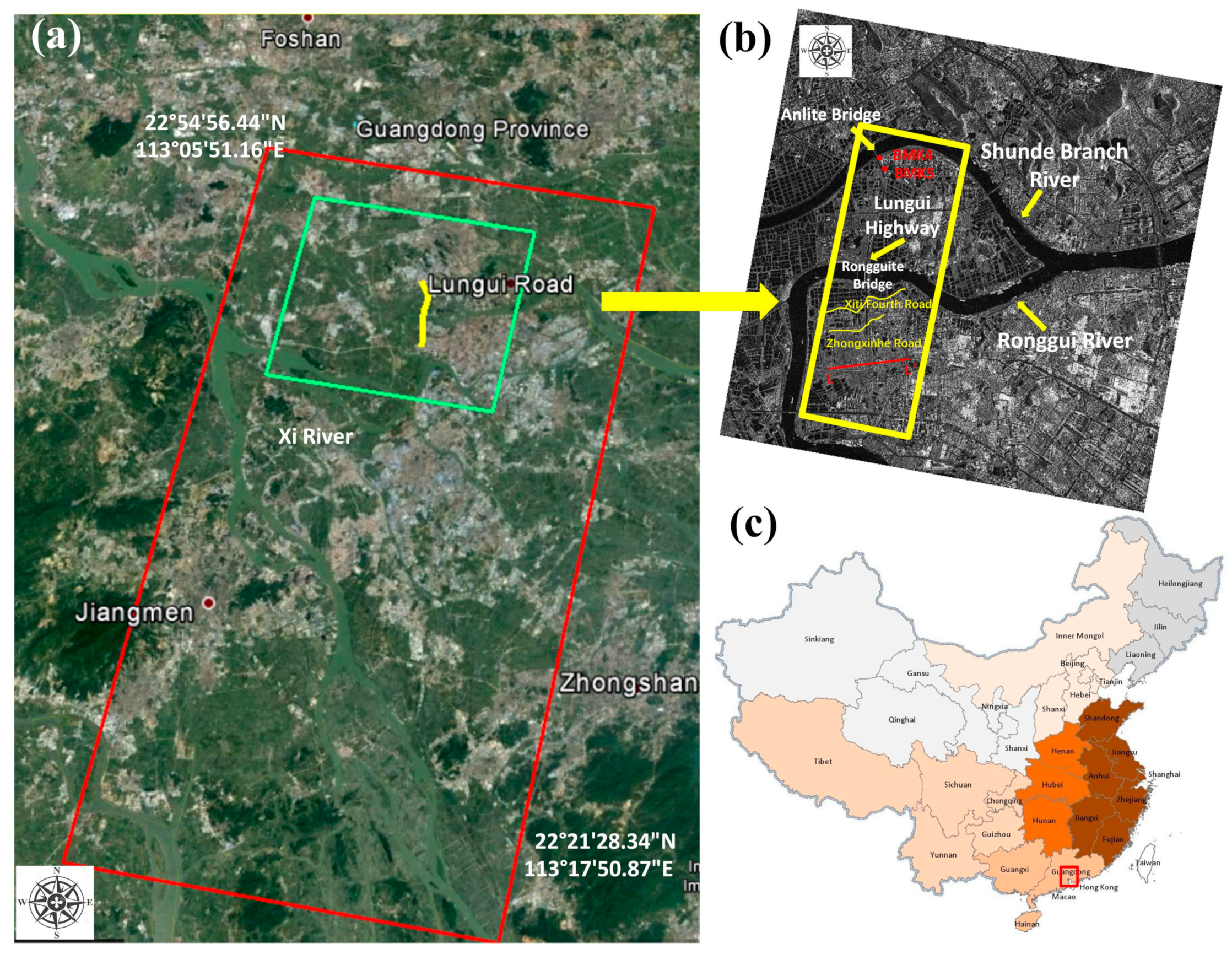
4.1. Geological Background of Study Area
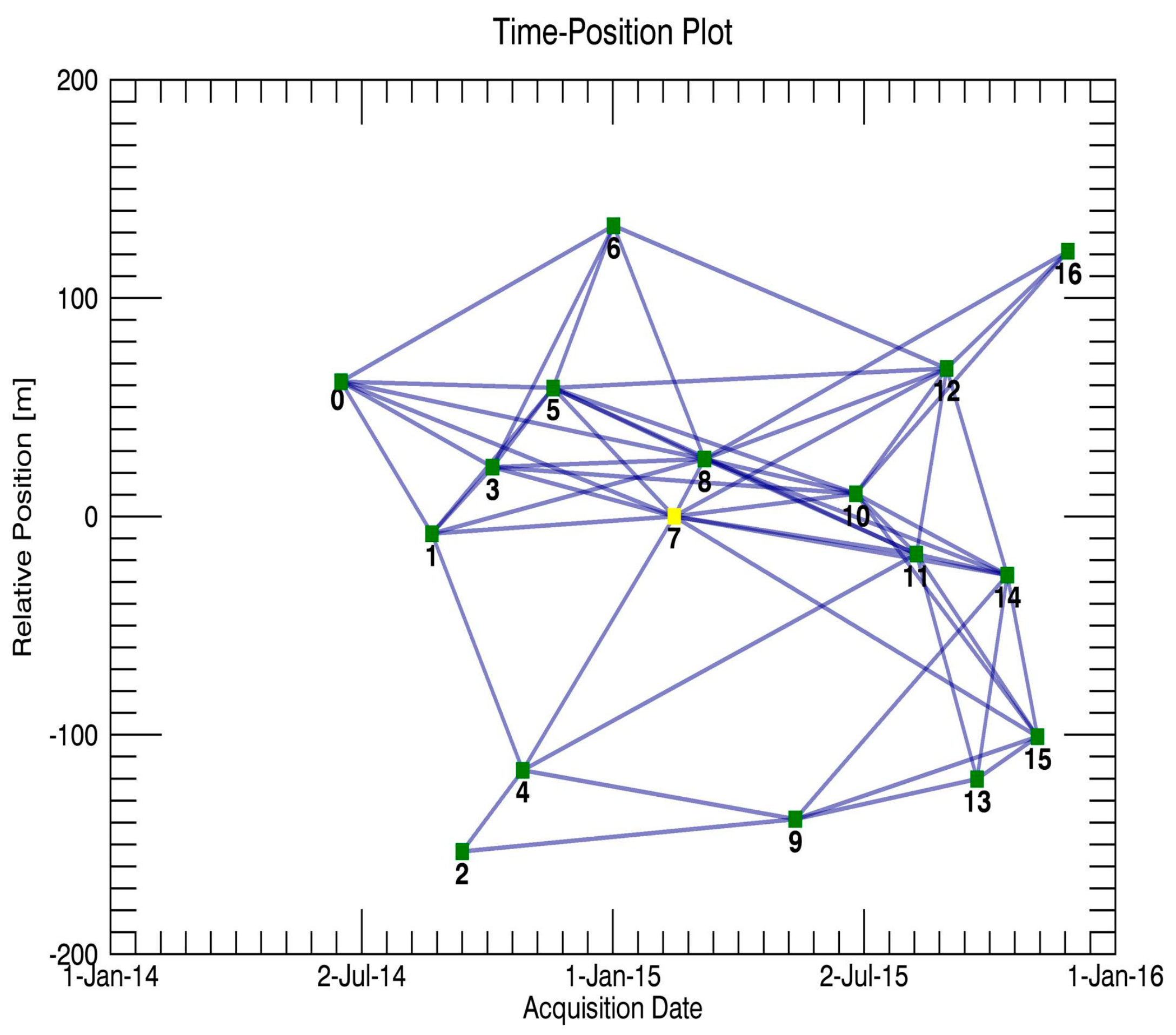
4.2. SAR Acquisition and Data Processing
4.3. Experimental Results
5. Discussions
5.1. Potential Reasons for the Deformation
- (1).
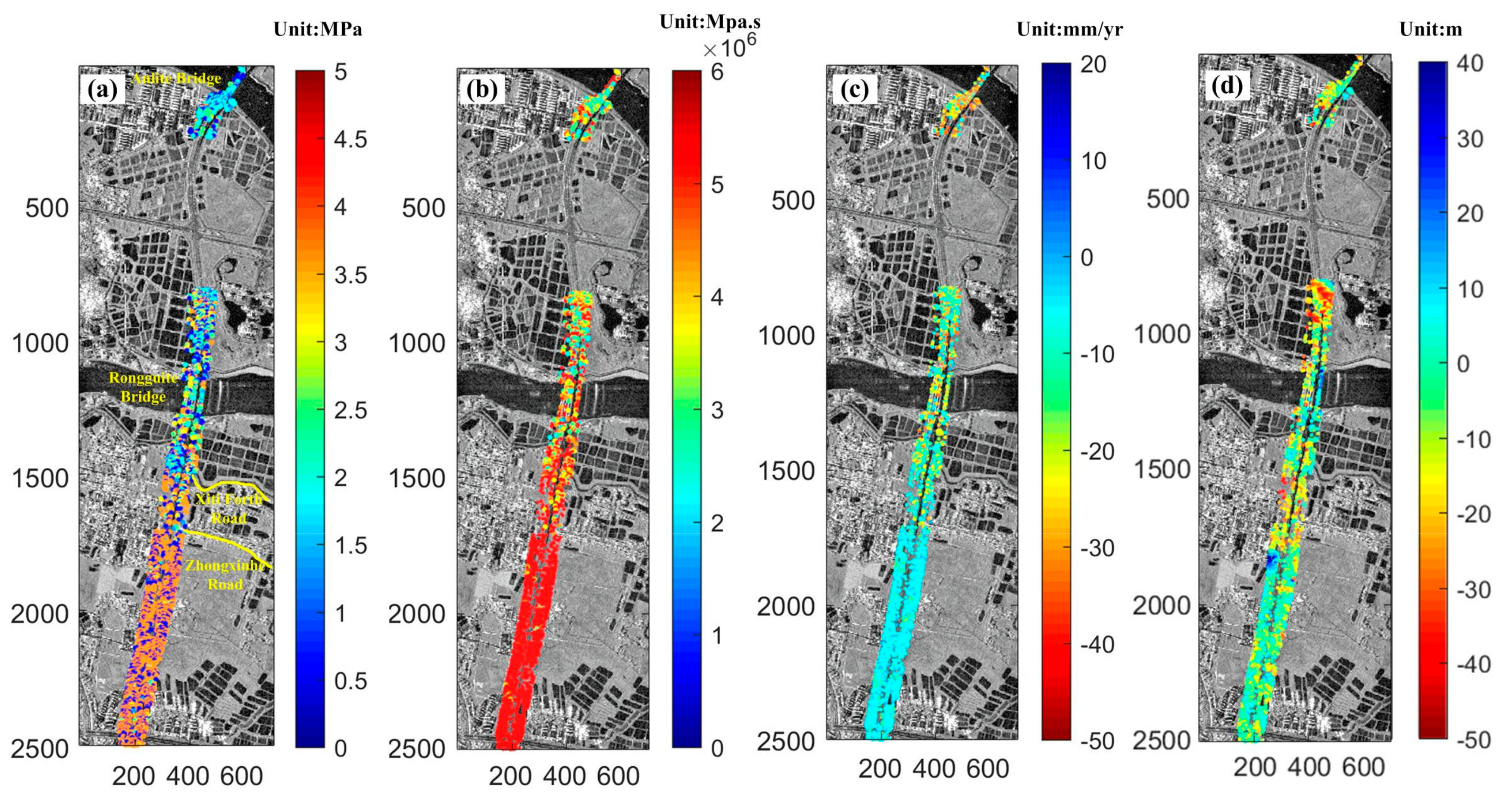
- The magnitude of the obtained elastic modulus and viscosity parameters reflect the aforementioned deformation characteristics. It can be obviously seen, from Figure 8 and Figure 9, that the bottom area was under a relatively stable deformation, with higher elastic modulus and viscosity values. Under the condition of unidirectional stress, the elastic modulus equals the stress divided by the strain along the direction [37]. As Equation (4) shows, deformation can be understood as a temporal integration of strain. Therefore, when the external load is constant, the stress can be considered a constant, and the higher the elastic modulus is, the lower the deformation performs. The physical parameter viscosity (also known as the viscosity coefficient) is a measure to describe the viscosity of a fluid, which is a demonstration of the fluid flow dynamics for its internal friction phenomenon [38]. Higher viscosity reflects greater friction in fluid. In this paper, viscosity is treated as the parameter that reflects the internal friction property of soil mass and its ability to resist deformation. The higher the value of the viscosity, the greater the friction resistance between the soil mass is and, thus, less strain and deformation. This is the key reason why the areas with low deformation showed a higher magnitude of elastic modulus and viscosity.
- (2).
- As described in Section 4.1, with densely distributed ponds around the upper stretch of the highway, mucky clay and silt dominated the geological content of the clay, and the soft soil layer of the upper segment was relatively thicker (with a thickness of 12.93–19.50 m). In addition, the water system around this stretch was well-developed and, thus, the ground subsidence was more obvious. In contrast, the areas below Zhongxinhe Road in the image were mainly urban districts, where the silt content in the soil of the road foundation was lower, with mealy sand and silty clay as the dominant geotechnical content. Furthermore, compared to the upper stretch of the highway, the average thickness of the soft soil layer was only 3.57–7.62 m, with a lower water discharge flow under the surface and an advanced drainage system in the urban areas. As a result, the settlement was much weaker.
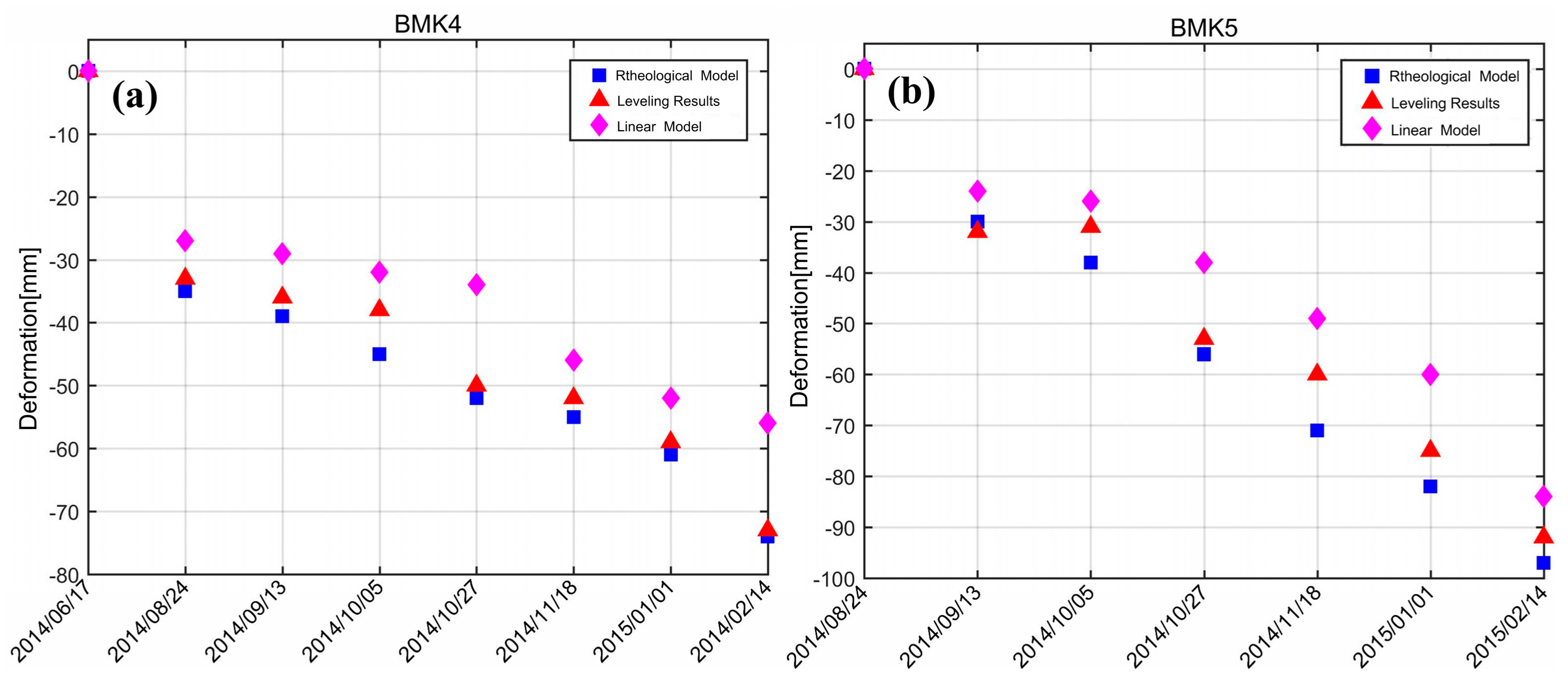
5.2. Temporal Deformation Characteristics over Feature Points
- (1).
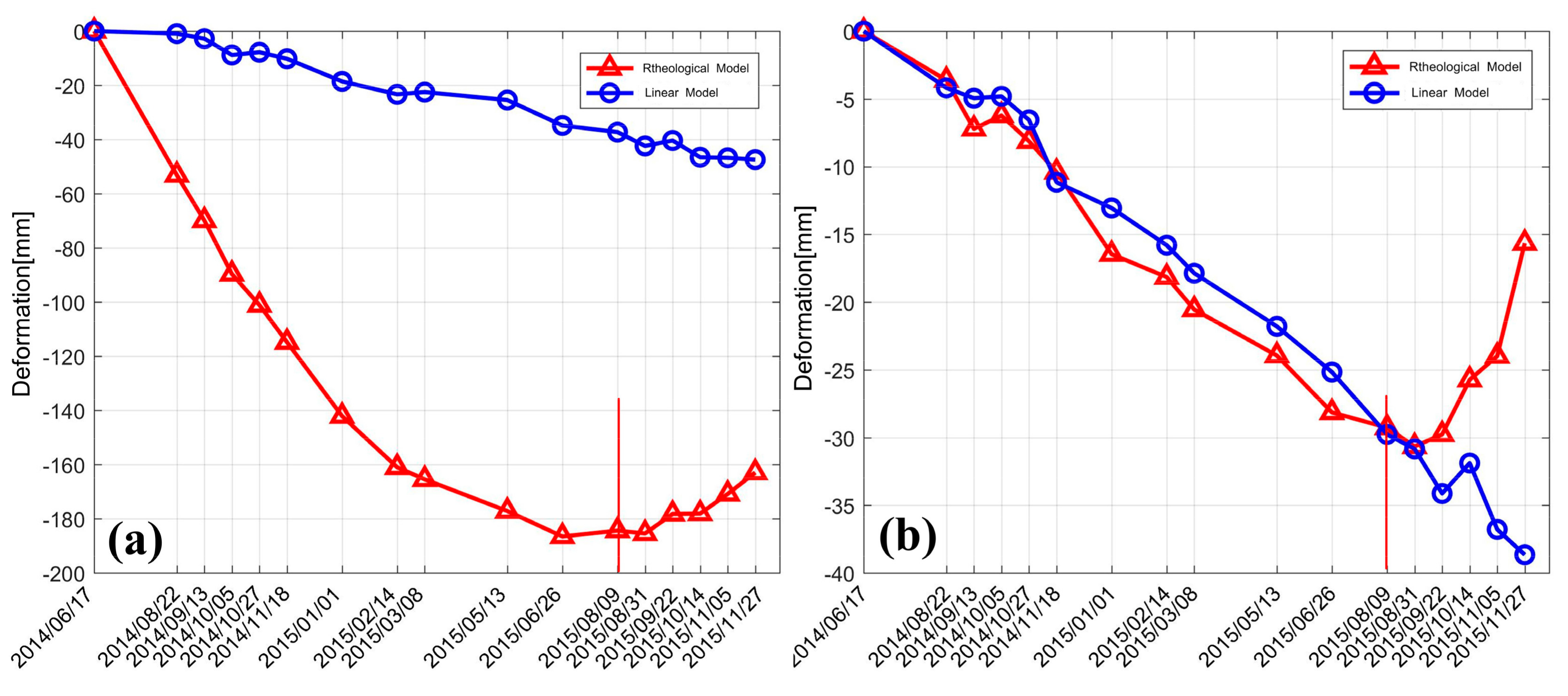
- Soft clay has the property of mellow soil, large natural water content, and high compressibility. During the period of June 2014 to June 2015, under the conditions of constant external load, the void between the soil mass was being compressed and the inner water was being released; thus, the deformation during this period was characterized as obvious subsidence with a decreasing velocity.
- (2).
- Second, as discussed in Section 4.2, a stretch in the middle of the test highway was still undergoing road surfacing from June 2014 to November 2014, and compaction of the soft soil layer in the middle section may have accelerated the subsidence phenomena in nearby stretches.
- (3).
- With the passage of time, when the natural compression of the soil reaches its limit and the porosity ratio drops to the minimum, the deformation caused by the early external load and extravasation of the inner water in the soft soil ceases. Consequently, the subsequent deformation was mainly affected by external environmental factors. According to precipitation data provided by the Fuoshan Meteorological Bureau, the annual precipitation in 2015 was 2055.2 mm, 20% higher than previous years. The spatial and temporal distributions of annual precipitation were extremely asymmetric, being three or four times higher in October and December. Extreme weather events, such as thunderstorms, wind, hail, and tornadoes occurred frequently, and disasters induced by rainstorms and typhoons were obvious. Under the combined influence of high trough and low vortex, continuous precipitation had occurred in the city from 27 August 2015. The average rainfall amount was 127.3 mm in Fuoshan city, with 100–250 mm recorded at 65% of the automatic stations, and 250 mm at Shunde automatic station [39]. Due to the increase of rainfall, both water content and discharge in the water system correspondingly increased. With accelerated flow speed, perched ground water in the upper layer of the subgrade increased due to the impact of rainfall and the supply from the surrounding water system. This is the key reason we suppose as the cause of the subsidence recovery that occurred from August 2015.
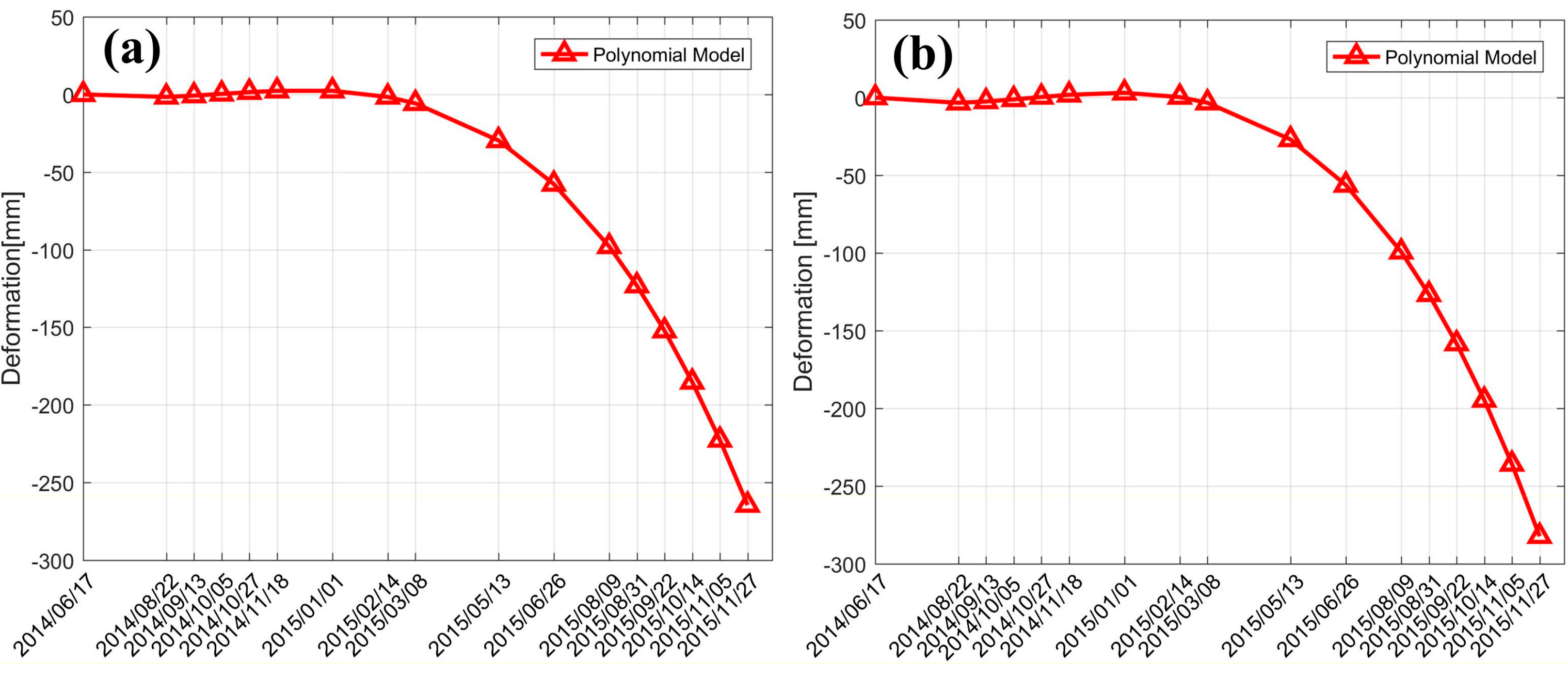
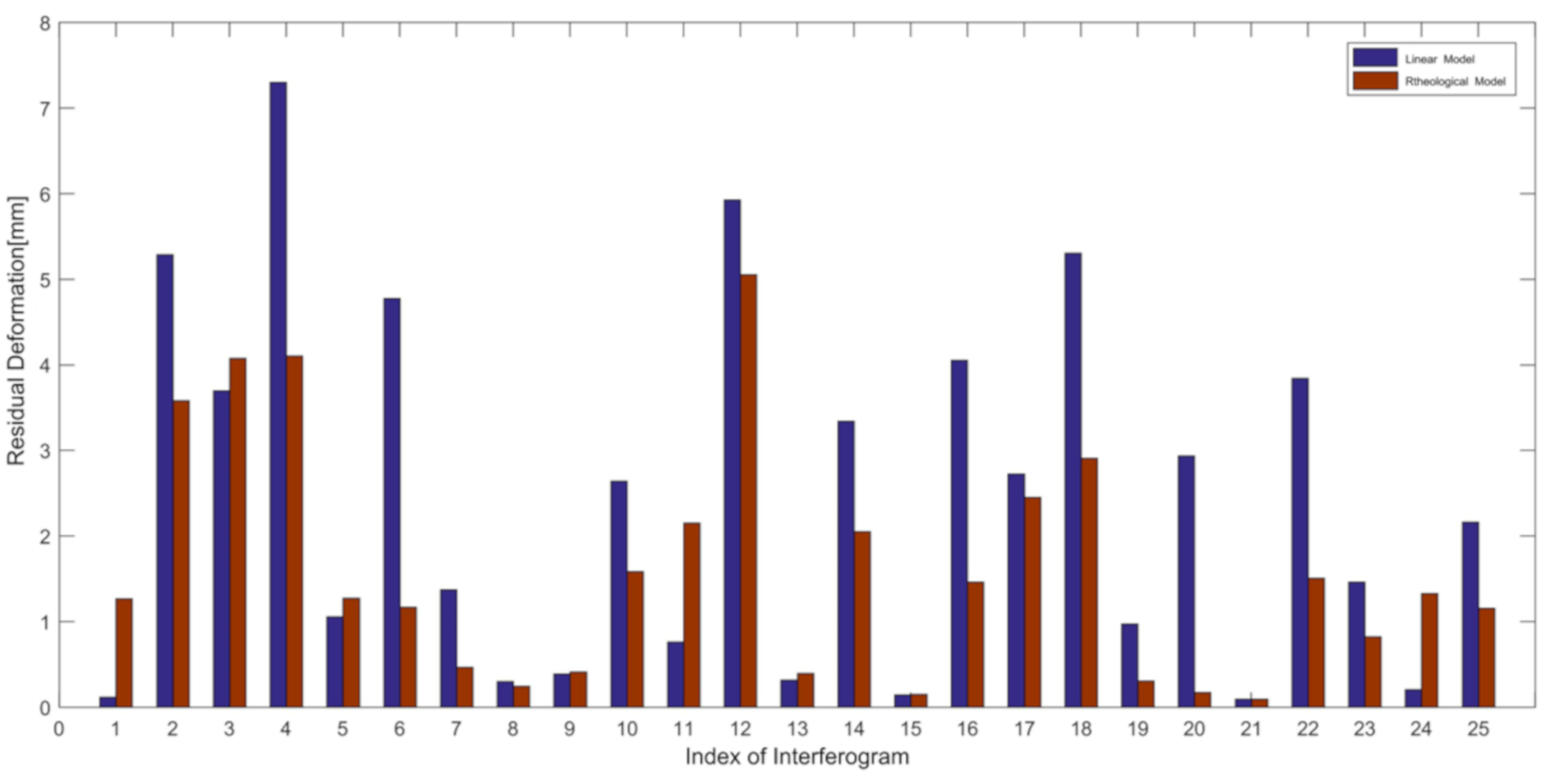
5.3. Comparative Analysis with other Non-Linear Time-Series Models
5.4. Accuracy Evaluation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xue, X.; Song, L.; Jia, L.; Le, Y.; Ge, H. New prediction method for postconstruction settlement of soft-soil roadbed of expressway. Chin. J. Geotech. Eng. 2011, 33, 125–130. [Google Scholar]
- Zhang, J.; Peng, J.; Zheng, J.; Yao, Y. Characterisation of stress and moisture-dependent resilient behaviour for compacted clays in south china. Road Mater. Pavement Des. 2018, 1–14. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic: New York, NY, USA, 2001. [Google Scholar]
- Zebker, H.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.J. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Z.; Ding, X.; Jung, H.S.; Feng, G.; Lee, C.W. Mapping ground surface deformation using temporarily coherent point SAR interferometry: Application to Los Angeles Basin. Remote Sens. Environ. 2012, 117, 429–439. [Google Scholar] [CrossRef]
- Hu, X.; Oommen, T.; Lu, Z.; Wang, T.; Kim, J.W. Consolidation settlement of Salt Lake County tailings impoundment revealed by time-series InSAR observations from multiple radar satellites. Remote Sens. Environ. 2017, 202, 199–209. [Google Scholar] [CrossRef]
- Zhu, J.; Li, Z.; Hu, J. Research progress and methods of InSAR for deformation monitoring. Acta Geod. Cartogr. Sin. 2017, 46, 1717–1733. [Google Scholar]
- Lin, H.; Ma, P.; Wang, W. Urban infrastructure health monitoring with spaceborne aperture radar interferometry. Acta Geod. Cartogr. Sin. 2017, 46, 1421–1433. [Google Scholar]
- Qin, X.; Yang, M.; Wang, H.; Yang, T.; Lin, J.; Liao, M. Application of high-resolution PS-InSAR in deformation characteristics probe of urban rail transit. Acta Geod. Cartogr. Sin. 2016, 45, 713–721. [Google Scholar]
- Tapete, D.; Morelli, S.; Fanti, R.; Casagli, N. Localizing deformation along the elevation of linear structures: An experiment with space-borne InSAR and RTK GPS on the Roman aqueducts in Rome, Italy. Appl. Geogr. 2015, 58, 65–83. [Google Scholar] [CrossRef]
- Lazecky, M.; Perissin, D.; Bakon, M.; De Sousa, J.M.; Hlavacova, I.; Real, N. Potential of satellite InSAR techniques for monitoring of bridge deformations. In Proceedings of the 2015 IEEE Joint Urban Remote Sensing Event (JURSE), Lausanne, Switzerland, 30 March–1 April 2015; pp. 1–4. [Google Scholar]
- Dong, S.; Samsonov, S.; Yin, H.; Ye, S.; Cao, Y. Time-series analysis of subsidence associated with rapid urbanization in Shanghai, China measured with SBAS InSAR method. Environ. Earth Sci. 2014, 72, 677–691. [Google Scholar] [CrossRef]
- Yu, B.; Liu, G.; Li, Z.; Zhang, R.; Jia, H.; Wang, X.; Cai, G. Subsidence detection by TerraSAR-X interferometry on a network of natural persistent scatterers and artificial corner reflectors. Comput. Geosci. 2013, 58, 126–136. [Google Scholar] [CrossRef]
- Xing, X.M.; Wen, D.; Chang, H.C.; Chen, L.F.; Yuan, Z.H. Highway deformation monitoring based on an integrated CRInSAR algorithm—Simulation and real data validation. Int. J. Pattern Recognit. Artif. Intell. 2018, 32, 1850036. [Google Scholar] [CrossRef]
- Dai, K.; Liu, G.; Li, Z.; Ma, D.; Wang, X.; Zhang, B.; Tang, J.; Li, G. Monitoring highway stability in permafrost regions with x-band temporary scatterers stacking InSAR. Sensors 2018, 18, 1871. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Yang, T.; Yang, M.; Zhang, L.; Liao, M. Health diagnosis of major transportation infrastructures in Shanghai metropolis using high-resolution persistent scatterer interferometry. Sensors 2017, 17, 2770. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, Y.; Jin, M.; Jing, Y.; Liu, Y.; Wei, S.; Wei, J.; Chen, Y. Monitoring land subsidence in Wuhan city (China) using the SBAS-InSAR method with radarsat-2 imagery data. Sensors 2019, 19, 743. [Google Scholar] [CrossRef] [PubMed]
- Cusson, D.; Trischuk, K.; Hébert, D.; Hewus, G.; Gara, M.; Ghuman, P. Satellite-based InSAR monitoring of highway bridges—Validation case study on the north-channel bridge in Ontario, Canada. Transp. Res. Rec. J. Trans. Res. Board 2018, 2672, 76–86. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514, 1–13. [Google Scholar] [CrossRef]
- Li, S.S.; Li, Z.W.; Hu, J.; Sun, Q.; Yu, X.Y. Investigation of the seasonal oscillation of the permafrost over Qinghai-Tibet plateau with SBAS-InSAR algorithm. Chin. J. Geophys. 2013, 56, 1476–1486. [Google Scholar]
- Xing, X.M.; Zhu, J.; Wang, Y.; Yang, Y. Time series ground subsidence inversion in mining area based on CRInSAR and PSInSAR integration. J. Cent. South Univ. 2013, 20, 2498–2509. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, H.a.; Sun, G. Deformation model of time series interferometric SAR techniques. Acta Geod. Cartogr. Sin. 2012, 41, 864–869. [Google Scholar]
- Hetland, E.; Musé, P.; Simons, M.; Lin, Y.; Agram, P.; DiCaprio, C. Multiscale InSAR time series (MINTS) analysis of surface deformation. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Huang, Y. Research on the Settlement of Embankment and Mechanism of Pavement for Freeway; Central South University: Changsha, China, 2010. [Google Scholar]
- Zhao, W.; Shi, J. Consolidation and Rtheology for Soft Clay; Hohao University Press: Nanjing, China, 1996. [Google Scholar]
- Huang, M. Highway Engineering Materials Rheology; Southwest Jiaotong University Press: Chengdu, China, 2010. [Google Scholar]
- You, S.; Zhang, Z.; Hongguang, J.I. A thermodynamic constitutive model for creep behavior of rocks and its application. J. Univ. Min. Technol. 2016, 45, 507–513. [Google Scholar]
- Zhao, R.; Li, Z.; Feng, G.; Wang, Q.; Hu, J. Monitoring surface deformation over permafrost with an improved SBAS-InSAR algorithm: With emphasis on climatic factors modeling. Remote Sens. Environ. 2016, 184, 276–287. [Google Scholar] [CrossRef]
- Liu, L.; Yan, Q.; Sun, H. Study on model of rheological property of soft clay. Rock Soil Mech. 2006, 27, 214–217. [Google Scholar]
- Tian, Y. Genetic Algorithms Research Based on Nonlinear Least Squares Estimation; Wuhan University: Wuhan, China, 2003. [Google Scholar]
- Yang, Z.; Li, Z.; Zhu, J.; Yi, H.; Hu, J.; Feng, G. Deriving dynamic subsidence of coal mining areas using InSAR and logistic model. Remote Sens. 2017, 9, 125. [Google Scholar] [CrossRef]
- Li, T. Deformation Monitoring by Multi-Temporal InSAR with Both Point and Distributed Scatterers; Southwest Jiaotong University: Chengdu, China, 2014. [Google Scholar]
- Costantini, M.; Rosen, P.A. A Generalized Phase Unwrapping Approach for Sparse Data. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Hamburg, Germany, 28 June–2 July 1999. [Google Scholar]
- Shi, S. Shear strength, modulus of rigity and young’s modulus of concrete. China Civil Engin. J. 1999, 32, 47–52. [Google Scholar]
- Xiangjun, F. Viscosity (rigidity coefficient) of high concentration turbid water. J. Hydraul. Eng. 1982, 3, 59–65. [Google Scholar]
- Main Climatic Characteristics and Typical Weather Event of Fuoshan. Available online: www.fs121.com/foreportinfo.aspx?Id=132832 (accessed on 1 December 2016).



| Rheological Parameters | (m) | |||
|---|---|---|---|---|
| RMSE | ±1.5870 (3.5%) | ±0.1741 (0.8%) | ±3.5 (1.3%) | ±0.29 (5.4%) |
| Image No. | Acquisition Date (yyyy/mm/dd) | Normal Baseline (m) | Temporal Baseline (Days) |
|---|---|---|---|
| 1 | 2014/06/17 | −71.50 | 198 |
| 2 | 2014/08/22 | −137.97 | 132 |
| 3 | 2014/09/13 | −286.33 | 110 |
| 4 | 2014/10/05 | −110.85 | 88 |
| 5 | 2014/10/27 | −249.06 | 66 |
| 6 | 2014/11/18 | −74.56 | 44 |
| 7 | 2015/01/01 | 0 | 0 |
| 8 | 2015/02/14 | −133.14 | 44 |
| 9 | 2015/03/08 | −106.99 | 66 |
| 10 | 2015/05/13 | −271.51 | 132 |
| 11 | 2015/06/26 | −122.85 | 176 |
| 12 | 2015/08/09 | −149.22 | 220 |
| 13 | 2015/08/31 | −65.63 | 242 |
| 14 | 2015/09/22 | −253.29 | 264 |
| 15 | 2015/10/14 | −159.34 | 286 |
| 16 | 2015/11/05 | −233.83 | 308 |
| 17 | 2015/11/27 | −11.87 | 330 |
| BMK4 | BMK5 | RMSE | |
|---|---|---|---|
| Linear velocity model | ±10.3 | ±11.0 | ±10.7 |
| Rheological model | ±3.4 | ±6.5 | ±5.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, X.; Chen, L.; Yuan, Z.; Shi, Z. An Improved Time-Series Model Considering Rheological Parameters for Surface Deformation Monitoring of Soft Clay Subgrade. Sensors 2019, 19, 3073. https://doi.org/10.3390/s19143073
Xing X, Chen L, Yuan Z, Shi Z. An Improved Time-Series Model Considering Rheological Parameters for Surface Deformation Monitoring of Soft Clay Subgrade. Sensors. 2019; 19(14):3073. https://doi.org/10.3390/s19143073
Chicago/Turabian StyleXing, Xuemin, Lifu Chen, Zhihui Yuan, and Zhenning Shi. 2019. "An Improved Time-Series Model Considering Rheological Parameters for Surface Deformation Monitoring of Soft Clay Subgrade" Sensors 19, no. 14: 3073. https://doi.org/10.3390/s19143073
APA StyleXing, X., Chen, L., Yuan, Z., & Shi, Z. (2019). An Improved Time-Series Model Considering Rheological Parameters for Surface Deformation Monitoring of Soft Clay Subgrade. Sensors, 19(14), 3073. https://doi.org/10.3390/s19143073




