A Fiber Bragg Grating Sensing Structure for the Design, Simulation and Stress Strain Monitoring of Human Puncture Surgery
Abstract
1. Introduction
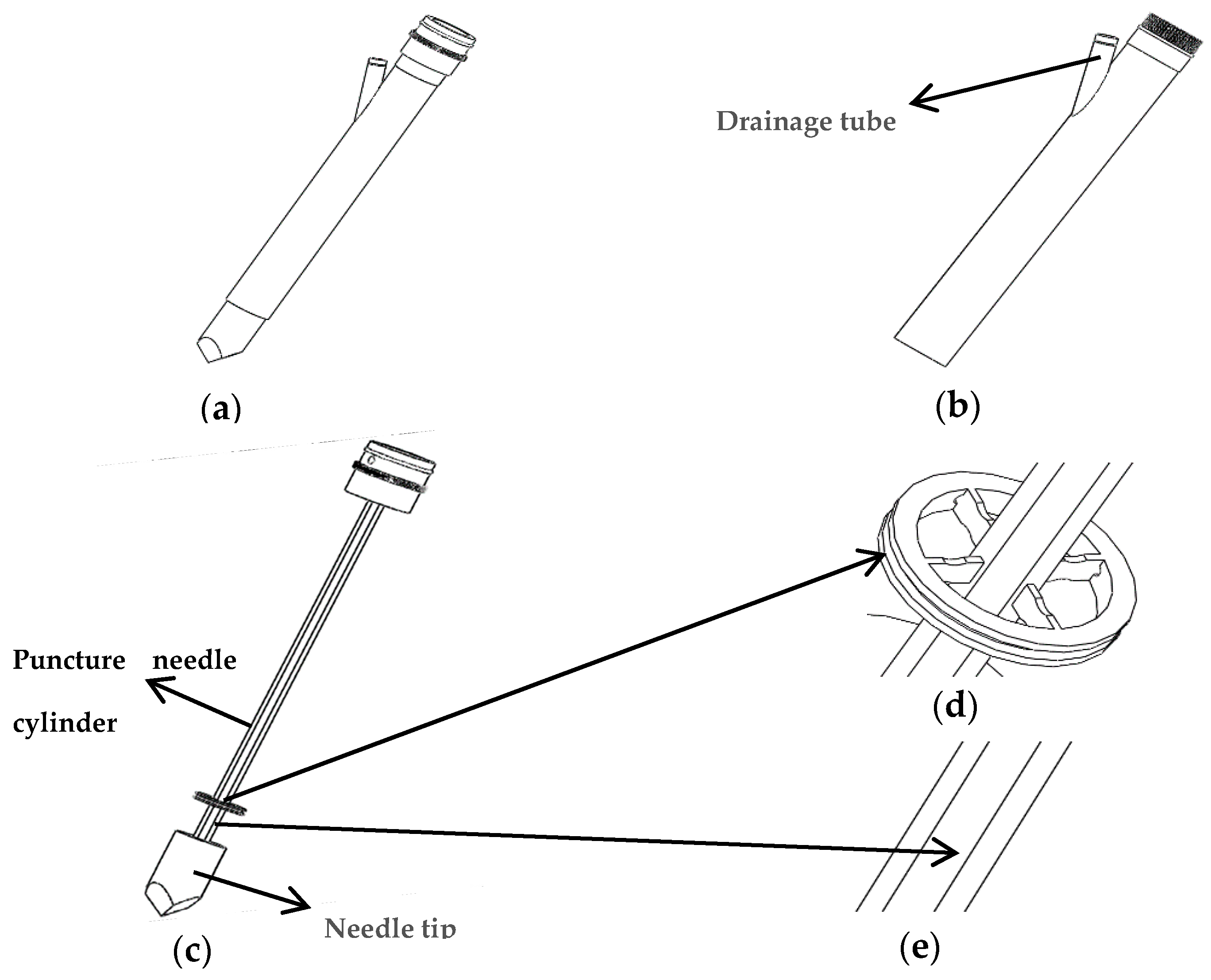
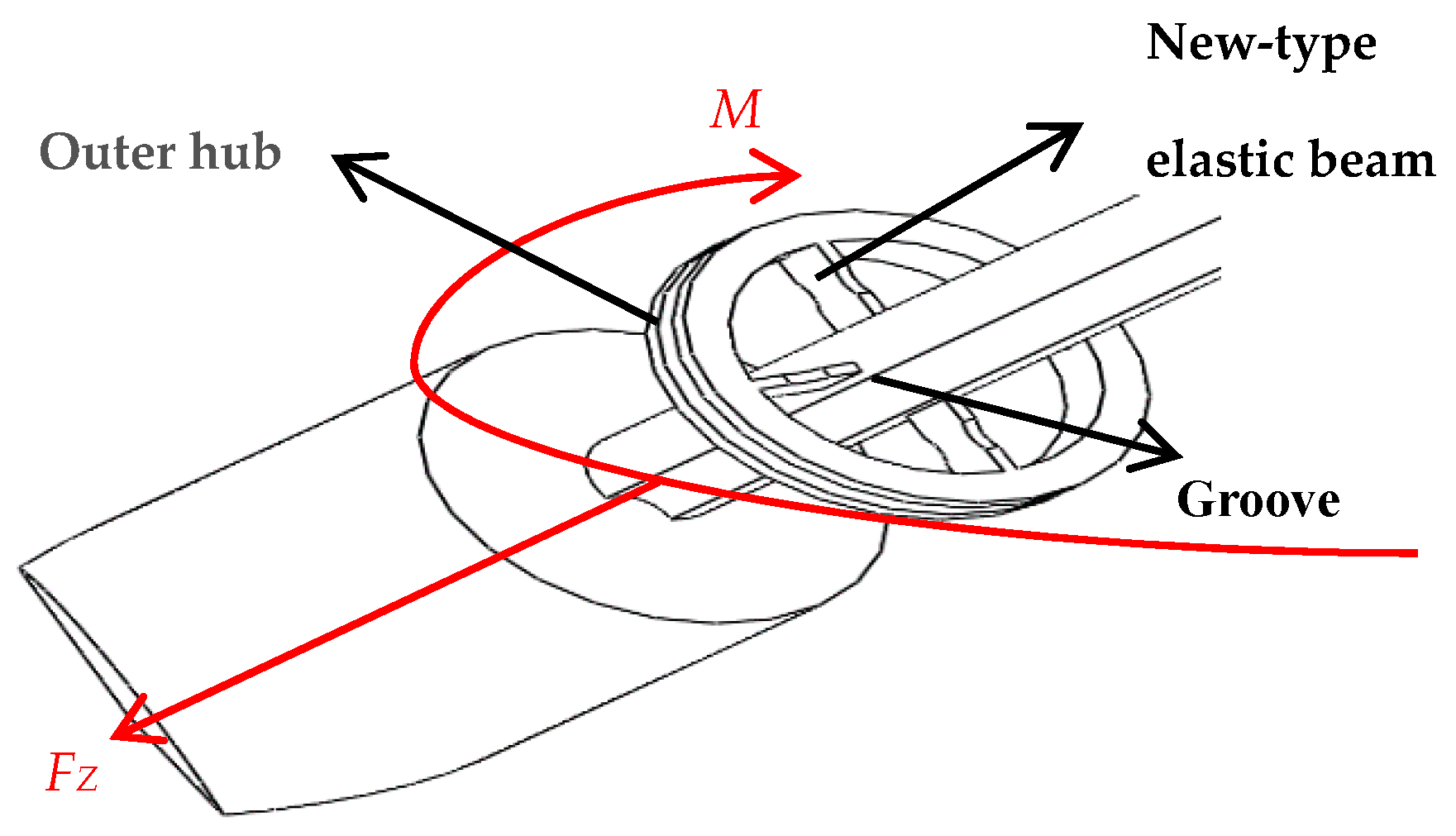
2. Structure Design of New-Type Puncturing Needle
3. Simulation and Implementation
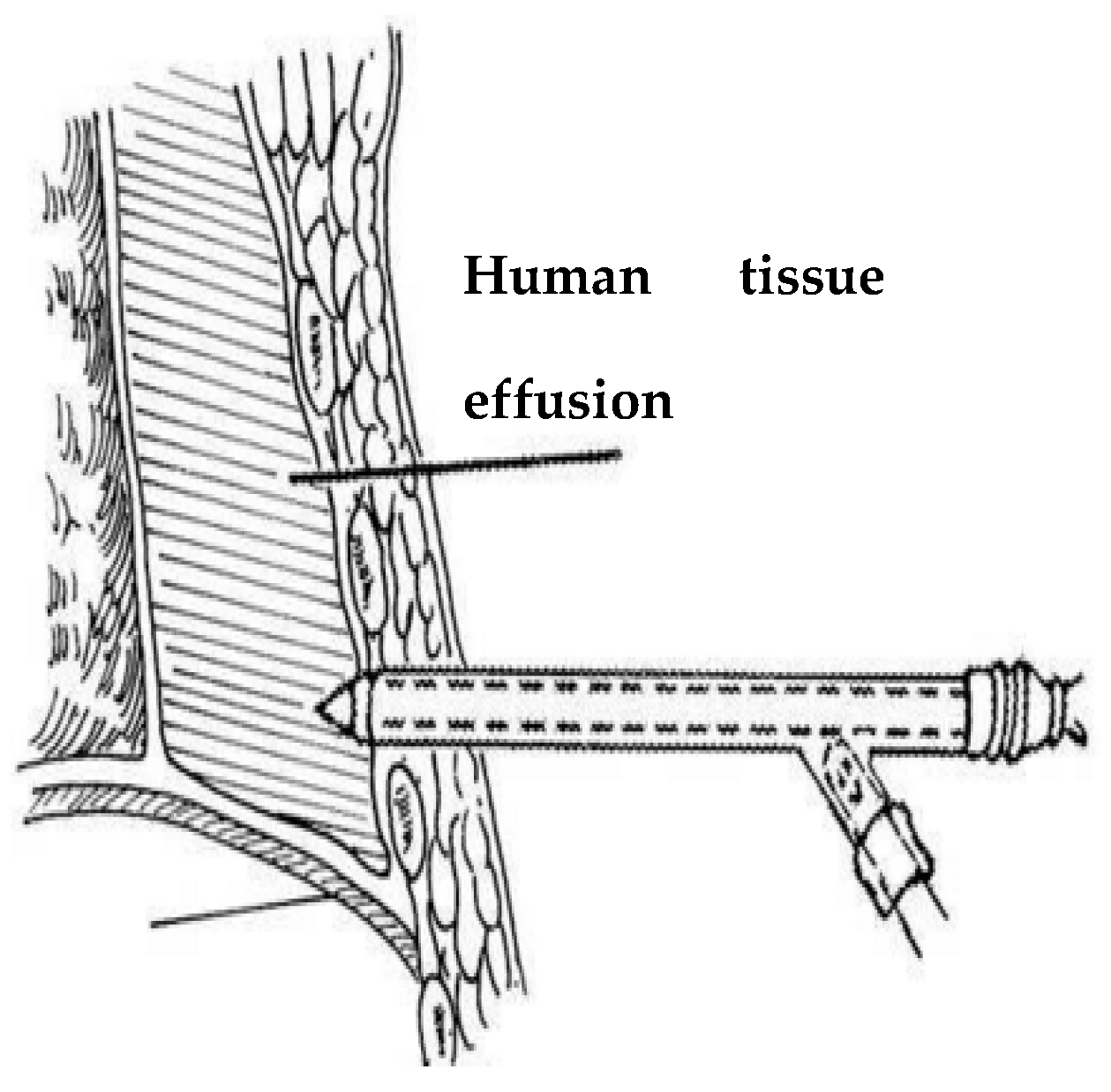
3.1. Principle of Operation
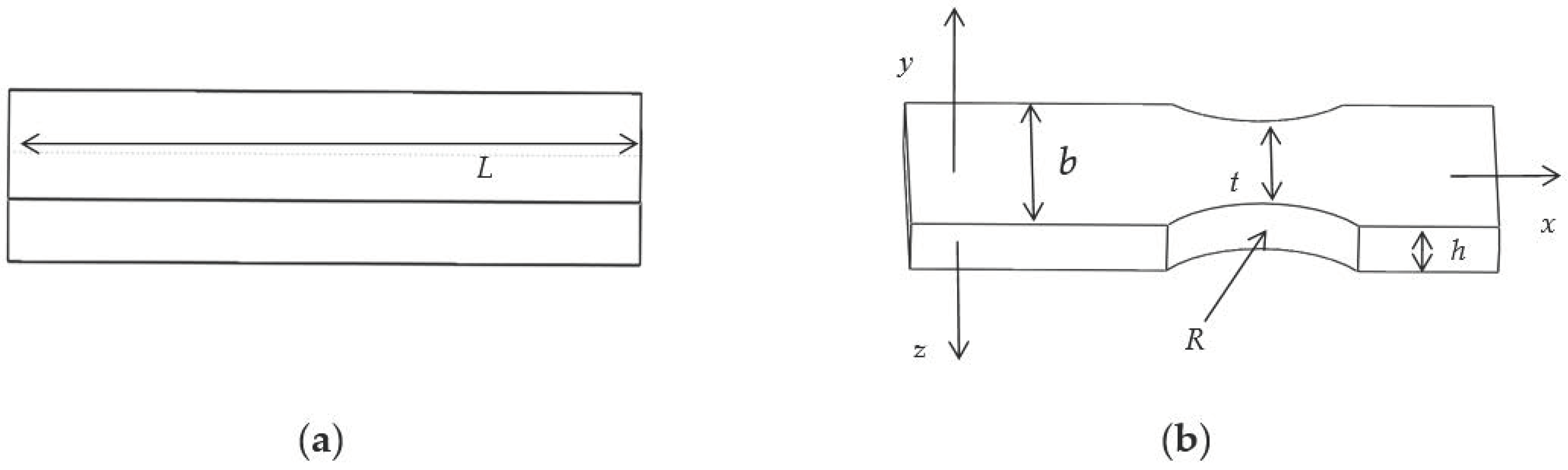
3.2. Force Simulation Analysis
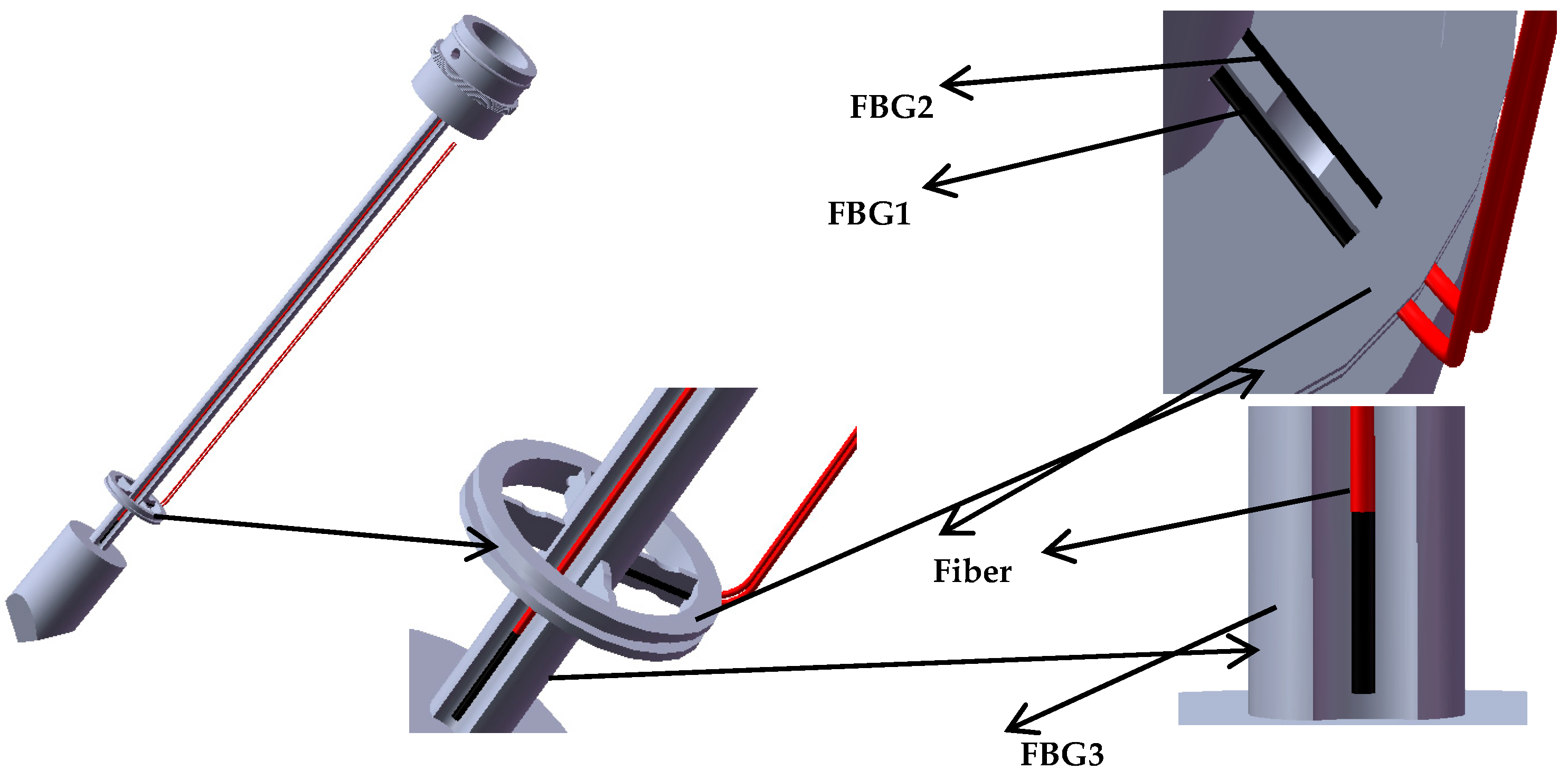
3.3. The FBG Sensor Paste
4. Calibration and Experiments
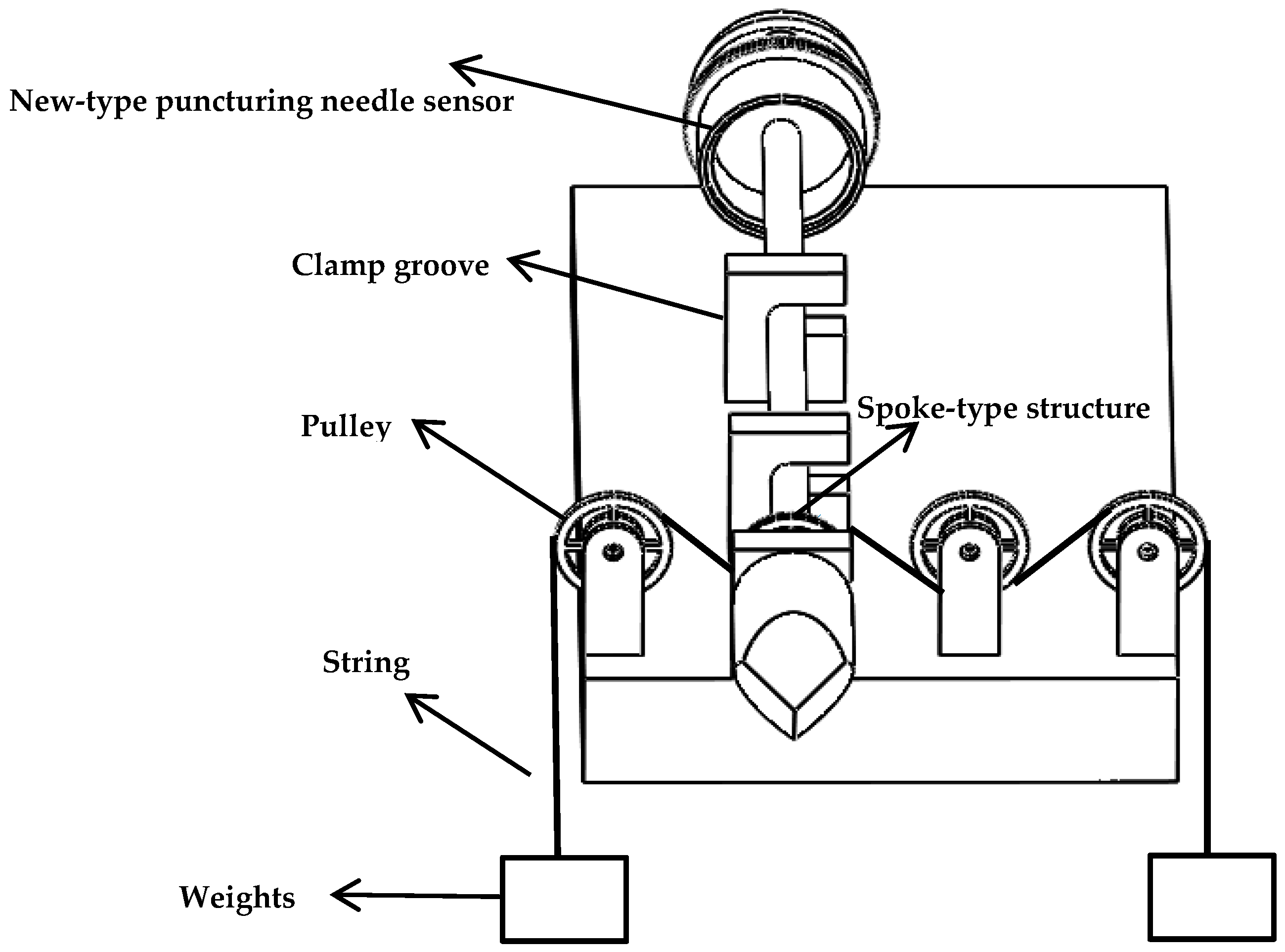
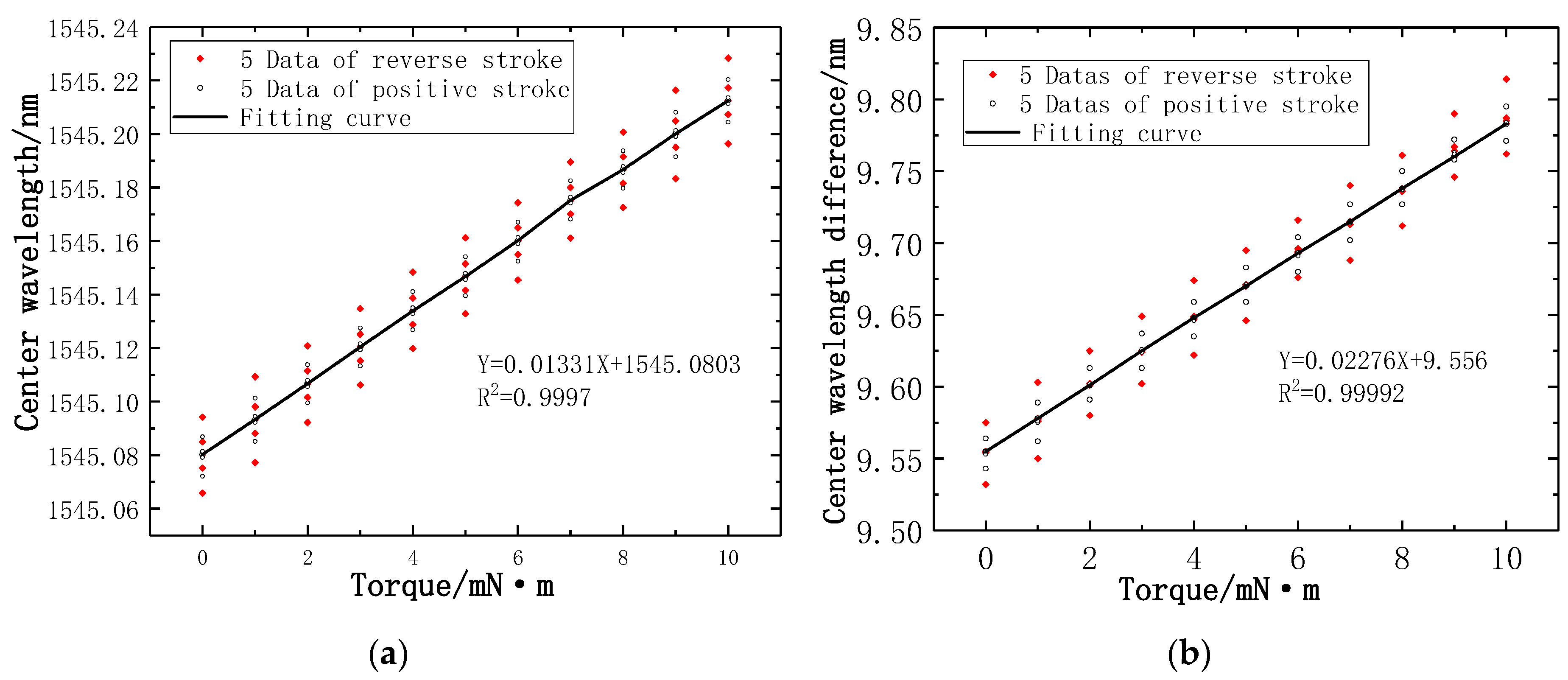
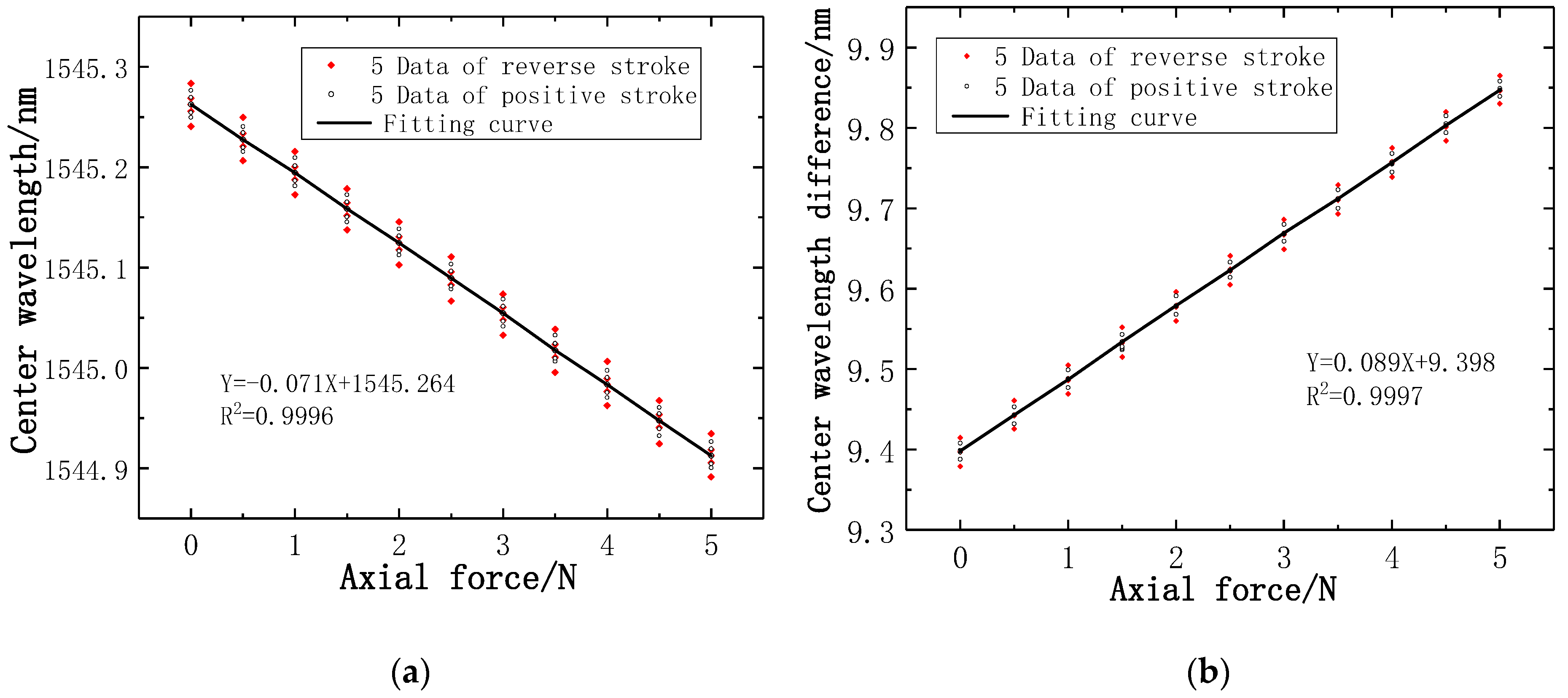
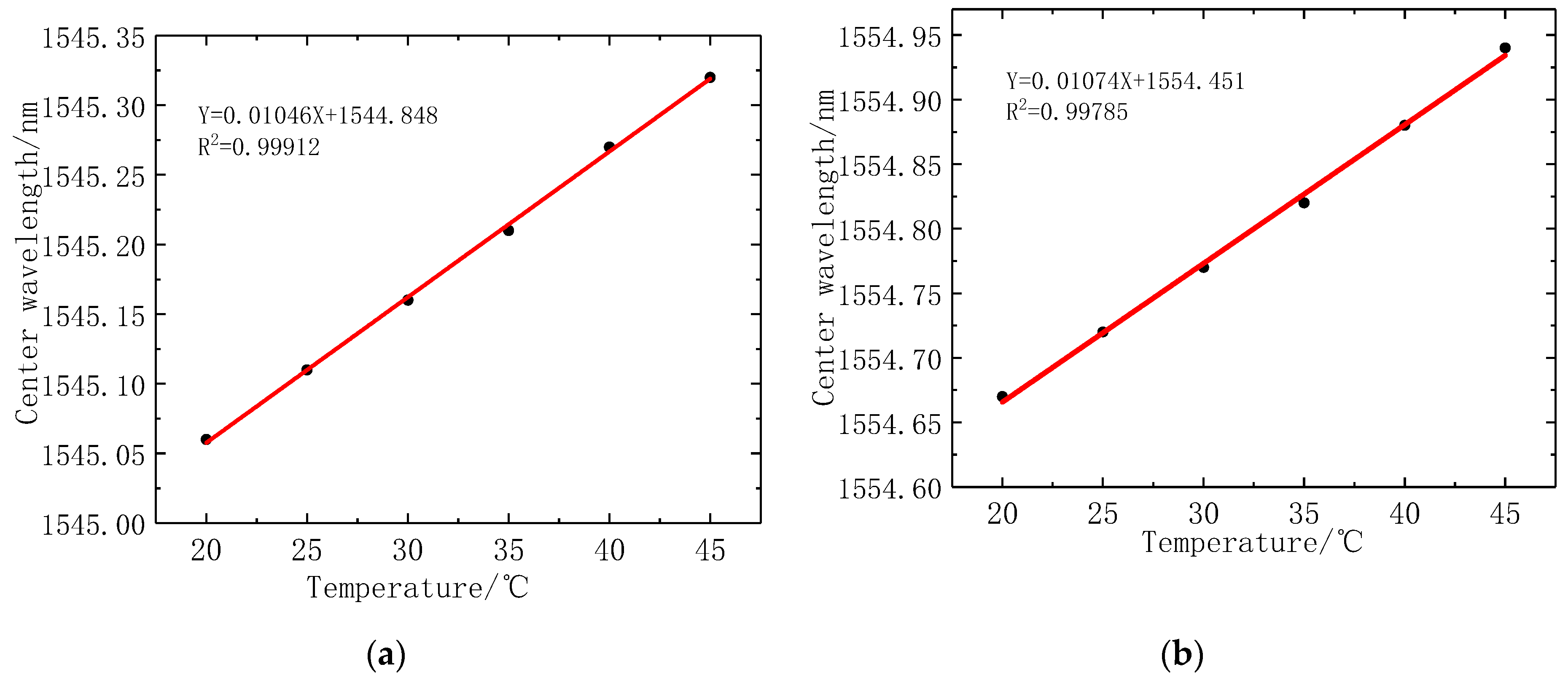
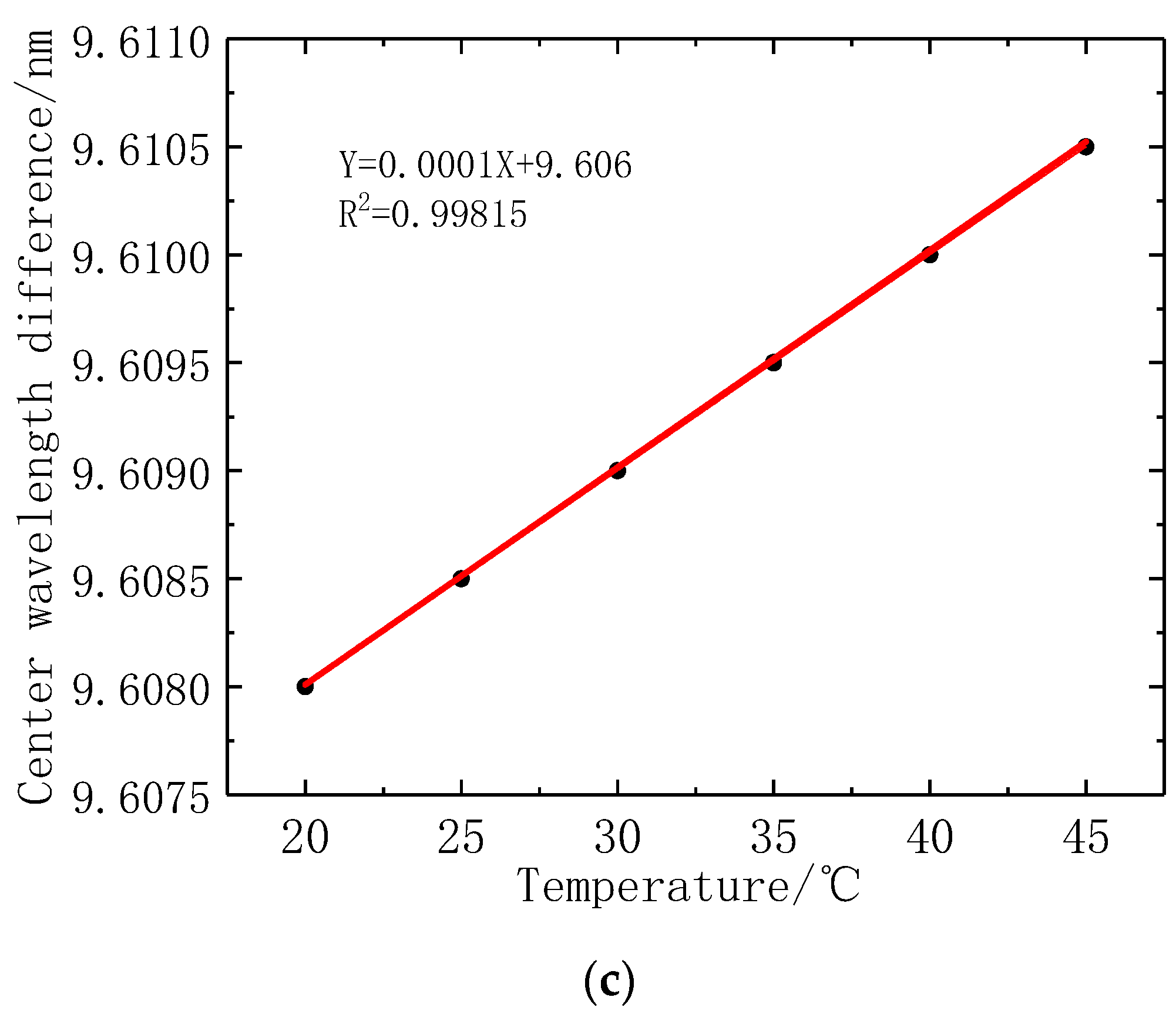
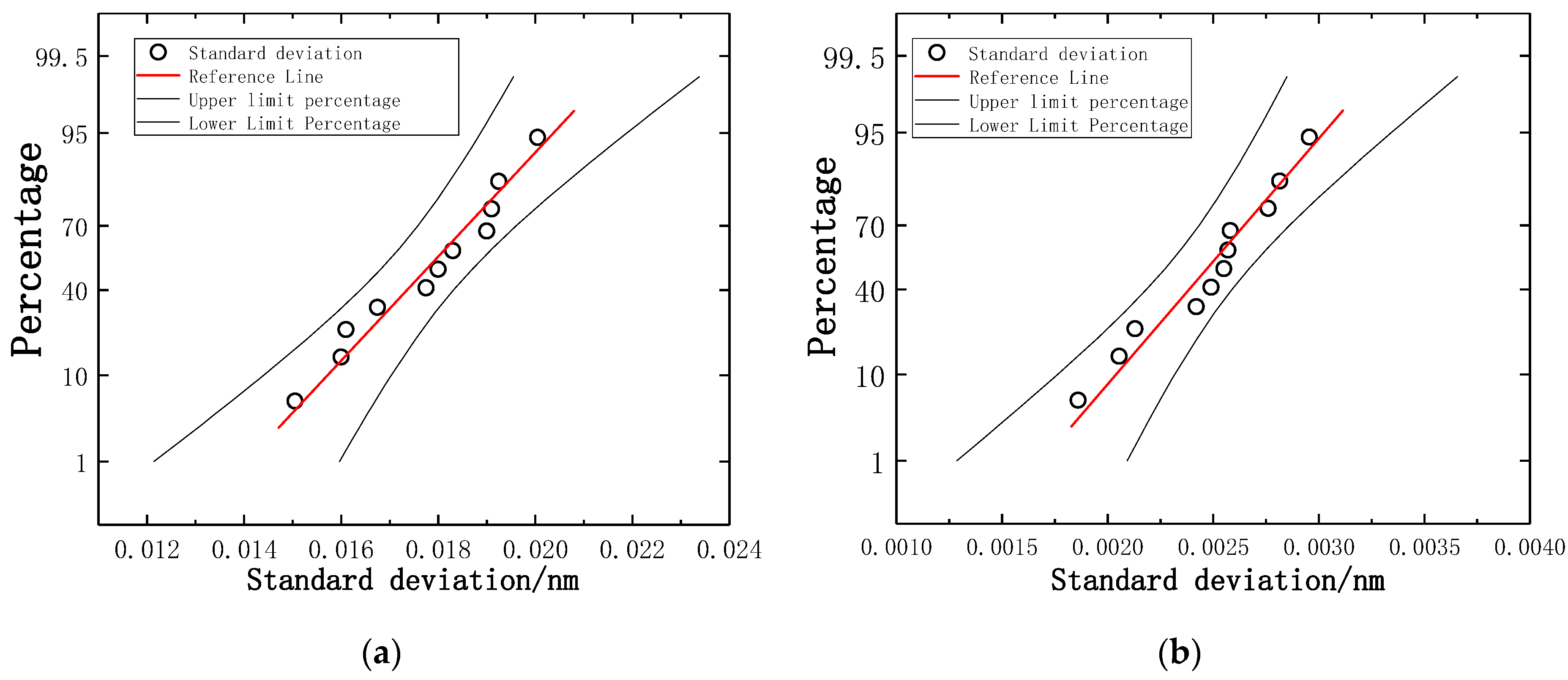
4.1. Calibration with Experimental Data
4.2. Experiment and Analysis
4.3. Performance of New-Type Sensors
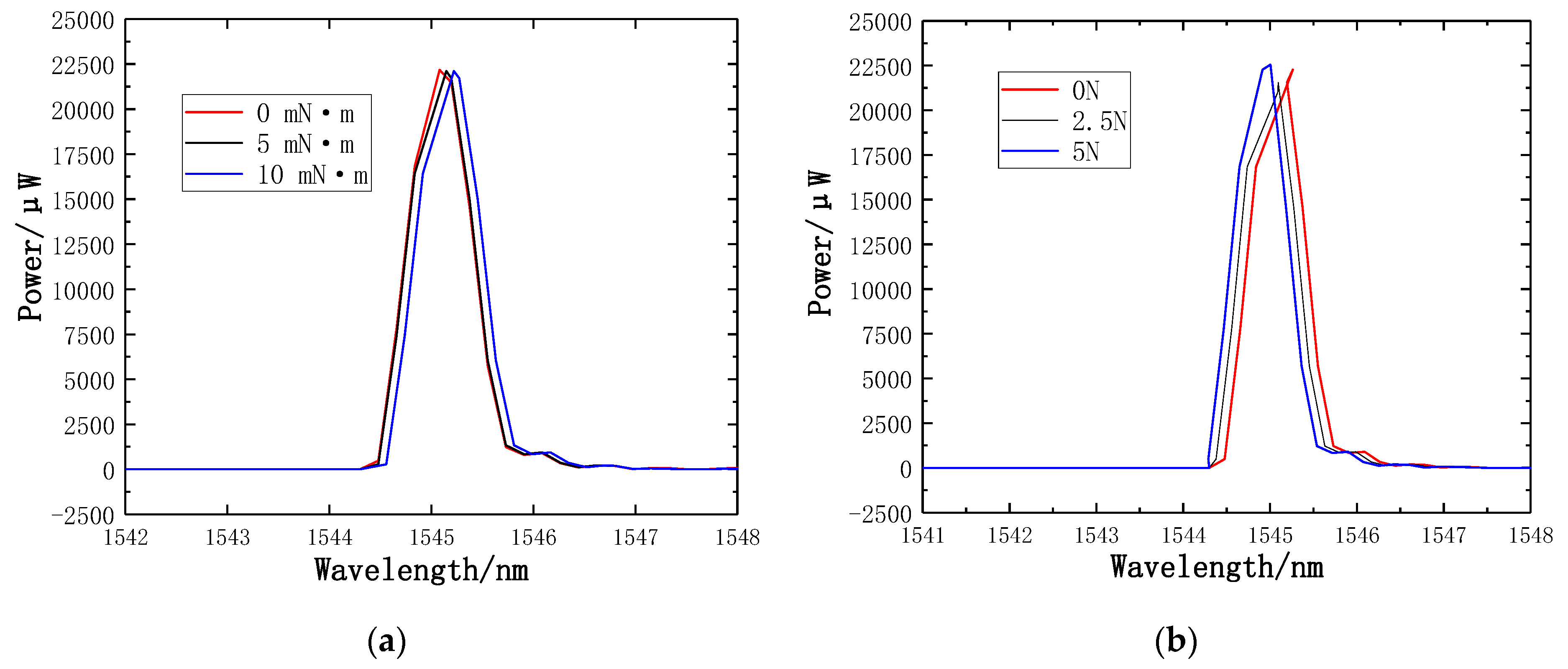
4.4. Transmission Spectra of the FBGs
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Robinson, T.N.; Stiegmann, G.V. Minimally invasive surgery. Endoscopy 2004, 36, 48–51. [Google Scholar] [PubMed]
- Redick, E.J. Minimally invasive surgery. IL G. Di Chir. 2003, 35, 171–177. [Google Scholar]
- Talamini, M.A. Development of Minimally Invasive Surgery at Johns Hopkins. Ann. Surg. 2018, 267 (Suppl. 2), S20. [Google Scholar] [CrossRef] [PubMed]
- Matsuoka, M.; Kashiwaba, M.; Koizumi, F. Sensation of an increased pressure in the thoracic cavity, pleural effusion, splenomegaly and lymphadenitis: Malignant lymphoma. Nihon Rinsho Jpn. J. Clin. Med. 1975, 146, 824. [Google Scholar]
- Huo, B.; Zhao, X.; Han, J.; Xu, W. Motion planning for flexible needle in multilayer tissue environment with obstacles. In Proceedings of the 2012 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Seoul, Korea, 14–17 Octomber 2012. [Google Scholar]
- Shelton, F.E., IV; Ouwerkerk, J.N.; Timperman, E.L. Robotically-Controlled Surgical Instrument Having Recording Capabilities. Patent Application WO/2012/166473, 12 June 2012. [Google Scholar]
- Rodrigues, P.L.; Rodrigues, N.F.; Fonseca, J.; Lima, E.; Vilaça, J.L. Kidney Targeting and Puncturing During Percutaneous Nephrolithotomy: Recent Advances and Future Perspectives. J. Endourol. 2013, 27, 826–834. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.; Rezvani, F.; Chang, K.J. Endoscopic ultrasound (EUS) and EUS-guided thoracentesis of pleural fluid. Gastroint. Endosc. 1997, 45, AB176. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Song, X.; Seneviratne, L.D.; Althoefer, K. Rolling Indentation Probe for Tissue Abnormality Identification during Minimally Invasive Surgery. IEEE Trans. Robot. 2011, 27, 450–460. [Google Scholar] [CrossRef]
- Liu, H.; Noonan, D.P.; Zweiri, Y.H.; Althoefer, K.A.; Seneviratne, L.D. The development of nonlinear viscoelastic model for the application of soft tissue identification. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, Sheraton Hotel and Marina, San Diego, CA, USA, 29 October–2 November 2007. [Google Scholar]
- Ahmadi, R.; Packirisamy, M.; Dargahi, J.; Cecere, R. Discretely Loaded Beam-Type Optical Fiber Tactile Sensor for Tissue Manipulation and Palpation in Minimally Invasive Robotic Surgery. IEEE Sens. J. 2012, 12, 22–32. [Google Scholar] [CrossRef]
- Shen, J.J.; Kalantari, M.; Kovecses, J.; Angeles, J.; Dargahi, J. Viscoelastic Modeling of the Contact Interaction Between a Tactile Sensor and an Atrial Tissue. IEEE Trans. Biomed. Eng. 2012, 59, 1727–1738. [Google Scholar] [CrossRef]
- King, C.H.; Culjat, M.O.; Franco, M.L.; Lewis, C.E.; Dutson, E.P.; Grundfest, W.S.; Bisley, J.W. Tactile Feedback Induces Reduced Grasping Force in Robot-Assisted Surgery. IEEE Trans. Haptics 2009, 2, 103–110. [Google Scholar] [CrossRef]
- Berkelman, P.J.; Whitcomb, L.L.; Taylor, R.H.; Jensen, P. A Miniature Microsurgical Instrument Tip Force Sensor for Enhanced Force Feedback during Robot-Assisted Manipulation. IEEE Trans. Robot. Autom. 2003, 19, 917–921. [Google Scholar] [CrossRef]
- Kuebler, B.; Seibold, U.; Hirzinger, G. Development of actuated and sensor integrated forceps for minimally invasive robotic surger. Int. J. Med. Robot. Comput. Assist. Surg. 2010, 1, 96–107. [Google Scholar] [CrossRef] [PubMed]
- Puangmali, P.; Althoefer, K.; Seneviratne, L.D.; Murphy, D.; Dasgupta, P. State-of-the-Art in Force and Tactile Sensing for Minimally Invasive Surgery. IEEE Sens. J. 2008, 8, 371–381. [Google Scholar] [CrossRef]
- Yu, F.T.S.; Yin, S. Fiber optic sensors. Opt. Eng. 2002, 478, 39–45. [Google Scholar]
- Omar, A.F. Fiber Optic Sensors: An Introduction for Engineers and Scientists. Sens. Rev. 2011, 33, 884–894. [Google Scholar]
- Grattan, K.T.V.; Sun, T. Fiber optic sensor technology: An overview. Sens. Actuators A Phys. 2000, 82, 40–61. [Google Scholar] [CrossRef]
- Broadway, C.; Rui, M.; Leal-Junior, A.G.; Marques, C.; Caucheteur, C. Towards commercial polymer fiber Bragg grating sensors: Review and applications. J. Light. Technol. 2018, 8724, 2605–2615. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Theodosiou, A.; Frizera-Neto, A.; Pontes, M.J.; Shafir, E.; Palchik, O.; Tal, N.; Zilberman, S.; Berkovic, G.; Antunes, P.; et al. Characterization of a new polymer optical fiber with enhanced sensing capabilities using a Bragg grating. Opt. Lett. 2018, 43, 4799. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Handa, J.; Gehlbach, P.; Iordachita, I. A Submillimetric 3-DOF Force Sensing Instrument with Integrated Fiber Bragg Grating for Retinal Microsurgery. IEEE Trans. Biomed. Eng. 2014, 61, 522–534. [Google Scholar] [PubMed]
- Liu, X.; Iordachita, I.I.; He, X.; Taylor, R.H.; Kang, J.U. Miniature fiber-optic force sensor based on low-coherence Fabry-Pérot interferometry for vitreoretinal microsurgery. Biomed. Opt. Express 2012, 3, 1062–1076. [Google Scholar] [CrossRef] [PubMed]
- Yip, M.C.; Yuen, S.G.; Howe, R.D. A Robust Uniaxial Force Sensor for Minimally Invasive Surgery. IEEE Trans. Biomed. Eng. 2010, 57, 1008–1011. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, R.; Dargahi, J.; Packirisamy, M.; Cecere, R. A new hybrid catheter-tip tactile sensor with relative hardness measuring capability for use in catheter-based heart surgery. In Proceedings of the 2010 IEEE Sensors, Kona, HI, USA, 1–4 November 2010. [Google Scholar]
- Yokoyama, K.; Nakagawa, H.; Shah, D.C.; Lambert, H.; Leo, G.; Aeby, N.; Ikeda, A.; Pitha, J.V.; Sharma, T.; Lazzara, R.; et al. Novel contact force sensor incorporated in irrigated radiofrequency ablation catheter predicts lesion size and incidence of steam pop and thrombus. Circ. Arrhythm. Electrophysiol. 2008, 1, 354. [Google Scholar] [CrossRef] [PubMed]
- Menciassi, A.; Eisinberg, A.; Scalari, G.; Anticoli, C.; Carrozza, M.; Dario, P. Force feedback-based microinstrument for measuring tissue properties and pulse in microsurgery. In Proceedings of the IEEE ICRA, Seoul, Korea, 21–26 May 2001; pp. 626–631. [Google Scholar]
- Bell, B.; Stankowski, S.; Moser, B.; Oliva, V.; Stieger, C.; Nolte, L.P.; Caversaccio, M.; Weber, S. Integrating optical fiber force sensors into microforceps for ORL microsurgery. IEEE Eng. Med. Biol. Soc. 2010, 2010, 1848–1851. [Google Scholar]
- Zhang, X. Silicon microsurgery-force sensor based on diffractive optical MEMS encoders. Sens. Rev. 2004, 24, 37–41. [Google Scholar] [CrossRef]
- Seibold, U.; Kubler, B.; Hirzinger, G. Prototype of Instrument for Minimally Invasive Surgery with 6-Axis Force Sensing Capability. In Proceedings of the IEEE ICRA, Barcelona, Spain, 18–22 April 2005; pp. 496–501. [Google Scholar]
- Puangmali, P.; Liu, H.; Seneviratne, L.D.; Dasgupta, P.; Althoefer, K. Miniature 3-Axis distal force sensor for minimally invasive surgical palpation. IEEE/ASME Trans. Mechatron. 2012, 17, 646–656. [Google Scholar] [CrossRef]
- Polygerinos, P.; Seneviratne, L.D.; Razavi, R.; Schaeffter, T.; Althoefer, K. Triaxial catheter-tip force sensor for MRI-guided cardiac procedures. IEEE/ASME Trans Mechatron. 2013, 18, 386–396. [Google Scholar] [CrossRef]
- Kesner, S.B.; Howe, R.D. Design Principles for Rapid Prototyping Forces Sensors Using 3-D Printing. IEEE/ASME Trans. Mechatron. 2011, 16, 866–870. [Google Scholar] [CrossRef] [PubMed]
- Roesthuis, R.J.; Kemp, M.; van den Dobbelsteen, J.J.; Misra, S. Three-Dimensional Needle Shape Reconstruction Using an Array of Fiber Bragg Grating Sensors. IEEE/ASME Trans. Mechatron. 2014, 19, 1115–1126. [Google Scholar] [CrossRef]
- Shang, W.; Su, H.; Li, G.; Fischer, G.S. Teleoperation System with Hybrid Pneumatic-Piezoelectric Actuation for MRI-Guided Needle Insertion with Haptic Feedback. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots & Systems, Tokyo, Japan, 3–7 November 2013. [Google Scholar]
- Brett, P.N.; Harrison, A.J.; Thomas, T.A. Schemes for the identification of tissue types and boundaries at the tool point for surgical needles. IEEE Trans. Inf. Technol. Biomed. 2000, 4, 30–36. [Google Scholar] [CrossRef]
- Berkelman, P.; Whitcomb, L.; Taylor, R.; Jensen, P. A Miniature Instrument Tip Force Sensor for Robot/ Human Cooperative Microsurgical Manipulation with Enhanced Force Feedback; Springer: Berlin, Germany, 2000; pp. 247–286. [Google Scholar]
- Song, H.; Kim, K.; Lee, J. Development of optical fiber Bragg grating force-reflection sensor system of medical application for safe minimally invasive robotic surgery. Rev. Sci. Instrum. 2011, 82, 074301. [Google Scholar] [CrossRef]
- Vidal, F.P.; John, N.W.; Healey, A.E.; Gould, D.A. Simulation of ultrasound guided needle puncture using patient specific data with 3D textures and volume haptics. Comput. Anim. Virtual Worlds 2010, 19, 111–127. [Google Scholar] [CrossRef]
- Guo, H.; Xiao, G.; Mrad, N.; Yao, J. Fiber Optic Sensors for Structural Health Monitoring of Air Platforms. Sensors 2011, 11, 3687–3705. [Google Scholar] [CrossRef] [PubMed]
- Jagtap, A.; Riviere, C. Applied force during vitreoretinal microsurgery with handheld instruments. In Proceedings of the International Conference of the IEEE Engineering in Medicine & Biology Society, San Francisco, CA, USA, 1–5 September 2004. [Google Scholar]
- Peirs, J.; Clijnen, J.; Reynaerts, D.; Van Brussel, H.; Herijgers, P.; Corteville, B.; Boone, S. A micro optical force sensor for force feedback during minimally invasive robotic surgery. Sens. Actuators A Phys. 2004, 115, 447–455. [Google Scholar] [CrossRef]
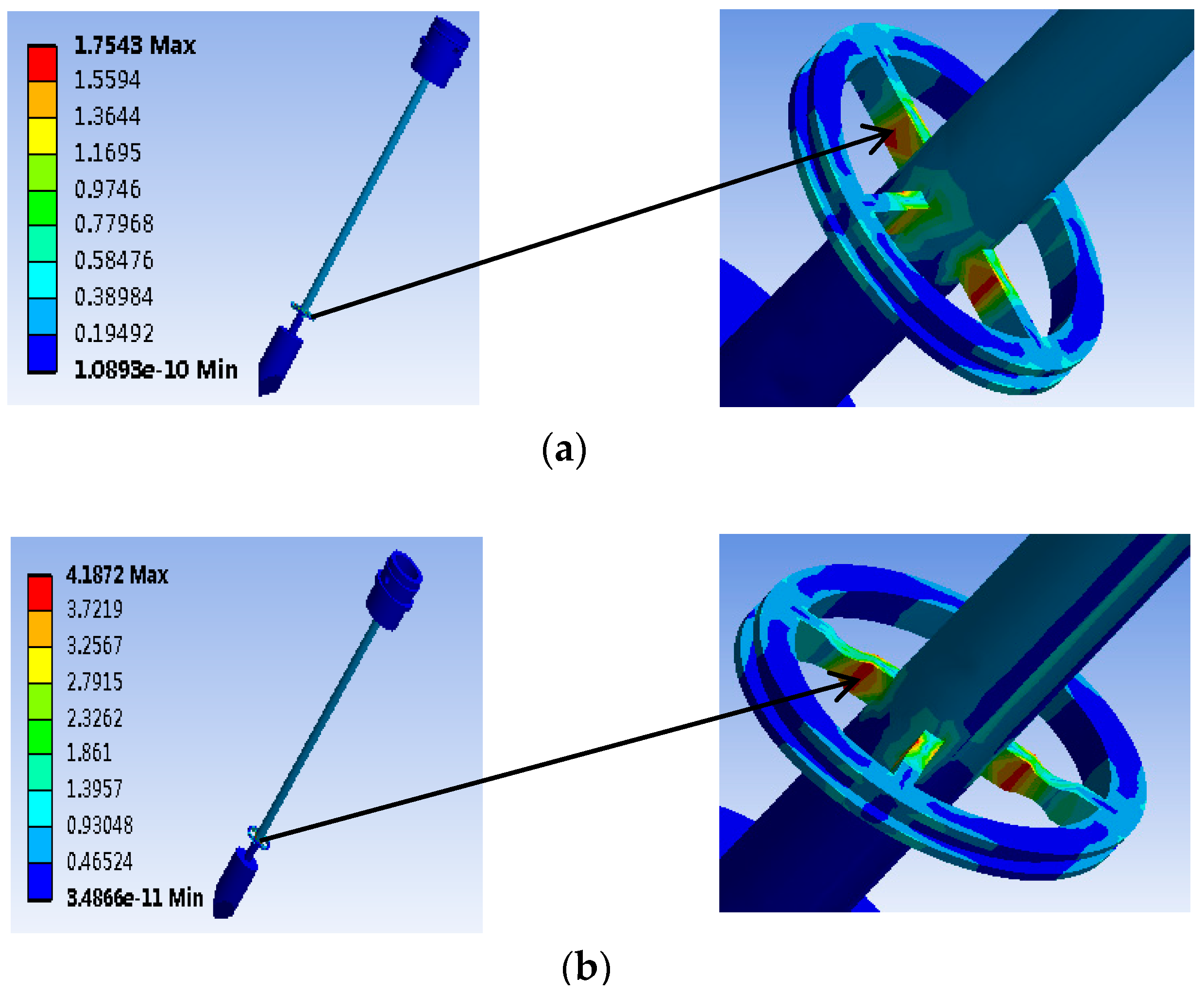
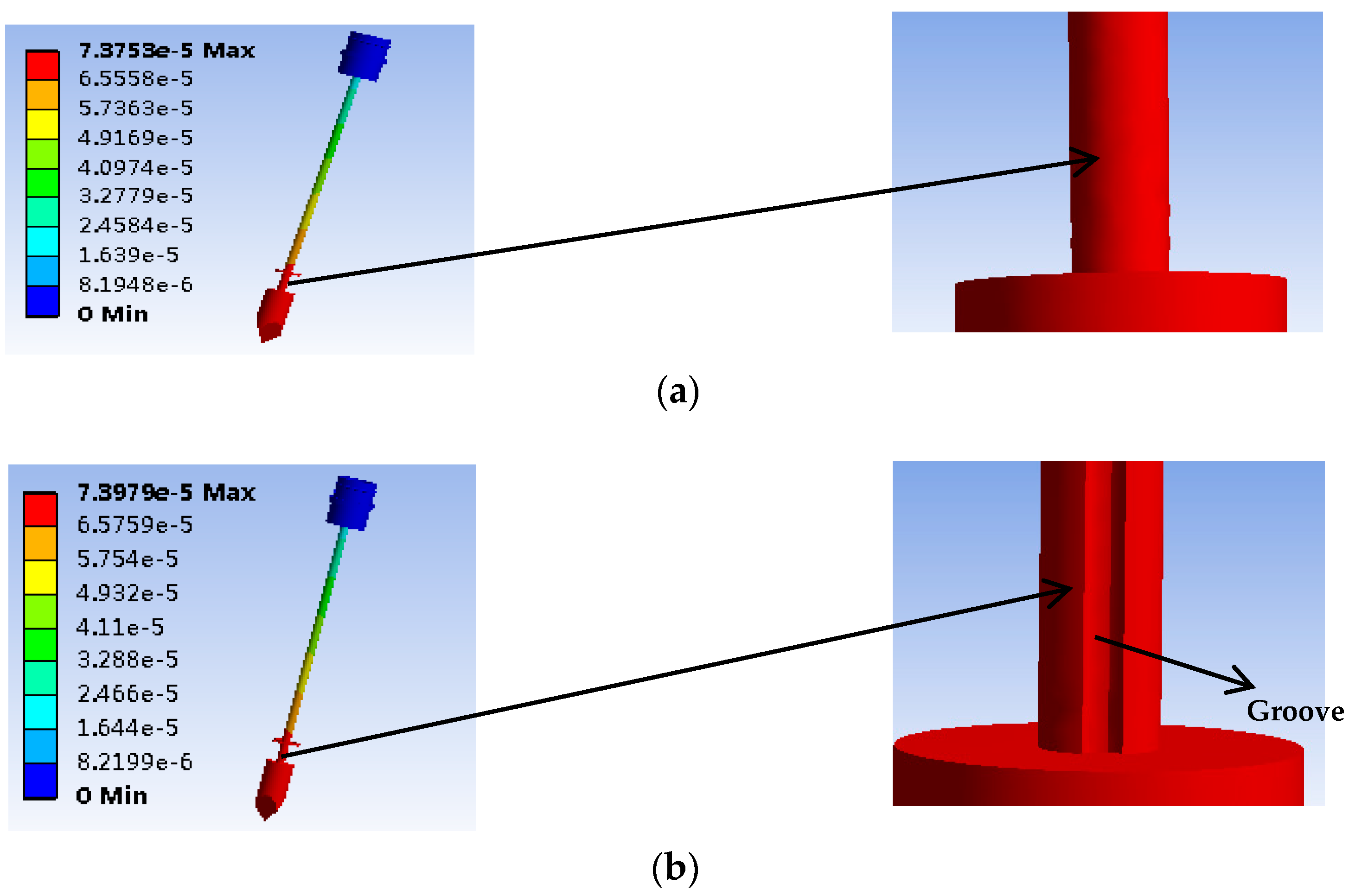
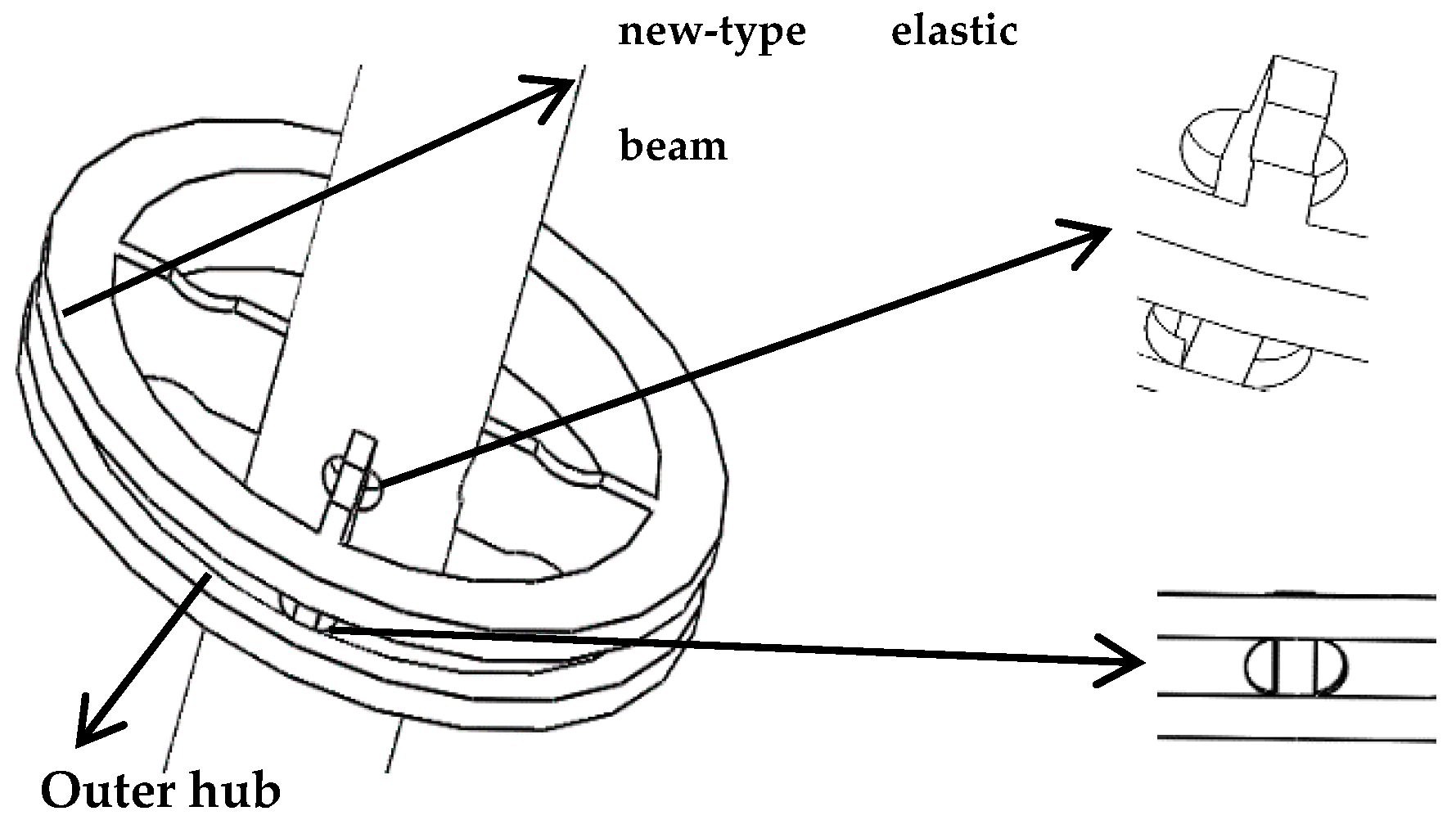
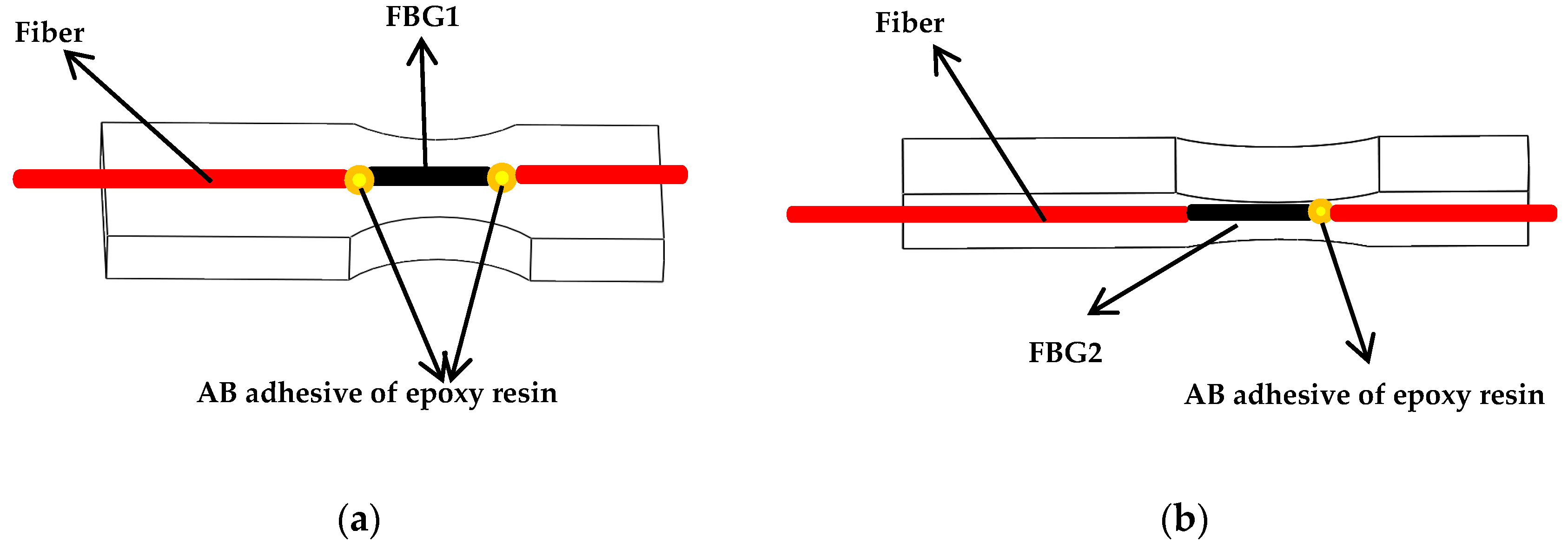

| Number | Length of Elastic Beam L/mm | Radial Width h/mm | Axial Thickness b/mm | Maximum Stress Intensity/MPa |
|---|---|---|---|---|
| 1 | 3 | 0.5 | 1.4 | 8.77 |
| 2 | 3 | 0.5 | 1.6 | 6.04 |
| 3 | 3 | 0.5 | 1.8 | 4.67 |
| 4 | 3 | 0.6 | 1.4 | 4.45 |
| 5 | 3 | 0.6 | 1.6 | 3.16 |
| 6 | 3 | 0.6 | 1.8 | 2.12 |
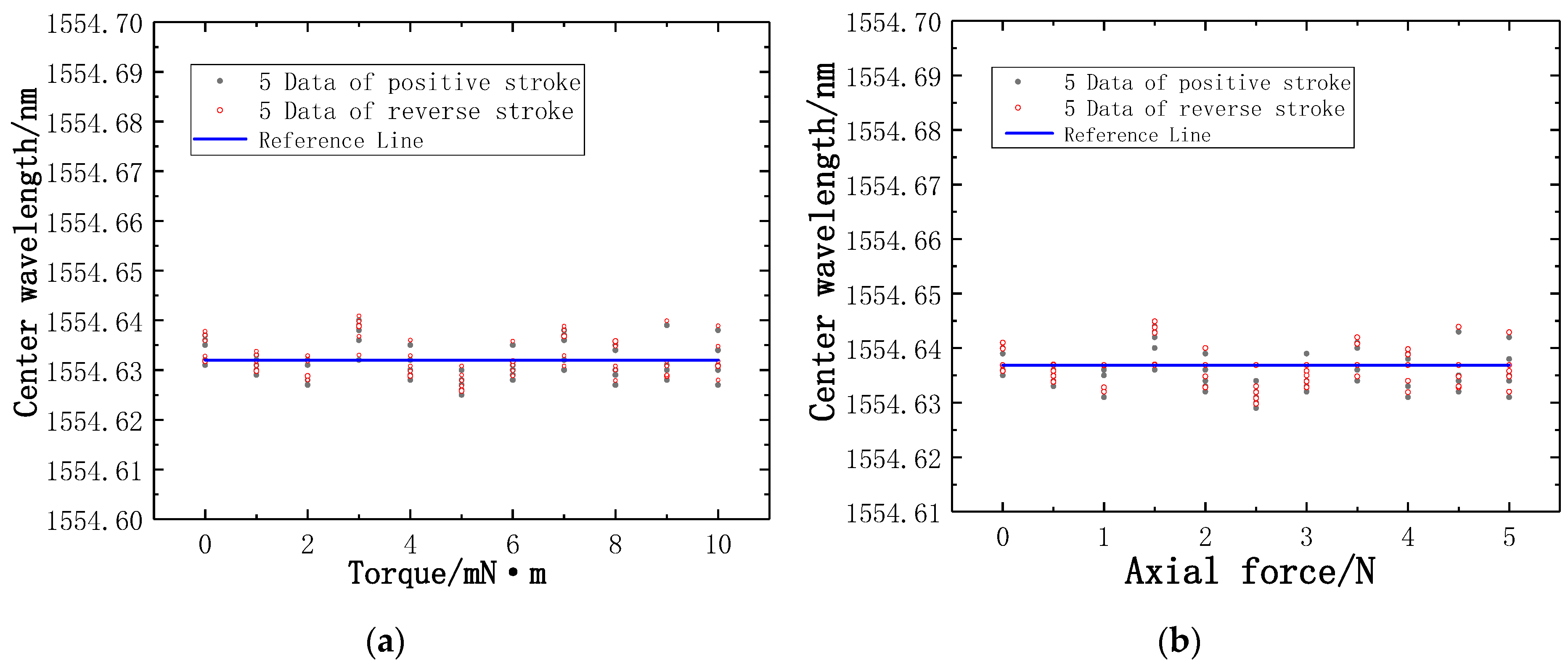
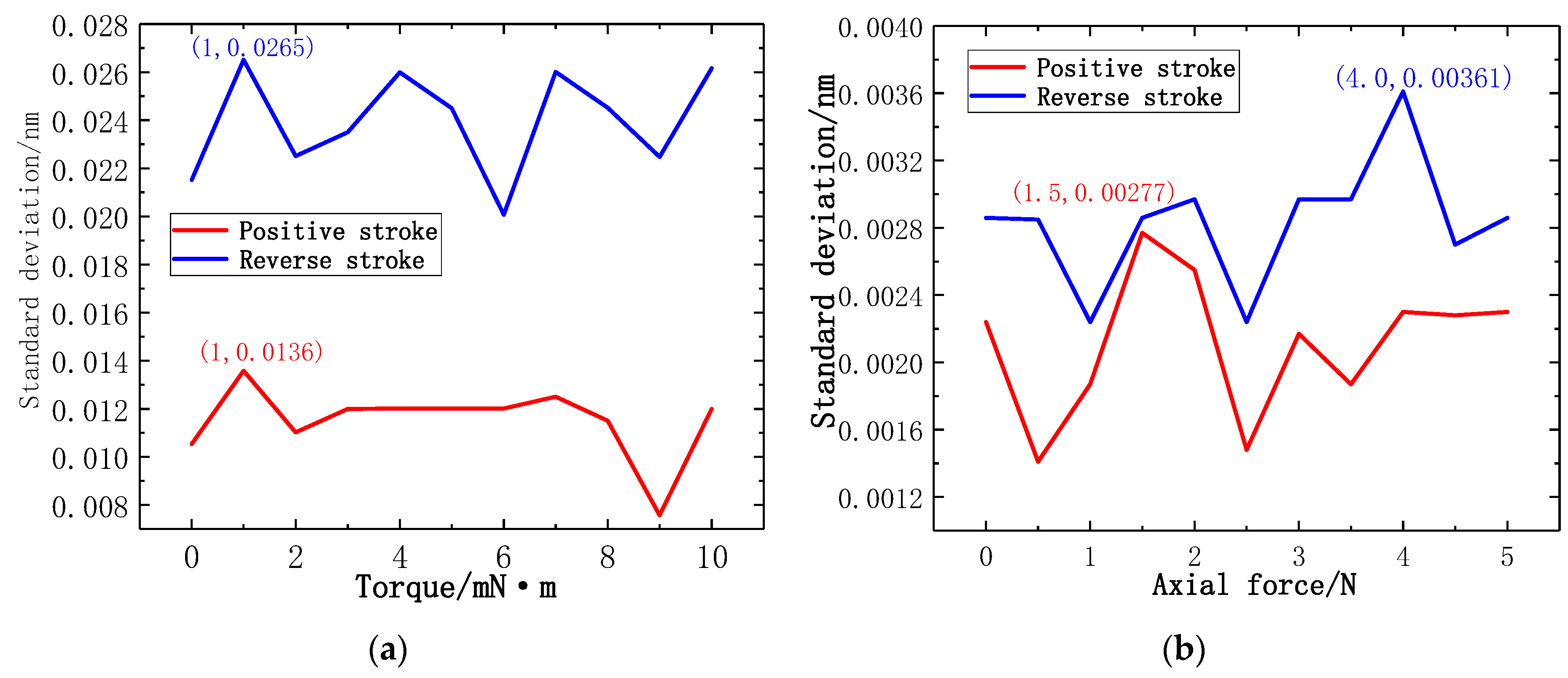
| Torque/mN·m | Standard Deviation of Positive Stroke/nm | Standard Deviation of Reverse Stroke/nm |
|---|---|---|
| 0 | 0.0105 | 0.0215 |
| 1 | 0.0136 | 0.0265 |
| 2 | 0.0110 | 0.0225 |
| 3 | 0.0120 | 0.0235 |
| 4 | 0.0120 | 0.0260 |
| 5 | 0.0121 | 0.0245 |
| 6 | 0.0121 | 0.0201 |
| 7 | 0.0125 | 0.0260 |
| 8 | 0.0115 | 0.0245 |
| 9 | 0.0076 | 0.0225 |
| 10 | 0.0120 | 0.0262 |
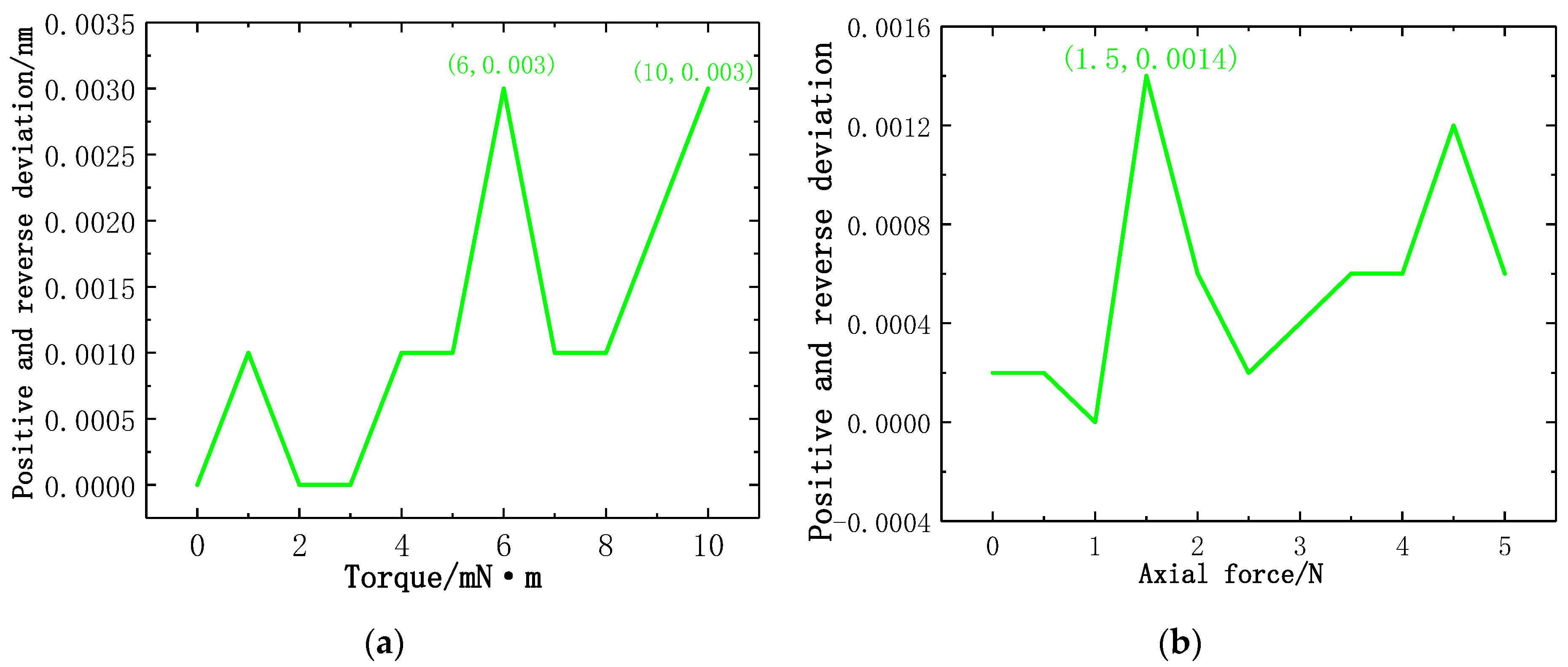
| Torque/mN·m | Positive Stroke Average Calibration Point/nm | Reverse Stroke Average Calibration Point/nm | Positive and Reverse Deviation/nm |
|---|---|---|---|
| 0 | 9.554 | 9.554 | 0.000 |
| 1 | 9.576 | 9.577 | 0.001 |
| 2 | 9.602 | 9.602 | 0.000 |
| 3 | 9.625 | 9.625 | 0.000 |
| 4 | 9.647 | 9.648 | 0.001 |
| 5 | 9.671 | 9.670 | 0.001 |
| 6 | 9.692 | 9.695 | 0.003 |
| 7 | 9.715 | 9.714 | 0.001 |
| 8 | 9.738 | 9.737 | 0.001 |
| 9 | 9.763 | 9.765 | 0.002 |
| 10 | 9.783 | 9.786 | 0.003 |
| Axial Force/N | Standard Deviation of Positive Stroke/nm | Standard Deviation of Reverse Stroke/nm |
|---|---|---|
| 0.0 | 0.00224 | 0.00286 |
| 0.5 | 0.00141 | 0.00285 |
| 1.0 | 0.00187 | 0.00224 |
| 1.5 | 0.00277 | 0.00286 |
| 2.0 | 0.00255 | 0.00297 |
| 2.5 | 0.00148 | 0.00224 |
| 3.0 | 0.00217 | 0.00297 |
| 3.5 | 0.00187 | 0.00297 |
| 4.0 | 0.00230 | 0.00361 |
| 4.5 | 0.00228 | 0.00270 |
| 5.0 | 0.00230 | 0.00286 |
| Axial Force/N | Positive Stroke Average Calibration Point/nm | Reverse Stroke Average Calibration Point/nm | Positive and Reverse Deviation/nm |
|---|---|---|---|
| 0.0 | 9.3980 | 9.3978 | 0.0002 |
| 0.5 | 9.4430 | 9.4428 | 0.0002 |
| 1.0 | 9.4870 | 9.4870 | 0.0000 |
| 1.5 | 9.5352 | 9.5338 | 0.0014 |
| 2.0 | 9.5790 | 9.5784 | 0.0006 |
| 2.5 | 9.6228 | 9.6230 | 0.0002 |
| 3.0 | 9.6688 | 9.6684 | 0.0004 |
| 3.5 | 9.7120 | 9.7114 | 0.0006 |
| 4.0 | 9.7564 | 9.7570 | 0.0006 |
| 4.5 | 9.8038 | 9.8026 | 0.0012 |
| 5.0 | 9.8474 | 9.8468 | 0.0006 |
| Sensor Type | Uses | Directivity | Sensitivity | Repeatability Error and Hysteresis Error | Resolution |
|---|---|---|---|---|---|
| New type of puncturing needle sensor | Puncture and drainage in MIS | Axial force and torque | 0.089 nm/N 22.8 pm/mN·m | Torque: YR = 0.81%FS, YH = 0.03%FS; Axial: YR = 0.11%FS, YH = 0.014%FS | Torque: 0.8 mN·m; Axial: 0.03 N |
| 5 mm Diameter tri-axial force sensor [42] | Force feedback during MIRS | Tri-axial | 10.3 mV/μm | No mention | 0.04 N |
| Miniature 3-Axis Distal Force Sensor [31] | MIS Palpation | 3-Axis | No mention | Hysteresis = 3.5%. | 0.02 N |
| Triaxial Catheter-Tip Force Sensor [32] | MRI-Guided Cardiac Procedures | Triaxial | 0.5V/N | Repeatability > 95% Hysteresis ratio = 5.3% | 0.01N |
| DOF Force Sensing Instrument [22] | Retinal Microsurgery | 3-DOF | No mention | Repeatability = 1.3 pm | Axial:1 mN; Transverse: 0.25 mN |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, P.; Huang, X.; Li, Y.; Liu, P.X. A Fiber Bragg Grating Sensing Structure for the Design, Simulation and Stress Strain Monitoring of Human Puncture Surgery. Sensors 2019, 19, 3066. https://doi.org/10.3390/s19143066
Xiong P, Huang X, Li Y, Liu PX. A Fiber Bragg Grating Sensing Structure for the Design, Simulation and Stress Strain Monitoring of Human Puncture Surgery. Sensors. 2019; 19(14):3066. https://doi.org/10.3390/s19143066
Chicago/Turabian StyleXiong, Pengwen, Xin Huang, Yulong Li, and Peter X. Liu. 2019. "A Fiber Bragg Grating Sensing Structure for the Design, Simulation and Stress Strain Monitoring of Human Puncture Surgery" Sensors 19, no. 14: 3066. https://doi.org/10.3390/s19143066
APA StyleXiong, P., Huang, X., Li, Y., & Liu, P. X. (2019). A Fiber Bragg Grating Sensing Structure for the Design, Simulation and Stress Strain Monitoring of Human Puncture Surgery. Sensors, 19(14), 3066. https://doi.org/10.3390/s19143066






