Scattering of Microwaves by a Passive Array Antenna Based on Amorphous Ferromagnetic Microwires for Wireless Sensors with Biomedical Applications
Abstract
1. Introduction
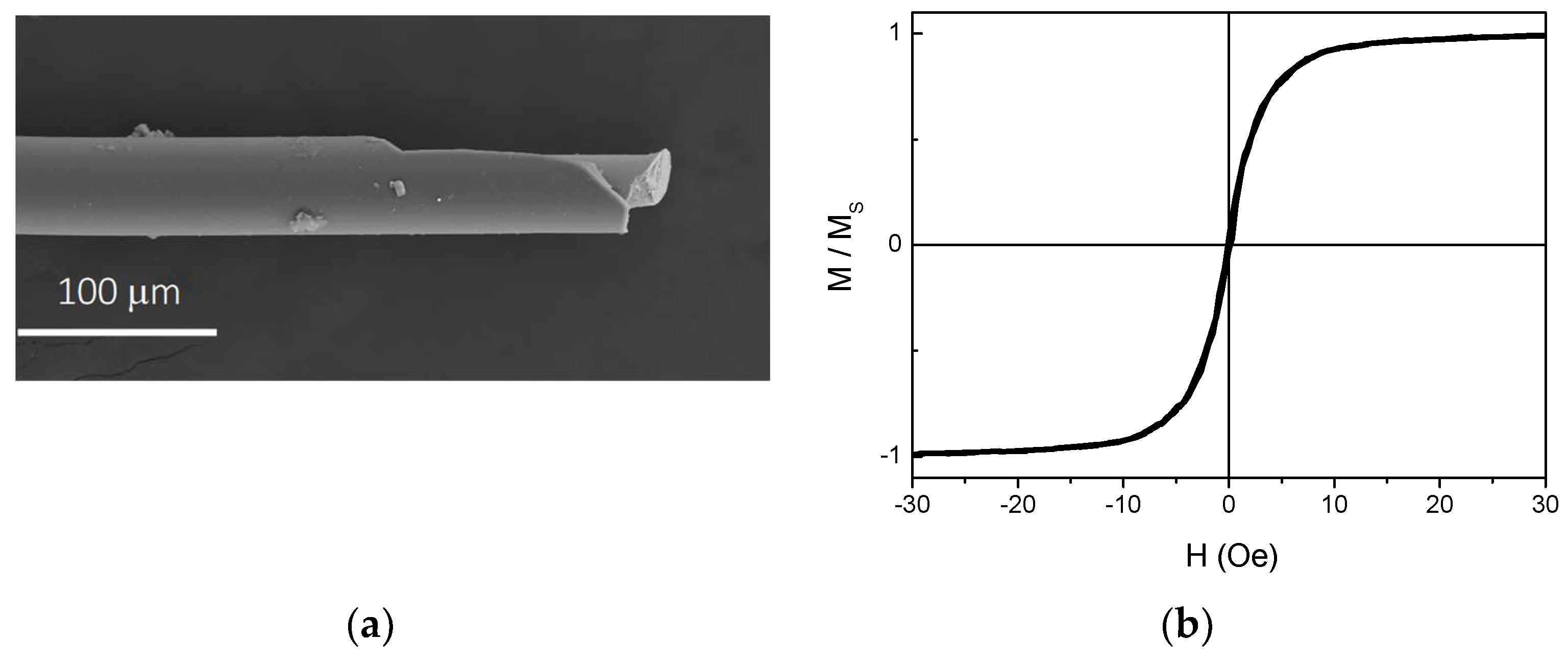
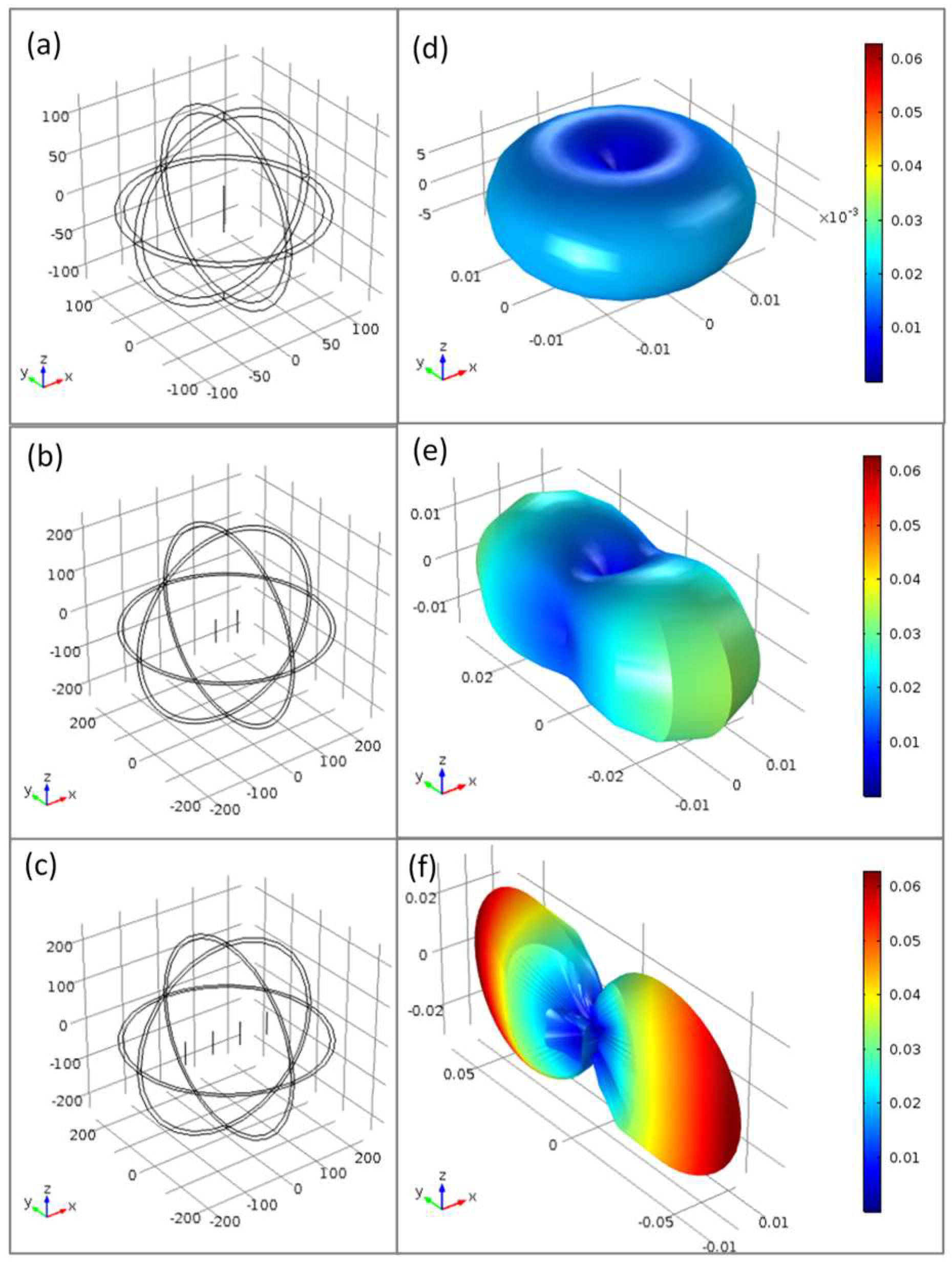
2. Materials and Methods
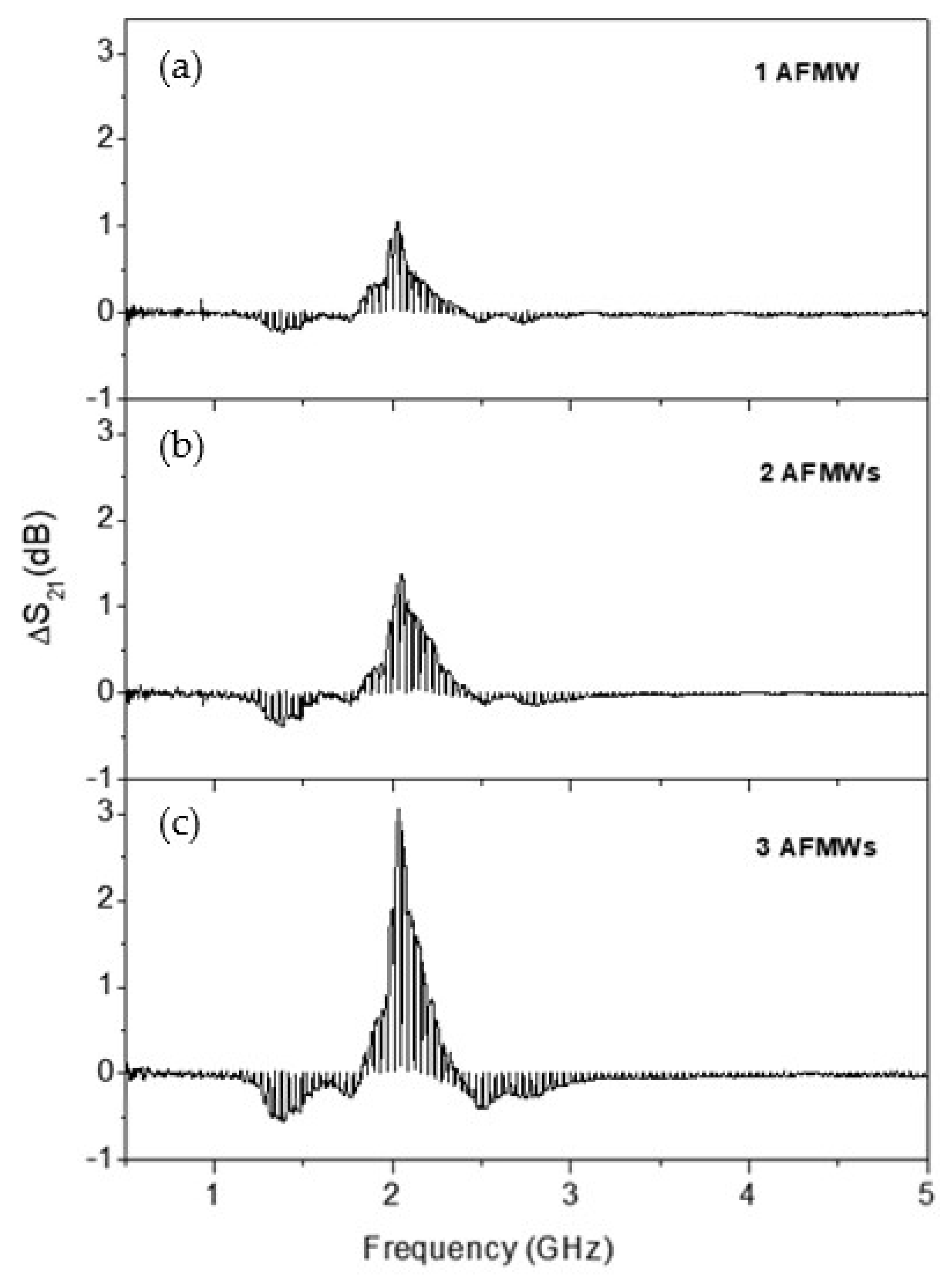
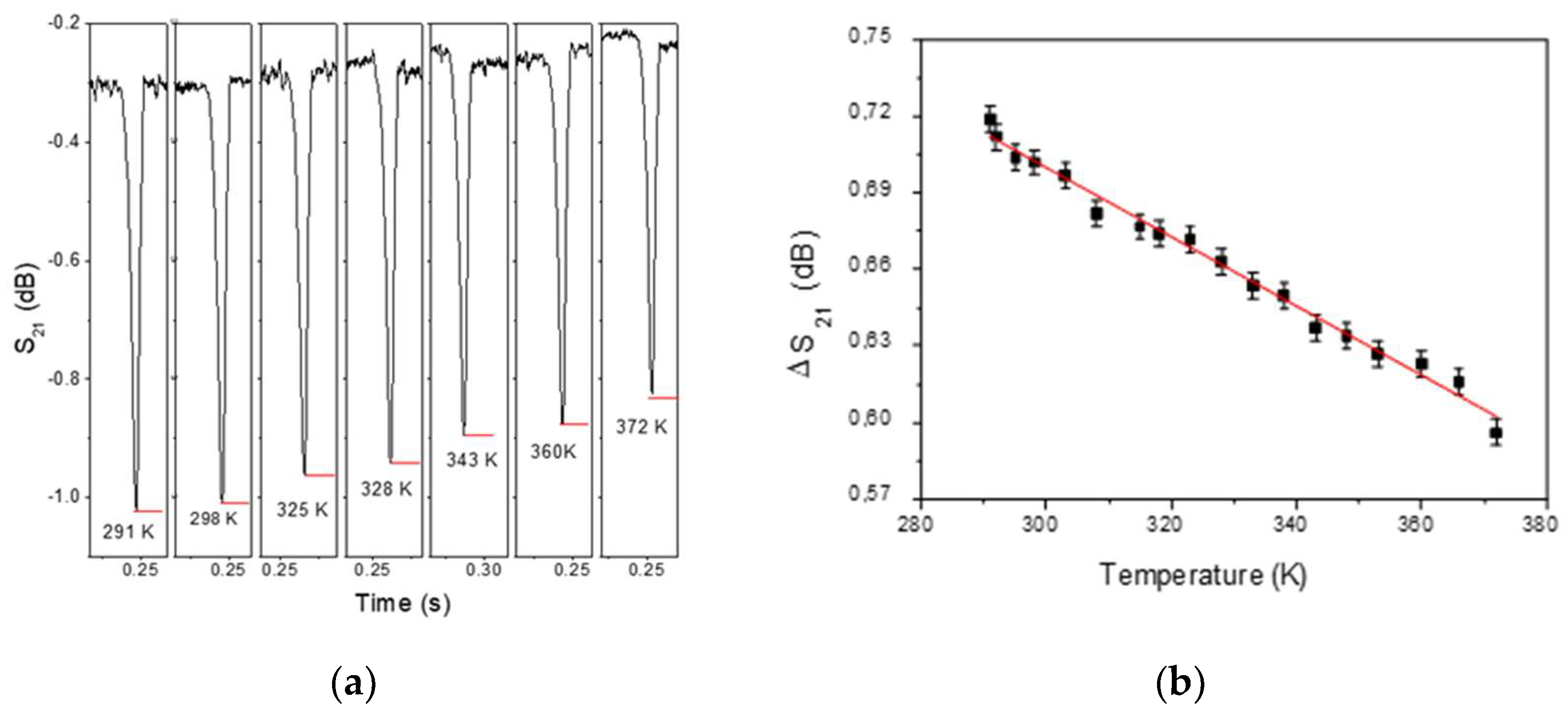
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chiriac, H.; Herea, D.-D.; Corodeanu, S. Microwire array for giant magneto-impedance detection of magnetic particles for biosensor prototype. J. Magn. Magn. Mater. 2007, 311, 425–428. [Google Scholar] [CrossRef]
- Marín, P.; López, M.; Agudo, P.; Vázquez, M.; Hernando, A. Applications of amorphous samples presenting high magnetomechanical coupling during the first stages of nanocrystallisation process. Sens. Actuators A 2001, 91, 218–222. [Google Scholar] [CrossRef]
- Beach, R.S.; Berkowitz, A.E. Giant magnetic field dependent impedance of amorphous FeCoSiB wire. Appl. Phys. Lett. 1994, 64, 3652–3654. [Google Scholar] [CrossRef]
- Paramonov, V.P.; Antonov, A.S.; Lagarikov, A.N. High frequency (1–1200 MHz) magnetoimpedance in CoFeSiB amorphous wires (abstract). J. Appl. Phys. 1996, 79, 6532. [Google Scholar] [CrossRef]
- Yelon, A.; Ménard, D.; Britel, M.; Ciureanu, P. Calculations of giant magnetoimpedance and of ferromagnetic resonance response are rigorously equivalent. Appl. Phys. Lett. 1996, 69, 3084. [Google Scholar] [CrossRef]
- Buznikov, N.A. The Effect of Surface Domain Structure on Low-Field Microwave Absorption of Magnetic Microwires. J. Phys. D: Appl. Phys. 2010, 43, 055002. [Google Scholar] [CrossRef]
- Liu, L.; Kong, L.B.; Lin, G.Q.; Matitsine, S.; Deng, C.R. Microwave permeability of ferromagnetic microwires composites/metamaterials and potential applications. IEEE Trans. Magn. 2008, 44, 3119–3122. [Google Scholar] [CrossRef]
- Qin, F.X.; Peng, H.X.; Pankratov, N.; Phan, M.H.; Panina, L.V.; Ipatov, M.; Zhukova, V.; Zhukov, A.; Gonzalez, J. Exceptional electromagnetic interference shielding properties of ferromagnetic microwires enabled polymer composites. J. Appl. Phys. 2010, 108, 044510. [Google Scholar] [CrossRef]
- Zhukova, V.; Larin, V.S.; Zhukov, A. Stress induced magnetic anisotropy and giant magnetoimpedance in Fe-rich glass-coated magnetic microwires. J. Appl. Phys. 2003, 94, 1115–1118. [Google Scholar] [CrossRef]
- Kraus, L.; Infante, G.; Frait, Z.; Vázquez, M. Ferromagnetic resonance in microwires and nanowires. Phys. Rev. B 2011, 83, 174438. [Google Scholar] [CrossRef]
- Zhukov, A.; González, J.; Blanco, J.M.; Vázquez, M.; Larin, V. Microwires coated by glass: A new family of soft and hard magnetic materials. J. Mater. Res. 2000, 15, 2107–2113. [Google Scholar] [CrossRef]
- Marín, P.; Marcos, M.; Hernando, A. High magnetomechanical coupling on magnetic microwire for sensors with biological applications. Appl. Phys. Lett. 2010, 96, 262512. [Google Scholar] [CrossRef]
- Kurlyandskaya, G.V.; Sánchez, M.L.; Hernando, B.; Prida, V.M.; Gorria, P.; Tejedor, M. Giant magnetoimpedance-based sensitive element as a model for biosensors. Appl. Phys. Lett. 2003, 82, 3053–3055. [Google Scholar] [CrossRef]
- Herrero-Gómez, C.; Aragón, A.M.; Hernando-Rydings, M.; Marín, P.; Hernando, A. Stress and field contactless sensor based on the scattering of electromagnetic waves by a single ferromagnetic microwire. Appl. Phys. Lett. 2014, 105, 092405. [Google Scholar] [CrossRef]
- Blyakhman, F.A.; Makarova, E.B.; Fadeyev, F.A.; Lugovets, D.V.; Safronov, A.P.; Shabadrov, P.A.; Shklyar, T.F.; Melnikov, G.Yu.; Orue, I.; Kurlyandskaya, G.V. The Contribution of Magnetic Nanoparticles to Ferrogel Biophysical Properties. Nanomaterials 2019, 9, 232. [Google Scholar] [CrossRef]
- Aragón, A.M.; Hernando-Rydings, M.; Hernando, A.; Marín, P. Liquid pressure wireless sensor based on magnetostrictive microwires for applications in cardiovascular localized diagnostic. AIP Adv. 2015, 5, 087132. [Google Scholar] [CrossRef]
- Chiriac, H.; Marinescu, C.S.; Óvári, T.A.; Neagu, M. Sensor applications of amorphous glass-covered wires. Sens. Actuators A 1999, 76, 208–212. [Google Scholar] [CrossRef]
- Atkinson, D.; Squire, P.T.; Maylin, M.G.; Gore, J. An integrating magnetic sensor based on the giant magneto-impedance effect. Sens. Actuators A 2000, 81, 82–85. [Google Scholar] [CrossRef]
- Panina, L.V.; Mohri, K. Magneto-impedance effect in amorphous wires. Appl. Phys. Lett. 1994, 65, 1189–1191. [Google Scholar] [CrossRef]
- Zhukova, V.; Ipatov, M.; Zhukov, A.; Gonzalez, J.; Blanco, J.M. GMI effect in ultra-thin glass-coated Co-rich amorphous wires. Sens. Actuators B 2007, 126, 232–234. [Google Scholar] [CrossRef]
- Bregar, V.B. Advantages of ferromagnetic nanoparticle composites in microwave absorbers. IEEE Trans. Magn. 2004, 40, 1679–1684. [Google Scholar] [CrossRef]
- Cramer, N.; Lucic, D.; Camley, R.E.; Celinski, Z. High aatenuation tunable microwave notch filters utilizing ferromagnetic resonance. J. Appl. Phys. 2000, 87, 6911–6913. [Google Scholar] [CrossRef]
- Pardavi-Horvath, M. Microwave applications of soft ferrites. J. Magn. Magn. Mater. 2000, 215–216, 171–183. [Google Scholar] [CrossRef]
- Shehreen, A.; Khanna, M.; Veenugopal, V.; Kuanr, B.K. Microwave monotithic filter and phase shifter using magnetic nanostructures. AIP Adv. 2018, 8, 056624. [Google Scholar]
- Kurlyandskaya, G.V.; Shcherbinin, S.V.; Volchkov, S.O.; Bhagat, S.M.; Calle, E.; Pérez, R.; Vazquez, M. Soft magnetic materials for sensor applications in the high frequency range. J. Magn. Magn. Matter. 2018, 459, 154–158. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Li, J.; Li, Y.; Chen, Y.; Xu, L. Design and fabrication of a miniaturized GMI magnetic sensor based on amorphous wire by MEMS technology. Sensors 2018, 183, 732. [Google Scholar]
- Hernando, A.; López-Domínguez, V.; Ricciardi, E.; Osiak, K.; Marín, P. Tuned scattering of electromagnetic waves by a finite length ferromagnetic microwire. IEEE Trans. Antenn. Propag. 2016, 105, 1112–1115. [Google Scholar] [CrossRef]
- López-Domínguez, V.; García, M.A.; Marín, P.; Hernando, A. Measurement of the magnetic permeability of amorphous magnetic microwires by using their antenna resonance. Rev. Sci. Instrum. 2017, 88, 124704. [Google Scholar] [CrossRef]
- Archilla, D.; Moya, A.; Hernando, A.; Marín, P. Optimization of tunable GHz micro-antennas based on Giant magnetoimpedance. J. Magn. Magn. Mater. 2019, 469, 289–295. [Google Scholar] [CrossRef]
- Panina, L.V.; Ipatov, M.; Zhukova, V.; Zhukov, A.; Gonzalez, J. Magnetic field effects in artificial dielectrics with arrays of magnetic wires at microwaves. J. Appl. Phys. 2011, 109, 053901. [Google Scholar] [CrossRef]
- Makhnovskiy, D.P.; Panina, L.V.; Garcia, C.; Zhukov, A.P.; Gonzalez, J. Experimental demonstration of tunable scattering spectra at microwave frequencies in composite media containing CoFeCrSiB glass-coated amorphous ferromagnetic wires and comparison with theory. Phys. Rev. B 2006, 74, 064205. [Google Scholar] [CrossRef]
- Luo, Y.; Peng, H.X.; Qin, F.X.; Ipatov, M.; Zhukova, V.; Zhukov, A.; Gonzalez. Fe-based ferromagnetic microwires enabled meta-composites. J. Appl. Phys. Lett. 2013, 103, 251902. [Google Scholar] [CrossRef]
- Lofland, S.E.; Bhagat, S.M.; Domínguez, M.; García-Beneytez, J. M.; Guerrero, F.; Vázquez, M. Low-field microwave magnetoimpedance in amorphous microwires. J. Appl. Phys. 1999, 85, 4442–4444. [Google Scholar] [CrossRef]
- Dominguez, M.; Garcia-Beneytez, J.M.; Vazquez, M.; Lofland, S.E.; Bhagat, S.M. Microwave response of amorphous microwires: magnetoimpedance and ferromagnetic resonance. J. Magn. Magn. Mater. 2002, 249, 117–121. [Google Scholar] [CrossRef]
- Hernando-Rydings, M.; Marín, P.; Aragon-Sanchez, A.; Bravo, E.; Lopez-Dominguez, V.; Martínez, I.; Fernandez, C.; Bilbao, A.; Serrano, F.; Vega, R.; et al. Development of a Telemetric System for Postoperative Follow-up of Vascular Surgery Procedures: In Vitro Model. J. Am. Heart Assoc. 2016, 5, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Rivero, G.; García-Páez, J.M.; Alvarez, L.; Multigner, M.; Valdes, J.; Carabias, I.; Spottorno, J.; Hernando, A. Sensor system for early detection of heart valve bioprostheses failure. Sens. Actuators A 2018, 142, 511–519. [Google Scholar] [CrossRef]
- Taylor, G.F. A Method of drawing metallic filaments and a discussion of their properties and uses. Phys. Rev. 1924, 23, 655–660. [Google Scholar] [CrossRef]
- Marín, P. Wireless stress sensor based on magnetic microwires. Magnetic Sensors—Development Trends and Applications. 2017. Chapter 2. Available online: https://www.intechopen.com/books/magnetic-sensors-development-trends-and-applications/wireless-stress-sensor-based-on-magnetic-microwires (accessed on 10 July 2019).
- Makhnovskiy, D.P.; Panina, L.V.; Mapps, D.J. Field-dependent surface impedance tensor in amorphous wires with two types of magnetic anisotropy: Helical and circumferential. Phys. Rev. B 2001, 63, 144424. [Google Scholar] [CrossRef]
- Hanson, G.W. Fundamental Transmitting Properties of Carbon Nanotube Antennas. IEEE Trans. Antennas Propag. 2005, 53, 3426–3435. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Maze-Merceur, G. Microwave characterization of 2-D random materials: numerical simulations and experiments. IEEE Trans. Microwave Theory Tech. 1998, 46, 1478–1483. [Google Scholar] [CrossRef]
- Semirov, A.V.; Derevyanko, M.S.; Bukreev, D.A.; Moiseev, A.A.; Kudryavtsev, V.O.; Safronov, A.P. Magnetoimpedance of cobalt-based amorphous ribbons/polymer composites. J. Magn. Magn. Mater. 2016, 415, 97–101. [Google Scholar] [CrossRef]
- Nabias, J.; Asfour, A.; Yonnet, J.-P. Temperature dependence of giant magnetoimpedance in amorphous microwires for sensor application. IEEE Trans. Magn. 2017, 53, 4001005. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moya, A.; Archilla, D.; Navarro, E.; Hernando, A.; Marín, P. Scattering of Microwaves by a Passive Array Antenna Based on Amorphous Ferromagnetic Microwires for Wireless Sensors with Biomedical Applications. Sensors 2019, 19, 3060. https://doi.org/10.3390/s19143060
Moya A, Archilla D, Navarro E, Hernando A, Marín P. Scattering of Microwaves by a Passive Array Antenna Based on Amorphous Ferromagnetic Microwires for Wireless Sensors with Biomedical Applications. Sensors. 2019; 19(14):3060. https://doi.org/10.3390/s19143060
Chicago/Turabian StyleMoya, Alberto, Diego Archilla, Elena Navarro, Antonio Hernando, and Pilar Marín. 2019. "Scattering of Microwaves by a Passive Array Antenna Based on Amorphous Ferromagnetic Microwires for Wireless Sensors with Biomedical Applications" Sensors 19, no. 14: 3060. https://doi.org/10.3390/s19143060
APA StyleMoya, A., Archilla, D., Navarro, E., Hernando, A., & Marín, P. (2019). Scattering of Microwaves by a Passive Array Antenna Based on Amorphous Ferromagnetic Microwires for Wireless Sensors with Biomedical Applications. Sensors, 19(14), 3060. https://doi.org/10.3390/s19143060






