Improved SH0 Guided Wave Transducers Based on Piezoelectric Fiber Patches †
Abstract
1. Introduction
2. Materials and Methods
2.1. A Short Review of SH0 Wave Generation with the SHPFP
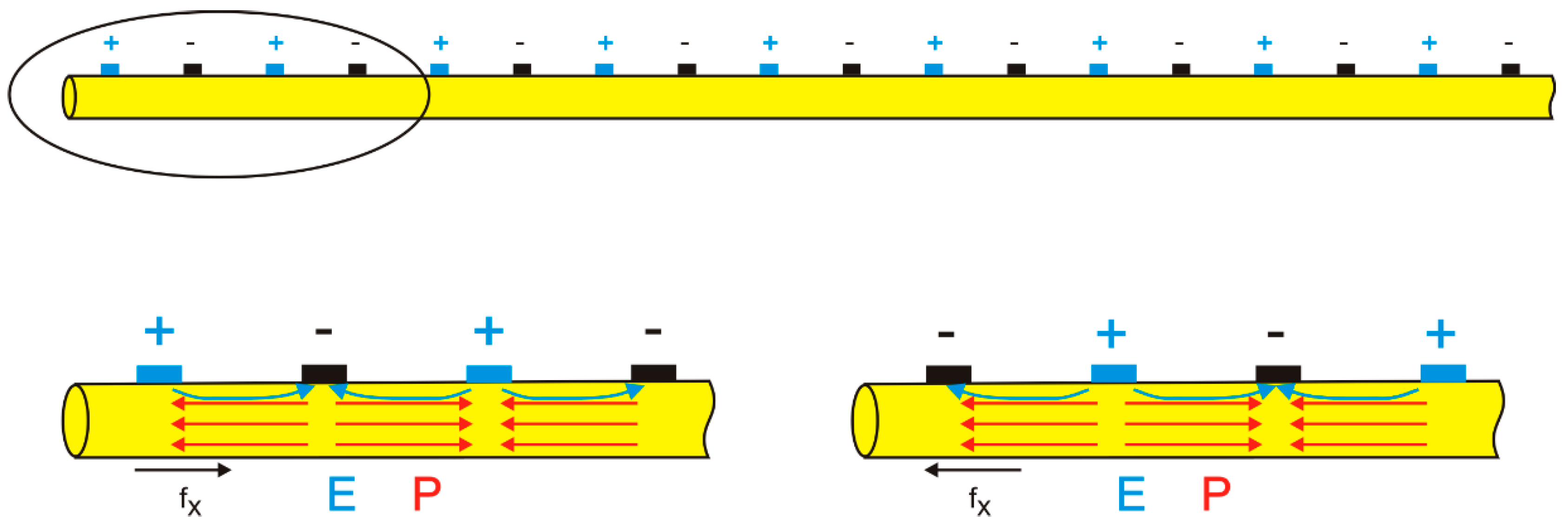
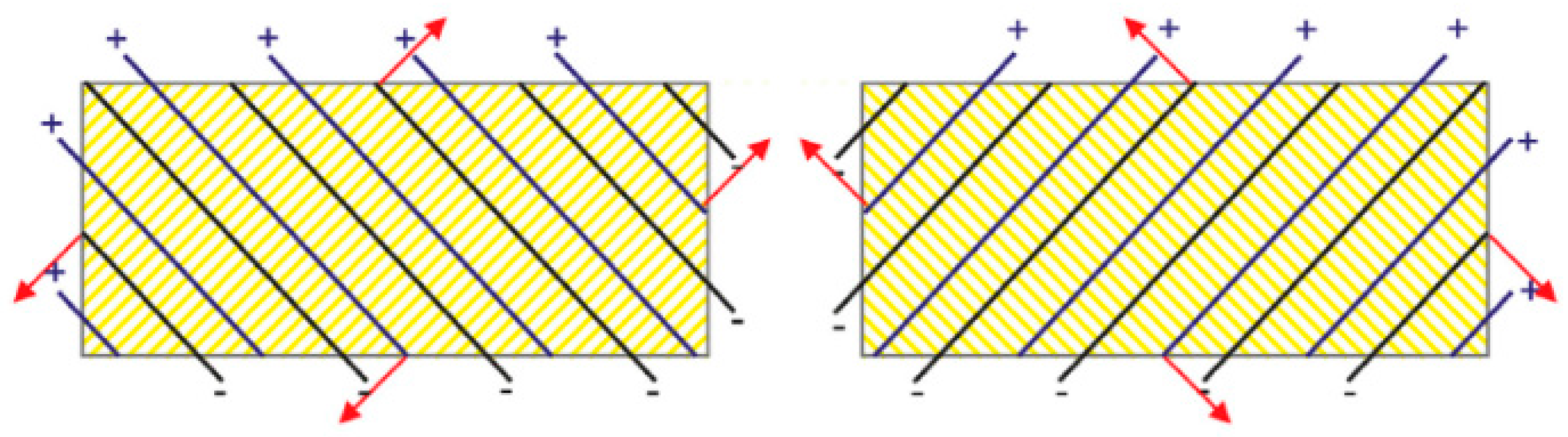
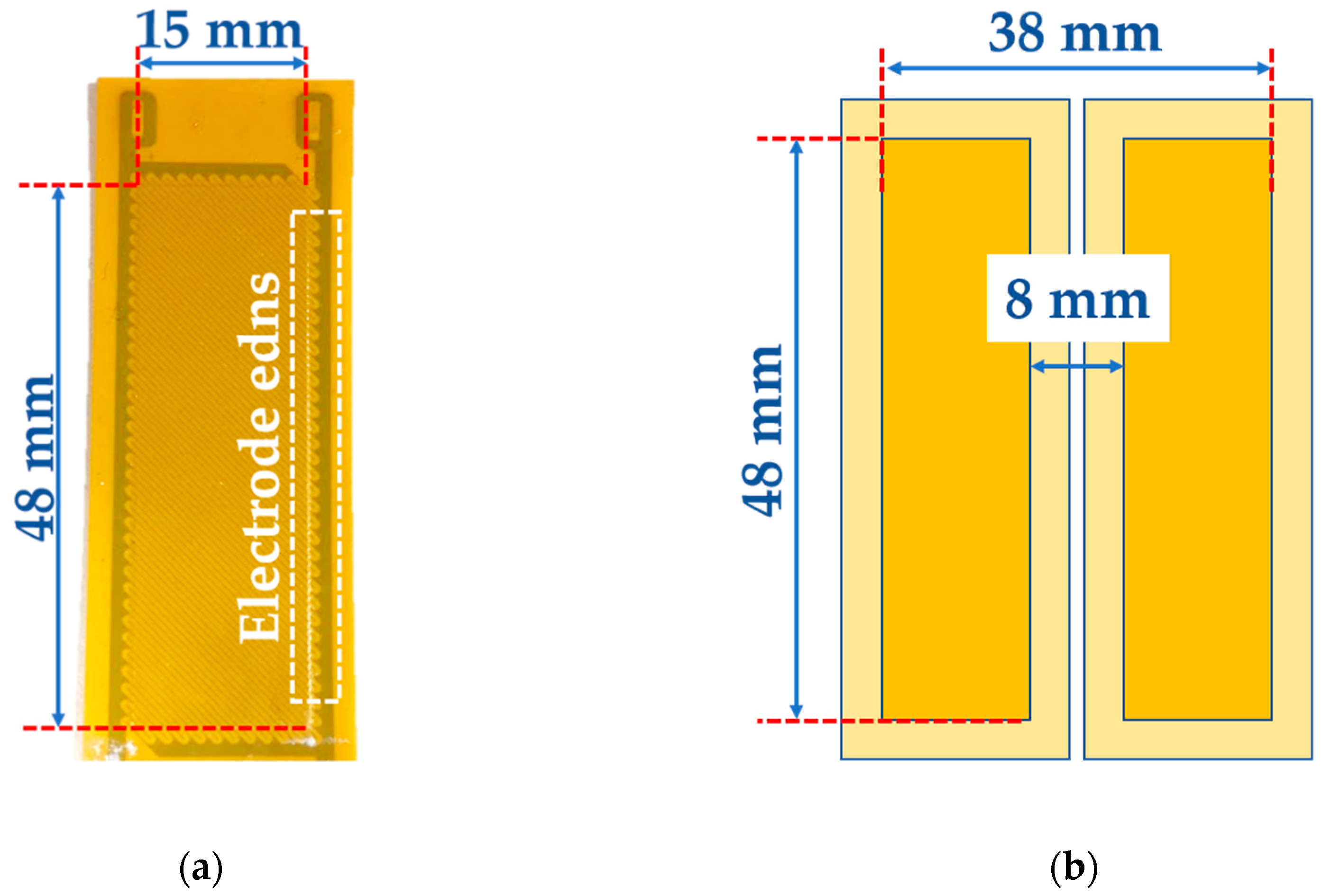
2.1.1. Piezoelectric Fiber Patches (PFPs) for Guided Wave Generation
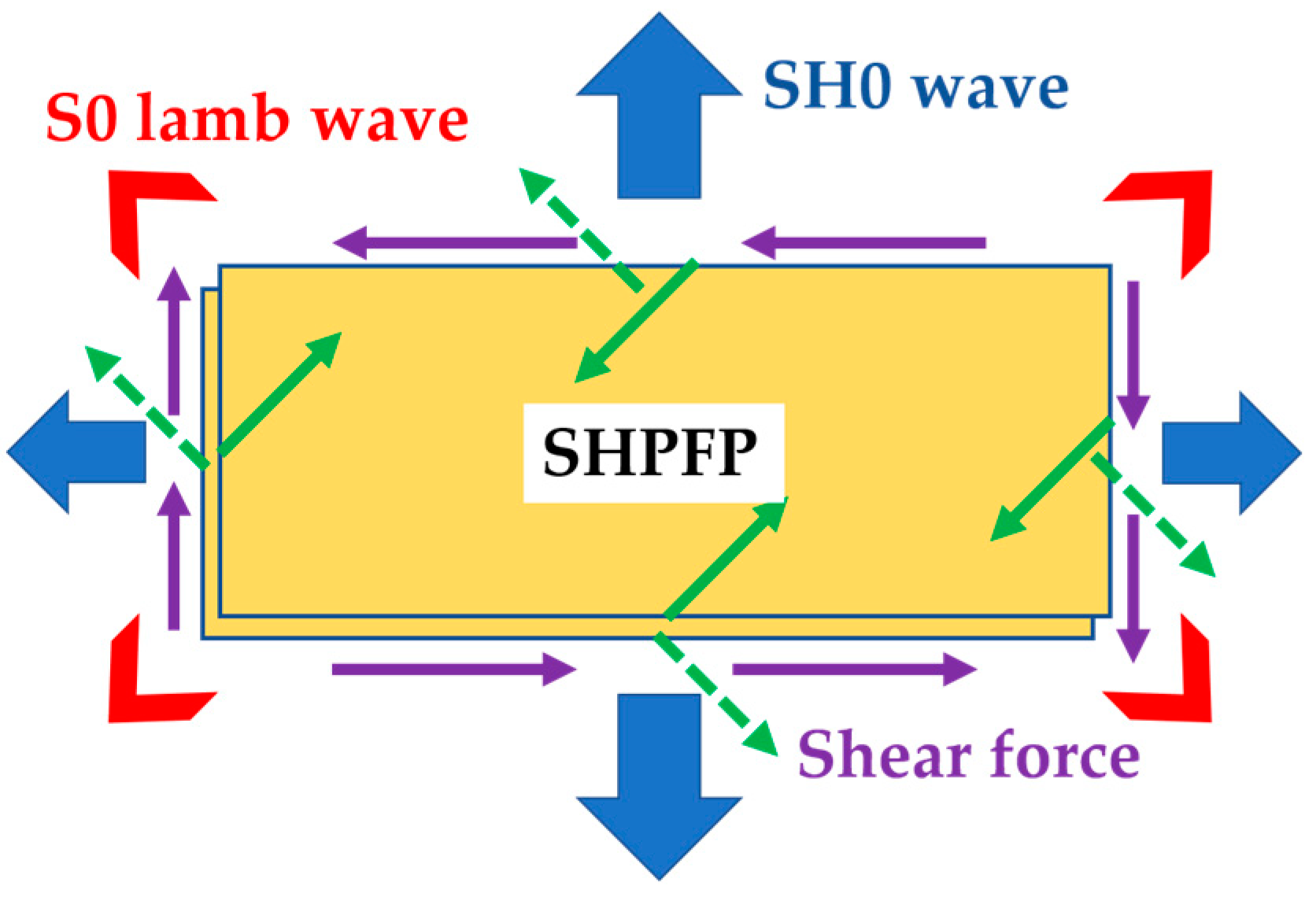
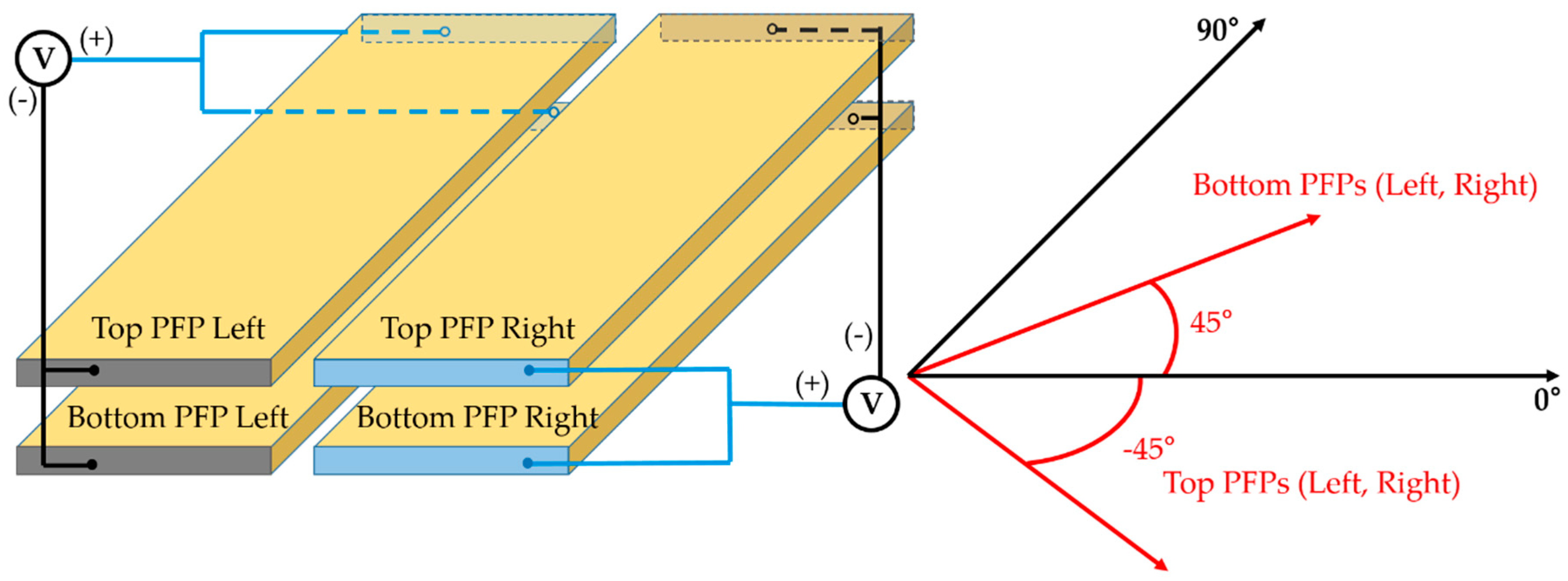
2.1.2. The Working Principle and Configuration of the SHPFP
2.1.3. Optimization Criteria
2.2. Modified Designs
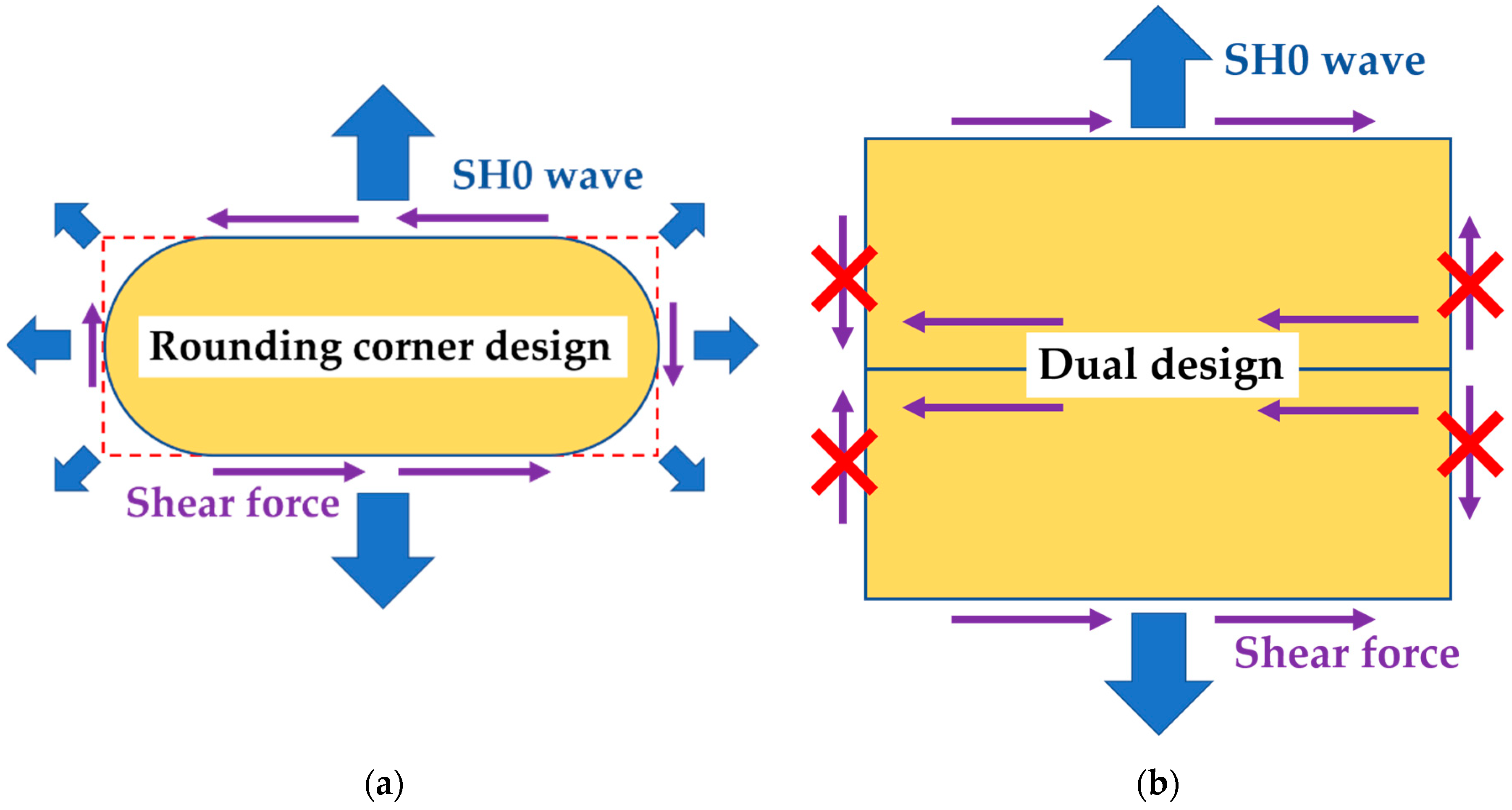
2.2.1. Change in the Transducer’s Shape (Rounded Corner SHPFP)
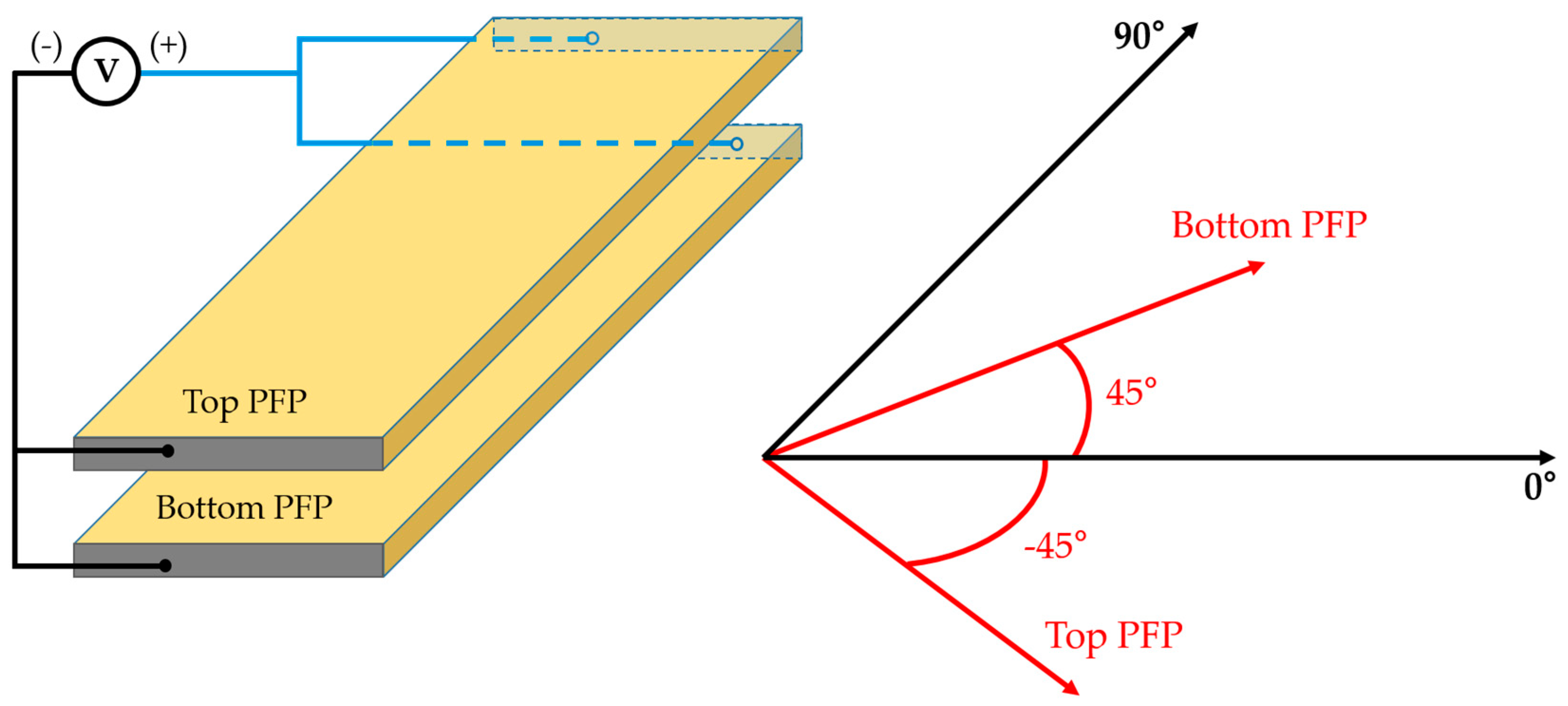
2.2.2. The Dual Transducer (Dual SHPFP)
2.3. Finite Element Method (FEM) Simulation Setup
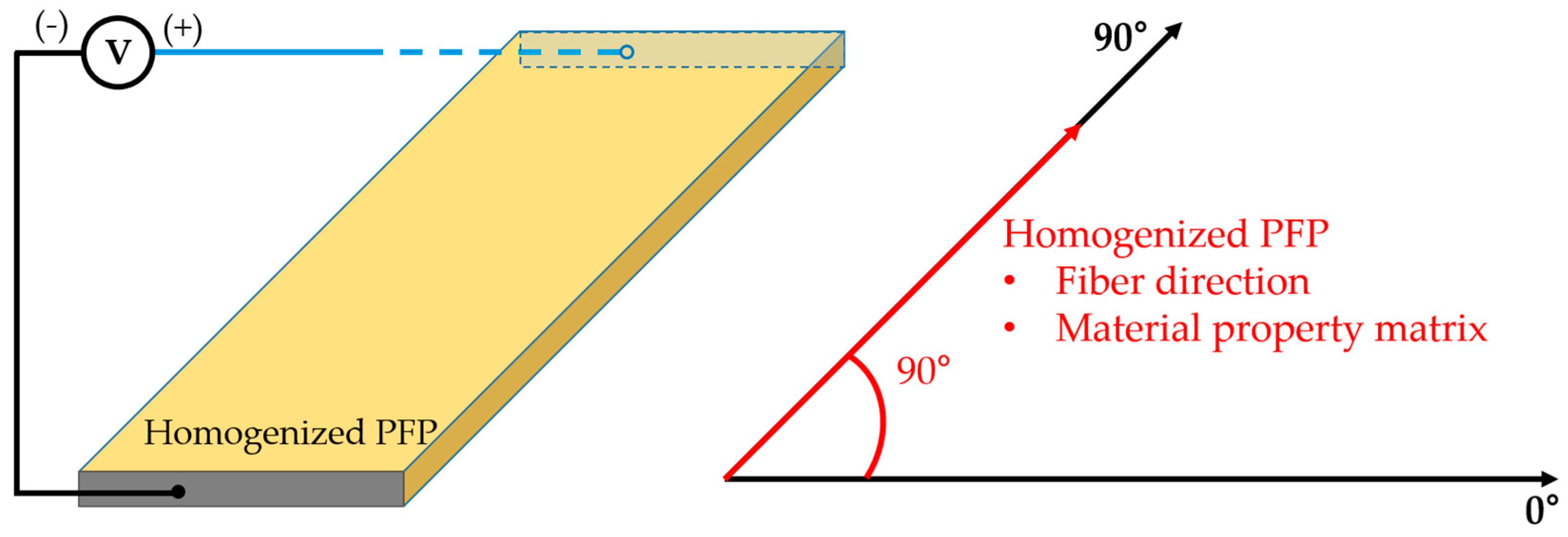
2.3.1. Homogenized PFP Model Verification
2.3.2. Modeling Details
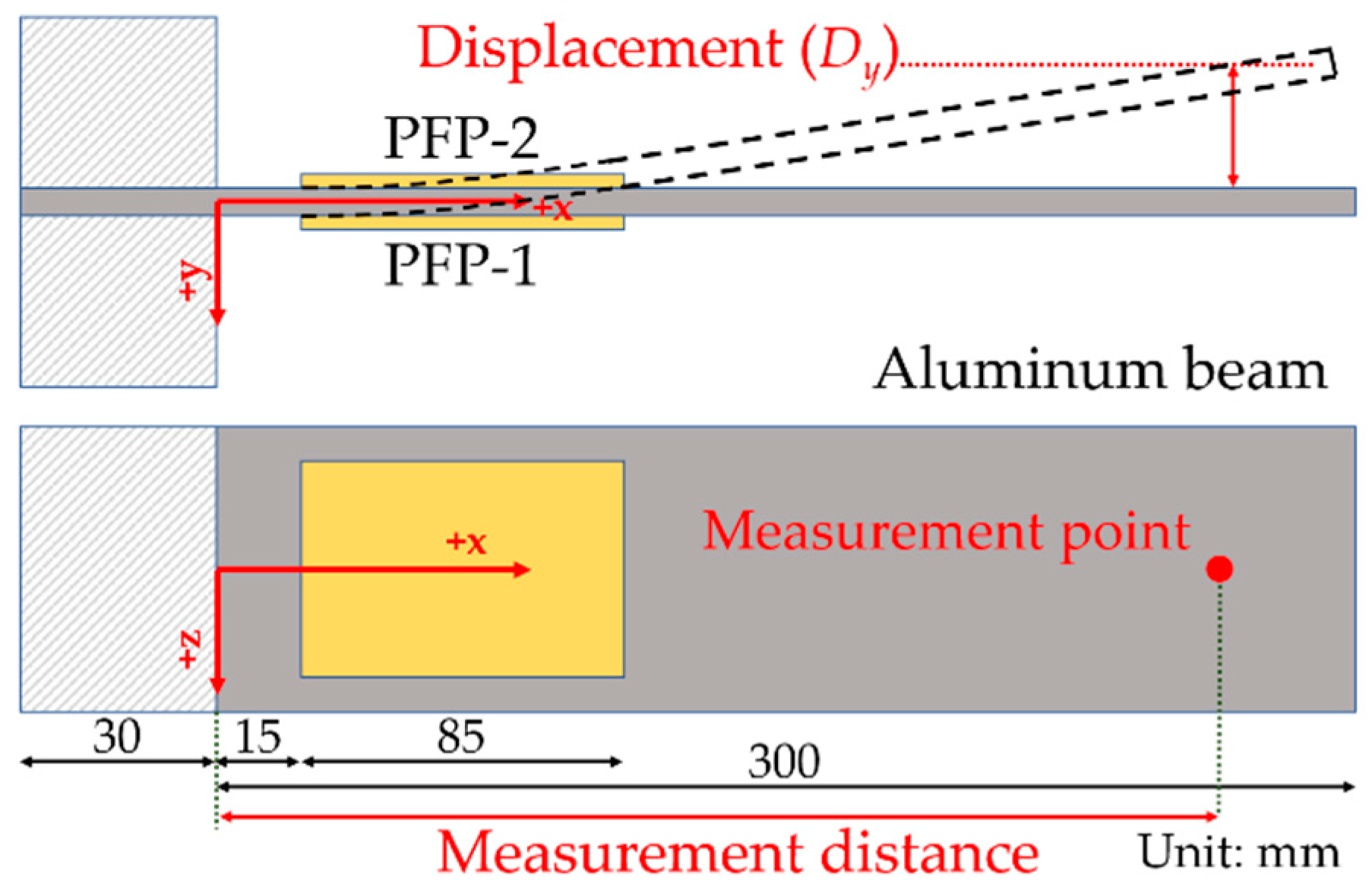
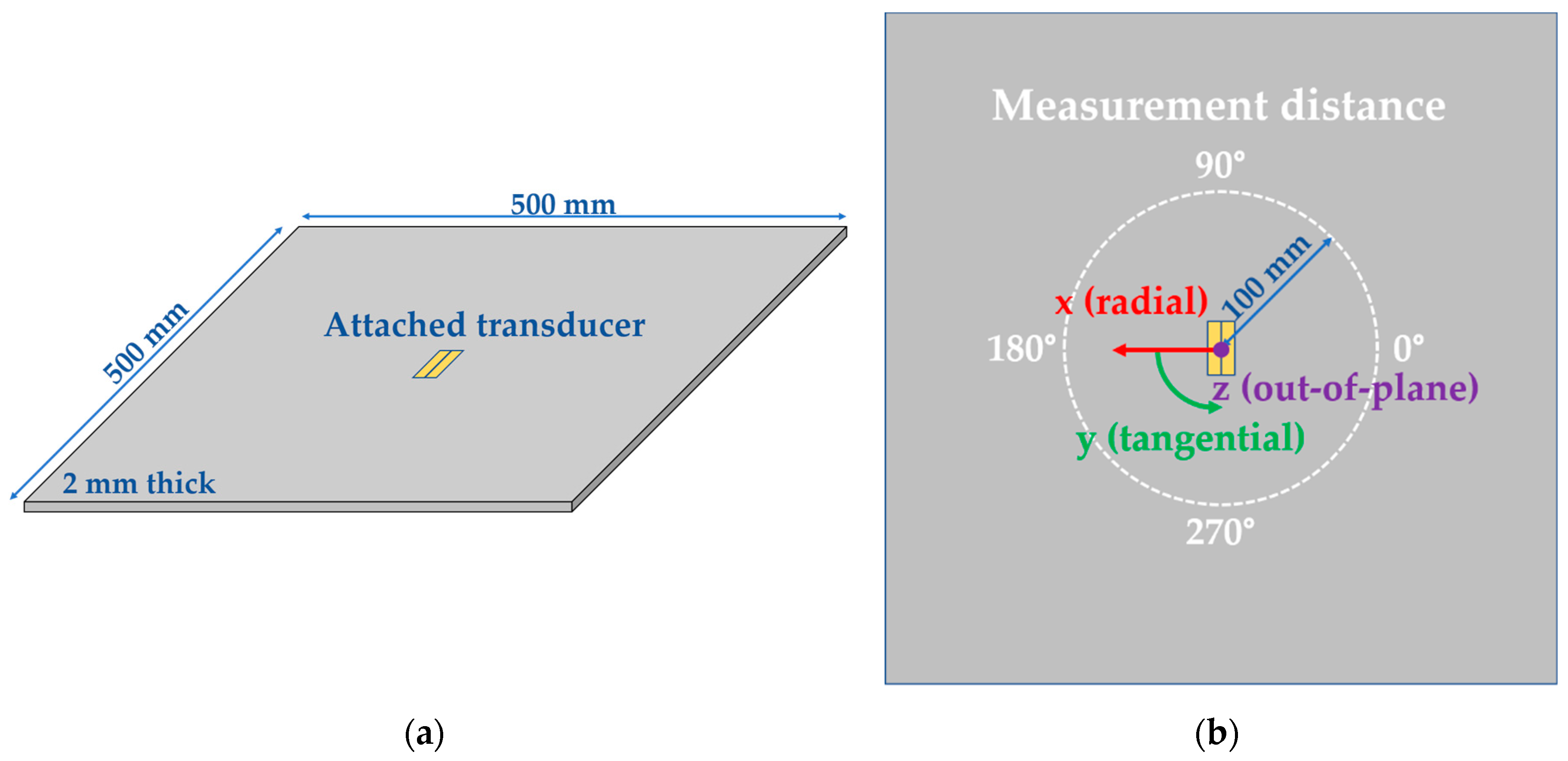
2.4. Experimental Setup
3. Results
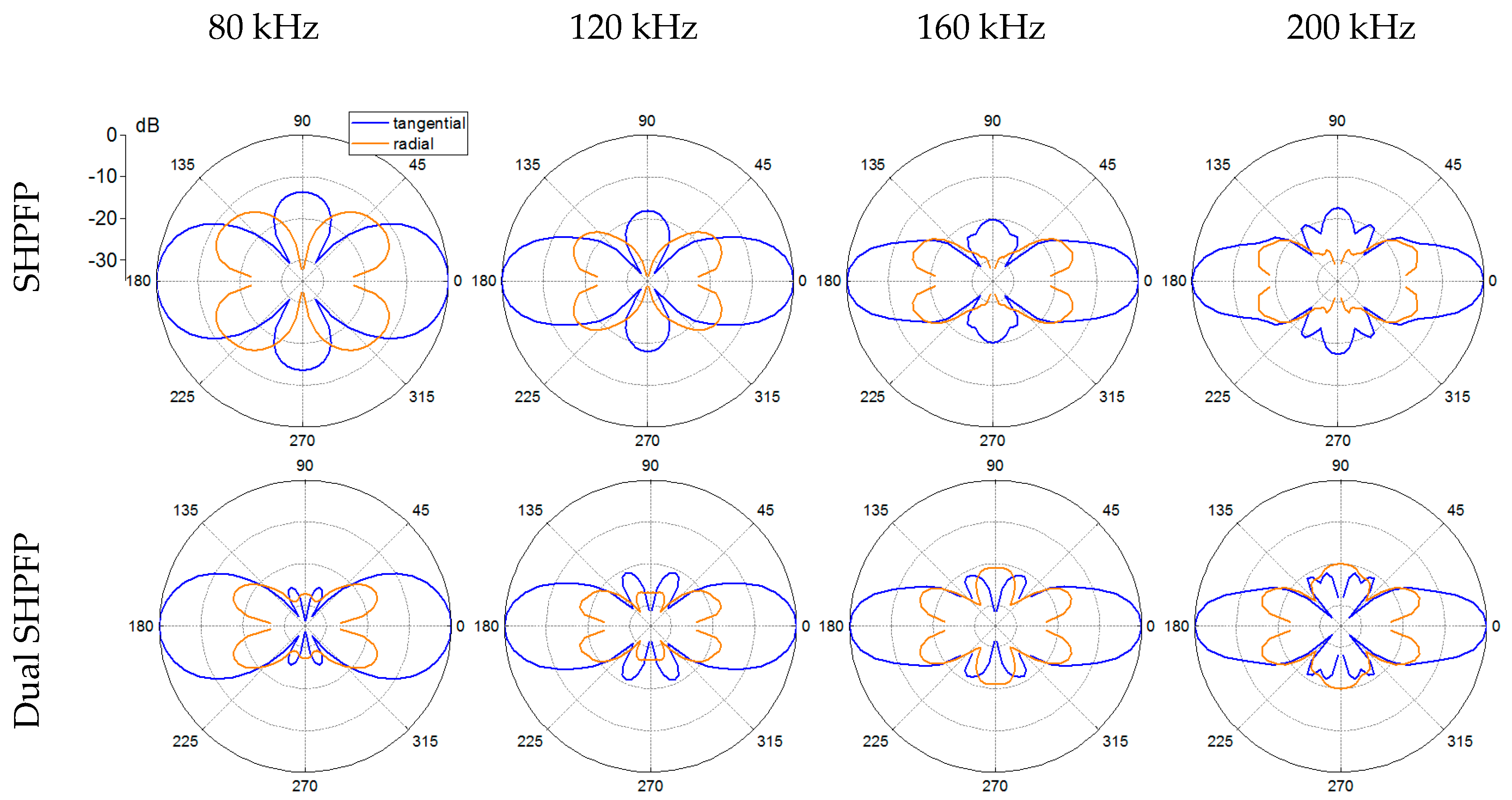
3.1. Results from the Simulation of the Modified Designs
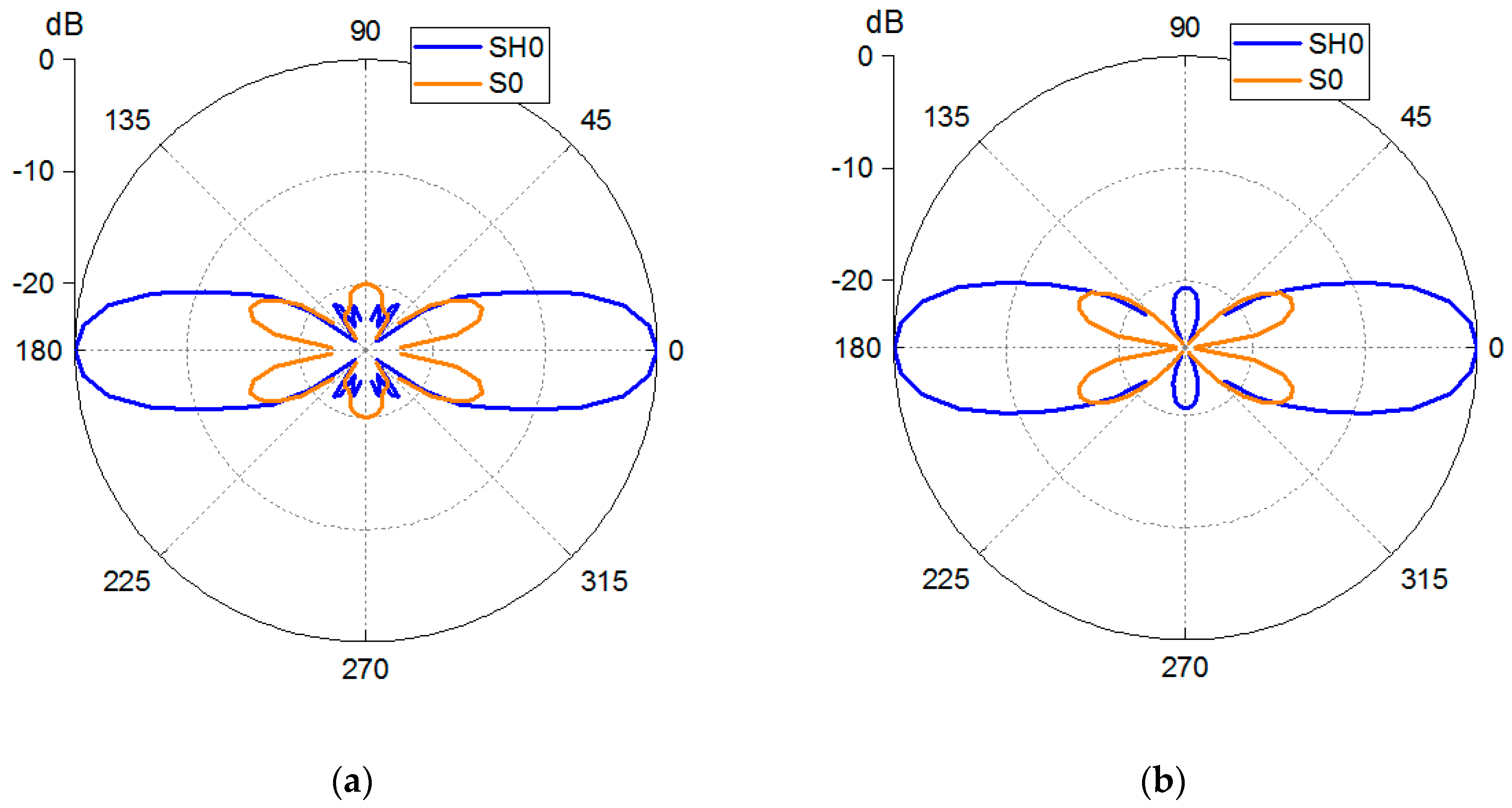
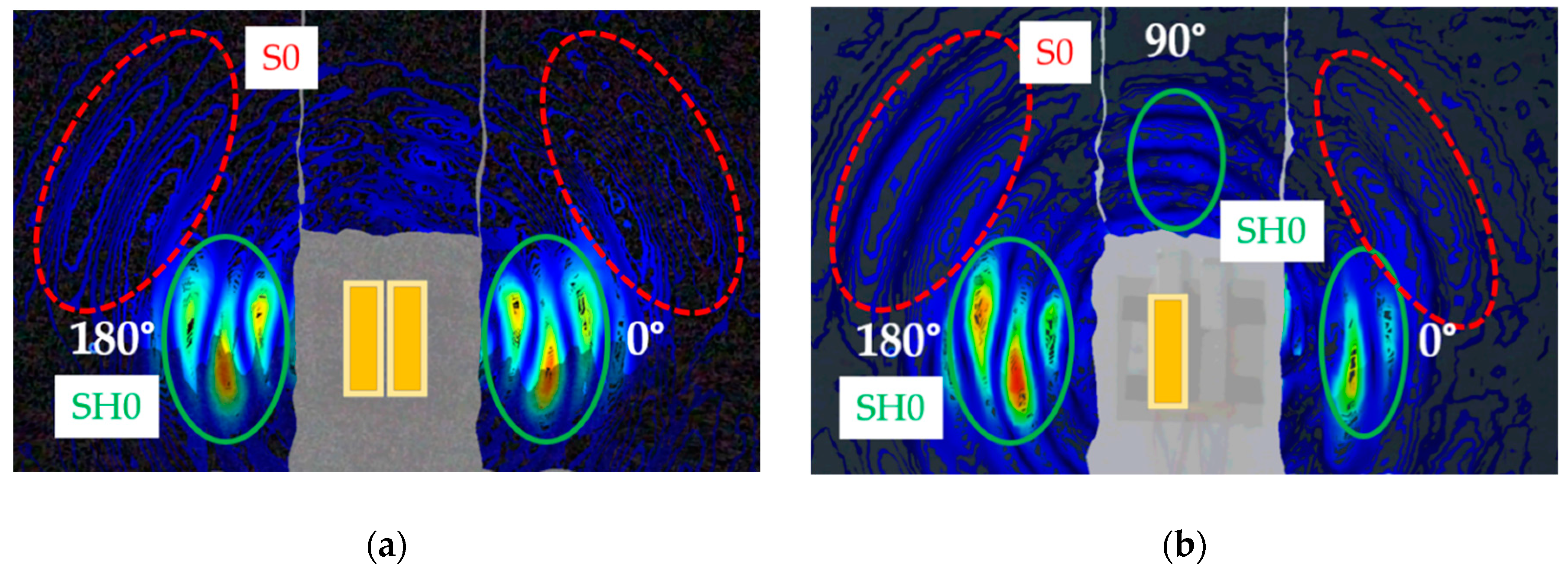
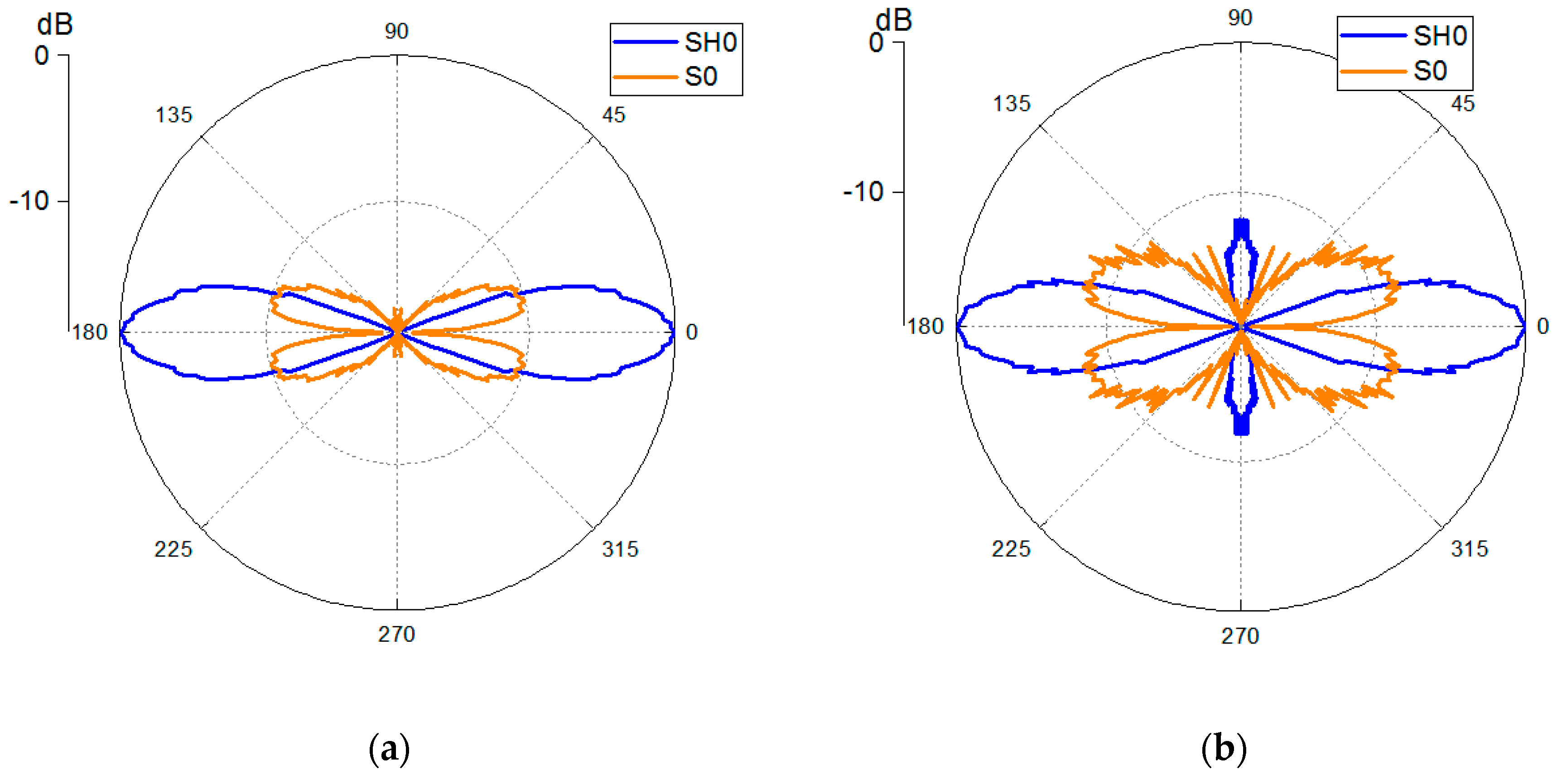
3.1.1. Rounded-Corner SHPFP
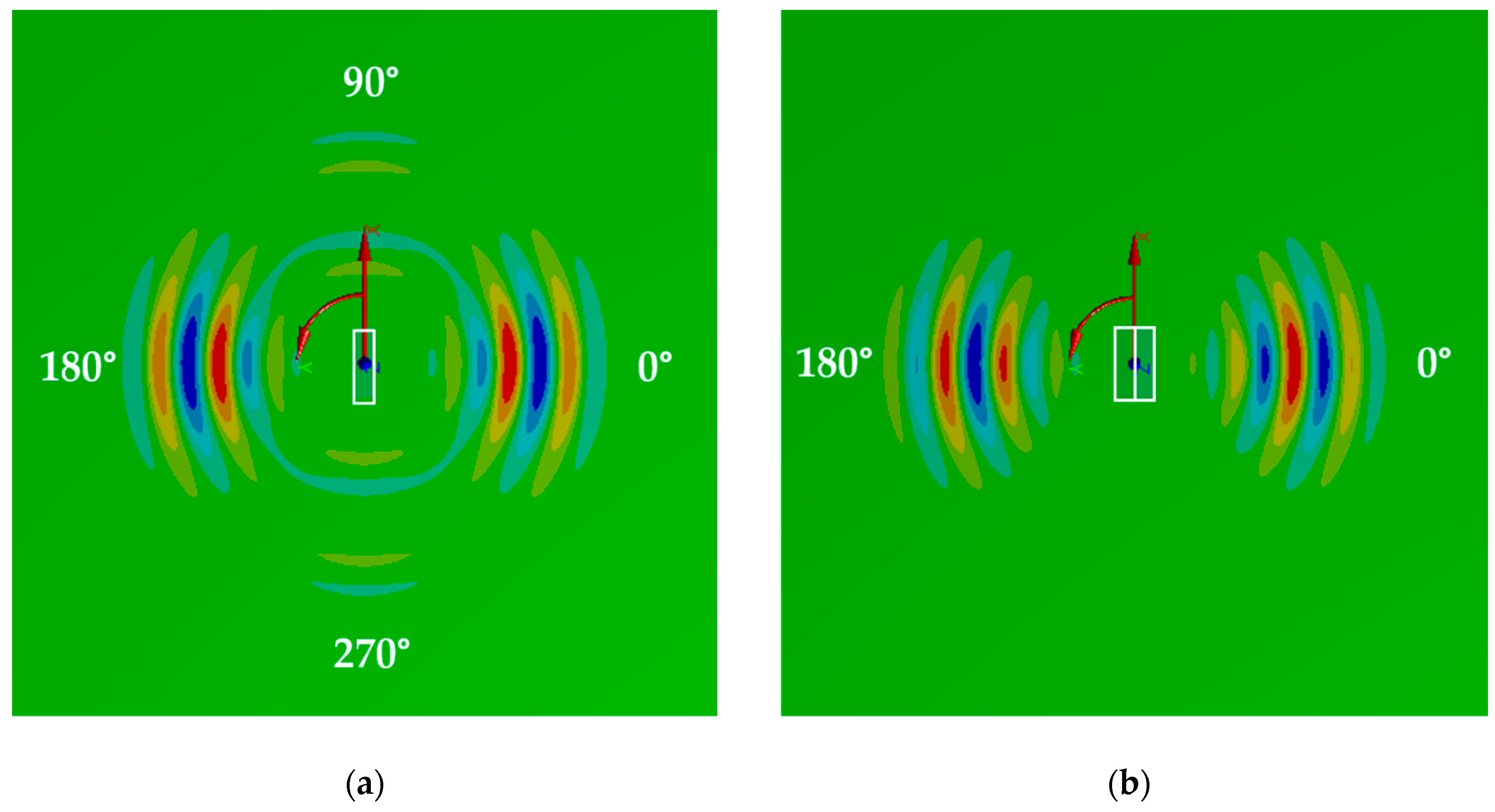
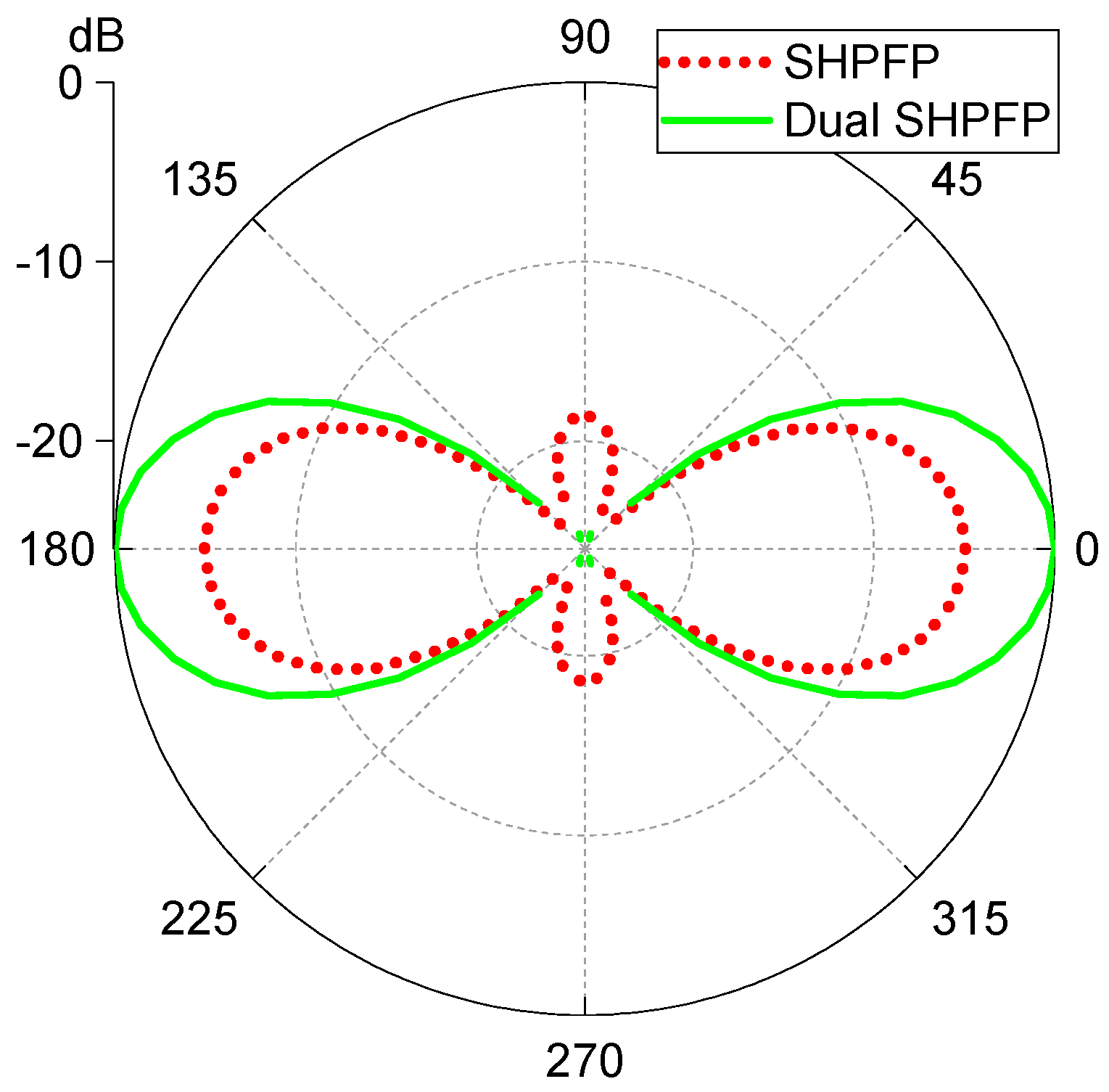
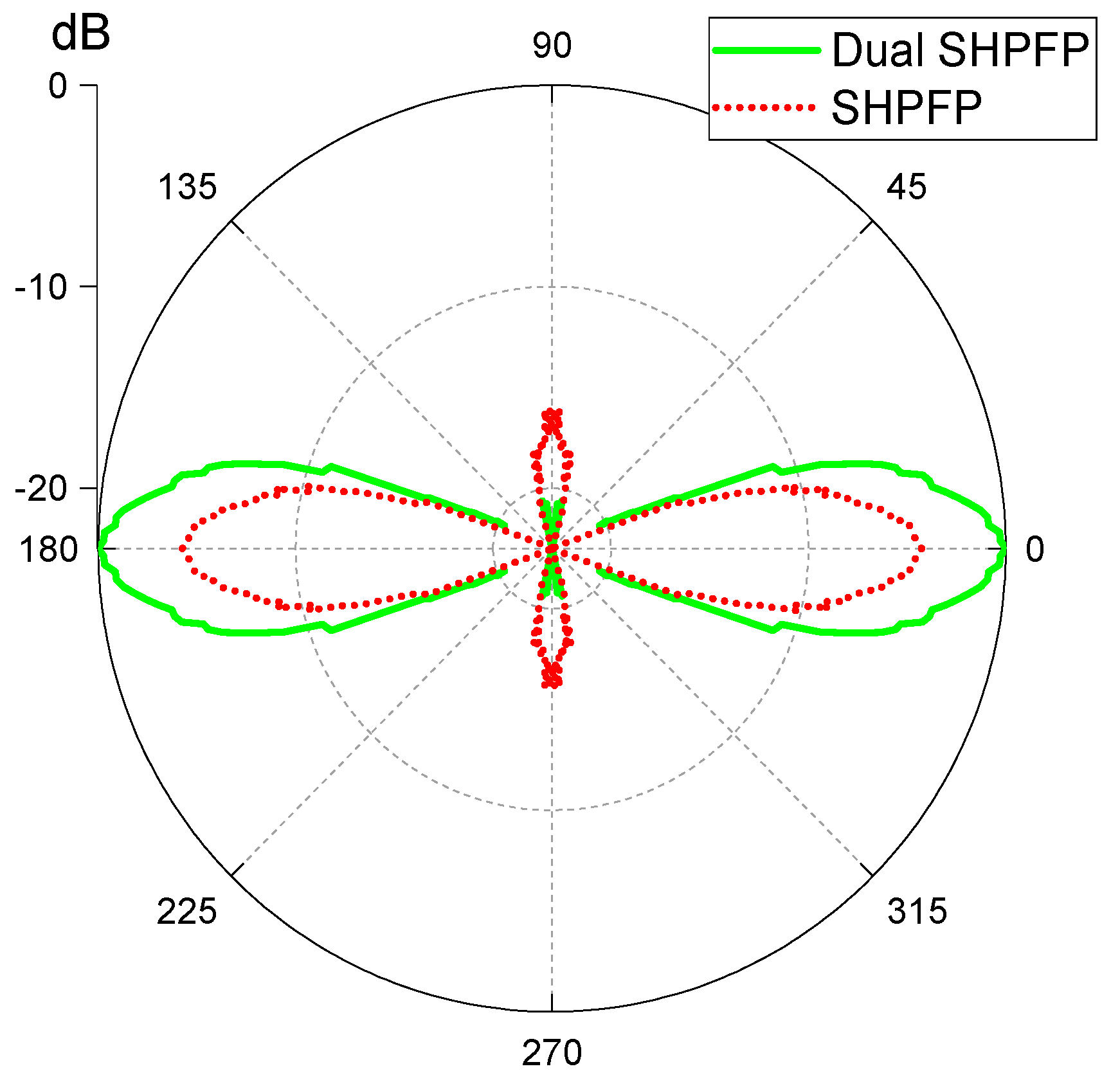
3.1.2. Dual SHPFP
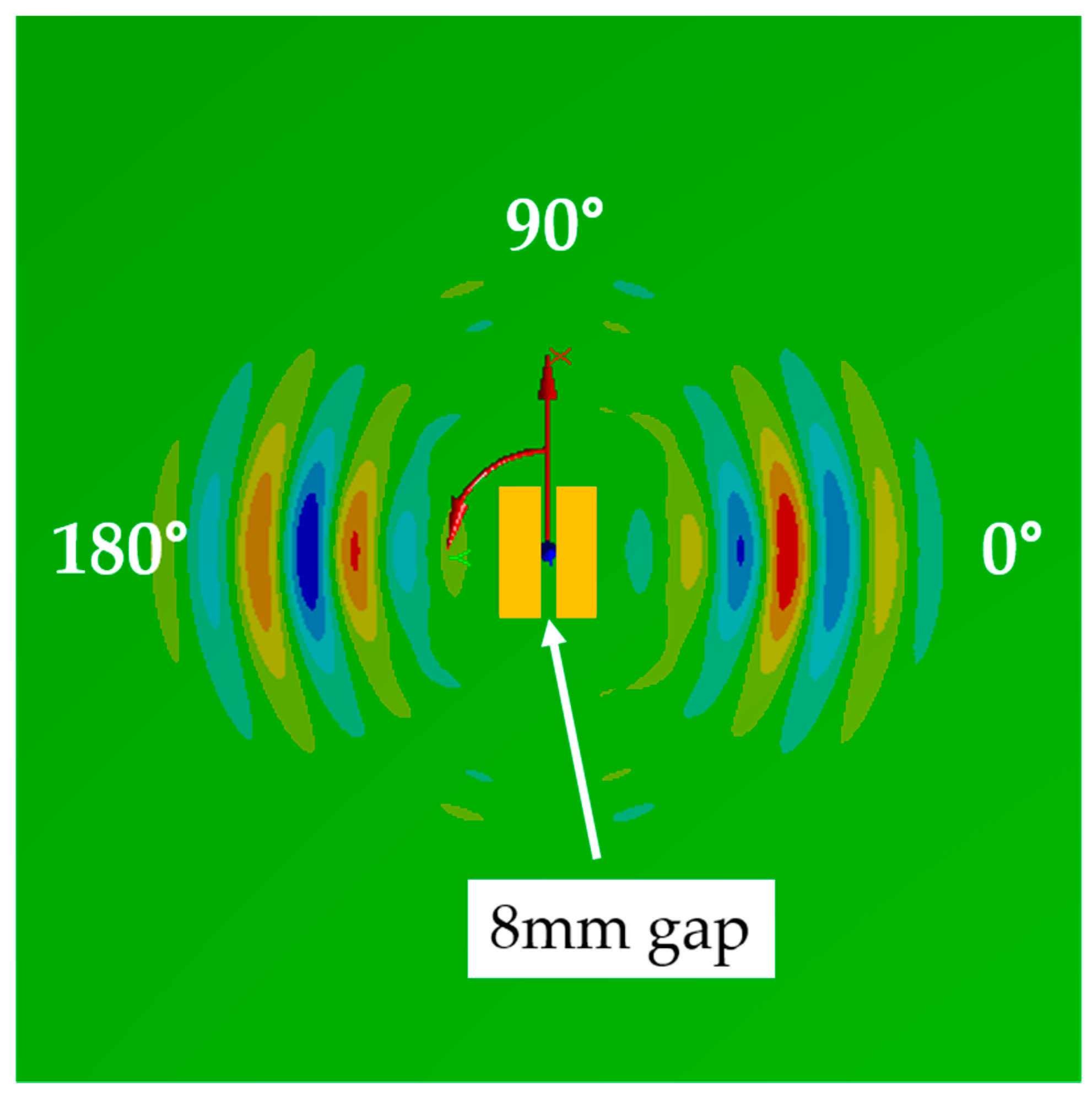
3.1.3. Dual SHPFP with an 8-mm Gap
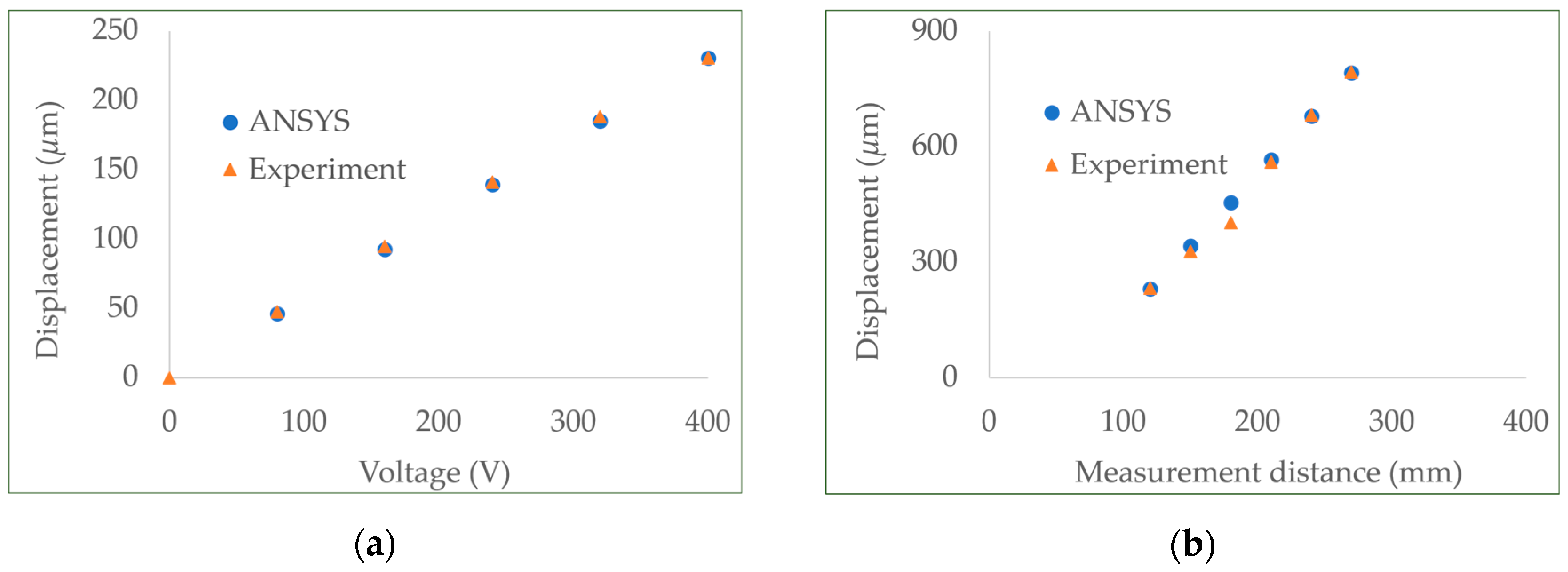
3.2. Experimental Results
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Giurgiutiu, V. Structural Health Monitoring: With Piezoelectric Wafer Active Sensors; Academic Press: Burlington, NJ, USA, 2007. [Google Scholar]
- Monkhouse, R.; Wilcox, P.; Cawley, P. Flexible interdigital PVDF transducers for the generation of Lamb waves in structures. Ultrasonics 1997, 35, 489–498. [Google Scholar] [CrossRef]
- Hall, J.S.; Michaels, J.E. Adaptive dispersion compensation for guided wave imaging. AIP Conf. Proc. 2012, 1430, 623–630. [Google Scholar]
- Thompson, R.B. Physical principles of measurements with EMAT transducers. Phys. Acoust. 1990, 19, 157–200. [Google Scholar]
- Wilcox, P.; Lowe, M.; Cawley, P. Omnidirectional guided wave inspection of large metallic plate structures using an EMAT array. IEEE Trans. UFFC 2005, 52, 653–665. [Google Scholar] [CrossRef]
- Kannan, E.; Maxfield, B.; Balasubramaniam, K. SHM of pipes using torsional waves generated by in situ magnetostrictive tapes. Smart Mater. Struct. 2007, 16, 2505–2515. [Google Scholar] [CrossRef]
- Lee, M.K.; Lee, J.S.; Kim, Y.Y. An SH wave magnetostrictive patch transducer for ultrasonic inspection of a plate-like structures. In Proceedings of the 2010 IEEE Ultrasonics Symposium (IUS), San Diego, CA, USA, 11–14 October 2010; pp. 1164–1165. [Google Scholar]
- Seung, H.M.; Kim, H.W.; Kim, Y.Y. Development of an omni-directional shear-horizontal wave magnetostrictive patch transducer for plates. Ultrasonics 2013, 53, 1304–1308. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.W.; Lee, J.K.; Kim, Y.Y. Circumferential phased array of shear-horizontal wave magnetostrictive patch transducers for pipe inspection. Ultrasonics 2013, 53, 423–431. [Google Scholar] [CrossRef]
- Köhler, B.; Gaul, T.; Lieske, U.; Schubert, F. Shear horizontal piezoelectric fiber patch transducers (SH-PFP) for guided elastic wave applications. NDT E Int. 2016, 82, 1–12. [Google Scholar] [CrossRef]
- Kamal, A.; Giurgiutiu, V. Shear horizontal wave excitation and reception with shear horizontal piezoelectric wafer active sensor (SH-PWAS). Smart Mater. Struct. 2014, 23, 085019. [Google Scholar] [CrossRef]
- Boivin, G.; Viens, M.; Belanger, P. Development of a low frequency shear horizontal piezoelectric transducer for the generation of plane SH waves. AIP Conf. Proc. 2016, 1706, 030019. [Google Scholar]
- Huan, Q.; Miao, H.; Li, F. A nearly perfect omnidirectional shear-horizontal (SH) wave transducer based on a thickness poled, thickness-shear (d15) piezoelectric ring. arXiv 2017, arXiv:1704.03629. [Google Scholar]
- Zhang, S.; Jiang, W.; Meyer, R.J., Jr.; Li, F.; Luo, J.; Cao, W. Measurements of face shear properties in relaxor-PbTiO3 single crystals. J. Appl. Phys. 2011, 110, 064106. [Google Scholar] [CrossRef]
- Zhou, W.; Li, H.; Yuan, F. Fundamental understanding of wave generation and reception using d 36 type piezoelectric transducers. Ultrasonics 2015, 57, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Dong, S.; Li, F. Excitation of fundamental shear horizontal wave by using face-shear (d36) piezoelectric ceramics. J. Appl. Phys. 2016, 119, 174101. [Google Scholar] [CrossRef]
- Miao, H.; Huan, Q.; Li, F. Excitation and reception of pure shear horizontal waves by using face-shear d24 mode piezoelectric wafers. arXiv 2016, arXiv:1604.03765. [Google Scholar]
- Miao, H.; Huan, Q.; Wang, Q.; Li, F. A new omnidirectional shear horizontal wave transducer using face-shear (d 24) piezoelectric ring array. Ultrasonics 2017, 74, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Belanger, P.; Boivin, G. Piezoceramic omnidirectional transduction of the fundamental shear horizontal guide wave mode. In Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, and Civil Infrastructure; International Society for Optics and Photonics: Bellingham, WA, USA, 2016; Volume 98040. [Google Scholar]
- Miao, H.; Huan, Q.; Li, F.; Kang, G. A variable-frequency bidirectional shear horizontal (SH) wave transducer based on dual face-shear (d24) piezoelectric wafers. Ultrasonics 2018, 89, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Mańka, M.; Rosiek, M.; Martowicz, A.; Stepinski, T.; Uhl, T. Lamb wave transducers made of piezoelectric macro-fiber composite. Struct. Control Health Monit. 2013, 20, 1138–1158. [Google Scholar]
- Köhler, B.; Schubert, F.; Barth, M.; Frankenstein, B. Selective excitation and detection of Lamb waves for SHM applications. In Proceedings of the Fourth European Workshop on Structural Health 2008, Krakow, Poland, 2–4 July 2008; pp. 706–714. [Google Scholar]
- Schubert, L.; Barth, M.; Klesse, T.; Köhler, B.; Frankenstein, B. Guided elastic waves and their impact interaction in CFRP structures characterized by 3D laser scanning vibrometry. In Proceedings of the 15th International Symposium on: Smart Structures and Materials Nondestructive Evaluation and Health Monitoring 2008, San Diego, CA, USA, 9–13 March 2008. [Google Scholar]
- Barth, M.; Köhler, B.; Schubert, L. 3D-Visualisation of Lamb waves by laser vibrometry. In Proceedings of the 4th European Workshop on Structural Health Monitoring 2008, Krakow, Poland, 2–4 July 2008; pp. 640–647. [Google Scholar]
- Kim, Y.; Köhler, B. Improved shear horizontal wave piezoelectric fiber patch (SH-PFP) for structural health monitoring applications. In Proceedings of the 10th International Symposium on NDT in Aerospace, Dresden, Germany, 24–26 October 2018. [Google Scholar]
- Sachau, D.; Wierach, P.; Monner, H.P.; Schönecker, A. Smart structures based on thin piezoceramic plates. Funct. Mater. 2000, 13, 520–524. [Google Scholar]
- Beckert, W.; Kreher, W.S. Modelling piezoelectric modules with interdigitated electrode structures. Comput. Mater. Sci. 2003, 26, 36–45. [Google Scholar] [CrossRef]
- Weight, J.P. A model for the propagation of short pulses of ultrasound in a solid. J. Acoust. Soc. Am. 1978, 81, 815–826. [Google Scholar] [CrossRef]
- Hamilton, R.; Hayward, G. The Modelling, Design and Applications of Controllable Composite Transducers. In Ultrasonics International 91: Conference Proceedings; Butterworth Heinemann: Oxford, UK, 1991; p. 367. [Google Scholar]
- Williams, R.B.; Inman, D.J.; Wilkie, W.K. Nonlinear response of the macro fiber composite actuator to monotonically increasing excitation voltage. J. Intell. Mater. Syst. Struct. 2006, 17, 601–608. [Google Scholar] [CrossRef]
- Bowen, C.R.; Giddings, P.F.; Salo, A.I.; Kim, H.A. Modeling and Characterization of Piezoelectrically Actuated Bistable Composites. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1737–1749. [Google Scholar] [CrossRef] [PubMed]
- Auld, B. General electromechanical reciprocity relations applied to the calculation of elastic wave scattering coefficients. Wave Motion 1979, 1, 3–10. [Google Scholar] [CrossRef]
- Koehler, B.; Frankenstein, B.; Schubert, F.; Barth, M. Novel piezoelectric fiber transducers for mode selective excitation and detection of lamb waves. AIP Conf. Proc. 2009, 1096, 982–989. [Google Scholar]
- Stepinski, T.; Mańka, M.; Martowicz, A. Interdigital Lamb Wave Transducers for Applications in Structural Health Monitoring. NDT E Int. 2016, 86, 199–210. [Google Scholar] [CrossRef]

| Properties | Value |
|---|---|
| (GPa) | 29.4 |
| (GPa) | 15.2 |
| (GPa) | 6.06 |
| 0.312 | |
| 0.16 | |
| (pm/V) | 467 |
| (pm/V) | −210 |
| (pm/V) | −210 |
| 712 | |
| 1.7 | |
| 737 |
| SHPFP Purity Ratio | Dual SHPFP Purity Ratio | Increment | |
|---|---|---|---|
| 80 | 3.977 | 6.493 | 160% |
| 100 | 5.304 | 10.707 | 202% |
| 120 | 6.010 | 7.427 | 124% |
| 140 | 5.372 | 7.053 | 131% |
| 160 | 5.488 | 6.081 | 111% |
| 180 | 5.452 | 5.814 | 107% |
| 200 | 5.477 | 5.595 | 102% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Gaul, T.; Köhler, B. Improved SH0 Guided Wave Transducers Based on Piezoelectric Fiber Patches. Sensors 2019, 19, 2990. https://doi.org/10.3390/s19132990
Kim Y, Gaul T, Köhler B. Improved SH0 Guided Wave Transducers Based on Piezoelectric Fiber Patches. Sensors. 2019; 19(13):2990. https://doi.org/10.3390/s19132990
Chicago/Turabian StyleKim, Yongtak, Tobias Gaul, and Bernd Köhler. 2019. "Improved SH0 Guided Wave Transducers Based on Piezoelectric Fiber Patches" Sensors 19, no. 13: 2990. https://doi.org/10.3390/s19132990
APA StyleKim, Y., Gaul, T., & Köhler, B. (2019). Improved SH0 Guided Wave Transducers Based on Piezoelectric Fiber Patches. Sensors, 19(13), 2990. https://doi.org/10.3390/s19132990





