An Efficient Framework for Estimating the Direction of Multiple Sound Sources Using Higher-Order Generalized Singular Value Decomposition
Abstract
1. Introduction
2. Preliminaries
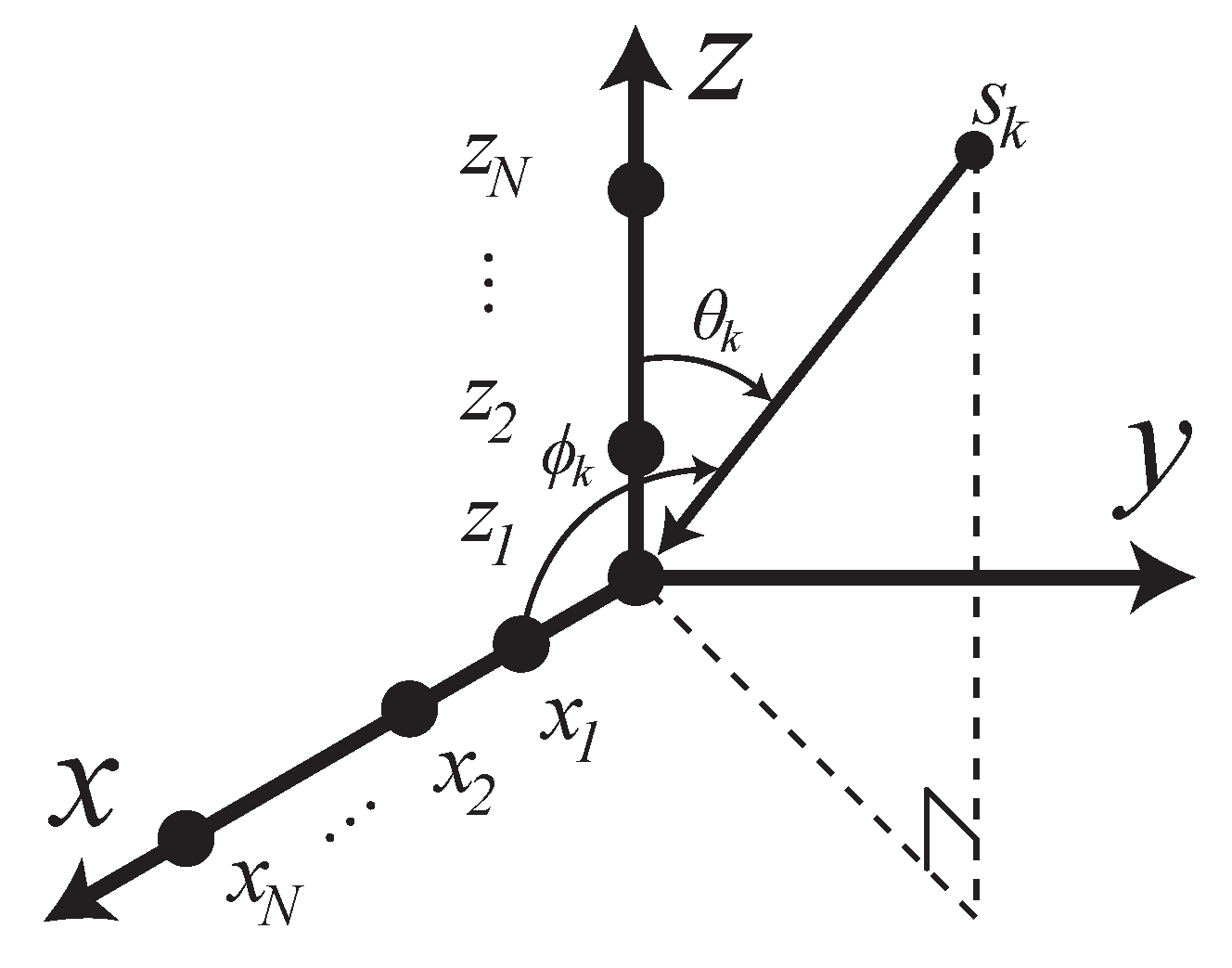
2.1. Data Model
2.2. Basic Assumptions
2.3. Transformation Problem
3. Proposed Method
3.1. Problem for Estimating the Transformation Matrix and Its Solution
3.2. Estimation of the Transformation Matrices by HOGSVD
3.3. DOA Estimation Scheme
3.3.1. DOA Estimation Scheme via MUSIC
3.3.2. DOA Estimation Scheme via ESPRIT
4. Numerical Simulations
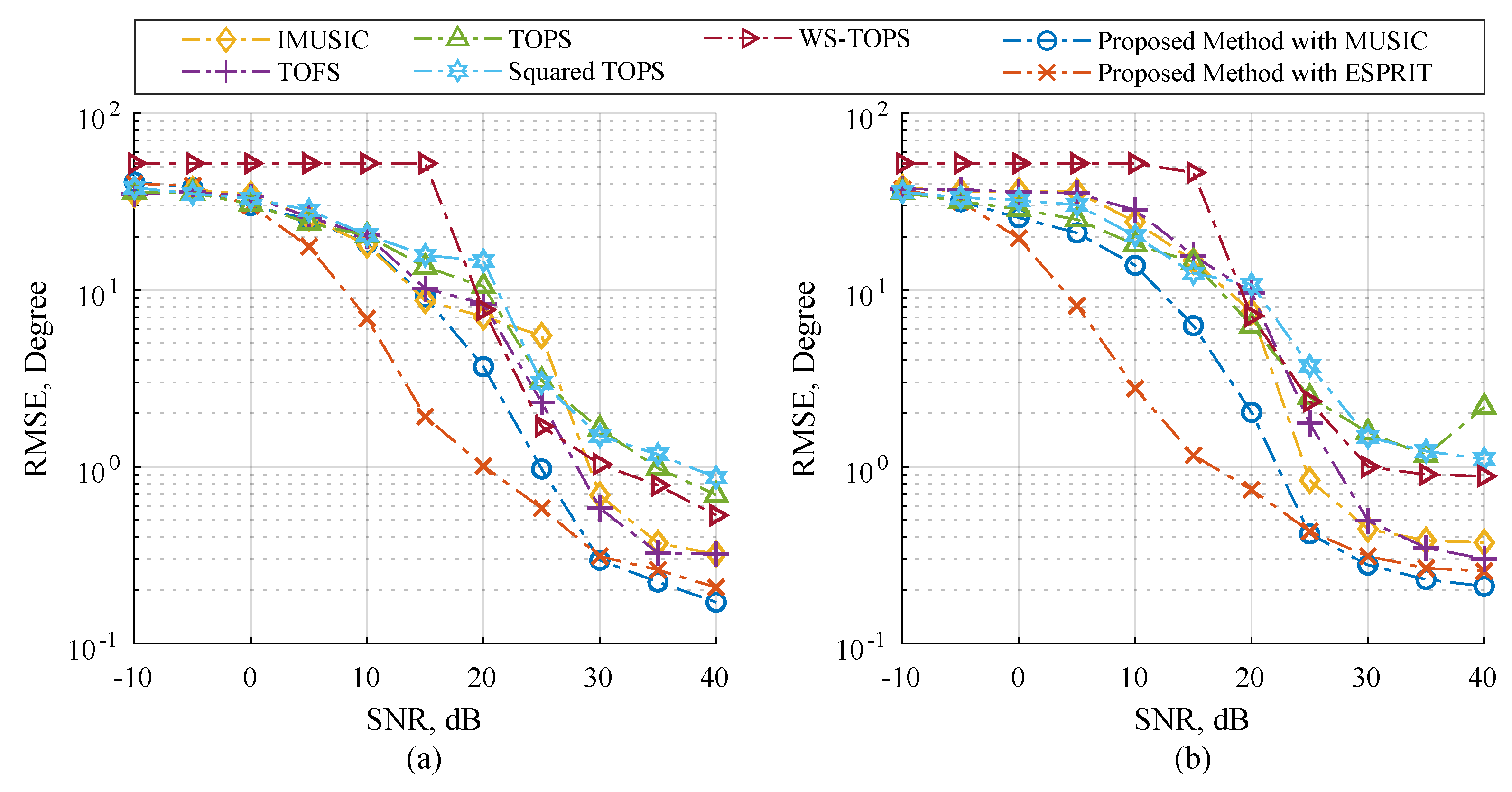
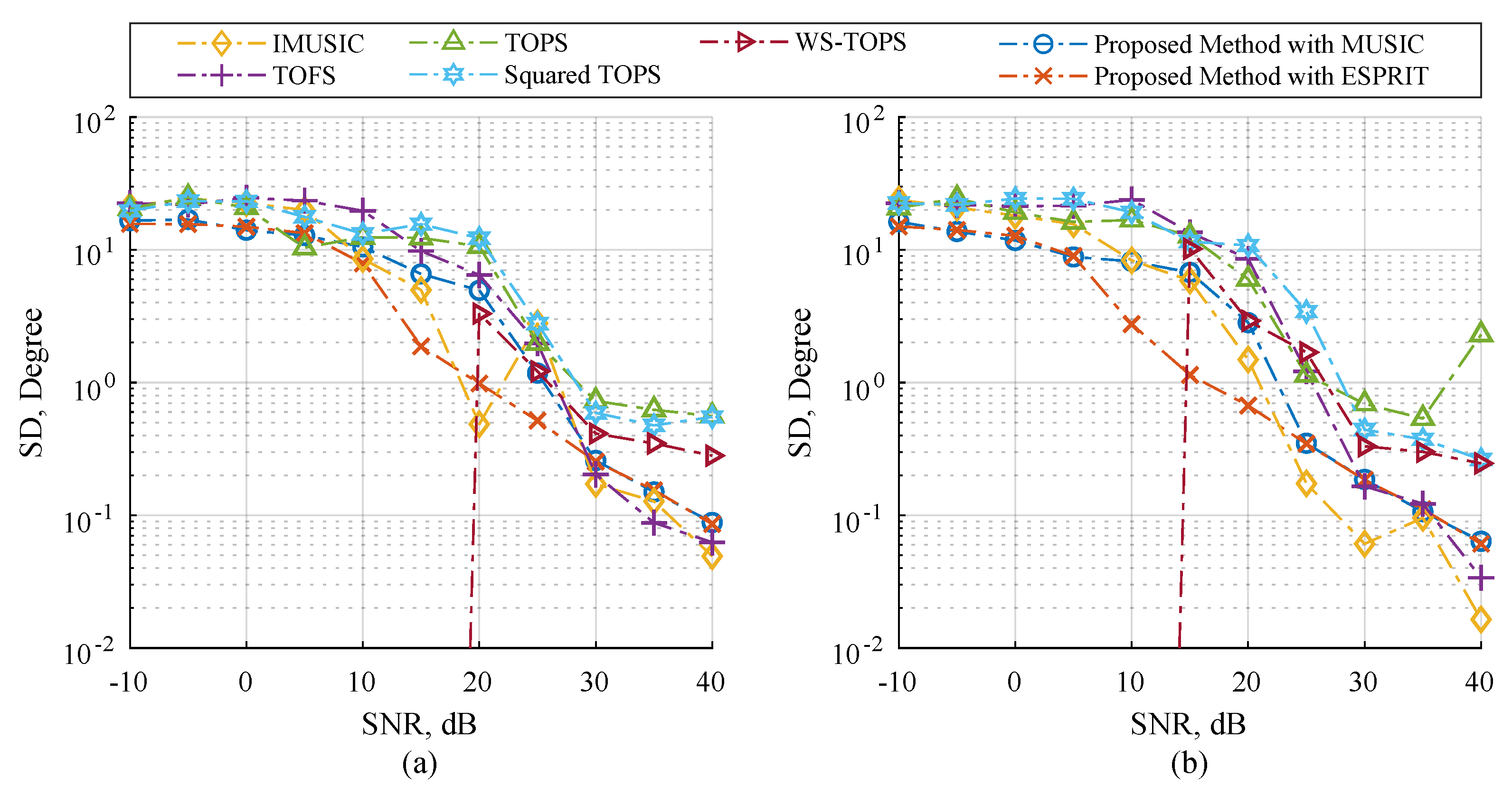
4.1. Scenario 1: Performance with Respect to Source Types
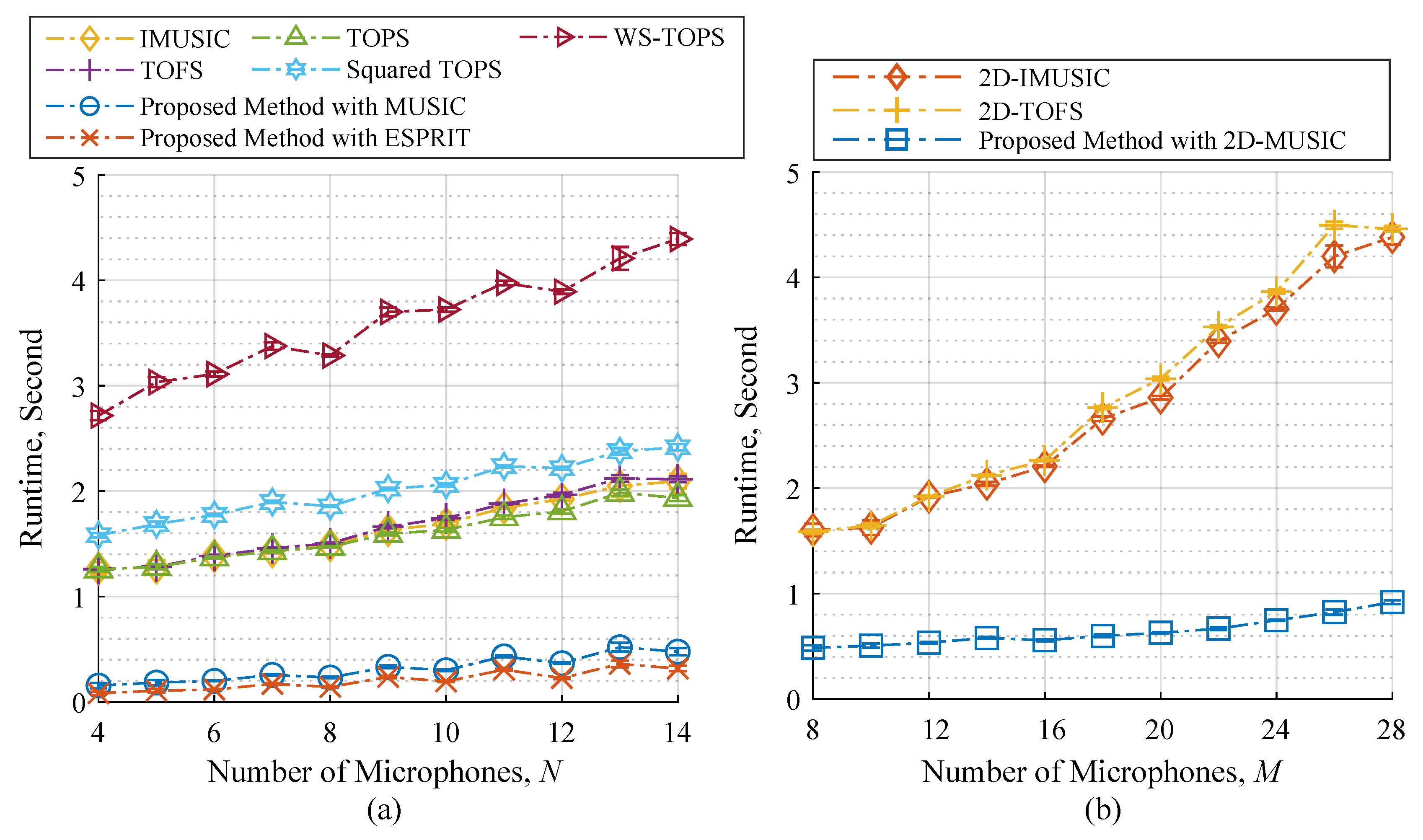
4.2. Scenario 2: Performance with Respect to the Number of Microphone Elements
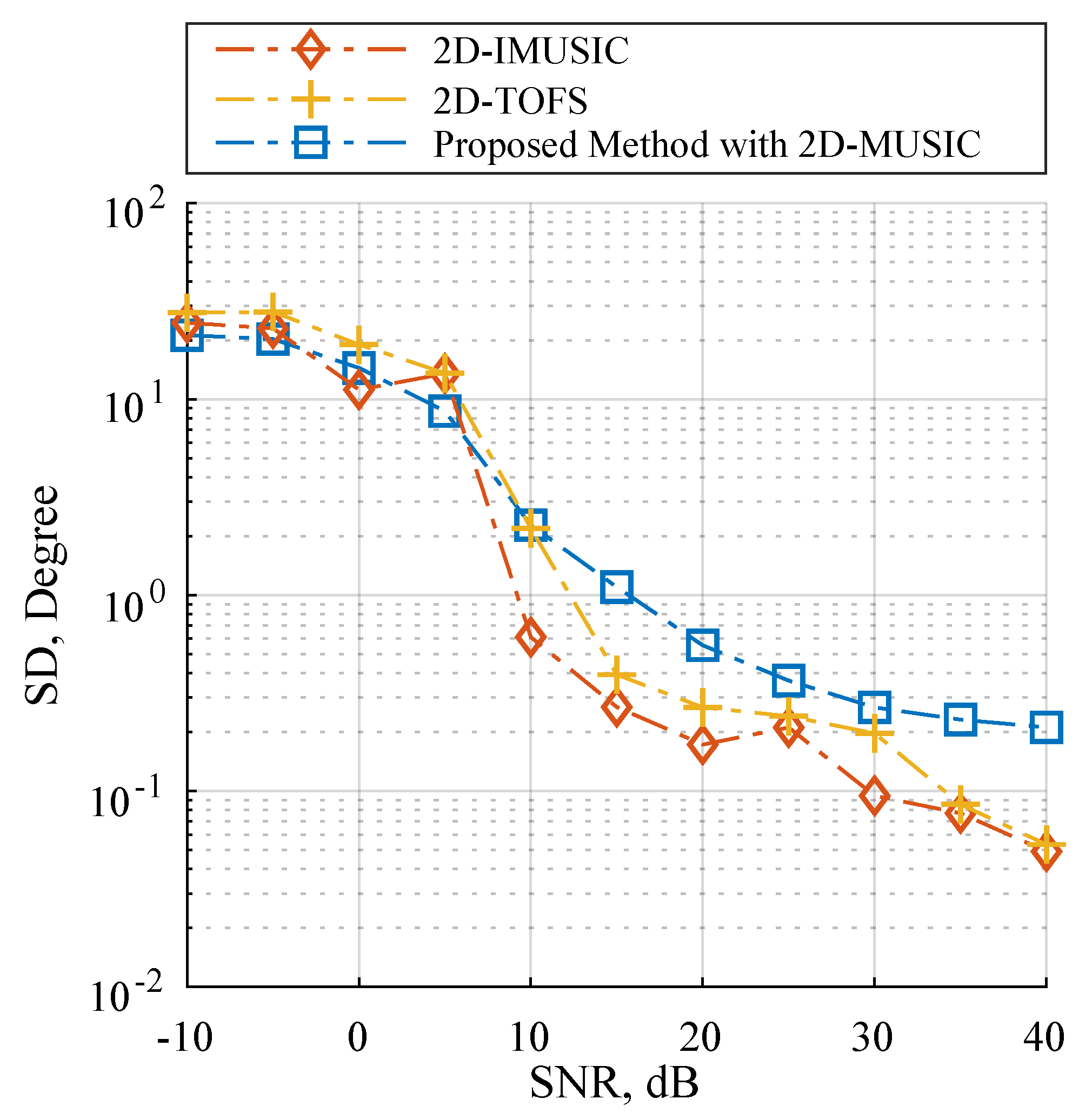
4.3. Scenario 3: Performance with Considering Automatic Pairing
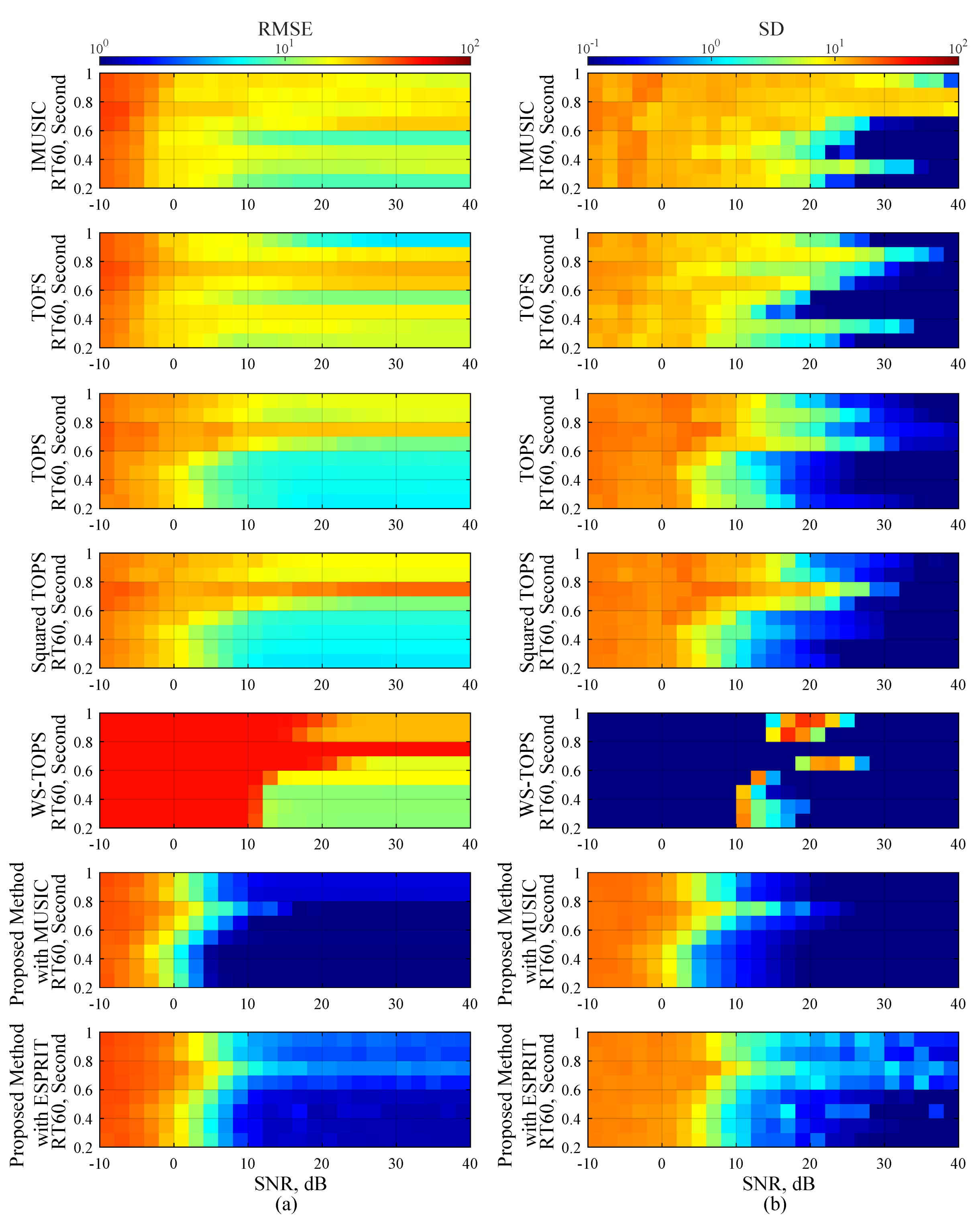
4.4. Scenario 4: Performance under Reverberation Environment
4.5. Computational Complexity
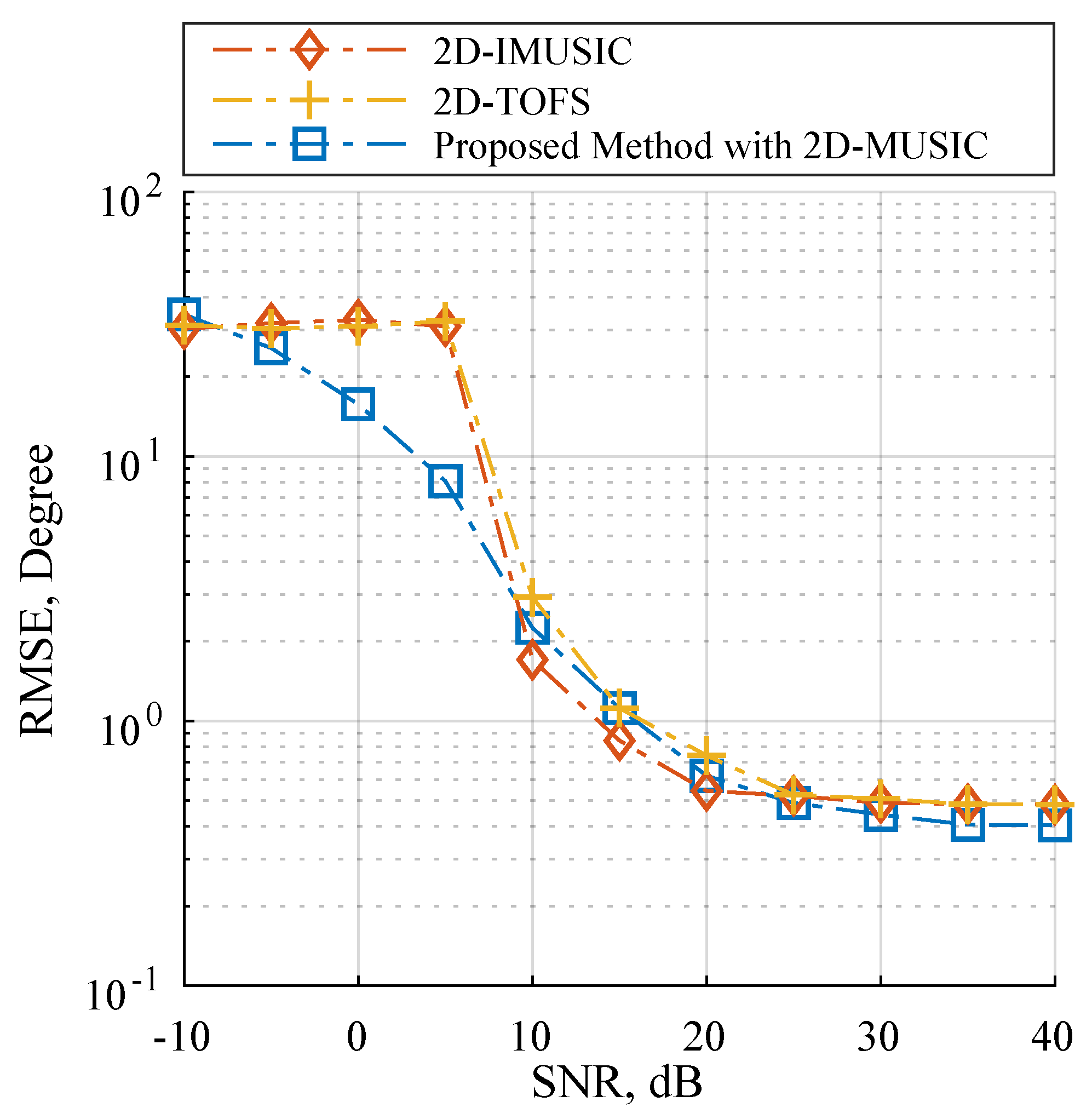
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
References
- Haykin, S.; Liu, K.R. Handbook on Array Processing and Sensor Networks; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Zekavat, R.; Buehrer, R.M. Handbook of Position Location: Theory, Practice and Advances, 1st ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Song, K.; Liu, Q.; Wang, Q. Olfaction and Hearing Based Mobile Robot Navigation for Odor/Sound Source Search. Sensors 2011, 11, 2129–2154. [Google Scholar] [CrossRef] [PubMed]
- Velasco, J.; Pizarro, D.; Macias-Guarasa, J. Source Localization with Acoustic Sensor Arrays Using Generative Model Based Fitting with Sparse Constraints. Sensors 2012, 12, 13781–13812. [Google Scholar] [CrossRef] [PubMed]
- Tiete, J.; Domínguez, F.; Silva, B.D.; Segers, L.; Steenhaut, K.; Touhafi, A. SoundCompass: A Distributed MEMS Microphone Array-Based Sensor for Sound Source Localization. Sensors 2014, 14, 1918–1949. [Google Scholar] [CrossRef] [PubMed]
- Clark, B.; Flint, J.A. Acoustical Direction Finding with Time-Modulated Arrays. Sensors 2016, 16, 2107. [Google Scholar] [CrossRef] [PubMed]
- Hoshiba, K.; Washizaki, K.; Wakabayashi, M.; Ishiki, T.; Kumon, M.; Bando, Y.; Gabriel, D.; Nakadai, K.; Okuno, H.G. Design of UAV-Embedded Microphone Array System for Sound Source Localization in Outdoor Environments. Sensors 2017, 17, 2535. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Li, B.; Yuan, X.; Zhou, Q.; Huang, J. A Robust Real Time Direction-of-Arrival Estimation Method for Sequential Movement Events of Vehicles. Sensors 2018, 18, 992. [Google Scholar] [CrossRef] [PubMed]
- Knapp, C.; Carter, G. The generalized correlation method for estimation of time delay. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 320–327. [Google Scholar] [CrossRef]
- Sawada, H.; Mukai, R.; Araki, S.; Makino, S. A robust and precise method for solving the permutation problem of frequency-domain blind source separation. IEEE Trans. Speech Audio Process. 2004, 12, 530–538. [Google Scholar] [CrossRef]
- Yokoi, K.; Hamada, N. ICA-Based Separation and DOA Estimation of Analog Modulated Signals in Multipath Environment. IEICE Trans. Commun. 2005, 88-B, 4246–4249. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Marcos, S.; Marsal, A.; Benidir, M. Performances analysis of the propagator method for source bearing estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP-94), Adelaide, SA, Australia, 19–22 April 1994; pp. IV/237–IV/240. [Google Scholar] [CrossRef]
- Marcos, S.; Marsal, A.; Benidir, M. The propagator method for source bearing estimation. Signal Process. 1995, 42, 121–138. [Google Scholar] [CrossRef]
- Hua, Y.; Sarkar, T.K.; Weiner, D.D. An L-shaped array for estimating 2-D directions of wave arrival. IEEE Trans. Antennas Propag. 1991, 39, 143–146. [Google Scholar] [CrossRef]
- Porozantzidou, M.G.; Chryssomallis, M.T. Azimuth and elevation angles estimation using 2-D MUSIC algorithm with an L-shape antenna. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, G.; Xin, J.; Zheng, N.; Sano, A. Computationally Efficient Subspace-Based Method for Two-Dimensional Direction Estimation With L-Shaped Array. IEEE Trans. Signal Process. 2011, 59, 3197–3212. [Google Scholar] [CrossRef]
- Nie, X.; Wei, P. Array Aperture Extension Algorithm for 2-D DOA Estimation with L-Shaped Array. Progress Electromagn. Res. Lett. 2015, 52, 63–69. [Google Scholar] [CrossRef]
- Tayem, N. Azimuth/Elevation Directional Finding with Automatic Pair Matching. Int. J. Antennas Propag. 2016, 2016, 5063450. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, H.; Chen, H.; Dong, Y.; Wang, L. A Low-Complexity Method for Two-Dimensional Direction-of-Arrival Estimation Using an L-Shaped Array. Sensors 2017, 17, 190. [Google Scholar] [CrossRef]
- Li, J.; Jiang, D. Joint Elevation and Azimuth Angles Estimation for L-Shaped Array. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 453–456. [Google Scholar] [CrossRef]
- Dong, Y.Y.; Chang, X. Computationally Efficient 2D DOA Estimation for L-Shaped Array with Unknown Mutual Coupling. Math. Probl. Eng. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Hsu, K.C.; Kiang, J.F. Joint Estimation of DOA and Frequency of Multiple Sources with Orthogonal Coprime Arrays. Sensors 2019, 19, 335. [Google Scholar] [CrossRef]
- Wu, T.; Deng, Z.; Li, Y.; Li, Z.; Huang, Y. Estimation of Two-Dimensional Non-Symmetric Incoherently Distributed Source with L-Shape Arrays. Sensors 2019, 19, 1226. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Hao, X.; Li, P.; Li, G. An Improved Two-Dimensional Direction-of-Arrival Estimation Algorithm for L-Shaped Nested Arrays with Small Sample Sizes. Sensors 2019, 19, 2176. [Google Scholar] [CrossRef] [PubMed]
- Omer, M.; Quadeer, A.A.; Al-Naffouri, T.Y.; Sharawi, M.S. An L-shaped microphone array configuration for impulsive acoustic source localization in 2-D using orthogonal clustering based time delay estimation. In Proceedings of the 1st International Conference on Communications, Signal Processing, and their Applications (ICCSPA), Sharjah, UAE, 12–14 February 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Wajid, M.; Kumar, A.; Bahl, R. Direction-of-arrival estimation algorithms using single acoustic vector-sensor. In Proceedings of the International Conference on Multimedia, Signal Processing and Communication Technologies (IMPACT), Aligarh, India, 24–26 November 2017; pp. 84–88. [Google Scholar] [CrossRef]
- Sugimoyo, Y.; Miyabe, S.; Yamada, T.; Makino, S.; Juang, B.H. An Extension of MUSIC Exploiting Higher-Order Moments via Nonlinear Mapping. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2016, E99.A, 1152–1162. [Google Scholar] [CrossRef]
- Suksiri, B.; Fukumoto, M. Multiple Frequency and Source Angle Estimation by Gaussian Mixture Model with Modified Microphone Array Data Model. J. Signal Process. 2017, 21, 163–166. [Google Scholar] [CrossRef][Green Version]
- Su, G.; Morf, M. The signal subspace approach for multiple wide-band emitter location. IEEE Trans. Acoust. Speech Signal Process. 1983, 31, 1502–1522. [Google Scholar] [CrossRef]
- Yu, H.; Liu, J.; Huang, Z.; Zhou, Y.; Xu, X. A New Method for Wideband DOA Estimation. In Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, Shanghai, China, 21–25 September 2007; pp. 598–601. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Kaplan, L.M.; McClellan, J.H. TOPS: New DOA estimator for wideband signals. IEEE Trans. Signal Process. 2006, 54, 1977–1989. [Google Scholar] [CrossRef]
- Okane, K.; Ohtsuki, T. Resolution Improvement of Wideband Direction-of-Arrival Estimation “Squared-TOPS”. In Proceedings of the IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Hirotaka, H.; Tomoaki, O. DOA estimation for wideband signals based on weighted Squared TOPS. EURASIP J. Wirel. Commun. Netw. 2016, 2016, 243. [Google Scholar] [CrossRef]
- Wang, H.; Kaveh, M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 823–831. [Google Scholar] [CrossRef]
- Hung, H.; Kaveh, M. Focussing matrices for coherent signal-subspace processing. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1272–1281. [Google Scholar] [CrossRef]
- Valaee, S.; Kabal, P. Wideband array processing using a two-sided correlation transformation. IEEE Trans. Signal Process. 1995, 43, 160–172. [Google Scholar] [CrossRef]
- Valaee, S.; Champagne, B.; Kabal, P. Localization of wideband signals using least-squares and total least-squares approaches. IEEE Trans. Signal Process. 1999, 47, 1213–1222. [Google Scholar] [CrossRef]
- Suksiri, B.; Fukumoto, M. A Computationally Efficient Wideband Direction-of-Arrival Estimation Method for L-Shaped Microphone Arrays. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Abdelbari, A. Direction of Arrival Estimation of Wideband RF Sources. Ph.D. Thesis, Near East University, Nicosia, Cyprus, 2018. [Google Scholar] [CrossRef]
- Ponnapalli, S.P.; Saunders, M.A.; Van Loan, C.F.; Alter, O. A Higher-Order Generalized Singular Value Decomposition for Comparison of Global mRNA Expression from Multiple Organisms. PLoS ONE 2011, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Xin, J.; Zheng, N.; Sano, A. Simple and Efficient Nonparametric Method for Estimating the Number of Signals Without Eigendecomposition. IEEE Trans. Signal Process. 2007, 55, 1405–1420. [Google Scholar] [CrossRef]
- Nadler, B. Nonparametric Detection of Signals by Information Theoretic Criteria: Performance Analysis and an Improved Estimator. IEEE Trans. Signal Process. 2010, 58, 2746–2756. [Google Scholar] [CrossRef]
- Diehl, R. Acoustic and auditory phonetics: The adaptive design of speech sound systems. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2008, 363, 965–978. [Google Scholar] [CrossRef] [PubMed]
- Van Der Veen, A.; Deprettere, E.F.; Swindlehurst, A.L. Subspace-based signal analysis using singular value decomposition. Proc. IEEE 1993, 81, 1277–1308. [Google Scholar] [CrossRef]
- Hogben, L. Discrete Mathematics and Its Applications. In Handbook of Linear Algebra; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Naidu, P. Sensor Array Signal Processing; Taylor & Francis: Abingdon-on-Thames, UK, 2000. [Google Scholar]
- Meyer, C.D. (Ed.) Matrix Analysis and Applied Linear Algebra; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Van Loan, C.F. Structured Matrix Computations from Structured Tensors: Lecture 6. In The Higher-Order Generalized Singular Value Decomposition; Cornell University: Ithaca, NY, USA, 2015. [Google Scholar]
- Wei, Y.; Guo, X. Pair-Matching Method by Signal Covariance Matrices for 2D-DOA Estimation. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1199–1202. [Google Scholar] [CrossRef]
- Lehmanna, E.A.; Johansson, A.M. Prediction of energy decay in room impulse responses simulated with an image-source model. J. Acoust. Soc. Am. 2008, 124, 269–277. [Google Scholar] [CrossRef] [PubMed]
- Gower, J.C.; Dijksterhuis, G.B. Procrustes Problems, 1st ed.; Oxford University Press: Oxford, UK, 2004. [Google Scholar] [CrossRef]




| Command Name | Command Counts | |
|---|---|---|
| HOGSVD in Equation (20) | Optimized HOGSVD in Equation (32) | |
| Matrix Addition/Subtraction | ||
| Element-wise Multiplication | 1 | 0 |
| Matrix Multiplication | ||
| Matrix Inversion | P | |
| QR Decomposition | 0 | 1 |
| Eigenvalue Decomposition (EVD) | 1 | 1 |
| Command Name | Complex Floating Point Operations per Command |
|---|---|
| Matrix Addition/Subtraction | |
| Element-wise Multiplication | |
| Matrix Multiplication | |
| Matrix Inversion (Gauss-Jordan elimination) | |
| QR Decomposition (Householder transformation) | |
| HOGSVD in Equation (20) without counting EVD | |
| Optimized HOGSVD in Equation (32) without counting EVD |
| Reverberation Time based on RT60 (Millisecond) | Axial Wall Plane | |||||
|---|---|---|---|---|---|---|
| Positive Direction | Negative Direction | |||||
| 200 | 0.7236 | 0.2021 | 0.6844 | 0.0792 | 0.2436 | 0.5586 |
| 300 | 0.7142 | 0.1687 | 0.7666 | 0.2650 | 0.2387 | 0.7043 |
| 400 | 0.7306 | 0.0555 | 0.7731 | 0.4091 | 0.8493 | 0.8587 |
| 500 | 0.5064 | 0.4974 | 0.8248 | 0.4189 | 0.8069 | 0.7572 |
| 600 | 0.6074 | 0.6299 | 0.8028 | 0.7599 | 0.6373 | 0.8209 |
| 700 | 0.7442 | 0.7624 | 0.8734 | 0.6922 | 0.6480 | 0.7893 |
| 800 | 0.6779 | 0.6827 | 0.7865 | 0.8045 | 0.8386 | 0.8430 |
| 900 | 0.6992 | 0.7111 | 0.7741 | 0.8752 | 0.8233 | 0.9081 |
| 1000 | 0.7622 | 0.7707 | 0.9394 | 0.8248 | 0.8192 | 0.8398 |
| Hardware Type/Parameter | Specification/Value |
|---|---|
| Audio Interface | Roland® Octa-capture (UA-1010) |
| Sampling Frequency | 48,000 Hz |
| Microphone Name | Behringer® C-2 studio condenser microphone |
| Number of Microphones | 8 |
| Pickup Patterns | Cardioid (8.9 mV/Pa; 20–20,000 Hz) |
| Diaphragm Diameter | 16 mm |
| Equivalent Noise Level | 19.0 dBA (IEC 651) |
| SNR Ratio | 75 dB |
| Microphone Structure | L-shaped Array |
| Spacing of Microphone | 9 cm |
| Incident Sources | RMSE of DOAs (Degree) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number | Position | Angle (Degree) | IMUSIC | TOFS | TOPS | Squared TOPS | WS-TOPS | Proposed Method with MUSIC | Proposed Method with ESPRIT |
| 1 | 96 | 0.3050 | 0.2050 | 1.0950 | 1.3350 | 0.5600 | 0.7750 | 0.7074 | |
| 86 | 0.5400 | 1.2600 | 1.2750 | 2.0150 | 0.6850 | 0.5700 | 0.6915 | ||
| Average | 0.4225 | 0.7325 | 1.1850 | 1.6750 | 0.6225 | 0.6725 | 0.6995 | ||
| 2 | 65 | 1.1857 | 1.7286 | 20.0143 | 28.5857 | 37.8714 | 1.5000 | 2.0284 | |
| 150 | 9.6000 | 6.6857 | 26.3571 | 39.7857 | 88.2000 | 8.8143 | 8.6800 | ||
| 55 | 1.0714 | 1.6857 | 22.2571 | 19.4000 | 32.2429 | 2.9714 | 3.8695 | ||
| 100 | 8.3714 | 8.3857 | 5.0143 | 6.7857 | 60.2286 | 6.6714 | 3.1630 | ||
| Average | 5.0571 | 4.6214 | 18.4107 | 23.6393 | 54.6357 | 4.9893 | 4.4353 | ||
| 3 | 58 | 2.1400 | 2.3900 | 46.5500 | 52.8100 | 40.9500 | 3.6600 | 4.0334 | |
| 55 | 55.0000 | 55.0000 | 55.0000 | 55.0000 | 55.0000 | 9.4300 | 4.1057 | ||
| 100 | 1.8400 | 2.0000 | 41.5700 | 62.4000 | 70.9100 | 1.8700 | 2.4554 | ||
| 95 | 95.0000 | 83.4200 | 52.4500 | 71.4800 | 95.0000 | 9.7700 | 5.8638 | ||
| 130 | 10.9300 | 11.8900 | 28.8300 | 32.2800 | 95.2400 | 8.2500 | 6.9071 | ||
| 120 | 26.9800 | 25.8400 | 16.1200 | 18.0100 | 91.2800 | 5.9400 | 7.3165 | ||
| Average | 31.9817 | 30.0900 | 40.0867 | 48.6633 | 74.7300 | 6.4867 | 5.1137 | ||
| Incident Sources | RMSE of DOAs (Degree) | ||||
|---|---|---|---|---|---|
| Number | Position | Angle (Degree) | 2D-IMUSIC | 2D-TOFS | Proposed Method with 2D-MUSIC |
| 1 | 96 | 0.9000 | 0.9000 | 0.9000 | |
| 86 | 0.4000 | 1.0500 | 0.7500 | ||
| Average | 0.6500 | 0.9750 | 0.8250 | ||
| 2 | 57 | 0.9500 | 1.1500 | 1.1000 | |
| 91 | 1.0500 | 1.8000 | 1.7000 | ||
| 139 | 4.9500 | 5.2000 | 5.4500 | ||
| 96 | 3.1500 | 3.3000 | 2.0500 | ||
| Average | 2.5250 | 2.8625 | 2.5750 | ||
| 3 | 48 | 0.9500 | 1.5500 | 1.9500 | |
| 86 | 1.4500 | 0.8000 | 2.4500 | ||
| 98 | 0.9000 | 1.8000 | 1.1500 | ||
| 95 | 1.4500 | 2.1500 | 2.6000 | ||
| 152 | 2.7000 | 2.4000 | 5.9000 | ||
| 95 | 4.5000 | 3.9000 | 1.4500 | ||
| Average | 1.9917 | 2.1000 | 2.5833 | ||
| 4 | 100 | 5.8095 | 6.5238 | 3.2857 | |
| 94 | 2.4286 | 2.6190 | 1.6667 | ||
| 51 | 1.2381 | 1.0952 | 2.5714 | ||
| 95 | 0.5714 | 0.6667 | 1.3333 | ||
| 134 | 1.9524 | 1.8571 | 3.9524 | ||
| 103 | 10.0952 | 10.2857 | 9.2857 | ||
| 153 | 7.4762 | 7.8095 | 7.8571 | ||
| 89 | 4.7143 | 4.7143 | 5.3810 | ||
| Average | 4.2857 | 4.4464 | 4.4167 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suksiri, B.; Fukumoto, M. An Efficient Framework for Estimating the Direction of Multiple Sound Sources Using Higher-Order Generalized Singular Value Decomposition. Sensors 2019, 19, 2977. https://doi.org/10.3390/s19132977
Suksiri B, Fukumoto M. An Efficient Framework for Estimating the Direction of Multiple Sound Sources Using Higher-Order Generalized Singular Value Decomposition. Sensors. 2019; 19(13):2977. https://doi.org/10.3390/s19132977
Chicago/Turabian StyleSuksiri, Bandhit, and Masahiro Fukumoto. 2019. "An Efficient Framework for Estimating the Direction of Multiple Sound Sources Using Higher-Order Generalized Singular Value Decomposition" Sensors 19, no. 13: 2977. https://doi.org/10.3390/s19132977
APA StyleSuksiri, B., & Fukumoto, M. (2019). An Efficient Framework for Estimating the Direction of Multiple Sound Sources Using Higher-Order Generalized Singular Value Decomposition. Sensors, 19(13), 2977. https://doi.org/10.3390/s19132977





