1. Introduction
In road-based mass transit systems, travel time (
TT) estimates are used for various key tasks. In operations’ planning, suitable time estimates are required for the preparation of timetables and to schedule services on the different routes. This type of planning is called long-term travel time planning. In operations’ monitoring, depending on the situation of the public transport vehicles and the conditions under which they operate the routes, travel time estimates are required to detect any potential significant deviations from the timetable and the scheduled services. This type of planning is called short-term
TT planning. According to the standards and recommendations of public transport agencies [
1],
TT is one of the key factors when providing quality of service. Users wish to travel on the public transport network in the shortest possible time using punctual services, and to be informed in the event of alterations in order to avoid waiting [
2].
In the context of road-based mass transit systems, short-term travel time forecasts estimate the time a public transport vehicle will take to reach points on the route that it has not yet passed. Due to a variety of different factors, such as demand, traffic conditions, weather conditions, etc., the development of models that provide reliable short-term TT predictions is a research challenge. In addition, for these types of predictions to be useful, they must be done in the shortest possible time, which means that the real-time parameter is an important feature. There are multiple studies that have proposed short-term TT prediction models. The common denominator in these studies is the fact that the proposed solutions take into account historical TT behaviour, modelled using different automatic learning techniques or statistics, and current TT behaviour on the route section for which TT is to be predicted. In these models, it is assumed that current TT behaviour resembles the TT observed in those vehicles that have recently travelled the section for which they want to make the prediction. This assumption about current TT behaviour is only possible when there is a planning of line services that guarantees that the sections for which TT is to be estimated will be covered by public transport vehicles with a certain frequency. In general, this situation occurs in the case of urban public transport systems where trips are planned by frequency of stops. However, in the case of intercity public transport, which is planned by timetable, it is not always possible to have representative TT values recently obtained from other vehicles. For this reason, most of the models proposed in the literature are applicable in contexts in which the routes of public transport vehicles are planned by frequency. But nowadays, especially with public transport service planning models that take into account last-mile problems in rural areas, it is also necessary to make TT predictions for intercity transport, since these models require synchronisation between buses and other types of vehicles, such as taxis.
In this paper, a short-term TT prediction model based on profile similarity is proposed. The proposed prediction model is based on the similarity between historical TT behaviour, represented by representative profiles obtained through clustering techniques, and TT behaviour observed in the vehicle itself. This paper contains four main contributions. The first is that the proposed method may be used for predicting TT in contexts where there is no recent TT information for other vehicles; it can therefore be used in the case of intercity transport. Second, the prediction may be made autonomously in the vehicle itself without the need to communicate with a control centre. Third, due to the computational cost and parameterisation of the techniques used, the proposed TT prediction model may be applied continuously to all the routes of a transport network at less cost than alternative methods, which generally require more complex learning and testing processes. Fourth, due to the way that historical TT behaviour is represented, the model not only provides short-term TT predictions, but also provides information on TT behaviour that is useful when making long-term predictions and for analysing its variability and identifying the factors that affect it.
In addition to this introduction, this paper contains four more sections. The section that follows is a review of short-term TT prediction models in the context of road-based mass transit systems. The proposed prediction model is described in the third Section. The results obtained through applying this model to a real case are presented in the fourth Section. The last Section presents the conclusions.
2. Related Works
This section reviews the proposals for short-term
TT prediction models on routes run by public transport buses. Depending on the techniques used to carry out the predictions, these proposals may be classified into three groups: prediction models based on historical average models (
HAM), prediction models based on machine learning regression (
MLR), and prediction models based on state-based time-series (
STS). Regardless of the theoretical foundations on which these prediction techniques are based, there are three common aspects. First, public transport routes for which
TT predictions are to be made are modelled as a sequence of segments the endpoints of which may be stops or time control points. Second, the historical data used to implement the different proposals come from records obtained from the automatic vehicle location (
AVL) systems and/or the automatic passenger counting (
APC) systems installed in public transport vehicles. Third, short-term
TT predictions for a public transport vehicle are done by taking as input the
TT obtained by the vehicle on the route segments already travelled, and the data from the last vehicles to have travelled the route segments that said vehicle has not yet travelled. At this initial point of the review it should be mentioned that the works published on these prediction methods are generally lacking in their analysis of the input variables used to make
TT predictions. We could, however, mention the works of Yetiskul and Senbil [
3] and Comi et al. [
4], which analysed the variables that affect
TT behaviour in order to provide useful information for long-term
TT planning. The former analysed
TT behaviour in the Turkish city of Ankara. Using statistical variables, the authors studied how time, space and service factors affect
TT. The latter was carried out in the city of Rome and consisted of an analysis based on time series designed to obtain
TT behaviour patterns depending on time factors, and on how these patterns were influenced by traffic conditions. Based on this analysis, the authors developed a long-term
TT prediction model based on time series. The review that follows is structured according to the theoretical model used by the proposed techniques, excluding those based on
HAM because they were the initial proposals that have already been improved upon by proposals based on other more recent models.
The aim of the models based on
MLR methods is to infer the value of a dependent variable, in this case
TT, by means of a mathematical function based on a set of independent variables, this function being the result of a prior learning process. The techniques used in the studies include artificial neural networks (
ANN); particularly multilayer perceptron (
MLP) networks; support vector machine using the radial-basis function (
RBF) as the kernel regression function;
k-nearest neighbours (
KNN) with the Euclidean distance being the most used metric; and decision tree regression (
DTR). Yu et al. [
5] proposed a prediction model based on
SVM, using
RBF as the kernel function. In this proposal, it is interesting to note that for the
TT prediction not only is
TT taken into account, but also an attribute that indicates the weather conditions (sunny day or rainy day) and the time of day in relation to demand (peak or off-peak). The
SVM model uses an input vector consisting of three variables—the segment, the
TT in the current segment, and the last
TT value for the next segment—and the output data are the estimated times for the segments not yet travelled by the vehicle. Chang et al. [
6] proposed a prediction model based on the
KNN method. The data used are the records provided by the
AVL systems. To make the prediction, the proposed model uses a set of historical data to obtain
TT patterns, one for each day of the week; these patterns are called historical patterns. The vehicles that operate on the route for which
TT is to be predicted communicate the times that they pass through the time control points to a central system. These are averaged, and a vector that characterises current
TT for the route is obtained. To make the prediction, the historical
k patterns closest to this vector are obtained using the Euclidean distance metric. Lee et al. [
7] propose a
TT prediction framework in which the vehicle’s arrival times, obtained from its
AVL systems, are stored in a historical record. These historical records are processed using the
k-means and
v-means clustering techniques in order to obtain different groups that represent significantly different
TT behaviours. In order to make the prediction, the times provided by the last vehicle that completed or is travelling on a route for which the
TT are to be predicted are used as input data. Taking these current trajectory times to classify the
TT to be predicted, the cluster with the pattern that most closely approximates the current times of the vehicle is sought. The
TT predictions for the following route points will be the average
TT from the data records that match this cluster. Gurmu et al. [
8] proposes using an
ANN model for real-time
TT prediction using Global Positioning System (
GPS) data. Gal et al. [
9] proposes a combined method that uses a model based on queueing theory to obtain a first approximation of the prediction and a model based on
DTR. The queueing theory model is based on the snapshot principle, using as input data the times that the last buses went through the stops. To implement the
DTR-based method, the authors studied different techniques: random forest (
RF), extremely randomised trees (
ET), AdaBoost (
AB), gradient tree boosting (
GB) and an improved version of the gradient tree boosting technique (
GBLAD), which produced the best results. Arhin and Stinson [
10] proposes a prediction method based on a regression model that takes into account different factors (independent variables) that affect
TT (dependent variable). These factors are passengers boarding, passengers alighting, passenger load, dwell time, segment length, bus stops, signalised intersections, access approaches and mid-segment crosswalks. The
TT is the result of evaluating a function based on these factors, each weighted by a regression factor. Zhang et al. [
11] uses a prediction method based on
SVM. The data used in this proposal come from
AVL systems. With historical records of traffic flow for different types of day and times of day, the authors constructed a training set to obtain a decision function that generates the prediction by combining current traffic data and the arrival times of the vehicles operating on the route.
Prediction methods that employ
STS models are based on the assumption that the value of the variable to be predicted is a function of a linear or non-linear combination of the historical values of the state variable or variables. Shalaby and Farhan [
12] proposes a prediction system based on Kalman filters (
KF). The objective of this proposal was to predict
TT between stops (nonstop running time) and the time that the vehicle spends at the stops on the route (dwell time). The data used are the records from the
AVL and
APC systems. Vanajakshi et al. [
13] proposes a prediction method based on
KF. The data used for the prediction are the
GPS data obtained manually over 10 days because the buses did not have
AVL systems. Song et al. [
14] proposes a prediction model in which the
TT between two consecutive stops on a route depends on the speed of the vehicle, which varies as it accelerates and decelerates, and by the time the vehicle is stationary because of traffic signals. This
TT behaviour is predicted by an exponential smoothing function. In this proposal, predictions are made using two sets of data from two different sources: the records provided by the
AVL systems and simulated Radio Frequency Identification (
RFID) data. The public transport vehicles considered in this paper were buses and taxis. The authors concluded that with
RFID data, better prediction results are obtained.
There are also proposals that use the
MLR and
STS models in combination. Chen et al. [
15] proposes the combined use of an
ANN model and a
KF algorithm to predict
TT. This model takes as input data the most recent information on the arrival time of the vehicle at a time point on the route and the prediction provided by the
ANN model with historical data to predict, using a
KF algorithm, the
TT between two points on the route that have not yet been reached. The data were collected by
APC systems. Bai et al. [
16] proposes a combined prediction method in which an
SVM model and a
KF algorithm are used. The
KF predictions were used to make short-term
TT predictions. To do this, the prediction made by the
SVM model and the
TT taken by the last bus to travel along the segment of the route for which
TT is to be predicted were taken as initial data. The authors compared the proposed model (
SVM-KF) with four alternative models: an
ANN model, a
KF model, an
SVM model, and a combined
ANN-KF model. The results indicated that the proposed combined model,
SVM-KF, performed better on the three road segments that were analysed.
Other studies have compared the different prediction models. In the specific context of a bus line in Macae (Brazil), Fan and Gurmu [
17] conducted a comparative study on three of the most used models. To carry out this study, only data provided by the
AVL systems were used. The models considered in this study were
HAM,
KF and
ANN. Of the three models analysed, the
ANN prediction model produced the best results. In the context of three Indian cities (Surat, Mysore, and Chennai), Jairam [
18] analysed the behaviour of the
KNN,
KF and auto-regressive integrated moving average (
ARIMA) prediction models. The study was conducted with the data provided by the
AVL systems, analysing three routes (one in each of the cities). The models were analysed over a week and, from the results obtained, the authors concluded that the different prediction models provided similar results for route segments used exclusively by public transport vehicles. However, on segments of the route used by both public transport vehicles and private transport vehicles, the model that combined the
KNN-KF techniques produced the best results. Hua et al. [
19] compared prediction methods based on
ANN,
SVM and Linear Regression, introducing three Forgetting Factor Functions; the aim was to develop a prediction model using actual multi-route bus arrival time data from previous stops as inputs.
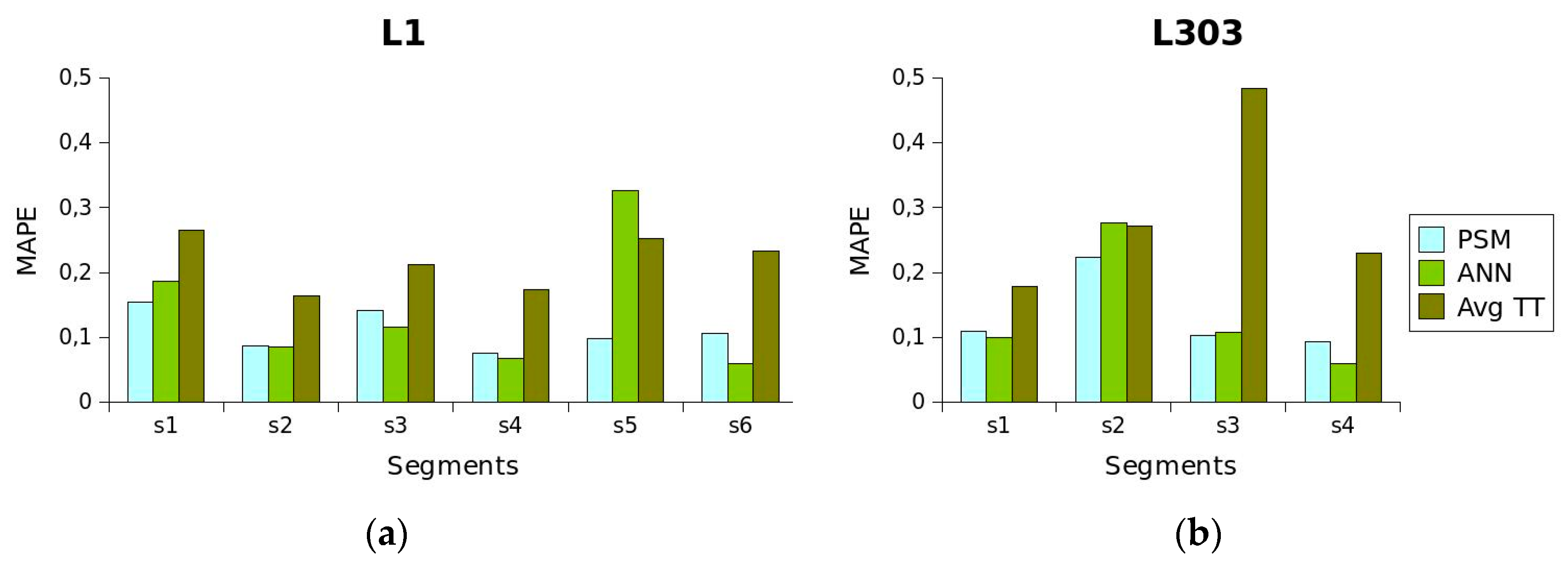
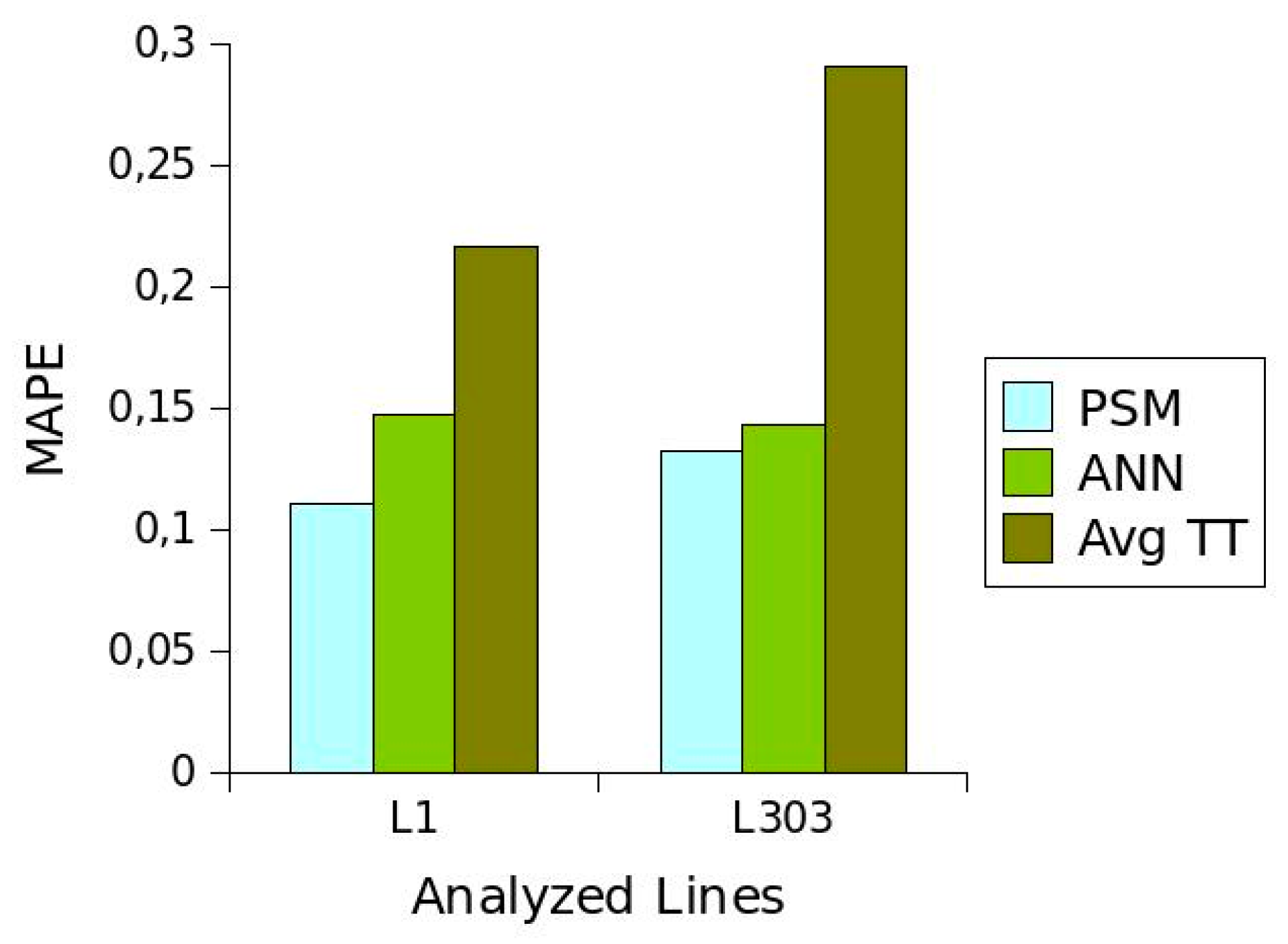
Table 1 shows the advantages and disadvantages of the different short-term
TT prediction methods. Considering these properties, the method proposed in this article is characterised by providing a predictive power similar to
ANN. In addition, the proposed method provides information on
TT behaviour that can be used for planning schedules and is more easily applicable to all routes of a transport network than methods with greater predictive power.
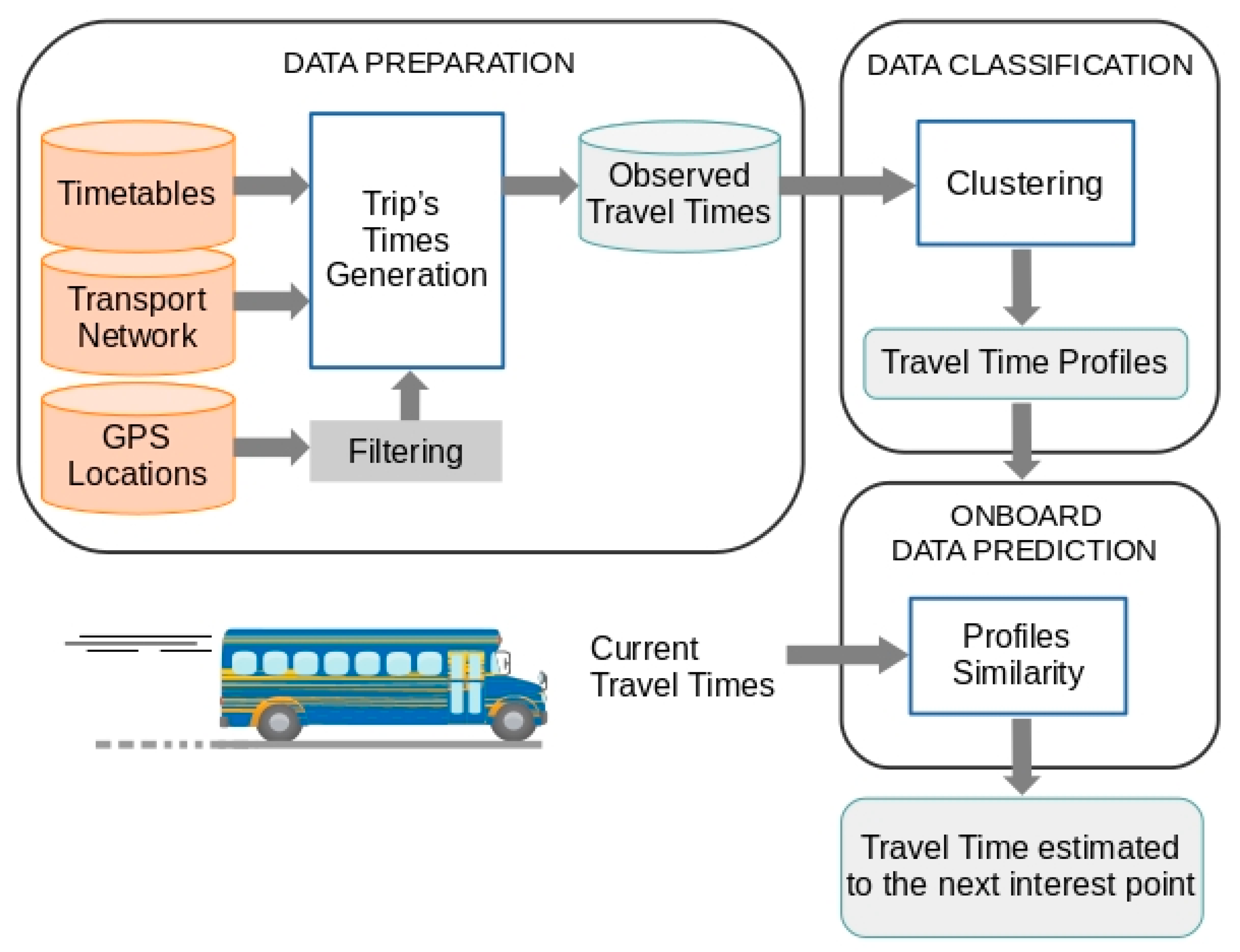
3. Travel Time Prediction Model Based on Profile Similarity (PSM)
As discussed in the previous section, in the context of regular road passenger transport, the short-term
TT prediction methods take into account historical
TT behaviour, modelled using different techniques such as
ANN,
SVM,
STS, etc., and current behaviour, usually represented by the time taken by the vehicle to travel the last segment it has completed. The proposed method is based on the idea that it is possible to predict short-term
TT using the representative elements from a classification process to represent historical behaviour, and the
TT observed at all points of interest through which the vehicle has already passed to represent current
TT behaviour (see
Figure 1). Considering these working principles, the proposed prediction method has some interesting properties in relation to the techniques described in the review of the previous section. These properties are:
Historical TT behaviour models that use patterns obtained through clustering techniques are much less costly, from the computational point of view, than the techniques usually used for this purpose, such as ANN, SVM and STS.
The historical TT behaviour model can be applied to all routes on a transport network more easily than when using the alternative techniques mentioned above. In a TT prediction scenario for all the routes on a public transport network, representing historical TT behaviour by means of clustering techniques would first require the appropriate number of classes to be determined for each route. This could be done systematically using metrics that measure the quality of the resulting clusters. However, the use, for example, of ANN or SVM, to model TT behaviour on all the routes would require different configurations that would have to be obtained through learning and validation processes.
A third advantage, resulting from the two previous advantages, is that the continuous evolution of the representation of historical behaviour by means of clustering techniques is less costly than with the alternative techniques mentioned above. This continuous evolution is necessary because TT depends on external factors that are variable over time.
For the representative elements obtained through a clustering process to reflect historical TT behaviour, a significant sample of TT is needed. As explained in the review of the previous section, there are mainly two data sources from which to obtain a sample of historical TT values: AVL and APC. Although the proposed method is independent of the data source that is used to obtain the historical TT data records, in the use case presented in the fourth Section AVL systems are used as the data source. In this implementation, the basic data are the GPS locations of the vehicle. In order to carry out this analysis of the routes, it is also necessary to handle data of a different nature, which are typically used in public transport operations (transport network design and operations control).
3.1. Formal Model Framework
The objective of the proposed method is to estimate short-term
TT in a context of regular passenger road transport planned by timetable. As already mentioned above, this type of
TT prediction is executed and is valid during the trip made by a public transport bus as it operates a particular route. In this section, entities related to the proposed method are presented and formalised.
Table 2 includes the notation used for the model entities.
3.1.1. Definition of the Entities Used by the Model
The first entity to be formalised is the public transport line. For the purposes of this paper, a line is defined as systematic, scheduled route taken by public transport buses. Systematic means that the bus always follows the same route and stops at a series of pre-established stops that do not vary. Scheduled means that there is a schedule that establishes when the buses must run the route. The operation of a line by a public transport vehicle shall be termed a trip. In the model,
L represents a generic line and a specific line is specified by means of the notation
Lc, where the subscript
c is an integer value that uniquely identifies the line. Trips on
Lc are specified by means of the notation
Ec, where
c is the identifier of the line. In the model, time is specified by the notations
T and
t.
T represents a time interval and
t represents a moment of time, which is the minimum unit of time. All trips by line
Lc that have been made over a period of time
T are specified by the notation
Ec,T. Similarly, a trip that has begun at a moment of time
t is specified by means of the notation
ec,t. Stops on the route of
Lc are represented by the notation
Sc. In the context of this study, stops on a route for which the
TT is to be predicted are called points of interest and are represented by
Pc. Points of interest on the route of
Lc are designated by the notation
Pc,i, where the subscript
i identifies the point of interest and its value matches the order in which the bus passes them following the planned route. For example,
Pc,1 is the first point of interest through which the vehicles pass when operating route
c. When selecting points of interest, the only restriction is that the first stop of the route cannot be a point of interest. The section of the route that runs from one point of interest to the next is called a route segment (see
Figure 2). In this figure, the blue rectangles represent the stops and the red circles, the points of interest.
In the context of regular passenger road transport,
TT is the result of the sum of two times: dwell time,
DT, and nonstop running time,
RT.
DT represents the time that the vehicle is stationary at stops for passengers to board or alight from the vehicle.
RT represents the time taken by the vehicle to go from one stop on the route to the next. If a route has
N stops, then the total
TT of a trip is:
The term arrival time is the time at which the vehicle arrives at that stop. The arrival times observed at the points of interest on trip ec,t are represented by OPTc,t. If Lc has N points of interest, then the arrival times of each entity OPTc,t are recorded as an array of N integer values. The set comprising the arrival times on all trips on a route completed by Lc in a time period T is represented by OPTc,T. The prediction made by the proposed model consists of estimating the time that elapses between the vehicle reaching point of interest i and point of interest i + 1. Therefore, the DT at point of interest i is included in this time.
3.1.2. The k-Medoid Clustering Technique
Clustering methods are classification techniques that group large sets of elements, characterised by a set of attributes, using similarity criteria. For the purposes of this study, clustering techniques have two interesting properties. The first is that they do not require prior learning and the second is that there are metrics that measure the quality of the resulting clusters. In the proposed model, assuming the formulation stated above, given a significant period of time T and a route Lc, the set of elements to be classified is composed by all the trips on route Lc that have been completed in period T—i.e., dataset Ec,T representing all trips ec,t. These trips are represented by the TT observed at each point of interest OPTc,t and the dataset of all the representations of all trips Ec,T is represented by OPTc,T. If in the prediction of TT, n points of interest have been defined on Lc, then each element OPTc,t, is represented by an n-tuple (TT1, TT2, …, TTn), which corresponds to the TT observed on trip ec,t.
In the proposed methodology, the historical
TT behaviour profiles are obtained by the
k-medoids method [
20]. This method belongs to the group of non-hierarchical clustering techniques, and any distance metric can be used to measure the similarity between two elements. The grouping criterion is to cluster data around the most representative objects, called the “medoid”, of the dataset. The most representative object is the most centrally located point. Therefore, this representative object is a pre-existing object from the sample and not an object that is generated in the classification process. This property means that the
k-medoids technique responds well in the event of outliers. The most used distance metrics in the
k-medoids technique are the Euclidean distance and Manhattan distance metrics. Equations (2) and (3) express the Euclidean and Manhattan distances, between two objects,
Xi and
Xj, for a set of
Q objects, each object being represented by
n attributes. Equation (2) is the Euclidean distance and Equation (3) the Manhattan distance.
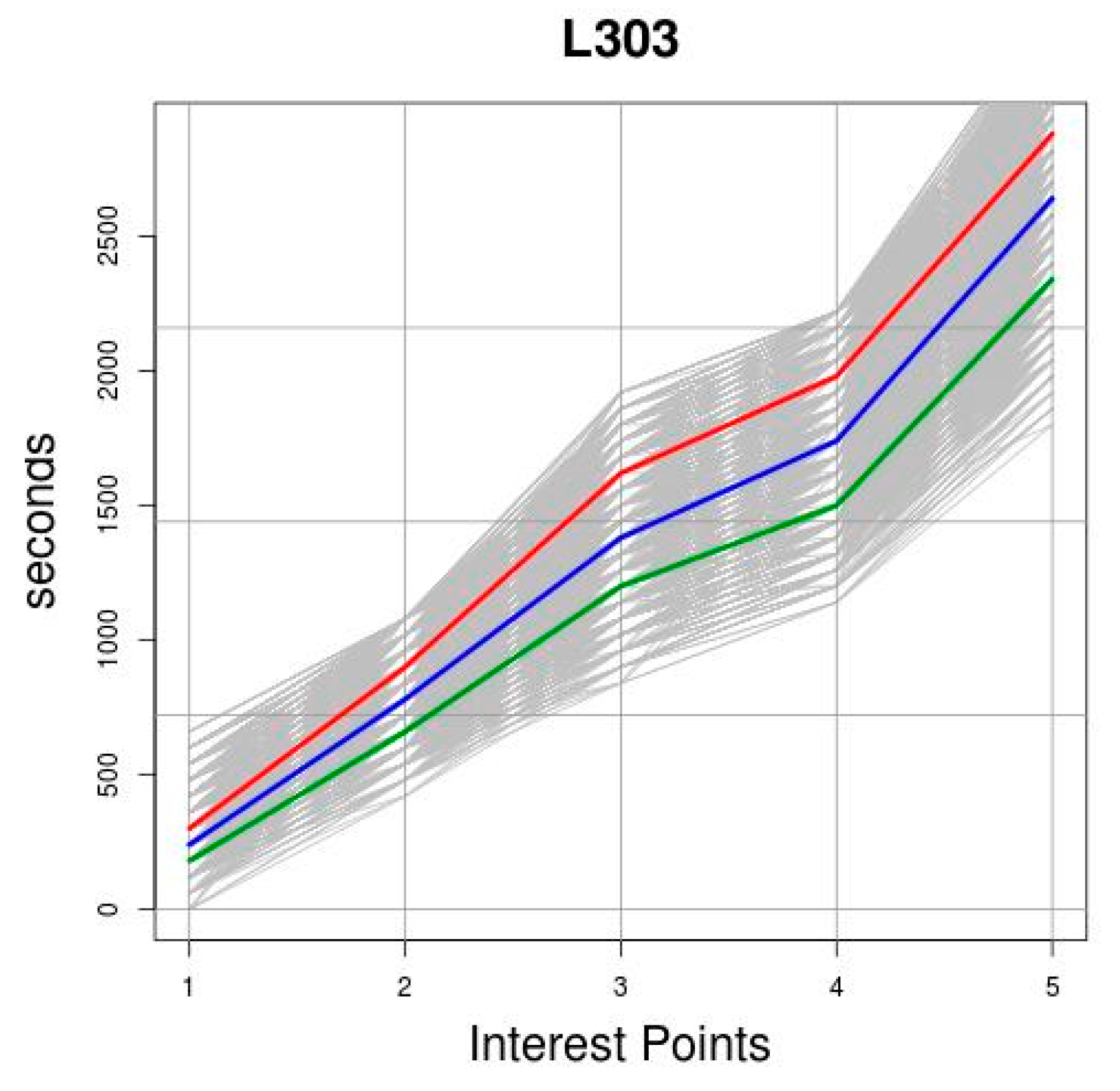
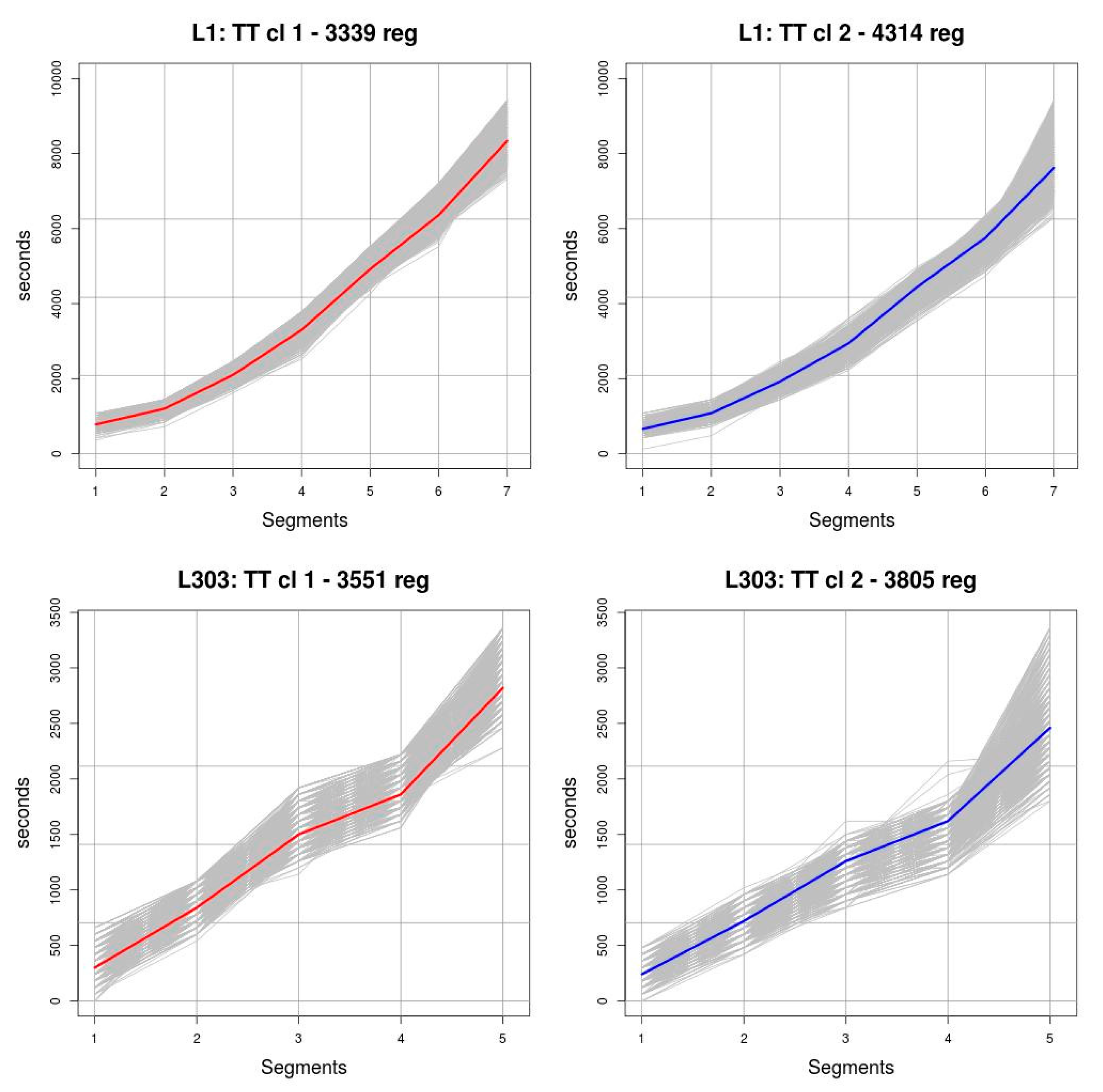
An example of clustering using the
k-medoids technique is shown in
Figure 3. On the horizontal axis the points of interest are represented and on the vertical axis the observed
TT, measured in seconds, at the points of interest of a route. Each grey curve represents the
TT recorded for a trip,
OPTc,t. The dataset
OPTc,T is formed by all the
OPTc,t curves. The red, blue and green curves represent the medoids, which are the representative object of each of the three resulting clusters.
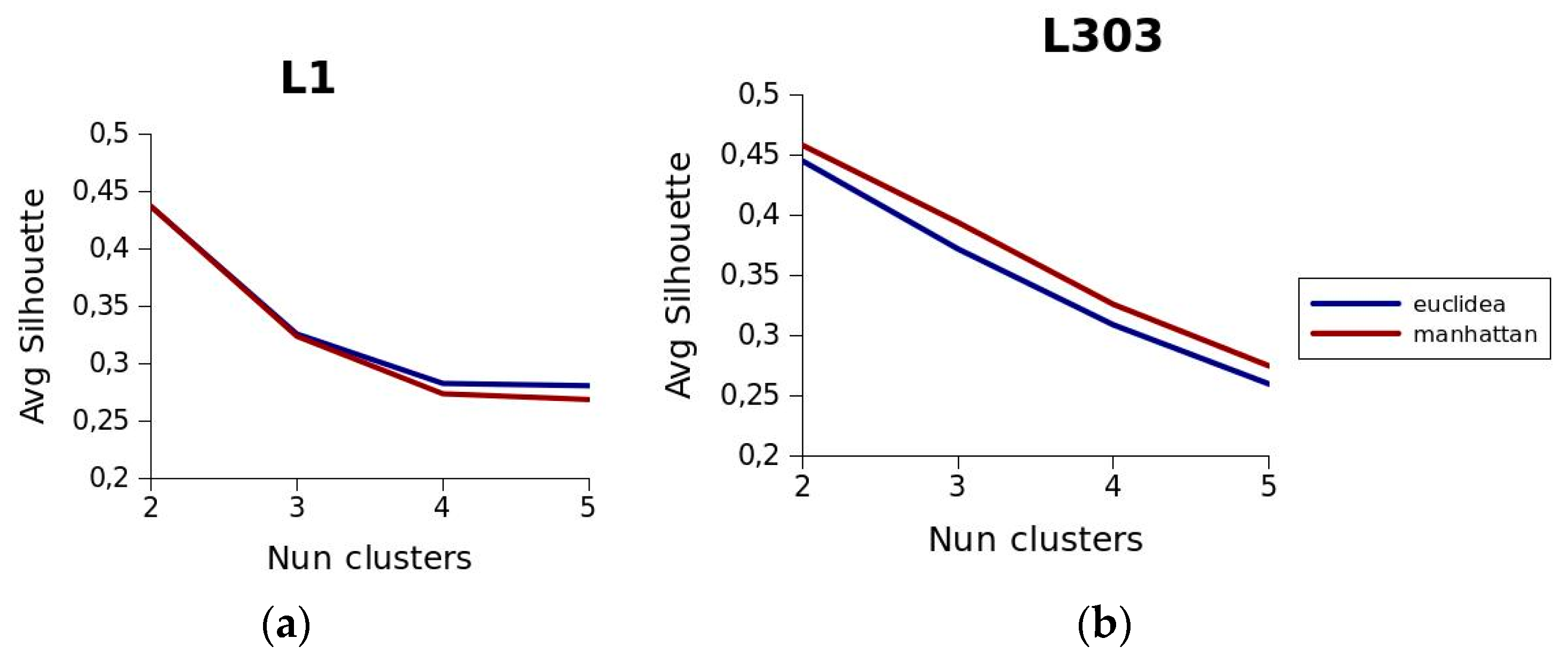
To evaluate the validity of a clustering solution there are different criteria, which may be classified into three categories: external indices, which measure the extent to which cluster labels match externally-supplied class labels; internal indices, which measure the intrinsic information of each dataset; and relative indices, which are used to compare several different clustering solutions. For the purposes of this study, an internal index was chosen to measure the quality of the clusters: the silhouette function [
21]. This measures the consistency of the cluster based on a comparison of the tightness and separation of the elements of each segment generated. This is computed by the following expression:
In expression (4), Ai is the average distance from object i to the other objects within the cluster and Bi is the smallest average distance from i to all the objects of each of the clusters to which i does not belong. The values returned by the silhouette function are in the range −1 and 1. A value close to 1 indicates a high degree of consistency in the resulting clusters and, conversely, a value close to −1 indicates that the resulting clusters have little consistency.
3.2. Travel Time Prediction Scheme
Taking the concept of point of interest, if we assume that a vehicle is at point
Pi of the sequence of points of interest on route
Lc, the objective of the proposed method is to estimate the
TT required to reach the next point in the sequence of points of interest of the route, i.e., the
TT to reach point
Pi+1. The recent history for that vehicle, located at point of interest
Pi, is represented by a set of ordered values that represent the
TT observed when going through the points of interest already travelled, represented by the
i-tuple (
TT1,
TT2, …,
TTi). Past history, in period
T, is represented by the medoids resulting from applying the
k-medoid clustering technique to the set
OPTc,T, these medoids represent the historical profiles of the
TT. When the vehicle is at
Pi, the
TT to reach point
Pi+1 is estimated in two steps. In the first step, from the observed
TT (
TT1,
TT2, …,
TTi) the medoid that has the most similar behaviour to the
TT behaviour recorded up to point
Pi is selected. The similarity metric used is the same as that used in the clustering process through which the medoids were obtained. Once the most similar medoid has been selected, then the prediction of the
TT for segment
Si, i.e., to reach point
Pi+1, is:
In Equation (5), PTTi+1 represents the prediction of the TT taken to reach point Pi+1. TTi is the TT observed at point Pi and Mk is the medoid to which the recorded TT are most similar. Mk,i and Mk,i+1 represent the attributes i and i + 1 of this medoid, i.e., the TT that represent the historical behaviours at points Pi and Pj+1 of the k cluster.
Next, the short-term TT prediction algorithm is described for trip ec,t that is completed in vehicle V.
Data:
K: number of clusters used to represent historical TT behaviour;
{M1, …, Mk}: set of k-medoids that represent TT behaviour on trips on route Lc;
i: last control point through which V has passed on trip ec,t;
TT1→i: observed arrival time at interest points 1, 2, …, i on trip ec,t (recent behaviour);
Mk,1→i: for the k-medoid, values of the arrival time at interest points 1, 2, …, i (historical behaviour);
PTTi+1: objective of the algorithm, which is to predict TT at interest point i + 1.
Step 1. Obtain the medoid that most resembles the observed TT behaviour up to the last interest point that V has passed on trip ec,t. Dist(a,b) is the function that evaluates the distance metric that is used to assess similarity.
Dmin = ∞
For (j = 1 to K) do
Do
D = Dist(Mk,1→i, TTi→1)
If (D < Dmin)
Begin
k = j
Dmin = D
End
End
Step 2. Estimate PTTi+1
PTTi+1 = TTi + Mk,i+1 − Mk,i
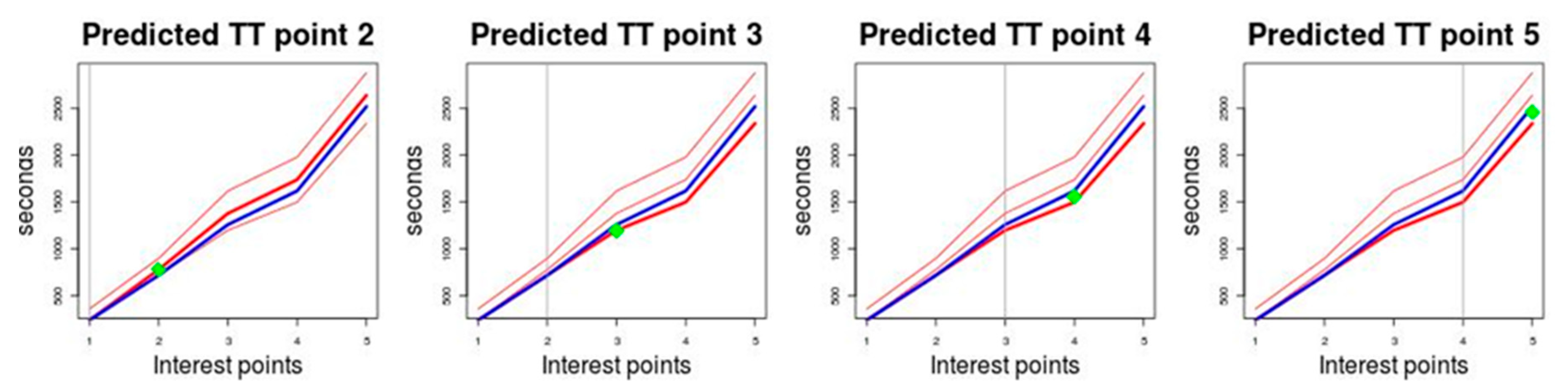
The prediction method is illustrated graphically in
Figure 4. This illustrates the prediction for a route on which five points of interest have been defined and that are represented on the horizontal axis. The
TT measured in seconds is represented on the vertical axis. The historical behaviour is represented by three medoids that have been drawn in red. The blue graph represents the
TT of the test trip for which the prediction is being made and the green dot is the
TT value predicted for the different points of interest.
Table 3 illustrates the prediction method numerically with an example prediction of a trip. The route in this example has five points of interest, columns
P1,
P2,
P3,
P4 and
P5. The historical
TT behaviour is represented by three medoids, rows
M1,
M2 and
M3. The observed
TT up to each of the points of interest is displayed in row
TT. As the vehicle reaches each point of interest, the medoid with the behaviour that is most similar to the
TT observed on the trip is selected, using Manhattan distance as the similarity metric. Rows
D(
TT,
M1),
D(
TT,
M2) and
D(
TT,
M3) contain the values resulting from calculating this distance between
TT and
M1,
M2 y
M3, respectively. At point of interest
P1, we calculated the distance between the
TT observed at this point, which was 180, and the values of the medoids at this point, which were 360 for
M1, 240 for
M2 and 240 for
M3. The Manhattan distance values obtained were 180 for
D(
TT,
M1), 60 for
D(
TT,
M2) and 60 for
D(
TT,
M3). Since the minimum distance value obtained was 60 and it was obtained with two medoids,
M2 and
M3, the first medoid that produced this minimum value, in this case
M2, was selected for this method. The predicted
TT values at each point
Pi are displayed in row
PTT. The
TT prediction to reach point of interest
P2 will be made taking medoid
M2 as the historical reference and the prediction will be calculated, according to Equation (5), by adding to the
TT observed at
P1, which is 180 s, the difference between the
TT value of
M2 at point
P2, which is 780 s, and the value of
M2 at point P
1, which is 240 s. Therefore, the value of the
TT prediction to reach P
2 is 720 s. The
TT prediction to reach point
P3 would be carried out analogously to this, but in this case the
TT profile on the trip will consist of two values (180,720) and the historical
TT behaviour profiles will be (360,900) according to
M1, (240,780) according to
M2 and (240,720) according to
M3. At this point the historical profile that is most similar to the profile observed on the trip is that represented by medoid
M3. As shown in
Table 3, at the rest of the points of interest,
M3 is the medoid with a profile most similar to the observed
TT values and therefore its
TT values will be those used to make the predictions at the other points.