Application of Logging While Drilling Tool in Formation Boundary Detection and Geo-steering
Abstract
1. Introduction
2. Forward Modeling
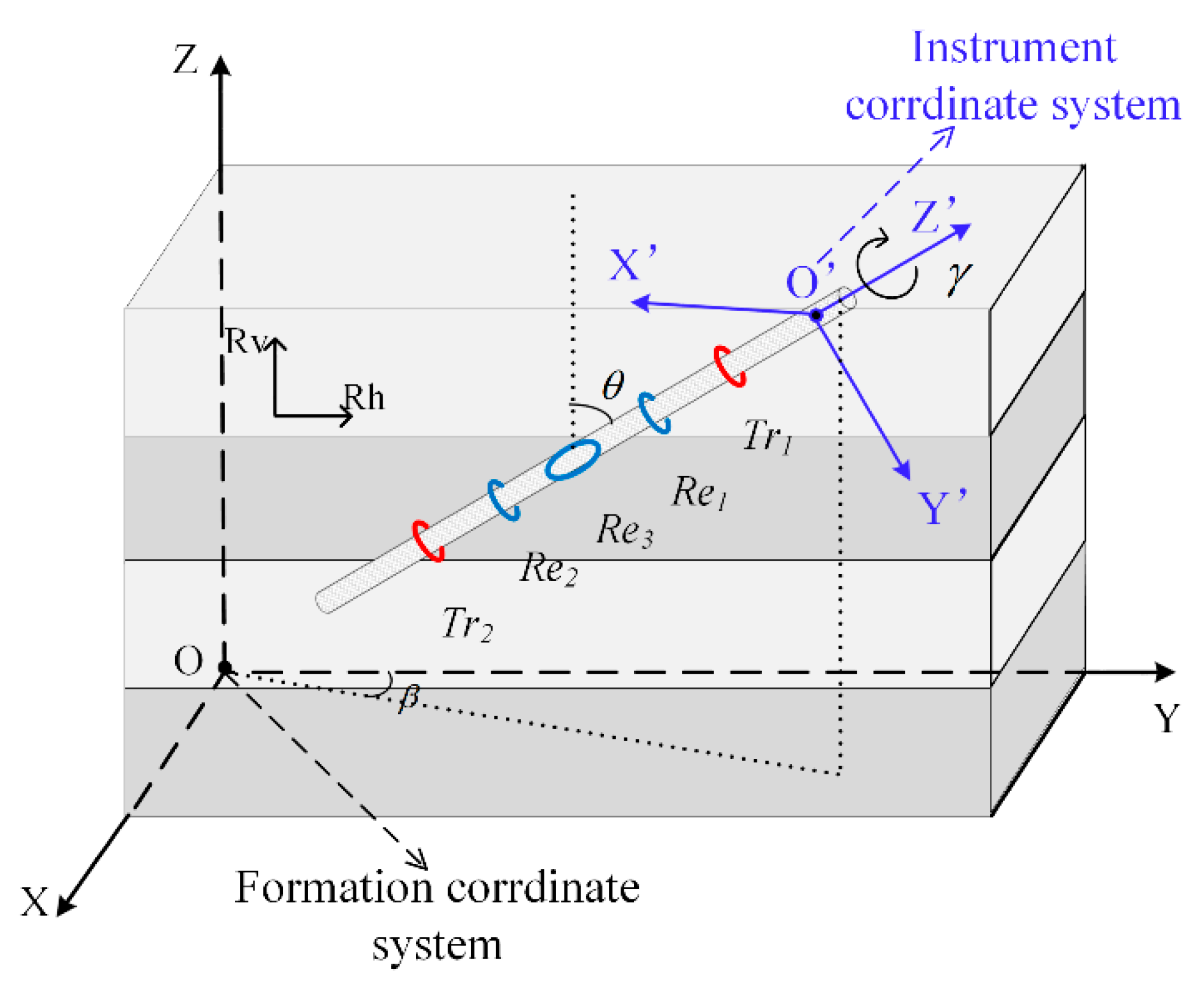
2.1. Theory of Forward Modeling
2.2. The Continued Fraction Summation
3. Inversion Modeling
3.1. Theory of Inversion Modeling
3.2. The Constraint Algorithm
4. Results and Discussions
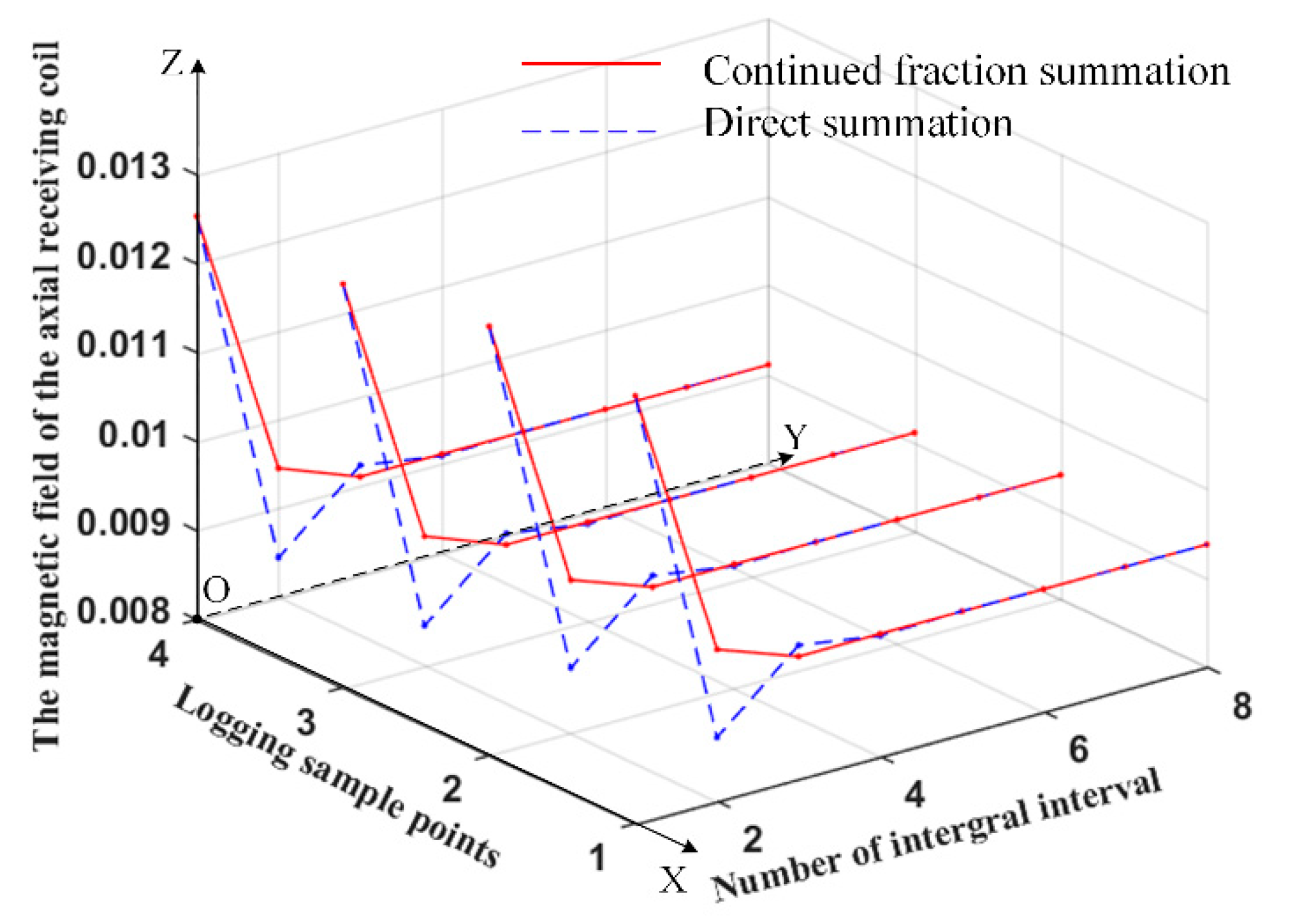
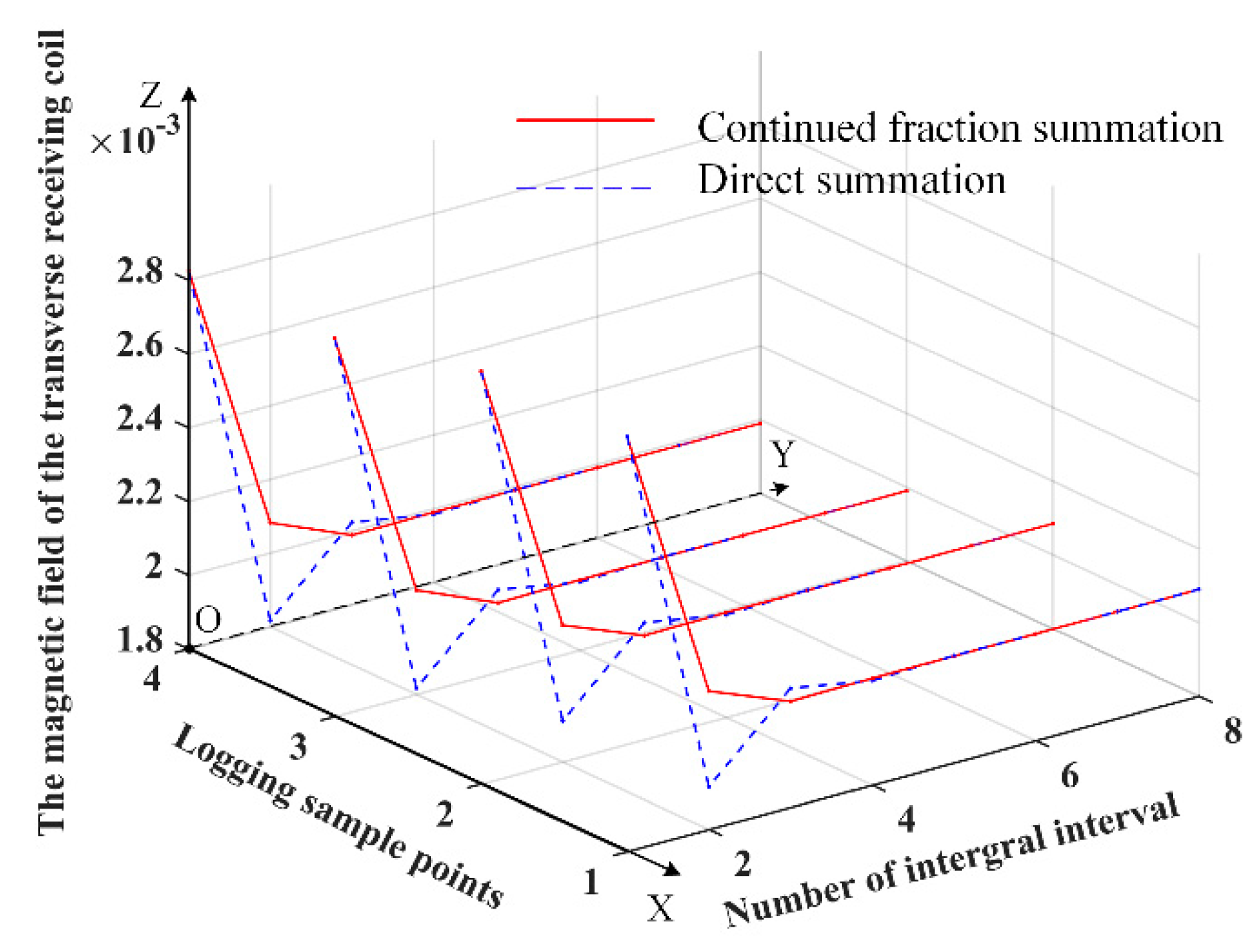
4.1. Convergence Comparison between Continued Fraction Summation and Direct Summation
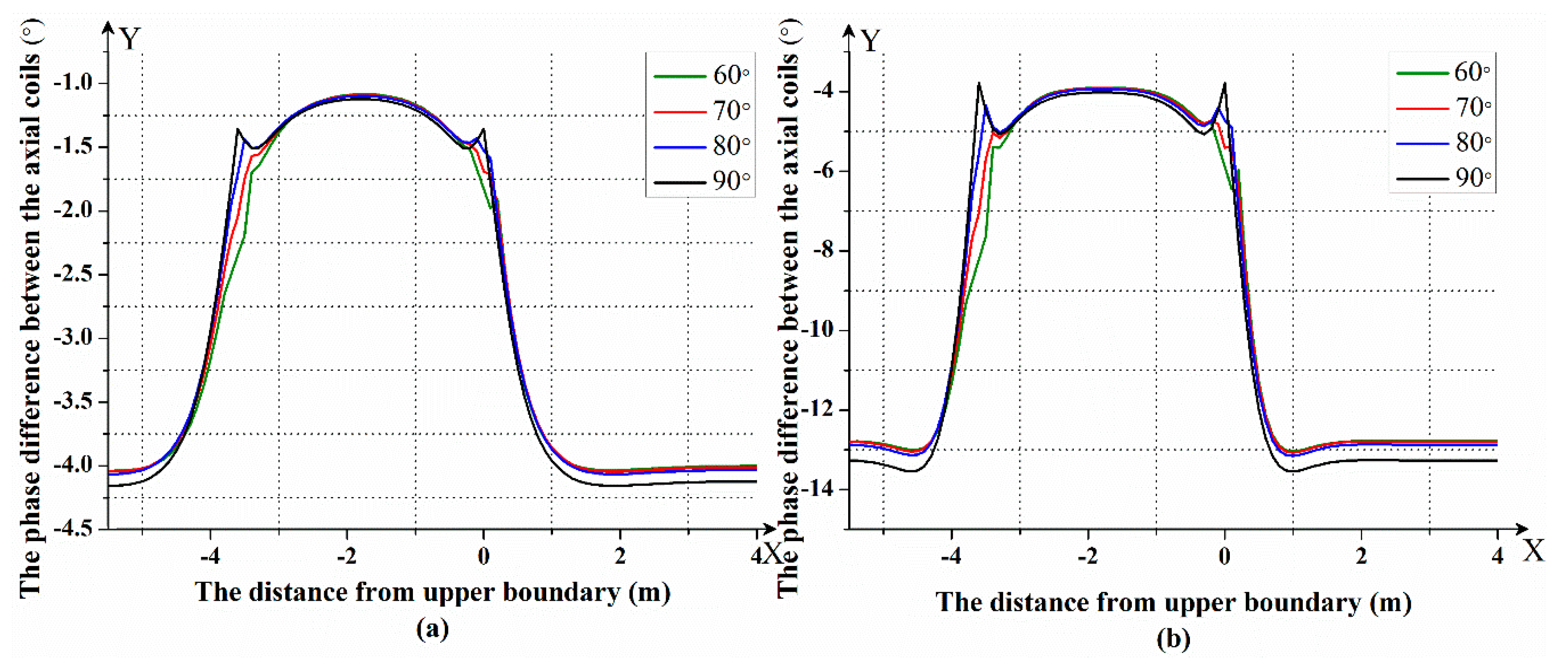
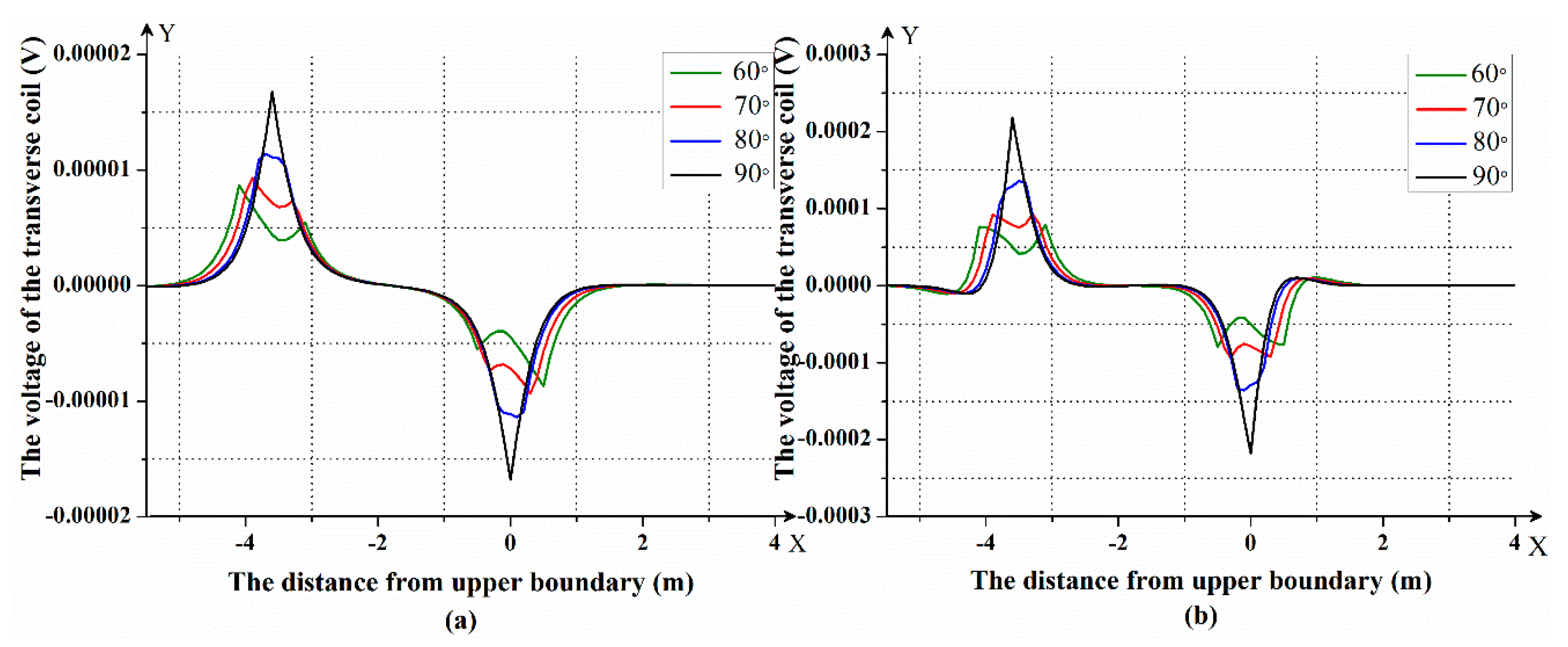
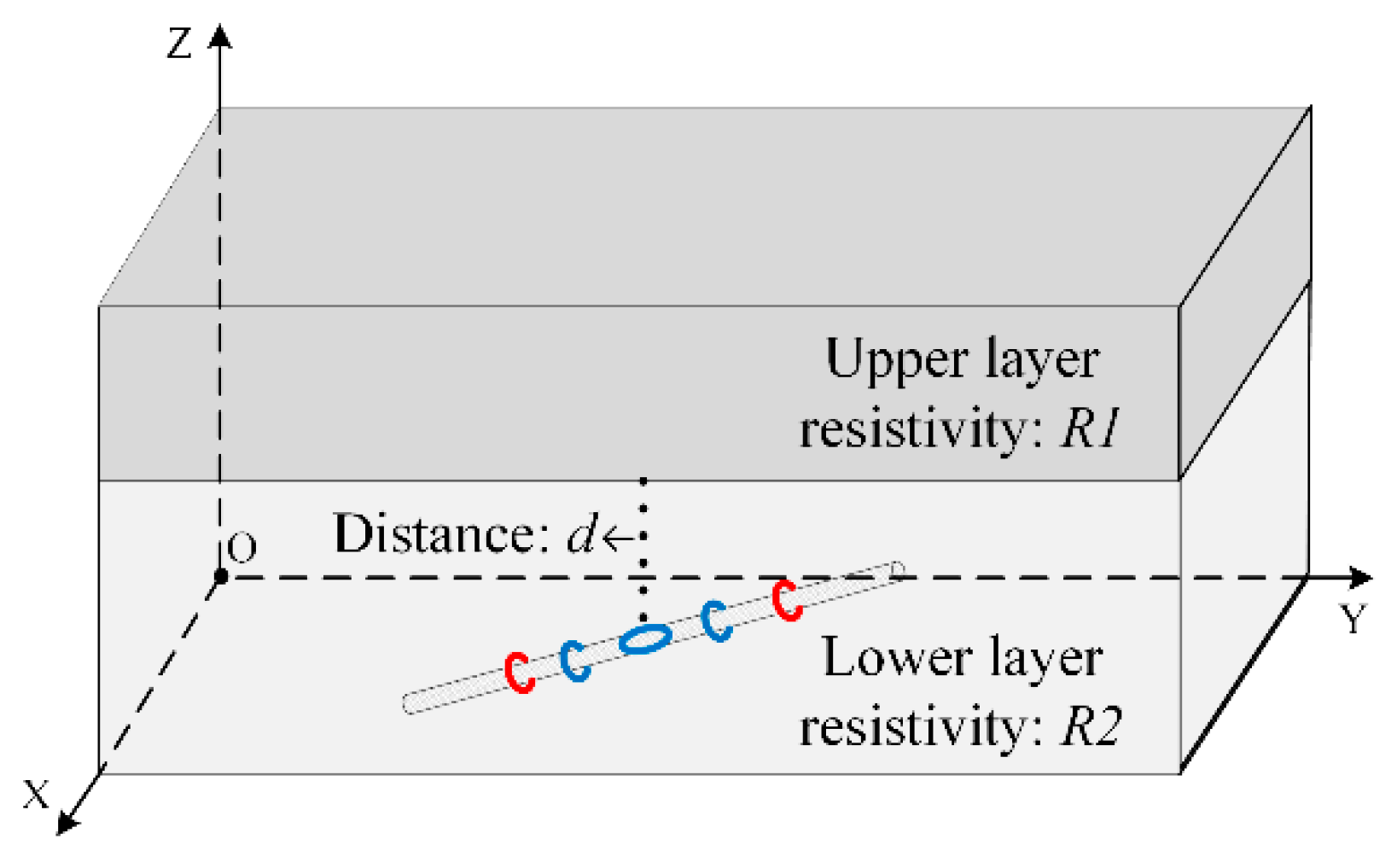
4.2. The Simulation of Forward Modeling
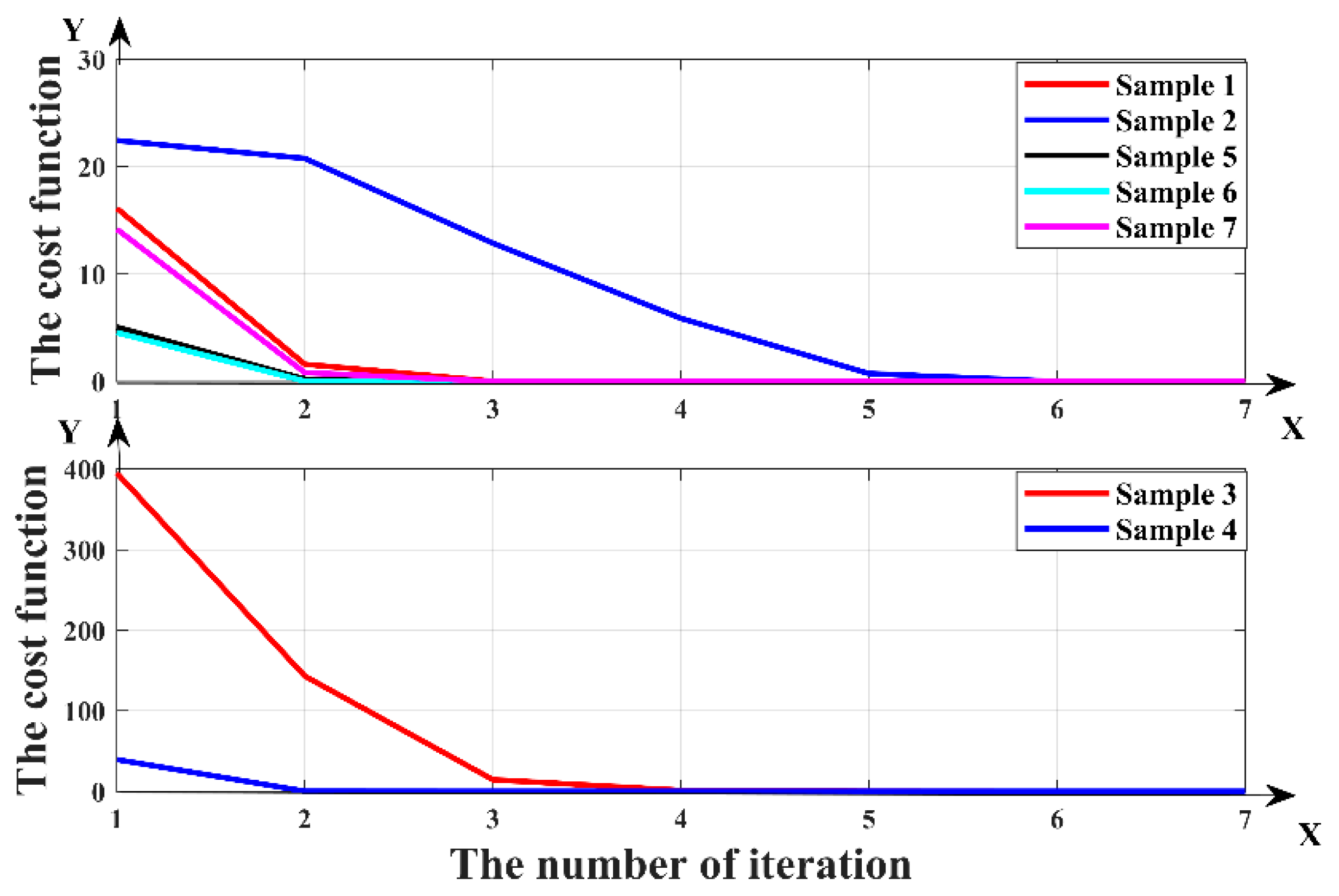
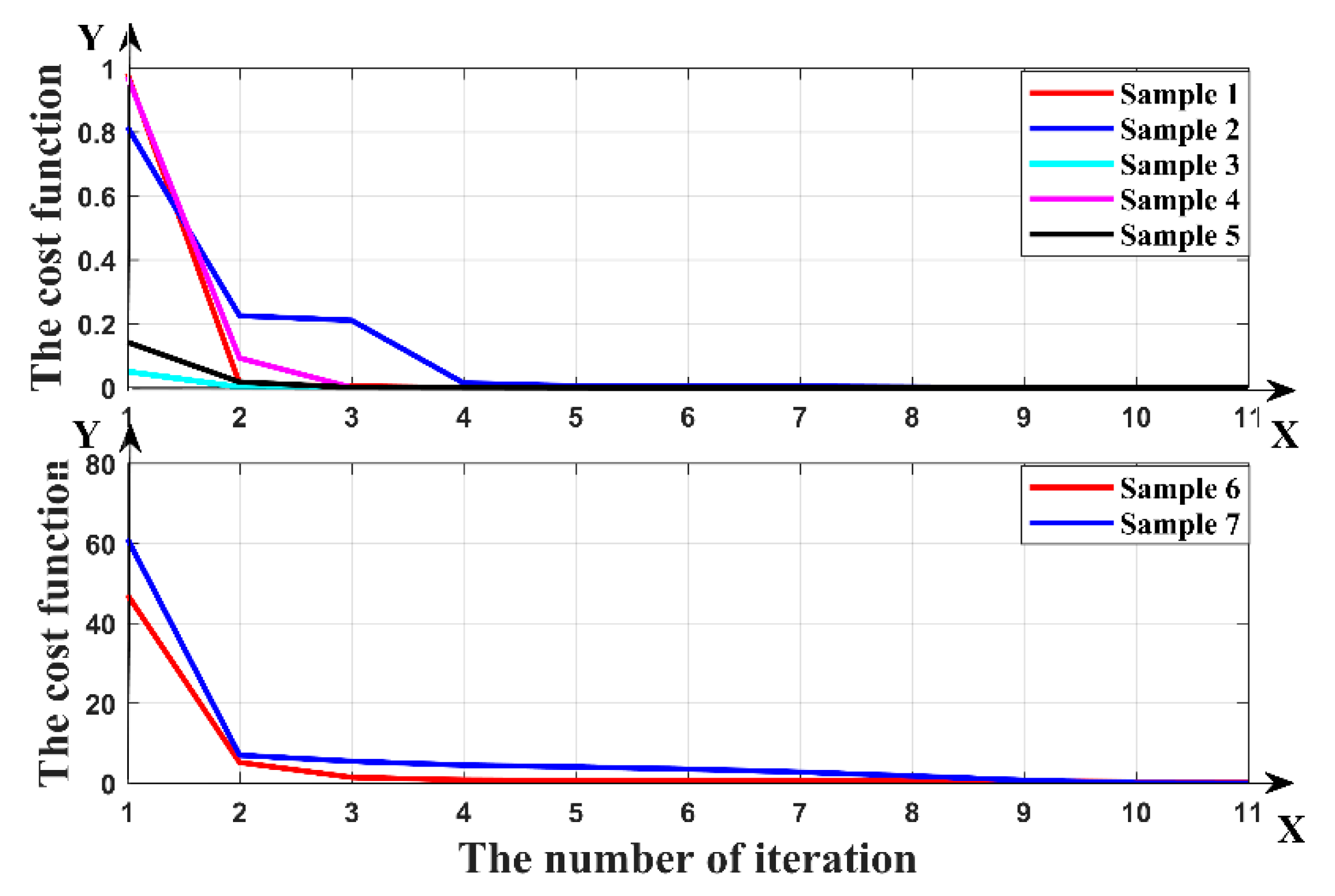
4.3. Results of Inversion Modeling
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Trujillo, M.Á.; Martínez-de Dios, J.R.; Martín, C.; Viguria, A.; Ollero, A. Novel Aerial Manipulator for Accurate and Robust Industrial NDT Contact Inspection: A New Tool for the Oil and Gas Inspection Industry. Sensors 2019, 19, 1305. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Chemali, R.; Hart, E.; Cairns, P. Real-Time Formation Imaging, Dip, And Azimuth While Drilling From Compensated Deep Directional Resistivity; Society of Petrophysicists and Well-Log Analysts: Houston, TX, USA, 2007. [Google Scholar]
- Ijasan, O.; Torresverdín, C.; Preeg, W.E. Inversion-based petrophysical interpretation of logging-while-drilling nuclear and resistivity measurements. Geophysics 2013, 78, D473–D489. [Google Scholar] [CrossRef]
- Lei, W.; Hu, L.; Fan, Y.; Wu, Z. Sensitivity analysis and inversion processing of azimuthal resistivity LWD measurements. J. Geophys. Eng. 2018, 15, 2339–2349. [Google Scholar]
- Yang, J. Method and tool for directional electromagnetic well logging. U.S. Patent No. 9,389,332, 12 July 2016. [Google Scholar]
- Liu, H. Logging-While-Drilling (LWD); Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Chimedsurong, Z.; nian, W.H. Forward Modeling of Induction Well Logging Tools in Dipping Boreholes and Their Response. Chin. J. Comput. Phys. 2003, 20, 161–168. [Google Scholar]
- Doll, H.G. Introduction to induction logging and application to logging of wells drilled with oil base mud. J. Pet. Technol. 1949, 1, 148–162. [Google Scholar] [CrossRef]
- Tang, C.-M. Electromagnetic fields due to dipole antennas embedded in stratified anisotropic media. IEEE Trans. Antennas Propag. 1979, 27, 665–670. [Google Scholar] [CrossRef]
- Eroglu, A.; Lee, Y.; Lee, J. Dyadic Green’s functions for multi-layered uniaxially anisotropic media with arbitrarily oriented optic axes. IET Microw. Antennas Propag. 2011, 5, 1779–1788. [Google Scholar] [CrossRef]
- Zhong, L.; Li, J.; Bhardwaj, A.; Shen, L.C.; Liu, R.C. Computation of Triaxial Induction Logging Tools in Layered Anisotropic Dipping Formations. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1148–1163. [Google Scholar] [CrossRef]
- Bo, D.; Ling, Y.; Liu, C.; Zheng, Y.; Hui, L.; Dang, R.; Sun, B. A Uniform Linear Multi-Coil Array-Based Borehole Transient Electromagnetic System for Non-Destructive Evaluations of Downhole Casings. Sensors 2018, 18, 2707. [Google Scholar]
- Zhang, Z. 1-D Modeling and Inversion of Triaxial Induction Logging Tool in Layered Anisotropic Medium. Dissertations & Theses Gradworks, University of Houston, 2011. [Google Scholar]
- Zhu, G.; Xiang, C.; Kong, F.; Li, K. A continued fraction method for modeling and inversion of triaxial induction logging tool. In Proceedings of the Microwaves, Radar and Remote Sensing Symposium (MRRS), Kyiv, Ukraine, 29–31 August 2017; pp. 201–204. [Google Scholar]
- Bakr, S.A.; Pardo, D.; Torres-Verdín, C. Fast inversion of logging-while-drilling resistivity measurements acquired in multiple wells. Geophysics 2017, 82, E111–E120. [Google Scholar] [CrossRef]
- Wang, X.; Fu, Z.; Wang, Y.; Liu, R.; Chen, L. A Non-Destructive Testing Method for Fault Detection of Substation Grounding Grids. Sensors 2019, 19, 2046. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Yan, S.; Li, B. A Novel Method of Localization for Moving Objects with an Alternating Magnetic Field. Sensors 2017, 17, 923. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.I.; Barber, T.D.; Habashy, T.M. The Interpretation and Inversion of Fully Triaxial Induction Data; A Sensitivity Study. Earth Moon Planets 2002, 66, 99–128. [Google Scholar]
- Yu, L.; Xiao, J. A fast inversion method for multicomponent induction log data. In SEG Technical Program Expanded Abstracts 2001; Society of Exploration Geophysicists: Houston, TX, USA, 2001; pp. 361–364. [Google Scholar]
- Lu, X.; Alumbaugh, D.L. One-dimensional inversion of three-component induction logging in anisotropic media. In SEG Technical Program Expanded Abstracts 2001; Society of Exploration Geophysicists: Houston, TX, USA, 2001; pp. 376–380. [Google Scholar]
- Heriyanto, M.; Srigutomo, W. 1-D DC Resistivity Inversion Using Singular Value Decomposition and Levenberg-Marquardt’s Inversion Schemes. J. Phys. Conf. Ser. 2017, 877, 012066. [Google Scholar] [CrossRef]
- Pardo, D.; Torres-Verdín, C. Fast 1D inversion of logging-while-drilling resistivity measurements for improved estimation of formation resistivity in high-angle and horizontal wells. Geophysics 2015, 80, E111–E124. [Google Scholar] [CrossRef]
- Xing, G.; Wang, H.; Zhu, D. A New Combined Measurement Method of the Electromagnetic Propagation Resistivity Logging. IEEE Geosci. Remote Sens. Lett. 2008, 5, 430–432. [Google Scholar] [CrossRef]
- Wang, W.; Geng, Y.; Wang, K.; Si, J.; Fiaux, J. Dynamic Toolface Estimation for Rotary Steerable Drilling System. Sensors 2018, 18, 2944. [Google Scholar] [CrossRef]
- Hardman, R.H. Theory of induction sonde in dipping beds. Geophysics 1986, 51, 800. [Google Scholar] [CrossRef]
- Shahriari, M.; Rojas, S.; Pardo, D.; Rodríguez-Rozas, A.; Bakr, S.; Calo, V.; Muga, I. A numerical 1.5 D method for the rapid simulation of geophysical resistivity measurements. Geosciences 2018, 8, 225. [Google Scholar] [CrossRef]
- Huang, M.; Shen, L.C. Computation of induction logs in multiple-layer dipping formation. IEEE Trans. Geosci. Remote Sens. 1989, 27, 259–267. [Google Scholar] [CrossRef]
- Jie, G.; Liu, F.P.; Bao, D.Z.; Xi, C.; Zhang, Y.L. Study on forward modeling of through-casing resistivity logging. Sci. China 2008, 51, 207–211. [Google Scholar]
- Cesarano, C.; Ricci, P.E. The legendre polynomials as a basis for Bessel functions. Int. J. Pure Appl. Math. 2016, 111, 129–139. [Google Scholar] [CrossRef][Green Version]
- Yoshida, Y.; Bowler, J.R. Computation of eddy current probe response due to a long crack based on a vector potential integral formulation. Int. J. Appl. Electromagn. Mech. 1999, 10, 77–89. [Google Scholar] [CrossRef]
- Hänggi, P.; Rösel, F.; Trautmann, D. Continued fraction expansions in scattering theory and statistical non-equilibrium mechanics. Zeitschrift Für Naturforschung A 1978, 33, 402–417. [Google Scholar] [CrossRef]
- Singh, U.K.; Tiwari, R.K.; Singh, S.B. One-dimensional inversion of geo-electrical resistivity sounding data using artificial neural networks—A case study. Comput. Geosci. 2005, 31, 99–108. [Google Scholar] [CrossRef]
- Golsorkhi, N.A.; Tehrani, H.A. Levenberg-Marquardt method for solving the inverse heat transfer problems. J. Math. Comput. Sci. 2014, 13, 300–310. [Google Scholar] [CrossRef]
- Pardo, D.; Calo, V.M.; Torres-Verdín, C.; Nam, M.J. Fourier series expansion in a non-orthogonal system of coordinates for the simulation of 3D-DC borehole resistivity measurements. Comput. Methods Appl. Mech. Eng. 2008, 197, 3836–3849. [Google Scholar] [CrossRef]
- Kleefeld, A.; Reißel, M. The Levenberg–Marquardt method applied to a parameter estimation problem arising from electrical resistivity tomography. Appl. Math. Comput. 2011, 217, 4490–4501. [Google Scholar] [CrossRef]
- Schellenberg, D. Identifikation und Optimierung im Kontext technischer Anwendungen; VDI: Düsseldorf, Germany, 2017. [Google Scholar]
| Sample | True Values | Initial Values | Iterations | Inversion Vesults | |||
|---|---|---|---|---|---|---|---|
| R2 (Ω∙m) | d (m) | R2 (Ω∙m) | d (m) | R2 (Ω∙m) | d (m) | ||
| 1 | 10.00 | −0.40 | 4.00 | −0.30 | 5 | 10.00 | −0.40 |
| 2 | 10.00 | −0.40 | 4.00 | −0.10 | 7 | 10.00 | −0.40 |
| 3 | 10.00 | 0.10 | 5.00 | 0.40 | 6 | 10.00 | 0.10 |
| 4 | 10.00 | −0.10 | 6.00 | 0.70 | 5 | 10.00 | −0.10 |
| 5 | 4.00 | 0.20 | 6.00 | 0.50 | 5 | 4.00 | 0.20 |
| 6 | 8.00 | −0.20 | 10.00 | −0.50 | 4 | 8.00 | −0.20 |
| 7 | 8.00 | −0.10 | 10.00 | −0.70 | 5 | 8.00 | −0.10 |
| Sample | True Values | Initial Values | Iterations | Inversion Results | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R1 (Ω∙m) | R2 (Ω∙m) | d (m) | R1 (Ω∙m) | R2 (Ω∙m) | d (m) | R1 (Ω∙m) | R2 (Ω∙m) | d (m) | ||
| 1 | 5.00 | 18.00 | 0.20 | 10.00 | 13.00 | 0.40 | 5 | 5.00 | 18.00 | 0.20 |
| 2 | 5.00 | 18.00 | 0.20 | 8.00 | 13.00 | −0.40 | 11 | 5.00 | 18.00 | 0.20 |
| 3 | 10.00 | 18.00 | −0.20 | 8.00 | 13.00 | −0.40 | 5 | 10.00 | 18.00 | −0.20 |
| 4 | 10.00 | 15.00 | −0.10 | 13.00 | 19.00 | −0.30 | 4 | 10.00 | 15.00 | −0.09 |
| 5 | 10.00 | 15.00 | 0.10 | 15.00 | 17.00 | 0.20 | 5 | 10.00 | 15.00 | 0.10 |
| 6 | 10.00 | 5.00 | −0.10 | 15.00 | 17.00 | 0.03 | 15 | 10.00 | 5.00 | −0.10 |
| 7 | 11.00 | 3.00 | −0.50 | 13.00 | 19.00 | 0.00 | 11 | 10.99 | 3.00 | −0.50 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, G.; Gao, M.; Kong, F.; Li, K. Application of Logging While Drilling Tool in Formation Boundary Detection and Geo-steering. Sensors 2019, 19, 2754. https://doi.org/10.3390/s19122754
Zhu G, Gao M, Kong F, Li K. Application of Logging While Drilling Tool in Formation Boundary Detection and Geo-steering. Sensors. 2019; 19(12):2754. https://doi.org/10.3390/s19122754
Chicago/Turabian StyleZhu, Gaoyang, Muzhi Gao, Fanmin Kong, and Kang Li. 2019. "Application of Logging While Drilling Tool in Formation Boundary Detection and Geo-steering" Sensors 19, no. 12: 2754. https://doi.org/10.3390/s19122754
APA StyleZhu, G., Gao, M., Kong, F., & Li, K. (2019). Application of Logging While Drilling Tool in Formation Boundary Detection and Geo-steering. Sensors, 19(12), 2754. https://doi.org/10.3390/s19122754





