1. Introduction
Through the deployment of numerous IoT sensors, smart environments can attempt to recognise the goal of a human from the actions they perform, and thus become more context-aware. Despite recent advances in Goal Recognition (GR) techniques [
1,
2], a person’s goal often cannot be determined until their plan nears completion. This is because the plans to reach different goals can initially be identical. Nonetheless, recognising a human’s goal promptly is important in many situations. In environments where security is essential, such as airports [
3], improved goal distinctiveness can allow security personnel to intercept a person sooner. In a kitchen environment [
4,
5], by minimising the number of observations required to recognise a human’s goal, a robot can provide earlier assistance [
6].
By redesigning an environment, our work aims to improve the distinctiveness of goals. We have identified two ways Goal Recognition Design (GRD) can affect human-inhabited environments. First, actions in the available plans can be replaced, e.g., by changing an item’s location, the act of taking it from its first location is replaced with taking it from a different location. Second, the possibility of performing an action can be removed, e.g., a barrier or ornament can be placed to prevent a human from navigating between two positions. The resulting environment design potentially improves the accuracy of GR approaches, such as [
7,
8,
9], and requires fewer distinct actions to be detected. In some cases, this reduction could lead to fewer, cheaper or less privacy invasive sensors being deployed in context-aware smart environments.
To clarify the principle of GRD, an example is provided.
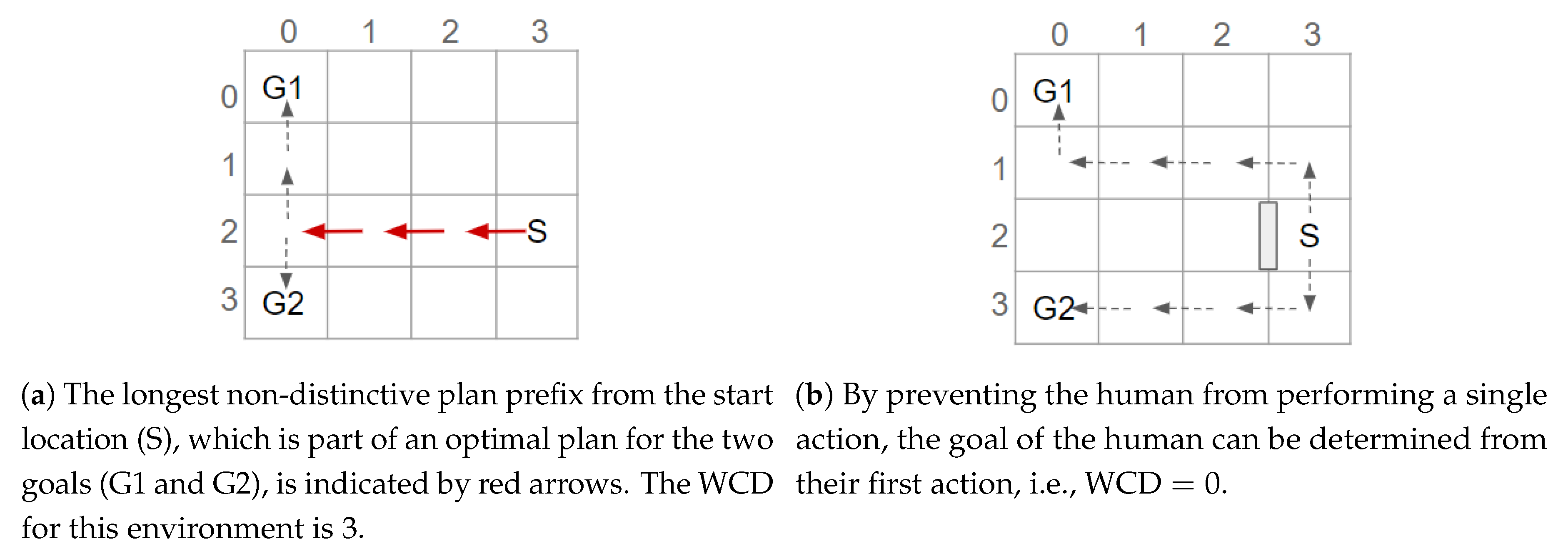
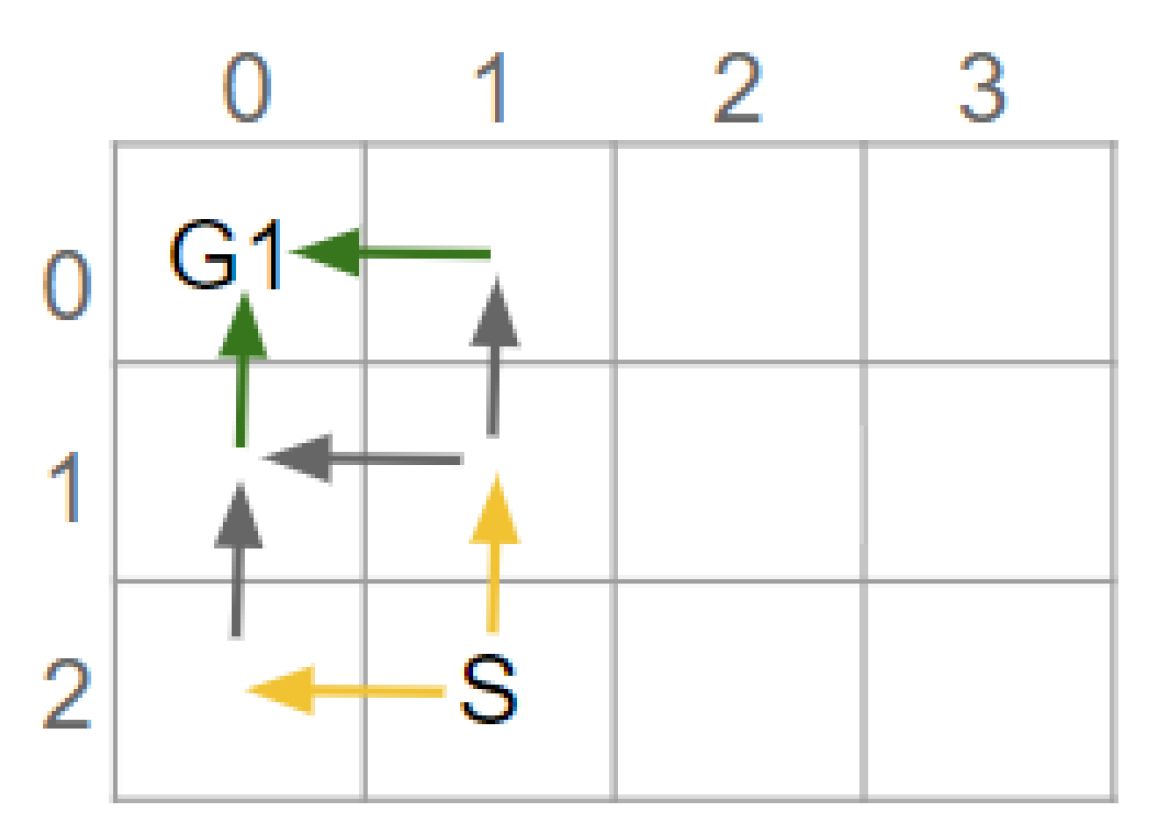
Figure 1 shows two potential goals. These goals could indicate the locations of the gates in an airport [
10]. To recognise which goal a human is aiming to reach, their actions are observed; however, depending on which route is taken, initially the human’s goal cannot be determined. At worst the plans to reach these goals have a non-distinctive prefix containing 3 actions, i.e., the Worst Case Distinctiveness (WCD) is 3. By placing an obstacle to prevent a person from moving between positions (3,2) and (2,2), the WCD of the environment is reduced to 0. In other words, after the environment is redesigned only 1 (discrete) action needs to be observed before the human’s goal is discernible. The term goal recognition design and the WCD metric were introduced by Keren et al. [
10].
GRD is a more complex problem than task planning. In task planning the aim is (normally) to find an optimal plan to reach a goal, whereas in GRD there are multiple goals defined and all optimal plans containing non-distinctive prefixes must be found before the environment can be redesigned. Current approaches to GRD [
12,
13,
14,
15] usually focus on removing the ability to perform actions or placing order constraints on the actions. To our knowledge, this paper is the first to propose state changes that cause actions in the plans to be replaced, which could result in the length of a plan as well as its non-distinctive prefix changing. As the lengths of the plans can change, we propose a new metric, complementary to WCD, to measure the distinctiveness of an environment.
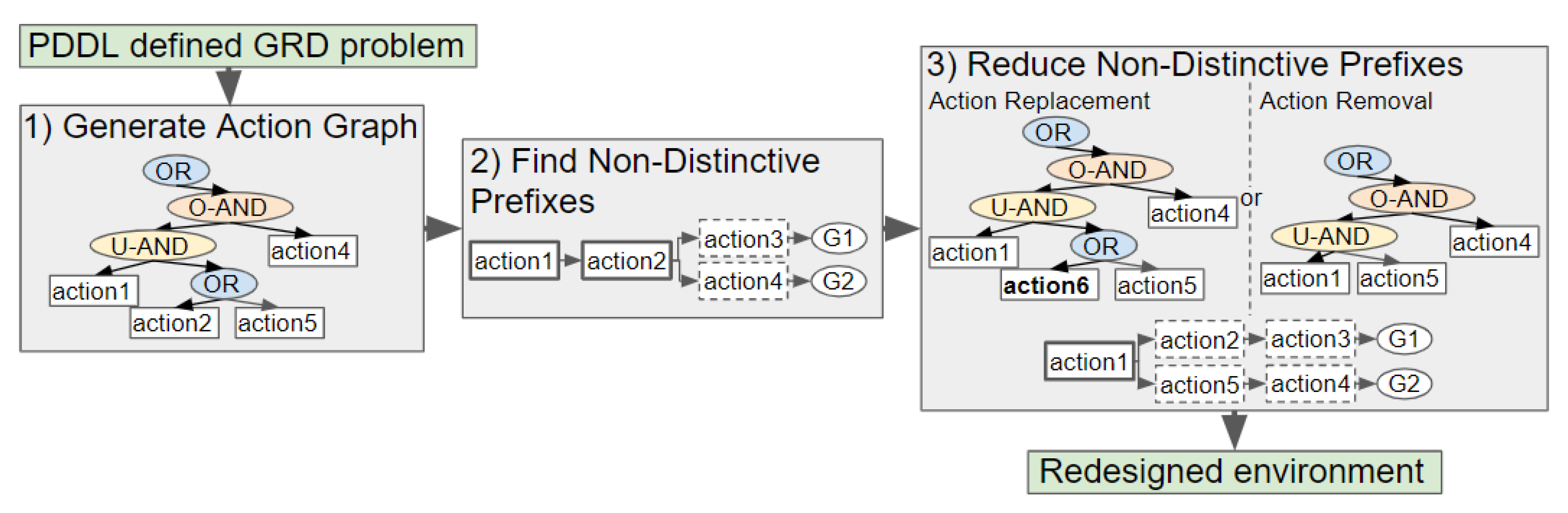
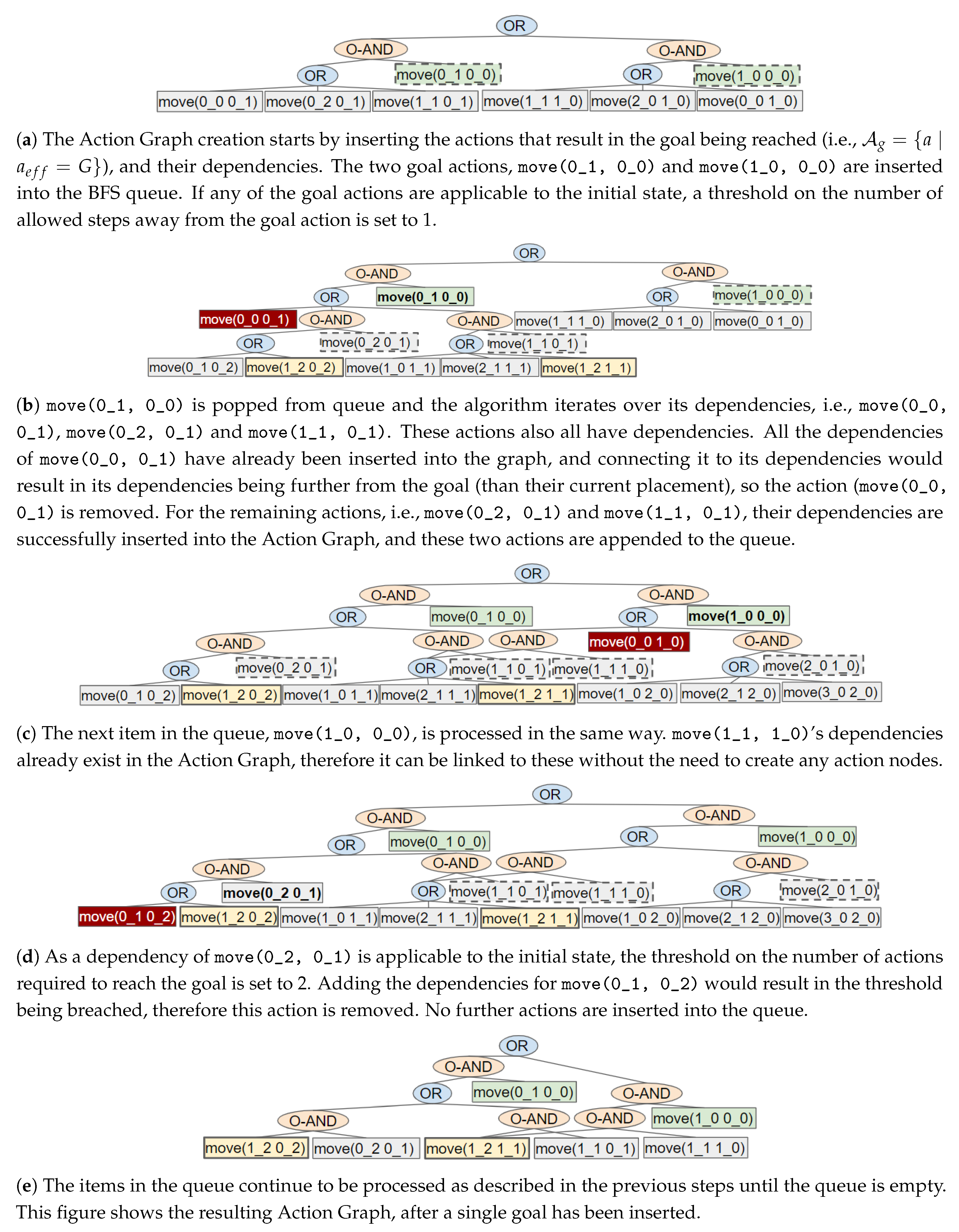
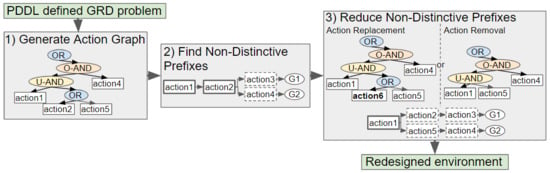
Our novel approach to GRD transforms a problem defined in Planning Domain Definition Language (PDDL), a popular domain-independent language to model the behaviour of deterministic agents, into an Action Graph. Non-distinctive plan prefixes are extracted from the graph, and processed to determine which actions should be removed or replaced to increase the goals’ distinctiveness. Two methods for selecting which actions to replace, namely exhaustive and a less computationally expensive method Shrink–Reduce, are introduced and compared to one another. An overview of our approach is provided in
Figure 2.
In our previous work [
11], we described a new method for generating an Action Graph for navigation problems. In the current paper, we introduce a new distinctiveness metric, expand the graph creation method to domains with fewer constraints on the order of actions, provide a new algorithm to find the non-distinctive prefixes, and develop a method to change the state of the environment so that actions are replaced. Our approach is not applicable to domains in which cycles exist within the goals’ plans, as Action Graphs are acyclic and no action is repeated within its structure. Moreover, the world is assumed to be fully observable; however, after redesigning the environment fewer actions tend to require observing. The algorithms are evaluated on a grid-based navigation domain, and on a kitchen domain developed by Ramírez and Geffner [
7] from the work of Wu et al. [
16]. While a domain from [
7] is used, a comparison to their approach is not provided as their approach performs GR and not GRD.
Section 2 provides an overview of related work.
Section 3 states the formal definition of GRD problems and briefly mentions the GR methods that inspired our approach. The metrics to measure the distinctiveness of an environment are presented in
Section 4.
Section 5 describes the structure and construction of an Action Graph. The algorithm to find all the non-distinctive plan prefixes in an Action Graph is introduced in
Section 6.
Section 7 describes how the actions to replace are selected. How actions are removed to increase the distinctiveness is described in
Section 8. Finally, we present experimental results in
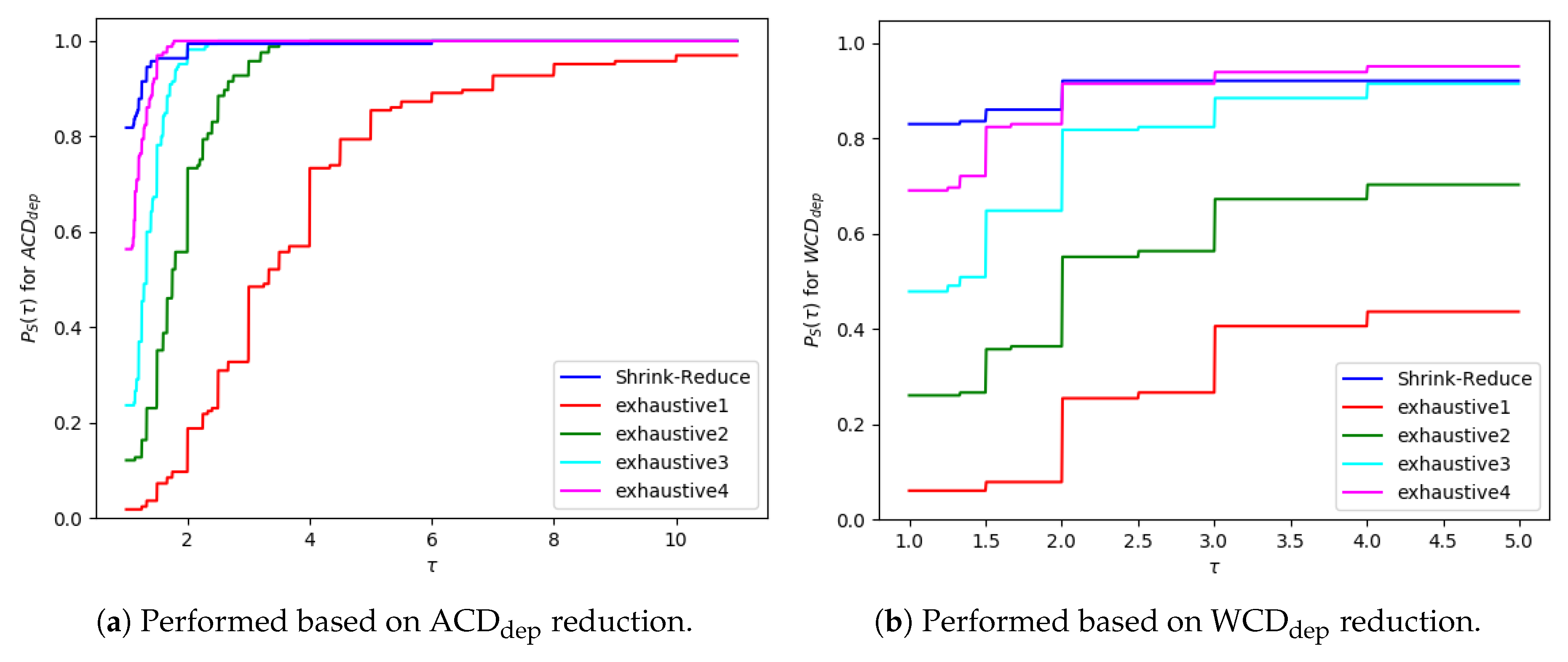
Section 9, by measuring the computational efficiency of our Shrink–Reduce action replacement heuristic and comparing our action removal method to a state-of-the-art approach [
10].
2. Related Work
The term goal recognition design was coined by Keren et al. [
10]. In their approach the WCD of a problem is calculated by transforming a GRD problem into multiple planning problems containing pairs of goals. An optimal plan, with the longest possible non-distinctive prefix, to each pair of goals is searched for. The longest non-distinctive plan prefix, across all joint plans, is the WCD. To reduce WCD an increasing number of actions are removed until either the WCD is 0, or the search space has been exhausted, in which case the best environment design discovered so far is returned. Their pruned-reduce method improves the computational efficiency by reducing the number of action combinations whose removal requires testing. We compare our solution to their pruned-reduce algorithm, and show that for navigation domains we have greatly reduced the time required to solve goal recognition design problems. Further to removing actions, their approach has been extended to action conditioning, in which a partial ordering is enforced [
15]. We do not investigate enforcing action ordering, as our focus is on human-inhabited environments, and it is difficult to force action order constraints on humans; but further to their work, we explore domains in which modifications to the state cause actions within a plan to be replaced and that result in the plan’s length changing. Their approach has also been extended for non-optimal agents [
17], and to determine where to place sensors within the environment [
18]. In this paper we assume the agent/human is optimal and do not investigate sensor placement.
Wayllace et al. [
12,
14] investigate goal recognition design involving stochastic action outcomes with Markov Decision Processes (MDPs). To calculate WCD, a MDP is created for each goal, the states that are common to pairs of goals are discovered and the Bellman equation is used to calculate the cost of reaching a state. To reduce the WCD their algorithm removes a set of actions, checks that the optimal cost to reach a goal has not been affected, and calculates the WCD to find out if it has been reduced. Their approach creates a MDP multiple times for each of the goals, which results in large computational costs. In our approach a single model (Action Graph) is created, which contains the actions to reach all goals, moreover it is only created once.
In [
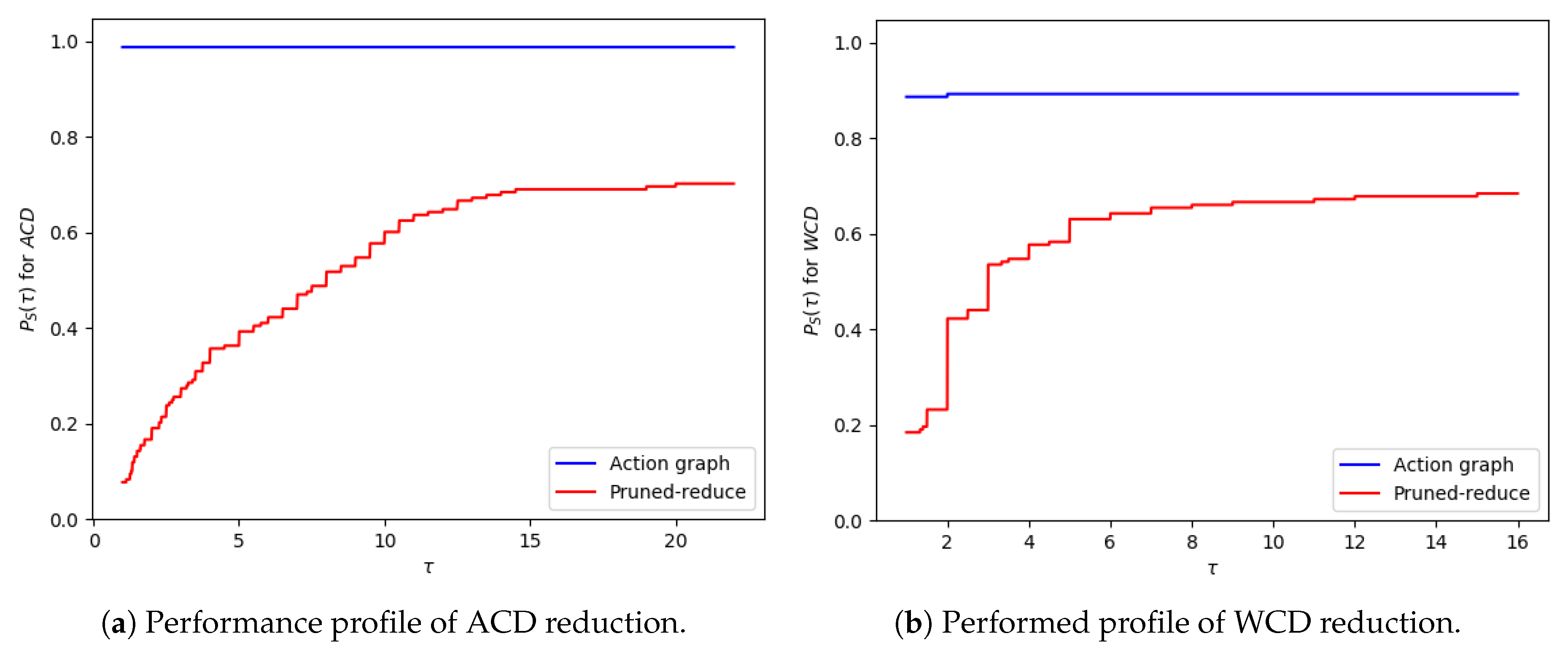
19], a new metric is introduced, namely expected-case distinctiveness (ECD), which is applicable to stochastic domains and solves a shortcoming of WCD. WCD only incorporates knowledge of the least distinctive pair of goals, rather than all goals’ distinctiveness. To solve this, ECD is calculated recursively, starting from the actions applicable to the initial state and ending with the actions furthest from that state (i.e., that result in a goal state). The resulting ECD is the sum of all weighted plan lengths, with the weights based on prior probabilities of an agent choosing a certain goal. We also introduce a new metric which addresses the mentioned shortcoming of WCD, but for a deterministic setting. Moreover, our metric also accounts for the length of both the plan and non-distinctive prefix being altered during the environment design process.
Son et al. [
13] propose an approach based on Answer Set Programming (ASP), as an alternative to PDDL, to reduce the computational cost. Their results only show a maximum of two actions being removed, which greatly limits how much WCD can be reduced. Our approach takes PDDL as input, as we build on the work from [
20], which performed well (i.e., computational time and accuracy) on goal recognition problems.
Planning libraries were provided as input to the goal recognition design method by Mirsky et al. [
21]. Further, they introduce plan recognition design, in which the aim is to make the plans, rather than goals, distinctive. They present a brute-force method, which gradually removes a higher number of rules from the planning library, and a constraint-based search method. Their constraint-based search attempts to remove different combinations of rules within the non-distinctive plans starting from the rules contained within the least distinctive plans. Like Mirsky et al. [
21] and Keren et al. [
15], we developed an exhaustive strategy and less computationally expensive method but, rather than preventing actions, removing rules or constraining the order actions must be performed in, our approach changes the state of the environment in such a way that the actions within plans are replaced by others (with the same effects), which could affect the length of the plans as well as the non-distinctive prefixes.
4. Distinctiveness Metric
The WCD metric proposed in [
10] only provides knowledge about the longest non-distinctive prefix for a set of goals
, rather than considering the overall distinctiveness of the goals and the structures of the plans. In this section, several examples are provided to illustrate the shortcomings of the WCD metric and additional metrics are proposed.
Whilst redesigning the environment, the distinctiveness of some goals (
) can be increased without affecting the WCD. We, therefore, propose finding the longest non-distinctive prefix for each goal and calculating the average length of these, namely the average distinctiveness (ACD). An example is provided to demonstrate the advantage of calculating ACD over WCD. Suppose there are three goals, all requiring a different item to be taken from the same cupboard. The plans are shown in
Figure 3a, from which it is clear that the WCD of these goals is 1. After redesigning the environment, by moving
item3 from
cupboard1, G3 becomes fully distinctive (
Figure 3b). The environment has arguably been made more distinctive but the WCD does not reflect this, i.e., it is still 1. The ACD of the initial environment is also 1, i.e.,
, but after
item3 has been moved, the ACD is reduced to
.
A second drawback of WCD (and also of ACD) is that these metrics only capture the lengths of the non-distinctive plan prefixes and not the structure of the plans. In other words, WCD lacks knowledge of the dependencies between actions, and thus the possible plan permutations. The more dependants a non-distinctive action has, the less distinctive that action is. If an action has one distinct dependant, then only one change is required to make it fully distinctive. When the state of the environment is redesigned, both the WCD and the ACD metrics could be reduced without the goals becoming necessarily more distinctive, or vice-versa. For this reason, we introduce modified versions of WCD and ACD, i.e., and .
To calculate these, if a non-distinctive action is required to fulfil multiple actions’ precondition(s), that action is counted multiple times. More precisely, each action a in the longest non-distinctive prefix is counted C times, with C equalling the number of actions (including the goal itself) for which a is a dependency. Dependencies are defined in this paper as actions that set one or more of the dependant’s preconditions, e.g., action 1 is said to be dependent on action 2 if action 2 fulfils one (or more) of action 1’s preconditions, i.e., . If multiple options exist the longest list of dependencies is selected.
The calculation for
is defined by Equation (
1), in which
is the number of actions counted, as described above, in the longest prefix common to both
and
. In the calculation of
, the averaging operation is replaced by finding the maximum, see Equation (
2). Note, the operator
p is non-commutative:
is not necessarily equal to
. Algorithmic details on how
p can be discovered are provided in
Section 6. For clarification several examples in which
, and the reduction differs, are provided next.
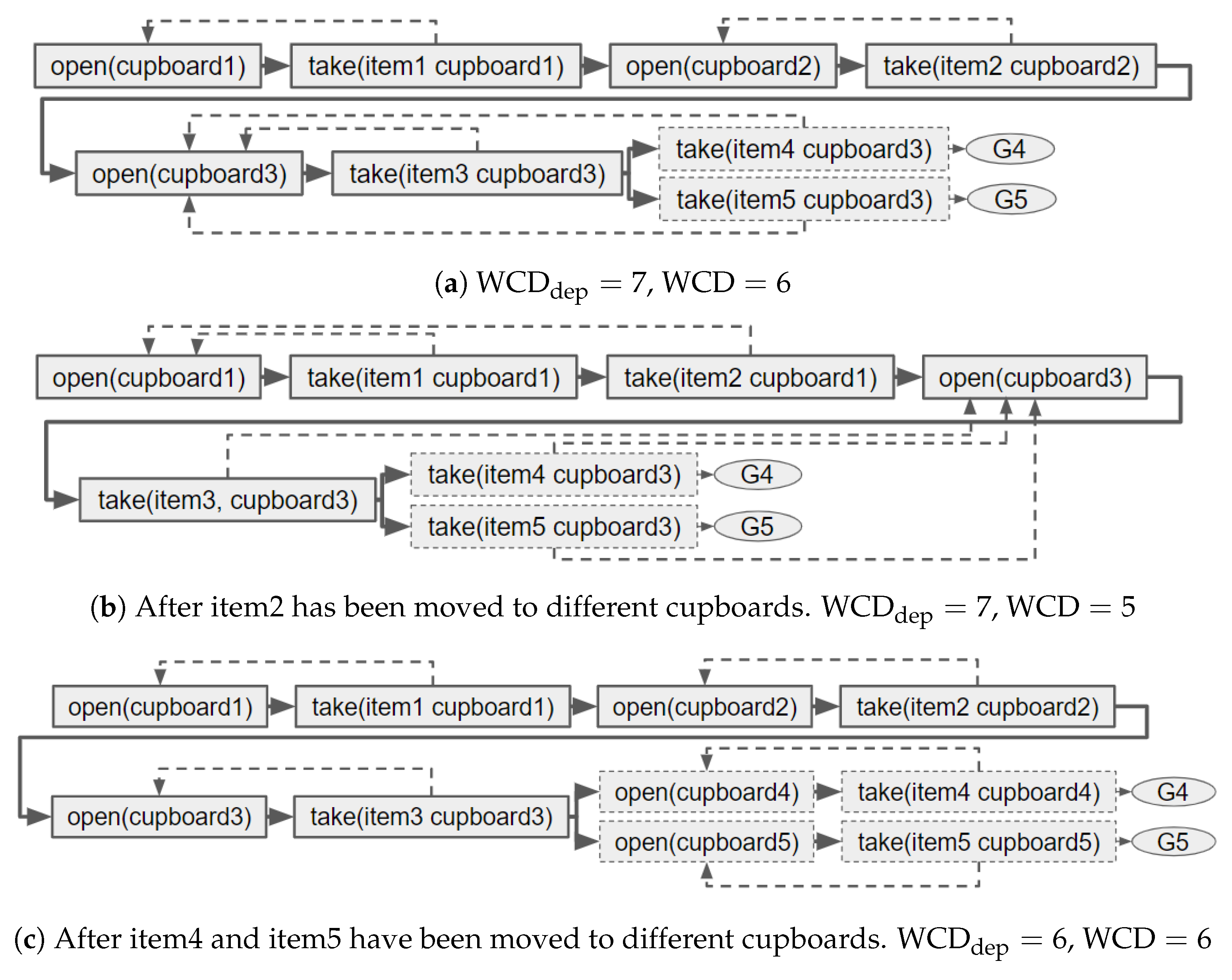
In the example shown in
Figure 4a, each of the 2 goals requires taking
item1,
item2 and
item3. These items are all in different cupboards that must be opened before the item can be taken. Therefore, the WCD for this environment is 6. The
is 7, as both these goals require a second (unique) item to be taken from
cupboard3, so opening
cupboard3 is counted twice. If during the design process
item2 is moved into
cupboard1 the WCD is reduced to 5 but the
is not reduced (
Figure 4b). When items are moved into a single cupboard the plans, as well as non-distinctive prefixes, become shorter. Therefore, a GRD approach that aims to reduce WCD could simply move all items into the same cupboard. A better solution would be to put the items unique to a goal in a cupboard not required by any another goal since, depending on which plan permutation is selected, this enables the goal to be recognised after a single observation. Note, making plans shorter may be desired by the human; however, it is not the primary aim of our work.
In the same scenario, it is also possible that
is reduced when WCD is not.
Figure 4c shows the example after such a change occurs. If the items unique to both plans are moved into different cupboards (which are also not contained within the non-distinctive prefix),
is reduced but WCD remains the same. This reduction reflects the fact that, due to the different plan permutations, the human’s first action could now be distinctive (i.e., if they open
cupboard4 their goal must be G4).
The non-distinctive prefix does not necessary equal the non-distinctive prefix . For example, if item4 is moved to cupboard4 and item5 remains in cupboard3, then , whereas (i.e., the opening of cupboard3 is counted twice). G4 is more distinctive than G5, as to maximise G5’s distinctiveness one item’s state needs to be changed, but modifying G4’s plan will not increase the distinctiveness.
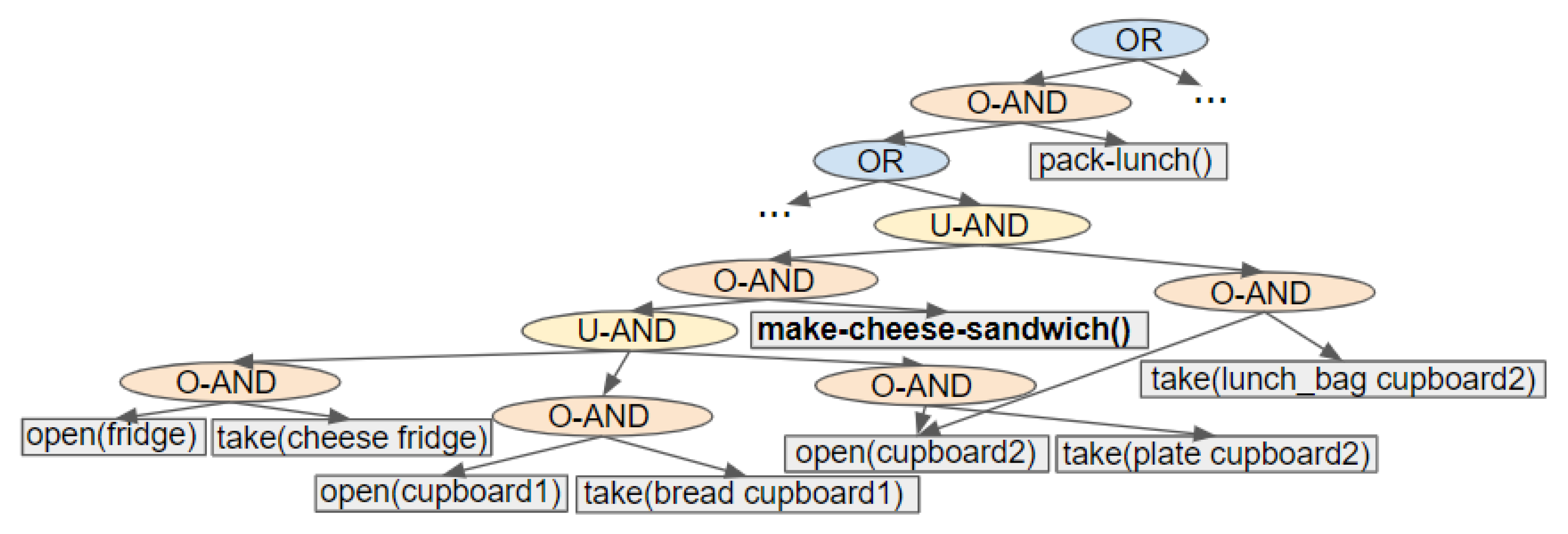
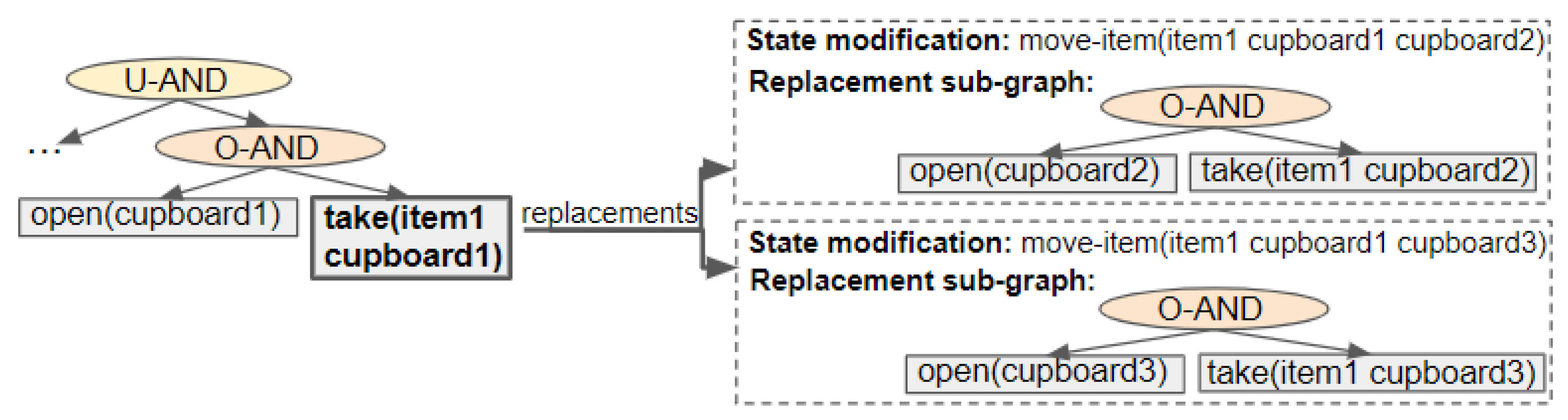
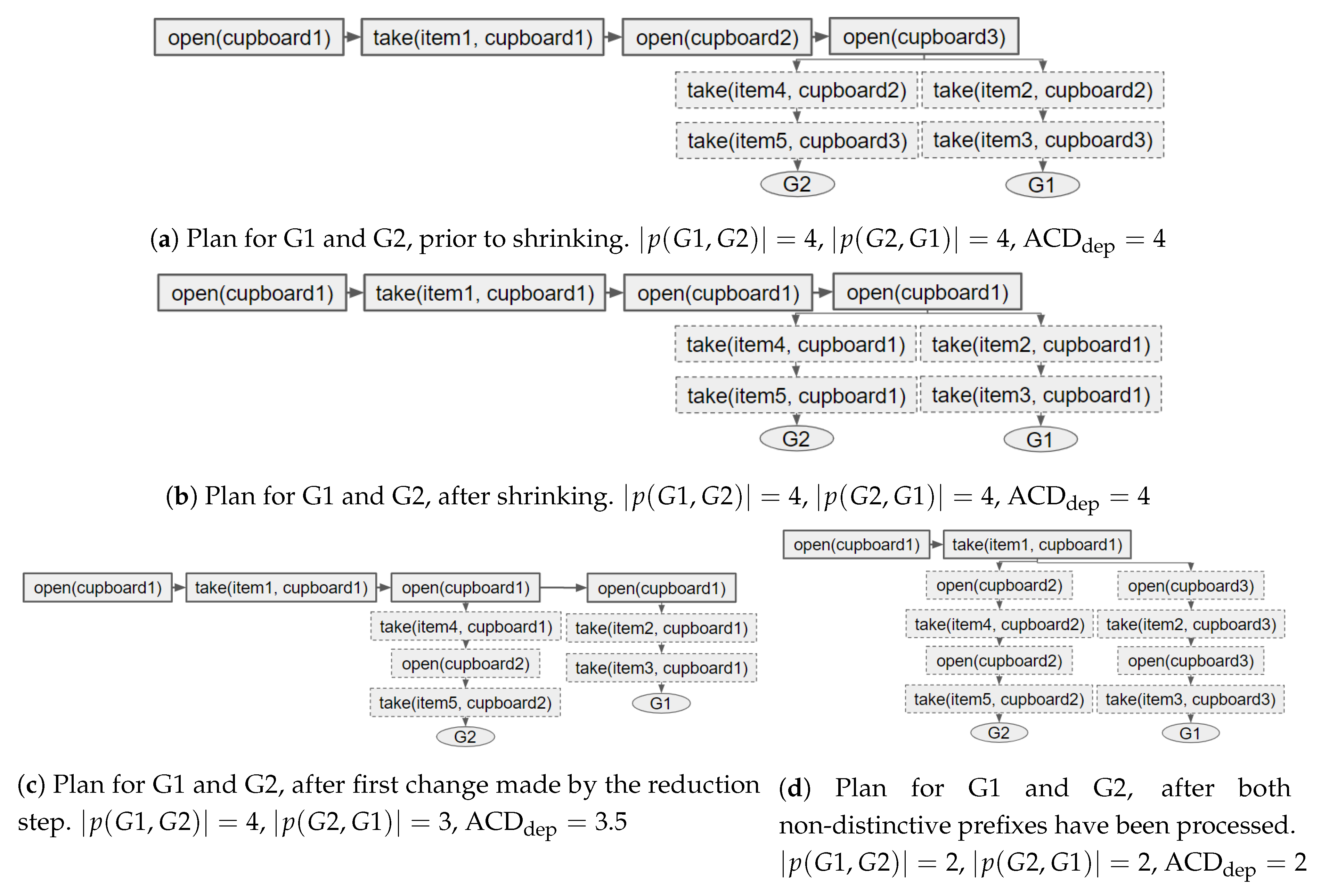
8. Performing Action Removal to Reduce ACD
As described in our previous work [
11], by removing the possibility of performing an action and, consequently, modifying the state of the environment, the goals
can be made more distinctive (i.e., the
reduced). This type of state modification is applied to a navigation domain, as it is the only human-inhabited environment, we can think of, in which it is feasible to remove actions (e.g., by placing obstacles). As mentioned above, for such a domain only the optimal plans are contained within the Action Graph; thus, during the action removal process the cost of the optimal is not increased. Rather than simply exhaustively removing parts of the graph, a much less computationally expensive algorithm has been developed. This section first provides an overview of how the non-distinctive prefixes are processed, before providing the details. In
Figure 11,
Figure 12 and
Figure 13, taken from our previous paper [
11], some simple examples are provided to illustrate how our approach works. An example is also provided in a video supplied as
Supplementary Materials. Our approach is applicable to environments of any size with any number of goals.
A video showing the Shrink–Reduce process, for an example problem, has been provided as
Supplementary Materials. The unconstrained and constrained Action Graph creation algorithms are demonstrated in the videos provided as
Supplementary Materials.
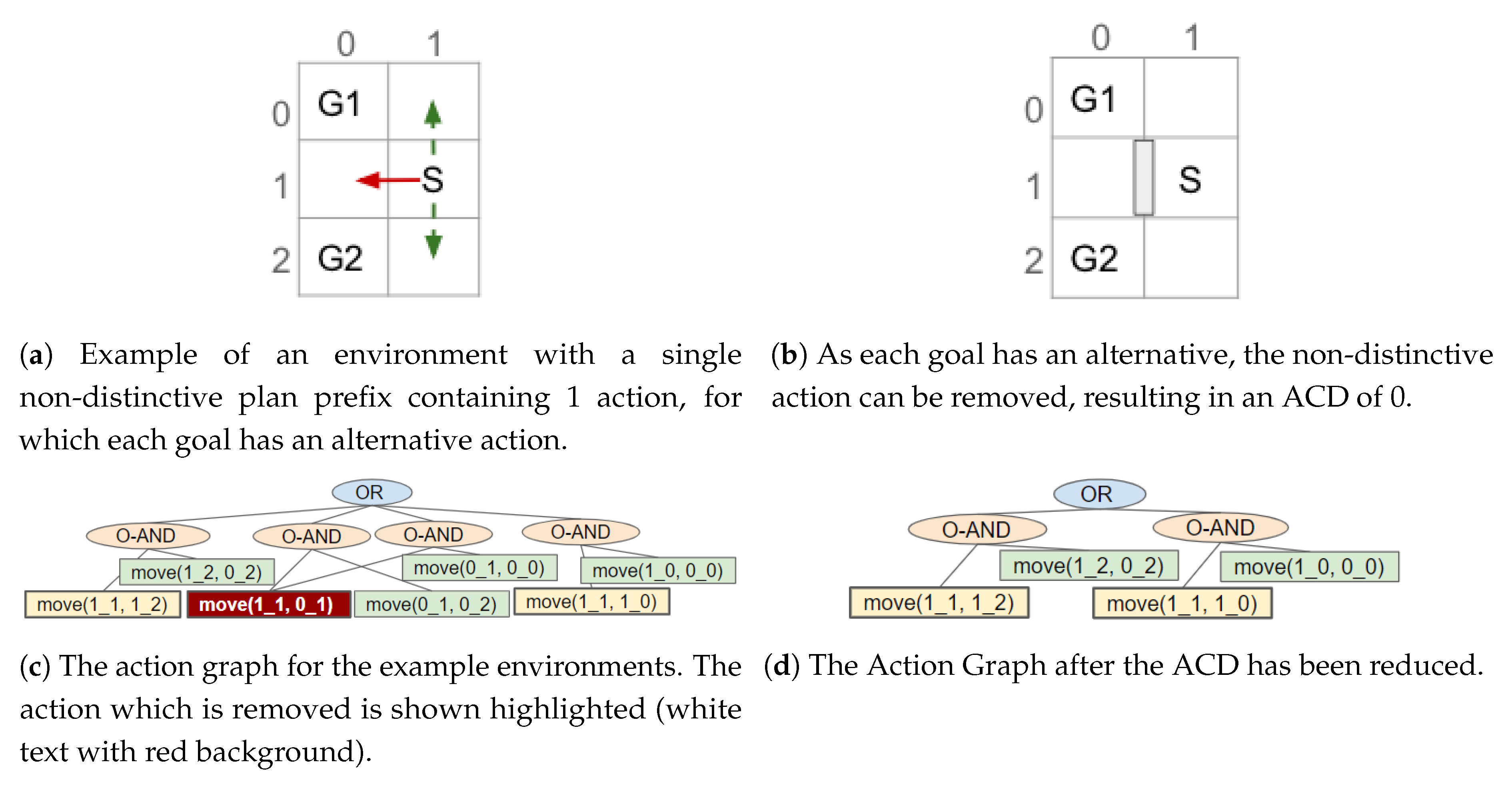
The list of non-distinctive plan prefixes is sorted, most costly first, so that the worst is processed first. In turn each prefix is taken from the list and its actions iterated over to discover if: (1) all goals an action belongs to have a (unique) alternative action; (2) a sub-set of the goals the non-distinctive prefix belongs to have an alternative; or (3) all the non-distinctive prefix’s goals have an action with an non-unique alternative. These points are expanded on below. The actions are iterated over in order because if an action at the start of the prefix can be removed, the remainder of the prefix is no-longer valid. If the algorithm were to start from the last action, in a plan containing the non-distinctive prefix, it would be more difficult to reduce the distinctiveness (i.e., more actions would require removing).
A goal has an alternative action if an action (or if the action has dependencies its single
ORDERED-AND parent) has an
OR node as a direct parent and another of the
OR node’s children belong to that goal. If so, an action can be removed without causing the goal to become unreachable. Moreover, the alternative cannot belong to any of the other goals the (non-distinctive) action belongs to as removing this action would have no effect on the goals’ distinctiveness. If all the goals with a plan containing the non-distinctive action have an alternative, the action is removed. An example is provided in
Figure 11.
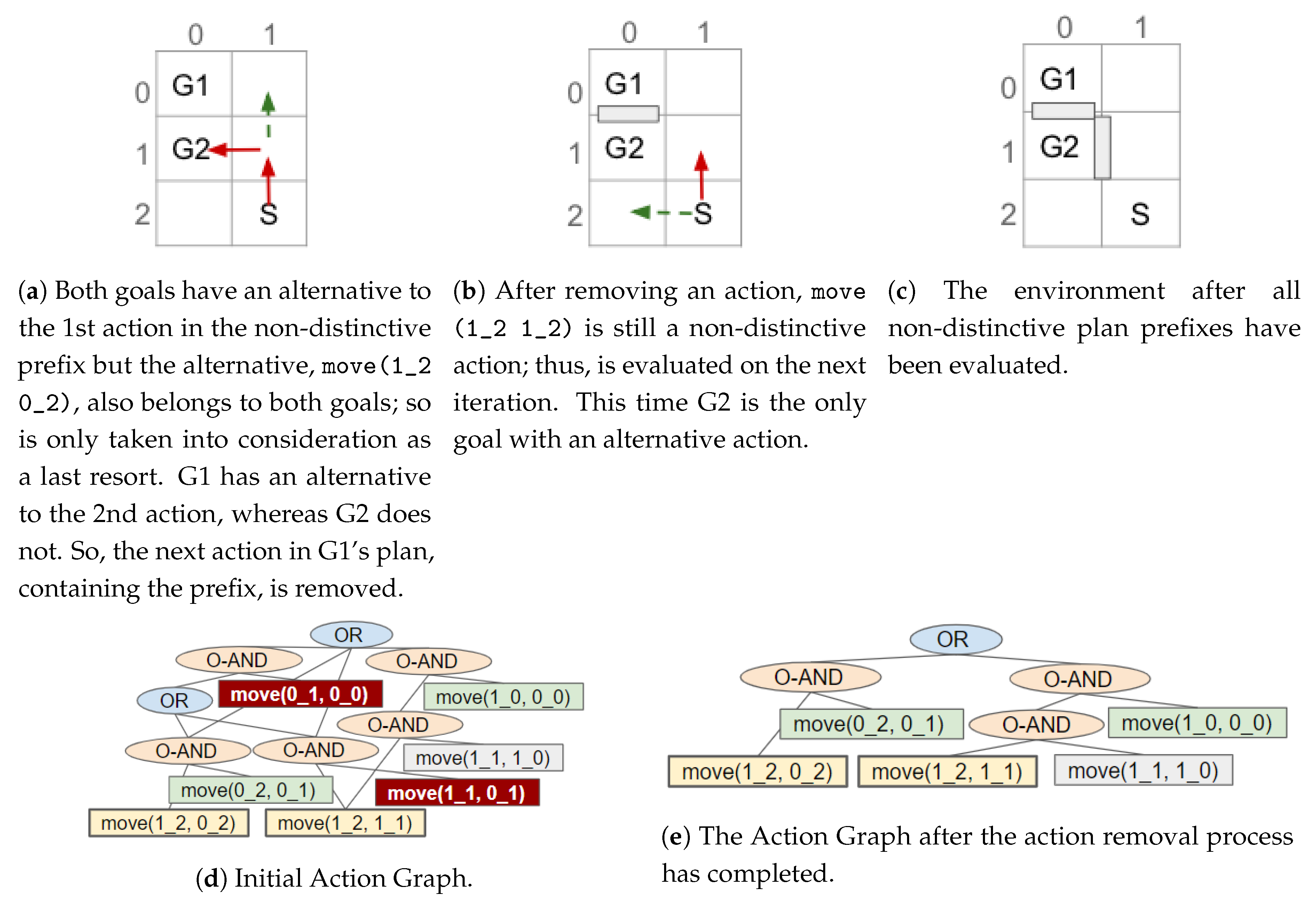
After checking all actions in a non-distinctive prefix, if only a subset of the goals have alternative actions, the action(s) directly after the non-distinctive prefix in their plans is removed. As a result, those goals can only be reached by their alternative (possibly more distinctive) plan(s). An example is shown in
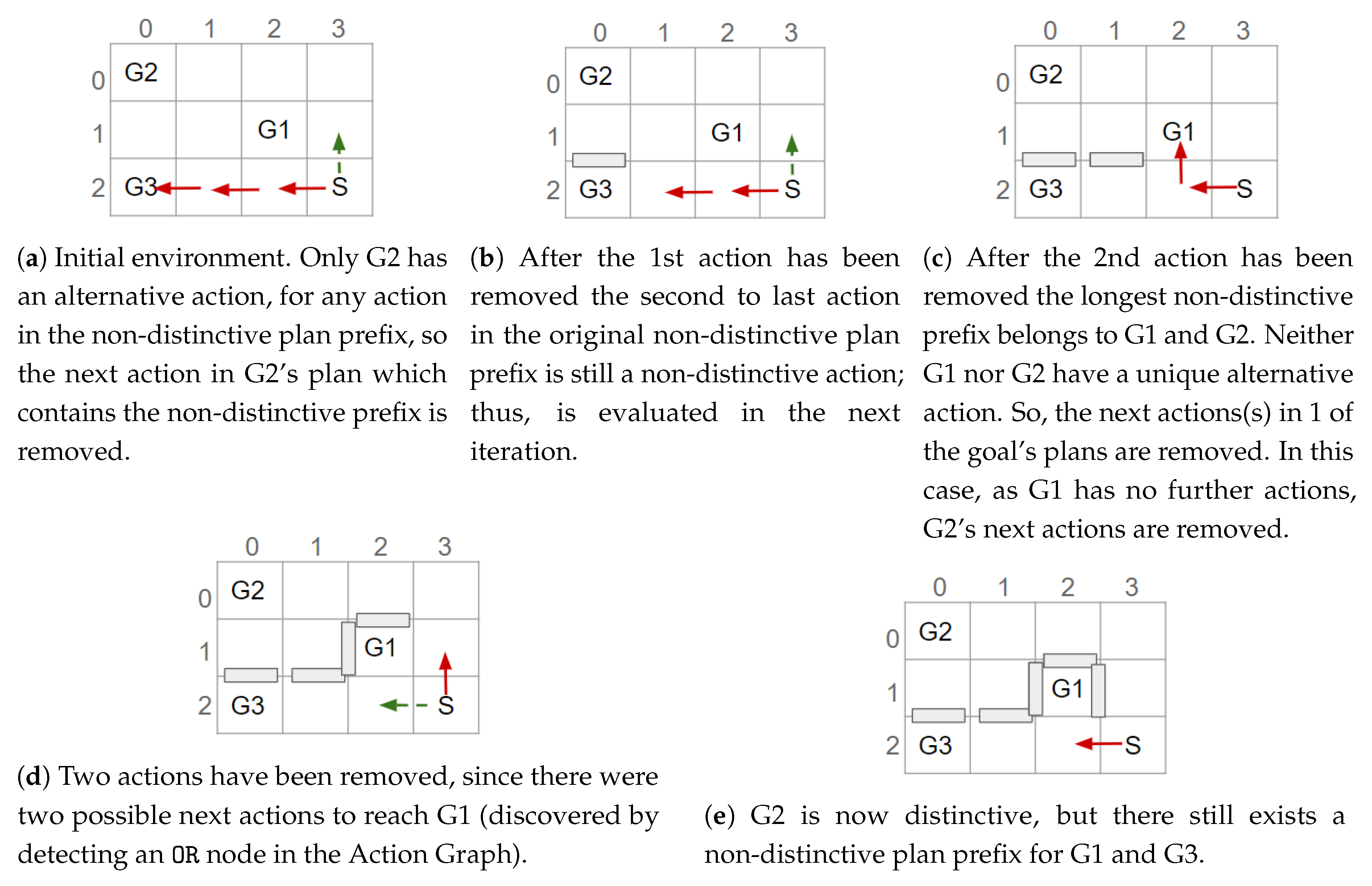
Figure 12. Otherwise, when all the non-distinctive prefix’s goals have an action (in the non-distinctive prefix) with an non-unique alternative, i.e., the alternative(s) belongs to more than one of the action’s goals, the next (distinctive) action(s) for one of the goals is removed (see
Figure 13c,d). This prevents the non-distinctive prefix being valid for that goal, thus making it more distinctive. Our action removal method always checks that the action removed will not interfere with any of the other goals, which do not have an alternative, to prevent them from becoming unreachable.
Once an action has been removed, which nodes belong to which goal is re-evaluated (see
Section 6); and the actions in the non-distinctive prefix, prior to any removed action, are checked to see if they should be inserted into the list of non-distinctive plan prefixes (e.g.,
Figure 12a,b). Actions, that are not the last action in the prefix, should be re-processed as it may be possible to further reduce the length of the non-distinctive prefix (e.g.,
Figure 13a–c). The last action in the prefix will not be processed again, if it is still a non-distinctive action then the ACD will not be reduced to 0. An example of an environment in which the ACD cannot be reduced to 0, and the steps our algorithm performs, is shown in
Figure 13.
10. Conclusions
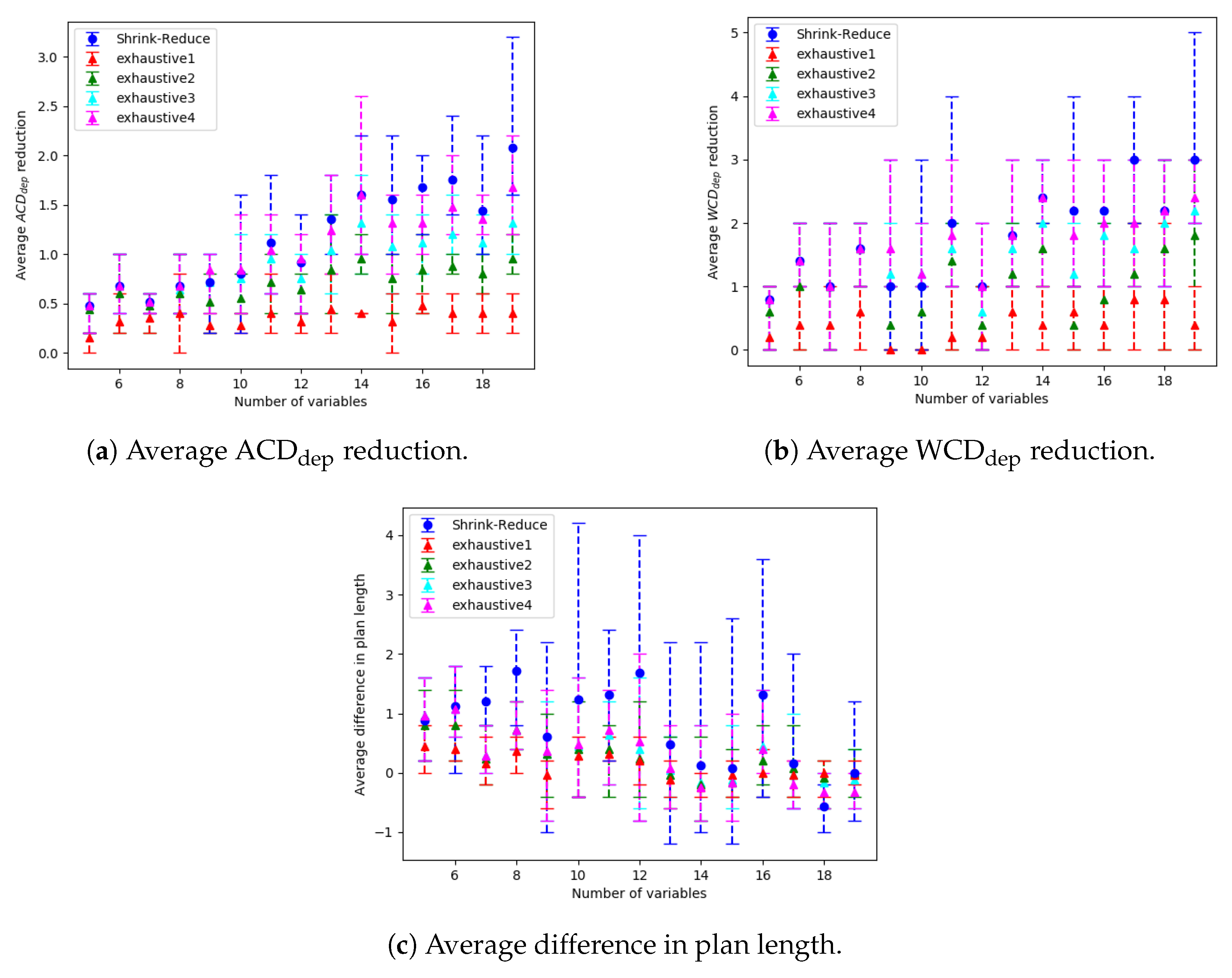
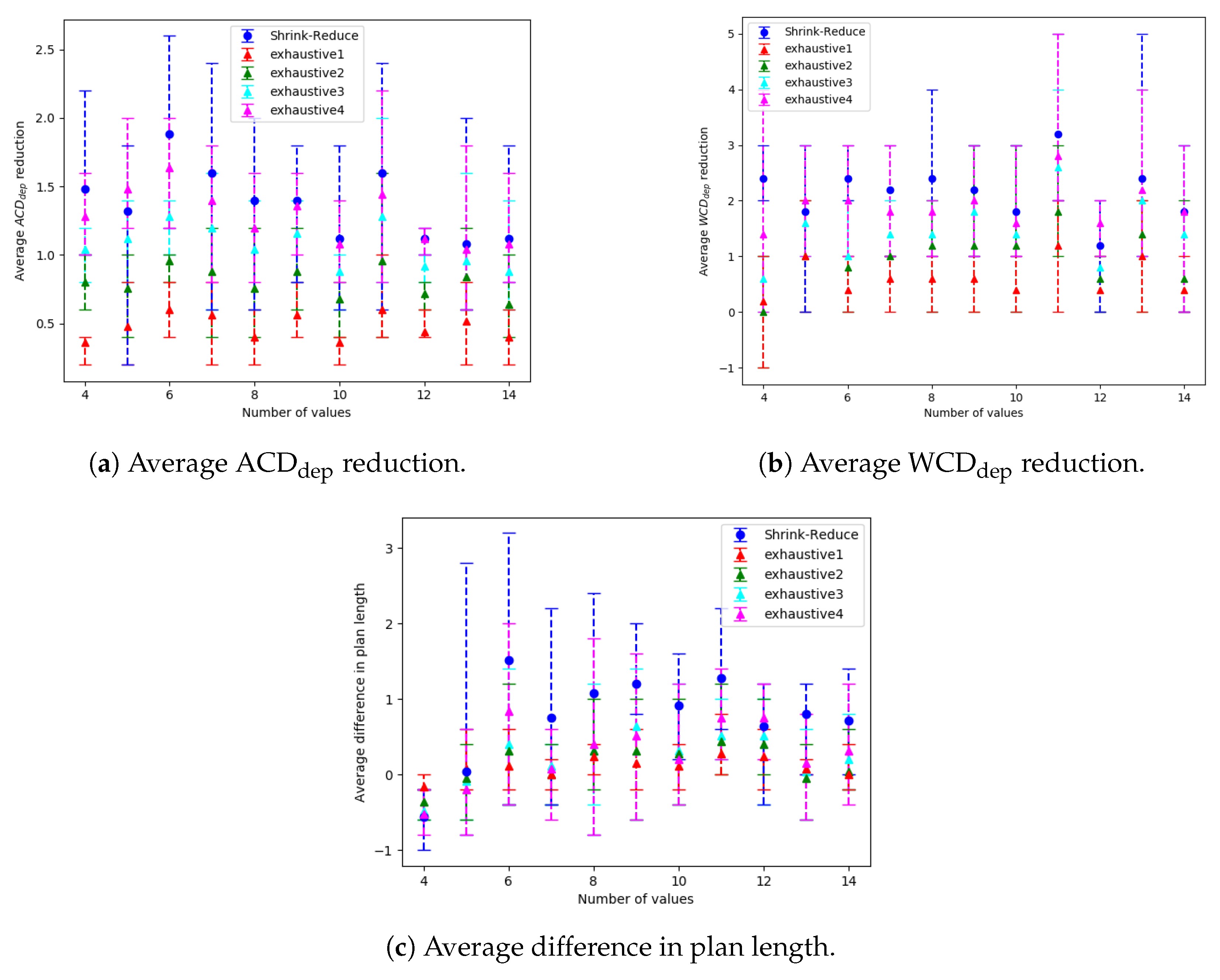
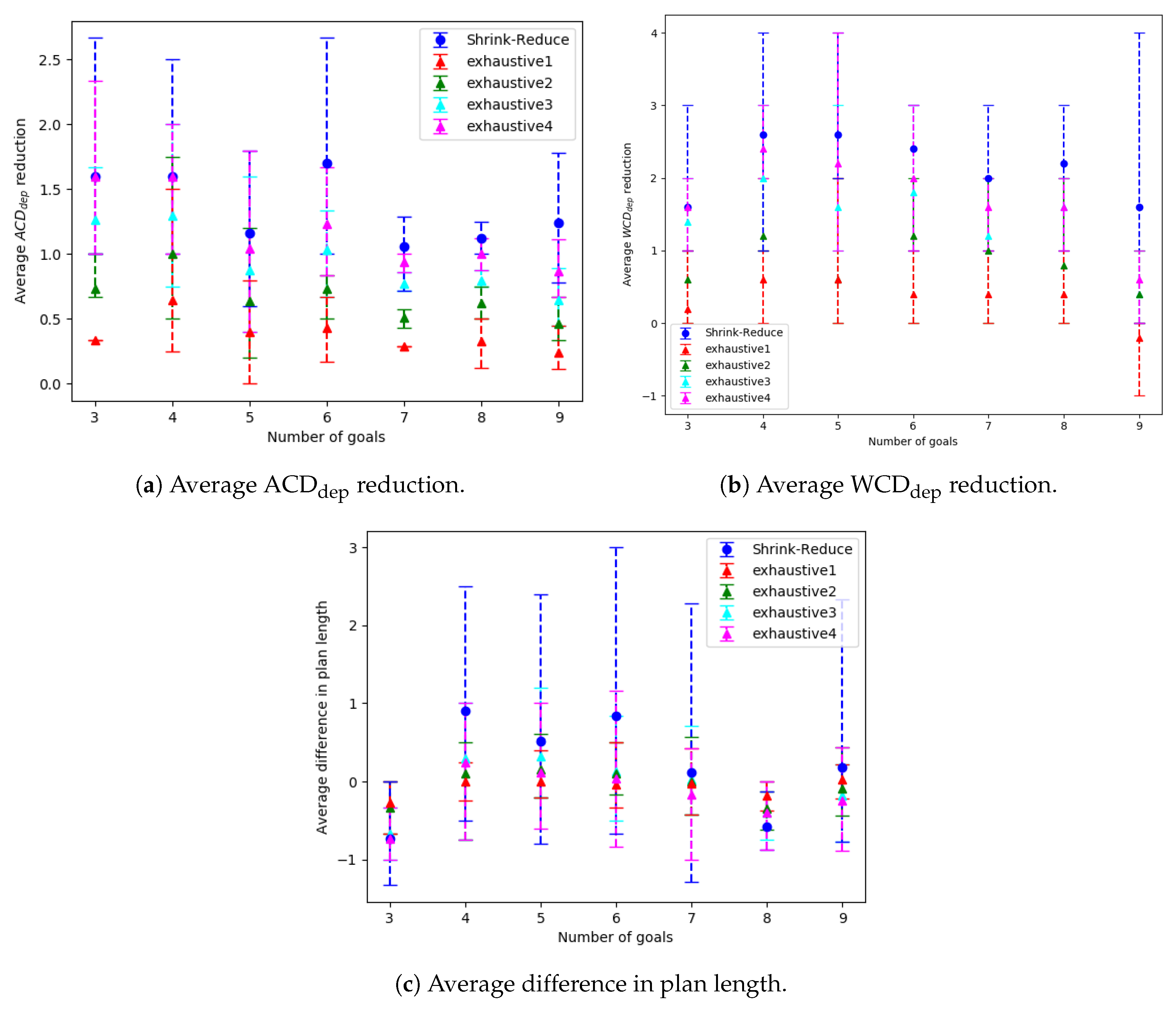
As the plans to reach different goals can start with the same actions, a human’s goal often cannot be recognised until their plan nears completion. By redesigning an environment, our work enables the goal of a human to be recognised after fewer observations. This is achieved through transforming a PDDL defined Goal Recognition Design (GRD) problem into an Action Graph, by means of a Breadth First Search (BFS) from each of the goal states to the initial world state. The non-distinctive plan prefixes are then extracted to calculate how distinctive the goals are, i.e., the
and
. Subsequently, these prefixes are processed to determine which actions can be replaced or removed. Our Shrink–Reduce method replaces actions by first shrinking the plans, then reducing the non-distinctive prefixes. Shrink–Reduce is less computational expensive than an exhaustive approach; however, when ran on kitchen domain Shrink–Reduce only reduces the
by 1, whereas exhaustive reduces
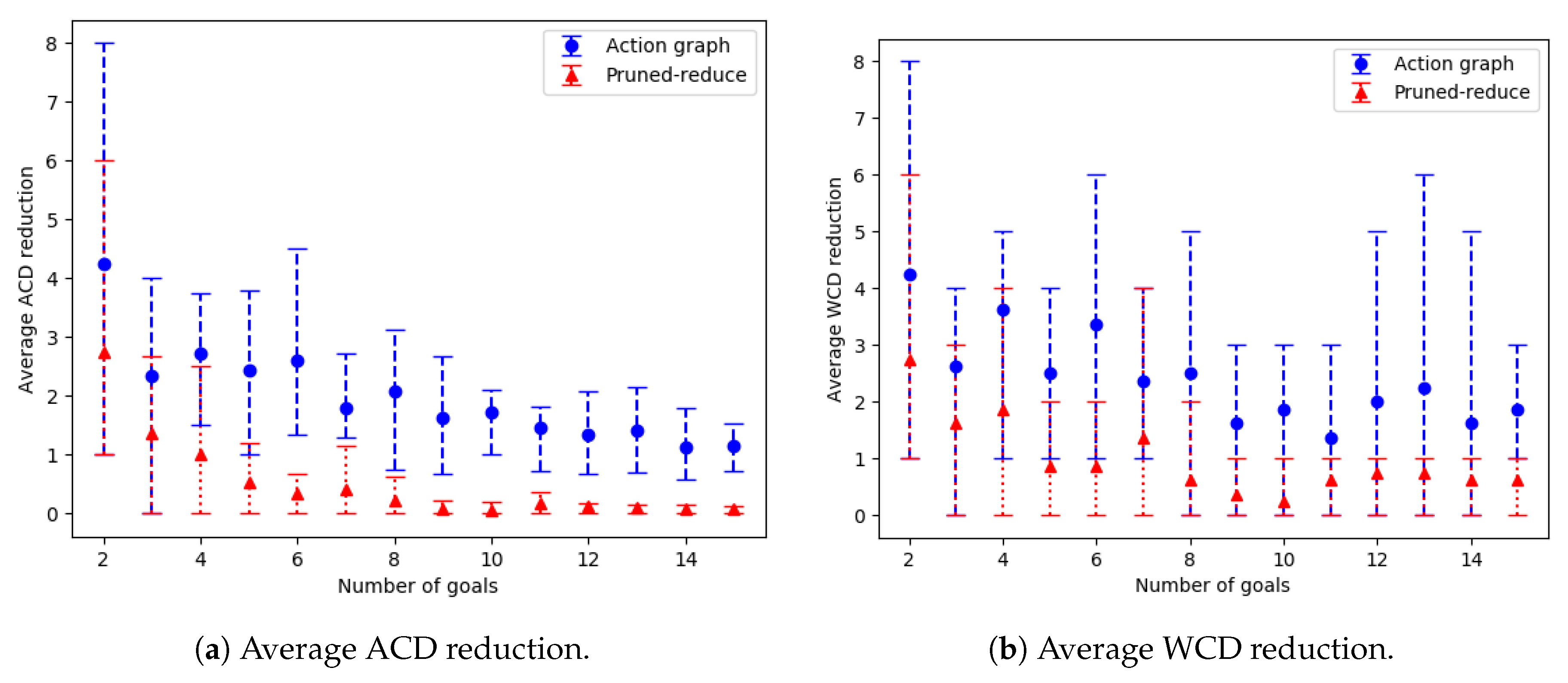
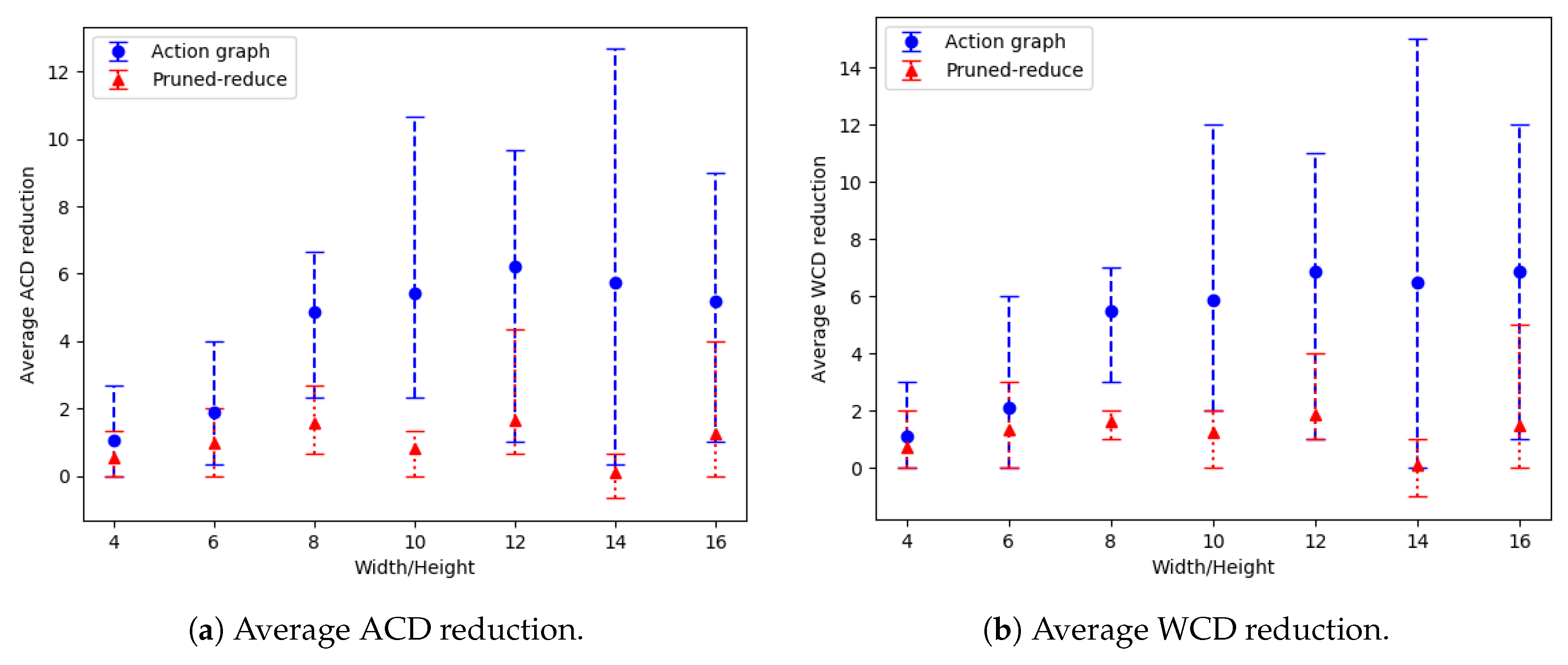
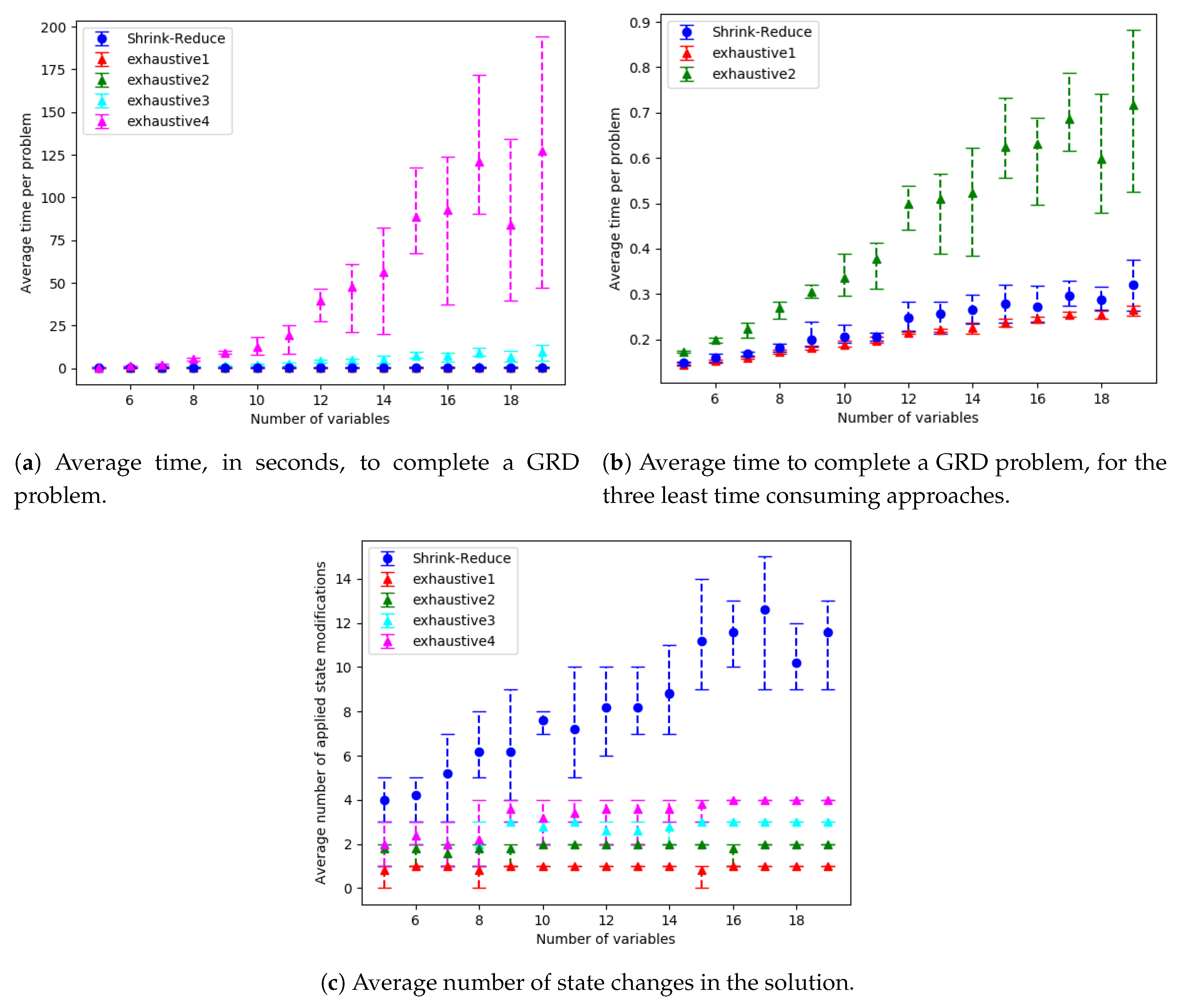
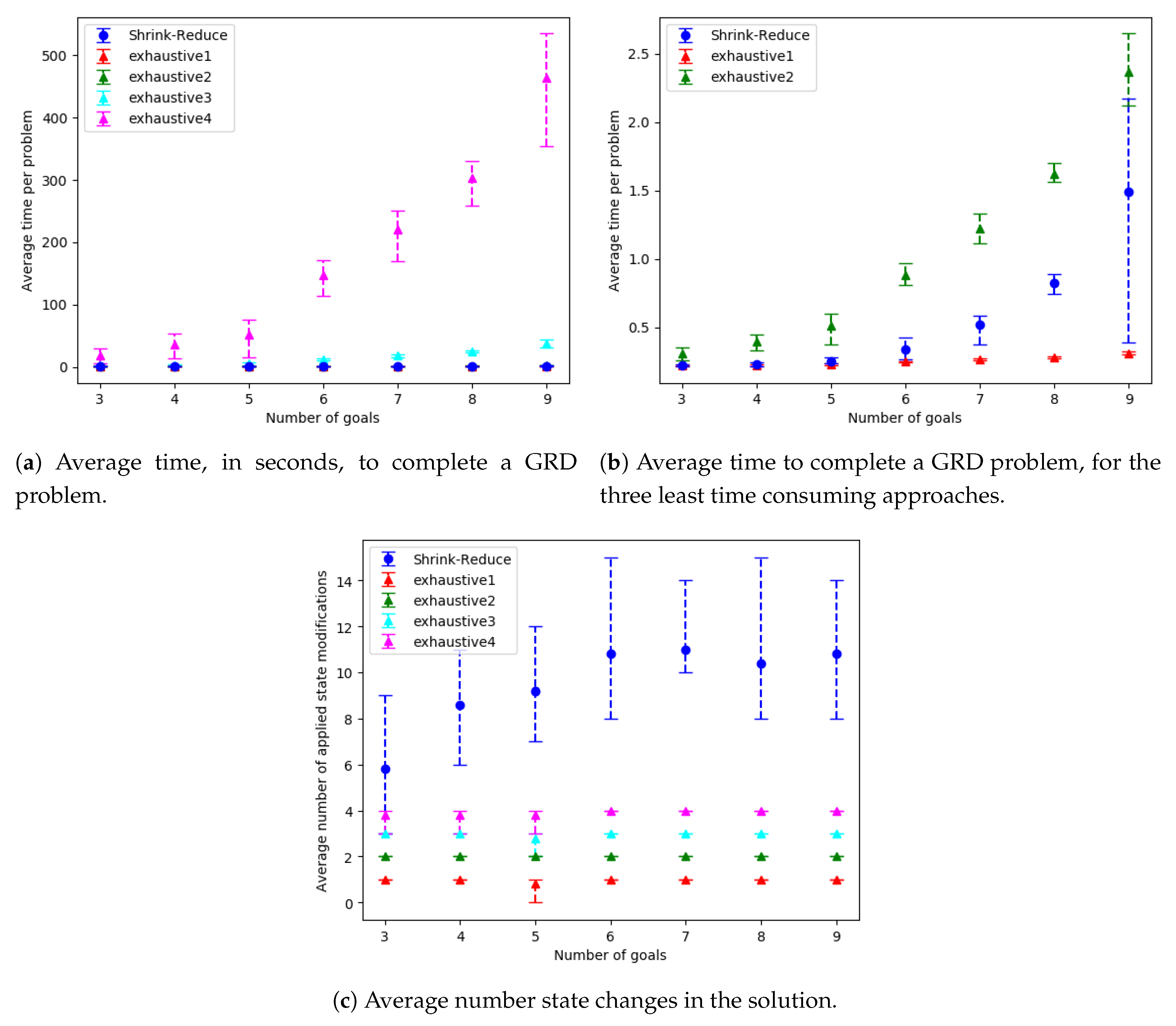
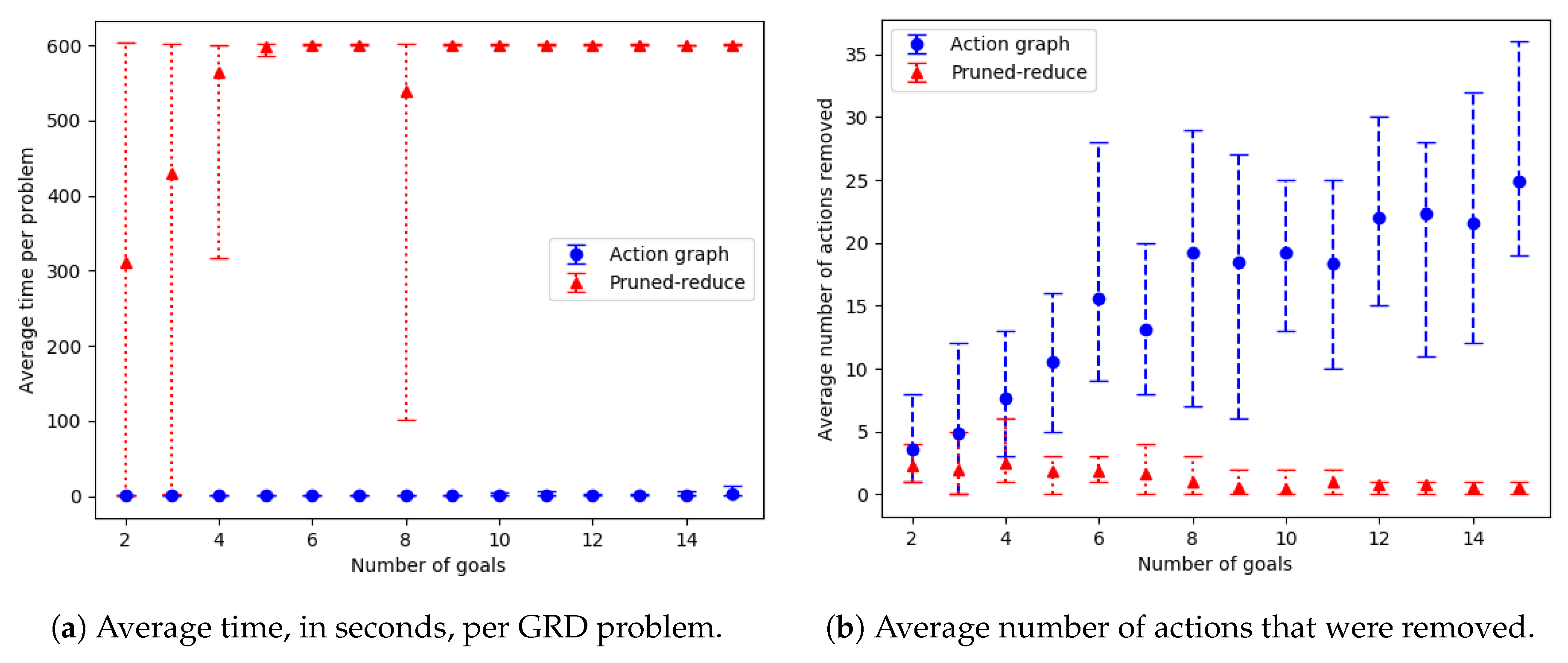
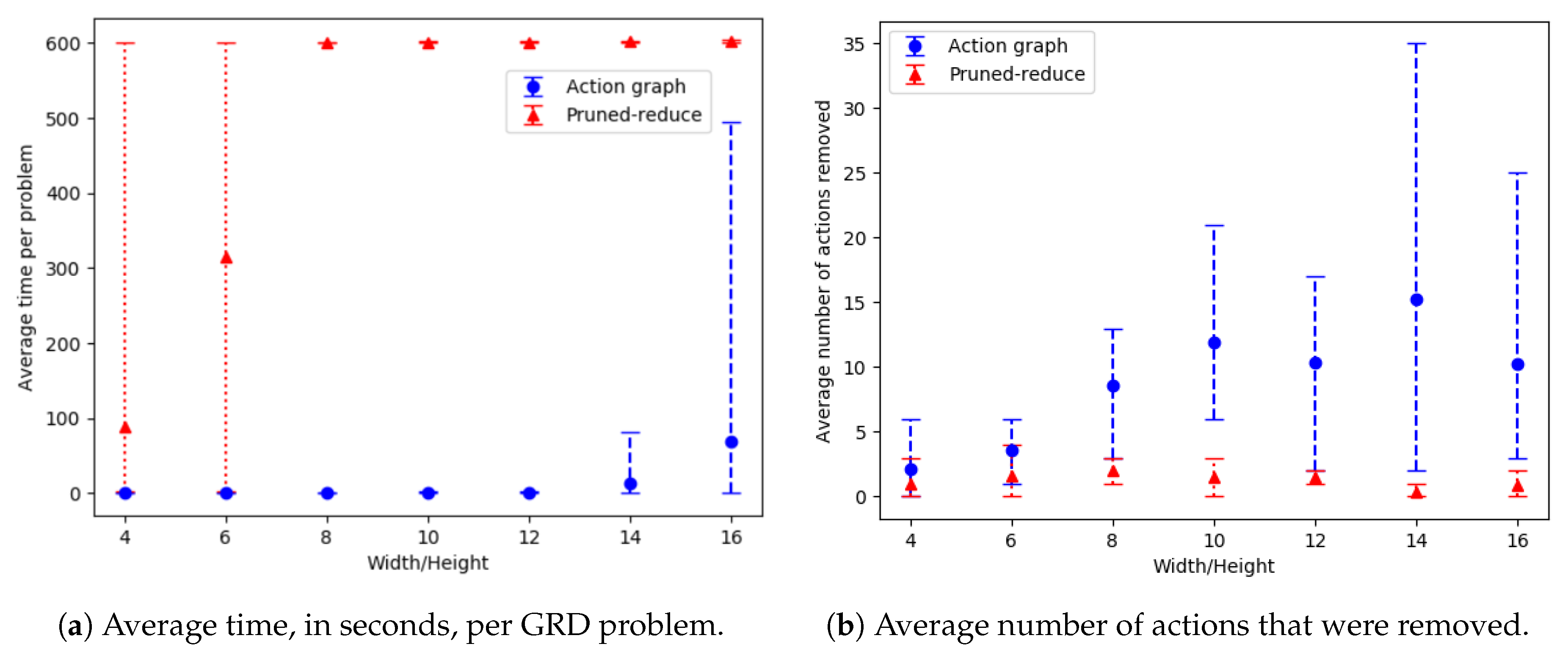
by 1.67. Our action removal method is shown to increase the distinctiveness of various grid-based navigation problems, with a width/height ranging from 4 to 16 and between 2 to 14 randomly selected goals, by an average of 3.27 actions in an average time of 4.69 s, whereas a state-of-the-art approach, namely pruned-reduce [
10], often breaches a 10 min time limit.
Action Graphs are acyclic and no actions are repeated, therefore domains in which an action has different dependencies under varying circumstances are not currently solvable by our approach. For instance, if to reach one goal a human must retrieve
item1 before taking
item2, but to reach another goal the human must take
item3 before
item2, the action to retrieve
item2 has different dependencies. For many domains, e.g., the kitchen domain, this strict ordering is not required, as humans are unlikely to adhere to a fixed ordering of actions, but for other domains this may be required. In future work, we will consider enabling actions to be repeated within an Action Graph. For domains such as the barman domain [
43], in which different cocktails are created, a combination of our unconstrained method (as ingredients can be added in any order) and constrained method (as grasping and leaving a shot requires an optimal plan) will be required.
In future work we intend to apply our Action Graph approach to other, closely related, research domains. For instance, GRD with stochastic actions [
14,
44], plan recognition design [
21], goal recognition [
8] and task planning (e.g., plan legibility [
45,
46]). Future experiments will hopefully demonstrate how Action Graphs can help all agents in collaborative smart environments to become more aware of each other’s intentions.
Further to contextual-awareness in human-inhabited environments, our work is applicable to numerous application areas. In human computer interaction scenarios, detecting a network intruder’s intentions [
21,
26,
47] or offering a user assistance [
48,
49] can also benefit from recognising the user’s goal sooner. In video game development [
50] often the world is designed so the player’s goal can be recognised, thus enabling the non-playable characters to assist or thwart them; moreover these characters’ plans can also be modelled as an Action Graph. Action Graphs could allow robots to learn from humans. For instance, the graph could be built from observations or their structure adjusted to match the order humans perform actions. We hope this paper will inspire researchers in these domains, to incorporate our Action Graph approach into their work.