The Fiber-Optic Rotational Seismograph—Laboratory Tests and Field Application
Abstract
1. Introduction
2. Construction and Laboratory Investigation of the Fiber-Optic Rotational Seismograph—FOSREM®
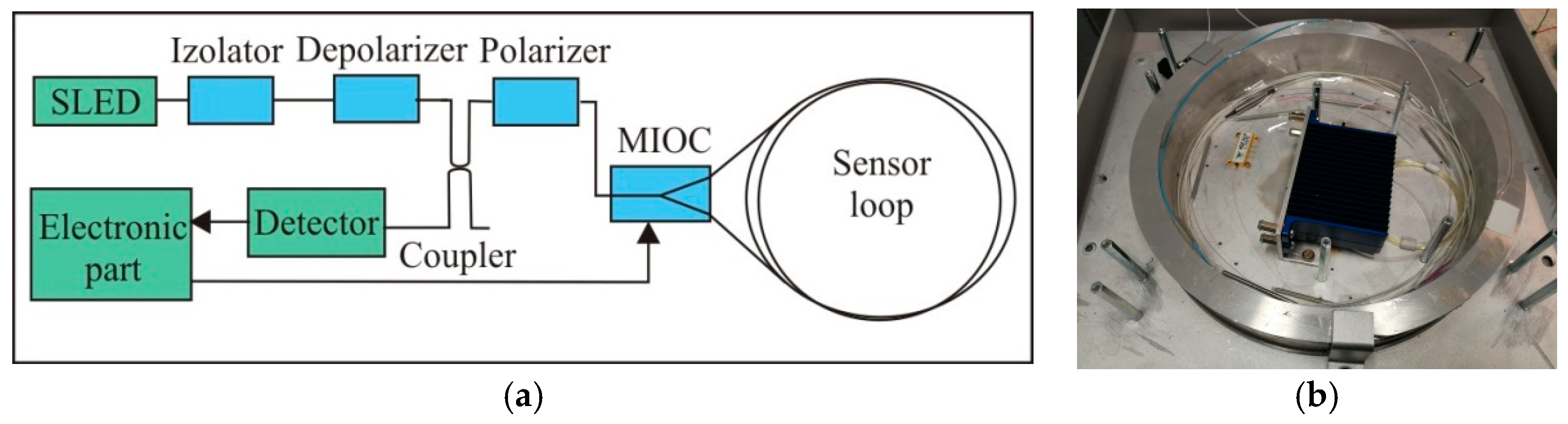
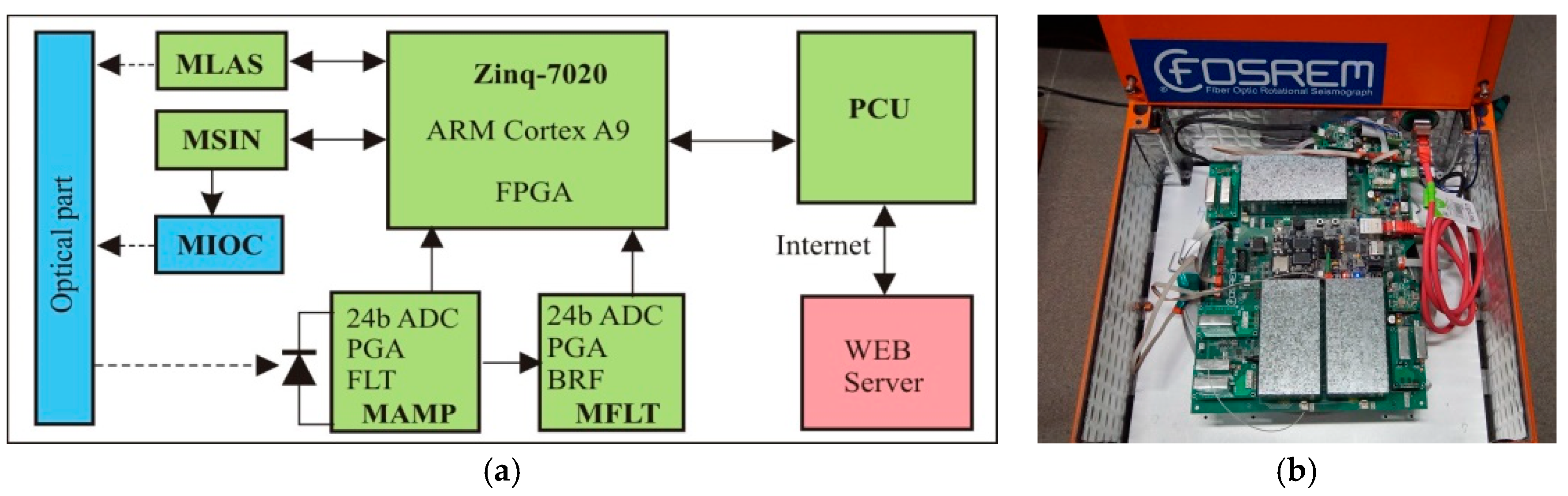
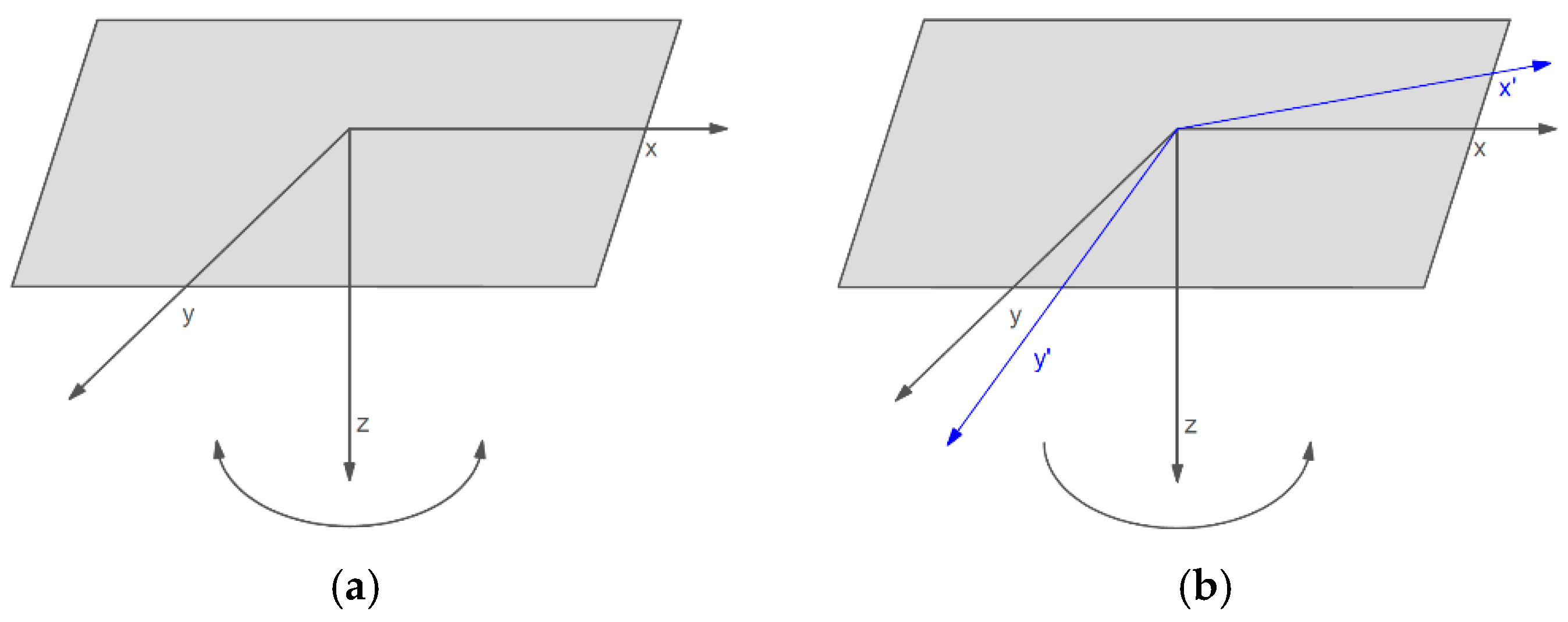
2.1. FOSREM® Construction
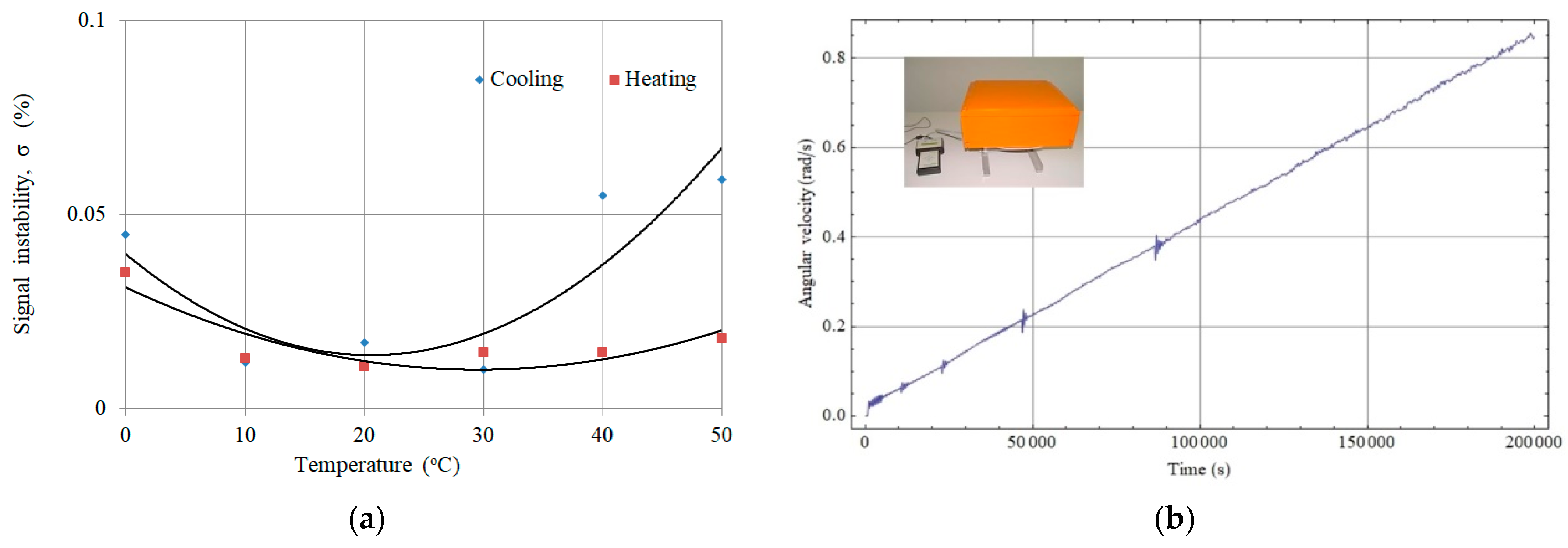
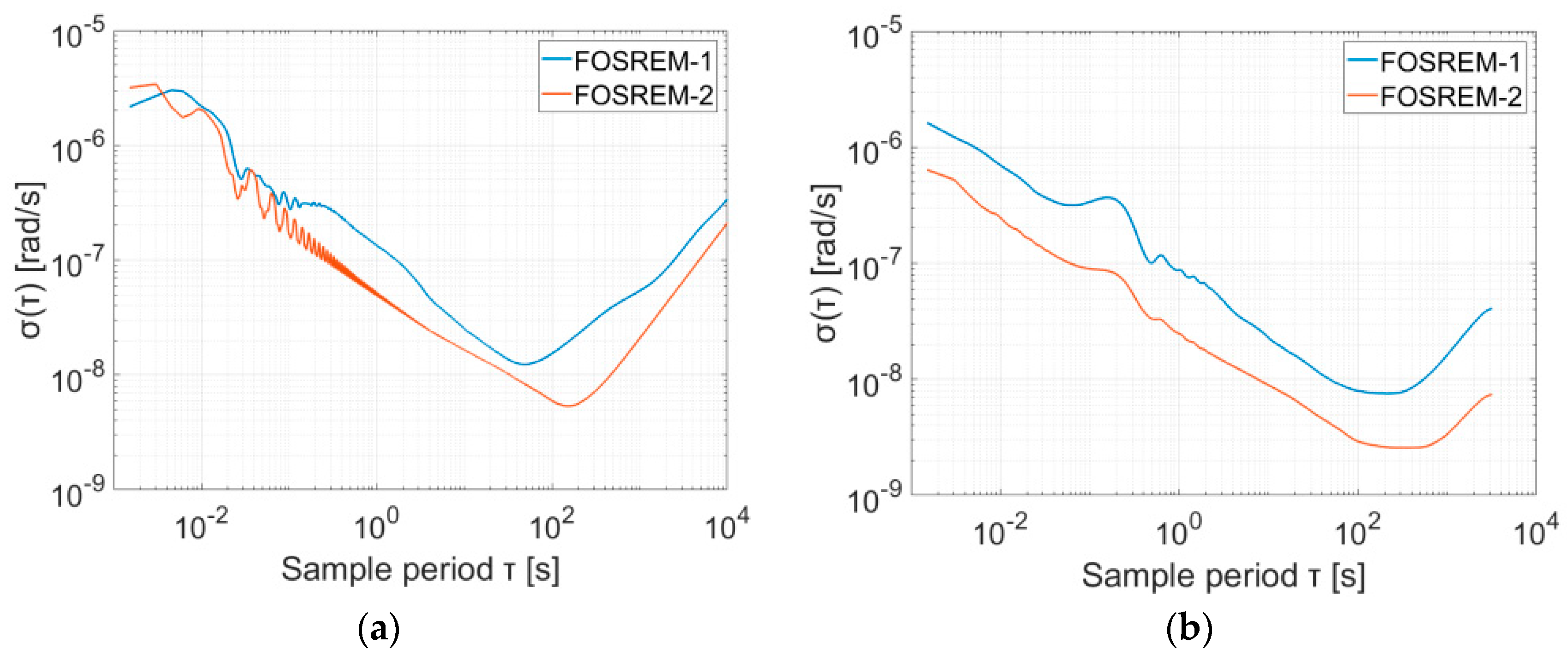
2.2. Results of Laboratory Investigation
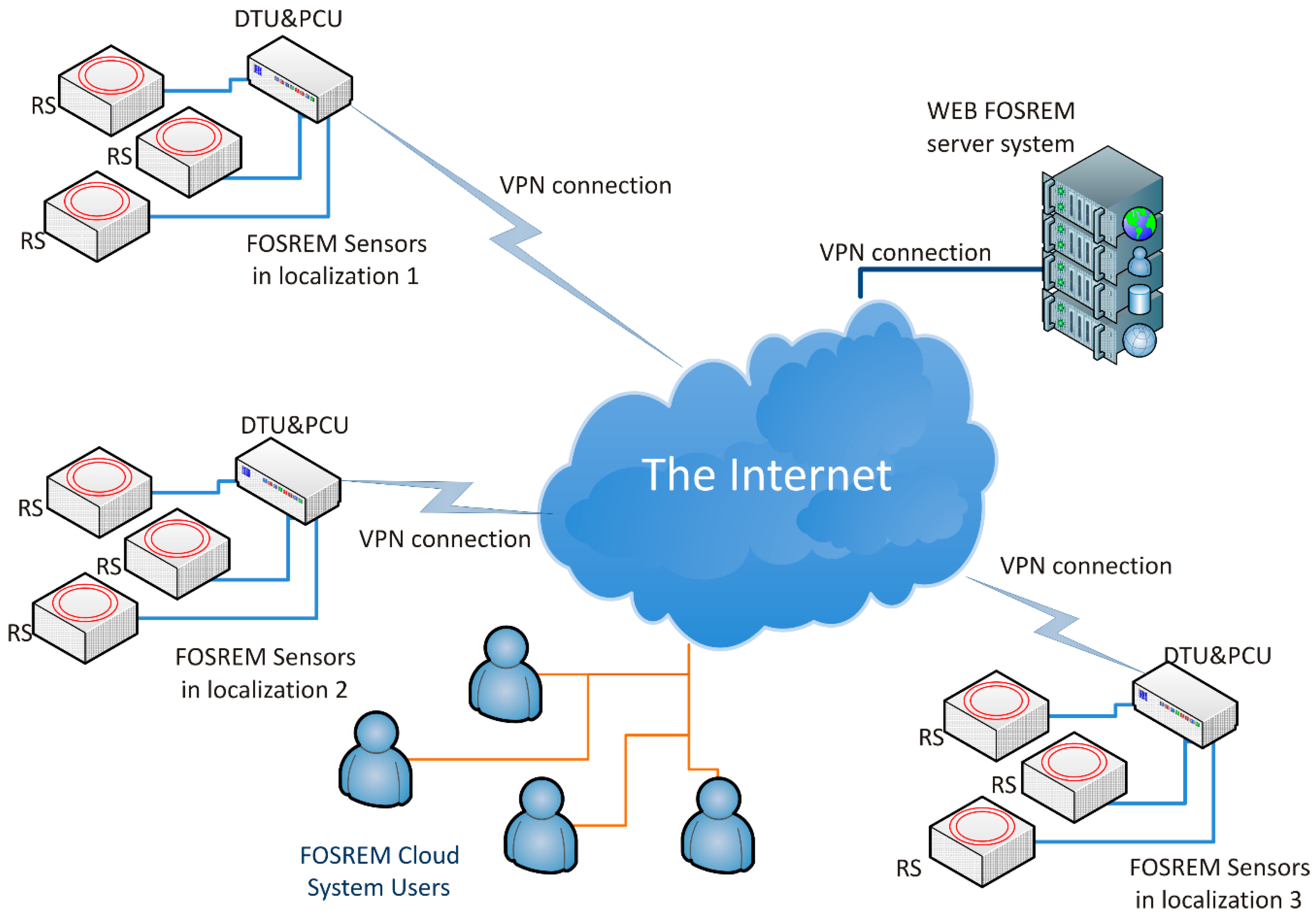
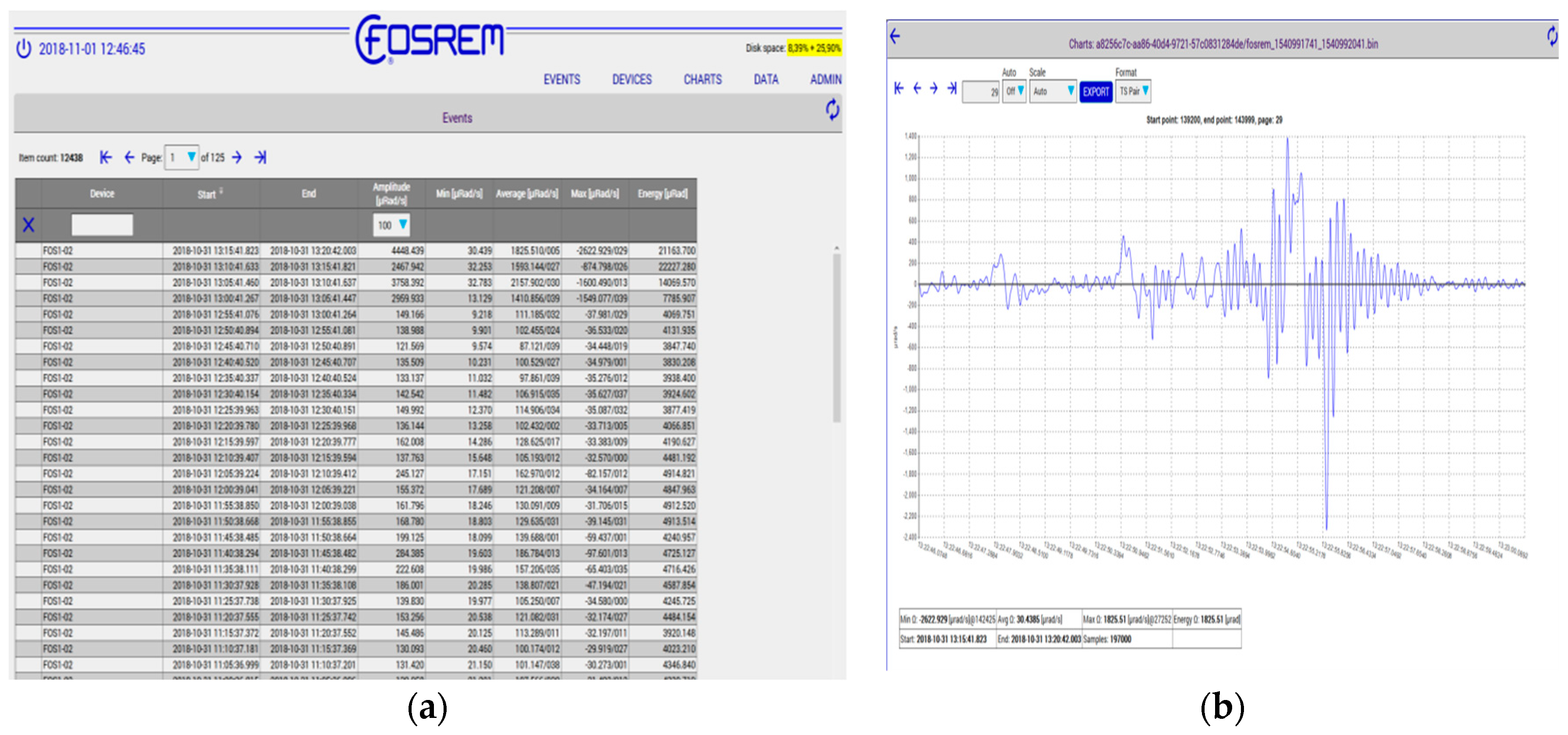
3. FOSREM® in the Field Application
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, W.H.K.; Celebi, M.; Todorovska, M.I.; Igel, H. Introduction to the special issue on rotational seismology and engineering applications. Bull. Seismol. Soc. Am. 2009, 99, 945–957. [Google Scholar] [CrossRef]
- Spudich, P.; Fletcher, J.B. Observation and prediction of dynamic ground strains, tilts, and torsions caused by the Mw 6.0 2004 Parkfield, California earthquake and aftershocks, derived from USPAR Array observations. Bull. Seismol. Soc. Am. 2008, 98, 1898–1914. [Google Scholar] [CrossRef]
- Takeo, M.; Ito, H.M. What can be learned from rotational motions excited by earthquakes? Geophys. J. Int. 1997, 129, 319–329. [Google Scholar] [CrossRef]
- Trifunac, M.D. A note on rotational components of earthquake motions on ground surface for incident body waves. Soil Dyn. Earthq. Eng. 1982, 1, 11–19. [Google Scholar] [CrossRef]
- Kurzych, A.; Teisseyre, K.P.; Krajewski, Z.; Jaroszewicz, L.R. Rotational components of the seismic fields caused by local events. In Earthquake Engineering—From Engineering Seismology to Optimal Seismic Design of Engineering Structures, 1st ed.; Moustafa, A., Ed.; Intech: Rijeka, Croatia, 2015; pp. 163–188. [Google Scholar]
- Brokešová, J.; Málek, J.; Štrunc, J. Rotational Seismic Sensor System, Seismic Measuring Set Containing that System, and Seismic Survey Method. Patent No. CZ 301217 B6, 8 December 2009. [Google Scholar]
- Brokešová, J.; Málek, J. Six-degree-of-freedom near-source seismic motions I: Rotation-to-translation relations and synthetic examples. J. Seismol. 2015, 19, 491–509. [Google Scholar] [CrossRef]
- D’Alessandro, A.; D’Anna, G. Suitability of low-cost three-axis MEMS accelerometers in strong-motion seismology: Tests on the LIS331DLH (iPhone) accelerometer. Bull. Seismol. Soc. Am. 2013, 103, 2906–2913. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Hautmann, J.N.; Velikoseltsev, A.; Wassermann, J.; Igel, H.; Otero, J.; Vernon, F.; Wells, J.P. Ring laser measurements of ground rotations for seismology. Bull. Seismol. Soc. Am. 2009, 99, 1190–1198. [Google Scholar] [CrossRef]
- Jaroszewicz, L.R.; Krajewski, Z.; Kowalski, H.; Mazur, G.; Zinówko, P.; Kowalski, J. AFORS Autonomous Fibre-Optic Rotational Seismograph: Design and application. Acta Geophys. 2011, 59, 578–596. [Google Scholar] [CrossRef]
- Jaroszewicz, L.; Kurzych, A.; Krajewski, Z.; Marć, P.; Kowalski, J.; Bobra, P.; Zembaty, Z.; Sakowicz, B.; Jankowski, R. Review of the usefulness of various rotational seismometers with laboratory results of fibre-optic ones tested for engineering applications. Sensors 2016, 16, 2161. [Google Scholar] [CrossRef] [PubMed]
- Jaroszewicz, L.R.; Krajewski, Z.; Teisseyre, K.P. Usefulness of AFORS–Autonomous Fibre-Optic Rotational Seismograph for investigation of rotational phenomena. J. Seismol. 2012, 16, 573–586. [Google Scholar] [CrossRef]
- Kurzych, A.; Jaroszewicz, L.R.; Krajewski, Z.; Sakowicz, B.; Kowalski, J.K.; Marć, P. Fibre-optic Sagnac interferometer in a FOG minimum configuration as instrumental challenge for rotational seismology. J. Lightwave Technol. 2018, 36, 879–884. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Jaroszewicz, L.R.; Kurzych, A.; Krajewski, Z.; Kowalski, J.K.; Kowalski, H.A.; Teisseyre, K.P. Innovative fiber-optic rotational seismograph. In Proceedings of the 7th International Symposium on Sensor Science (I3S 2019), Napoli, Italy, 9–11 May 2019. [Google Scholar]
- Jaroszewicz, L.R.; Krajewski, Z.; Kurzych, A.; Marc, P.; Lipinski, S.; Kowalski, J.K.; Bobra, P.; Zembaty, Z.; Jankowski, R.; Teisseyre, K.P. Recording rotational motions at a new set-up uses’ earthquakes simulation. In Proceedings of the 4th International Working Group on Rotational Seismology Meeting, Tutzing, Germany, 20–23 June 2016; Available online: http://www.rotational-seismology.org/events/workshops/Presentations_2016/presentations/Jaroszewicz_talk/view (accessed on 23 May 2019).
- LeFevre, H.C. The Fiber Optic Gyroscope, 2nd ed.; Artech House: Norwood, MA, USA, 2014; pp. 38–53. [Google Scholar]
- Sagnac, G. L’ether lumineux demontre par l’effet du vent relatif d’Etherdanus un interferometre en rotation uniforme. C.R. Acad. Sci. 1913, 95, 708–710. [Google Scholar]
- Kurzych, A.; Kowalski, J.K.; Sakowicz, B.; Krajewski, Z.; Jaroszewicz, L.R. The laboratory investigation of the innovative sensor for torsional effects in engineering structures’ monitoring. Opto-Electron. Rev. 2016, 24, 134–143. [Google Scholar] [CrossRef]
- Arditty, H.J.; Puech, C.; Papuchon, M. Device for Measuring a Phase Shift Which is Not Reciprocally Produced in a Ring Interferometer. U.S. Patent #5,056,919, 15 October 1991. [Google Scholar]
- Dai, X.; Zhao, X.; Cai, B.; Yang, G.; Zhou, K.; Liu, C. Quantitative analysis of the Shupe reduction in a fiber-optic Sagnac interferometer. Opt. Eng. 2002, 41, 1155–1156. [Google Scholar] [CrossRef]
- Ezekiel, S.; Davis, J.L.; Hellwarth, R.W. Observation of intensity-induced nonreciprocity in a fiber-optic gyroscope. Opt. Lett. 1982, 7, 457–459. [Google Scholar] [CrossRef] [PubMed]
- IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Interferometric Fiber Optic Gyros; IEEE-SA Standards Board: New York, NY, USA, 1997.
- Variance, A. Allan Variance: Noise Analysis for Gyroscopes. Freescale Semiconductor Application Note AN5087. 2015. [Google Scholar]
- Hall, G. Pearson’s Correlation Coefficient. Available online: http://www.hep.ph.ic. ac.uk/~hallg/UG_2015/ Pearsons.pdf (accessed on 13 March 2018).

| Sturdy Flat Floor | Active Optical Table | |||
|---|---|---|---|---|
| ARW [rad/√s] | BI [rad/s] | ARW [rad/√s] | BI [rad/s] | |
| FOSREM-1 | 1.33 × 10−7 | 1.81 × 10−8 | 8.66 × 10−8 | 1.13 × 10−8 |
| FOSREM-2 | 5.26 × 10−8 | 8.08 × 10−9 | 2.45 × 10−8 | 3.91 × 10−9 |
| Device | Recorded Torsion Event | Recorded Tilt Event | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Date | Time | Max. Amplitude [rad/s] | EF [rad] | Pc | Date | Time | Max. Amplitude [rad/s] | EF [rad] | Pc | |
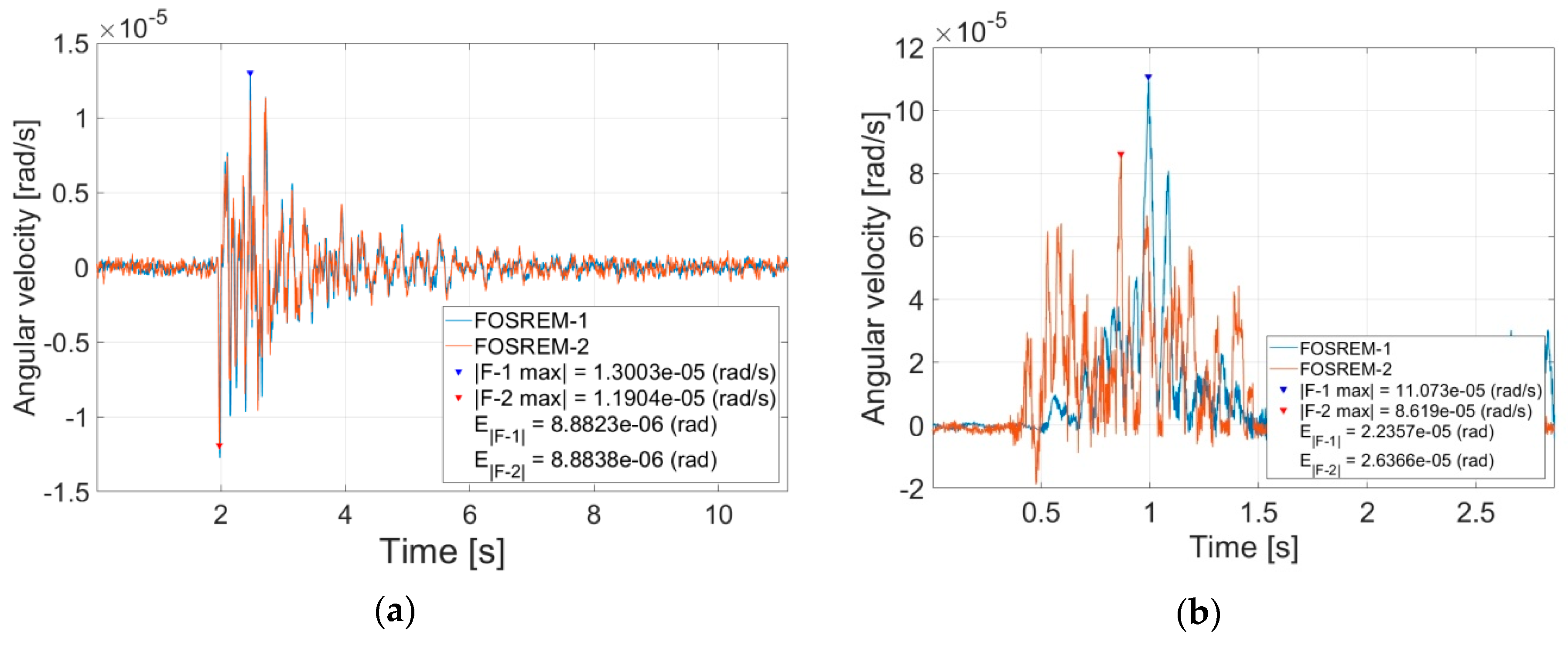
| FOSREM-1 FOSREM-2 | 29 August 17 | 11:02:34 | 2.68 × 10−5 3.25 × 10−5 | 1.31 × 10−5 1.91 × 10−5 | 0.99 | 8 December 17 | 13:01:41 | 9.61 × 10−5 9.31 × 10−5 | 2.19 × 10−5 2.20 × 10−5 | 0.71 |
| FOSREM-1 FOSREM-2 | 29 August 17 | 11:08:12 | 1.23 × 10−5 1.21 × 10−5 | 9.00 × 10−6 9.12 × 10−6 | 0.98 | 13 December 17 | 11:15:27 | 1.11 × 10−4 8.62 × 10−5 | 2.34 × 10−5 2.64 × 10−5 | 0.57 |
| FOSREM-1 FOSREM-2 | 1 December 17 | 12:19:10 | 1.30 × 10−5 1.19 × 10−5 | 8.88 × 10−6 8.88 × 10−6 | 0.98 | 11 January 18 | 11:27:05 | 7.97 × 10−6 8.46 × 10−6 | 1.89 × 10−6 1.61 × 10−6 | 0.59 |
| FOSREM-1 FOSREM-2 | 13 December 17 | 18:25:43 | 3.03 × 10−6 3.26 × 10−6 | 2.22 × 10−6 2.56 × 10−6 | 0.93 | 18 January 18 | 9:44:34 | 5.21 × 10−5 5.47 × 10−5 | 1.52 × 10−5 1.23 × 10−5 | 0.59 |
| FOSREM-1 FOSREM-2 | 13 December 17 | 18:25:58 | 1.78 × 10−6 2.08 × 10−6 | 1.18 × 10−6 1.52 × 10−6 | 0.92 | 25 January 18 | 11:55:33 | 9.35 × 10−4 8.76 × 10−4 | 1.03 × 10−4 1.17 × 10−4 | 0.67 |
| FOSREM-1 FOSREM-2 | 14 December 17 | 08:06:24 | 6.04 × 10−6 6.13 × 10−6 | 4.26 × 10−6 4.80 × 10−6 | 0.97 | 26 January 18 | 11:11:18 | 2.34 × 10−4 2.21 × 10−4 | 3.77 × 10−5 3.78 × 10−5 | 0.60 |
| FOSREM-1 FOSREM-2 | 8 January 18 | 08:09:02 | 3.88 × 10−6 3.44 × 10−6 | 4.43 × 10−6 4.66 × 10−6 | 0.95 | 26 January 18 | 11:11:43 | 4.99 × 10−4 6.61 × 10−4 | 4.92 × 10−5 5.82 × 10−5 | 0.57 |
| FOSREM-1 FOSREM-2 | 8 January 18 | 08:09:57 | 1.18 × 10−5 1.29 × 10−5 | 9.31 × 10−6 9.56 × 10−6 | 0.98 | 26 January 18 | 11:11:58 | 4.98 × 10−4 4.78 × 10−4 | 5.76 × 10−5 4.95 × 10−5 | 0.73 |
| FOSREM-1 FOSREM-2 | 26 January 18 | 11:14:23 | 1.42 × 10−5 1.40 × 10−5 | 1.22 × 10−5 1.21 × 10−5 | 0.97 | 3 February 18 | 10:14:21 | 2.40 × 10−4 2.85 × 10−4 | 4.25 × 10−5 5.64 × 10−5 | 0.61 |
| Average value of Pc for torsion event | 0.96 ± 0.03 | Average value of Pc for tilt event | 0.63 ± 0.06 | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaroszewicz, L.R.; Kurzych, A.; Krajewski, Z.; Dudek, M.; Kowalski, J.K.; Teisseyre, K.P. The Fiber-Optic Rotational Seismograph—Laboratory Tests and Field Application. Sensors 2019, 19, 2699. https://doi.org/10.3390/s19122699
Jaroszewicz LR, Kurzych A, Krajewski Z, Dudek M, Kowalski JK, Teisseyre KP. The Fiber-Optic Rotational Seismograph—Laboratory Tests and Field Application. Sensors. 2019; 19(12):2699. https://doi.org/10.3390/s19122699
Chicago/Turabian StyleJaroszewicz, Leszek R., Anna Kurzych, Zbigniew Krajewski, Michał Dudek, Jerzy K. Kowalski, and Krzysztof P. Teisseyre. 2019. "The Fiber-Optic Rotational Seismograph—Laboratory Tests and Field Application" Sensors 19, no. 12: 2699. https://doi.org/10.3390/s19122699
APA StyleJaroszewicz, L. R., Kurzych, A., Krajewski, Z., Dudek, M., Kowalski, J. K., & Teisseyre, K. P. (2019). The Fiber-Optic Rotational Seismograph—Laboratory Tests and Field Application. Sensors, 19(12), 2699. https://doi.org/10.3390/s19122699









