A Novel Ensemble Artificial Intelligence Approach for Gully Erosion Mapping in a Semi-Arid Watershed (Iran)
Abstract
1. Introduction
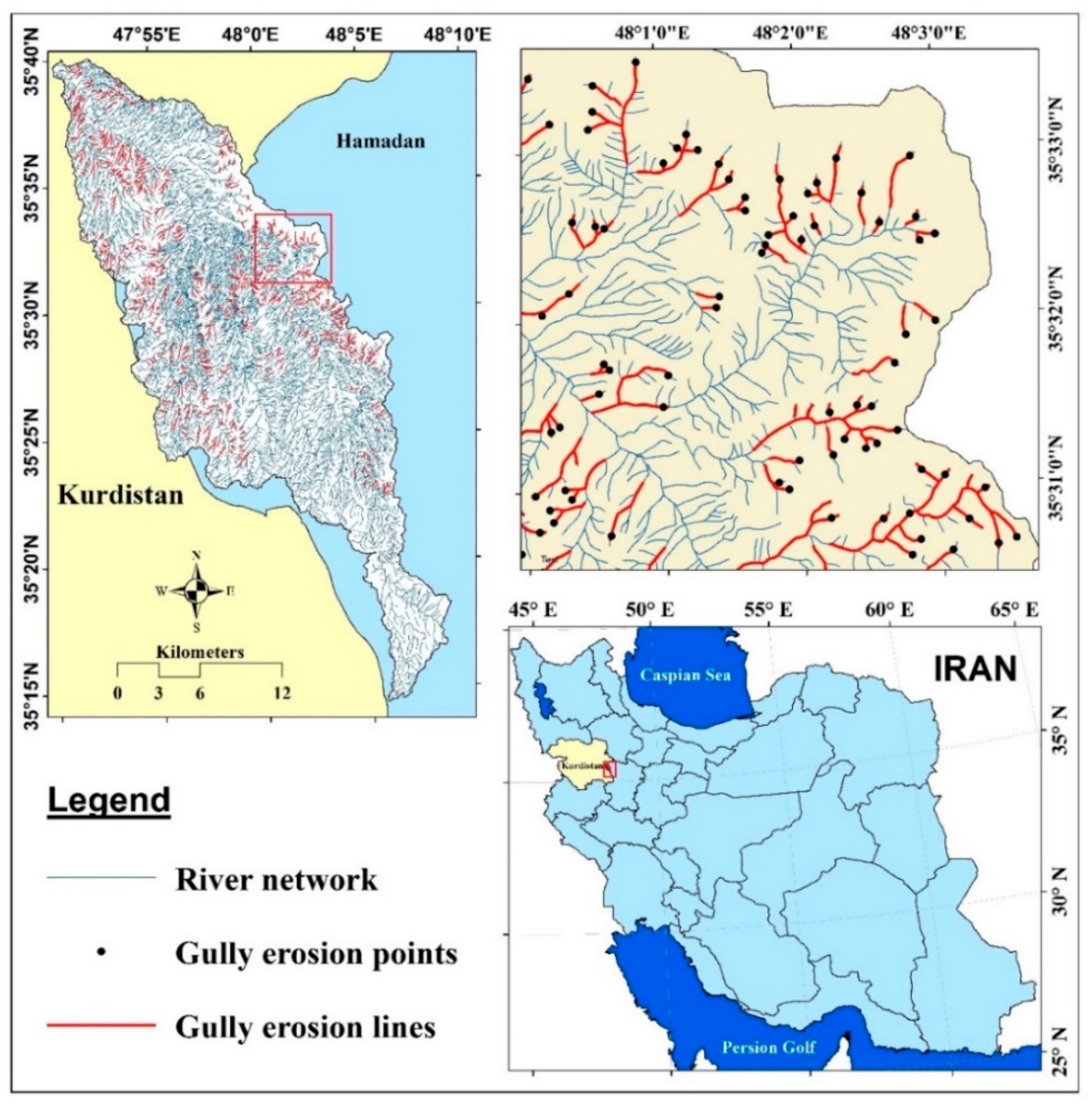
2. Description of Study Area
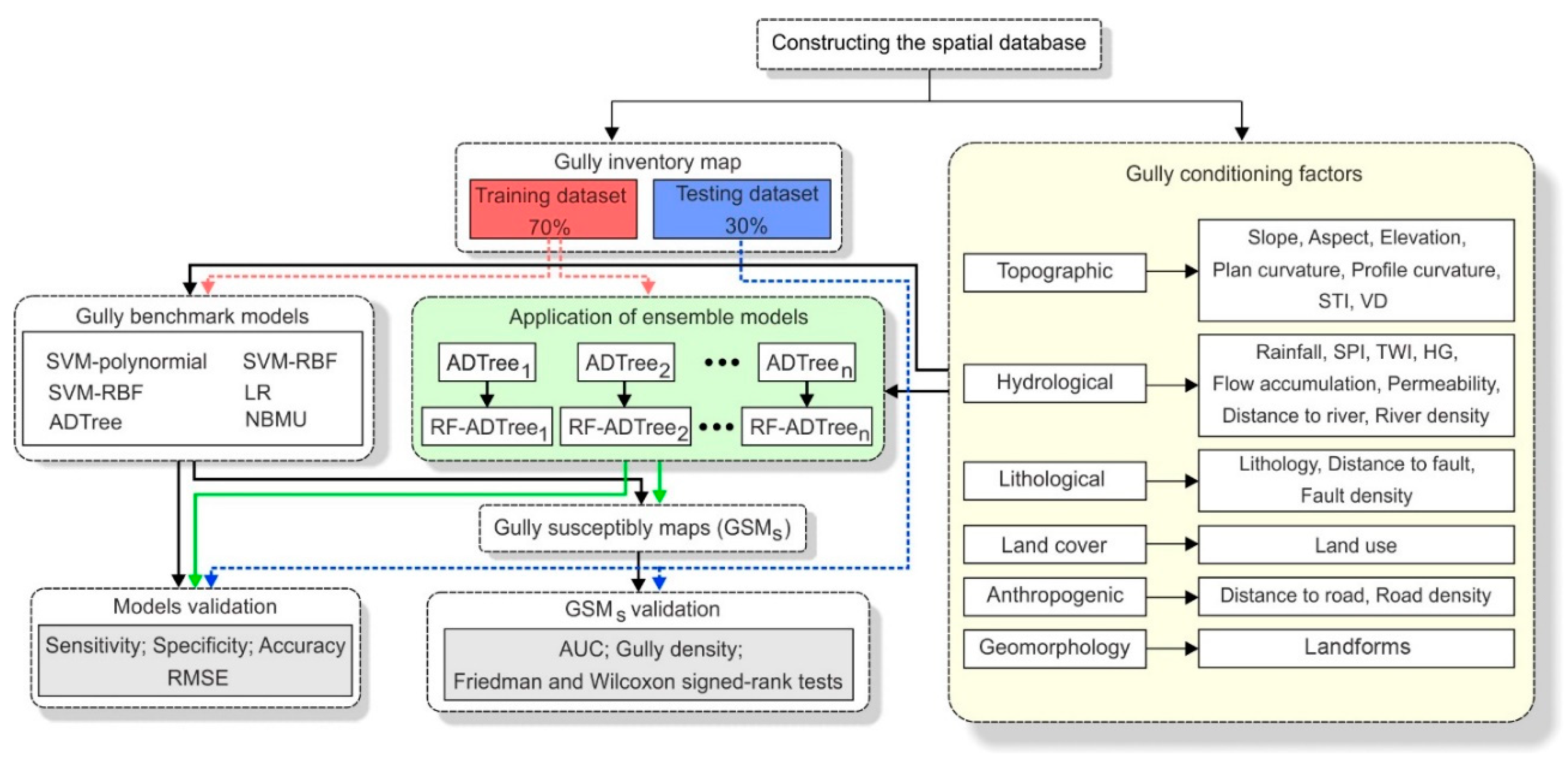
3. Data Acquisition
3.1. Gully Inventory Map
3.2. Gully Erosion Conditioning Factors
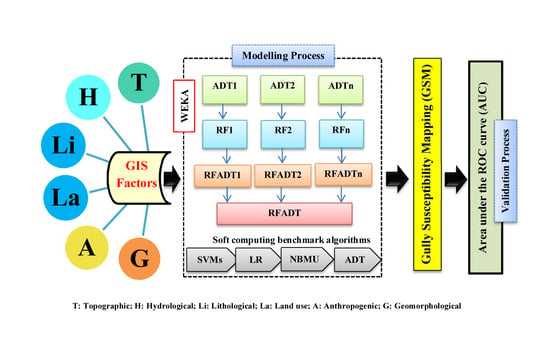
4. Background of Machine Learning Methods
4.1. Support Vector Machine Classifier
4.2. Logistic Regression Classifier
4.3. Naïve Bayes Multinomial Updatable Classifier
4.4. Alternating Decision Tree Classifier
4.5. Rotation Forest Ensemble Classifier
4.6. Factor Selection Using Information Gain Ratio (IGR)
4.7. Development of Gully Erosion Maps
4.8. Evaluation and Comparison Methods
4.8.1. Statistical Index-Bases Measures
4.8.2. Receiver Operating Characteristic (ROC)
4.8.3. Freidman and Wilcoxon Sign Rank Tests
4.8.4. Gully Density
5. Result and Analysis
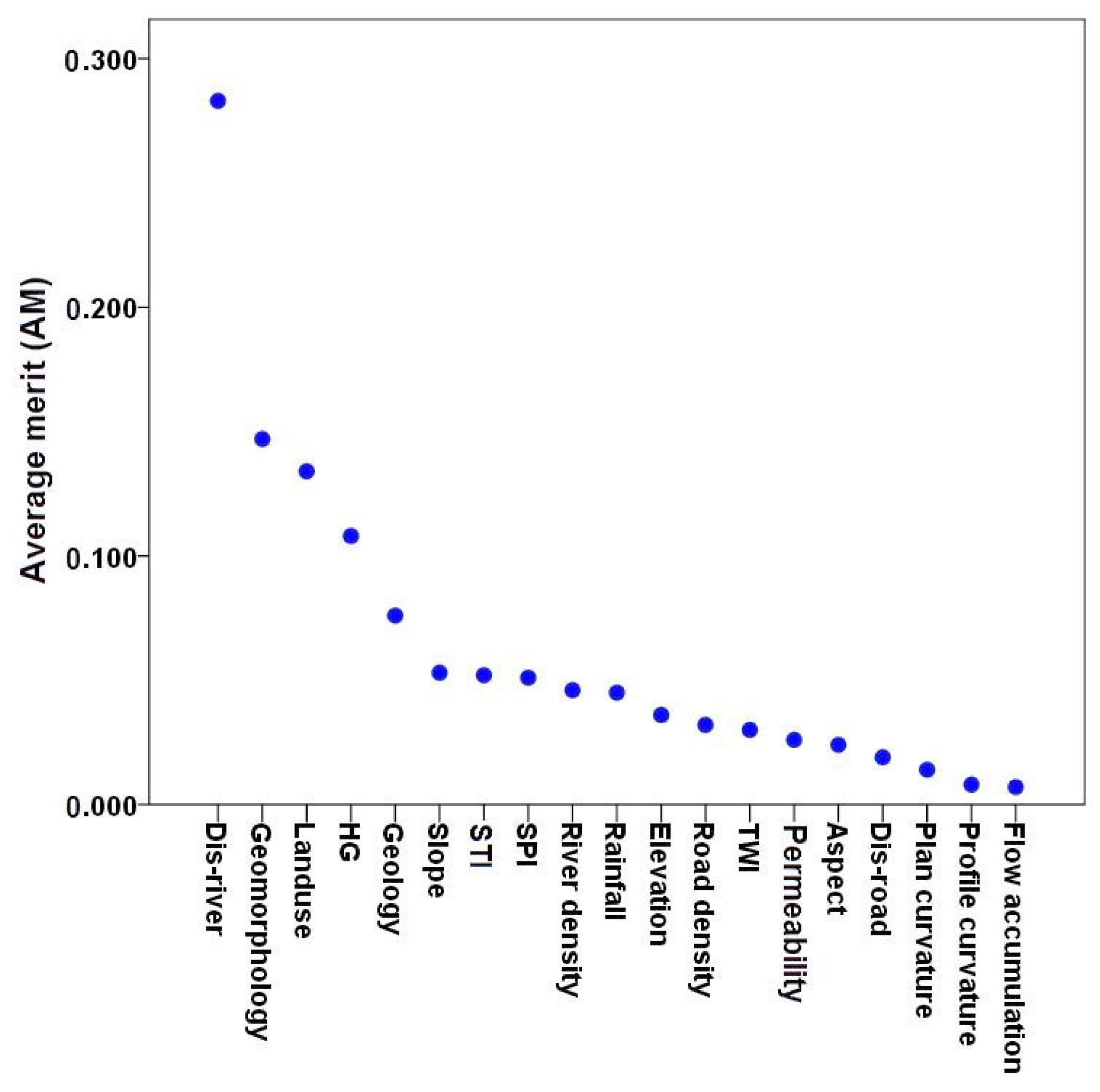
5.1. The Most Important Factors in Gully Modelling by IGR
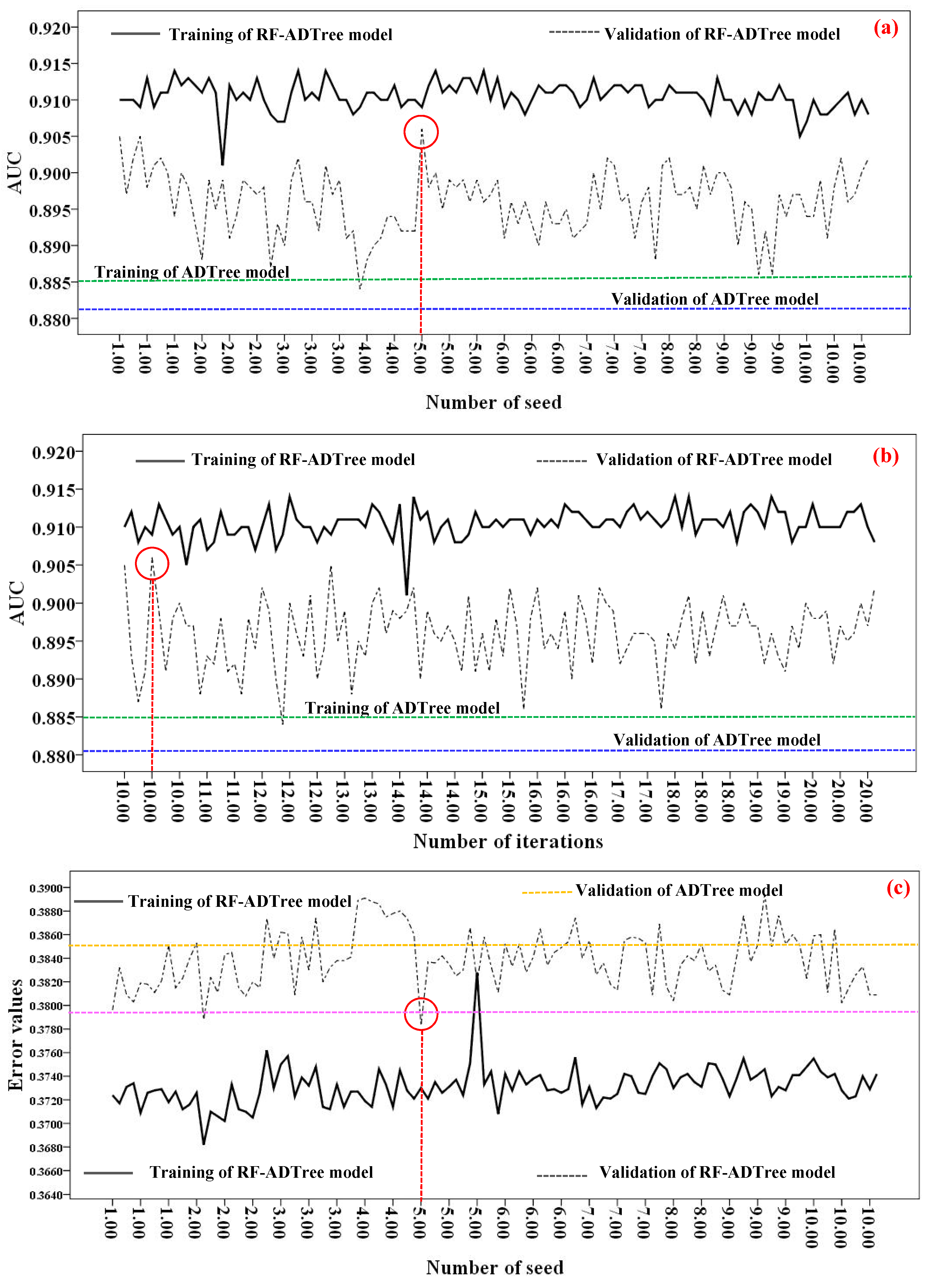
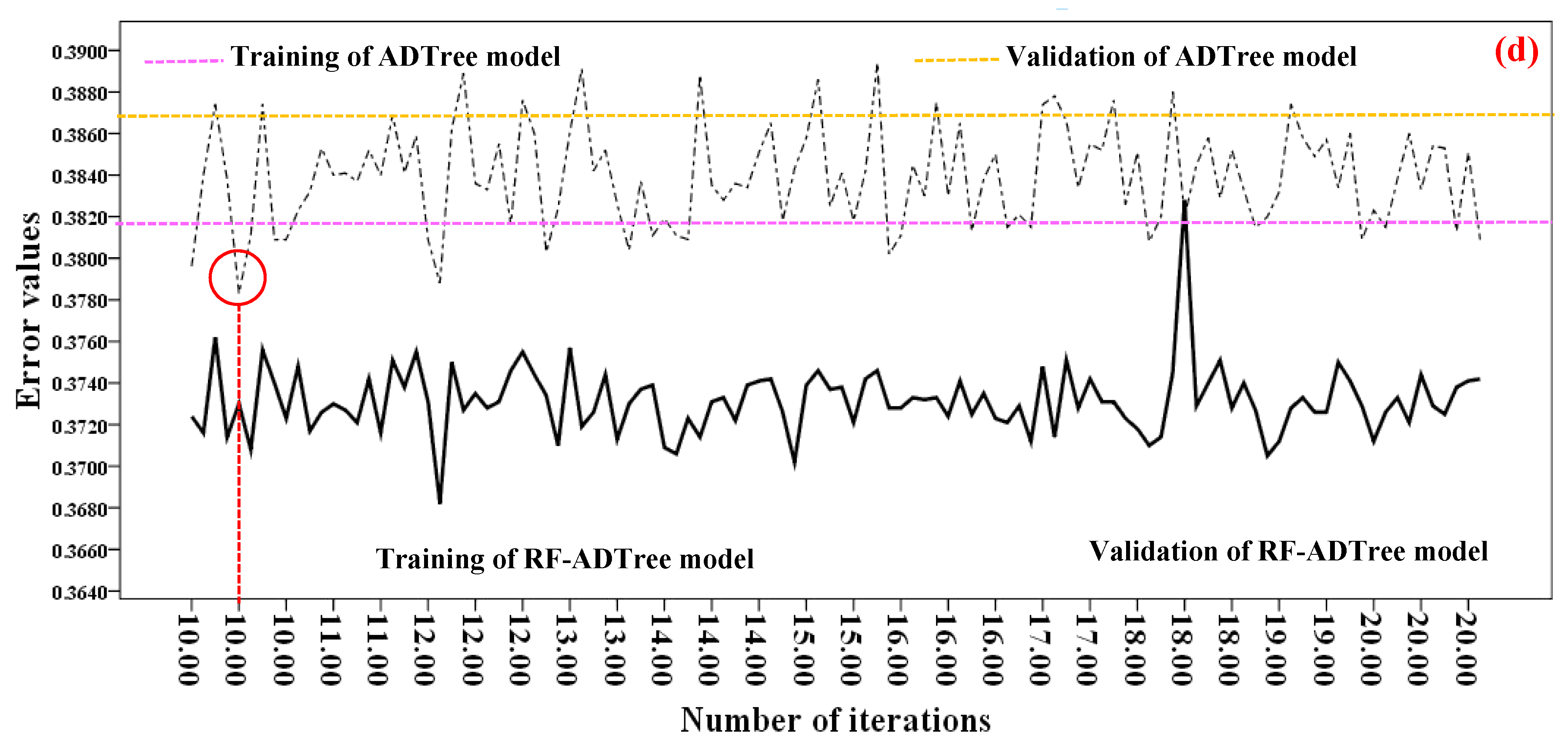
5.2. Gully Modeling Procedure or Optimization
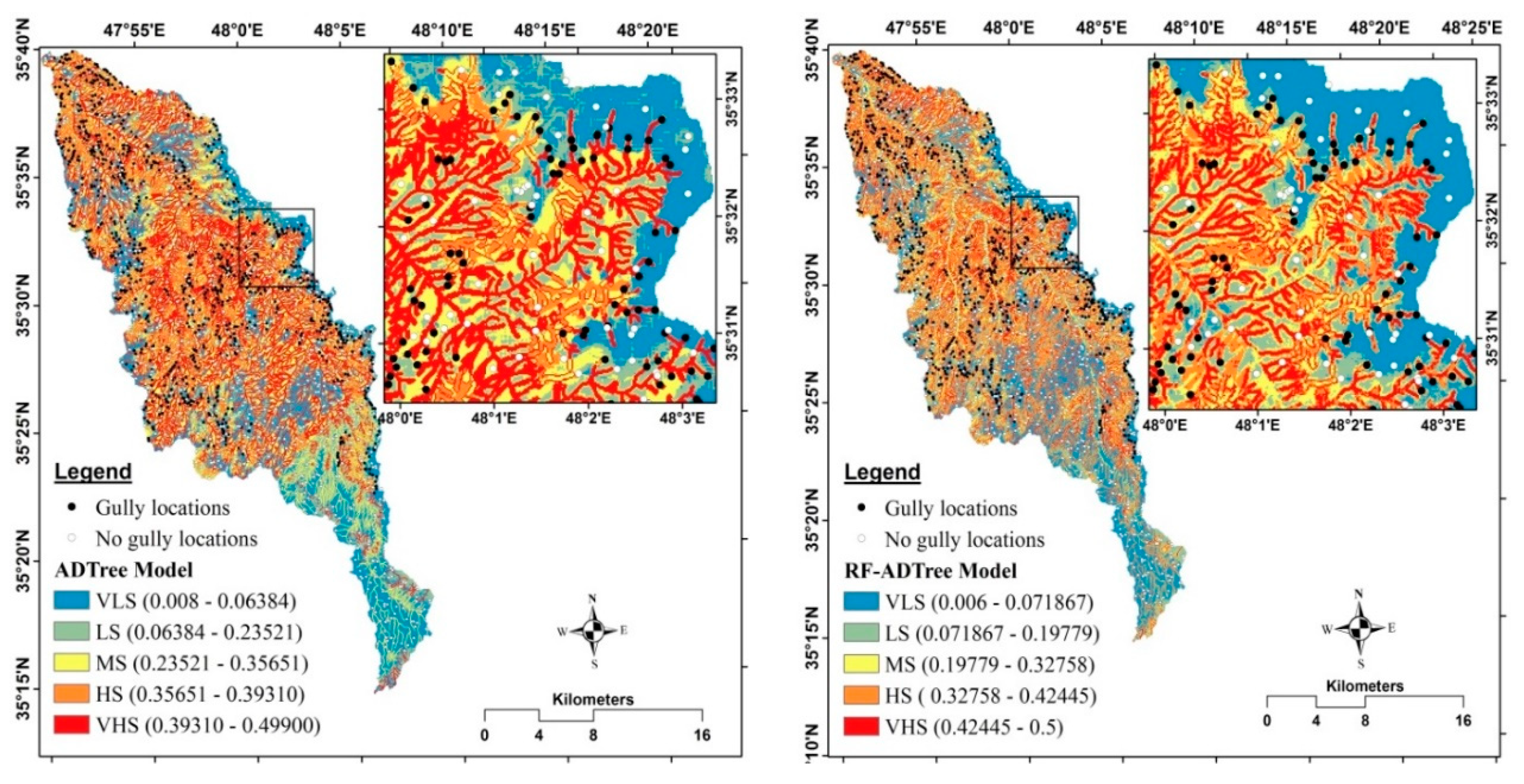
5.3. Development of Gully Erosion Maps
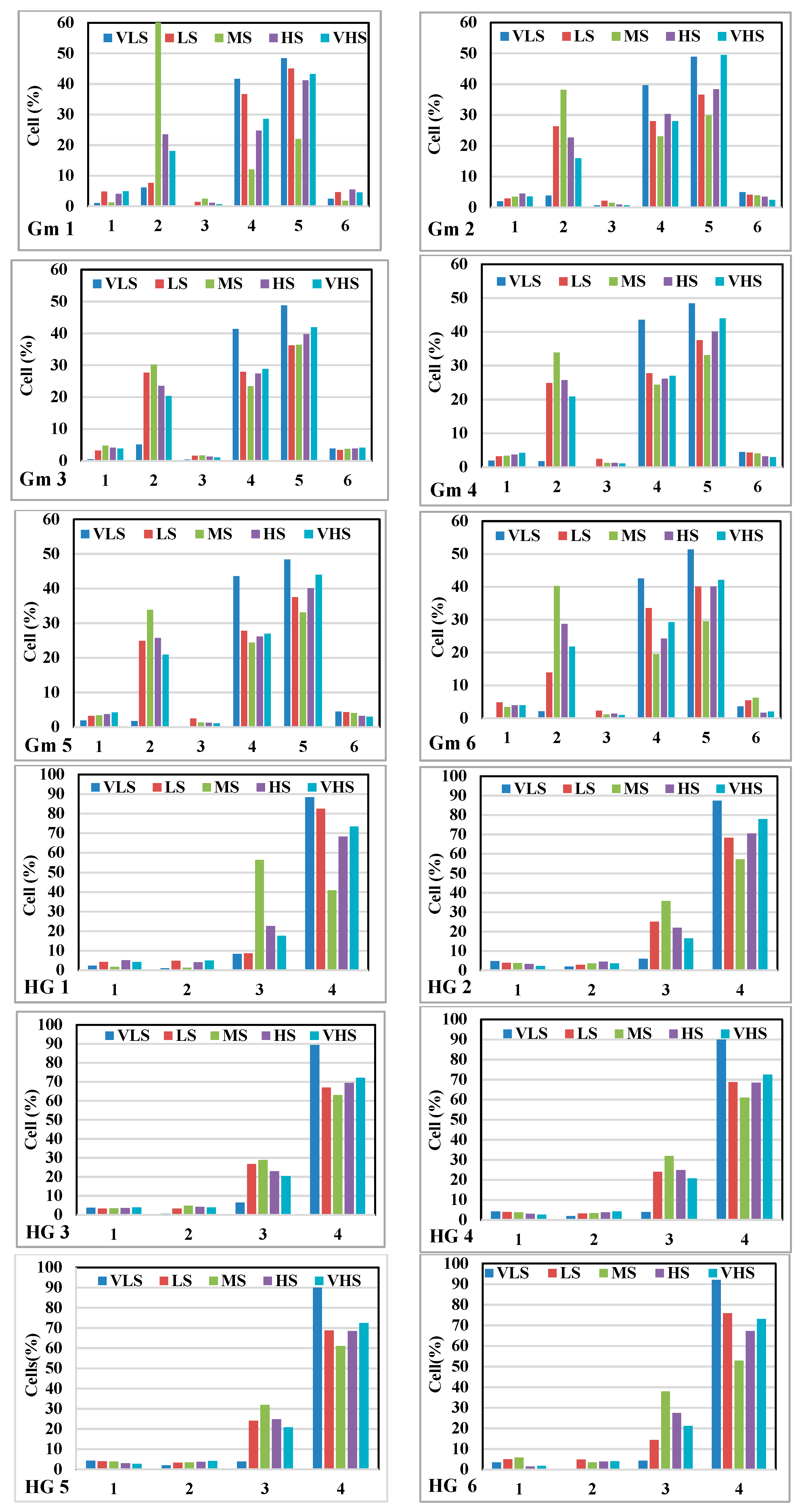
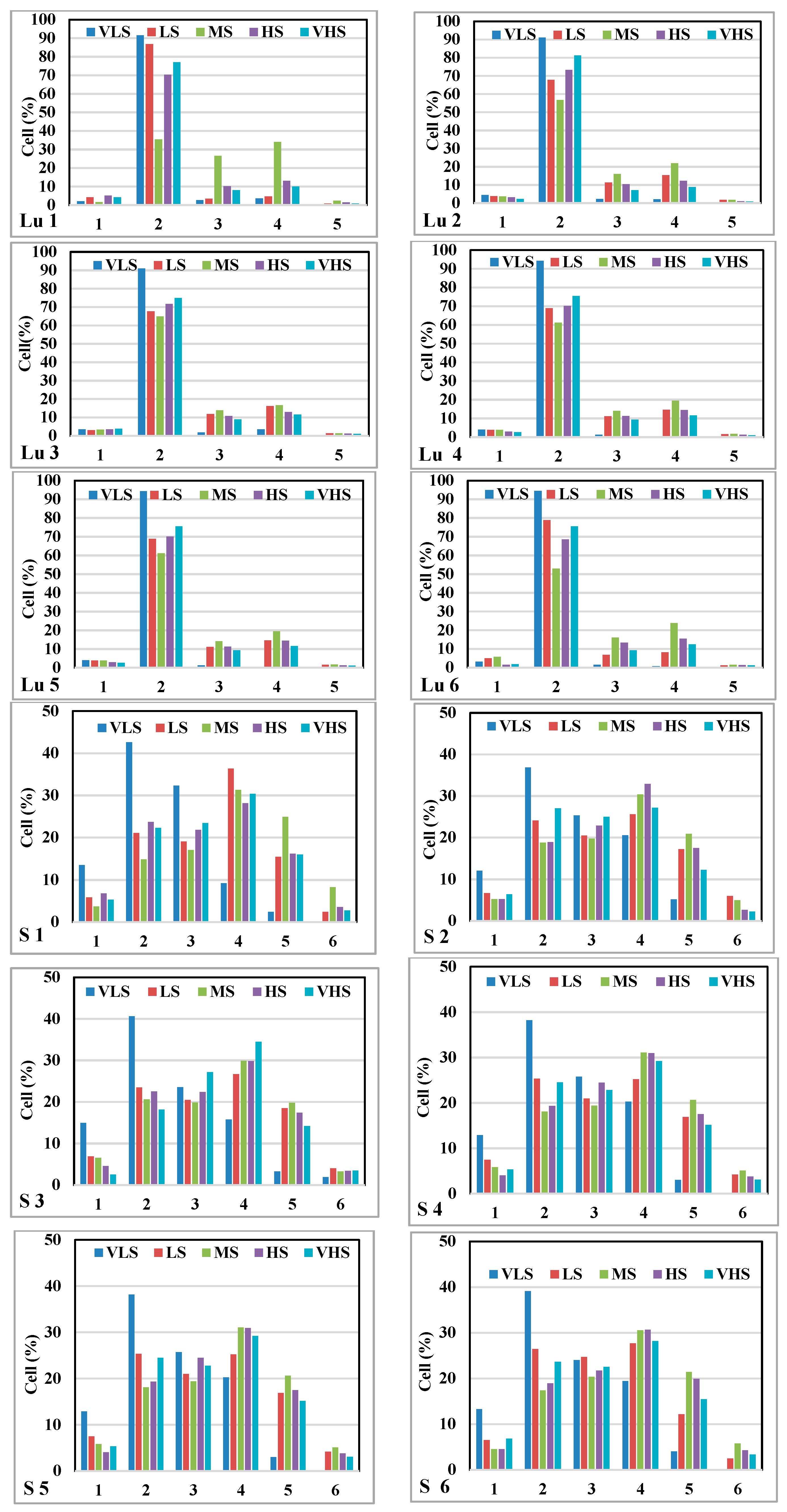
5.4. The Contribution of the Sixth Most Important Factors Using GESMs
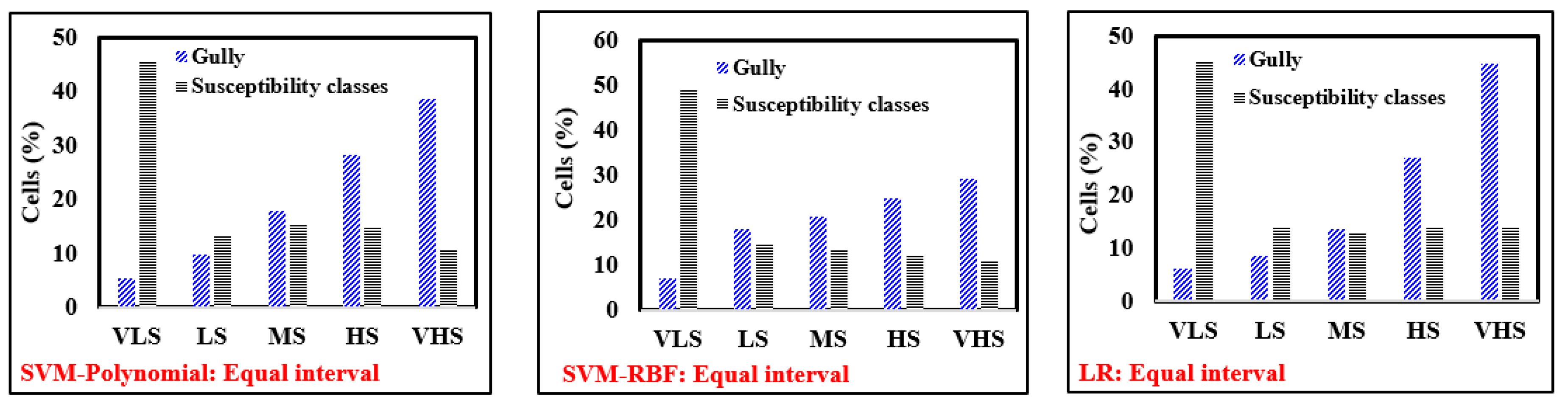
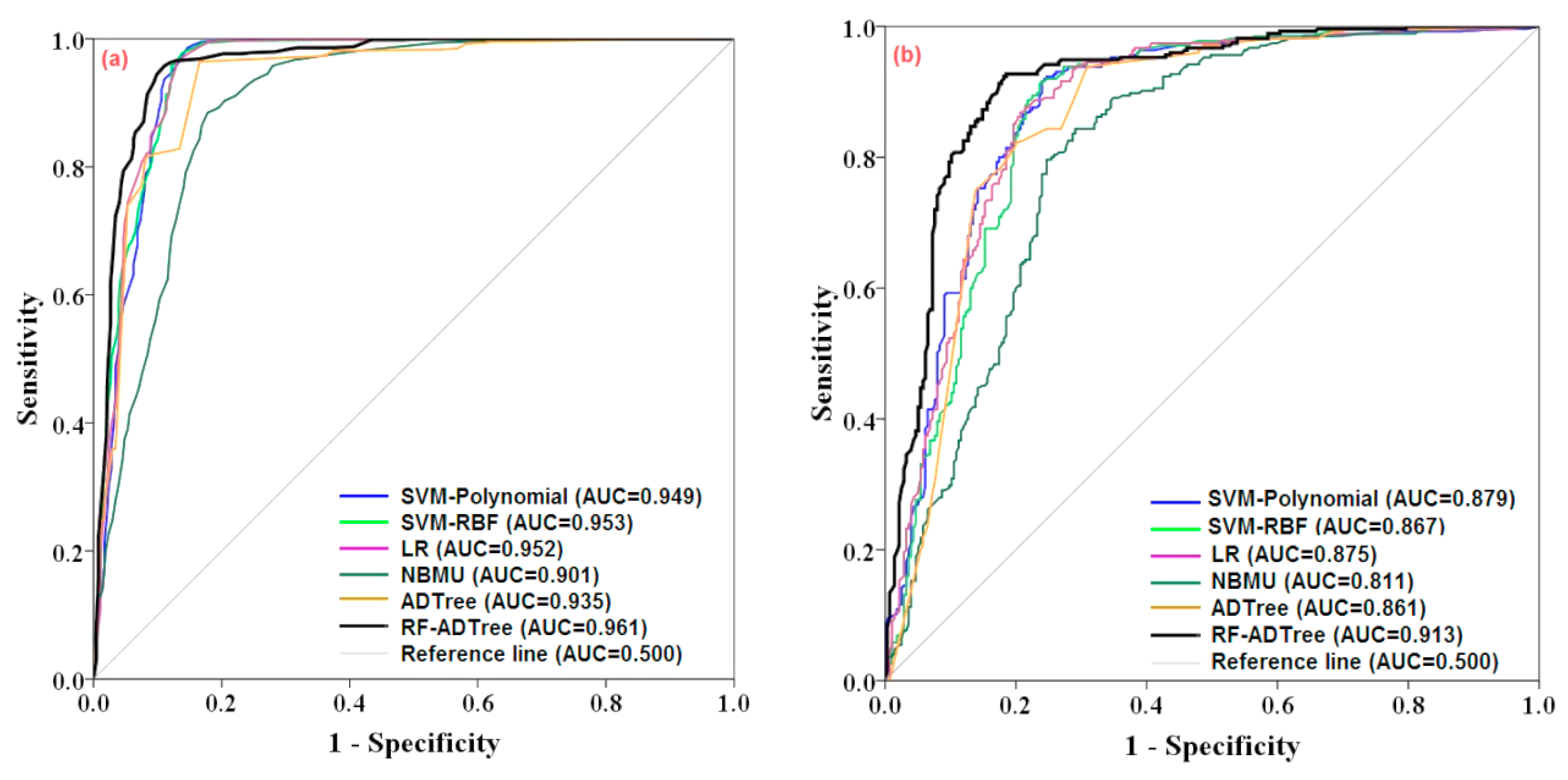
5.5. Evaluation and Comparison of Gully Erosion Maps
5.6. Statistical Tests
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lal, R. Offsetting global CO2 emissions by restoration of degraded soils and intensification of world agriculture and forestry. Land Degrad. Dev. 2003, 14, 309–322. [Google Scholar] [CrossRef]
- Ayele, G.K.; Gessess, A.A.; Addisie, M.B.; Tilahun, S.A.; Tebebu, T.Y.; Tenessa, D.B.; Langendoen, E.J.; Nicholson, C.F.; Steenhuis, T.S. A biophysical and economic assessment of a community-based rehabilitated gully in the ethiopian highlands. Land Degrad. Dev. 2016, 27, 270–280. [Google Scholar] [CrossRef]
- Kosmas, C.; Danalatos, N.; Cammeraat, L.H.; Chabart, M.; Diamantopoulos, J.; Farand, R.; Gutierrez, L.; Jacob, A.; Marques, H.; Martinez-Fernandez, J. The effect of land use on runoff and soil erosion rates under mediterranean conditions. Catena 1997, 29, 45–59. [Google Scholar] [CrossRef]
- Bryan, R.B. Soil erodibility and processes of water erosion on hillslope. Geomorphology 2000, 32, 385–415. [Google Scholar]
- Poesen, J.; Nachtergaele, J.; Verstraeten, G.; Valentin, C. Gully erosion and environmental change: Importance and research needs. Catena 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Valentin, C.; Poesen, J.; Li, Y. Gully erosion: Impacts, factors and control. Catena 2005, 63, 132–153. [Google Scholar] [CrossRef]
- Poesen, J.; Vandekerckhove, L.; Nachtergaele, J.; Oostwoud Wijdenes, D.; Verstraeten, G.; van Wesemael, B. Gully erosion in dryland environments. In Dryland Rivers: Hydrology and Geomorphology of Semi-Arid Channels; Bull, L.J., Kirkby, M.J., Eds.; Wiley: Chichester, UK, 2002; pp. 229–262. [Google Scholar]
- Poesen, J.; Vandaele, K.; Van Wesemael, B. Contribution of gully erosion to sediment production on cultivated lands and rangelands. IAHS Publ. Ser. Proc. Rep. Int. Assoc. Hydrol. Sci. 1996, 236, 251–266. [Google Scholar]
- Soil Science Society of America. Glossary of Soil Science Terms; Soil Science Society of America: Madison, WI, USA, 2001. [Google Scholar]
- Kociuba, W.; Janicki, G.; Rodzik, J.; Stępniewski, K. Comparison of volumetric and remote sensing methods (tls) for assessing the development of a permanent forested loess gully. Nat. Hazards 2015, 79, 139–158. [Google Scholar] [CrossRef]
- Gawrysiak, L.; Harasimiuk, M. Spatial Diversity of Gully Density of the Lublin Upland and Roztocze Hills (se Poland); Annales Universitatis Mariae Curie-Sklodowska; De Gruyter Open Sp. z oo: Lublin, Polandcity, 2012; p. 27. [Google Scholar]
- Janicki, G.; Rejman, J.; Zgłobicki, W.; Poesen, J.; Starkel, L.; Agnesi, V.; Angileri, S.; Cappadonia, C.; Conoscenti, C.; Rotigliano, E. Human impact on gully erosion. Landf. Anal. 2011, 17, 1–229. [Google Scholar]
- Poesen, J. Gully typology and gully control measures in the european loess belt. In Farm Land Erosion; Elsevier: Amsterdam, The Netherlands, 1993; pp. 221–239. [Google Scholar]
- Brice, J.C. Erosion and Deposition in the Loess-Mantled Great Plains, Medicine Creek Drainage Basin, Nebraska; US Government Printing Office: Washington, DC, USA, 1966.
- Poesen, J.; Govers, G. Gully Erosion in the Loam Belt of Belgium: Typology and Control Measures; In Soil Erosion on Agricultural Land, Proceedings of a workshop sponsored by the British Geomorphological Research Group, Coventry, UK, January 1989; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1990; pp. 513–530. [Google Scholar]
- Mazaeva, O.; Pelinen, V.; Janicki, G. Development of Bank Gullies on the Shore Zone of the Bratsk Reservoir (Russia). In Annales Universitatis Mariae Curie-Sklodowska; De Gruyter Open Sp. z oo: Lublin, Poland, 2014; p. 117. [Google Scholar]
- Najafi. Land and agricultural lands in iran. Mon. Dehati Mag. 2005, 24, 17–24. (In Persian) [Google Scholar]
- Pulley, S.; Ellery, W.N.; Lagesse, J.V.; Schlegel, P.K.; McNamara, S.J. Gully erosion as a mechanism for wetland formation: An examination of two contrasting landscapes. Land Degrad. Dev. 2018, 29, 1756–1767. [Google Scholar] [CrossRef]
- Zakerinejad, R.; Märker, M. Prediction of gully erosion susceptibilities using detailed terrain analysis and maximum entropy modeling: A case study in the mazayejan plain, southwest iran. Geogr. Fis. Din. Quat. 2014, 37, 67–76. [Google Scholar]
- Svoray, T.; Michailov, E.; Cohen, A.; Rokah, L.; Sturm, A. Predicting gully initiation: Comparing data mining techniques, analytical hierarchy processes and the topographic threshold. Earth Surf. Process. Landf. 2012, 37, 607–619. [Google Scholar] [CrossRef]
- Conforti, M.; Aucelli, P.P.; Robustelli, G.; Scarciglia, F. Geomorphology and gis analysis for mapping gully erosion susceptibility in the turbolo stream catchment (northern calabria, italy). Nat. Hazards 2011, 56, 881–898. [Google Scholar] [CrossRef]
- Rahmati, O.; Haghizadeh, A.; Pourghasemi, H.R.; Noormohamadi, F. Gully erosion susceptibility mapping: The role of gis-based bivariate statistical models and their comparison. Nat. Hazards 2016, 82, 1231–1258. [Google Scholar] [CrossRef]
- Azareh, A.; Rahmati, O.; Rafiei-Sardooi, E.; Sankey, J.B.; Lee, S.; Shahabi, H.; Ahmad, B.B. Modelling gully-erosion susceptibility in a semi-arid region, Iran: Investigation of applicability of certainty factor and maximum entropy models. Sci. Total Environ. 2018, 655, 684–696. [Google Scholar] [CrossRef]
- Dube, F.; Nhapi, I.; Murwira, A.; Gumindoga, W.; Goldin, J.; Mashauri, D. Potential of weight of evidence modelling for gully erosion hazard assessment in mbire district–zimbabwe. Phys. Chem. Earth Parts A/B/C 2014, 67, 145–152. [Google Scholar] [CrossRef]
- Al-Abadi, A.M.; Al-Ali, A.K. Susceptibility mapping of gully erosion using gis-based statistical bivariate models: A case study from ali al-gharbi district, maysan governorate, southern iraq. Environ. Earth Sci. 2018, 77, 249. [Google Scholar] [CrossRef]
- Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluating the influence of geo-environmental factors on gully erosion in a semi-arid region of Iran: An integrated framework. Sci. Total Environ. 2017, 579, 913–927. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Pourghasemi, H.R.; Lee, S.; Yamani, M. Gis-based gully erosion susceptibility mapping: A comparison among three data-driven models and ahp knowledge-based technique. Environ. Earth Sci. 2018, 77, 628. [Google Scholar] [CrossRef]
- Chaplot, V.; Le Brozec, E.C.; Silvera, N.; Valentin, C. Spatial and temporal assessment of linear erosion in catchments under sloping lands of northern laos. Catena 2005, 63, 167–184. [Google Scholar] [CrossRef]
- Vanwalleghem, T.; Van Den Eeckhaut, M.; Poesen, J.; Govers, G.; Deckers, J. Spatial analysis of factors controlling the presence of closed depressions and gullies under forest: Application of rare event logistic regression. Geomorphology 2008, 95, 504–517. [Google Scholar] [CrossRef]
- Conoscenti, C.; Angileri, S.; Cappadonia, C.; Rotigliano, E.; Agnesi, V.; Märker, M. Gully erosion susceptibility assessment by means of gis-based logistic regression: A case of sicily (Italy). Geomorphology 2014, 204, 399–411. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Yousefi, S.; Kornejady, A.; Cerdà, A. Performance assessment of individual and ensemble data-mining techniques for gully erosion modeling. Sci. Total Environ. 2017, 609, 764–775. [Google Scholar] [CrossRef]
- Kheir, R.B.; Wilson, J.; Deng, Y. Use of terrain variables for mapping gully erosion susceptibility in lebanon. Earth Surf. Process. Landf. J. Br. Geomorphol. Res.Group 2007, 32, 1770–1782. [Google Scholar] [CrossRef]
- Märker, M.; Pelacani, S.; Schröder, B. A functional entity approach to predict soil erosion processes in a small plio-pleistocene mediterranean catchment in northern chianti, italy. Geomorphology 2011, 125, 530–540. [Google Scholar] [CrossRef]
- Kuhnert, P.M.; Henderson, A.K.; Bartley, R.; Herr, A. Incorporating uncertainty in gully erosion calculations using the random forests modelling approach. Environmetrics 2010, 21, 493–509. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K. Gully erosion zonation mapping using integrated geographically weighted regression with certainty factor and random forest models in gis. J. Environ. Manag. 2019, 232, 928–942. [Google Scholar] [CrossRef]
- Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Bui, D.T.; Pham, B.T.; Khosravi, K. A novel hybrid artificial intelligence approach for flood susceptibility assessment. Environ. Model. Softw. 2017, 95, 229–245. [Google Scholar] [CrossRef]
- Hong, H.; Panahi, M.; Shirzadi, A.; Ma, T.; Liu, J.; Zhu, A.-X.; Chen, W.; Kougias, I.; Kazakis, N. Flood susceptibility assessment in hengfeng area coupling adaptive neuro-fuzzy inference system with genetic algorithm and differential evolution. Sci. Total Environ. 2018, 621, 1124–1141. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Bui, D.T. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at haraz watershed, northern iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Valavi, R.; Shahabi, H.; Chapi, K.; Shirzadi, A. Novel forecasting approaches using combination of machine learning and statistical models for flood susceptibility mapping. J. Environ. Manag. 2018, 217, 1–11. [Google Scholar] [CrossRef]
- Ahmadlou, M.; Karimi, M.; Alizadeh, S.; Shirzadi, A.; Parvinnejhad, D.; Shahabi, H.; Panahi, M. Flood susceptibility assessment using integration of adaptive network-based fuzzy inference system (anfis) and biogeography-based optimization (bbo) and bat algorithms (ba). Geocarto Int. 2018, 1–21. [Google Scholar] [CrossRef]
- Bui, D.T.; Panahi, M.; Shahabi, H.; Singh, V.P.; Shirzadi, A.; Chapi, K.; Khosravi, K.; Chen, W.; Panahi, S.; Li, S. Novel hybrid evolutionary algorithms for spatial prediction of floods. Sci. Rep. 2018, 8, 15364. [Google Scholar] [CrossRef]
- Miraki, S.; Zanganeh, S.H.; Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Pham, B.T. Mapping groundwater potential using a novel hybrid intelligence approach. Water Resour. Manag. 2018, 33, 281–302. [Google Scholar] [CrossRef]
- Rahmati, O.; Naghibi, S.A.; Shahabi, H.; Bui, D.T.; Pradhan, B.; Azareh, A.; Rafiei-Sardooi, E.; Samani, A.N.; Melesse, A.M. Groundwater spring potential modelling: Comprising the capability and robustness of three different modeling approaches. J. Hydrol. 2018, 565, 248–261. [Google Scholar] [CrossRef]
- Tien Bui, D.; Khosravi, K.; Li, S.; Shahabi, H.; Panahi, M.; Singh, V.; Chapi, K.; Shirzadi, A.; Panahi, S.; Chen, W. New hybrids of anfis with several optimization algorithms for flood susceptibility modeling. Water 2018, 10, 1210. [Google Scholar] [CrossRef]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve bayes tree classifiers for a landslide susceptibility assessment in langao county, china. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Li, T.; Guo, C.; Hong, H.; Li, W.; Pan, D.; Hui, J.; Ma, M. A novel ensemble approach of bivariate statistical-based logistic model tree classifier for landslide susceptibility assessment. Geocarto Int. 2018, 33, 1398–1420. [Google Scholar] [CrossRef]
- Pham, B.T.; Shirzadi, A.; Bui, D.T.; Prakash, I.; Dholakia, M. A hybrid machine learning ensemble approach based on a radial basis function neural network and rotation forest for landslide susceptibility modeling: A case study in the himalayan area, India. Int. J. Sediment Res. 2018, 33, 157–170. [Google Scholar] [CrossRef]
- Abedini, M.; Ghasemian, B.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Pham, B.T.; Bin Ahmad, B.; Tien Bui, D. A novel hybrid approach of bayesian logistic regression and its ensembles for landslide susceptibility assessment. Geocarto Int. 2018. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hoang, N.-D.; Pham, B.; Bui, Q.-T.; Tran, C.-T.; Panahi, M.; Bin Ahamd, B. A novel integrated approach of relevance vector machine optimized by imperialist competitive algorithm for spatial modeling of shallow landslides. Remote Sens. 2018, 10, 1538. [Google Scholar] [CrossRef]
- Jaafari, A.; Panahi, M.; Pham, B.T.; Shahabi, H.; Bui, D.T.; Rezaie, F.; Lee, S. Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena 2019, 175, 430–445. [Google Scholar] [CrossRef]
- Nguyen, V.V.; Pham, B.T.; Vu, B.T.; Prakash, I.; Jha, S.; Shahabi, H.; Shirzadi, A.; Ba, D.N.; Kumar, R.; Chatterjee, J.M. Hybrid machine learning approaches for landslide susceptibility modeling. Forests 2019, 10, 157. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Omidvar, E.; Shirzadi, A.; Geertsema, M.; Clague, J.J.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Chapi, K. Shallow landslide prediction using a novel hybrid functional machine learning algorithm. Remote Sens. 2019, 11, 931. [Google Scholar] [CrossRef]
- Zhang, T.; Han, L.; Chen, W.; Shahabi, H. Hybrid integration approach of entropy with logistic regression and support vector machine for landslide susceptibility modeling. Entropy 2018, 20, 884. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.; Zhang, T.; Zhang, L.; Chai, H. Landslide susceptibility modeling based on gis and novel bagging-based kernel logistic regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Ahmad, B.; Panahi, M.; Hong, H. Landslide detection and susceptibility mapping by airsar data using support vector machine and index of entropy models in cameron highlands, malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using gis-based machine learning techniques for chongren county, Jiangxi province, china. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.-X.; Li, S. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2018. [Google Scholar] [CrossRef]
- Shadman Roodposhti, M.; Aryal, J.; Shahabi, H.; Safarrad, T. Fuzzy shannon entropy: A hybrid gis-based landslide susceptibility mapping method. Entropy 2016, 18, 343. [Google Scholar] [CrossRef]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid artificial intelligence models based on a neuro-fuzzy system and metaheuristic optimization algorithms for spatial prediction of wildfire probability. Agric. Forest Meteorol. 2019, 266, 198–207. [Google Scholar] [CrossRef]
- Taheri, K.; Shahabi, H.; Chapi, K.; Shirzadi, A.; Gutiérrez, F.; Khosravi, K. Sinkhole susceptibility mapping: A comparison between bayes-based machine learning algorithms. Land Degrad. Dev. 2019, 30, 730–745. [Google Scholar] [CrossRef]
- Roodposhti, M.S.; Safarrad, T.; Shahabi, H. Drought sensitivity mapping using two one-class support vector machine algorithms. Atmos. Res. 2017, 193, 73–82. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Pradhan, B.; Chen, W.; Khosravi, K.; Panahi, M.; Bin Ahmad, B.; Saro, L. Land subsidence susceptibility mapping in south korea using machine learning algorithms. Sensors 2018, 18, 2464. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.-X.; Chen, W.; Ahmad, B.B. Landslide susceptibility mapping using j48 decision tree with adaboost, bagging and rotation forest ensembles in the guangchang area (China). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Rodriguez, J.J.; Kuncheva, L.I.; Alonso, C.J. Rotation forest: A new classifier ensemble method. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef]
- Du, P.; Samat, A.; Waske, B.; Liu, S.; Li, Z. Random forest and rotation forest for fully polarized sar image classification using polarimetric and spatial features. ISPRS J. Photogram. Remote Sens. 2015, 105, 38–53. [Google Scholar] [CrossRef]
- Nguyen, Q.-K.; Tien Bui, D.; Hoang, N.-D.; Trinh, P.; Nguyen, V.-H.; Yilmaz, I. A novel hybrid approach based on instance based learning classifier and rotation forest ensemble for spatial prediction of rainfall-induced shallow landslides using gis. Sustainability 2017, 9, 813. [Google Scholar] [CrossRef]
- Zhu, H.-J.; You, Z.-H.; Zhu, Z.-X.; Shi, W.-L.; Chen, X.; Cheng, L. Droiddet: Effective and robust detection of android malware using static analysis along with rotation forest model. Neurocomputing 2018, 272, 638–646. [Google Scholar] [CrossRef]
- Agnesi, V.; Angileri, S.; Cappadonia, C.; Conoscenti, C.; Rotigliano, E. Multi parametric gis analysis to assess gully erosion susceptibility: A test in southern sicily, italy. Landf. Anal. 2011, 17, 15–20. [Google Scholar]
- Wang, L.; Wei, S.; Horton, R.; Shao, M.A. Effects of vegetation and slope aspect on water budget in the hill and gully region of the loess plateau of china. Catena 2011, 87, 90–100. [Google Scholar] [CrossRef]
- Pauchard, A.; Alaback, P.B. Influence of elevation, land use, and landscape context on patterns of alien plant invasions along roadsides in protected areas of south-central chile. Conserv. Biol. 2004, 18, 238–248. [Google Scholar] [CrossRef]
- Zhu, H.; Tang, G.; Qian, K.; Liu, H. Extraction and analysis of gully head of loess plateau in china based on digital elevation model. Chin. Geogr. Sci. 2014, 24, 328–338. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, Á.; Conoscenti, C.; Angileri, S.E.; Rotigliano, E.; Schnabel, S. Using topographical attributes to evaluate gully erosion proneness (susceptibility) in two mediterranean basins: Advantages and limitations. Nat. Hazards 2015, 79, 291–314. [Google Scholar] [CrossRef]
- Cerdan, O.; Le Bissonnais, Y.; Couturier, A.; Bourennane, H.; Souchère, V. Rill erosion on cultivated hillslopes during two extreme rainfall events in normandy, france. Soil Tillage Res. 2002, 67, 99–108. [Google Scholar] [CrossRef]
- Moore, I.D.; Wilson, J.P. Length-slope factors for the revised universal soil loss equation: Simplified method of estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Woltemade, C.J. Impact of residential soil disturbance on infiltration rate and stormwater runoff 1. J. Am. Water Resour. Assoc. 2010, 46, 700–711. [Google Scholar] [CrossRef]
- Danladi, A.; Ray, H. An analysis of some soil properties along gully erosion sites under different land use areas of gombe metropolis, gombe state, nigeria. J. Geogr. Reg. Plan. 2014, 7, 86–96. [Google Scholar]
- El Maaoui, M.A.; Felfoul, M.S.; Boussema, M.R.; Snane, M.H. Sediment yield from irregularly shaped gullies located on the fortuna lithologic formation in semi-arid area of tunisia. Catena 2012, 93, 97–104. [Google Scholar] [CrossRef]
- Lesschen, J.; Kok, K.; Verburg, P.; Cammeraat, L. Identification of vulnerable areas for gully erosion under different scenarios of land abandonment in southeast spain. Catena 2007, 71, 110–121. [Google Scholar] [CrossRef]
- Billi, P.; Dramis, F. Geomorphological investigation on gully erosion in the rift valley and the northern highlands of ethiopia. Catena 2003, 50, 353–368. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hong, H.; Liu, J.; Zhu, A.-X.; Shahabi, H.; Pham, B.T.; Chen, W.; Pradhan, B.; Bui, D.T. A novel hybrid integration model using support vector machines and random subspace for weather-triggered landslide susceptibility assessment in the wuning area (china). Environ. Earth Sci. 2017, 76, 652. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A novel hybrid intelligent model of support vector machines and the multiboost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2018, 78, 2865–2886. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in gis. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood susceptibility assessment using gis-based support vector machine model with different kernel types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Cortez, P.; Morais, A.D.J.R. A Data Mining Approach to Predict Forest Fires Using Meteorological Data; Associação Portuguesa para a Inteligência Artificial (APPIA): Guimarães, Portugal, 2007. [Google Scholar]
- Tien Bui, D.; Le, K.-T.T.; Nguyen, V.C.; Le, H.D.; Revhaug, I. Tropical forest fire susceptibility mapping at the cat ba national park area, hai phong city, vietnam, using gis-based kernel logistic regression. Remote Sens. 2016, 8, 347. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Colkesen, I. A kernel functions analysis for support vector machines for land cover classification. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 352–359. [Google Scholar] [CrossRef]
- Tu, J.V. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Bagley, S.C.; White, H.; Golomb, B.A. Logistic regression in the medical literature: Standards for use and reporting, with particular attention to one medical domain. J. Clin. Epidemiol. 2001, 54, 979–985. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemesbow, S. Goodness of fit tests for the multiple logistic regression model. Commun. Stat. Theory Methods 1980, 9, 1043–1069. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I. Evaluation and comparison of logitboost ensemble, fisher’s linear discriminant analysis, logistic regression, and support vector machines methods for landslide susceptibility mapping. Geocarto Int. 2017, 34, 316–333. [Google Scholar] [CrossRef]
- Pradhan, B. Flood susceptible mapping and risk area delineation using logistic regression, GIS and remote sensing. J. Spat. Hydrol. 2010, 9, 33–49. [Google Scholar]
- Chen, J.; Huang, H.; Tian, S.; Qu, Y. Feature selection for text classification with naïve bayes. Expert Syst. Appl. 2009, 36, 5432–5435. [Google Scholar] [CrossRef]
- Kim, S.-B.; Han, K.-S.; Rim, H.-C.; Myaeng, S.H. Some effective techniques for naive bayes text classification. IEEE Trans. Knowl. Data Eng. 2006, 18, 1457–1466. [Google Scholar]
- Subbalakshmi, G.; Ramesh, K.; Rao, M.C. Decision support in heart disease prediction system using naive bayes. Indian J. Comput. Sci. Eng. (IJCSE) 2011, 2, 170–176. [Google Scholar]
- Bhargavi, P.; Jyothi, S. Applying naive bayes data mining technique for classification of agricultural land soils. Int. J. Comput. Sci. Netw. Secur. 2009, 9, 117–122. [Google Scholar]
- Li, Y.; Anderson-Sprecher, R. Facies identification from well logs: A comparison of discriminant analysis and naïve bayes classifier. J. Petrol. Sci. Eng. 2006, 53, 149–157. [Google Scholar] [CrossRef]
- Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow landslide susceptibility assessment using a novel hybrid intelligence approach. Environ. Earth Sci. 2017, 76, 60. [Google Scholar] [CrossRef]
- Freund, Y.; Mason, L. The Alternating Decision Tree Learning Algorithm; ICML: New York, NY, USA, 1999; pp. 124–133. [Google Scholar]
- Chen, W.; Xie, X.; Peng, J.; Wang, J.; Duan, Z.; Hong, H. Gis-based landslide susceptibility modelling: A comparative assessment of kernel logistic regression, naïve-bayes tree, and alternating decision tree models. Geomat. Nat. Hazards Risk 2017, 8, 950–973. [Google Scholar] [CrossRef]
- De Comité, F.; Gilleron, R.; Tommasi, M. Learning multi-label alternating decision trees from texts and data. In Proceedings of the International Workshop on Machine Learning and Data Mining in Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2003; pp. 35–49. [Google Scholar]
- Berk, R.A. Classification and regression trees (cart). In Statistical Learning from a Regression Perspective; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–65. [Google Scholar]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Ozcift, A. Svm feature selection based rotation forest ensemble classifiers to improve computer-aided diagnosis of parkinson disease. J. Med. Syst. 2012, 36, 2141–2147. [Google Scholar] [CrossRef]
- Shirzadi, A.; Solaimani, K.; Roshan, M.H.; Kavian, A.; Chapi, K.; Shahabi, H.; Keesstra, S.; Ahmad, B.B.; Bui, D.T. Uncertainties of prediction accuracy in shallow landslide modeling: Sample size and raster resolution. Catena 2019, 178, 172–188. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4. 5: Programs for Empirical Learning; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Bui, D.T.; Ho, T.-C.; Pradhan, B.; Pham, B.-T.; Nhu, V.-H.; Revhaug, I. Gis-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with adaboost, bagging, and multiboost ensemble frameworks. Environ. Earth Sci. 2016, 75, 1101. [Google Scholar]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y. Landslide spatial modelling using novel bivariate statistical based naïve bayes, rbf classifier, and rbf network machine learning algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Bui, D.T. Landslide susceptibility modeling using reduced error pruning trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Panahi, S.; Li, S.; Jaafari, A.; Ahmad, B.B. Applying population-based evolutionary algorithms and a neuro-fuzzy system for modeling landslide susceptibility. Catena 2019, 172, 212–231. [Google Scholar] [CrossRef]
- Shirzadi, A.; Soliamani, K.; Habibnejhad, M.; Kavian, A.; Chapi, K.; Shahabi, H.; Chen, W.; Khosravi, K.; Thai Pham, B.; Pradhan, B. Novel GIS based machine learning algorithms for shallow landslide susceptibility mapping. Sensors 2018, 18, 3777. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the gis-based data mining techniques of best-first decision tree, random forest, and naïve bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Vanmaercke, M.; Poesen, J.; Van Mele, B.; Demuzere, M.; Bruynseels, A.; Golosov, V.; Bezerra, J.F.R.; Bolysov, S.; Dvinskih, A.; Frankl, A. How fast do gully headcuts retreat? Earth-Sci. Rev. 2016, 154, 336–355. [Google Scholar] [CrossRef]
- Ballabio, C.; Sterlacchini, S. Support vector machines for landslide susceptibility mapping: The staffora river basin case study, italy. Math. Geosci. 2012, 44, 47–70. [Google Scholar] [CrossRef]
- Wijdenes, D.J.O.; Poesen, J.; Vandekerckhove, L.; Ghesquiere, M. Spatial distibution of gully head activity and sediment supply along an ephemeral channel in a mediterranean environment. Catena 2000, 39, 147–167. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Yamani, M.; Pourghasemi, H.R.; Lombardo, L. Spatial modelling of gully erosion using evidential belief function, logistic regression, and a new ensemble of evidential belief function–logistic regression algorithm. Land Degrad. Dev. 2018, 29, 4035–4049. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Dholakia, M.; Prakash, I.; Pham, H.V.; Mehmood, K.; Le, H.Q. A novel ensemble classifier of rotation forest and naïve bayer for landslide susceptibility assessment at the luc yen district, yen bai province (viet nam) using gis. Geomat. Nat. Hazards Risk 2017, 8, 649–671. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen, V.-T.; Ngo, V.-L.; Trinh, P.T.; Ngo, H.T.T.; Bui, D.T. A novel hybrid model of rotation forest based functional trees for landslide susceptibility mapping: A case study at kon tum province, Vietnam. In Proceedings of the International Conference on Geo-Spatial Technologies and Earth Resources, Hanoi, Vietnam, 5–6 October 2017; pp. 186–201. [Google Scholar]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Optimization of landslide conditioning factors using very high-resolution airborne laser scanning (lidar) data at catchment scale. Remote Sens. Environ. 2014, 152, 150–165. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Revhaug, I.; Tran, C.T. A comparative assessment between the application of fuzzy unordered rules induction algorithm and j48 decision tree models in spatial prediction of shallow landslides at lang son city, vietnam. In Remote Sensing Applications in Environmental Research; Springer: Berlin/Heidelberg, Germany, 2014; pp. 87–111. [Google Scholar]
- Francis, J.; Tontisirin, N.; Anantsuksomsri, S.; Vink, J.; Zhong, V. Alternative strategies for mapping acs estimates and error of estimation. In Emerging Techniques in Applied Demography; Springer: Berlin/Heidelberg, Germany, 2015; pp. 247–273. [Google Scholar]
- Umar, Z.; Pradhan, B.; Ahmad, A.; Jebur, M.N.; Tehrany, M.S. Earthquake induced landslide susceptibility mapping using an integrated ensemble frequency ratio and logistic regression models in west sumatera province, indonesia. Catena 2014, 118, 124–135. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M. Rotation forest fuzzy rule-based classifier ensemble for spatial prediction of landslides using gis. Nat. Hazards 2016, 83, 97–127. [Google Scholar] [CrossRef]
- Neilsen, R.D.; Hjelmfelt, A.T. Hydrologic soil group assignment. Proc. Water Resour. Eng. 1998, 10, 1297–1302. [Google Scholar]




| No. | Factors | Classes | Classification Method | |
|---|---|---|---|---|
| Topographic | 1 | Slope (o) | (1) 0–2; (2) 2–5; (3) 5–10; (4) 10–15; (5) 15–20; (6) >20 | Manual |
| 2 | Aspect | (1) Flat; (2) North; (3) Northeast; (4) East; (5) Southeast; (6) South; (7) Southwest; (8) West; (9) Northwest | Azimuth | |
| 3 | Elevation (m) | (1) 1612–1700; (2) 1700–1800; (3) 1800–1900; (4) 1900–2000; (5) 2000–2100; (6) 2100–2200; (7) 2200–2300; (8) 2300–2400 | Manual | |
| 4 | Plan curvature (m−1) | (1) [(−5.67)–(−0.736)]; (2) [(−0.736)–(−0.188)]; (3) [(−0.188)–0.149]; (4) [0.149–0.697]; (5) [0.6974–5.08] | Natural break | |
| 5 | Profile curvature (m−1) | (1) [(−6.357)–(−0.972)]; (2) [(−0.972)–(−0.187)]; (3) [(−0.187)–0.317]; (4) [0.317–1.1]; (5) [1.1–7.94] | Natural break | |
| 6 | STI | (1) 0–1.286; (2) 1.286–2.894; (3) 2.894–5.145; (4) 5.145–8.468; (5) 8.468–27.33 | Natural break | |
| 7 | VD | (1) 0–48.231; (2) 48.231–108.520; (3) 108.520–176.340; (4) 176.340–254.720; (5) 254.720–384.340 | Natural break | |
| Hydrological | 8 | Rainfall (mm) | (1) 261–286; (2) 286–298; (3) 298–306; (4) 306–312; (5) 312–322 | Natural break |
| 9 | SPI | (1) 0–112.4; (2) 112.4–224.8; (3) 224.8–401.5; (4) 401.5–722.7; (5) 722.7–4095 | Natural break | |
| 10 | TWI | (1) 1–3; (2) 3–4; (3) 4–5; (4) 5–6; (5) 6–9.059 | Natural break | |
| 11 | HG | (1) A; (2) B; (3) C; (4) D | HG type | |
| 12 | Flow accumulation | (1) 0–5; (2) 5–10; (3) 10–20; (4) 20–30; (5) >30 | Manual | |
| 13 | Permeability | (1) Low; (2) Moderate; (3) High | Permeability type | |
| 14 | Distance to river (m) | (1) 0–20; (2) 20–40; (3) 40–60; (4) 60–80; (5) >80 | Manual | |
| 15 | River density (km/km2) | (1) 0–2.775; (2) 2.775–4.810; (3) 4.810–6.598; (4) 6.598–8.694; (5) 8.694–15.72 | Natural break | |
| Lithological | 16 | Lithology | (1) JL; (2) JS; (3) Mm; (4) PLb; (5) Pcg; (6) Plm; (7) Plt; (8) Qal; (9) Qc; (10) Qtr; (11) Qt1; (12) Qt2 | Lithology type |
| 17 | Distance to fault (m) | (1) 0–100; (2) 100–200; (3) 200–500; (4) 500–1000; (5) >1000 | Manual | |
| 18 | Fault density (km/km2) | (1) 0–0.287; (2) 0.287–0.823; (3) 0.823–1.270; (4) 1.270–1.820; (5) 1.820–2.440 | Natural break | |
| Land cover | 19 | Land use | (1) Wood land; (2) Dry-farming and cultivated lands; (3) Poor pastures; (4) Semi-dense pastures; (5) Destroyed pastures | Land use type |
| Anthropogenic | 20 | Distance to road (m) | (1) 0–100; (2) 100–200; (3) 200–300; (4) 300–500; (5) >500 | Manual |
| 21 | Road density (km/km2) | (1) 0–0.684; (2) 0.684–1.750; (3) 1.750–2.570; (4) 2.570–3.690; (5) 3.690–6.980 | Natural break | |
| Geomorphology | 22 | Geomorphology | (1) The valley plain unit (2) Hilly unit; (3) Mountain unit; (4) New plain unit; (5) Old plain unit; (6) Fluvial sediment unit | Geomorphology type |
| Model Name | Description of Parameters |
|---|---|
| RF-ADTree | Classifier: ADTree; MaxGroup: 3; MinGroup: 3; Number of iterations: 10; Number of Groups: False; Projection Filter: PCA; Removed Percentage: 50; Number of seeds: 5 |
| ADTree | Number of Boosting Iterations: 10; Random Seed: 0; Save Instance Data: false; Search Path: Expand all Paths |
| LR | Maximum Its: −1; Ridge: 1.0 × 108 |
| SVM-PolyKernel | Build Logistic Models: True; C: 1; Check turned Off: False; Epsilon: 1.0 × 1012: Filter Type: Not normalization/standardization; Kernel: PolyKernel; Number of folds: −1; Tolerance Parameter: 0.001 |
| SVM-RBF | Build Logistic Models: True; C: 1; Check turned Off: False; Epsilon: 1.0 × 1012: Filter Type: Not normalization/standardization; Kernel: RBF; Number of folds: −1; Tolerance Parameter: 0.001 |
| NBMU | - |
| Measures | NBMU | SVM-Polynomial | SVM-RBF | LR | ADTree | RF-ADTree |
|---|---|---|---|---|---|---|
| True positive | 466 | 461 | 494 | 470 | 476 | 501 |
| True negative | 513 | 574 | 558 | 550 | 551 | 570 |
| False positive | 174 | 179 | 146 | 170 | 164 | 139 |
| False negative | 127 | 66 | 82 | 90 | 89 | 70 |
| Sensitivity (%) | 0.786 | 0.875 | 0.858 | 0.839 | 0.842 | 0.877 |
| Specificity (%) | 0.747 | 0.762 | 0.793 | 0.764 | 0.771 | 0.804 |
| Accuracy (%) | 0.765 | 0.809 | 0.822 | 0.797 | 0.802 | 0.837 |
| RMSE | 0.398 | 0.378 | 0.375 | 0.376 | 0.379 | 0.373 |
| AUC | 0.844 | 0.871 | 0.895 | 0.876 | 0.885 | 0.909 |
| Measures | NBMU | SVM-Polynomial | SVM-RBF | LR | ADTree | RF-ADTree |
|---|---|---|---|---|---|---|
| True positive | 201 | 195 | 198 | 201 | 204 | 213 |
| True negative | 210 | 244 | 227 | 236 | 240 | 240 |
| False positive | 74 | 80 | 77 | 47 | 71 | 62 |
| False negative | 65 | 31 | 48 | 39 | 35 | 35 |
| Sensitivity (%) | 0.756 | 0.863 | 0.805 | 0.838 | 0.854 | 0.859 |
| Specificity (%) | 0.739 | 0.753 | 0.747 | 0.834 | 0.772 | 0.795 |
| Accuracy (%) | 0.747 | 0.798 | 0.773 | 0.836 | 0.807 | 0.824 |
| RMSE | 0.403 | 0.380 | 0.381 | 0.380 | 0.384 | 0.378 |
| AUC | 0.843 | 0.863 | 0.873 | 0.869 | 0.882 | 0.906 |
| No. | Gully Models | Mean Ranks | χ2 | Sig. |
|---|---|---|---|---|
| 1 | SVM-Polynomial | 2.29 | 2040 | 0.000 |
| 2 | SVM-RBF | 2.71 | ||
| 3 | LR | 3.06 | ||
| 4 | NBMU | 3.49 | ||
| 5 | ADTree | 4.65 | ||
| 6 | RF-ADTree | 4.80 |
| No. | Pairwise Comparison | NPD | NND | z-value | p-value | Significance |
|---|---|---|---|---|---|---|
| 1 | SVM-Polynomial vs. SVM-RBF | 303 | 540 | −9.755 | 0.000 | Yes |
| 2 | SVM-Polynomial vs. LR | 245 | 700 | −13.424 | 0.000 | Yes |
| 3 | SVM-Polynomial vs. NBMU | 349 | 905 | −9.343 | 0.000 | Yes |
| 4 | SVM-Polynomial vs. ADTree | 196 | 1057 | −23.838 | 0.000 | Yes |
| 5 | SVM-Polynomial vs. RF-ADTree | 129 | 1126 | −26.125 | 0.000 | Yes |
| 6 | SVM-RBF vs. LR | 325 | 568 | −4.621 | 0.000 | Yes |
| 7 | SVM-RBF vs. NBMU | 434 | 813 | −3.536 | 0.000 | Yes |
| 8 | SVM-RBF vs. ADTree | 234 | 1009 | −21.050 | 0.000 | Yes |
| 9 | SVM-RBF vs. RF-ADTree | 194 | 1049 | −23.189 | 0.000 | Yes |
| 10 | LR vs. NBMU | 448 | 780 | −2.020 | 0.043 | Yes |
| 11 | LR vs. ADTree | 273 | 978 | −19.344 | 0.000 | Yes |
| 12 | LR vs. RF-ADTree | 222 | 1019 | −21.772 | 0.000 | Yes |
| 13 | NBMU vs. ADTree | 291 | 916 | −19.038 | 0.000 | Yes |
| 14 | NBMU vs. RF-ADTree | 249 | 919 | −19.714 | 0.000 | Yes |
| 15 | ADTree vs. RF-ADTree | 578 | 591 | −0.616 | 0.538 | No |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tien Bui, D.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Omidavr, E.; Pham, B.T.; Talebpour Asl, D.; Khaledian, H.; Pradhan, B.; Panahi, M.; et al. A Novel Ensemble Artificial Intelligence Approach for Gully Erosion Mapping in a Semi-Arid Watershed (Iran). Sensors 2019, 19, 2444. https://doi.org/10.3390/s19112444
Tien Bui D, Shirzadi A, Shahabi H, Chapi K, Omidavr E, Pham BT, Talebpour Asl D, Khaledian H, Pradhan B, Panahi M, et al. A Novel Ensemble Artificial Intelligence Approach for Gully Erosion Mapping in a Semi-Arid Watershed (Iran). Sensors. 2019; 19(11):2444. https://doi.org/10.3390/s19112444
Chicago/Turabian StyleTien Bui, Dieu, Ataollah Shirzadi, Himan Shahabi, Kamran Chapi, Ebrahim Omidavr, Binh Thai Pham, Dawood Talebpour Asl, Hossein Khaledian, Biswajeet Pradhan, Mahdi Panahi, and et al. 2019. "A Novel Ensemble Artificial Intelligence Approach for Gully Erosion Mapping in a Semi-Arid Watershed (Iran)" Sensors 19, no. 11: 2444. https://doi.org/10.3390/s19112444
APA StyleTien Bui, D., Shirzadi, A., Shahabi, H., Chapi, K., Omidavr, E., Pham, B. T., Talebpour Asl, D., Khaledian, H., Pradhan, B., Panahi, M., Bin Ahmad, B., Rahmani, H., Gróf, G., & Lee, S. (2019). A Novel Ensemble Artificial Intelligence Approach for Gully Erosion Mapping in a Semi-Arid Watershed (Iran). Sensors, 19(11), 2444. https://doi.org/10.3390/s19112444