1. Introduction
With the development of Industry 4.0, wireless sensor networks (WSNs) have great application prospects for industrial scenarios due to their advantages over traditional wired networks [
1,
2,
3,
4]. However, fully-automated mechanized operations and the wireless communication environments make the industrial wireless sensor networks (IWSNs) have stronger requirements for high security and low latency [
5]. M.Luvisotto et al. [
6] mentioned that the response delay in IWSNs should be in milliseconds. Moreover, under the edge computing (EC) system in IWSNs, some sensor nodes are in some completely security-free environments because there are no redundant computing resources and transmission resources. Therefore, lightweight authentication is urgently needed to enhance the security of IWSNs while ensuring low latency. The encrypted methods [
7,
8] are too heavy to support the nodes due to complex computing. I. Bhardwaj et al. [
9] did some lightweight processing on the password, but their method still cannot meet some specific requirements. Some other researchers proposed a fast cross-authentication scheme that combines non-cryptographic and cryptographic algorithms to solve the security and latency issues [
10]. In addition, the heterogeneous nature of the IWSNs makes traditional encryption-based authentication methods more complex to implement or manage. However, physical (PHY) layer methods provide some new approaches to protect the lightweightIWSNs. The high authentication rate and low cost are especially valued for such applications. By introducing deep learning (DL) into the PHY-layer authentication method, under the EC system, the training is performed under the edge devices, and the sensor nodes almost do not bear any extra costs.
D. Christin et al. [
1] surveyed related WSN technologies dedicated to industrial automation from the aspects of security and quality of service (QoS). The work in [
4] presented a QoS framework for IWSNs guaranteeing the delay bound and the target reliability. N. Neshenko et al. [
11] surveyed the challenges and research problems in the Internet of Things (IoT) including intrusion detection systems, threat modeling, and emerging technologies. However, the papers mentioned above only address the security and reliability issues from the perspective of the system architecture or simply give a direction for future research. L. Xiao et al. [
12] proposed a method to enhance the security of underwater sensor networks exploiting the power delay profile of the underwater acoustic channel to discriminate the sensors. The article [
13] presented a two-factor user authentication protocol using the hash function that protects against other attacks in wireless sensor networks, with the exception of denial of service (DoS) and node attacks. However, the traditional security methods have relatively large requirements on computing resources and communication resources, which cannot meet the requirement of low latency.
PHY-layer authentication can achieve lightweight authentication and effectively address the tradeoff between the security and low latency requirement of the wireless sensor networks in industrial scenarios. The PHY-layer authentication methods can distinguish the legitimate sensor nodes and illegal ones by physical layer channel information, such as channel state information (CSI) [
14,
15,
16,
17], received signal strength indicator (RSSI) [
18,
19,
20], received signal strength (RSS) [
21], and the radio frequency (RF) fingerprint [
22,
23]. However, the PHY-layer authentication methods mentioned above based on the hypothesis test are mostly compared with a threshold to distinguish users, which makes it difficult to discriminate multi-nodes at the same time. Authenticating multi-nodes simultaneously is a multi-classification problem, which needs to be solved urgently.
Deep learning has a large number of applications, such as computer vision, image classification, pattern recognition [
24,
25,
26], and so on. There are considerable research works using deep learning in wireless communications, such as in channel estimation and channel prediction. P. Illy et al. used machine learning to enhance the security of edge computing by implementing intrusion detection [
27]. The paper [
28] used the deep neural network to estimate the CSIs in orthogonal frequency division multiplexing (OFDM) systems. The work in [
29] proposed a Raleigh fading channel prediction scheme with a deep learning method. N. Wang et al. [
30] proposed a physical-layer authentication scheme based on extreme learning machine to detect spoofing attack. The DL-based PHY-layer authentication methods proposed in this paper can achieve multi-user authentication in a short time.
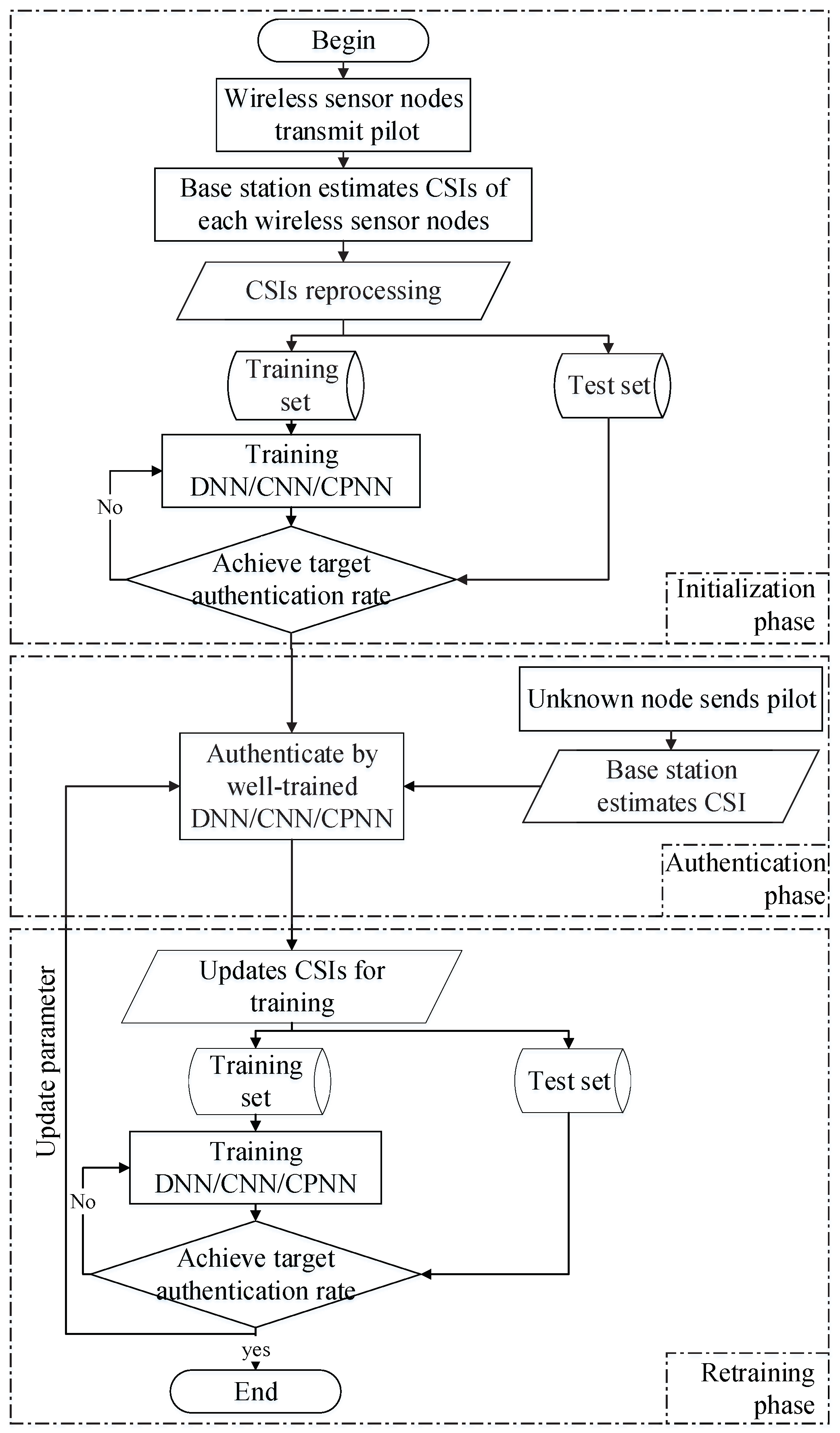
Unlike the traditional test-threshold-based PHY-layer authentication, the DL-based PHY-layer authentication methods can distinguish multiple sensor nodes simultaneously and maintain excellent performance. In the EC system, multi-sensor nodes need to be authenticated simultaneously, which is suitable for using the DL-based methods. The DL-based authentication methods are usually divided into the offline training phase and online authentication phase. The PHY-layer authentication framework we proposed in this paper also includes an online retraining process. In summary, the DL-based sensor nodes’ authentication algorithms proposed in this paper, utilizing the spatial diversity of wireless channels, can discriminate the sensor nodes without the test thresholds and have more practical application values. The main contributions of our work can be summarized as follows:
We propose a DL-based PHY-layer authentication framework to enhance the security of industrial sensor networks. We also briefly explore the applications of the framework for practical industrial scenarios.
Three different algorithms are adopted to implement the PHY-layer authentication in IWSNs, including the deep neural network (DNN)-based sensor nodes’ authentication method, the convolutional neural network (CNN)-based sensor nodes’ authentication method, and the convolution preprocessing neural network (CPNN)-based sensor nodes’ authentication method.
Simulation results show that the proposed algorithms can achieve better performance. In addition, the experiments in the engineering center with USRPs validate their utility in practical industrial environments.
The rest of this paper is organized as follows. We present the preliminaries and system model in
Section 2 and
Section 3, respectively. The DL-based PHY-layer authentication method in industrial wireless sensor networks is proposed in
Section 4. We provide numerical experiments in
Section 5. The experiment in a practical environment and conclusions are presented in
Section 6 and
Section 7, respectively.
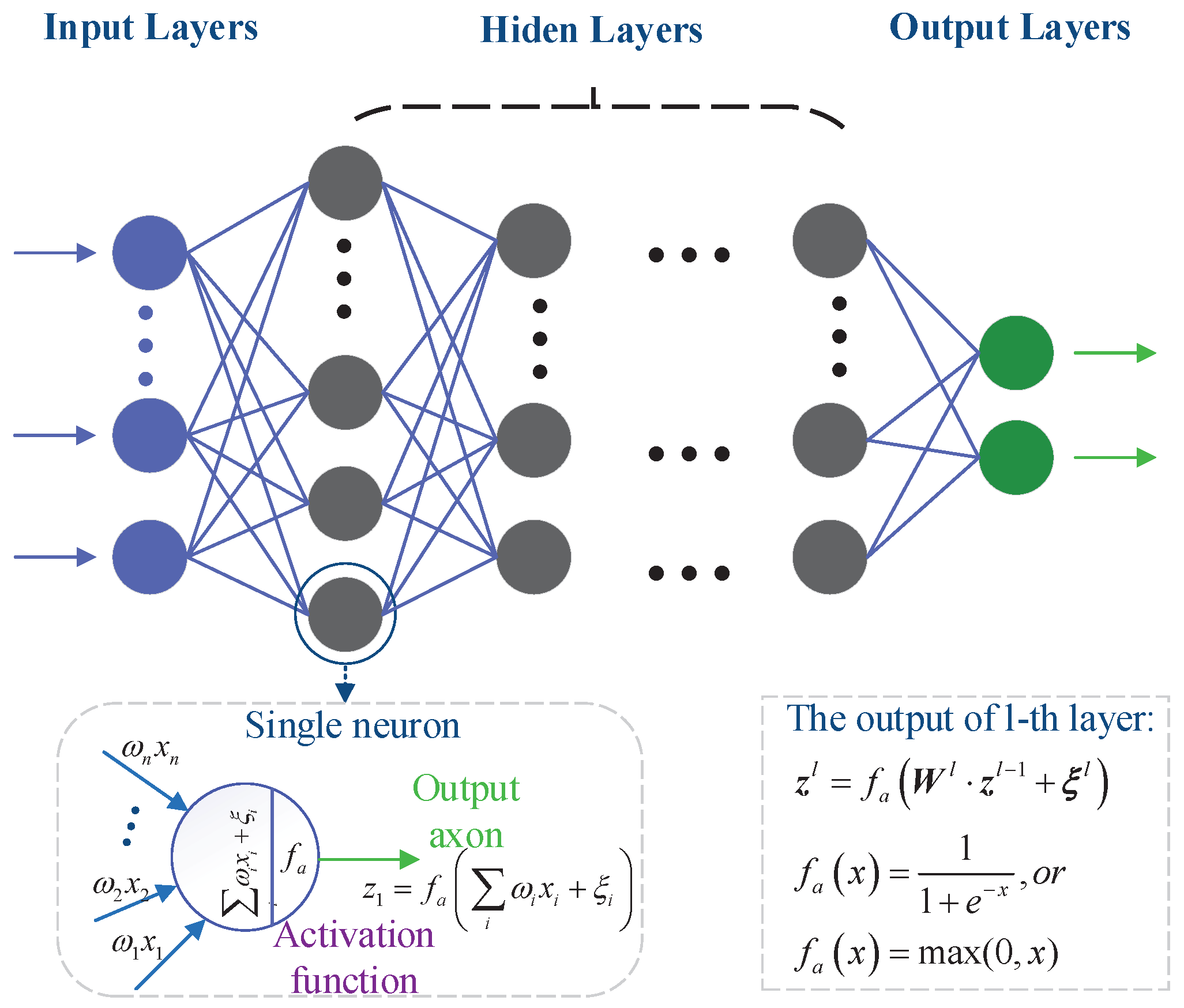
The symbols used in this article are briefly described as follows. Uppercase bold letters are used for the matrix (e.g., , ) and lowercase bold letters for vectors (e.g., , ). The elements are represented by the letters with subscripts and not bold (e.g., , ).
4. Deep Learning-Based Sensor Nodes’ Authentication Algorithms
In our previous work, we briefly introduced the physical layer channel authentication based on CNN [
31]. This paper will further improve the CNN algorithm and propose a rapid-DNN-based PHY-layer authentication algorithm to meet the low latency requirements of industrial wireless sensor networks.
4.1. DNN-Based Sensor Nodes’ Authentication
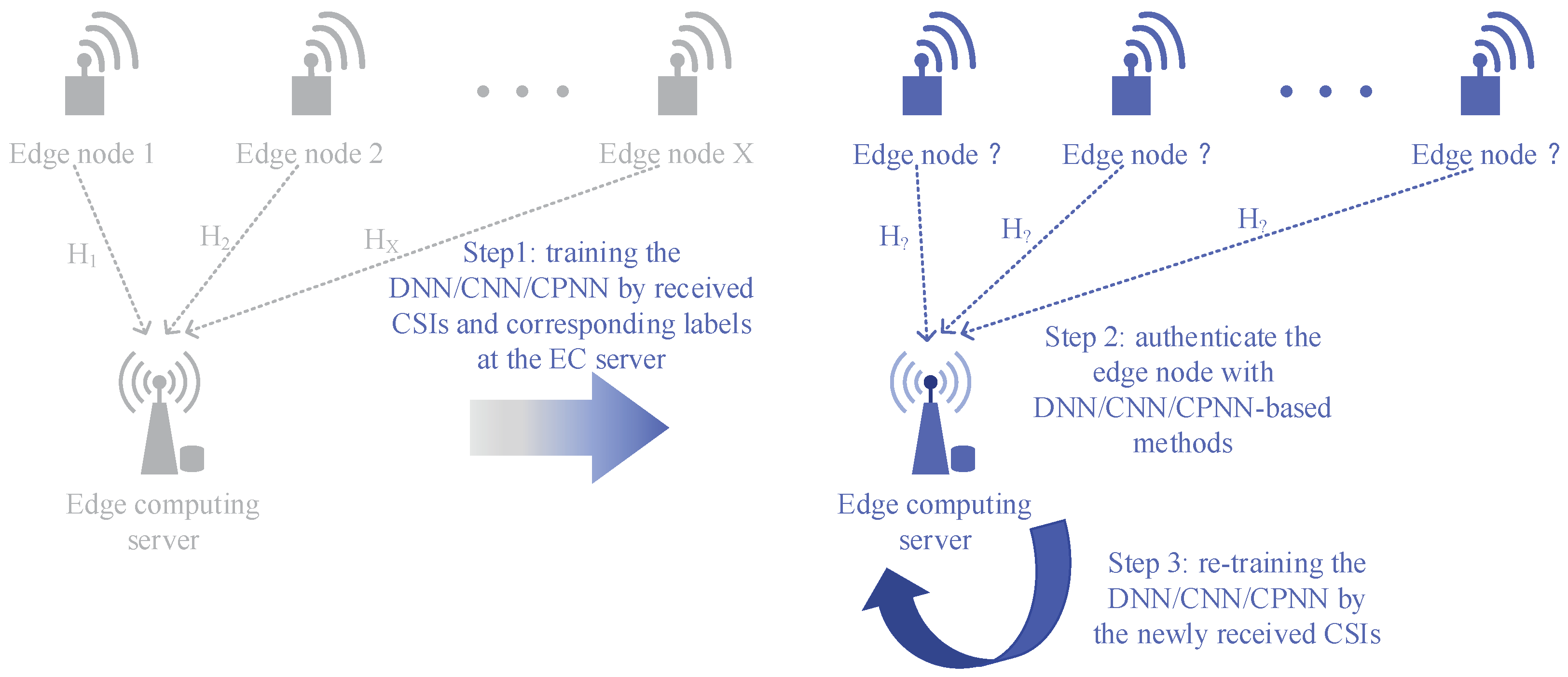
The DNN-based PHY-layer authentication in industrial wireless sensor networks uses the DNN to implement sensor nodes’ authentication. In the initialization phase, the base station collects channel state information of each sensor node and performs the corresponding labeling according to the upper layer protocol authentication (e.g., EAP, AKA). The DNN was trained by the collected information to obtain the initial neural network parameters. In the authentication phase, the CSI of the unknown sensor node will be authenticated by the well-trained DNN in the initialization phase. After the new CSI has been authenticated, the dataset will be trained again for the next authentication.
| Algorithm 1 DNN-based sensor nodes’ authentication. |
| Input: The CSI to authenticate |
| Output: The label of unknown CSI , the new weight matrix , and threshold vector of DNN |
| 1: Initialize all connection weights , and thresholds in the network will be obtained through the training of DNN, using the pre-acquired dataset ; |
| 2: Compute by well-trained DNN; |
| 3: Update the training set by ; |
| 4: Retrain the DNN by the new dataset and get new weight matrix and threshold vector ; |
| 5: Return , , . |
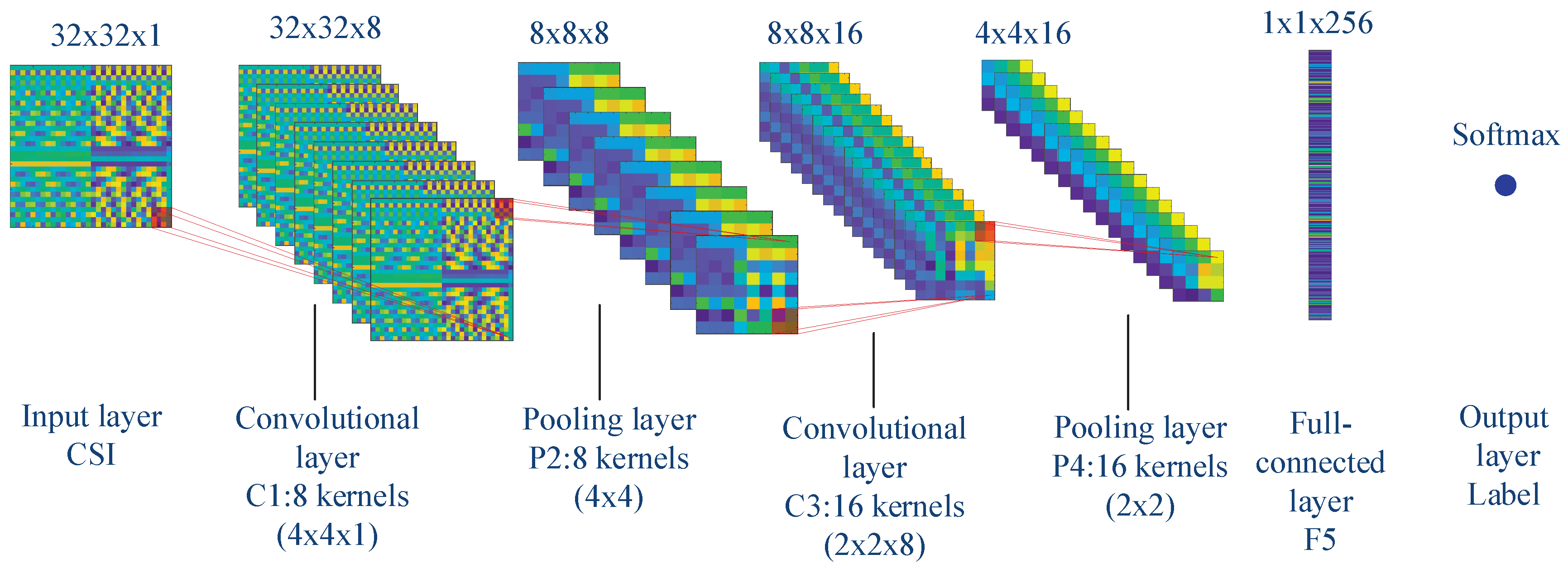
4.2. CNN-Based Sensor Nodes’ Authentication
The CNN-based sensor nodes’ authentication method is more like the DNN-based sensor nodes’ authentication. They have the same steps except that the authenticated neural network changes from DNN to CNN. In the initialization phase, the CNN will be trained by the pre-acquired dataset of different sensor nodes. Then, the CSI will be authenticated by the well-trained CNN. At last, the CNN will be retrained after the dataset is updated.
| Algorithm 2 CNN-based sensor nodes’ authentication. |
| Input: The CSI to authenticate |
| Output: The label of unknown CSI , the new weight matrix , and threshold vector of CNN |
| 1: Initialize all connection weights , and thresholds in the network will be obtained through the training of CNN, using the pre-acquired dataset ; |
| 2: Compute by the well-trained CNN; |
| 3: Update the training set by ; |
| 4: Retrain the CNN by the new dataset and get new weight matrix and threshold vector ; |
| 5: Return , , . |
4.3. Convolution Pre-Processing Neural Network-based Sensor Nodes’ Authentication
The convolution pre-processing neural network-based sensor nodes’ authentication method we propose in this paper has shorter training time and higher authentication accuracy. The core idea is to perform offline convolution preprocessing on the CSIs before training the neural network. The convolution preprocessing can effectively reduce the data dimension and extract the feature information of the CSIs, while the convolution kernels are trained by pre-obtained CSIs and corresponding labels. After convolution, activation, and pooling by the convolution kernels, the CSIs become . The latter’s dimensions are much smaller than the former’s. For the CPNN-based sensor node authentication method, the convolution kernels need to be calculated by the pre-obtained CSIs. Then, the neural network is trained by the new dataset in the initialization phase to get the weight matrix and threshold vector .
| Algorithm 3 CPNN-based sensor nodes’ authentication. |
| Input: The CSI to authenticate |
| Output: The label of unknown CSI , the new weight matrix , and threshold vector of CPNN |
| 1: Initialize: training the CNN by the pre-acquired CSIs to obtain the convolution kernels ; the dataset obtained by convolution; the weights and thresholds in the neural network will be obtained through the training of CPNN, using dataset ; |
| 2: Convolution pre-processing of the CSI into ; |
| 3: Compute by the well-trained CPNN; |
| 4: Update the training set by ; |
| 5: Retrain the CPNN by the new dataset, and get new weight matrix and threshold vector ; |
| 6: Return , , . |
4.4. Complexity Analysis
We compare the computational complexity of each sensor nodes’ authentication methods in this section. The initialization phase was performed offline, and we will not discuss its computational resources and latency issues. In the authentication phase, the DNN-based sensor nodes’ authentication method needs to perform:
As shown in
Table 1, the computational complexity of the mathematical operation of DNN-based method is almost
, where
denotes the number of neurons in the
layer in DNN. In our numerical experiments, we used a five-layer DNN in which the number of neurons in each layer was 1024, 120, 60, 25, 4. Therefore, the computational complexity is almost
. The CNN-based sensor nodes’ authentication method needs to perform:
The computational complexity of the mathematical operation of the CNN-based method is almost , where indicates the number of convolution operations in the layer. and denote the dimensions and the number of convolution kernels in the layer. and represent the number of neurons in the fully-connected and output layers. In our numerical experiments, we used eight convolution kernels with dimensions of and 16 convolution kernels with dimensions of . The dimensions of the input layer and fully-connected layer were and , respectively. Therefore, the computational complexity of the CNN-based method was almost . The CPNN-based sensor nodes’ authentication method needs to perform convolution pre-processing on CSI, and the computation complexity of pre-processing was relatively small. The computational complexity of the CPNN-based method is , which is almost the same as that of the DNN-based method, where denotes the number of convolution operations in pre-processing and denotes the dimensions of the CSI after being processed in the layer. and denote the dimension and number of convolution kernels in pre-processing, respectively. There were 16 convolution kernels of size in the pre-processing of the CPNN-based method. There were four convolution steps. The computational complexity of the CPNN-based method was almost .
During the retraining phase, the number of parameters that needed to be trained is shown in
Table 2. The DNN-based sensor nodes’ authentication method needs to train weight matrix
and threshold vector
, in which it needs to train
parameters. There were almost
parameters for the DNN-based sensor nodes’ authentication method in our numerical experiments. The CNN-based sensor nodes’ authentication method needs to train convolution kernels
and threshold vector
, which needed to train
parameters. In our numerical experiments, only
parameters needed to be trained. The CPNN-based authentication method needed to train weight matrix
and threshold vector
. Like the DNN-based method, the parameters of CPNN-based method depended on the number of neurons in each layer. However, the dimension of the input in the CPNN-based method was much smaller than the DNN-based method. The number of neurons in each layer of CPNN was 256, 50, 25, 12, and 4. There were almost
parameters that needed to be trained in the retraining phase.
5. Numerical Experiments
Simulations have been performed to evaluate the performance of DL-based PHY-layer authentication for industrial wireless sensor networks. We performed the simulations under different nodes and analyzed the impact of the number of sensor nodes on the authentication success rate. We also compared the performance of different algorithms under different numbers of sensor nodes. Cost J denotes the value of the loss function, which is calculated by (6) or (7). The authentication rate is defined as the probability of discriminating the wireless sensor nodes.
We considered the tapped delay line (TDL) model to simulate Raleigh fading channels with multipath delays [
32]. The TDL model uses a set of non-frequency selective fading generators (such as the FWGN model or the Jakes model), where each generator is independent of each other and has an average power of one. The channel state information of different transmitters can be generated by:
where
denotes the number of taps of the filters. We set the normalized Doppler shift
, and six paths with different power delays were selected to synthesize the channels of different wireless sensor nodes. For more realistic consideration, the time delay of the first five paths of the sensor nodes was the same, which was 0 second (s),
s,
s,
s, and
s, respectively. When there were twelve sensor nodes, the time delay of the sixth path of each sensor node was as shown in
Table 3.
When there were four sensor nodes, the sixth paths of each sensor node were s, s, s, s, respectively. Sampling interval s; the signal to noise ratio (SNR) of the simulation channel was 4 dB; the number of subcarriers was ; the number of pilot intervals and of the cyclic prefix length were and , respectively.
We used a five-layer neural network for the DNN-based sensor nodes’ authentication method, where the numbers of neurons in the hidden layer were 120, 60, and 25. The size of the input layer was determined by the CSI dimension, and the size of the output layer was determined by the number of sensor nodes. The convolutional neural network used in the CNN-based algorithm had seven layers, which were an input layer, two convolution layers, two pooling layers, one fully-connected layer, and an output layer. The two convolutional layers respectively used eight convolution kernels of size and 16 convolution kernels of size , respectively. For the CPNN-based algorithm, it had 16 convolution kernels of size for the convolution pre-processing. In the authentication phase and retraining phase, we used a five-layer neural network for the CPNN-based algorithm, where the numbers of neurons in the hidden layer were 50, 25, and 12. Moreover, the adaptive moment estimation (Adam) accelerated gradient algorithm and minibatch skill was used for the accelerating of the neural networks’ training.
As shown in
Figure 5a, the x-axis is the number of neural network iterations and the y-axis is the cost function value. As the number of iterations increased, the cost function value decreased. In addition, the fewer the sensor nodes, the faster the cost function value dropped. We can visually see the authentication rate under different sensor nodes from
Figure 5b. After 30 iterations, the authenticate rates tended to be stable. However, the authentication rate of four sensor nodes was higher than that of six sensor nodes, and the authentication rate of 12 sensor nodes was the lowest. Specifically, after 30 iterations, the authentication rates of 4 sensor nodes, 6 sensor nodes, 8 sensor nodes, and 12 sensor nodes was 95.5%, 80.83%, 77.25%, and 66.5%, respectively.
By discussing the authentication success rate under different numbers of hidden layers, we researched the robustness of the DL-based authentication method. The DNN-based algorithm had the most excellent performance. Therefore, we considered the influence of different hidden layer numbers on the authentication rate under the DNN-based method. As shown in
Figure 6a, the authentication rate of the DNN-based method with different numbers of hidden layers increased as the iterations increased. The greater the number of hidden layers, the faster the convergence of the neural network’s performance. The authentication success rate of the DNN-based method with different hidden layers after the training was stabilized are shown in
Figure 6b. As the number of hidden layers increased, the authentication success rate increased. However, due to the inherent characteristics of the specific wireless channels, the performance of the DNN-based method did not continue to grow and tended to be stable, after the number of hidden layers was increased to a certain number.
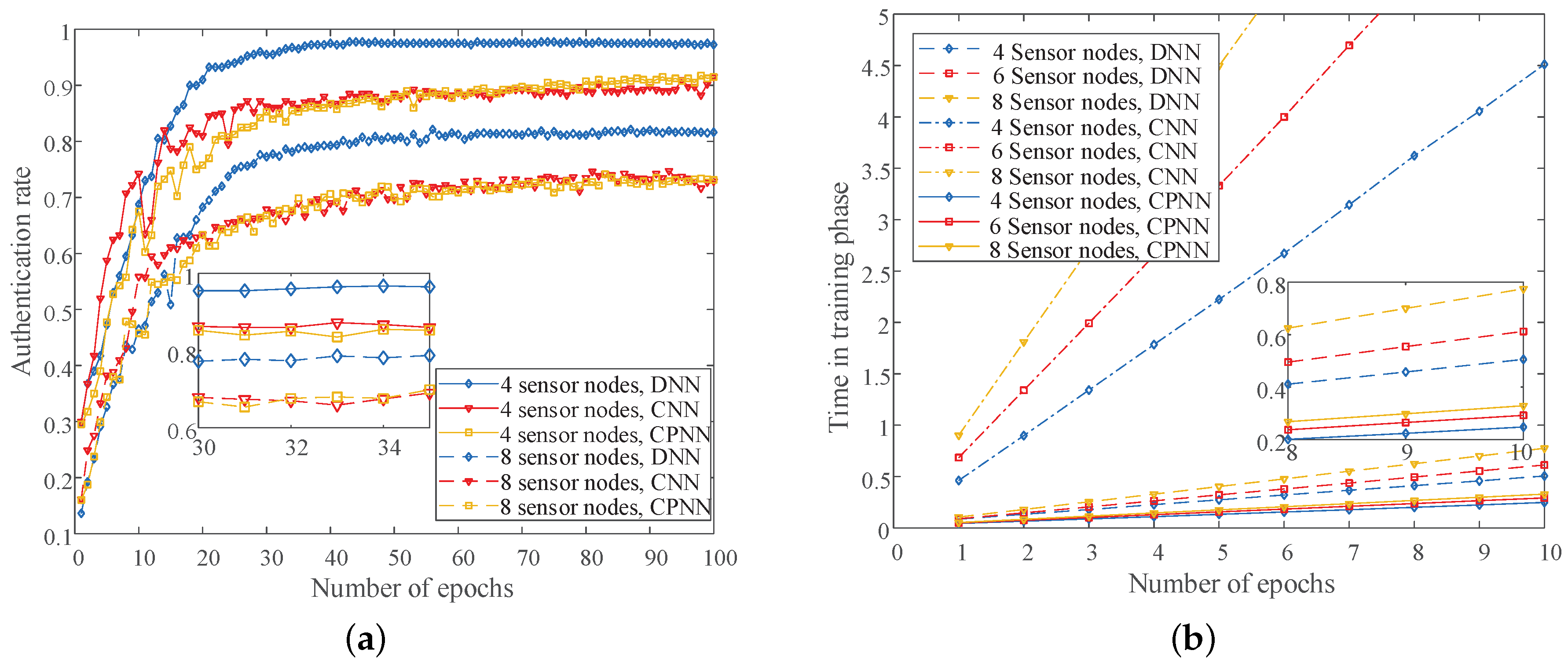
In addition, we performed simulation analysis on the authentication performance of different algorithms under different numbers of sensor nodes. As shown in
Figure 7a, the DNN-based method had the best performance, because it had many parameters. For example, the authentication rates of the DNN-based method were 95.5% and 77.25% under four sensor nodes and eight sensor nodes, respectively. The CNN-based algorithm had the worst performance, because of the convolution and pooling and more or less lost some information of CSIs. For example, the authentication rates of the CNN-based method were 86.25% and 67.87% under four sensor nodes and eight sensor nodes. Another CPNN-based method we proposed in this paper was similar in performance to the CNN-based method. The authentication rates of CPNN-based algorithm were 85.25% and 66.75% under four sensor nodes and eight sensor nodes. However, the CPNN-based method had the shortest training time compared to the DNN-based algorithm and CNN-based algorithm, as shown in
Figure 7b. Therefore, it has a better application prospect in the actual industrial wireless sensor network. We can see that the CNN-based method had the longest training time, followed by the DNN-based method.
In summary, the DNN-based sensor nodes’ authentication had the best authenticate performance and a relatively limited training time. However, its training parameters will grow exponentially as the dimensions of CSI become larger. Therefore, the DNN-based algorithm is suitable for a shorter CSI authentication scheme. The CNN-based sensor nodes’ authentication method effectively reduced the parameters that the neural network needed to train. However, due to the convolution operation and the pooling operation, it did not meet the requirements of saving training time, especially when the dimension of CSI was relatively small. At last, the CPNN-based sensor nodes’ authentication method can effectively solve the problem of training time and authentication performance. It has an unparalleled advantage in practical industrial wireless sensor network applications.
6. Experiments In Practical Environment
Experiments have been performed with universal software radio peripherals (USRPs) to evaluate the authentication performance of the proposed DL-based PHY-layer authentication algorithms in industrial wireless sensor networks. The experimental simulations were performed at the school’s engineering center, which has a large number of industrial facilities, such as computer numerical control (CNC) engraving and milling, CNC lathe, and so on. As shown in
Figure 8, five radio sensor nodes equipped with industrial computer and USRPs were placed in a
factory. The base station was equipped with 8 antennas in Position 2, and the other sensor nodes were equipped with 2, 4, or 8 antennas in Positions 1, 3, 4, and 5. The distances between sensor nodes and the base station varied from 5–25 meters (m). In this experiment, we set the carrier frequency
gigahertz (GHz), the interval of subcarriers
kilohertz (kHz), and the number of subcarriers
. The transmitting power of USRPs was 15 dBm, and the transmission gain was 20 dB. The practical view of the engineering center is shown in
Figure 9.
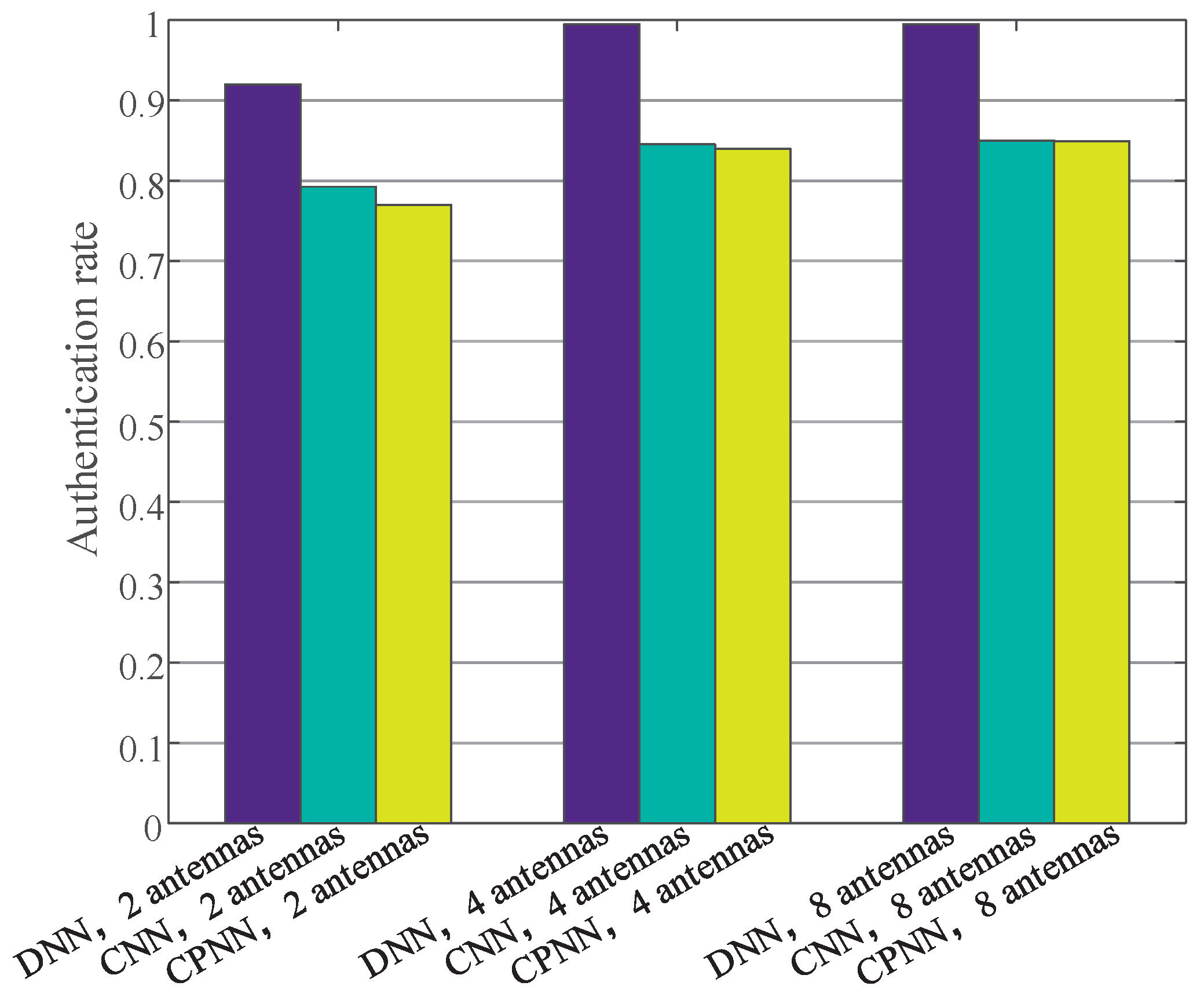
We tested the authentication rates of sensor nodes with different antennas in different locations. As shown in
Figure 10, as the number of antennas increased, the authentication success rate increased correspondingly. For example, the authentication rate of the DNN-based algorithm with 2 antennas was 92%, while the authentication rate of the DNN-based algorithm with 4 antennas and 8 antennas was 99.5% and 99.5%, respectively. From the histograms of different colors, we can see that the DNN-based sensor nodes’ authentication method had the best performance. For example, the authentication rate of DNN-based algorithm with 8 antennas was 99.5%, while the authentication rate of the CNN-based algorithm with 8 antennas was 85%. In addition, the CPNN-based algorithm had the same performance as the CNN-based algorithm. However, the retraining time of the CPNN-based method was much shorter than that of the CNN-based algorithm.