1. Introduction
Owing to its better environmental stability, an interferometric displacement measurement technique based on diffraction grating is an alternative to a laser interferometer for identifying the position of a wafer stage in a photolithography scanner [
1,
2,
3]. For ultraprecision positioning of the wafer stage in a nonvacuum environment, the sensor and the displacements calculation algorithm are critical to the performance of the measurement system [
4]. The algorithm is used to calculate the precise 6-DOF displacement of the wafer stage in real time using phase shifts and eliminate a rotation–translation coupling (similar to tilt-to-length coupling in a laser interferometer) and geometric errors, such as the Abbe and cosine errors [
5,
6,
7].
For a multiple-DOF measurement system, the displacements calculation algorithm can be regarded as a method to solve unknown displacements by using known sensor readings. One simple approach is establishing a linear readings–displacements model using various approximations and deriving its closed-form solutions. Although this method has high resolution and excellent real-time performance, its calculation precision degrades with an increase in the rotation range because its nonlinearities such as rotation–translation coupling and geometric errors are neglected [
8,
9,
10]. To achieve ultraprecise displacements calculation, establishing a precise readings–displacements model is a prerequisite. It is a common practice to use affine transformation to establish an exact functional relationship among displacements of the sensor and the measured object, and to consider the sensor reading as a linear function of the displacements of the sensor [
11,
12]. For a grating interferometer system, this modeling method ignores the nonlinear relationship between the phase shift and the displacements of the encoder (DOE) caused by rotation–translation coupling. Moreover, the model established by this method has no closed-form solution and can only be solved precisely by an iterative numerical algorithm, which has a large computational effort and cannot meet the requirements of real-time measurement [
13]. In a similar study on the laser interferometer system, Gao et al. analyzed the changes of the external optical path of the laser interferometer caused by rotation using the above modeling method, and they established a precise model containing tilt-to-length coupling. The closed-form solution is derived after nonlinear model reduction using information from symmetrically arranged additional interferometers [
4]. However, because absolute symmetry does not exist in actual measurement due to manufacturing and assembly errors, the method is still not precise enough. Ultraprecision requires a complex computational model, while real-time performance requires a simple model; therefore, it is challenging to achieve both goals simultaneously.
In this paper, we present an algorithm that can calculate the 6-DOF DOWS in a photolithography scanner in real time with ultraprecision. According to the two factors that cause the phase shift of the grating interferometer based on the Doppler effect—the diffraction spot displacements and the change in the internal and external effective optical paths—the exact relationship between the phase shift of each grating interferometer and the 6-DOF DOWS is established with affine transformation. To solve the DOWS in this complex model in real time, a polynomial approximation (PA) algorithm is presented in which model reduction is achieved by the frequency domain characteristics of the nonlinearities.
2. Readings-displacements Modeling Method
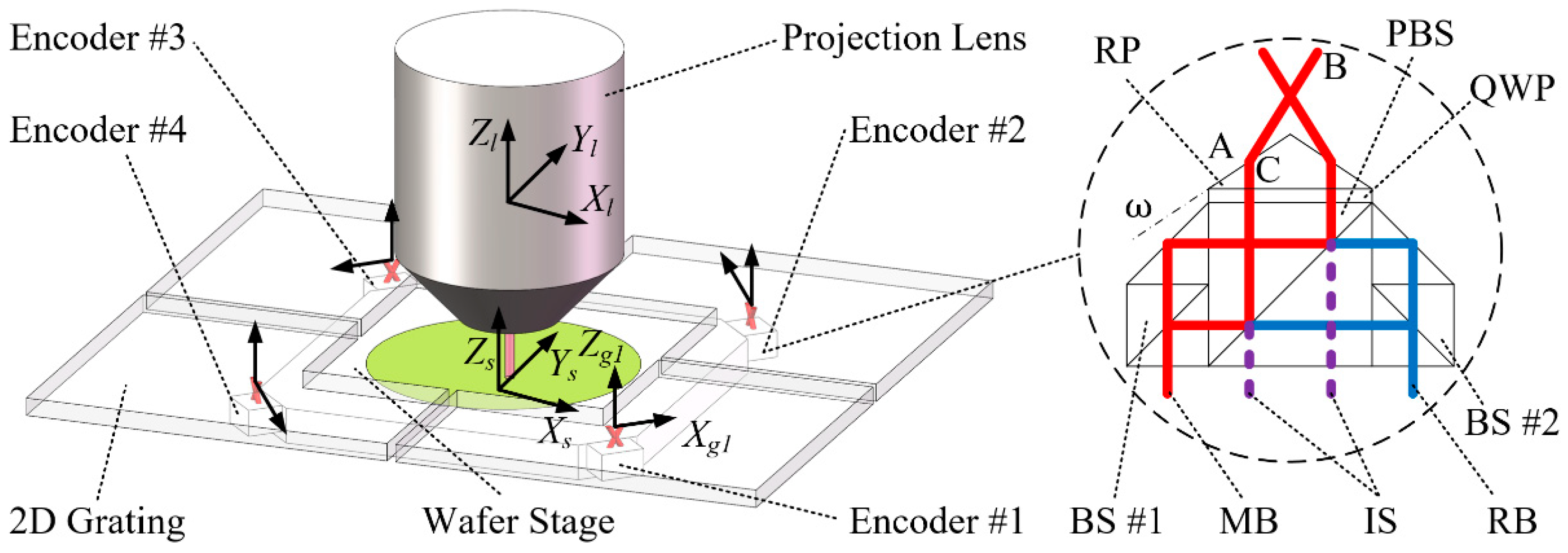
As shown in
Figure 1, most advanced photolithography scanners adopt a planar motor drive system and a grating interferometer displacements measurement system [
14]. The measurement system comprises four grating interferometers and is used to measure the 6-DOF DOWS relative to the projection lens. During the exposure process of the photolithography scanner, the wafer stage moves to some areas where only three encoders are active because another moves out of the area covered by the grating. Therefore, displacements calculation algorithms using both 4-active and 3-active encoder readings are necessary.
To establish the precise phase shift-DOWS model, the grating interferometer system of the wafer stage shown in
Figure 1 is reduced to some coordinate systems (CSs) and points, as shown in
Figure 2. The 6-DOF DOWS CS
relative to the projection lens CS
is the measured DOWS
. Points A, B, and C represent the key points in which the measuring beams change directions and are used to demonstrate the modeling method. When the relationship between the position of all key points and the DOWS is determined, the change
of the total length of all measuring beams and diffraction spot displacements
in the
direction can be calculated. Then, the phase shift
of interference signal can be given by
where
is the diffraction order,
is the grating pitch in the
direction,
is the refractive index in the air, and
is the wavelength of the laser.
The relationship between the DOE and , is more intuitive, and therefore, DOWS is first converted to the DOE in the CS . Rotational displacements can be transformed by the transformation matrix between the CS and CS , and the translational displacements are transformed by Equation (2). When the DOE is computed, the transformation from CS to CS can be represented by matrix . In the CS , the homogeneous matrix of point A that does not change with the DOE is a constant matrix . The computation of the homogeneous matrix of point B requires the use of geometric constraints for beam AB: the direction vector of beam AB can be calculated by the azimuth and the Littrow angle ; the Z coordinate of point B in the CS is 0. According to these constraints, Equation (3) is set to solve .
where
is a homogeneous matrix representing the translational DOE
of the grating interferometer #i;
represents the position
of encoder #i in the CS
;
is a transformation matrix representing the position and orientation of #i grating in the CS
;
is a rotation matrix corresponding to the
based on Euler angles (z-y-x extrinsic);
represents the transformation matrix formed by the DOWS
; and
is the number of active encoders.
where
is the length of the beam AB,
is the Z coordinate of point B in the CS
, and
is the Littrow angle.
According to the above method, we establish the relationship between the position of all key points and the DOE. Then,
and
can be obtained, and the phase shift
is derived. Because
contains several trigonometric and inverse trigonometric functions, it cannot be expressed by an explicit function, and its computational efficiency is very low. Considering that the three rotational displacements are very small,
can be simplified to a polynomial with the Taylor series expansion at the point
, as shown in
where
and
are the polynomials of
.
The order of Taylor’s expansion determines the precision of the polynomial’s reproduction of the original model, and the fourth-order Taylor expansion (cubic polynomial) can achieve an approximation precision on the order of picometers. In the practical application of the grating interferometer, the polynomial based on the design parameters cannot represent the precise nonlinearities owing to manufacturing and assembly errors. The polynomial calibrated by external sensors is more practical for the ultraprecision positioning of the wafer stage.
Equation (4) represents the phase shift-DOE model; however, the phase shift-DOWS model is required to calculate the DOWS. The DOE in Equation (4) is replaced by the DOWS by coordinate transformation, and the coefficients of polynomials are redetermined by the regression method. The phase shift-DOWS model of two interference signals
and
of the 2-DOF grating interferometer system in both 4-active and 3-active encoder modes can be derived as
where
is the redetermined coefficient of the polynomials.
3. Polynomial Approximation Algorithm with Substitution Variables
When the grating interferometer system reads out the phase shift, the DOWS can be calculated by solving Equation (5). However, due to the very complex nonlinearity, Equation (5) has only a numerical solution rather than a closed-form solution. To calculate the ultraprecision DOWS in real time, cubic polynomials of 6 or 8 normalized phase shift are employed to approximate the calculation process of two measurement modes. Owing to the complex nonlinear coupling in the phase shift, a cubic polynomial of about 120 terms is required to ensure that the calculation errors of translational displacements are less than 10 pm in a non-ideally manufactured and assembled measurement system. Such a large polynomial requires considerable computational effort to be used for real-time measurement of 10 kHz or higher bandwidths.
To further improve the real-time performance of the approximate model, a more efficient method for nonlinear model reduction is needed. The 6-DOF DOWS are set to sinusoidal motions at different frequencies, and the amplitude is set as the motion range of each DOF, as shown in
Figure 3a. As shown in
Figure 3b, six substitution variables
, which are only dependent with each displacement by linear fitting the normalized phase shift, are established by Equation (6). When each displacement is calculated using only the corresponding quasi-linear substitution variable, the frequency domain characteristics of the displacement calculation error are shown in
Figure 3c. The peak in the Fourier amplitude spectrum shows the magnitude and frequency of the error, which can be eliminated by adding a basis function corresponding to the error frequency to the PA model. By adding basis functions in the order of error amplitude from large to small until the precision requirement of the displacement calculation is satisfied, the PA model with the highest computational efficiency is established. As shown in Equation (7), the displacements calculation algorithm obtained by this method only requires 40 terms to ensure that the calculation errors of translational and rotational displacements are less than 10 pm and 1 nrad, respectively.
where
is the linear approximation coefficient matrix of the normalized phase shift to the DOWS and
is the coefficient matrix of the PA algorithm consisting of 40 basis functions of six substitution variables.