1. Introduction
Image registration is a core technology of image processing, particularly widely applied in the remote sensing community, such as change detection [
1,
2], image fusion, long-time remote sensing data analysis, surface displacement of landslides [
3,
4], photogrammetry [
5], etc. According to the comprehensive overview of image matching approaches [
6], image registration methods can be grouped into two categories: feature based registration methods and area based registration methods. For the feature based image registration methods, according to the utilized features, single pixel feature and multipixel feature, they can loosely be grouped into two categories. For the first category, its feature is the single pixel feature, such as ground control point (GCP). Its main procedures include feature detection, feature matching, transform model estimation and image warping [
7,
8,
9,
10]. Among these procedures, feature detection and feature matching are two core steps, and they are also two steps to which researchers devote much effort [
11]. After decades of development, feature detection approaches have developed from the initial handcrafted methods (Difference of Gaussian (DoG) [
12], Harris [
13], Hessian [
14] and Wavelet Features.) to the latest deep learning based approaches (TILDE [
15], CovDet [
16] and SuperPoint [
17]). For feature matching, the feature descriptors are vital for correct correspondence. Feature descriptors are also developed from hand-engineered descriptors (HoG [
18], DAISY [
19], etc.) to deep learning based descriptors (DDesc [
20], L2-Net [
21] and HardNet [
22]). Although the deep learning based feature detectors and descriptors are promising, the lack of available public remote sensing image matching data makes it hard to go beyond the hand-engineered approaches for the time being. Thus, the handcrafted features and descriptors are also the mainstream methods. However, these methods are originated from the field of computer vision and they have encountered many challenging problems when applied in the community of remote sensing images. Specially, the nonlinear radiation distortions of remote sensing images result in a dramatic drop in performance, even failure.
For the second category, its feature is multipixel features, such as lines and polygons. Here, we mainly introduce the multipixel feature captured by the Wavelet and Shearlet transform. Its main procedures include the selection of feature space, extraction of features, the selection of similarity metric and search strategy [
23,
24,
25,
26]. For the features identified by wavelet transform, they are isotropic textural features. For the features identified by Shearlet transform, they are anisotropic features, such as edges, roads, rivers and other edge-like features. The combination of features captured by the wavelet transform and Shearlet transform is more robust to the initial choice of global transform [
26]. In addition, the multiresolution nature of wavelet decomposition can accelerate the calculation of geometric transform model. In fact, these multipixel features are matched with an optimization scheme. Due to the non-convex characteristic of objective function, there exist some limitations of feature space in the practical application. For example, it is very difficult to conduct in the search space that consists of polynomial transformations to address more complex and spatially varying distortions within images. In addition, the final registration result is also sensitive to the similarity measurement and optimization method.
In recent years, image registration based on phase correlation has drawn extensive attention due to its three merits: high registration accuracy and robustness to noise and variation of gray value, constant processing time for the fixed size image, and ease of implementation and parallelization. The existing methods based on phase correlation can loosely be grouped into two categories. One category is determining the translation by precisely locating the main peak of Inverse Fourier Transform of the normalized cross-power. The other category is directly estimating the linear phase difference in the frequency domain. For the first category, the commonly used solutions are interpolation methods, such as 1D parabolic function, sinc function, modified sinc function and Gaussian function [
27,
28,
29]. However, the shortcomings of the method are sensitivity to noise and other errors. For the other category, the principle behind it is that the phase difference in the frequency domain is linear with respect to displacement in the spatial domain. The linear phase difference can be achieved by different approaches, such as least square fitting [
30], the combination of singular value decomposition and random sample consensus algorithm [
31], and low-rank factorization by modeling the noise with Gaussian mixtures model [
32]. The sub-pixel accuracy of phase correlation-based image registration is mainly affected by the noise, aliasing and border of the image. As suggested in [
30], abandoning Inverse Fourier Transform can alleviate the side effect caused by this noise and aliasing. Thus, most researchers have focused on precisely estimating the linear phase difference in the frequency domain rather than identifying the location of main peak by the introduction of Inverse Fourier Transform.
As for the effect of image border, it is caused by the implicit assumption of periodicity in the computation of Discrete Fourier Transform of an image. In almost all circumstances, it is not reasonable to assume that the opposite border of image is similar, so the assumed periodic image will lead to strong discontinuities across the image border. For the effect produced by the border of image, the commonly used approach is weighting the reference and sensed images with a window function in the spatial domain separately. However, the operation of weighting window function can cause additional negative effects, namely reducing the common and useful information for registration based on phase correlation, especially in the case of small patch-based matching or small overlap existence between image pairs.
To deal with the effect of image border, we applied a novel approach, image periodic decomposition method (decomposition method for short) to decompose the original image into two components, namely periodic image component and smooth image component. Then, we replaced the original image by the periodic image component, which can eliminate the effect of image border effectively and there is almost no loss of image information at the same time. Thus, the decomposition method can improve the estimation accuracy and success rate of image registration based on phase correlation, especially in the case of small image patches’ registration.
In this paper, our main contributions are two-fold: (1) a novel approach, image decomposition was utilized to eliminate the effect of image border, which degrades the accuracy and success rate of phase correlation-based image registration. Compared to the traditional weighted filtering approaches, the image decomposition method can not only eliminate the effect of image border, but also it rarely reduces information away from the image border. Thus, the decomposition method can improve the registration accuracy and success rate in some certain cases. Furthermore, it is easy to use and there are no parameters to tune. (2) We introduced a new concept of SSNR (Similar-to-Signal-Noise Ratio) to obtain a new view of the role of weighting window function; it can be more helpful to guide researchers to select a proper approach for eliminating the effect of image border to improve the registration accuracy and success rate in the practical applications.
This paper extends a preliminary version of [
33] by adding: (1) a detailed description of various methods of eliminating the effect of image border and the phenomenon of the effect of image border; (2) two groups of experiments about displacement estimation success rate and accuracy to further illustrate the advantages of the proposed method, and a further analysis of elimination of the effect of image border methods; (3) a thorough discussion of elimination of the effect of image border, and a new understanding of the role of window function.
The remainder of this paper is organized as follows.
Section 2 introduces the related work of elimination of the effect of image border.
Section 3 details the principle of image registration based on phase correlation and our proposed method of decomposition method. In
Section 4, three groups of experiments were carried out to illustrate the advantages of the decomposition method, compared to three other window functions, and further analysis was made to give more insights on eliminating the effect of image border. The discussion is given in
Section 5. The conclusions are drawn in
Section 6.
2. Related Work
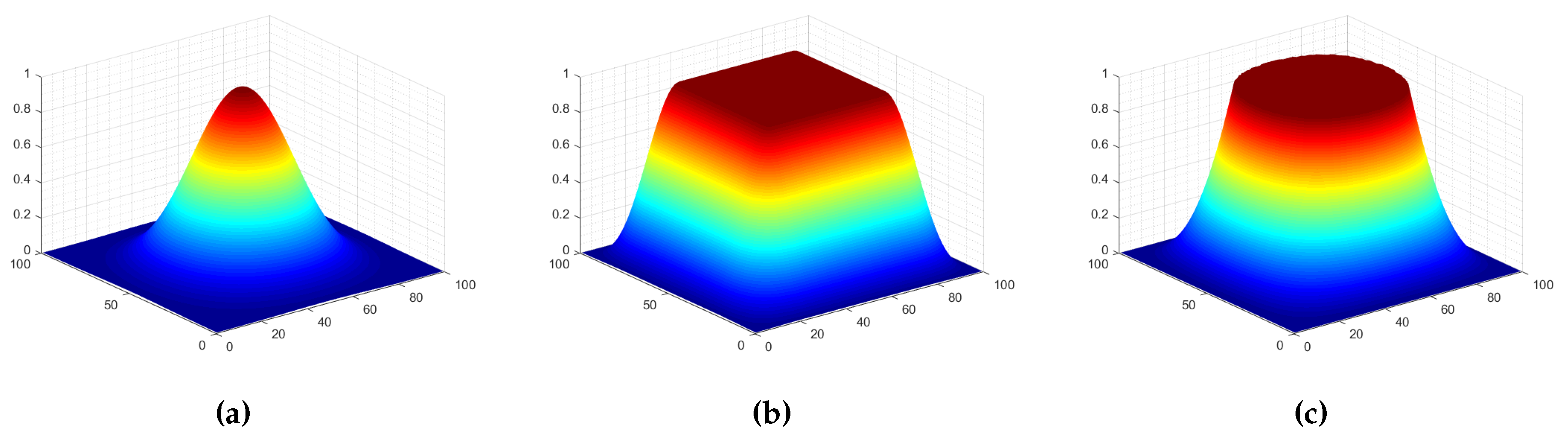
For the implicit periodicity property of Discrete Fourier Transform (DFT) and the nature of the image for which the opposite borders are not alike, the effect of image border always occurs in the process of image registration based on phase correlation. In the past research, various approaches are proposed to deal with the problem. Among them, three approaches are popular, namely Blackman window, raised-cosine window [
3] and flap-top window [
34].
For the Blackman window of length
N, its formula in one dimension is defined as follows:
It is a commonly used window function when using spectral analysis in the signal processing field. Its three-dimensional diagram is shown in
Figure 1a. Apparently, for an image patch weighted by the Blackman window, the discontinuities across the image border are smoothed out, but a significant amount of signal is also degraded.
Another window function, named raised-cosine [
3], was proposed to achieve a good balance between reducing effect of image border and the information retention of image. The one-dimensional expression of the raised-cosine window of length
N is given as follows:
where
,
M,
N are the sizes of the images,
k is the stretch factor. A three-dimensional diagram of it is shown in
Figure 1b.
The role of the aforementioned weighting window function is similar to the general filter in the spatial domain. The essences of these window functions are progressively making the border of the image fuzzy and preserving the content away from the border of image. In fact, in order to avoid adding new discontinuous information to the images, some content near the border will be subjected to varying degrees of fuzziness. The difference between the three window functions is how much the information near the image border is processed. It was further illustrated by the result of an image filtered by different window functions, as shown in
Figure 2. Here, the parameters of flat-top and raised-cosine window function are the same as ones in the
Figure 1.
Figure 2a is the original image,
Figure 2b–d are the resulting images after filtering by Blackman, flat-top and raised-cosine window function, respectively.
Figure 2e–h are the amplitude spectrum of
Figure 2a–d, respectively. From the bottom row in
Figure 2, the cross structure is distinct in the amplitude spectrum of original image, and disappeared in other three amplitude spectrums. This shows that the weighting window function can eliminate the effect of image border. However, for the Blackman window, it blurs out a large amount of the content of images and retains a fraction of content centered at the image unchanged. Blurring out a large amount of content means that some valuable information is degraded for registration based on phase correlation. This will reduce the accuracy of registration due to little common information left. For raised-cosine and flap-top, they blur the borders while keeping the content in the middle of the image unchanged as much as possible. However, some contents near the border are also degraded inevitably. Especially when the overlap of the image pairs is small, there is a dilemma that the common areas of image pairs are fuzzy and the common information is reduced to only a little. Consequently, this will lead to the failure of registration based on phase correlation due to the lack of a large amount of the common information.
Here, we aimed to solve the problem of effect of image border. A corresponding strategy is decomposition of an image. The concrete decomposition approach is decomposing the image into two images: one is periodic image and the other is smooth image. We finally discarded the smooth image and calculated the Discrete Fourier Transform only for the periodic image. This method only eliminates the effect of image border and rarely degrades the content near the image border.
4. Experiment and Analysis
To thoroughly analyze the role of different window functions and the proposed method (referenced as decomposition method), three subsets of experiments were carried out. The first one is about the comparison of success rate of image registration for different methods in the case of small patches’ registration. The second one and third one is about the comparison of registration accuracy for different methods in the case of displacement estimation as well as angle and scale estimation, respectively. In all of the following experiments, the parameter settings are the same. The roll-off factor, , of the raised-cosine window is set to 0.25. The stretch parameter, k, of the flat-top window is set to 2.7.
4.1. The Comparison of Image Registration Success Rate for Different Methods
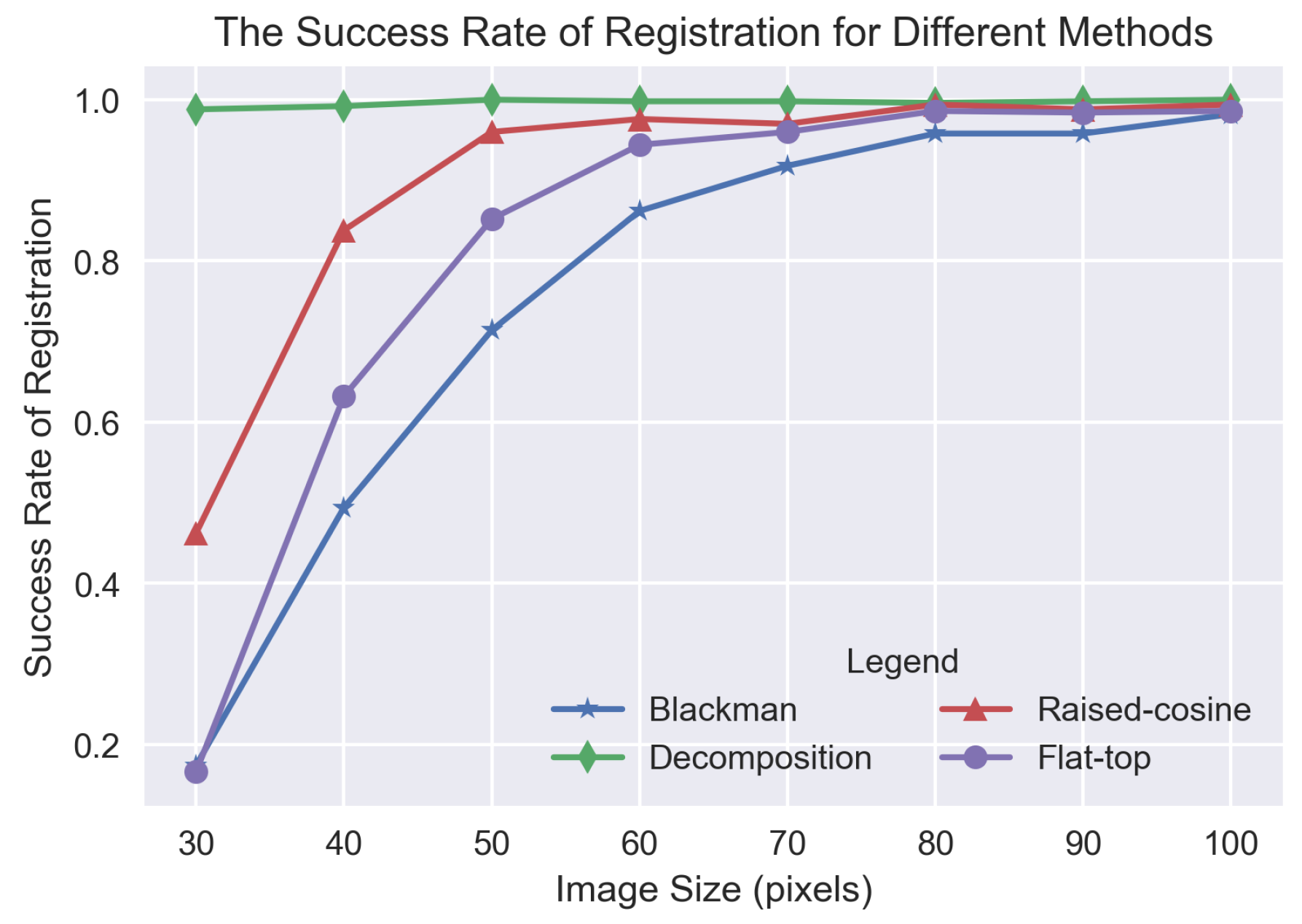
Various sizes of remote sensing images were applied to evaluate the success rate of image registration for different methods of eliminating the effect of image border. There are eight groups of remote sensing images, whose sizes vary from
to
pixels in a step of 10. For each group, 500 images are included. The content they covered are diverse, including man-made buildings, mountain, residential area and so on. For each image, a corresponding translated version is generated by randomly translating a displacement, ranging from
to
the size of the image. For each generated image pair, we utilized Blackman, raised-window, flat-top and the decomposition method to eliminate the effect of image border, respectively; then, the displacement is acquired by the phase correlation based method. Considering the characteristic of high estimation accuracy of the phase correlation based algorithm, the criteria of registration success is that the absolute error between the true displacement and the estimated displacement in both
x- and
y-directions is less than one pixel. The experiment results are shown in
Figure 5.
Apparently, regardless of the image size, the success rate of the decomposition method is highest and almost close to 1. For the other three methods, Blackman, raised-cosine and flat-top, the success rate is relatively low, especially when the image size is less than pixels. Among the three window functions, the registration success rate curve of Blackman is below those of the other two window functions, and the curve of raised-cosine is above those of the other two window functions. The difference between the success rate of different methods is mainly due to the fact that the information near the image border is subjected to varying degrees of degradation. For the decomposition method, very little information is degraded, which results in its high success rate in the case of large displacement of small image registration. For Blackman window function, it degrades a large amount of information near the image border, which reduces its success rate heavily. Especially when large displacement exists between small size images, the blurring of a large amount of information near the image border leads to little common information left between images. As the image size grows gradually, the phenomenon will be reduced, and the success rate will increase a lot.
4.2. The Comparison of Displacement Estimate Accuracy for Different Methods
To compare the performance of different methods in the case of displacement estimation, two hundred remote sensing images with the size of
pixels were applied. They cover a wide variety of content, including farmland, road, river, buildings and so on. To generate an image pair, each image was translated randomly by a displacement ranging from 1 pixel to
size of image. Blackman, raised-cosine, flat-top and decomposition method were utilized to eliminate the effect of image border, respectively. The translation was estimated by using the phase correlation based method. The mean absolute error
and
in the
x- and
y-directions, and RMSE in the
x- and
y-directions are reported in
Table 1.
From
Table 1, in terms of the mean absolute error of displacement in the
x- and
y-directions, the proposed method, the decomposition method obtained minimal error, and the other three methods, Blackman, raised-cosine and flat-top method, are also hard to rank. In terms of RMSE of absolute error, the proposed method obtained the minimal RMSE in the
y-direction and the second lowest RMSE in the
x-direction. In summary, we can roughly conclude that the decomposition method has better performance than the other three methods in the case of only displacement estimation. The reason why the three window functions are difficult to rank is that the amount of degraded information affecting the estimation accuracy is also related to the displacement between image pairs. Some detailed discussion is given in
Section 4.4.
4.3. The Comparison of Scale and Angle Estimation Accuracy for Different Methods
To compare the performance of different methods for eliminating the effect of image border in the case of scale and rotation transformation, a small subset of aerial images, from the USC-SIPI image database, are used in the test. There are thirty-seven images, whose sizes vary from
to
, and contents include man-made buildings, ports, mountain and so on. We shifted, rotated and scaled each image randomly to acquire their corresponding transformed images. The range of displacement is from zero to one-quarter of the image size, and the scale factor varied from 0.1 to 0.9, and rotation angle is from 30
to 90
. Here, three window function Blackman window, flat-top window and raised-cosine window weighting function and decomposition method were applied to eliminate the effect of image border. To quantitatively evaluate the performance of our proposed algorithm, two kinds of measurements are used. One is the success rate of registration in our test images subjected to certain transformation. The criteria of registration success is that the absolute error of scalar estimation is less than 0.01 and the absolute error of angle estimation is less than
. The other is the registration accuracy measurements, including the mean error and the root mean squared error (RMSE) of scalar and angle estimation in the case of registration success. To compare fairly, angle and scale factors are estimated by the same approach: multi-layer fractional Fourier Transform [
37]. The results of each method are summarized in
Table 2.
From
Table 2, we can see that, for the value of the indicators of the proposed algorithm, the decomposition method is best, which showed the superiority of eliminating the effect of image border. As for other algorithms, it is hard to tell the superiority of them directly according to these measurements. The raised-cosine window acquired higher success rate than Blackman, but its mean error of scalar and angle is higher than the one of Blackman. Theoretically, a raised-cosine window should have better performance on eliminating the effect of image border while preserving more information, but its performance depends on the roll-off factor
parameter tuning. In addition, it is very challenging to find an optimal
for all the images in a subset; in particular, there are scale differences and angle rotation. The same problem also exists in the flat-top algorithm. Thus, our proposed algorithm is easiest to use and has the highest performance.
4.4. Further Analysis of Eliminating the Effect of Image Border Methods
To learn more deeply and thoroughly about the role of different window functions for eliminating the effect of image border, an experiment about images with different sizes of
,
,
and
pixels were applied to evaluate the displacement estimation accuracy for different methods of eliminating the effect of image border. The number of images for each image set with the same size is 200. For each image, randomly translating it ranging from 1 to
size of image to generate a image pair. Then, for each image pair, Blackman, flat-top, raised-cosine and the decomposition method were applied to eliminate the effect of image border, respectively. The displacement estimation accuracy is measured by the mean absolute error
and
in the
x- and
y-directions. The experiment results were reported in
Table 3. For the images with
pixels, its result is directly referred from
Section 4.2.
For images with smaller size of , and pixels, we can see that the decomposition method acquired the minimum error of and , especially for the image size of pixels. While for images with larger size, or pixels, the estimated error of the decomposition method is larger than the one of window functions. This shows that the decomposition method no longer has an advantage than weighted function methods in the case of image with larger size.
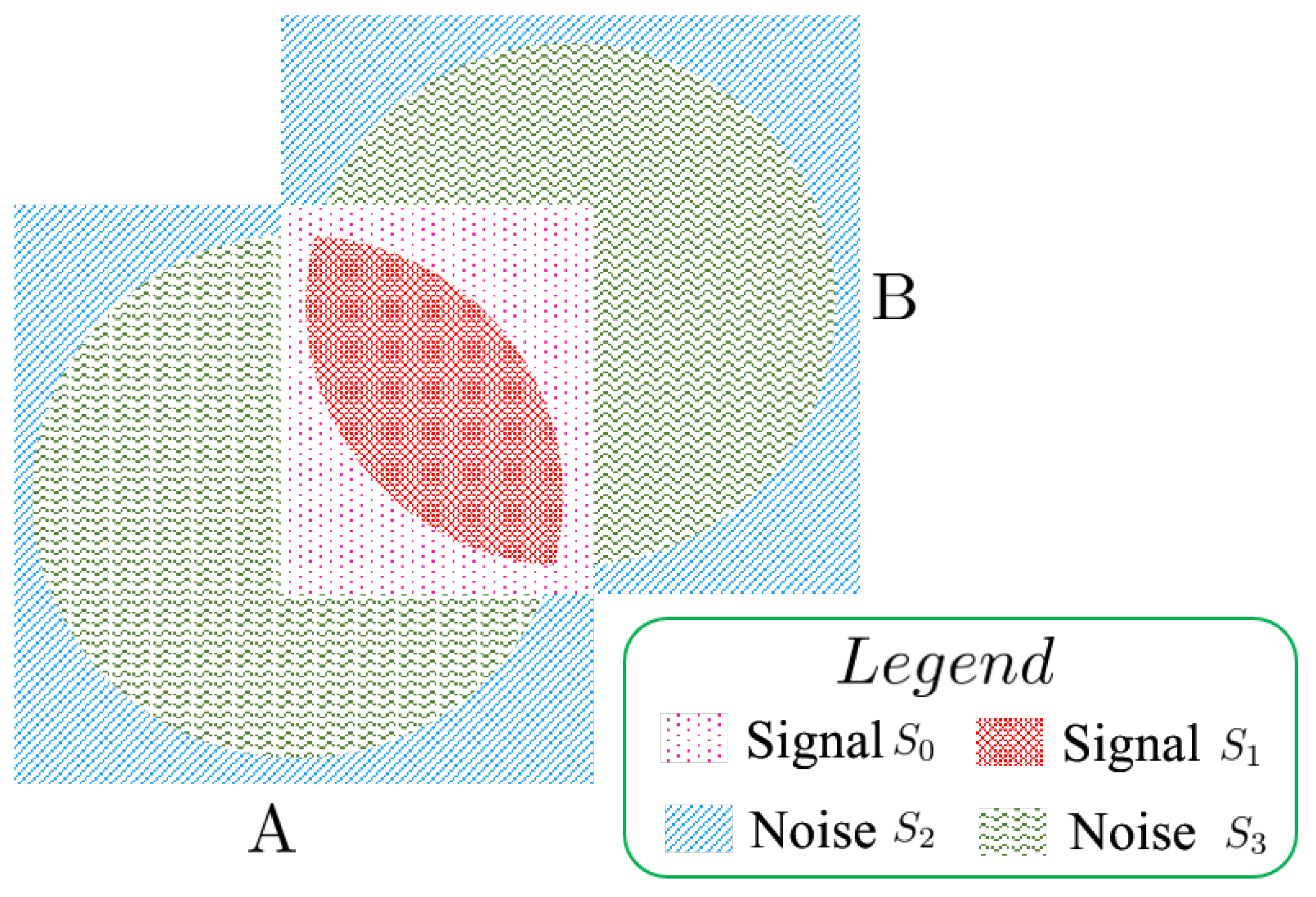
To explain the problem more clearly, we introduced a new concept of SSNR (Similar-to-Signal-Noise Ratio) for a pair of images, similar to signal-to-noise (SNR) in the field of signal processing. To explain the ANSR more clearly, a corresponding schematic diagram is shown in
Figure 6. Here, we assume that there are two images A and B, and a displacement relationship between them. A and B represent two images, respectively. Their corresponding weighted filtered window denoted by a circle is centered at the center of each image. It is worth noting that, for each image, their content not in the scope of the circle will suffer from varying degrees of degradation due to the filtering of weighted window function. To simplify, we assume that the content in the common area of the two images is exactly the same, namely that there are no content changes in the overlapping region.
We divide the information into four categories and render each category by a different pattern. They are shown in
Figure 6. For signal
, it denotes the information in the overlap and suffered from the degradation due to the filtering of weighted window function. For signal
, it denotes the information that is in the overlap and is free from the degradation due to the filtering of weighted window function. The difference between signal
and
is that one is degraded by the weighted window function and one is not. For noise
, it denotes the information that is not in the overlap and suffered from the degradation due to the filtering of weighted window function. For noise
, it denotes the information that is not in the overlap and is free from the degradation due to the filtering of weighted window function. The difference between signal
and
is that one is degraded by the weighted window function and one is not. The SSNR is expressed as
. All of the weighted window function, image size and the displacements between images affect the
,
,
and
.
Thus, the increase of SSNR is beneficial to the phase correlation-based image registration. When the SSNR becomes lower, it will reduce the estimation accuracy or even lead to the estimation failure of the phase correlation-based method. For large images with small displacements, after the operation of blurring by window function, the content retained in the central of images also has larger overlap. Thus, in this case, blurring these images may increase the SSNR because, although it degrades some information that has a corresponding piece in its transformed image, it also reduces the amount of the non-corresponding content of the image. Thus, the window function can not only eliminate the effect of image border, but also increase the SSNR, especially for the large images with small displacements. This is different from the existing understanding in the past research that the window function is only a tool of eliminating the effect of image border and produces side effects of reducing the amount of common information at the same time. The new understanding is helpful for researchers to select the best approaches of eliminating the effect of image border in different cases.
For the flat-top and raised-cosine method, their acquired estimation error for images with sizes of are significantly larger than the ones of Blackman and decomposition. This is due to the constant parameter setting of these two methods for images with varied sizes. This illustrates that the related parameter setting of the flat-top and raised-cosine method is sensitive to image size. For the different parameter settings of flat-top and raised-cosine, they control the amount of information that is blurred, which affected the SSNR of image pairs finally. Thus, in the practical application, the performance is sensitive to the fine-tuning of parameters of flat-top and raised-cosine, which reduced the ease of application of these two methods.
Through the above analysis, we get a new understanding that the degradation of content near the image border affects the SSNR of a pair of images. All of these factors, the translation, the image size and the amount of information degraded by the window function, affect the ANSR of a pair of images. For small size image with larger displacement, as
Section 4.1, the more the amount of information degraded, and the lower the SSNR of a pair of images, so the decomposition can obtain the highest success rate of registration. For image pairs with scale and rotation deformation, as
Section 4.3, a relationship that has been established is that degrading the information by the window function can lower the ANSR. However, regarding how the amount of degraded information affects the ANSR, it is hard to determine directly and is related to the amount of scale and rotation. Thus, the performance of three window functions is hard to rank. For large images with small displacements, the larger the amount of information blurred by window function, the higher the ANSR. Thus, the Blackman window function gets the best performance and the decomposition method has the worst performance. As for other cases, it is hard to directly determine the relationship between the amount of blurred information and the value of SSNR.
5. Discussion
To illustrate the advantages of the proposed method, the decomposition method for image registration based on phase correlation, three groups of experiments were carried out and the other three methods, raised-cosine window, Blackman window and flat-top window, were introduced for comparison. For the first group experiment, we evaluated the displacement estimation success rate of different methods for different sizes of images. The decomposition method always achieved the stable and high success rate than other methods for different sizes of image, especially for images with sizes less than pixels. For the second experiment, we compared the different mean absolute errors in the x- and y-directions , and RMSE in the x- and y-directions, and . The experiment results show that the decomposition method can always achieve the minimum error except for the measurement of , which is the second minimum, compared to other methods. The third experiment is about the estimation of scale and angle. The experimental results show that the decomposition method can acquire a higher success rate, a smaller absolute error and RMSE for the estimation of scale and angle. In addition, although all the test images in the experiment are square, the decomposition method is independent of the image aspect ratio because the decomposition method is carried out by the rigorous mathematical formula and all the involved mathematical operations are also independent of image aspect ratio.
Additionally, another group experiment of displacement estimation of images with five different sizes were carried out to give more insights on eliminating the effect of image border. An interesting experiment result was reported in which the decomposition method has a larger estimation error than weighted window filter methods in the case of images with a size of . Through the in-depth analysis, a new concept of SSNR, the ratio of the corresponding image content information to the non-corresponding image content information was introduced to interpret the results and a novel understanding of the role of weighted window filter function was gained. The window function can not only eliminate the effect of image border, but also affect the SSNR of image pair at the same time. The increment of SSNR is beneficial to image registration based on phase correlation. However, the value of SSNR is related to the image size, displacement and the amount and distribution of image content changes. Thus, in the practical application, it is difficult to select a general window function with fixed parameters to acquire the best performance in the different cases, while the decomposition method is easy to use and no parameters are required for tuning.
As for the efficiency of the proposed method, the image periodic decomposition method, its time complexity is mainly dependent on the calculation of smooth image component. Because the original image is equal to the sum of the periodic image and smooth image component, we can acquire the smooth component firstly and then acquire the periodic component by subtracting a smooth component from the original image—while, for solving a smooth component, its time complexity is
, which is the same as the time complexity of the phase correlation based image registration method. Here,
M and
N denote the width and height of image, respectively. Thus, the complexity of the proposed method is also
[
35].