Improving Discrimination in Color Vision Deficiency by Image Re-Coloring
Abstract
1. Introduction
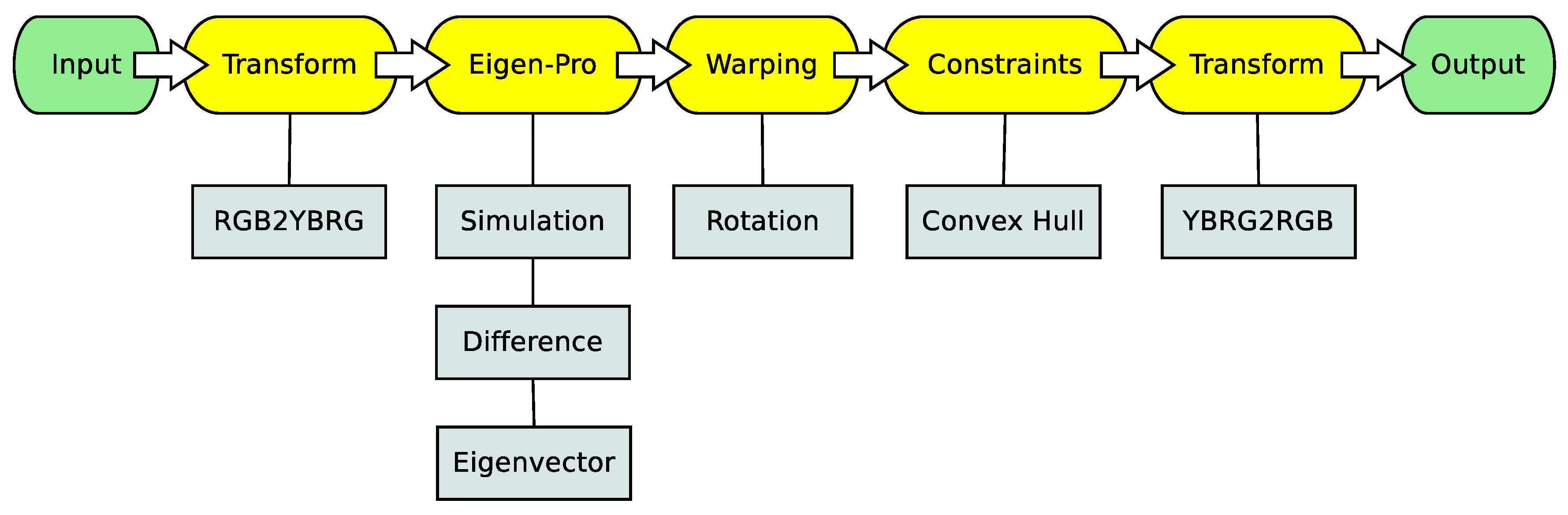
2. Approach
2.1. Color Transform
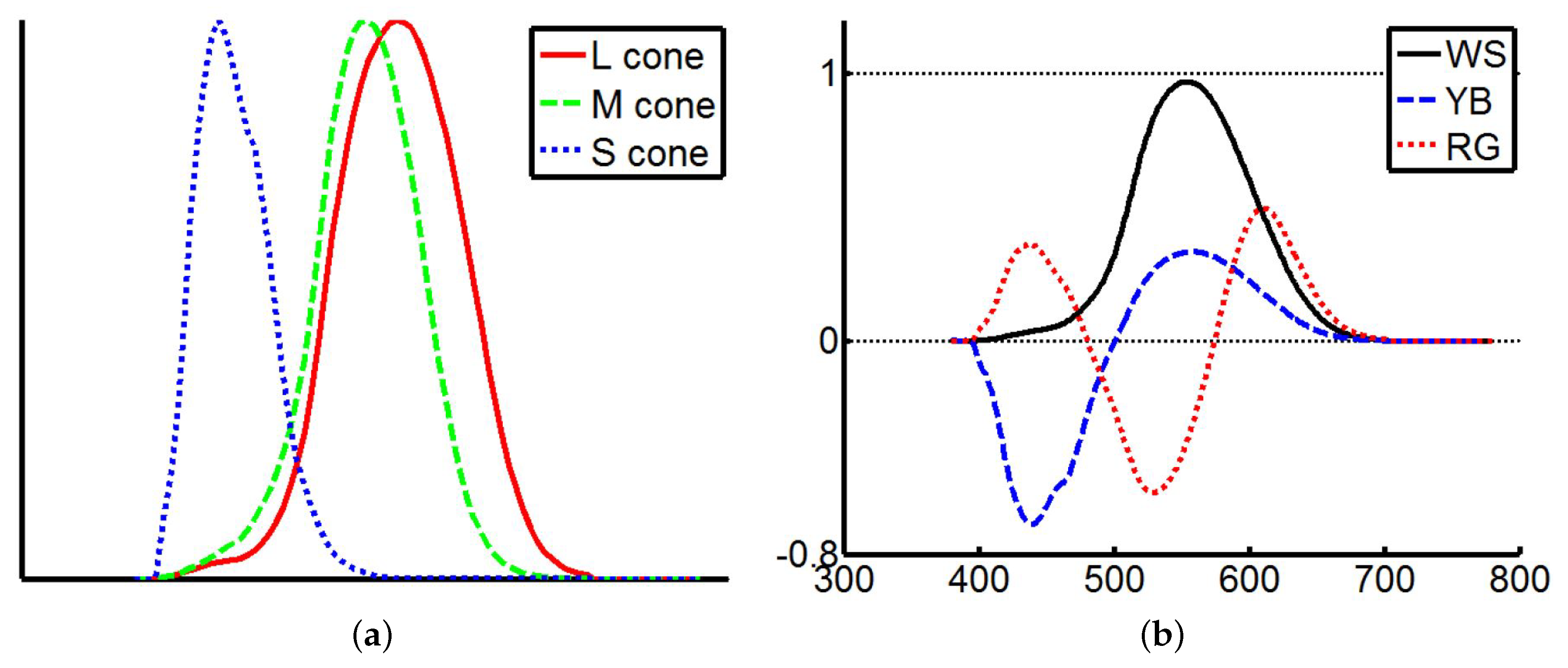
2.2. Eigenvector Processing
- Protanomaly: Shift L cone toward M cone, .
- Deuteranomaly: Shift M cone toward L cone, .
- Trianomaly: Shift S cone, .
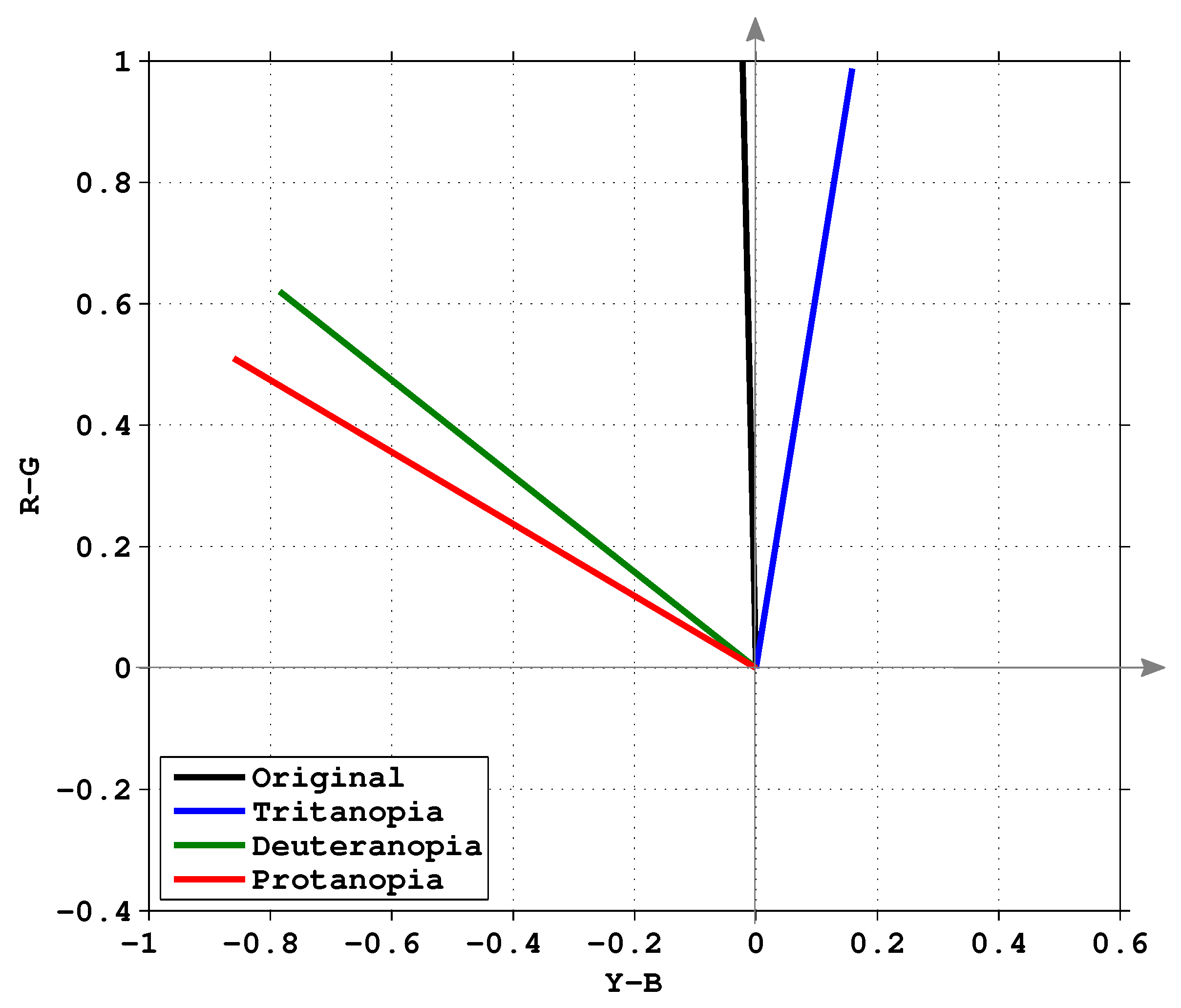
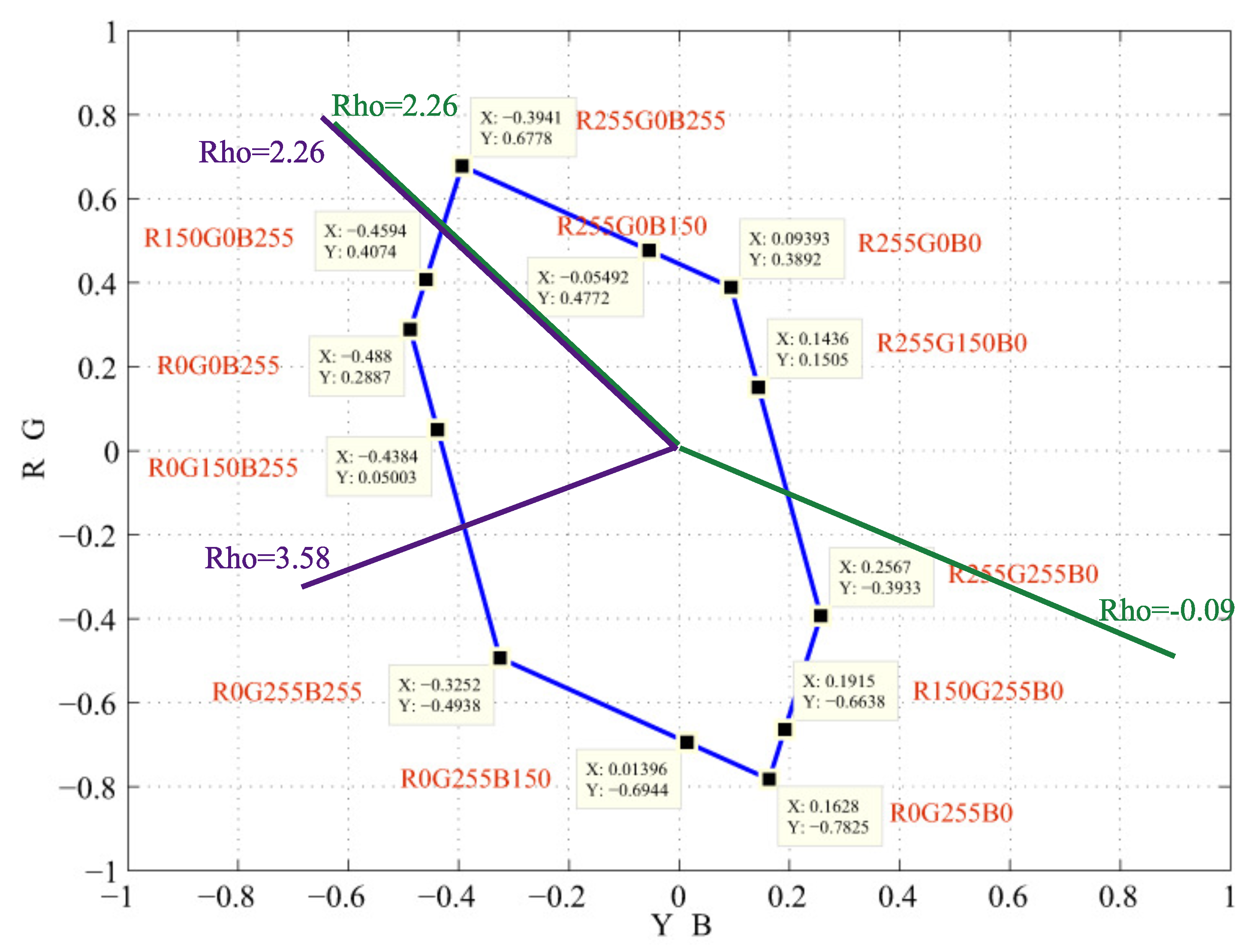
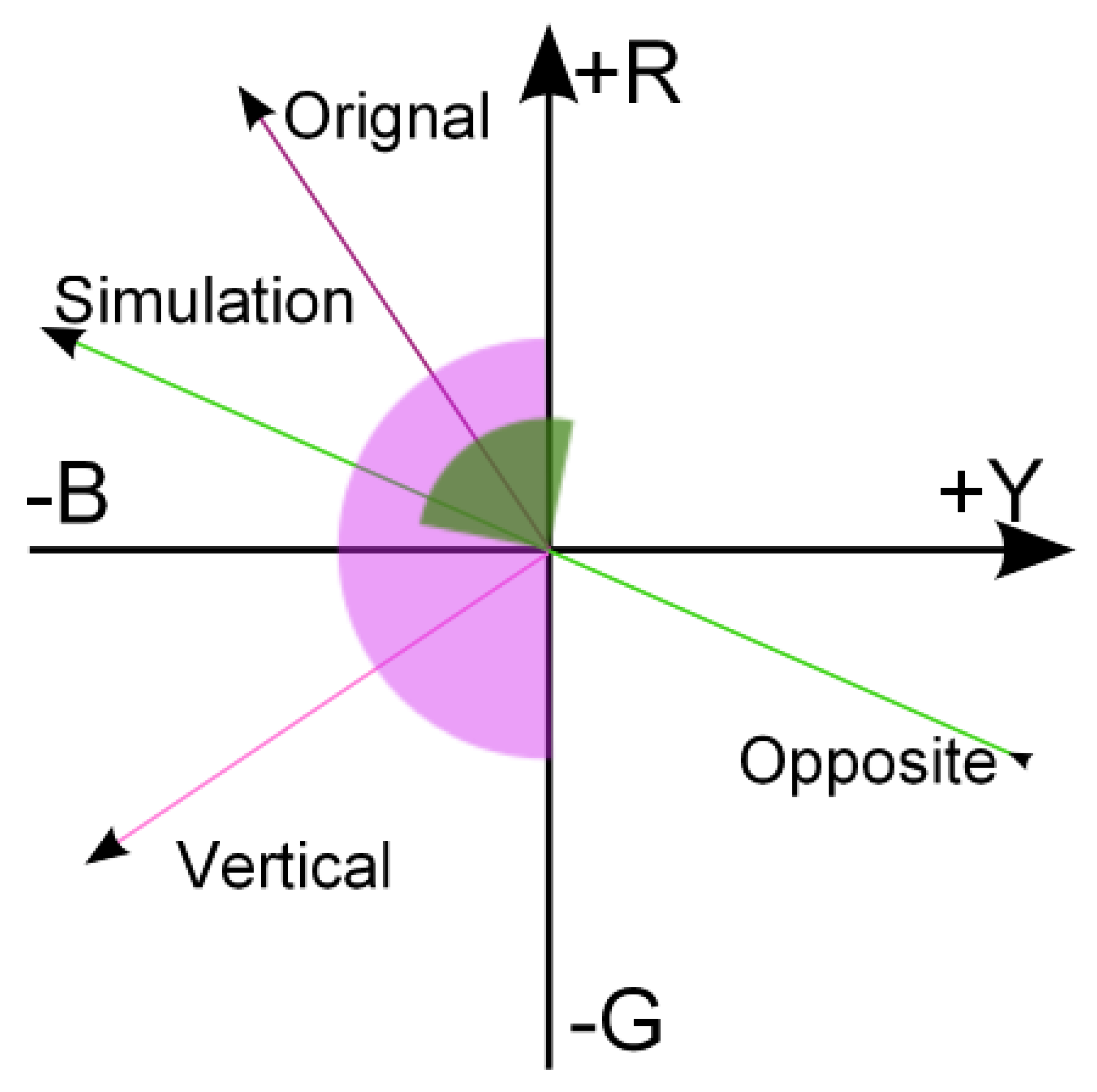
2.3. Color Warping
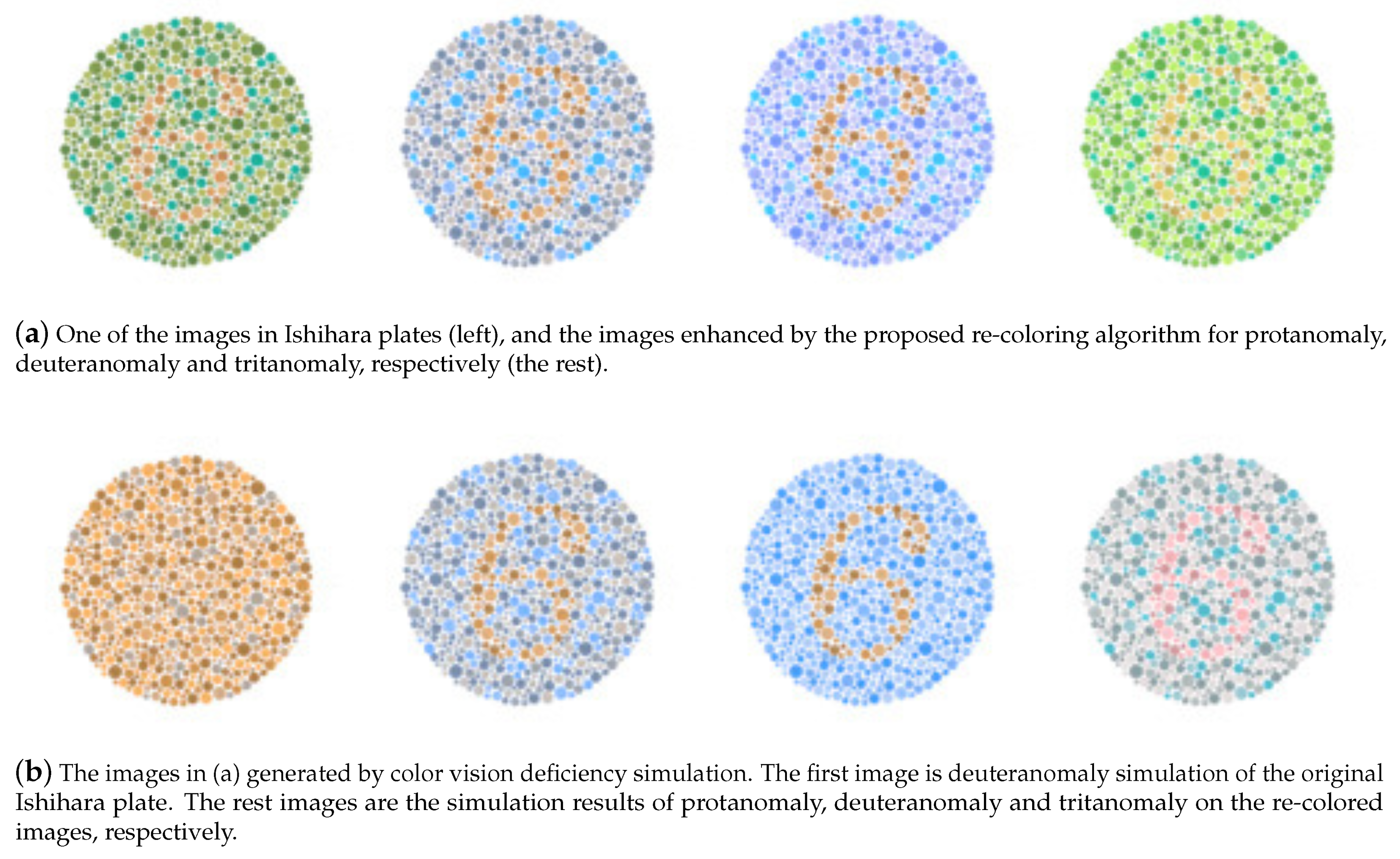
3. Experiments
3.1. Root Mean Square
3.2. Visual Difference Predictor
3.3. Human Subjective Evaluation
- : The input image is converted to the color space, projected to and equalized the and coordinates.
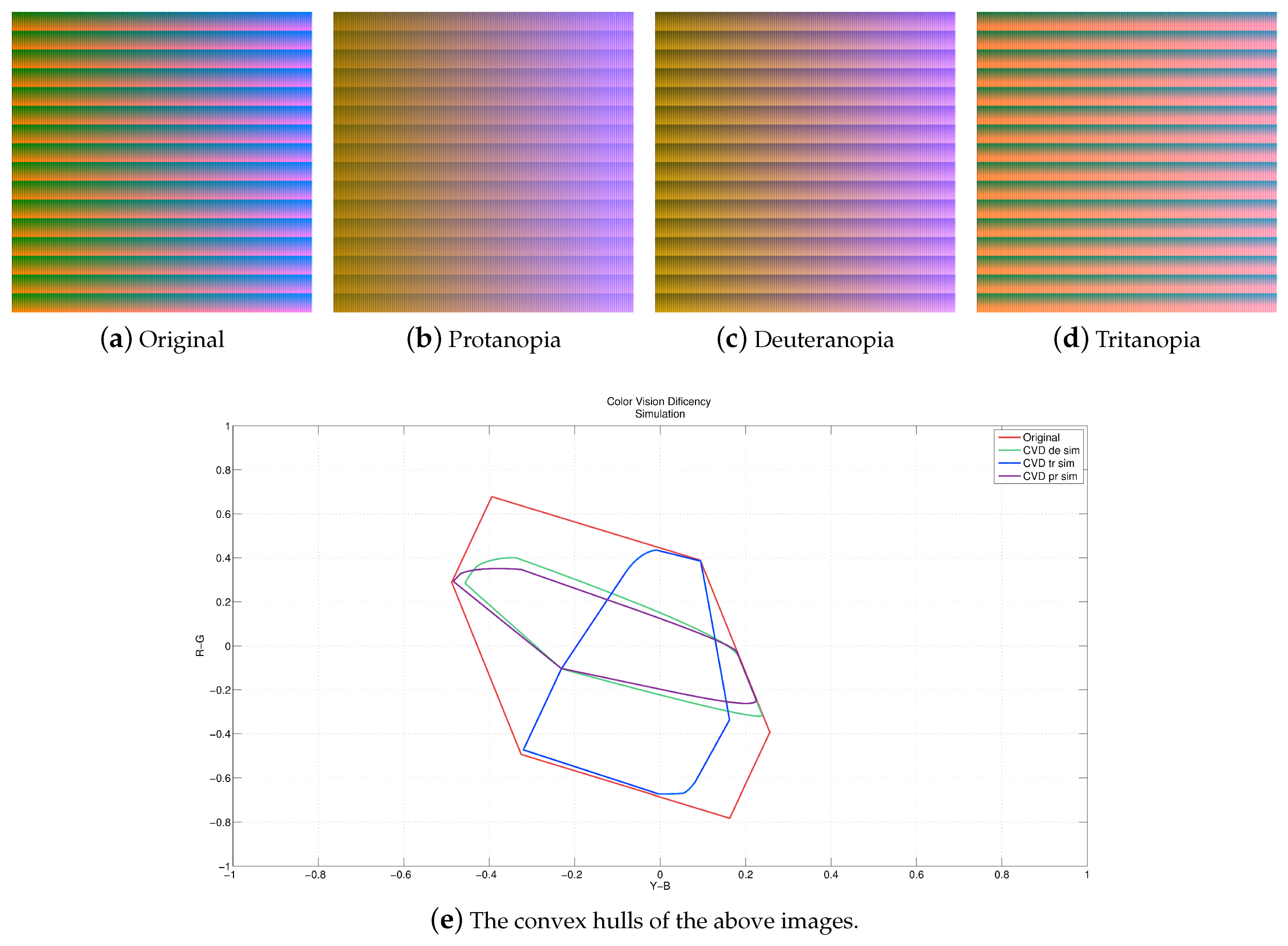
- : The input image is used to simulate the CVD view, and find the (R, G, B) difference between input and simulation images. A matrix is then used to enhance the color difference regions.
- : The input image is converted to the color space, and rotated to the non-confused color position.
- : The input image is used to simulate the CVD view, and the distances among the colors are used to obtain the discrepancy. The image is then converted to the , Y-B, R-G color space, and rotated the color difference regions.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wong, B. Points of view: Color blindness. Nat. Methods 2011, 8, 441. [Google Scholar] [CrossRef] [PubMed]
- Ishihara, S. Ishihara’s Tests for Color-Blindness, 38th ed.; Kanehara, Shuppan: Tokyo, Japan, 1990. [Google Scholar]
- Hunt, R. Colour Standards and Calculations. In The Reproduction of Colour; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2005; pp. 92–125. [Google Scholar] [CrossRef]
- Nathans, J.; Thomas, D.; Hogness, D.S. Molecular genetics of human color vision: The genes encoding blue, green, and red pigments. Science 1986, 232, 193–202. [Google Scholar] [CrossRef]
- Michael, K.; Charles, L. Psychophysics of Vision: The Perception of Color. Available online: https://www.ncbi.nlm.nih.gov/books/NBK11538/ (accessed on 30 April 2019).
- Colblindor Web Site. Available online: https://www.color-blindness.com/category/tools/ (accessed on 30 April 2019).
- Neitz, M.; Neitz, J. Numbers and ratios of visual pigment genes for normal red-green color vision. Science 1995, 267, 1013–1016. [Google Scholar] [CrossRef]
- Graham, C.; Hsia, Y. Color Defect and Color Theory Studies of normal and color-blind persons, including a subject color-blind in one eye but not in the other. Science 1958, 127, 675–682. [Google Scholar] [CrossRef]
- Fairchild, M. Color Appearance Models; The Wiley-IS&T Series in Imaging Science and Technology; Wiley: London, UK, 2013. [Google Scholar]
- Dolgin, E. Colour blindness corrected by gene therapy. Nature 2009, 2, 66–69. [Google Scholar] [CrossRef]
- Hunt, R.W.G.; Pointer, M.R. Measuring Colour; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Huang, J.B.; Wu, S.Y.; Chen, C.S. Enhancing Color Representation for the Color Vision Impaired. In Proceedings of the Workshop on Computer Vision Applications for the Visually Impaired, Marseille, France, 12–18 October 2008. [Google Scholar]
- Huang, J.B.; Chen, C.S.; Jen, T.C.; Wang, S.J. Image recolorization for the colorblind. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 1161–1164. [Google Scholar]
- Huang, C.R.; Chiu, K.C.; Chen, C.S. Key Color Priority Based Image Recoloring for Dichromats. In Advances in Multimedia Information Processing, Proceedings of the 11th Pacific Rim Conference on Multimedia, Shanghai, China, 21–24 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 637–647. [Google Scholar] [CrossRef]
- Chen, Y.S.; Hsu, Y.C. Computer vision on a colour blindness plate. Image Vis. Comput. 1995, 13, 463–478. [Google Scholar] [CrossRef]
- Rasche, K.; Geist, R.; Westall, J. Re-coloring Images for Gamuts of Lower Dimension. Comput. Graph. Forum 2005, 24, 423–432. [Google Scholar] [CrossRef]
- Rasche, K.; Geist, R.; Westall, J. Detail preserving reproduction of color images for monochromats and dichromats. IEEE Comput. Graph. Appl. 2005, 25, 22–30. [Google Scholar] [CrossRef]
- Lau, C.; Heidrich, W.; Mantiuk, R. Cluster-based color space optimizations. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 1172–1179. [Google Scholar]
- Lee, J.; Santos, W. An adaptative fuzzy-based system to evaluate color blindness. In Proceedings of the 17th International Conference on Systems, Signals and Image Processing (IWSSIP 2010), Rio de Janeiro, Brazil, 17–19 June 2010. [Google Scholar]
- Poret, S.; Dony, R.; Gregori, S. Image processing for colour blindness correction. In Proceedings of the 2009 IEEE Toronto International Conference Science and Technology for Humanity (TIC-STH), Toronto, ON, Canada, 26–27 September 2009; pp. 539–544. [Google Scholar]
- CIE Web Site. Available online: http://cie.co.at/ (accessed on 30 April 2019).
- Wright, W.D. Color Science, Concepts and Methods. Quantitative Data and Formulas. Phys. Bull. 1967, 18, 353. [Google Scholar] [CrossRef]
- Mantiuk, R.; Kim, K.J.; Rempel, A.G.; Heidrich, W. HDR-VDP-2: A Calibrated Visual Metric for Visibility and Quality Predictions in All Luminance Conditions. ACM Trans. Graph. 2011, 30, 40:1–40:14. [Google Scholar] [CrossRef]
- Moroney, N.; Fairchild, M.D.; Hunt, R.W.; Li, C.; Luo, M.R.; Newman, T. The CIECAM02 Color Appearance Model. Color Imaging Conf. 2002, 2002, 23–27. [Google Scholar]
- Brettel, H.; Viénot, F.; Mollon, J.D. Computerized simulation of color appearance for dichromats. J. Opt. Soc. Am. A 1997, 14, 2647–2655. [Google Scholar] [CrossRef]
- Wild, F. Outline of a Computational Theory of Human Vision. In Proceedings of the KI 2005 Workshop 7 Mixed-Reality as a Challenge to Image Understanding and Artificial Intelligence, Koblenz, Germany, 11 September 2005; p. 55. [Google Scholar]
- Busin, L.; Vandenbroucke, N.; Macaire, L. Color spaces and image segmentation. Adv. Imaging Electron Phys. 2008, 151, 65–168. [Google Scholar]
- Vrhel, M.; Saber, E.; Trussell, H. Color image generation and display technologies. IEEE Signal Process. Mag. 2005, 22, 23–33. [Google Scholar] [CrossRef]
- Sharma, G.; Trussell, H. Digital color imaging. IEEE Trans. Image Process. 1997, 6, 901–932. [Google Scholar] [CrossRef] [PubMed]
- Marguier, J.; Süsstrunk, S. Color matching functions for a perceptually uniform RGB space. In Proceedings of the ISCC/CIE Expert Symposium, Ottawa, ON, Canada, 16–17 May 2006. [Google Scholar]
- Huang, J.B.; Tseng, Y.C.; Wu, S.I.; Wang, S.J. Information preserving color transformation for protanopia and deuteranopia. IEEE Signal Process. Lett. 2007, 14, 711–714. [Google Scholar] [CrossRef]
- Ballard, D.H.; Brown, C.M. Computer Vision; Prentice Hall: Upper Saddle River, NJ, USA, 1982. [Google Scholar]
- Swain, M.J.; Ballard, D.H. Color indexing. Int. J. Comput. Vis. 1991, 7, 11–32. [Google Scholar] [CrossRef]
- Ingling, C.R.; Tsou, B.H.P. Orthogonal combination of the three visual channels. Vis. Res. 1977, 17, 1075–1082. [Google Scholar] [CrossRef]
- Machado, G.M.; Oliveira, M.M.; Fernandes, L.A. A physiologically-based model for simulation of color vision deficiency. IEEE Trans. Vis. Comput. Graph. 2009, 15, 1291–1298. [Google Scholar] [CrossRef]
- Smith, V.C.; Pokorny, J. Spectral sensitivity of the foveal cone photopigments between 400 and 500 nm. Vis. Res. 1975, 15, 161–171. [Google Scholar] [CrossRef]
- Kuhn, G.R.; Oliveira, M.M.; Fernandes, L.A. An efficient naturalness-preserving image-recoloring method for dichromats. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1747–1754. [Google Scholar] [CrossRef] [PubMed]
- Wikipedia. Institutional Review Board—Wikipedia. The Free Encyclopedia. Available online: http://en.wikipedia.org/wiki/Institutional_review_board (accessed on 1 July 2013).








| Type | Range | Peak Wavelength |
|---|---|---|
| S | 400–500 nm | 420–440 nm |
| M | 450–630 nm | 534–555 nm |
| L | 500–700 nm | 564–580 nm |
| Type | Male (%) | Female (%) |
|---|---|---|
| Protanopia | 1.0 | 0.02 |
| Deuteranopia | 1.1 | 0.01 |
| Trianopia | 0.002 | 0.001 |
| Protanomaly | 1.0 | 0.02 |
| Deuteranomaly | 4.9 | 0.38 |
| Tritanomaly | ∼0 | ∼0 |
| Total | 8.002 | 0.44 |
| Sensitivity | 0.6 |
|---|---|
| Protanopia | |
| Deuteranopia | |
| Tritanopia |
| Level | A | B | ||||||
| 5.45 | 83.64 | 5.45 | 5.45 | 45.45 | 9.09 | 9.09 | 36.36 | |
| 5.45 | 90.91 | 0.00 | 3.64 | 3.64 | 5.45 | 21.82 | 69.09 | |
| 1.82 | 72.73 | 14.55 | 10.90 | 20.00 | 3.64 | 25.45 | 50.91 | |
| 1.82 | 94.55 | 1.82 | 1.82 | 9.09 | 1.82 | 25.45 | 63.64 | |
| e | 1.89 | 91.67 | 0.00 | 8.33 | 0.00 | 5.45 | 20.00 | 74.55 |
| 0.00 | 41.82 | 12.73 | 45.45 | 5.36 | 8.93 | 44.64 | 41.07 | |
| 49.09 | 9.09 | 3.64 | 38.18 | 16.36 | 27.27 | 30.91 | 25.45 | |
| 14.81 | 20.37 | 16.67 | 48.15 | 12.37 | 9.09 | 50.91 | 27.27 | |
| Summary | 7.14 | 64.29 | 3.57 | 25.00 | 11.11 | 3.70 | 33.33 | 51.85 |
| Level | C | D | ||||||
| 9.09 | 5.45 | 54.55 | 30.91 | |||||
| 0.00 | 0.00 | 76.36 | 23.64 | 90.91 | 3.64 | 3.64 | 1.82 | |
| 9.09 | 14.55 | 43.64 | 32.73 | 69.09 | 9.09 | 16.36 | 5.45 | |
| 18.18 | 0.00 | 49.09 | 32.73 | 70.91 | 3.64 | 23.64 | 1.82 | |
| 14.55 | 1.82 | 63.64 | 20.00 | 88.89 | 0.00 | 7.41 | 3.70 | |
| 21.82 | 50.91 | 14.55 | 12.73 | 75.47 | 0.00 | 24.53 | 0.00 | |
| 16.36 | 30.91 | 32.73 | 20.00 | 18.18 | 32.73 | 32.73 | 16.36 | |
| 41.82 | 16.00 | 32.00 | 20.00 | 31.48 | 51.85 | 5.56 | 11.11 | |
| Summary | 9.68 | 12.90 | 58.06 | 19.35 | 76.00 | 12.00 | 8.00 | 4.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.-Y.; Chen, L.-Q.; Wang, M.-L. Improving Discrimination in Color Vision Deficiency by Image Re-Coloring. Sensors 2019, 19, 2250. https://doi.org/10.3390/s19102250
Lin H-Y, Chen L-Q, Wang M-L. Improving Discrimination in Color Vision Deficiency by Image Re-Coloring. Sensors. 2019; 19(10):2250. https://doi.org/10.3390/s19102250
Chicago/Turabian StyleLin, Huei-Yung, Li-Qi Chen, and Min-Liang Wang. 2019. "Improving Discrimination in Color Vision Deficiency by Image Re-Coloring" Sensors 19, no. 10: 2250. https://doi.org/10.3390/s19102250
APA StyleLin, H.-Y., Chen, L.-Q., & Wang, M.-L. (2019). Improving Discrimination in Color Vision Deficiency by Image Re-Coloring. Sensors, 19(10), 2250. https://doi.org/10.3390/s19102250





