Light-In-Flight Imaging by a Silicon Image Sensor: Toward the Theoretical Highest Frame Rate
Abstract
1. Introduction
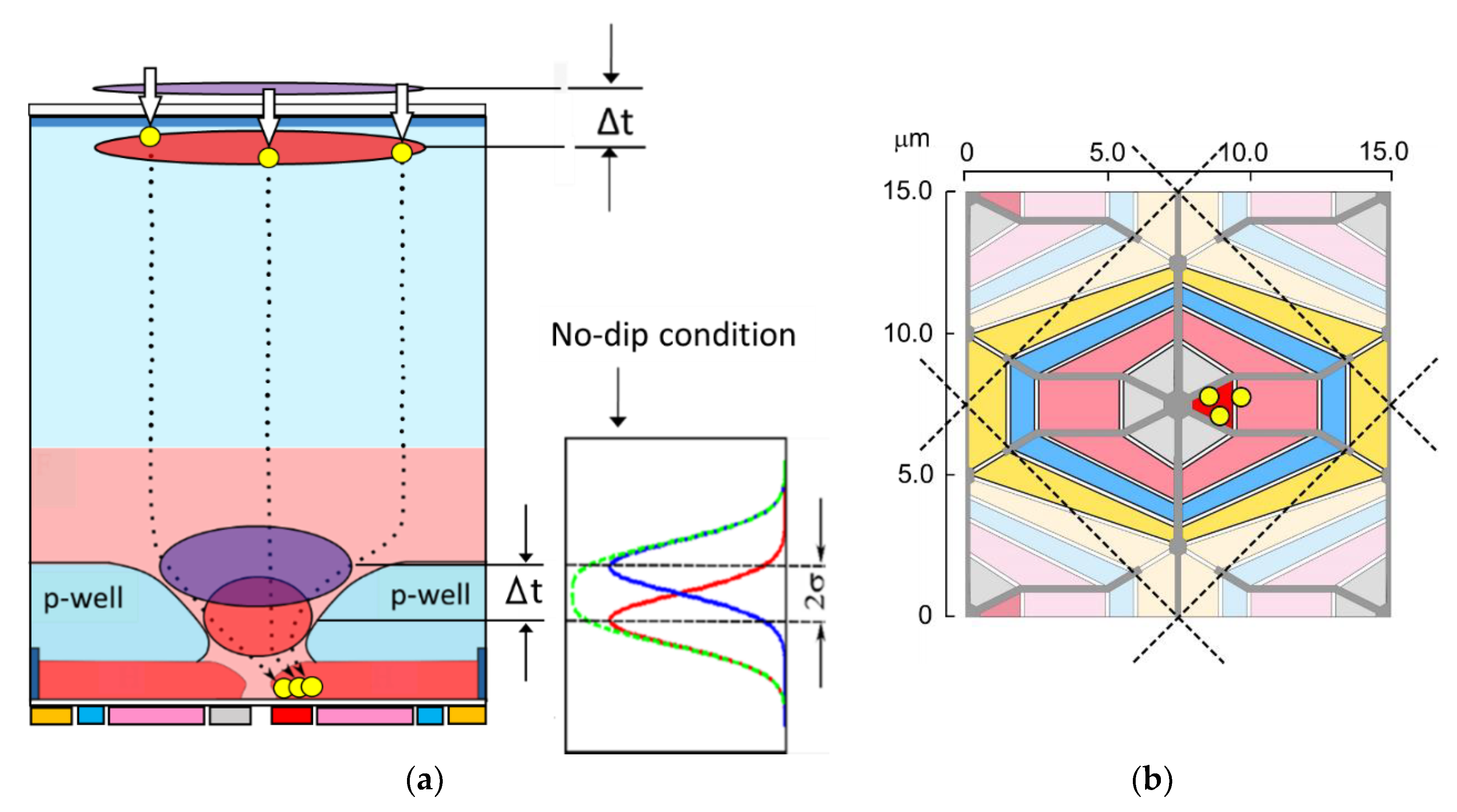
2. Light-in-Flight Captured by a Single Shot with a Silicon Image Sensor
2.1. BSI MCG Image Sensor
- (1)
- A backside-illuminated image sensor with the fill factor of 100%;
- (2)
- (3)
- (4)
- The silicon layer is 28 μm thick, which absorbs more than 99.9% of incident light with the wavelength less than 650 nm, preventing the remaining light after the absorption from directly intruding into the circuits on the front side and generating false signal electrons there.
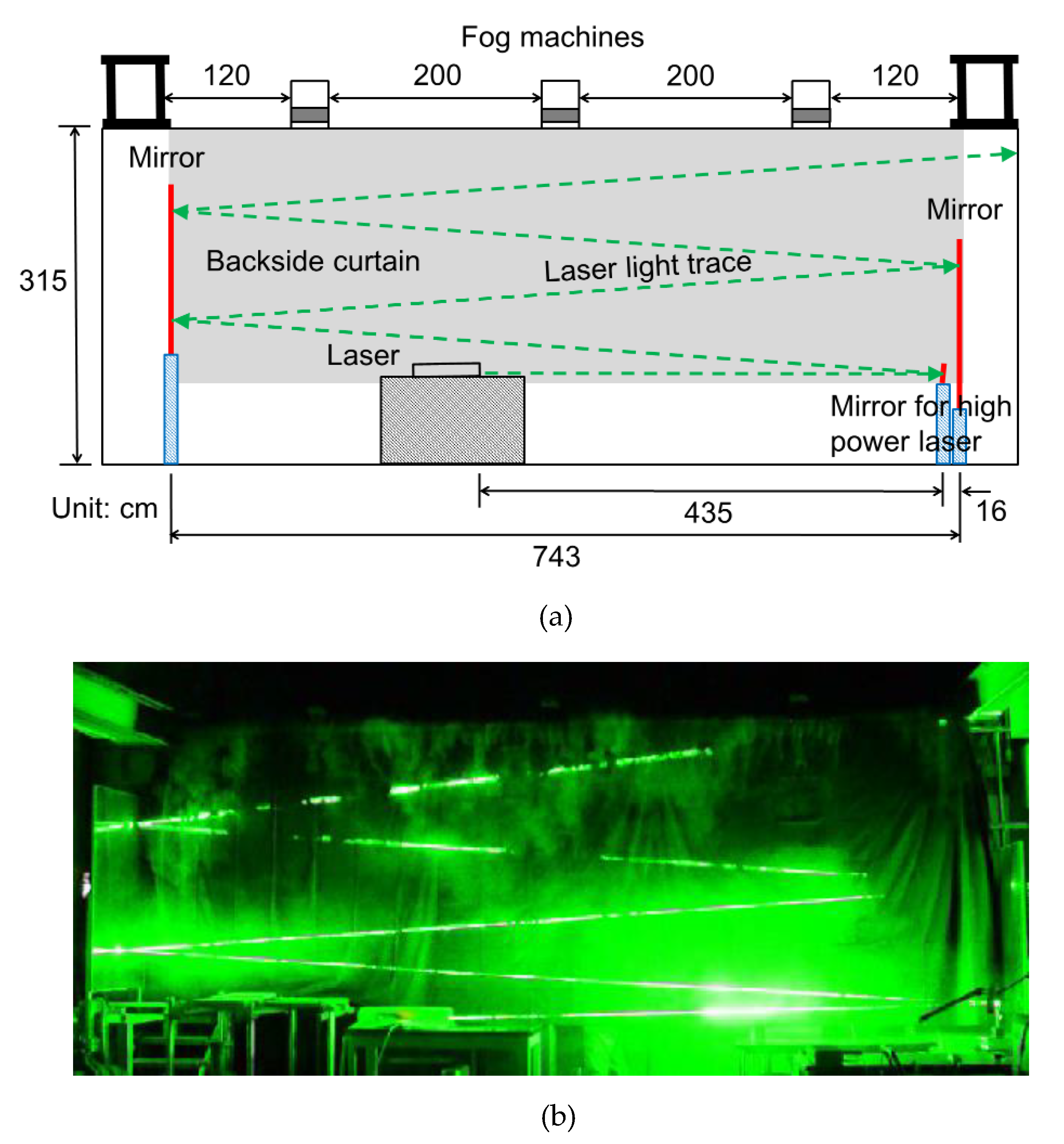
2.2. Experimental Setup
2.3. Timing Control
2.4. Captured Image
- (1)
- Blooming (overflow of signal charges from the pixels) at the local thick fog, especially near the mirrors, where the fog may have stagnated, or damage of the mirrors which may have caused additional strong emission of light;
- (2)
- the overlaps of the driving voltages, and;
- (3)
- tails before and after the main segment of the laser beam of the half-value width of 5 ns.
3. Suppression of Horizontal Motion of Signal Electrons for Ultimate-High-Speed
3.1. Surpression of Horizontal Motion of Signal Electrons
- (1)
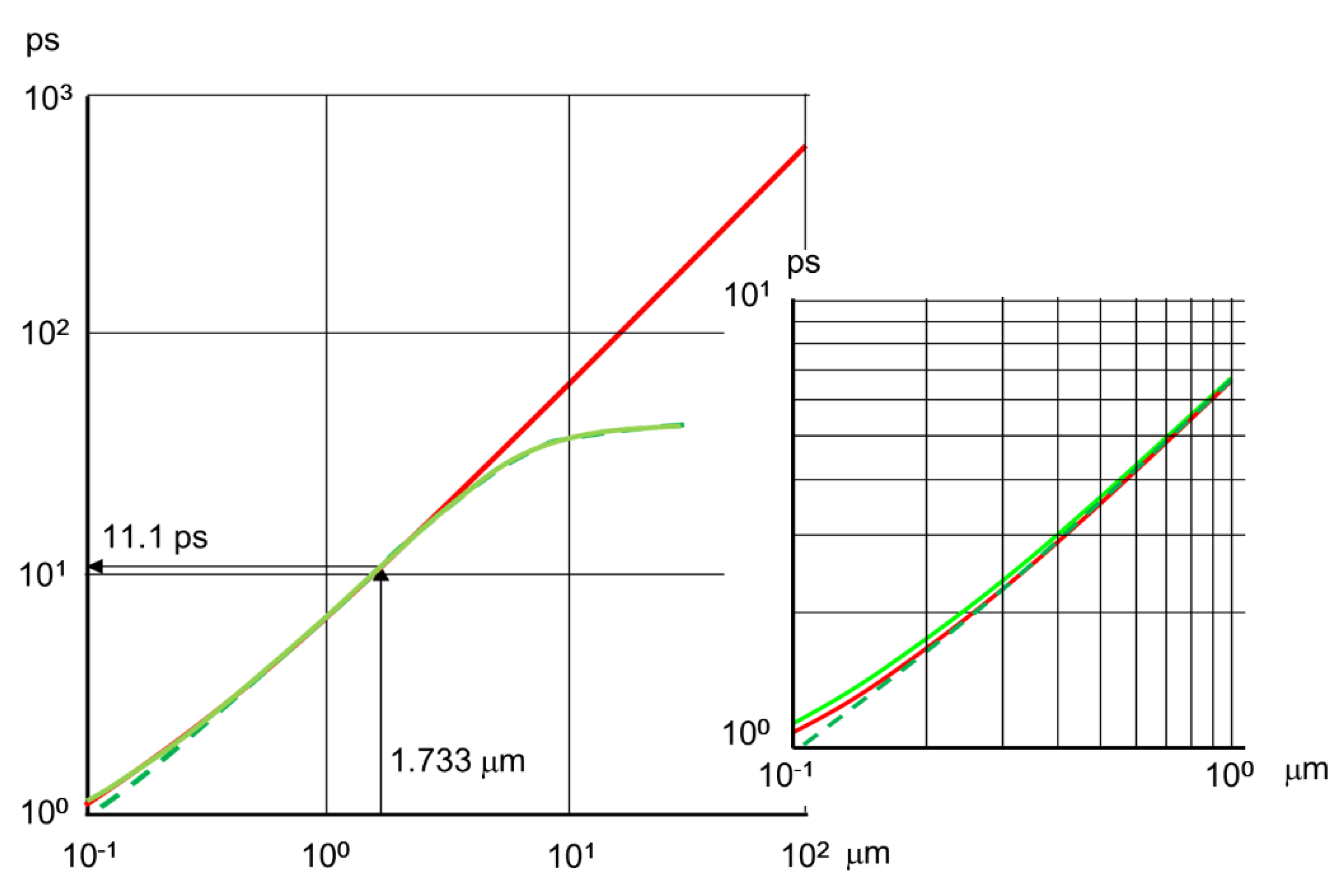
- The theoretical temporal resolution limitBy assuming the perfect suppression, the authors derived an expression of the theoretical temporal resolution limit of photo-conversion layers. The high accuracy of the expression was proved by comparison with the results of Monte Carlo simulations of the motion of signal electrons in silicon image sensors. The theoretical temporal resolution limit of silicon image sensors is 11.1 ps [15]. In this paper, the very high accuracy of the approximate expression is confirmed in comparison with the numerical calculation results of the strictly formulated expression that cannot be expressed with elementary functions.
- (2)
- Practical methods for the suppression of the horizontal motion:A frame interval of 50 ps can be achieved by a silicon image sensor with a silicon pipe in the middle of each pixel to suppress the horizontal motion of generated electrons [13]. While the pipe can be fabricated by an existing technology, the sensor requires a light focusing device such as a micro-lens or light-guide array on the backside. In this paper, a convex silicon pyramid is proposed for charge collection, which eliminates the requirement and will provide an image sensor with the time resolution better than 100 ps with 100% fill factor.
3.2. Comparison of the Approximaate Expression of Theoretical Highest Frame Rate with Numerical Calculation of the Strictly Formulated Expression
3.3. Suppression of Horizontal Motion of Electrons with Convex Pyramid Charge Collector
4. Further Evolution of BSI Multi-Collection-Gate Image Sensors
4.1. Pipeline Operation for More Frame Count and Signal Accumulation
4.2. Macro-pixel Image Sensor
4.3. Driver
5. Conclusions
- (1)
- The-state-of-the-art ultra-high-speed image sensorA silicon image sensor achieved the temporal resolution of 10 ns. Light in flight is captured with the image sensor.
- (2)
- The theoretical temporal resolution limitThe most critical issue for increasing the frame rate is suppression of the horizontal motion of signal electrons. Assuming the perfect suppression, an approximate expression of the theoretical temporal resolution limit was derived. The very high accuracy of the expression is confirmed in comparison with numerical calculation results of the expression rigorously formulated. The theoretical limit for silicon image sensors is 11.1 ps.
- (3)
- The practical temporal resolution limitThe convex pyramid charge collector is the most promising method to effectively suppress the horizontal motion, which achieves the temporal resolution of 100 ps, keeping the 100% fill factor.
Supplementary Materials
Supplementary File 1Author Contributions
Acknowledgments
Conflicts of Interest
References
- Abramson, N. Light-in-flight recording by holography. Opt. Lett. 1978, 3, 121. [Google Scholar] [CrossRef] [PubMed]
- Kubota, T.; Awatsuji, Y. Observation of light propagation by holography with a picosecond pulsed laser. Opt. Lett. 2002, 27, 815. [Google Scholar] [CrossRef]
- Kubota, T.; Awatsuji, Y. Femtosecond motion picture. IEICE Electron. Express 2005, 2, 298–304. [Google Scholar] [CrossRef]
- Kubota, T.; Komai, K.; Yamagiwa, M.; Awatsuji, Y. Moving picture recording and observation of three-dimensional image of femtosecond light pulse propagation. Opt. Express 2007, 15, 14348. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Liang, J.; Li, C.; Wang, L.V. Single-shot compressed ultrafast photography at one hundred billion frames per second. Nat. Cell Boil. 2014, 516, 74–77. [Google Scholar] [CrossRef]
- Liang, J.; Ma, C.; Zhu, L.; Chen, Y.; Gao, L.; Wang, L.V. Single-shot real-time video recording of a photonic Mach cone induced by a scattered light pulse. Sci. Adv. 2017, 3, e1601814. [Google Scholar] [CrossRef] [PubMed]
- Gariepy, G.; Krstajic, N.; Henderson, R.; Li, C.; Thomson, R.R.; Buller, G.S.; Heshmat, B.; Raskar, R.; Leach, J.; Faccio, D. Single-photon sensitive light-in-flight imaging. Nat. Commun. 2015, 6, 6021. [Google Scholar] [CrossRef] [PubMed]
- Velten, A.; Ramesh, R.; Di, W.; Adrian, J.; Belen, M.; Christopher, B.; Chinmaya, J.; Everett, L.; Moungi, B.; Diego, G. Femto-photography: Capturing and visualizing the propagation of light. ACM Trans. Graph 2013, 32, 1–8. [Google Scholar] [CrossRef]
- Etoh, T.; Mutoh, H. Back-Illuminated Image Device Having Signal Charges Suppressing Region. US Patent 7,345,268 B2 (JP 2003-000117), 26 December 2003. [Google Scholar]
- Etoh, T.G.; Nguyen, D.H.; Dao, S.V.T.; Vo, C.L.; Tanaka, M.; Takehara, K.; Okinaka, T.; Van Kuijk, H.; Klaassens, W.; Bosiers, J.; et al. A 16 Mfps 165kpixel backside-illuminated CCD. In Proceedings of the 2011 IEEE International Solid- State Circuits Conference—(ISSCC), San Francisco, CA, USA, 20–24 February 2011; pp. 406–407. [Google Scholar]
- Etoh, T.; Yamada, T.; Dao, V.T.S. Solid-State Apparatus. US Patent 9,503,663 B2 (JP 2012-128368), 24 August 2014. [Google Scholar]
- Etoh, T.G.; Dao, V.T.S.; Yamada, T.; Charbon, E.; Son, D. Toward One Giga Frames per Second—Evolution of in Situ Storage Image Sensors. Sensors 2013, 13, 4640–4658. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.Q.; Dao, V.T.S.; Shimonomura, K.; Takehara, K.; Etoh, T.G. Toward the Ultimate-High-Speed Image Sensor: From 10 ns to 50 ps. Sensors 2018, 18, 2407. [Google Scholar] [CrossRef] [PubMed]
- Lord Rayleigh, F.R.S. Investigations in optics, with special reference to the spectroscope. Philos. Mag. 1879, 5, 49. [Google Scholar] [CrossRef]
- Etoh, T.G.; Nguyen, A.Q.; Kamakura, Y.; Shimonomura, K.; Le, T.Y.; Mori, N.; Passaro, V.M.N. The Theoretical Highest Frame Rate of Silicon Image Sensors. Sensors 2017, 17, 483. [Google Scholar] [CrossRef]
- Etoh, T.G.; Nguyen, A.Q. Evolution of high-speed image sensors. In The Micro-World Observed by Ultra-High-Speed Cameras: We See What You Don’t See; Tsuji, K., Ed.; Springer: New York, NY, USA, 2017; pp. 81–102. [Google Scholar]
- Etoh, T. A high-speed video camera operating at 4,500 fps. J. Inst. Telev. Eng. Jpn. 1992, 46, 543–545. (In Japanese) [Google Scholar]
- Etoh, T.G.; Son, D.V.T.; Akino, T.K.; Akino, T.; Nishi, K.; Kureta, M.; Arai, M. Ultra-High-Speed Image Signal Accumulation Sensor. Sensors 2010, 10, 4100–4113. [Google Scholar] [CrossRef] [PubMed]
- Dao, V.T.S.; Ngo, N.; Nguyen, A.Q.; Morimoto, K.; Shimonomura, K.; Goetschalckx, P.; Haspeslagh, L.; De Moor, P.; Takehara, K.; Etoh, T.G. An image signal accumulation multi-collection-gate image sensor operating at 25 Mfps with 32 × 32 pixels and 1,220 in-pixel frame memory. Sensors 2018, 18, 3112. [Google Scholar] [CrossRef] [PubMed]
- Morel, F.; Le Normand, J.P.; Zint, C.V.; Uhring, W.; Hu, Y.; Mathiot, D. A Fast, High Resolution Imager for Nanosecond Light Pulse detections. Proc. SPIE 2004, 5451, 434–440. [Google Scholar]
- Sze, S.M.; Lee, M.K. Physics of Semiconductor Devices, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 66–67. [Google Scholar]
- Jacoboni, C.; Canali, C.; Ottaviani, G.; Quaranta, A.A. A review of some charge transport properties of silicon. Solid-State Electron. 1977, 20, 77–89. [Google Scholar] [CrossRef]
- Kunikiyo, T.; Takenaka, M.; Kamakura, Y.; Yamaji, M.; Mizuno, H.; Morifuji, M.; Taniguchi, K.; Hamaguchi, C. A Monte Carlo simulation of anisotropic electron transport in silicon including full band structure and anisotropic impact-ionization model. J. Appl. Phys. 1994, 75, 297–312. [Google Scholar] [CrossRef]
- Jones, M.H.; Jones, S.H. Optical Properties of Silicon 71502, Virginia Semiconductor Inc. Available online: https://www.univie.ac.at/photovoltaik/vorlesung/ss2014/unit4/optical_properties_silicon.pdf (accessed on 13 May 2018).
- Weber, G. X-Ray Attenuation & Absorption calcuLator. Available online: https://web-docs.gsi.de/~stoe_exp/web_programs/x_ray_absorption/index.php (accessed on 13 May 2018).
- Claus, L.; Fang, L.; Kay, R.; Kimmel, M.; Long, J.; Robertson, G.; Sanchez, M.; Stahoviak, J.; Trotter, L.; Porter, J.L. An overview of the Ultrafast X-ray Imager (UXI) program at Sandia Labs. Proc. SPIE 2015, 9591, 95910P. [Google Scholar]
- Pal1, P.; Sato, K.; Chandra, S. Fabrication techniques of convex corners in a (100)-silicon wafer using bulk micromachining: A review. J. Micromech. Microeng. 2007, 17, R111–R133. [Google Scholar] [CrossRef]
- Mavrokefalos, A.; Han, S.E.; Yerci, S.; Branham, M.S.; Chen, G. Efficient Light Trapping in Inverted Nanopyramid Thin Crystalline Silicon Membranes for Solar Cell Applications. Nano Lett. 2012, 12, 2792–2796. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, L.; Liu, Y.; Mei, Z.; Chen, W.; Li, J.; Liang, H.; Kuznetsov, A.; Xiaolong, D. Maskless inverted pyramid texturization of silicon. Sci. Rep. 2015, 5, 10843. [Google Scholar] [CrossRef] [PubMed]
- Pal, P.; Sato, K. Silicon Wet Bulk Michromachining; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Yokogawa, S.; Oshiyama, I.; Ikeda, H.; Ebiko, Y.; Hirano, T.; Saito, S.; Oinoue, T.; Hagimoto, Y.; Iwamoto, H. IR sensitivity enhancement of CMOS Image Sensor with diffractive light trapping pixels. Sci. Rep. 2017, 7, 3832. [Google Scholar] [CrossRef] [PubMed]
- Etoh, T.G.; Mutoh, H. Image Accumulation High-Speed Imaging Device. JP A2011-082925, 9 October 2009. (In Japanese). [Google Scholar]
- Mochizuki, F.; Kagawa, K.; Ok ihara, S.; Seo, M.-W.; Zhan, B.; Takasawa, T.; Yasutomi, K.; Kawahito, S. Single-Shot 200Mfps 5x3-Aperture Compressive CMOS Imager; ISSCC 2015, Digest of Technical Papers; IEEE: San Francisco, CA, USA, 2015; pp. 116–117. [Google Scholar]
- Zhang, C.; Dao, V.T.S.; Charbon, E.; Etoh, T.G. Pixel parallel localized driver design for a 128 × 256 pixel array 3D 1Gfps image sensor. In Proceedings of the 31st International Congress on High-Speed Imaging and Photonics, Osaka, Japan, 20 February 2017. [Google Scholar]




| Structure | BSI MCG Image Sensor |
|---|---|
| Shortest frame interval (Equivalent frame rate) | 10 ns (100 Mfps) |
| Frame and pixel counts | 5 frames for 576 × 512 × 2 pixels ** 10 frames for 575 × 512 pixels |
| Fill factor | 100% |
| Charge handling capacity | 7000 e− |
| Pixel size | 12.73 × 12.73 μm (Diagonal 18 μm) |
| Photoreceptive area | 10.368 × 9.216 mm |
| Process | 130 nm CMOS process modified for CCD |
| Structure | p-Well | Light/Electron Guide Pipe | Convex Pyramid Charge Collector |
|---|---|---|---|
| Cross sections |  |  |  |
| Temporal resolution 2σ | 990.0 ps | 49.0 ps | 87.5 ps |
| Vertical Field | 5 kV/cm * | 25 kV/cm * | 25 kV/cm * |
| Collection Ratio *** | 100% | 100% | 98% |
| Dark current | less | middle | large |
| X-ray | Applicable | Low efficiency | Ideal |
| Technical feasibility | Already applied | Existing technology | Process improvement |
| Requirement | Linear built-in potential **** | Micro lens/light guide necessary | High-quality convex pyramid unavailable |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Etoh, T.G.; Okinaka, T.; Takano, Y.; Takehara, K.; Nakano, H.; Shimonomura, K.; Ando, T.; Ngo, N.; Kamakura, Y.; Dao, V.T.S.; et al. Light-In-Flight Imaging by a Silicon Image Sensor: Toward the Theoretical Highest Frame Rate. Sensors 2019, 19, 2247. https://doi.org/10.3390/s19102247
Etoh TG, Okinaka T, Takano Y, Takehara K, Nakano H, Shimonomura K, Ando T, Ngo N, Kamakura Y, Dao VTS, et al. Light-In-Flight Imaging by a Silicon Image Sensor: Toward the Theoretical Highest Frame Rate. Sensors. 2019; 19(10):2247. https://doi.org/10.3390/s19102247
Chicago/Turabian StyleEtoh, Takeharu Goji, Tomoo Okinaka, Yasuhide Takano, Kohsei Takehara, Hitoshi Nakano, Kazuhiro Shimonomura, Taeko Ando, Nguyen Ngo, Yoshinari Kamakura, Vu Truong Son Dao, and et al. 2019. "Light-In-Flight Imaging by a Silicon Image Sensor: Toward the Theoretical Highest Frame Rate" Sensors 19, no. 10: 2247. https://doi.org/10.3390/s19102247
APA StyleEtoh, T. G., Okinaka, T., Takano, Y., Takehara, K., Nakano, H., Shimonomura, K., Ando, T., Ngo, N., Kamakura, Y., Dao, V. T. S., Nguyen, A. Q., Charbon, E., Zhang, C., De Moor, P., Goetschalckx, P., & Haspeslagh, L. (2019). Light-In-Flight Imaging by a Silicon Image Sensor: Toward the Theoretical Highest Frame Rate. Sensors, 19(10), 2247. https://doi.org/10.3390/s19102247






