Design of a Measurement System for Six-Degree-of-Freedom Geometric Errors of a Linear Guide of a Machine Tool
Abstract
1. Introduction
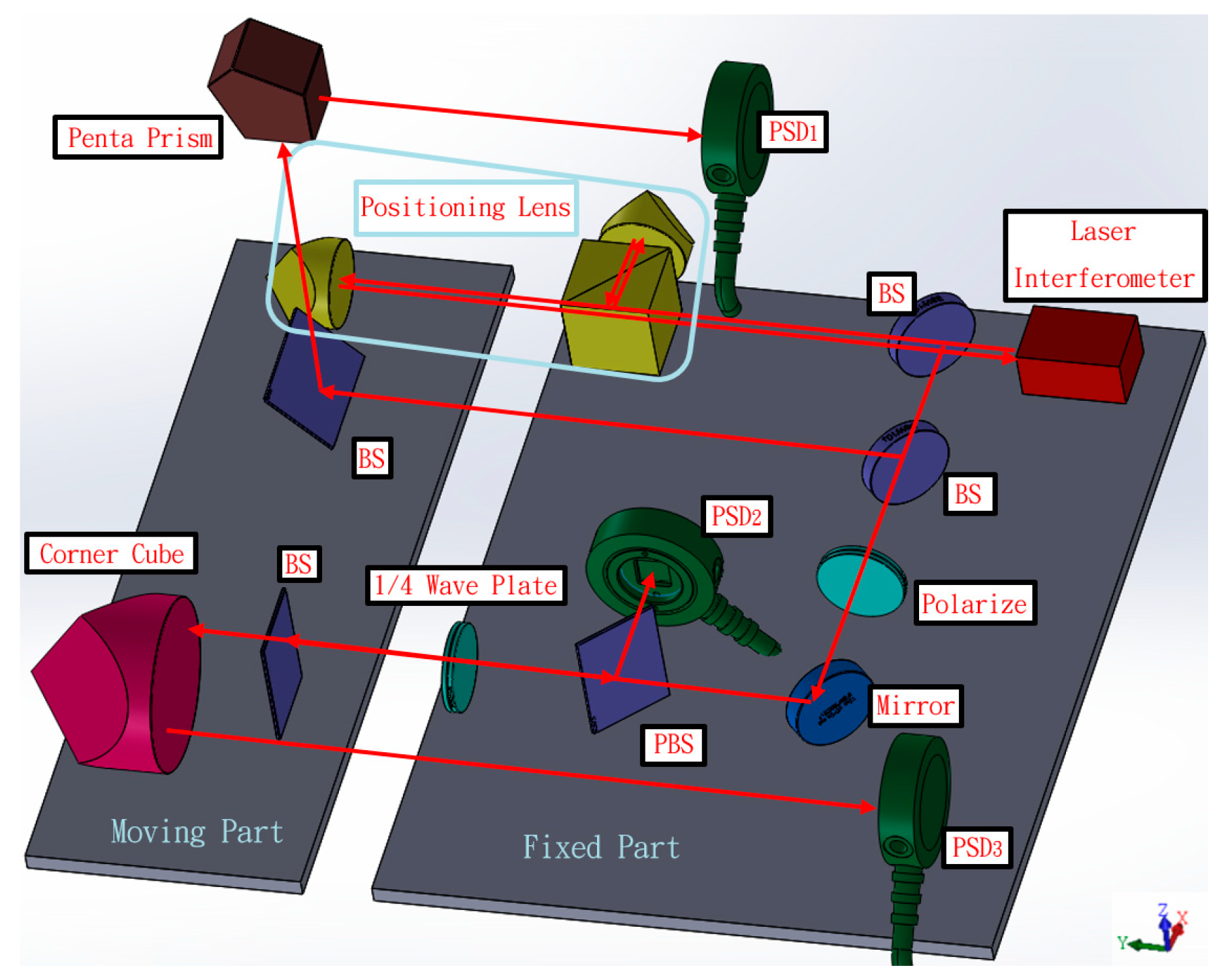
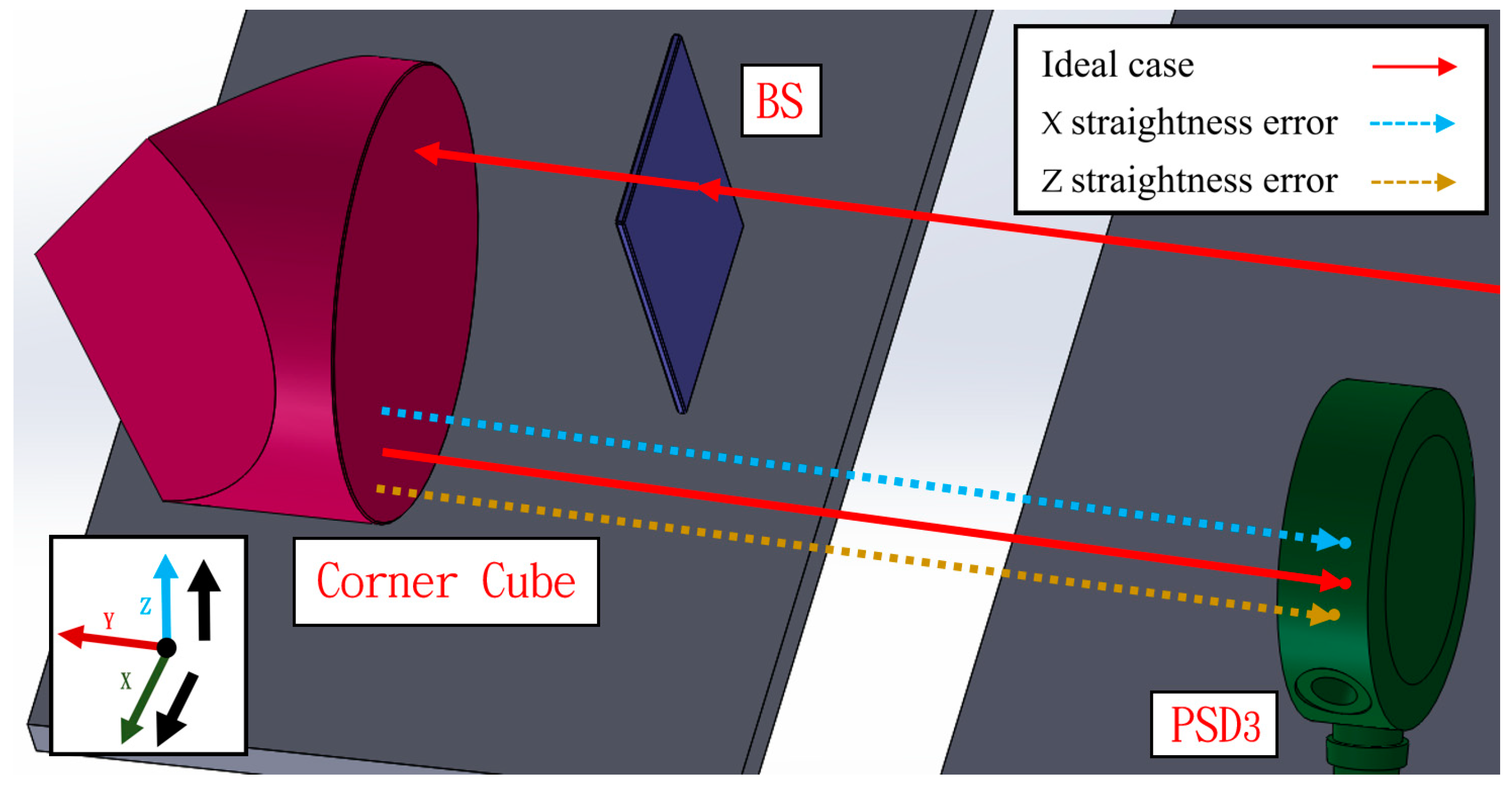
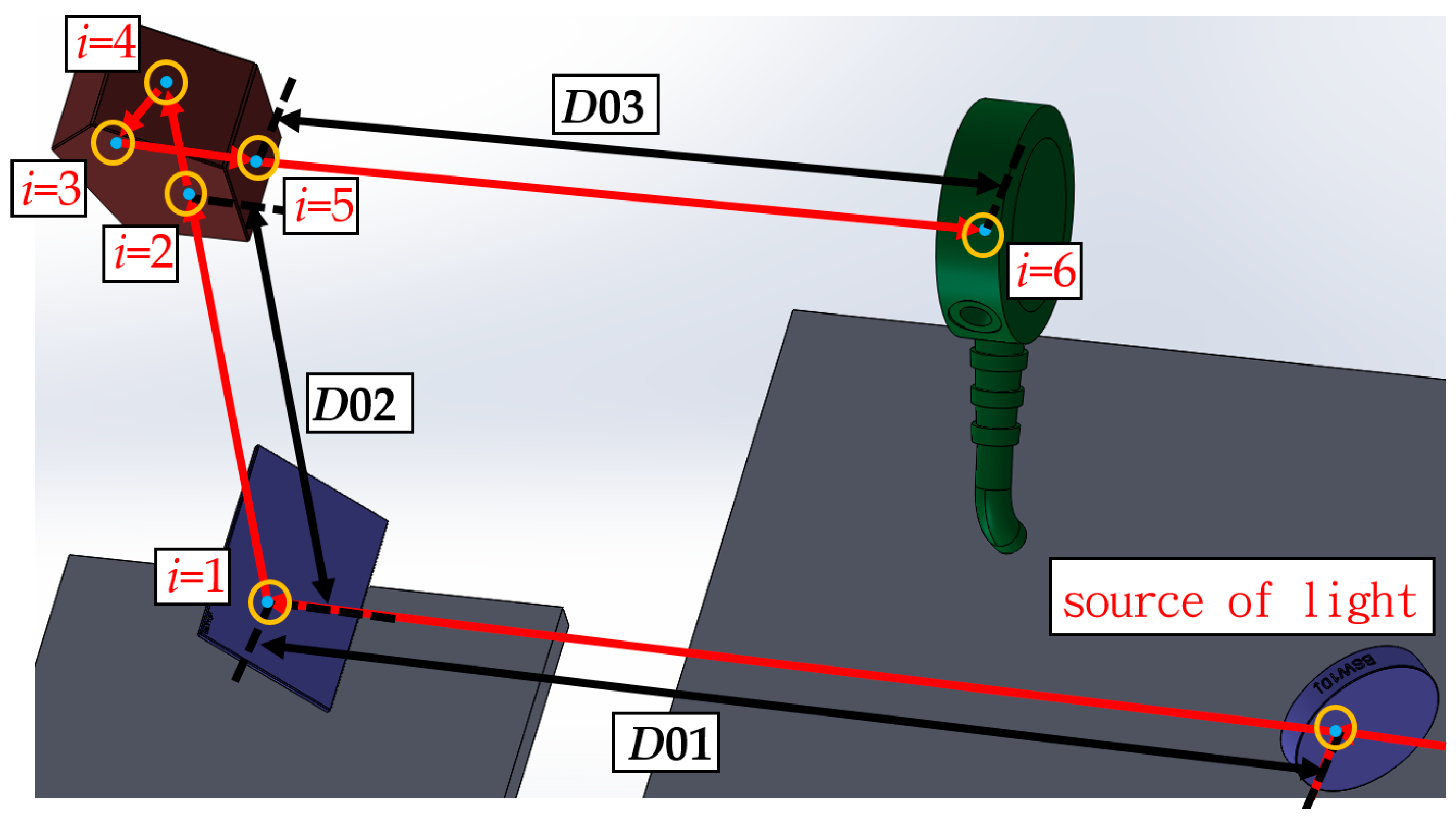
2. Structure Layout and Measuring Principle
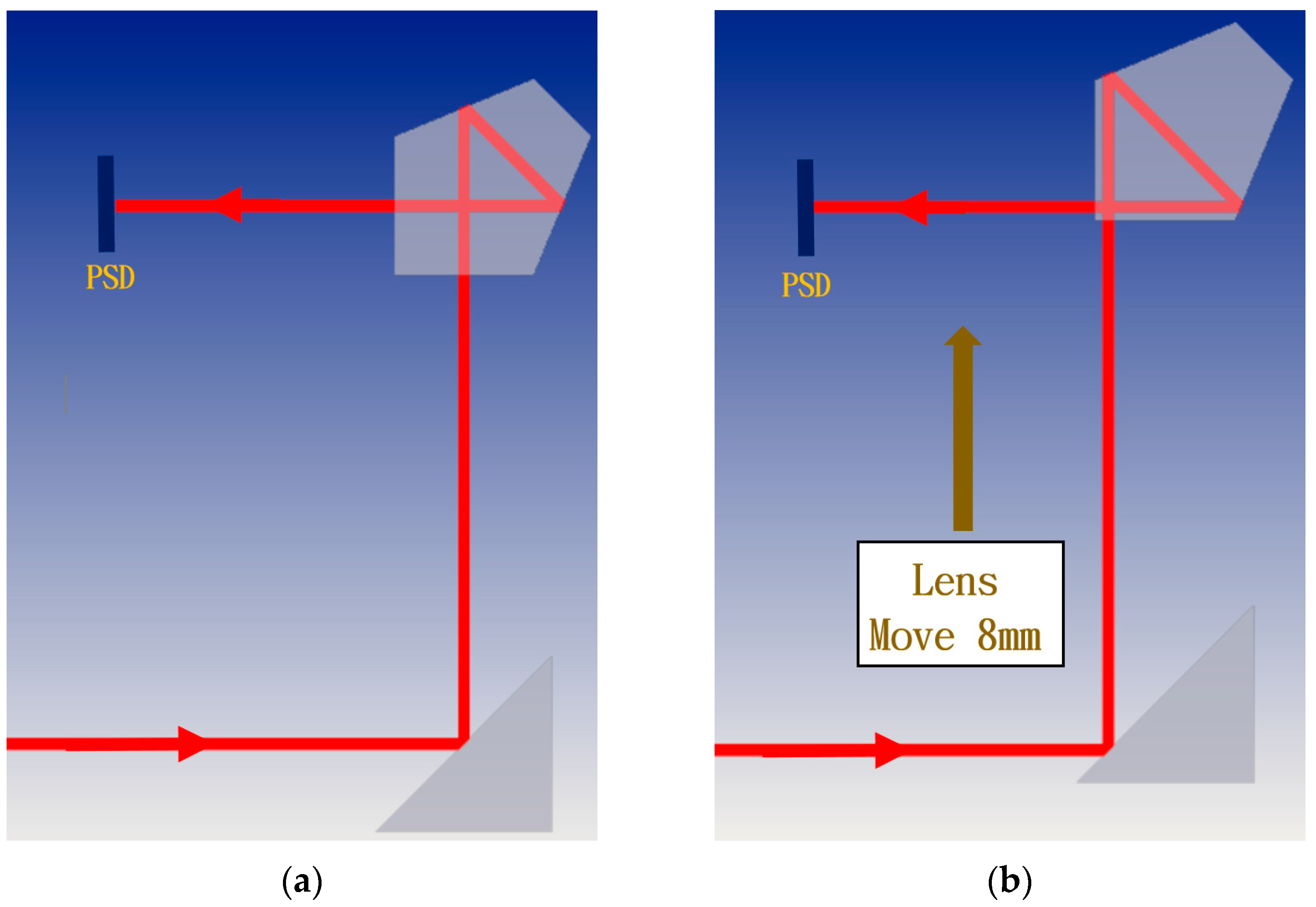
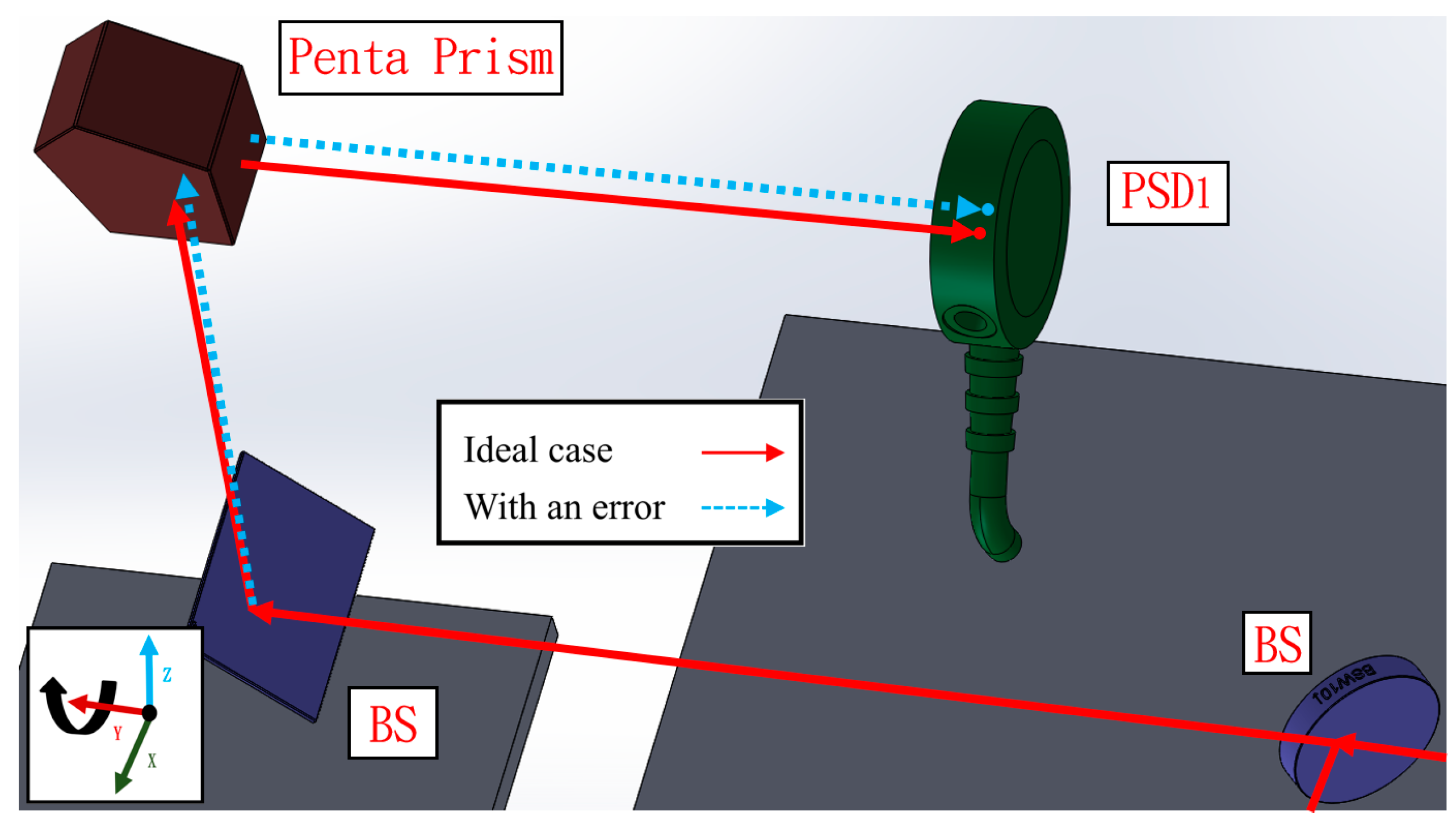
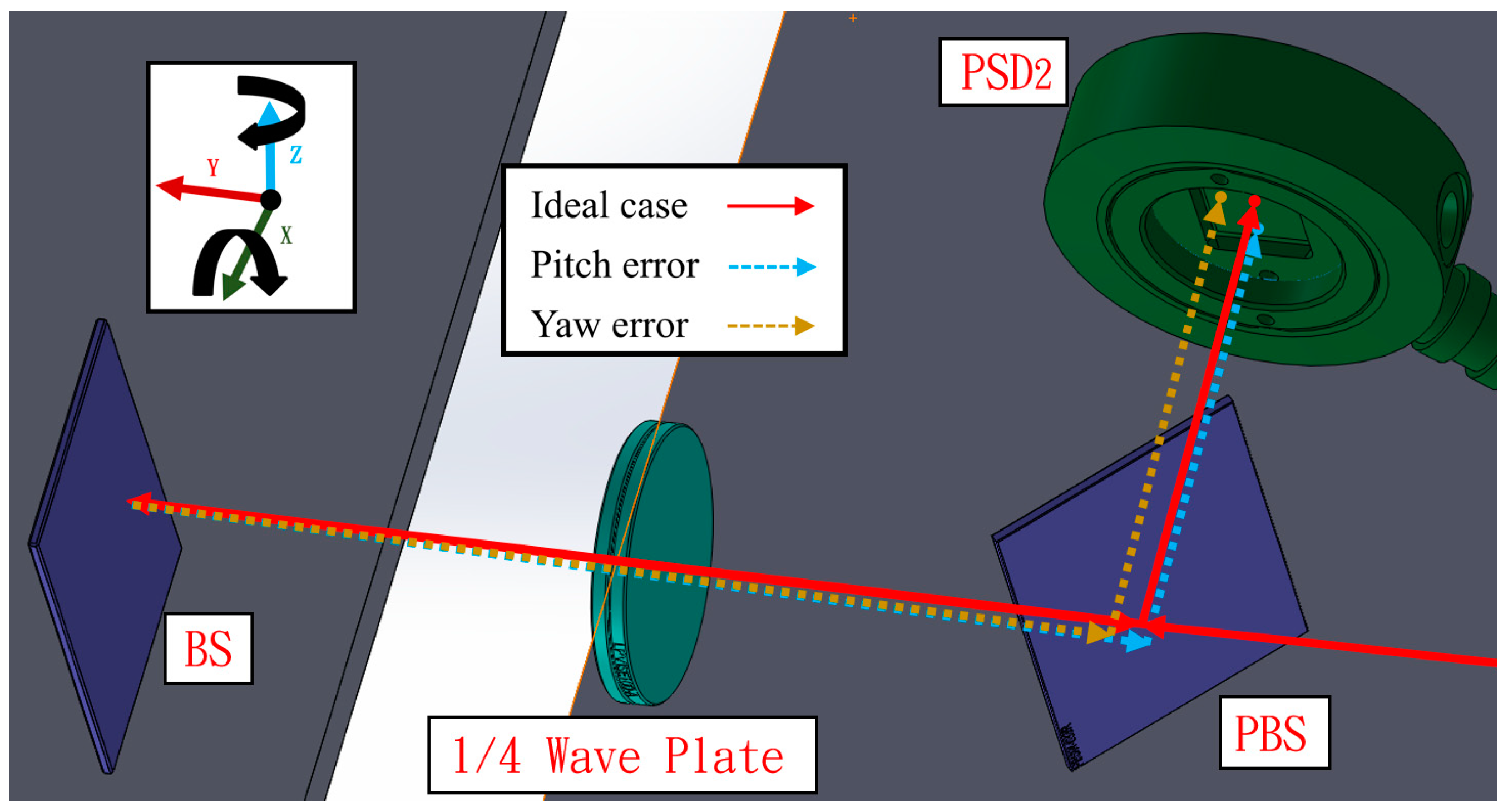
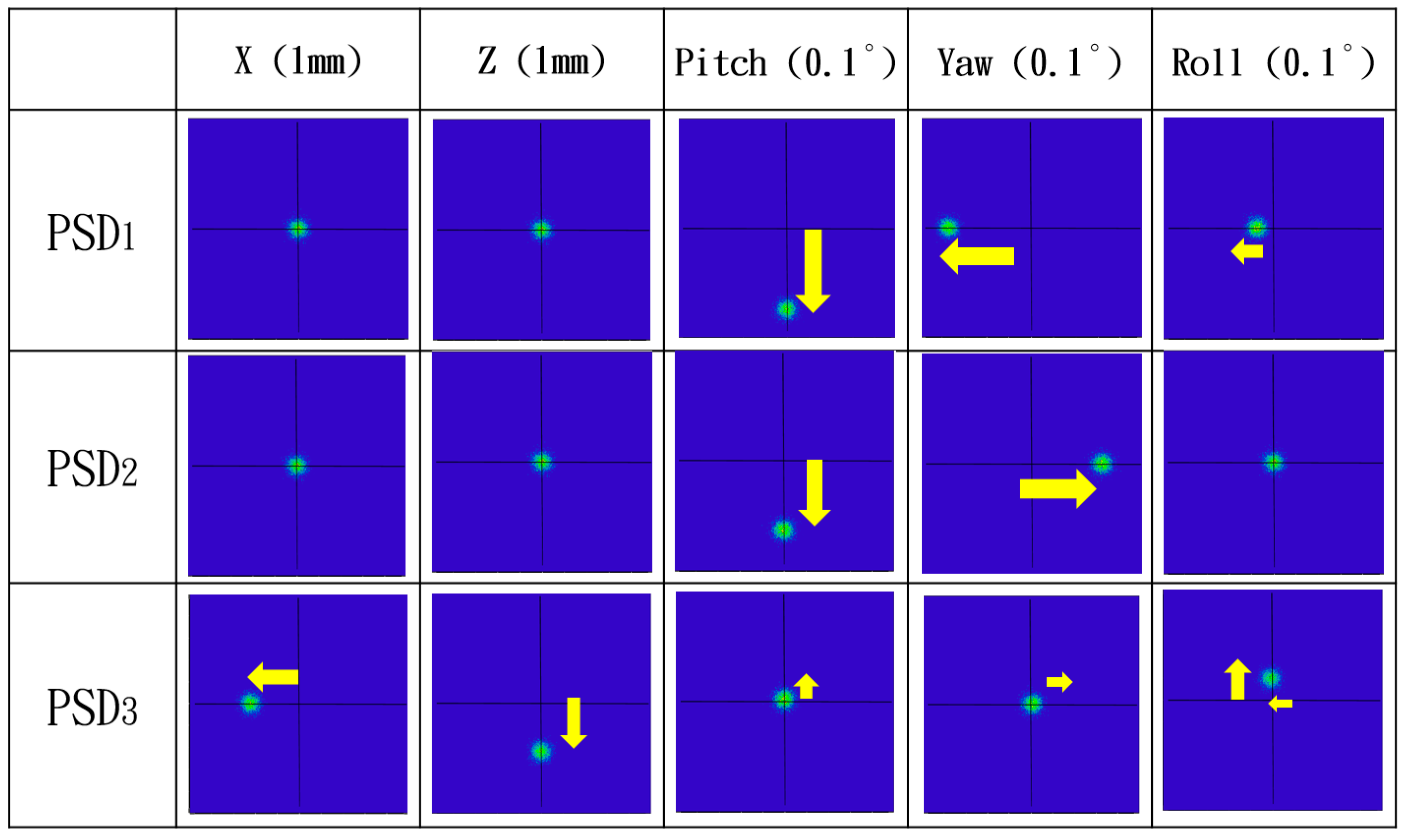
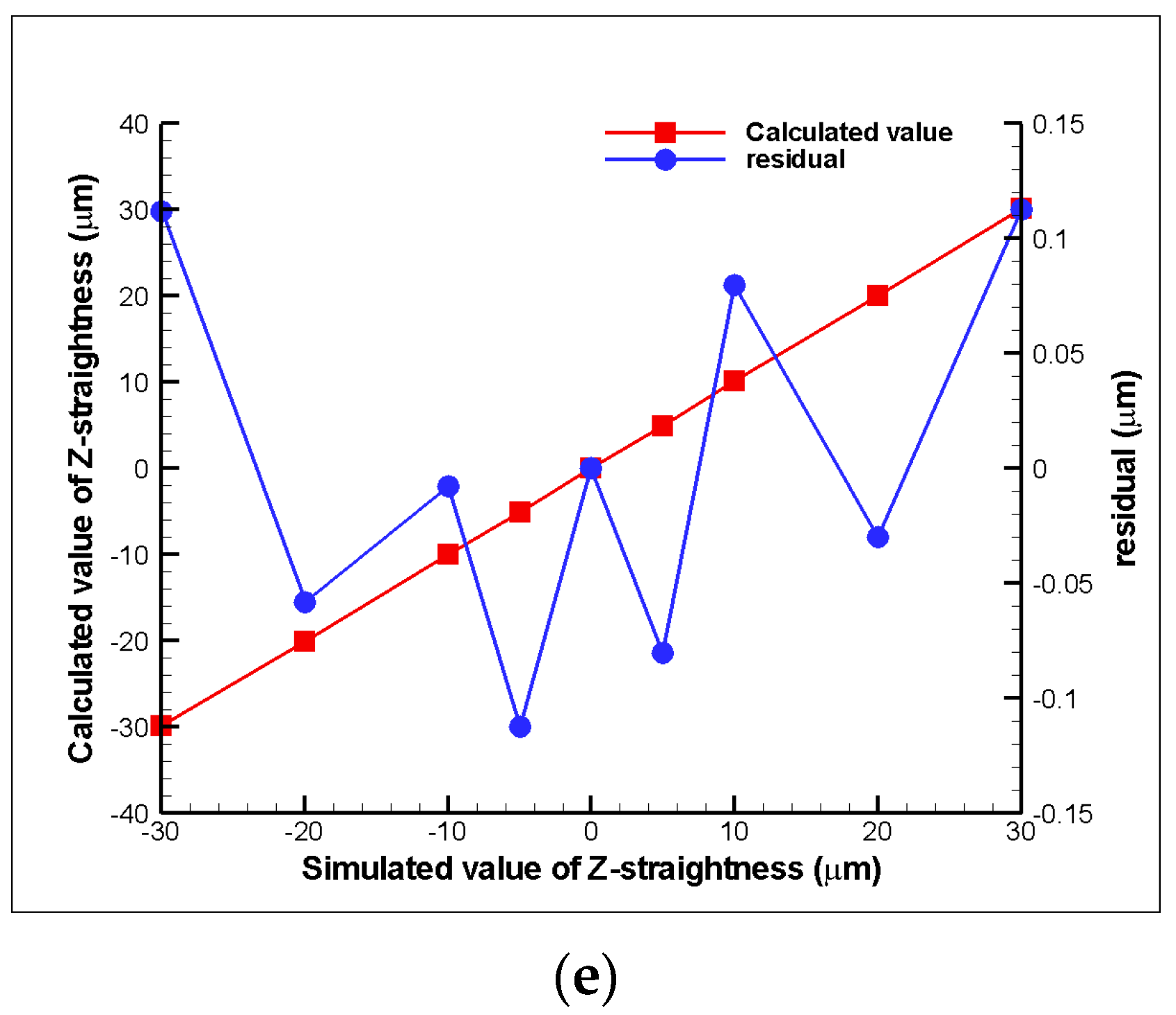
3. Numerical Simulation and Mathematical Model
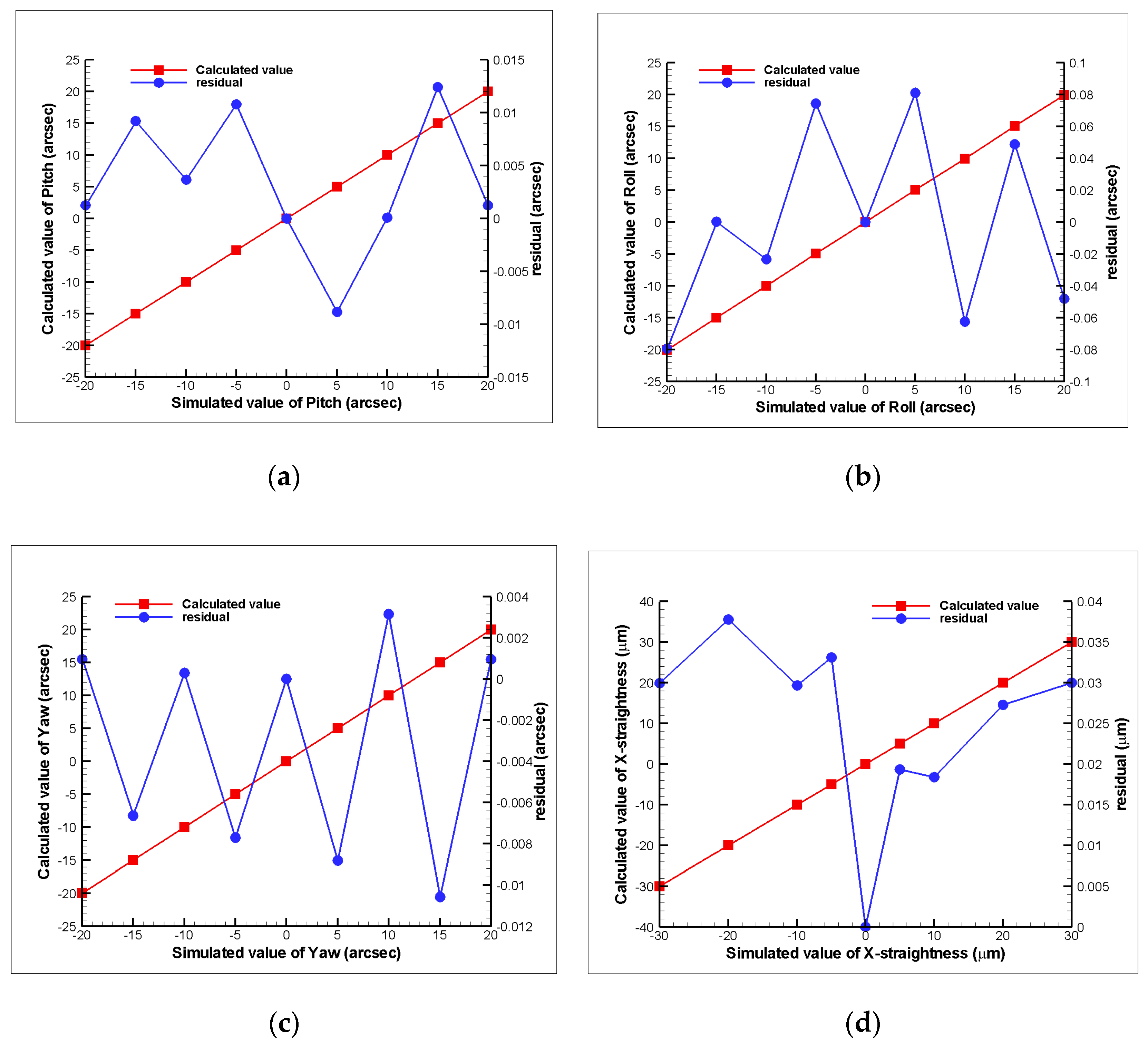
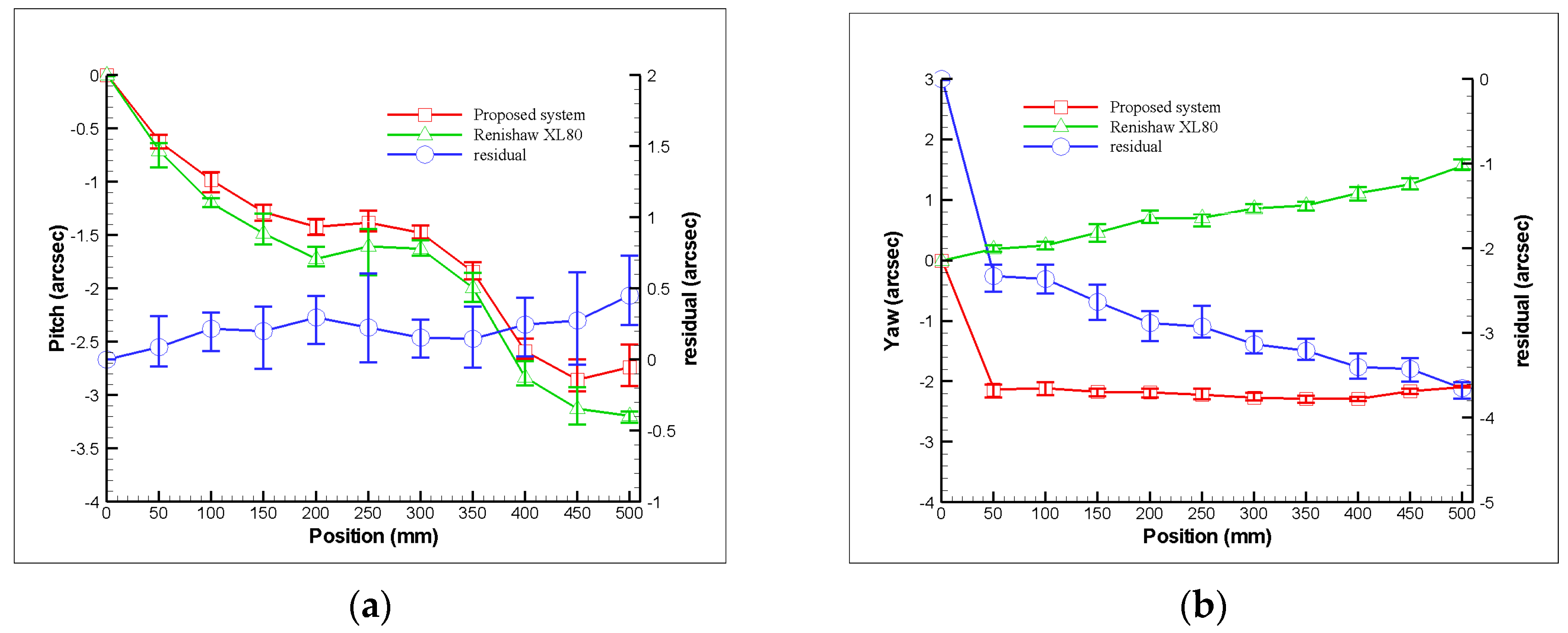
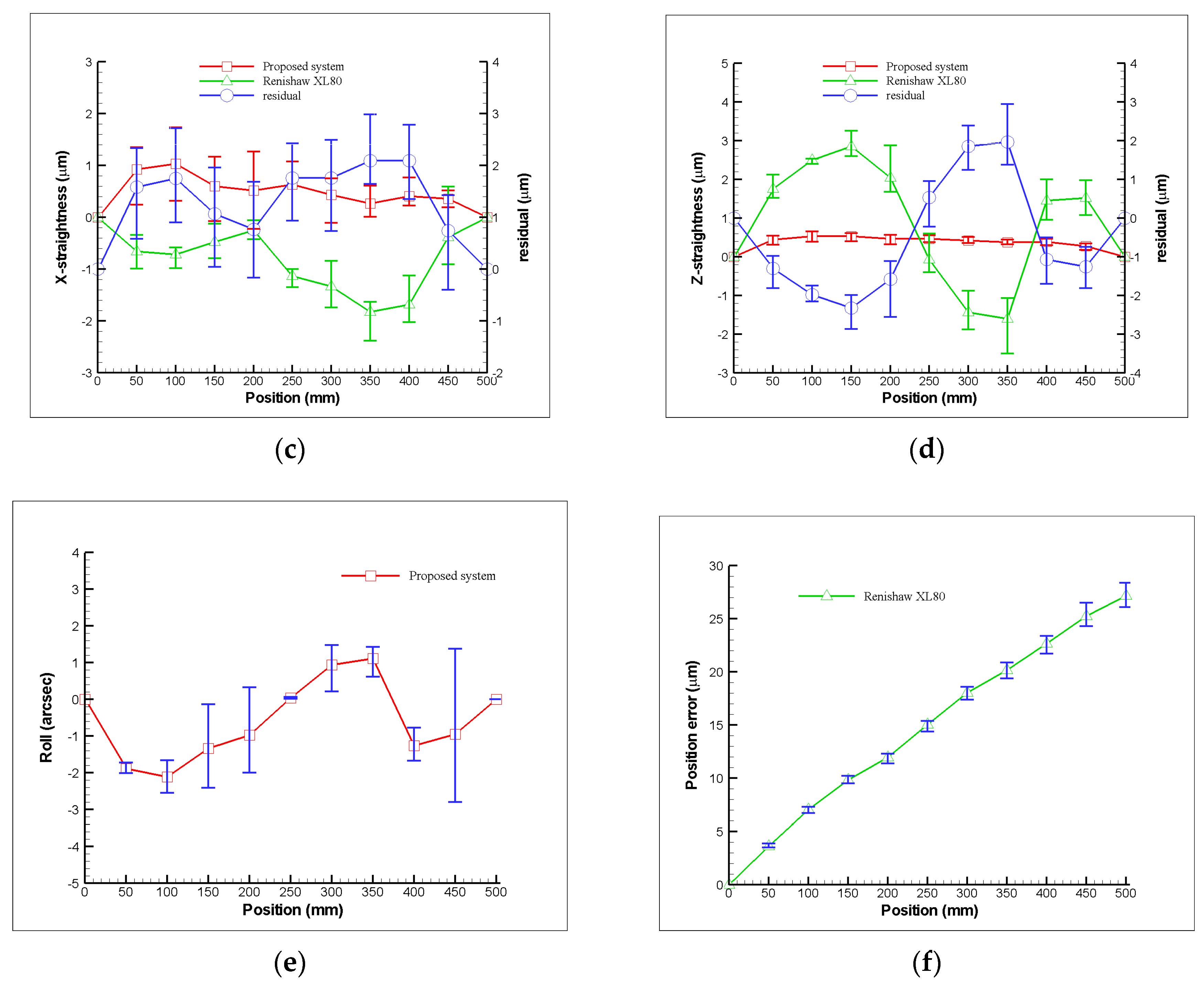
4. Experimental characterization
5. Conclusions
6. Patents
Author Contributions
Funding
Conflicts of Interest
References
- Lee, C.B.; Kim, G.H.; Lee, S.K. Uncertainty investigation of grating interferometry in six degree-of-freedom motion error measurements. Int. J. Precis. Eng. Manuf. 2012, 13, 1509–1515. [Google Scholar] [CrossRef]
- Lee, C.B.; Lee, S.K. Multi-degree-of-freedom motion error measurement in an ultraprecision machine using laser encoder—Review. J. Mech. Sci. Technol. 2013, 27, 141–152. [Google Scholar] [CrossRef]
- Liu, C.H.; Jywe, W.Y.; Hsu, C.C.; Hsu, T.H. Development of a laser-based high-precision six-degrees-of-freedom motion errors measuring system for linear stage. Rev. Sci. Instrum. 2005, 76, 055110. [Google Scholar] [CrossRef]
- Chen, Y.T.; Lin, W.C.; Liu, C.S. Design and experimental verification of novel six-degree-of freedom geometric error measurement system for linear stage. Opt. Lasers Eng. 2017, 92, 94–104. [Google Scholar] [CrossRef]
- Fan, K.C.; Chen, M.J. A 6-degree-of-freedom measurement system for the accuracy of X-Y stages. Precis. Eng. 2000, 24, 15–23. [Google Scholar] [CrossRef]
- Cui, C.; Feng, Q.; Zhang, B.; Zhao, Y. System for simultaneously measuring 6DOF geometric motion errors using a polarization maintaining fiber-coupled dual-frequency laser. Opt. Express 2016, 24, 6735–6748. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Mayor, R.; Ni, J. Development of a six-degree-of-freedom geometric error measurement system for a meso-scale machine tool. J. Manuf. Sci. Eng.-Trans. ASME 2005, 127, 857–865. [Google Scholar] [CrossRef]
- Feng, Q.; Zhang, B.; Cui, C.; Kuang, C.; Zhai, Y.; You, F. Development of a simple system for simultaneously measuring 6DOF geometric motion errors of a linear guide. Opt. Express 2013, 21, 25805–25819. [Google Scholar]
- Renishaw plc, “XL-80,” Renishaw. Available online: https://www.renishaw.com.tw/tw/xl-80-laser- system--8268 (accessed on 14 November 2018).
- Okafor, A.C.; Ertekin, Y.M. Vertical machining center accuracy characterization using laser interferometer, part one: Linear positional errors. J. Mater. Process. Technol. 2000, 105, 394–406. [Google Scholar] [CrossRef]
- Okafor, A.C.; Ertekin, Y.M. Vertical machining center accuracy characterization using laser interferometer, part two: Angular errors. J. Mater. Process. Technol. 2000, 105, 407–420. [Google Scholar] [CrossRef]
- Wang, W.; Kweon, S.H.; Hwang, C.S.; Kang, N.C.; Kim, Y.S.; Yang, S.H. Development of an optical measuring system for integrated geometric errors of a three-axis miniaturized machine tool. Int. J. Adv. Manuf. Technol. 2009, 43, 701–709. [Google Scholar] [CrossRef]
- Yu, X.; Gillmer, S.R.; Woody, S.C.; Ellis, J.D. Development of a compact, fiber-coupled, six degree-of-freedom measurement system for precision linear stage metrology. Rev. Sci. Instrum. 2016, 87, 065109. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.T.; Hu, J.C.; Chen, L.M. Study on fast and precise measurement of three-dimensional displacement using hall sensors. Adv. Mater. Res. 2013, 694–697, 1034–1038. [Google Scholar] [CrossRef]
- Allred, C.J.; Jolly, M.R.; Buckner, G.D. Real-time estimation of helicopter blade kinematics using integrated linear displacement sensors. Aerosp. Sci. Technol. 2015, 42, 274–286. [Google Scholar] [CrossRef]
- Mura, A. Six dof displacement measuring device based on a modified Stewart platform. Mechatronics 2011, 21, 1309–1316. [Google Scholar] [CrossRef]
- Mura, A. Multi-dofs MEMS displacement sensors based on the Stewart platform theory. Microsyst. Technol. 2012, 18, 575–579. [Google Scholar] [CrossRef]
- Mura, A. Sensitivity analysis of a six degrees of freedom displacement measuring device. Proc. Inst. Mech. Eng. C 2014, 228, 158–168. [Google Scholar] [CrossRef]
- Fan, K.C.; Chen, M.J.; Huang, W.M. A six-degree-of-freedom measurement system for the motion accuracy of linear stages. Int. J. Mach. Tools Manuf. 1998, 38, 155–164. [Google Scholar] [CrossRef]
- Chen, B.; Xu, B.; Yan, L.; Zhang, E.; Liu, Y. Laser straightness interferometer system with rotational error compensation and simultaneous measurement of six degrees of freedom error parameters. Opt. Express 2015, 23, 9052–9073. [Google Scholar] [CrossRef]
- Lou, Y.; Yan, L.; Chen, B.; Zhang, S. Laser homodyne straightness interferometer with simultaneous measurement of six degrees of freedom motion errors for precision linear stage metrology. Opt. Express 2017, 25, 6805–6821. [Google Scholar] [CrossRef]
- Gao, W.; Arai, Y.; Shibuya, A.; Kiyono, S.; Park, C.H. Measurement of multi-degree-of-freedom error motions of a precision linear air-bearing stage. Precis. Eng. 2006, 30, 97–103. [Google Scholar] [CrossRef]
- Gao, W.; Saito, Y.; Muto, H.; Arai, Y.; Shimizu, Y. A three-axis autocollimator for detection of angular error motions of a precision stage. CIRP Ann.-Manuf. Tech. 2011, 60, 515–518. [Google Scholar] [CrossRef]
- Kuang, C.F.; Hong, H.; Ni, J. A high-precision five-degree-of-freedom measurement system based on laser collimator and interferometry techniques. AIP Rev. Sci. Instrum. 2007, 78, 095105. [Google Scholar] [CrossRef] [PubMed]
- Feng, Q.; Zhang, B.; Kuang, C. Four degree-of-freedom geometric measurement system with common-path compensation for laser beam drift. Int. J. Precis. Eng. Manuf. 2008, 9, 26–31. [Google Scholar]
- Gao, S.; Zhang, B.; Feng, Q.; Cui, C.; Chen, S.; Zhao, Y. Errors crosstalk analysis and compensation in the simultaneous measuring system for five-degree-of-freedom geometric error. Appl. Opt. 2015, 54, 458–466. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, B.; Feng, Q. Measurement system and model for simultaneously measuring 6DOF geometric errors. Opt. Express 2017, 25, 20993–201007. [Google Scholar] [CrossRef]
- Chen, Y.T.; Huang, Y.S.; Liu, C.S. An optical sensor for measuring the position and slanting direction of flat surfaces. Sensors 2016, 16, 1061. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.S.; Pu, Y.F.; Chen, Y.T.; Luo, Y.T. Design of a measurement system for simultaneously measuring six-degree-of-freedom geometric errors of a long linear stage. Sensors 2018, 18, 3875. [Google Scholar] [CrossRef]
- Liu, C.S.; Lin, P.D. Determination of linear equations of position sensing detectors in small motion measurement systems. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 2010, 27, 2480–2487. [Google Scholar] [CrossRef]
- Liu, C.S.; Lin, P.D. Jacobian and Hessian matrices of optical path length for computing the wave front shape, irradiance, and caustics in optical systems. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 2012, 29, 2272–2280. [Google Scholar]
- Lin, P.D. New Computation Methods for Geometrical Optics; Springer: Singapore, 2013. [Google Scholar]
- Chang, Y.H.; Liu, C.S.; Chen, C.C. Design and characterization of a fast steering mirror compensation system based on double Porro prisms by a screw-ray tracing method. Sensors 2018, 18, 4046. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.S.; Lin, K.W. Numerical and experimental characterization of reducing geometrical fluctuations of laser beam based on rotating optical diffuser. Opt. Eng. 2014, 53, 122408. [Google Scholar] [CrossRef]
- Liu, C.S.; Jiang, S.H. A novel laser displacement sensor with improved robustness toward geometrical fluctuations of the laser beam. Meas. Sci. Technol. 2013, 24, 105101. [Google Scholar] [CrossRef]
- Liu, C.S.; Jiang, S.H. Precise autofocusing microscope with rapid response. Opt. Lasers Eng. 2015, 66, 294–300. [Google Scholar] [CrossRef]
- Liu, C.S.; Lin, Y.C.; Hu, P.H. Design and characterization of precise laser-based autofocusing microscope with reduced geometrical fluctuations. Microsyst. Technol. 2015, 19, 1717–1724. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.-S.; Lai, J.-J.; Luo, Y.-T. Design of a Measurement System for Six-Degree-of-Freedom Geometric Errors of a Linear Guide of a Machine Tool. Sensors 2019, 19, 5. https://doi.org/10.3390/s19010005
Liu C-S, Lai J-J, Luo Y-T. Design of a Measurement System for Six-Degree-of-Freedom Geometric Errors of a Linear Guide of a Machine Tool. Sensors. 2019; 19(1):5. https://doi.org/10.3390/s19010005
Chicago/Turabian StyleLiu, Chien-Sheng, Jia-Jun Lai, and Yong-Tai Luo. 2019. "Design of a Measurement System for Six-Degree-of-Freedom Geometric Errors of a Linear Guide of a Machine Tool" Sensors 19, no. 1: 5. https://doi.org/10.3390/s19010005
APA StyleLiu, C.-S., Lai, J.-J., & Luo, Y.-T. (2019). Design of a Measurement System for Six-Degree-of-Freedom Geometric Errors of a Linear Guide of a Machine Tool. Sensors, 19(1), 5. https://doi.org/10.3390/s19010005




