Towards Inertial Sensor Based Mobile Gait Analysis: Event-Detection and Spatio-Temporal Parameters
Abstract
1. Introduction
2. Materials and Methods
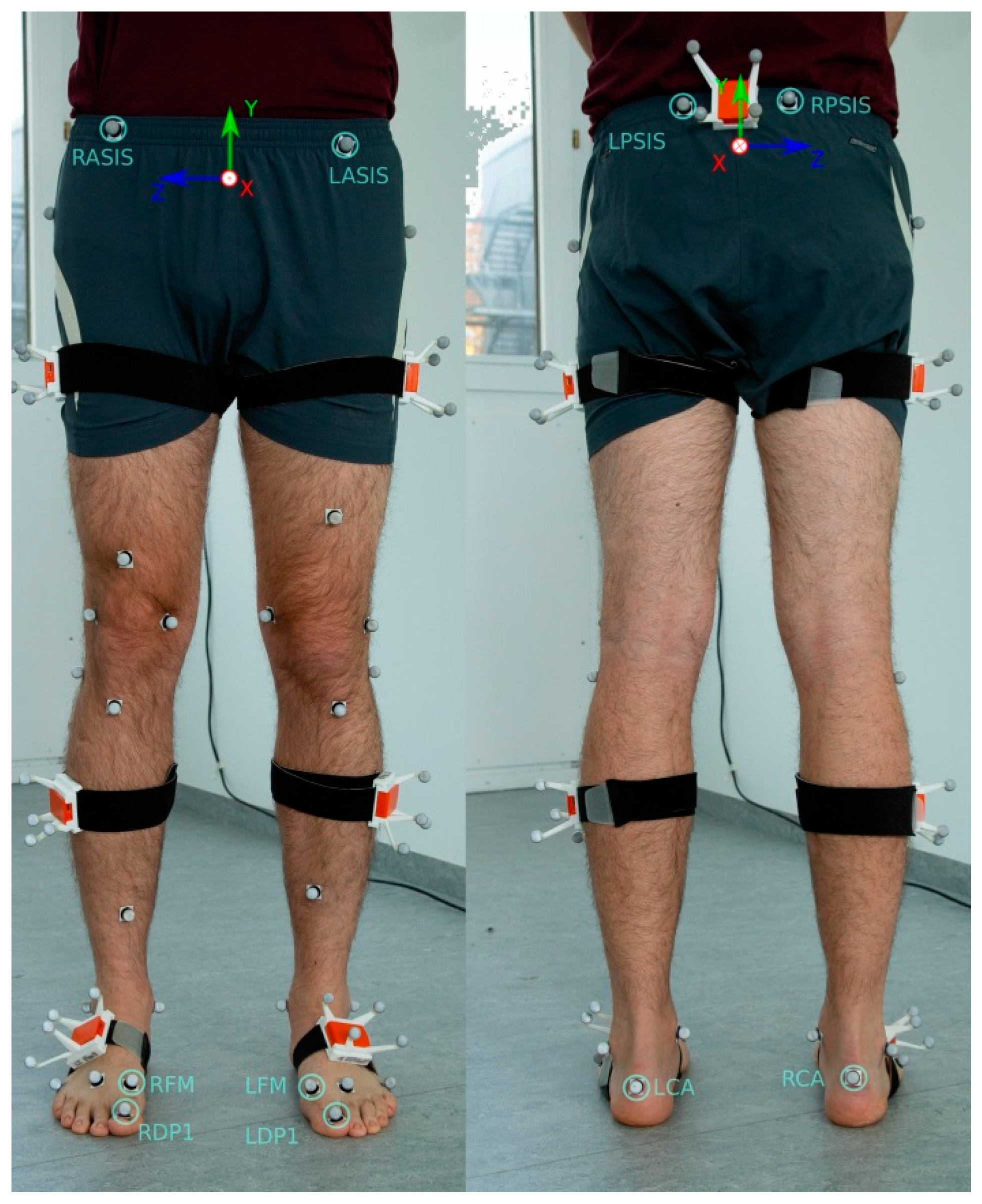
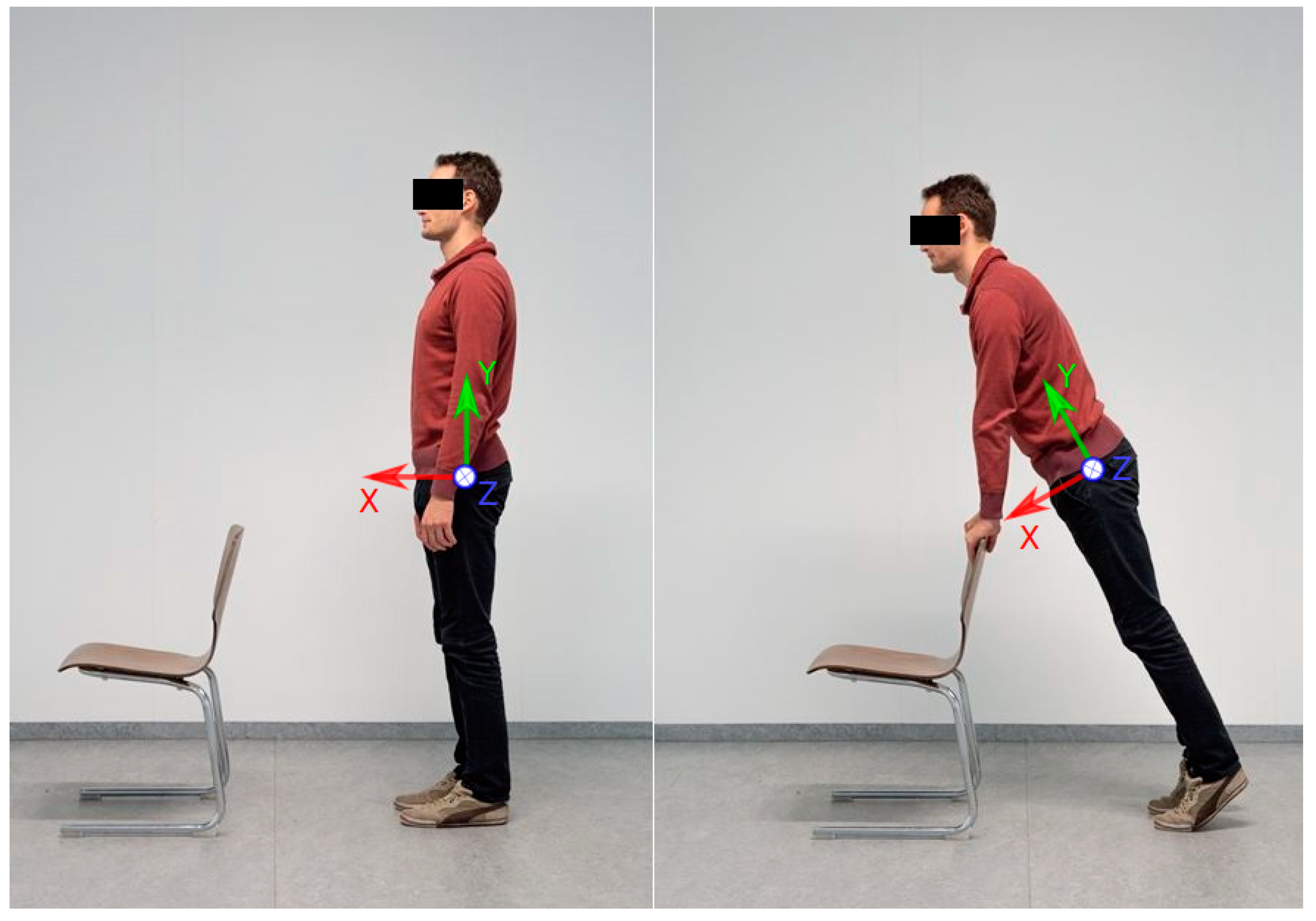
2.1. Subjects and Data Acquisition
2.2. Statistical Analysis
3. Results
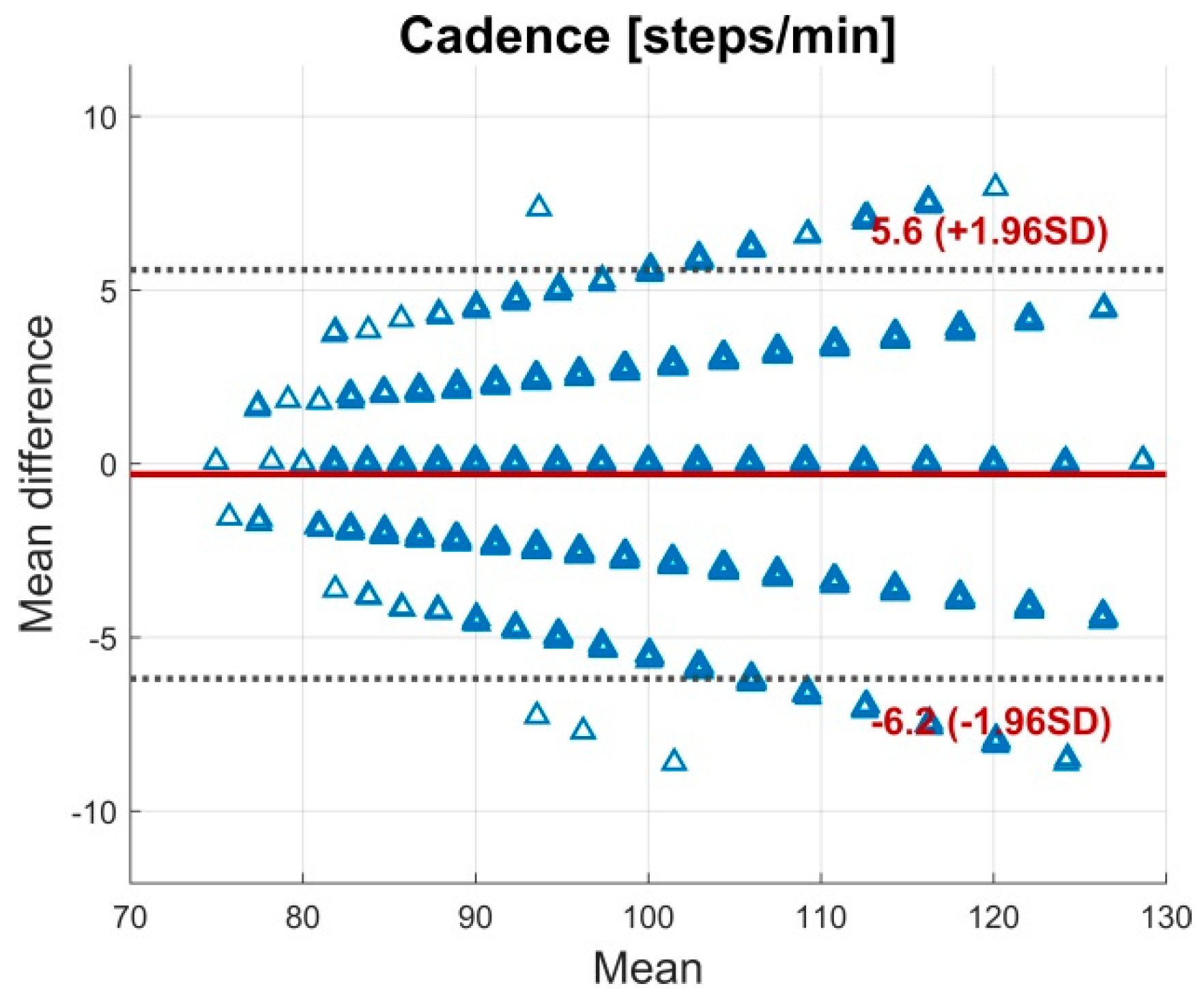
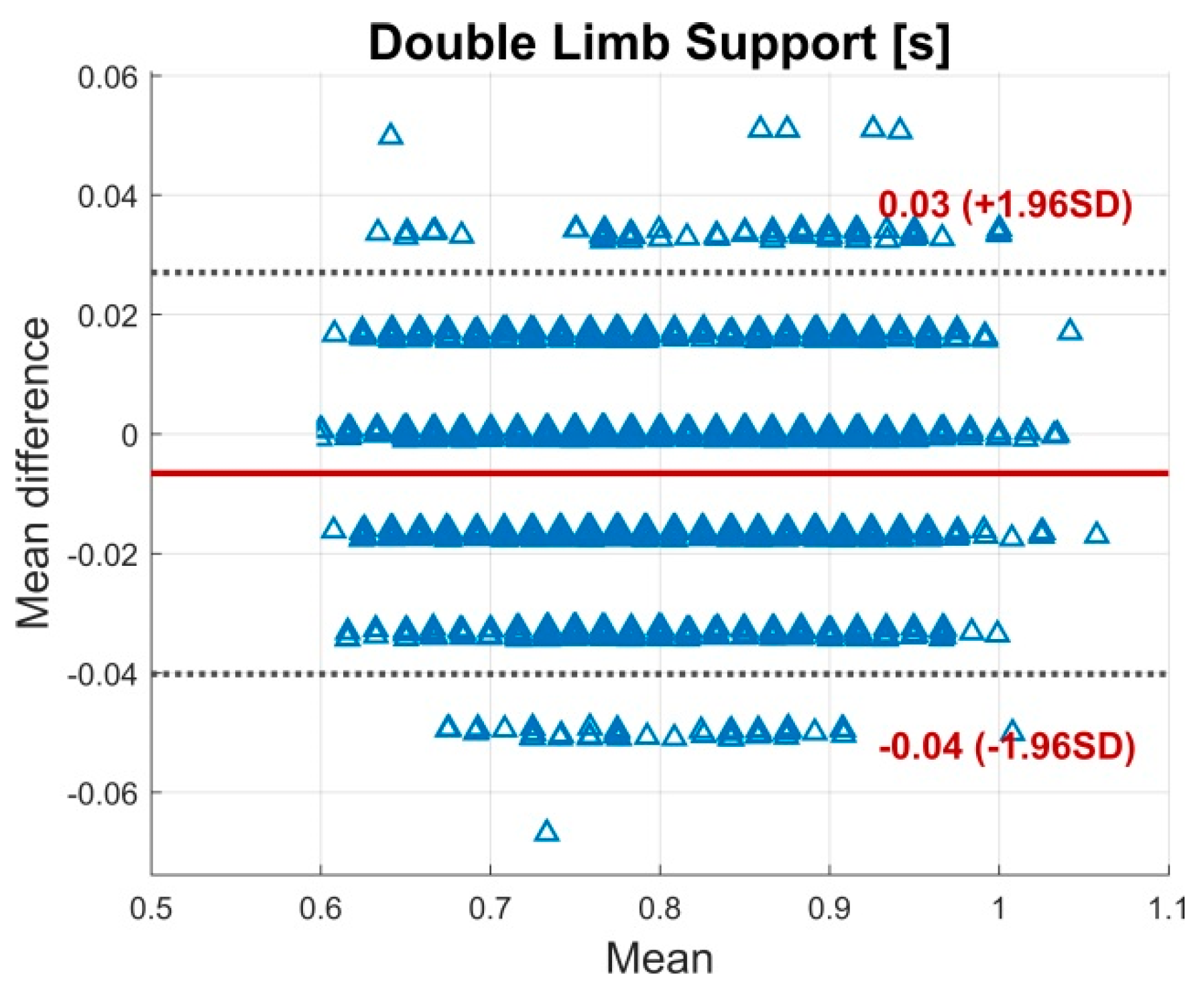
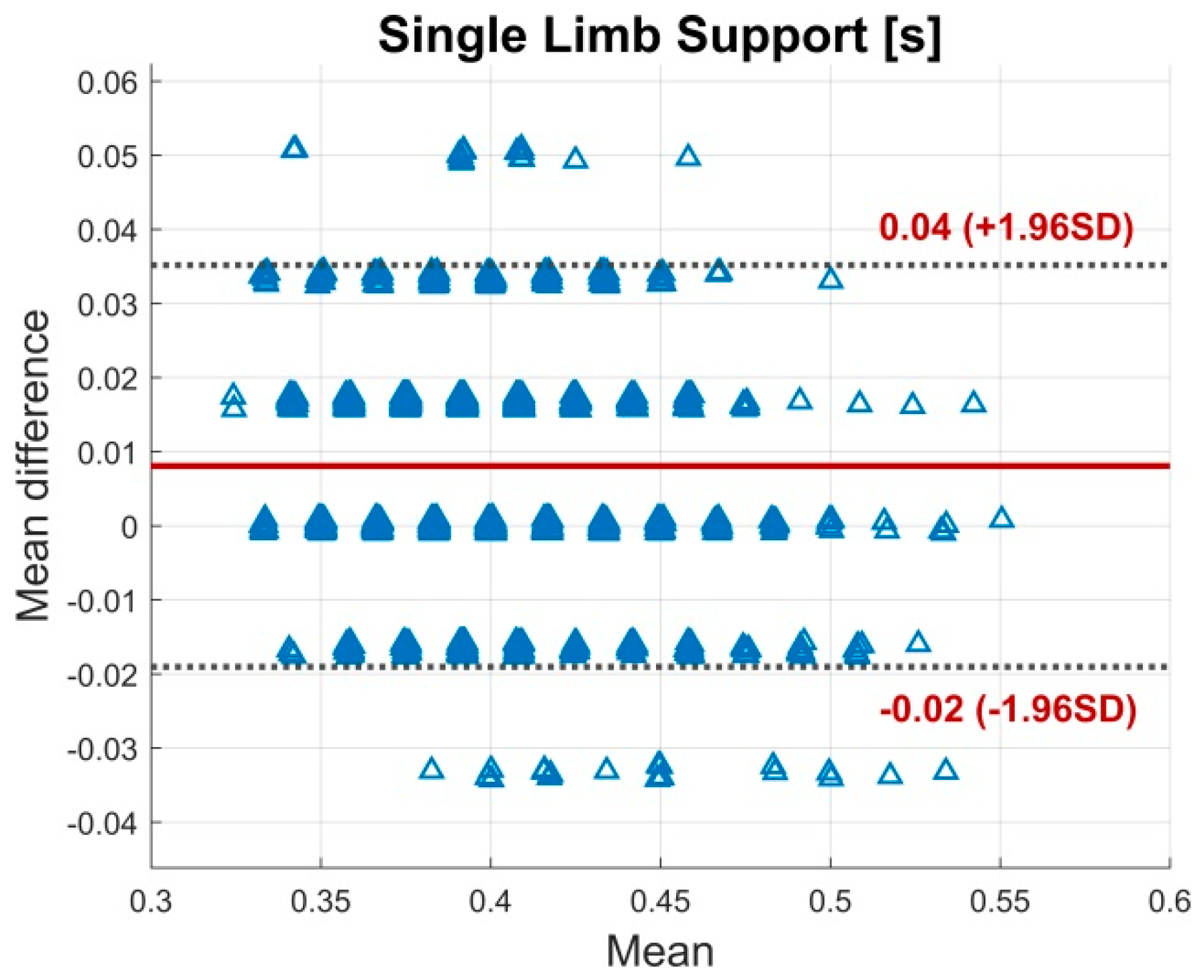
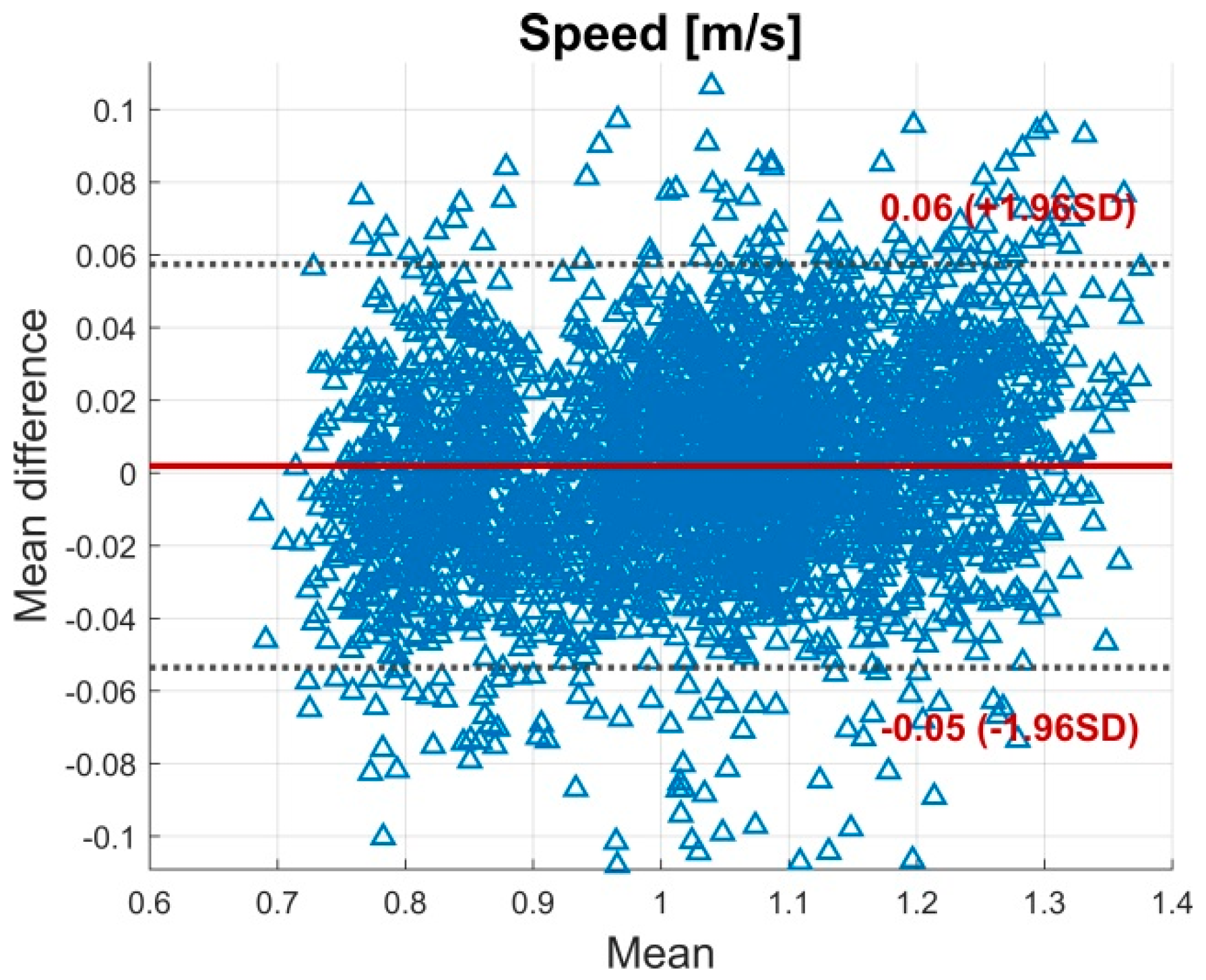
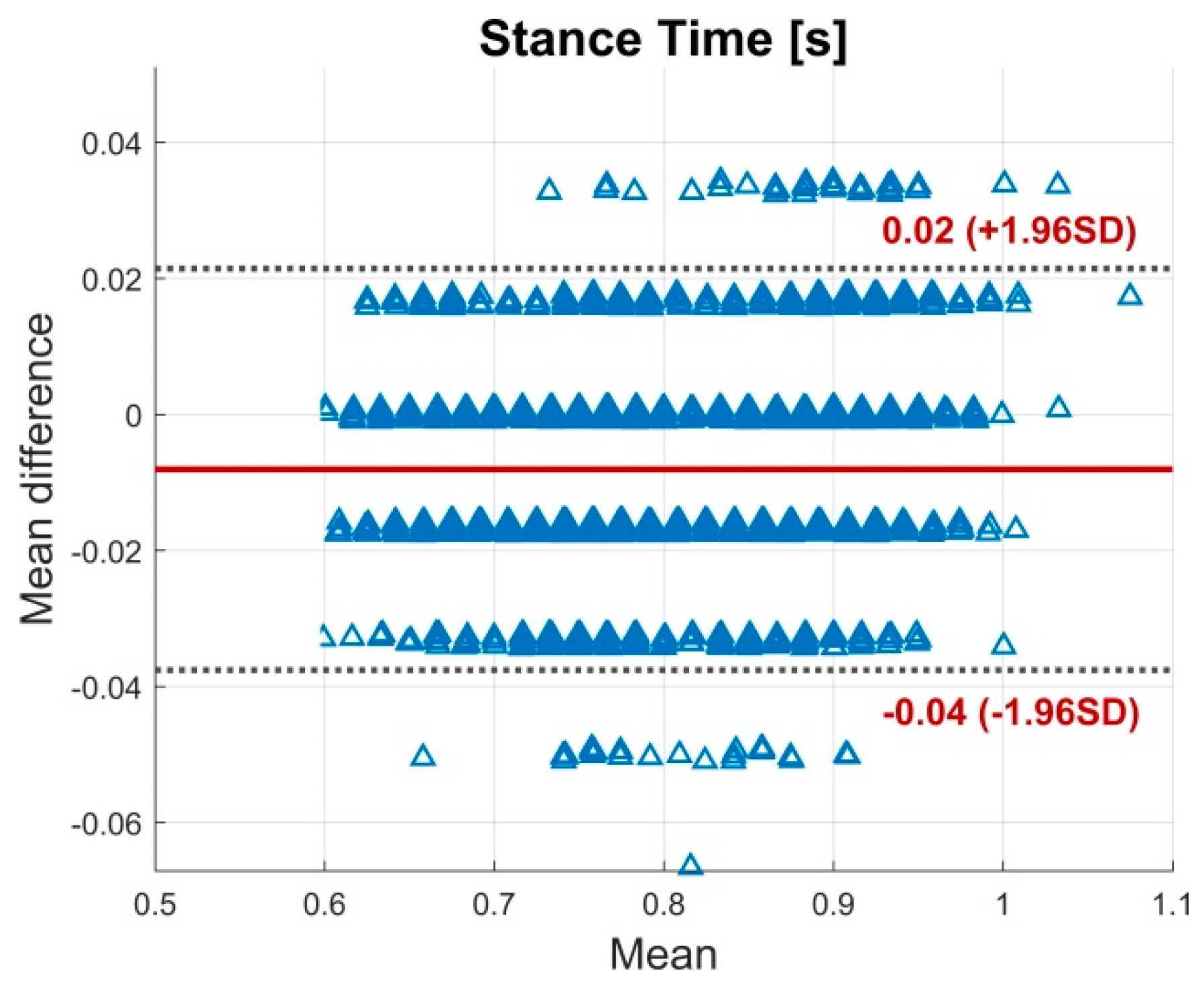
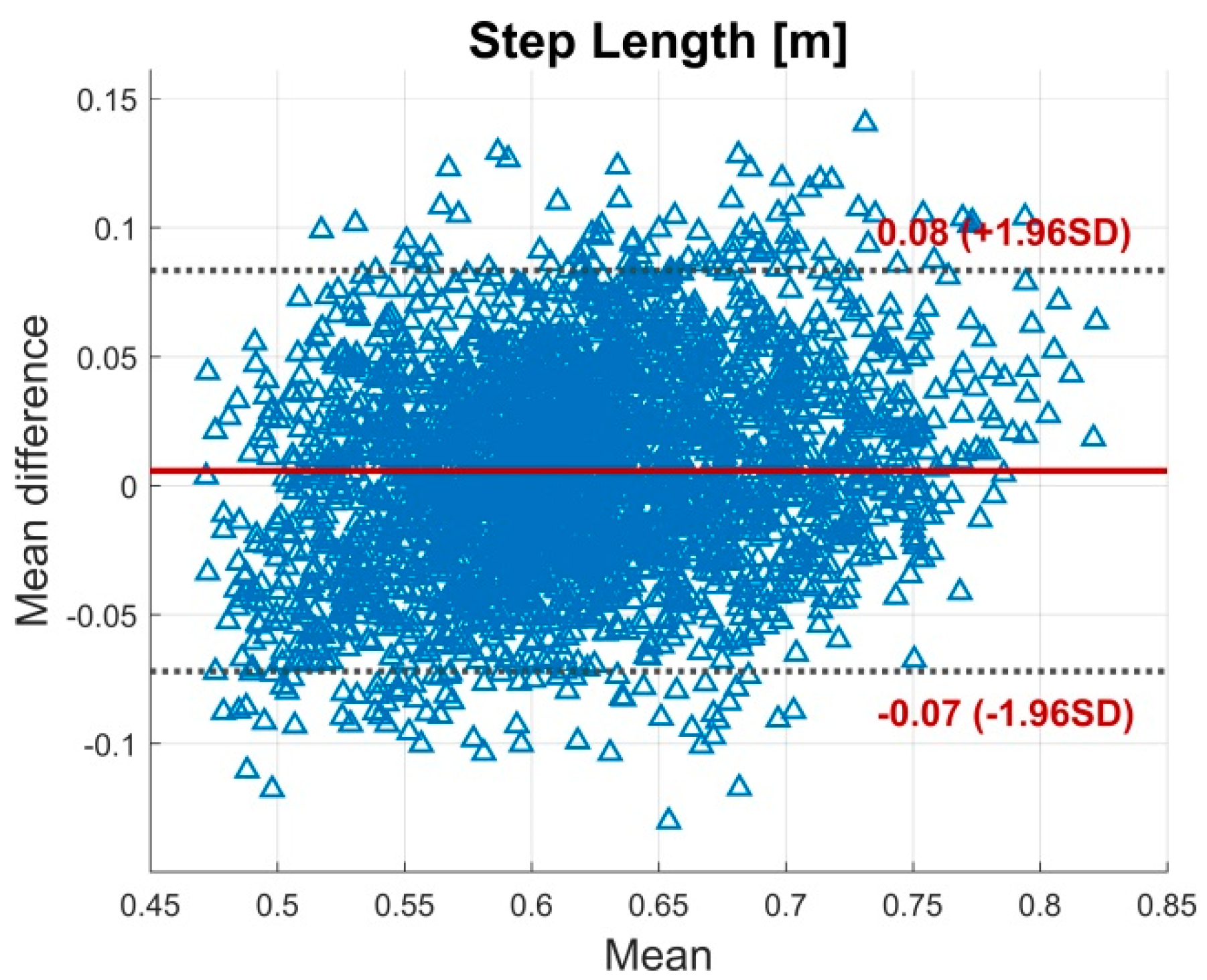
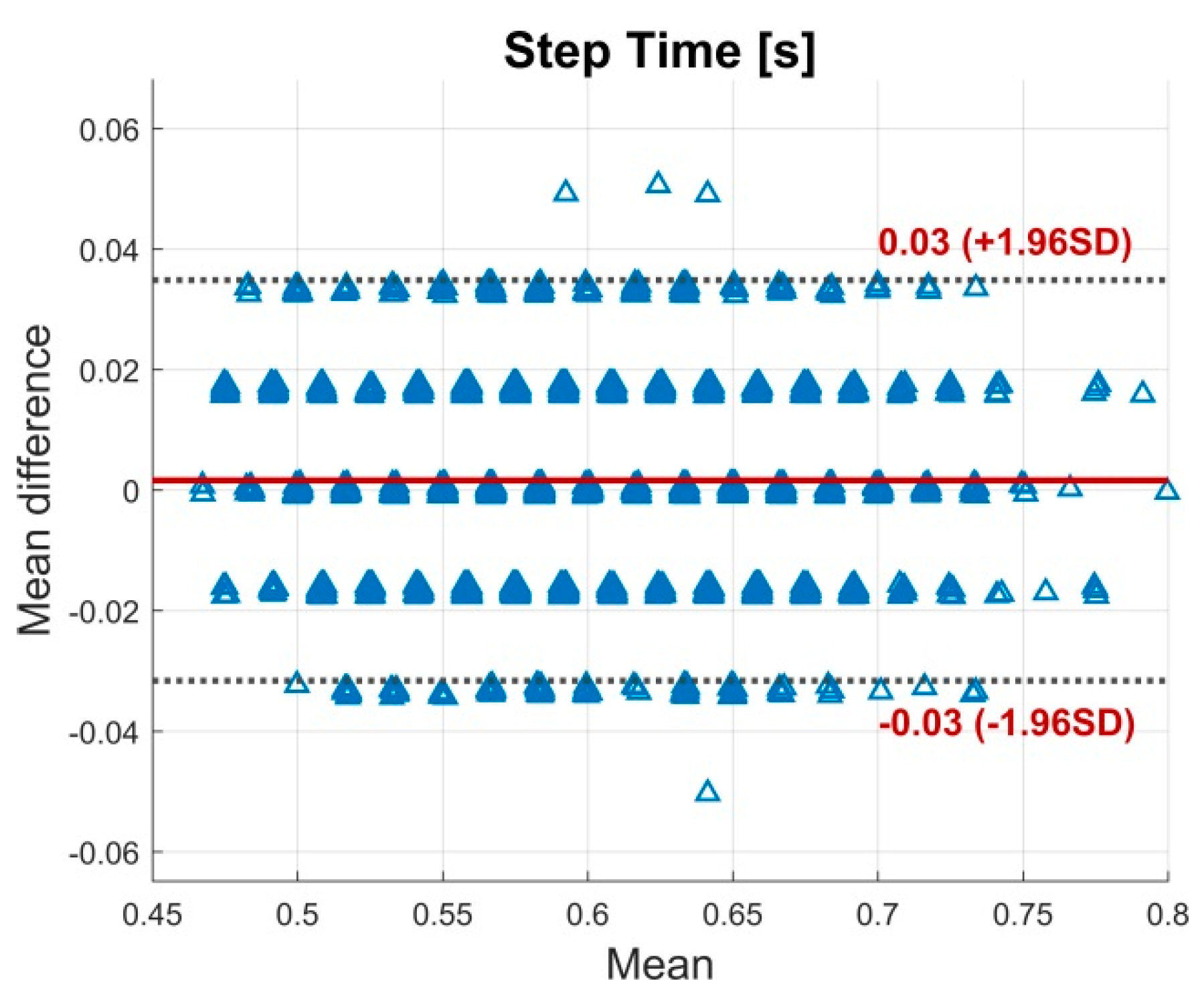
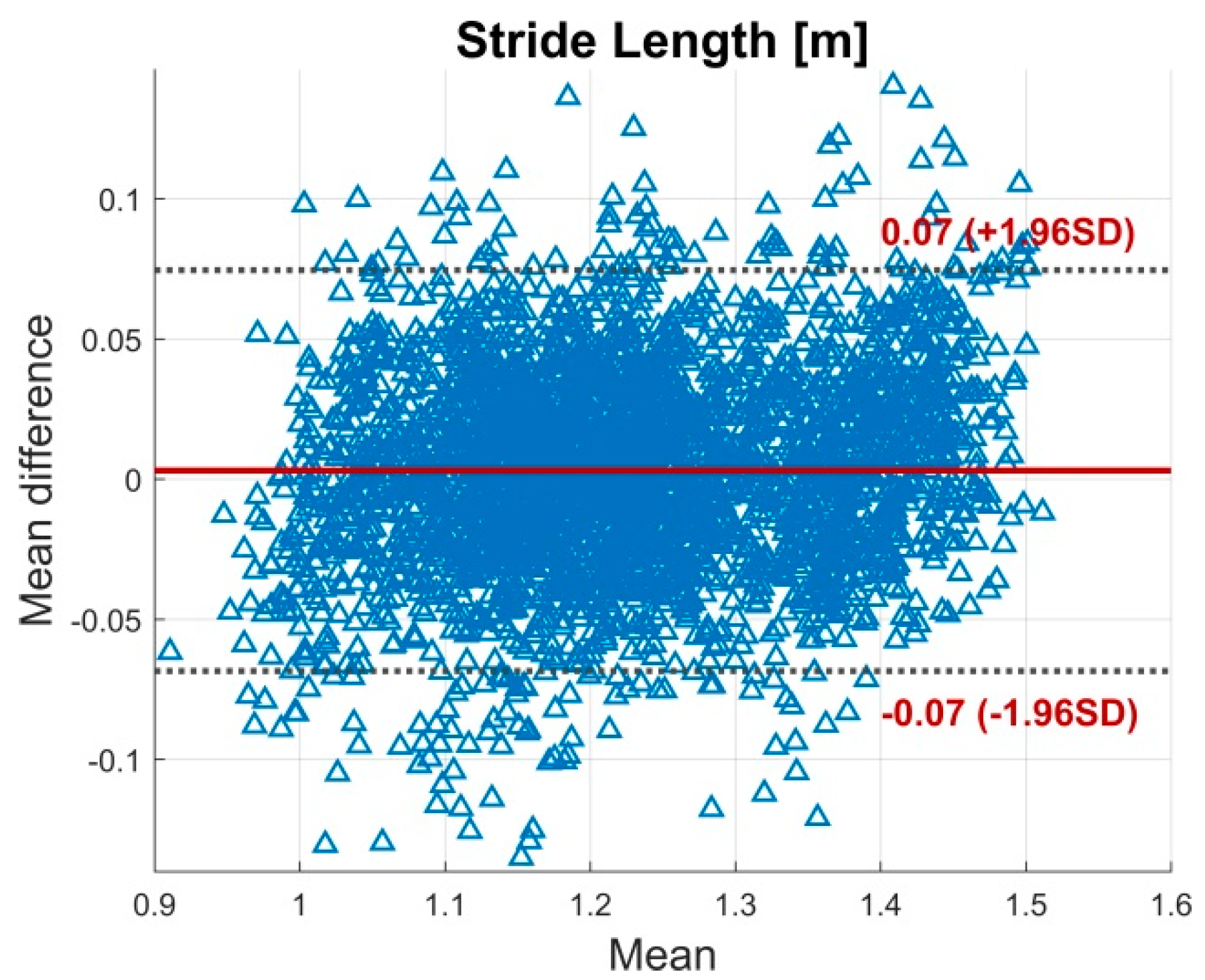
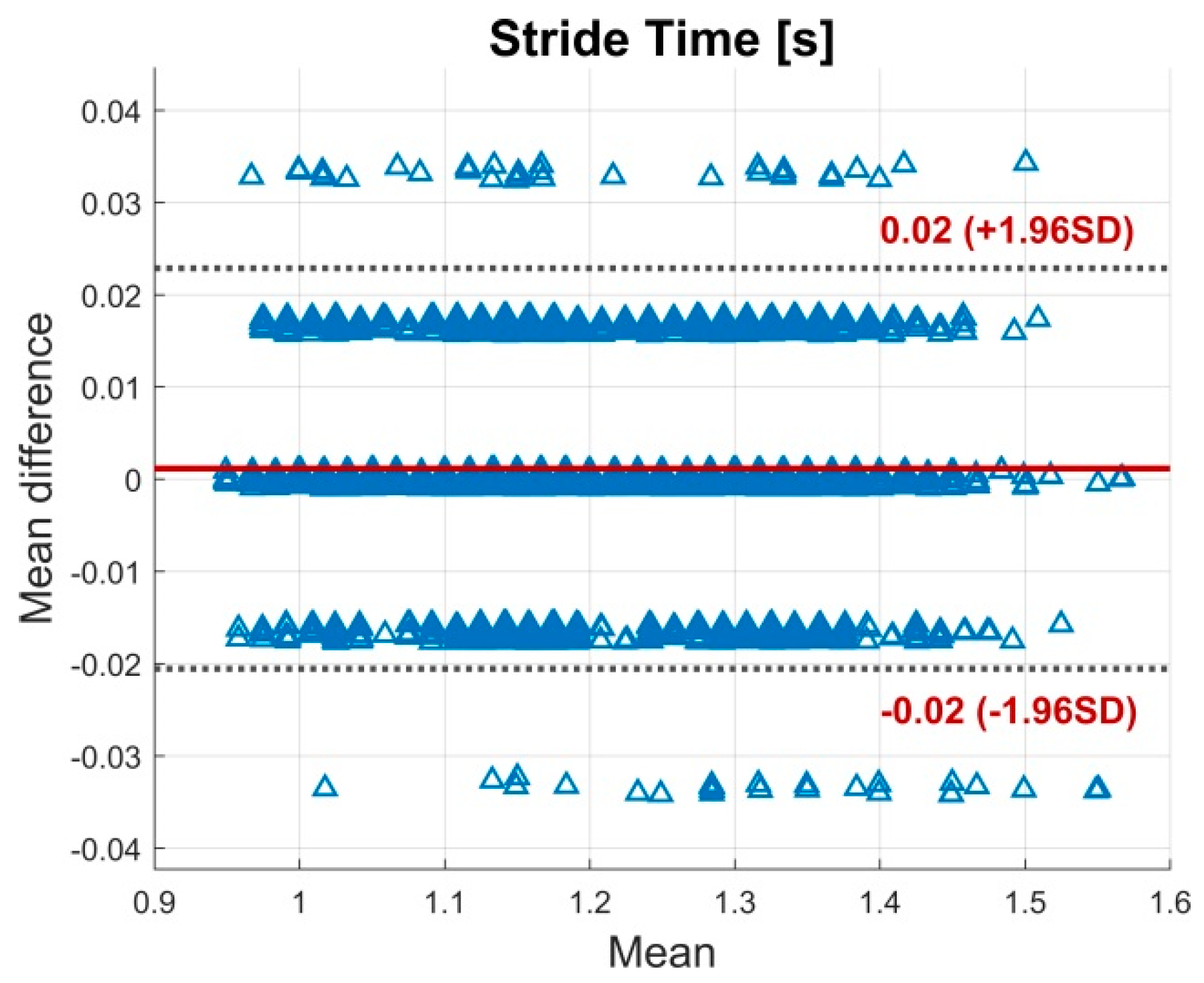
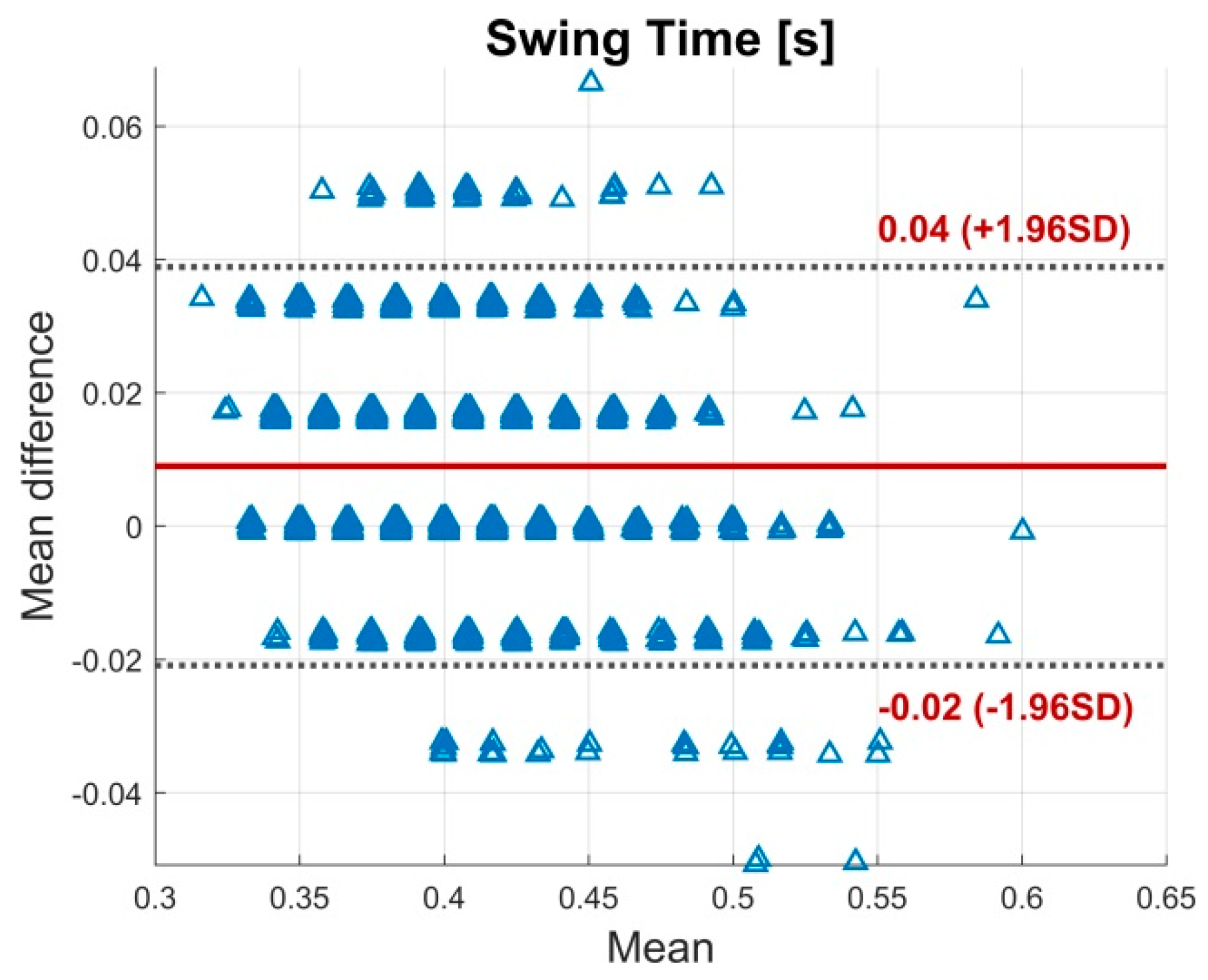
3.1. Validity
3.2. Test-Retest Reliability
4. Discussion
4.1. Validity
4.2. Test-Retest Reliability
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Ethical Statements
Appendix A
References
- Loske, S.; Nüesch, C.; Byrnes, K.S.; Fiebig, O.; Schären, S.; Mündermann, A.; Netzer, C. Decompression surgery improves gait quality in patients with symptomatic lumbar spinal stenosis. Spine J. 2018, 18, 2195–2204. [Google Scholar] [CrossRef] [PubMed]
- Zomar, B.O.; Bryant, D.; Hunter, S.; Howard, J.L.; Vasarhelyi, E.M.; Lanting, B.A. A randomised trial comparing spatio-temporal gait parameters after total hip arthroplasty between the direct anterior and direct lateral surgical approaches. HIP Int. 2018, 28, 478–484. [Google Scholar] [CrossRef] [PubMed]
- Steultjens, M.P.M.; Dekker, J.; van Baar, M.E.; Oostendorp, R.A.B.; Bijlsma, J.W.J. Range of joint motion and disability in patients with osteoarthritis of the knee or hip. Rheumatology 2000, 39, 955–961. [Google Scholar] [CrossRef] [PubMed]
- Bertoli, M.; Cereatti, A.; Trojaniello, D.; Avanzino, L.; Pelosin, E.; Del Din, S.; Rochester, L.; Ginis, P.; Bekkers, E.M.J.; Mirelman, A.; et al. Estimation of spatio-temporal parameters of gait from magneto-inertial measurement units: Multicenter validation among Parkinson, mildly cognitively impaired and healthy older adults. Biomed. Eng. OnLine 2018, 17, 58. [Google Scholar] [CrossRef] [PubMed]
- Pau, M.; Corona, F.; Pili, R.; Casula, C.; Guicciardi, M.; Cossu, G.; Murgia, M. Quantitative assessment of gait parameters in people with Parkinson’s disease in laboratory and clinical setting: Are the measures interchangeable? Neurol. Int. 2018, 10, 7729. [Google Scholar] [CrossRef] [PubMed]
- Leijendekkers, R.A.; Marra, M.A.; Kolk, S.; van Bon, G.; Schreurs, B.W.; Weerdesteyn, V.; Verdonschot, N. Gait symmetry and hip strength in women with developmental dysplasia following hip arthroplasty compared to healthy subjects: A cross-sectional study. PLoS ONE 2018, 13, e0193487. [Google Scholar] [CrossRef] [PubMed]
- Radzak, K.N.; Putnam, A.M.; Tamura, K.; Hetzler, R.K.; Stickley, C.D. Asymmetry between lower limbs during rested and fatigued state running gait in healthy individuals. Gait Posture 2017, 51, 268–274. [Google Scholar] [CrossRef] [PubMed]
- Picerno, P. 25 years of lower limb joint kinematics by using inertial and magnetic sensors: A review of methodological approaches. Gait Posture 2017, 51, 239–246. [Google Scholar] [CrossRef] [PubMed]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G.; Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends Supporting the In-Field Use of Wearable Inertial Sensors for Sport Performance Evaluation: A Systematic Review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef] [PubMed]
- Kianifar, R.; Lee, A.; Raina, S.; Kulic, D. Classification of Squat Quality with Inertial Measurement Units in the Single Leg Squat Mobility Test. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016. [Google Scholar]
- Robert-Lachaine, X.; Mecheri, H.; Larue, C.; Plamondon, A. Validation of inertial measurement units with an optoelectronic system for whole-body motion analysis. Med. Biol. Eng. Comput. 2017, 55, 609–619. [Google Scholar] [CrossRef]
- Al-Amri, M.; Nicholas, K.; Button, K.; Sparkes, V.; Sheeran, L.; Davies, J.L. Inertial Measurement Units for Clinical Movement Analysis: Reliability and Concurrent Validity. Sensors 2018, 18, 719. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Lach, J.; Lo, B.; Yang, G.Z. Toward Pervasive Gait Analysis With Wearable Sensors: A Systematic Review. IEEE J. Biomed. Health Inform. 2016, 20, 1521–1537. [Google Scholar] [CrossRef] [PubMed]
- Caldas, R.; Mundt, M.; Potthast, W.; Buarque de Lima Neto, F.; Markert, B. A systematic review of gait analysis methods based on inertial sensors and adaptive algorithms. Gait Posture 2017, 57, 204–210. [Google Scholar] [CrossRef] [PubMed]
- Seel, T.; Cermeño Escobar, V.; Raisch, J.; Schauer, T. Online Gait Phase Detection with Automatic Adaption to Gait Velocity Changes Using Accelerometers and Gyroscopes. Biomed. Tech. 2014, 59, S795–S798. [Google Scholar]
- Müller, P.; Seel, T.; Schauer, T. Experimental Evaluation of a Novel Inertial Sensor Based Realtime Gait Phase Detection Algorithm. Available online: https://www.control.tu-berlin.de/wiki/images/5/5e/Mueller_TAR2015.pdf (accessed on 26 November 2018).
- Schwesig, R.; Leuchte, S.; Fischer, D.; Ullmann, R.; Kluttig, A. Inertial sensor based reference gait data for healthy subjects. Gait Posture 2011, 33, 673–678. [Google Scholar] [CrossRef] [PubMed]
- Kluge, F.; Gaßner, H.; Hannink, J.; Pasluosta, C.; Klucken, J.; Eskofier, B.M. Towards Mobile Gait Analysis: Concurrent Validity and Test-Retest Reliability of an Inertial Measurement System for the Assessment of Spatio-Temporal Gait Parameters. Sensors 2017, 17, 1522. [Google Scholar] [CrossRef] [PubMed]
- Köse, A.; Cereatti, A.; Della Croce, U. Bilateral step length estimation using a single inertial measurement unit attached to the pelvis. J. NeuroEng. Rehabil. 2012, 9, 9. [Google Scholar] [CrossRef] [PubMed]
- Takeda, R.; Lisco, G.; Fujisawa, T.; Gastaldi, L.; Tohyama, H.; Tadano, S. Drift Removal for Improving the Accuracy of Gait Parameters Using Wearable Sensor Systems. Sensors 2014, 14, 23230–23247. [Google Scholar] [CrossRef]
- Bertuletti, S.; Cereatti, A.; Comotti, D.; Caldara, M.; Della Croce, U. Static and Dynamic Accuracy of an Innovative Miniaturized Wearable Platform for Short Range Distance Measurements for Human Movement Applications. Sensors 2017, 17, 1492. [Google Scholar] [CrossRef]
- Agostini, V.; Gastaldi, L.; Rosso, V.; Knaflitz, M.; Tadano, S. A Wearable Magneto-Inertial System for Gait Analysis (H-Gait): Validation on Normal Weight and Overweight/Obese Young Healthy Adults. Sensors 2017, 17, 2406. [Google Scholar] [CrossRef]
- Cimolin, V.; Capodaglio, P.; Cau, N.; Galli, M.; Santovito, C.; Patrizi, A.; Tringali, G.; Sartorio, A. Computation of spatio-temporal parameters in level walking using a single inertial system in lean and obese adolescents. Biomed. Eng. Biomed. Tech. 2017, 62. [Google Scholar] [CrossRef] [PubMed]
- Nüesch, C.; Roos, E.; Pagenstert, G.; Mündermann, A. Measuring joint kinematics of treadmill walking and running: Comparison between an inertial sensor based system and a camera-based system. J. Biomech. 2017, 57, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Donath, L.; Faude, O.; Lichtenstein, E.; Nüesch, C.; Mündermann, A. Validity and reliability of a portable gait analysis system for measuring spatiotemporal gait characteristics: Comparison to an instrumented treadmill. J. Neuroeng. Rehabil. 2016, 13, 6. [Google Scholar] [CrossRef] [PubMed]
- Donath, L.; Faude, O.; Lichtenstein, E.; Pagenstert, G.; Nüesch, C.; Mündermann, A. Mobile inertial sensor based gait analysis: Validity and reliability of spatiotemporal gait characteristics in healthy seniors. Gait Posture 2016, 49, 371–374. [Google Scholar] [CrossRef] [PubMed]
- Shull, P.B.; Jirattigalachote, W.; Hunt, M.A.; Cutkosky, M.R.; Delp, S.L. Quantified self and human movement: A review on the clinical impact of wearable sensing and feedback for gait analysis and intervention. Gait Posture 2014, 40, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Shull, P.B.; Lurie, K.L.; Cutkosky, M.R.; Besier, T.F. Training multi-parameter gaits to reduce the knee adduction moment with data-driven models and haptic feedback. J. Biomech. 2011, 44, 1605–1609. [Google Scholar] [CrossRef] [PubMed]
- Afzal, M.R.; Oh, M.-K.; Lee, C.-H.; Park, Y.S.; Yoon, J. A Portable Gait Asymmetry Rehabilitation System for Individuals with Stroke Using a Vibrotactile Feedback. BioMed Res. Int. 2015, 2015, 375638. [Google Scholar] [CrossRef]
- Crea, S.; Cipriani, C.; Donati, M.; Carrozza, M.C.; Vitiello, N. Providing Time-Discrete Gait Information by Wearable Feedback Apparatus for Lower-Limb Amputees: Usability and Functional Validation. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 250–257. [Google Scholar] [CrossRef]
- Seel, T.; Laidig, D.; Valtin, M.; Werner, C.; Raisch, J.; Schauer, T. Feedback control of foot eversion in the adaptive peroneal stimulator. In Proceedings of the 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; pp. 1482–1487. [Google Scholar]
- Valtin, M.; Seel, T.; Raisch, J.; Schauer, T. Iterative learning control of drop foot stimulation with array electrodes for selective muscle activation. In Proceedings of the 19th World Congress The International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Teufl, W.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Validity, Test-Retest Reliability and Long-Term Stability of Magnetometer Free Inertial Sensor Based 3D Joint Kinematics. Sensors 2018, 18, 1980. [Google Scholar] [CrossRef]
- Leardini, A.; Sawacha, Z.; Paolini, G.; Ingrosso, S.; Nativo, R.; Benedetti, M.G. A new anatomically based protocol for gait analysis in children. Gait Posture 2007, 26, 560–571. [Google Scholar] [CrossRef]
- Palermo, E.; Rossi, S.; Marini, F.; Patanè, F.; Cappa, P. Experimental evaluation of accuracy and repeatability of a novel body-to-sensor calibration procedure for inertial sensor-based gait analysis. Measurement 2014, 52, 145–155. [Google Scholar] [CrossRef]
- Miezal, M.; Taetz, B.; Bleser, G. On Inertial Body Tracking in the Presence of Model Calibration Errors. Sensors 2016, 16, 1132. [Google Scholar] [CrossRef] [PubMed]
- Miezal, M.; Taetz, B.; Bleser, G. Real-time inertial lower body kinematics and ground contact estimation at anatomical foot points for agile human locomotion. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May– 3 June 2017; pp. 3256–3263. [Google Scholar]
- Carbone, V.; Fluit, R.; Pellikaan, P.; van der Krogt, M.M.; Janssen, D.; Damsgaard, M.; Vigneron, L.; Feilkas, T.; Koopman, H.F.J.M.; Verdonschot, N. TLEM 2.0—A comprehensive musculoskeletal geometry dataset for subject-specific modeling of lower extremity. J. Biomech. 2015, 48, 734–741. [Google Scholar] [CrossRef] [PubMed]
- Dreyfuss, H. The Measure of Man: Human Factors in Design; Whitney Library of Design: New York, NY, USA, 1967; ISBN 978-0-8230-7370-2. [Google Scholar]
- Zeni, J.; Richards, J.; Higginson, J.S. Two simple methods for determining gait events during treadmill and overground walking using kinematic data. Gait Posture 2008, 27, 710–714. [Google Scholar] [CrossRef] [PubMed]
- Mcgraw, K.; Wong, S.P. Forming Inferences About Some Intraclass Correlation Coefficients. Psychol. Methods 1996, 1, 30–46. [Google Scholar] [CrossRef]
- Cicchetti, D.V. Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology. Psychol. Assess. 1994, 6, 284–290. [Google Scholar] [CrossRef]
- Banks, J.J.; Chang, W.-R.; Xu, X.; Chang, C.-C. Using horizontal heel displacement to identify heel strike instants in normal gait. Gait Posture 2015, 42, 101–103. [Google Scholar] [CrossRef]
- Storm, F.A.; Buckley, C.J.; Mazzà, C. Gait event-detection in laboratory and real life settings: Accuracy of ankle and waist sensor based methods. Gait Posture 2016, 50, 42–46. [Google Scholar] [CrossRef]
- Taetz, B.; Bleser, G.; Miezal, M. Towards self-calibrating inertial body motion capture. In Proceedings of the Information Fusion (FUSION), In Proceedings of 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; pp. 1751–1759. [Google Scholar]
- Seel, T.; Raisch, J.; Schauer, T. IMU-Based Joint Angle Measurement for Gait Analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef]
- Trojaniello, D.; Cereatti, A.; Pelosin, E.; Avanzino, L.; Mirelman, A.; Hausdorff, J.M.; Della Croce, U. Estimation of step-by-step spatio-temporal parameters of normal and impaired gait using shank-mounted magneto-inertial sensors: Application to elderly, hemiparetic, parkinsonian and choreic gait. J. Neuroeng. Rehabil. 2014, 11, 152. [Google Scholar] [CrossRef]
- Beauchet, O.; Allali, G.; Annweiler, C.; Bridenbaugh, S.; Assal, F.; Kressig, R.W.; Herrmann, F.R. Gait Variability among Healthy Adults: Low and High Stride-to-Stride Variability Are Both a Reflection of Gait Stability. Gerontology 2009, 55, 702–706. [Google Scholar] [CrossRef] [PubMed]
- Stolze, H. Typical features of cerebellar ataxic gait. J. Neurol. Neurosurg. Psychiatry 2002, 73, 310–312. [Google Scholar] [CrossRef]
- Ilg, W.; Golla, H.; Thier, P.; Giese, M.A. Specific influences of cerebellar dysfunctions on gait. Brain 2007, 130, 786–798. [Google Scholar] [CrossRef] [PubMed]
- Müller, B.; Ilg, W.; Giese, M.A.; Ludolph, N. Validation of enhanced kinect sensor based motion capturing for gait assessment. PLoS ONE 2017, 12, e0175813. [Google Scholar] [CrossRef] [PubMed]
- Shorter, K.A.; Wu, A.; Kuo, A.D. The high cost of swing leg circumduction during human walking. Gait Posture 2017, 54, 265–270. [Google Scholar] [CrossRef] [PubMed]
- Awad, L.N.; Bae, J.; Kudzia, P.; Long, A.; Hendron, K.; Holt, K.G.; O’Donnell, K.; Ellis, T.D.; Walsh, C.J. Reducing Circumduction and Hip Hiking During Hemiparetic Walking Through Targeted Assistance of the Paretic Limb Using a Soft Robotic Exosuit. Am. J. Phys. Med. Rehabil. 2017, 96, S157–S164. [Google Scholar] [CrossRef] [PubMed]
- Shiotani, M.; Watanabe, T. A preliminary study on evaluation of circumduction movement during gait with wireless inertial sensors. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 5828–5831. [Google Scholar]
- Watanabe, T.; Saito, H. Tests of wireless wearable sensor system in joint angle measurement of lower limbs. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 5469–5472. [Google Scholar]
- Robert-Lachaine, X.; Mecheri, H.; Larue, C.; Plamondon, A. Accuracy and repeatability of single-pose calibration of inertial measurement units for whole-body motion analysis. Gait Posture 2017, 54, 80–86. [Google Scholar] [CrossRef]
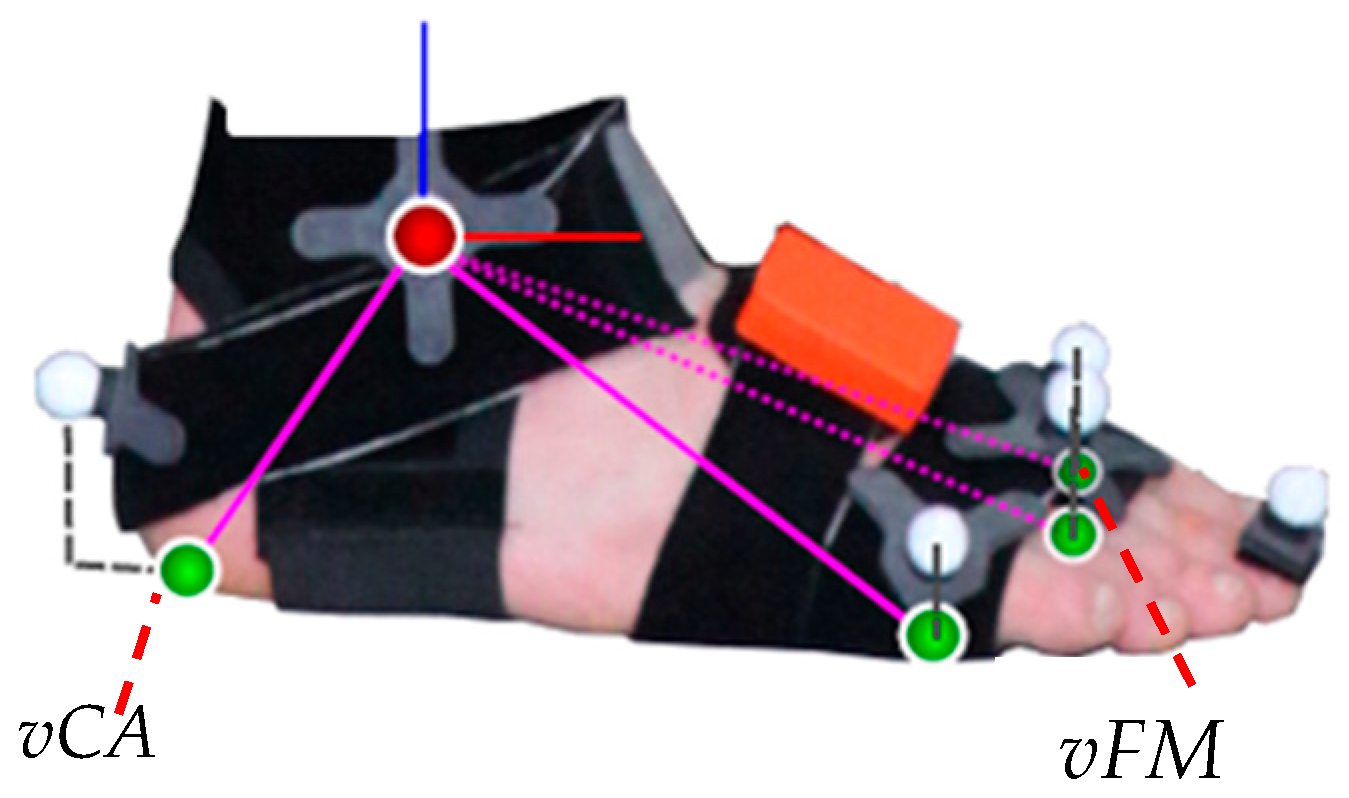


| Parameter | Description |
|---|---|
| Step Length (m) * | Distance between the CA marker positions of the left and right foot projected on the ground at two consecutive contralateral ICs |
| Stride Length (m) | Distance between the CA marker positions of one foot projected on the ground at two consecutive ipsilateral ICs |
| Step Width (m) * | Orthogonal distance between the line of the CA marker positions of one foot projected on the ground at two consecutive ipsilateral ICs and the CA marker position of the contralateral foot at the contralateral IC |
| Swing Width (m) * | Minimal distance between both CA markers during the swing phase |
| Step Time (s) | Period between two consecutive ICs of the left and right foot |
| Stride Time (s) | Period between two consecutive ICs of the ipsilateral foot |
| Cadence (steps/min) | 60 divided by step time |
| Single Limb Support (s) | Period between contralateral TC and contralateral IC |
| Double Limb Support (s) | Stride time minus Single limb support |
| Stance Time (s) | Period between IC and TC of one foot |
| Swing Time (s) | Period between TC and IC of one foot |
| Speed (m/s) | Stride length divided by Stride time [4] |
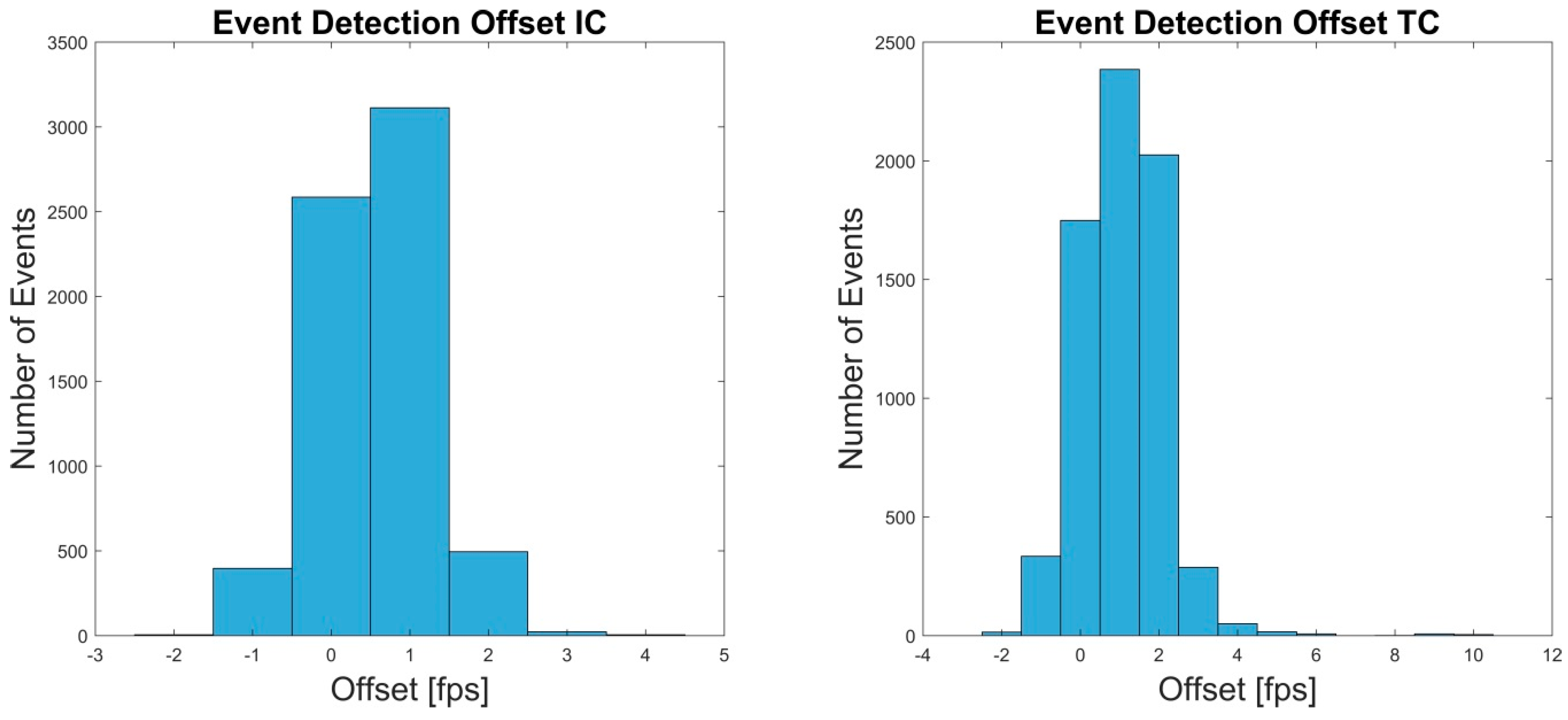
| Test 1 | Total | Total Errors | False-Positive | False-Negative | % Error | Offset (SD) (s) |
|---|---|---|---|---|---|---|
| IC | 6619 | 1 | 1 | 0 | 0.02 | 0.008 (0.007) |
| TC | 6796 | 80 | 44 | 36 | 1.17 | 0.016 (0.010) |
| OMC | IMU | p Value | Mean Error | RMSE | Relative RMSE (%) | Bias | |
|---|---|---|---|---|---|---|---|
| Step Length (m) | 0.61 ± 0.06 | 0.62 ± 0.07 | <0.05 | 0.006 | 0.04 (0.03−0.04) | 6.69 | 0.006 (0.08) |
| Stride Length (m) | 1.21 ± 0.12 | 1.22 ± 0.12 | 0.39 | 0.005 | 0.04 (0.03−0.04) | 2.98 | 0.005 (0.07) |
| Step Width (m) | 0.09 ± 0.03 | 0.10 ± 0.03 | <0.05 | 0.008 | 0.03 (0.02−0.03) | 34.34 | 0.008 (0.06) |
| Swing Width (m) | 0.09 ± 0.02 | 0.08 ± 0.03 | <0.05 | −0.008 | 0.03 (0.02−0.03) | 35.20 | −0.008 (0.06) |
| Step Time (s) | 0.60 ± 0.06 | 0.60 ± 0.06 | 0.33 | 0.002 | 0.02 (0.01−0.02) | 2.94 | 0.002 (0.03) |
| Stride Time (s) | 1.20 ± 0.11 | 1.20 ± 0.11 | 0.63 | 0.002 | 0.01 (0.01−0.01) | 0.90 | 0.002 (0.02) |
| Cadence (steps/min) | 101.09 ± 10.02 | 100.79 ± 9.76 | 0.33 | −0.296 | 3.10 (2.23−2.87) | 3.07 | −0.296 (6.05) |
| Single Limb Support (s) | 0.39 ± 0.03 | 0.40 ± 0.03 | <0.05 | 0.008 | 0.02 (0.01−0.02) | 4.26 | 0.008 (0.03) |
| Double Limb Support (s) | 0.81 ± 0.09 | 0.80 ± 0.09 | <0.05 | −0.006 | 0.02 (0.02−0.02) | 2.32 | −0.006 (0.04) |
| Stance Time (s) | 0.80 ± 0.09 | 0.80 ± 0.09 | <0.05 | −0.008 | 0.02 (0.01−0.02) | 2.10 | −0.008 (0.03) |
| Swing Time (s) | 0.39 ± 0.03 | 0.40 ± 0.03 | <0.05 | 0.010 | 0.02 (0.01−0.02) | 4.40 | 0.010 (0.03) |
| Speed (m/s) | 1.03 ± 0.14 | 1.03 ± 0.15 | 0.57 | 0.003 | 0.03 (0.02−0.03) | 2.72 | 0.003 (0.05) |
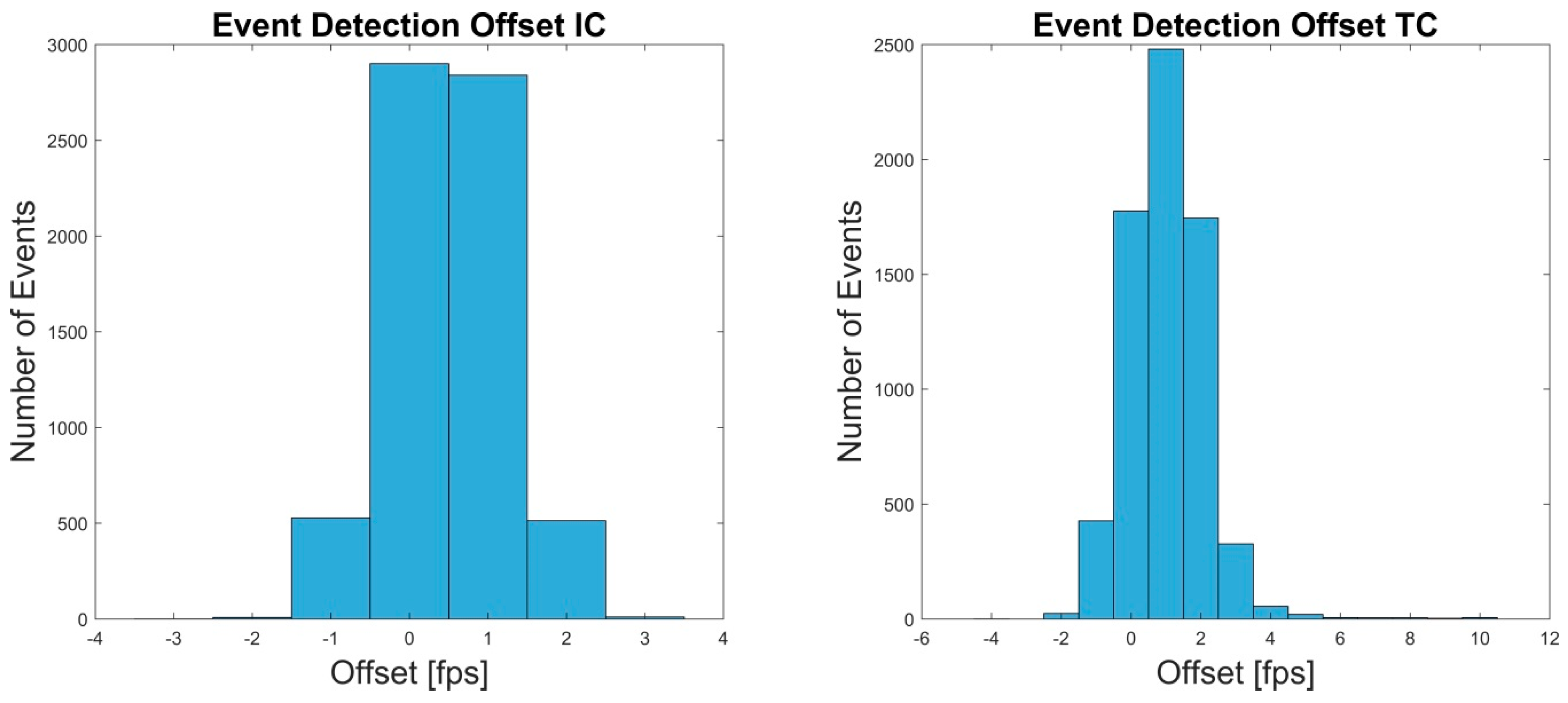
| Retest | Total | Total Errors | False-Positive | False-Negative | % Error | Offset (SD) (s) |
|---|---|---|---|---|---|---|
| IC | 6802 | 15 | 7 | 8 | 0.22 | 0.007 (0.008) |
| TC | 6780 | 105 | 58 | 47 | 1.55 | 0.015 (0.010) |
| Parameter | ICC OMC | ICC IMU |
|---|---|---|
| Step Length (m) | 0.88 | 0.67 |
| Stride Length (m) | 0.87 | 0.88 |
| Step Width (m) | 0.67 | 0.25 |
| Swing Width (m) | 0.90 | 0.69 |
| Step Time (s) | 0.87 | 0.87 |
| Stride Time (m) | 0.92 | 0.91 |
| Cadence (steps/min) | 0.87 | 0.87 |
| Single Limb Support (m) | 0.82 | 0.85 |
| Double Limb Support (m) | 0.89 | 0.90 |
| Stance Time (s) | 0.92 | 0.92 |
| Swing Time (s) | 0.81 | 0.73 |
| Speed (m/s) | 0.91 | 0.92 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teufl, W.; Lorenz, M.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Towards Inertial Sensor Based Mobile Gait Analysis: Event-Detection and Spatio-Temporal Parameters. Sensors 2019, 19, 38. https://doi.org/10.3390/s19010038
Teufl W, Lorenz M, Miezal M, Taetz B, Fröhlich M, Bleser G. Towards Inertial Sensor Based Mobile Gait Analysis: Event-Detection and Spatio-Temporal Parameters. Sensors. 2019; 19(1):38. https://doi.org/10.3390/s19010038
Chicago/Turabian StyleTeufl, Wolfgang, Michael Lorenz, Markus Miezal, Bertram Taetz, Michael Fröhlich, and Gabriele Bleser. 2019. "Towards Inertial Sensor Based Mobile Gait Analysis: Event-Detection and Spatio-Temporal Parameters" Sensors 19, no. 1: 38. https://doi.org/10.3390/s19010038
APA StyleTeufl, W., Lorenz, M., Miezal, M., Taetz, B., Fröhlich, M., & Bleser, G. (2019). Towards Inertial Sensor Based Mobile Gait Analysis: Event-Detection and Spatio-Temporal Parameters. Sensors, 19(1), 38. https://doi.org/10.3390/s19010038






