Low-Dose Computed Tomography Image Super-Resolution Reconstruction via Random Forests
Abstract
:1. Introduction
2. Background
2.1. Sparse Representation
2.2. Coupled Dictionary Learning
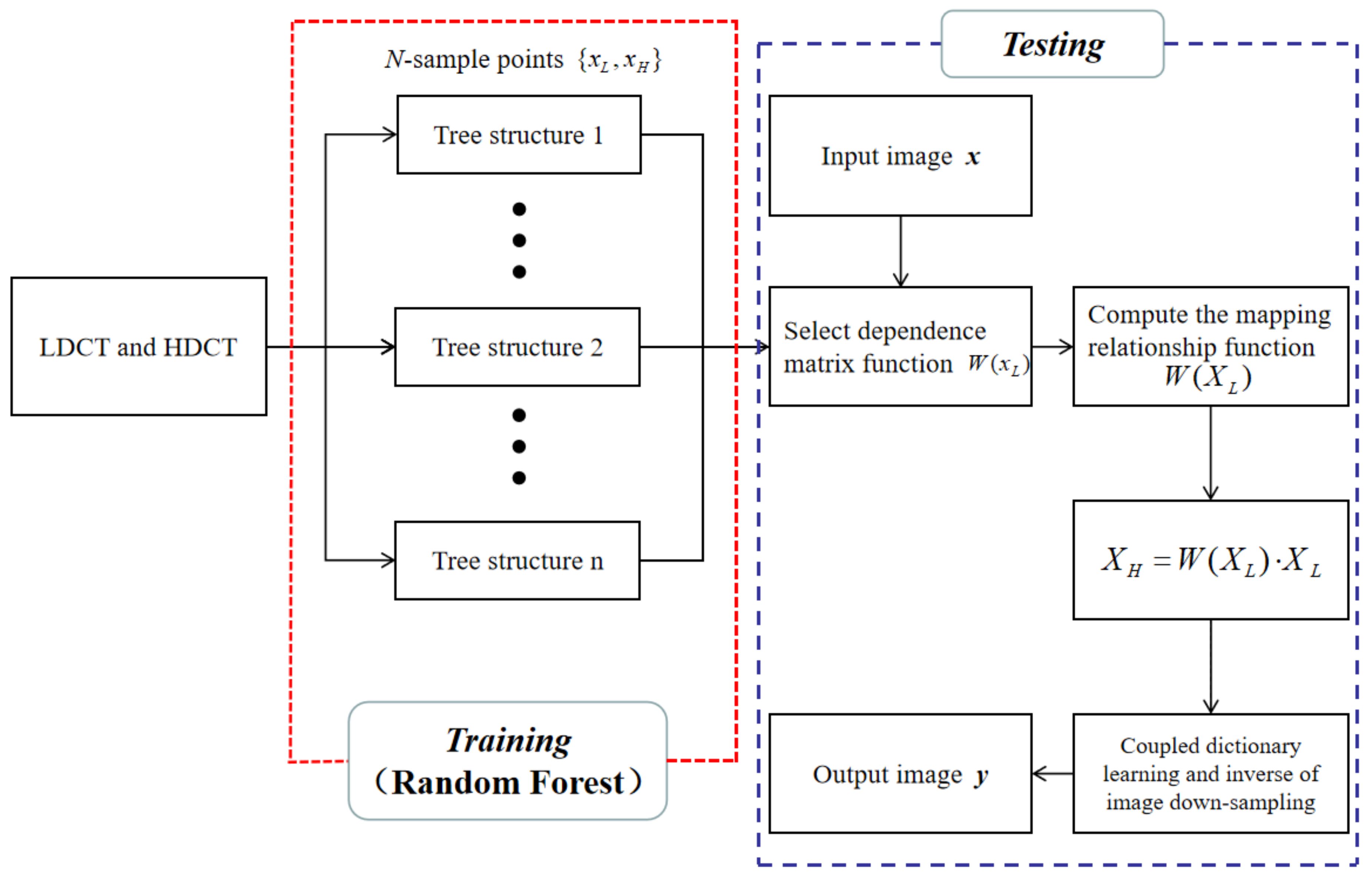
3. Proposed Reconstruction Method
3.1. Mapping Relation Function Learning
3.2. Tree Structure Learning
3.3. The Method Scheme
4. Experiments and Results
4.1. Experimental Parameters and Evaluation Function
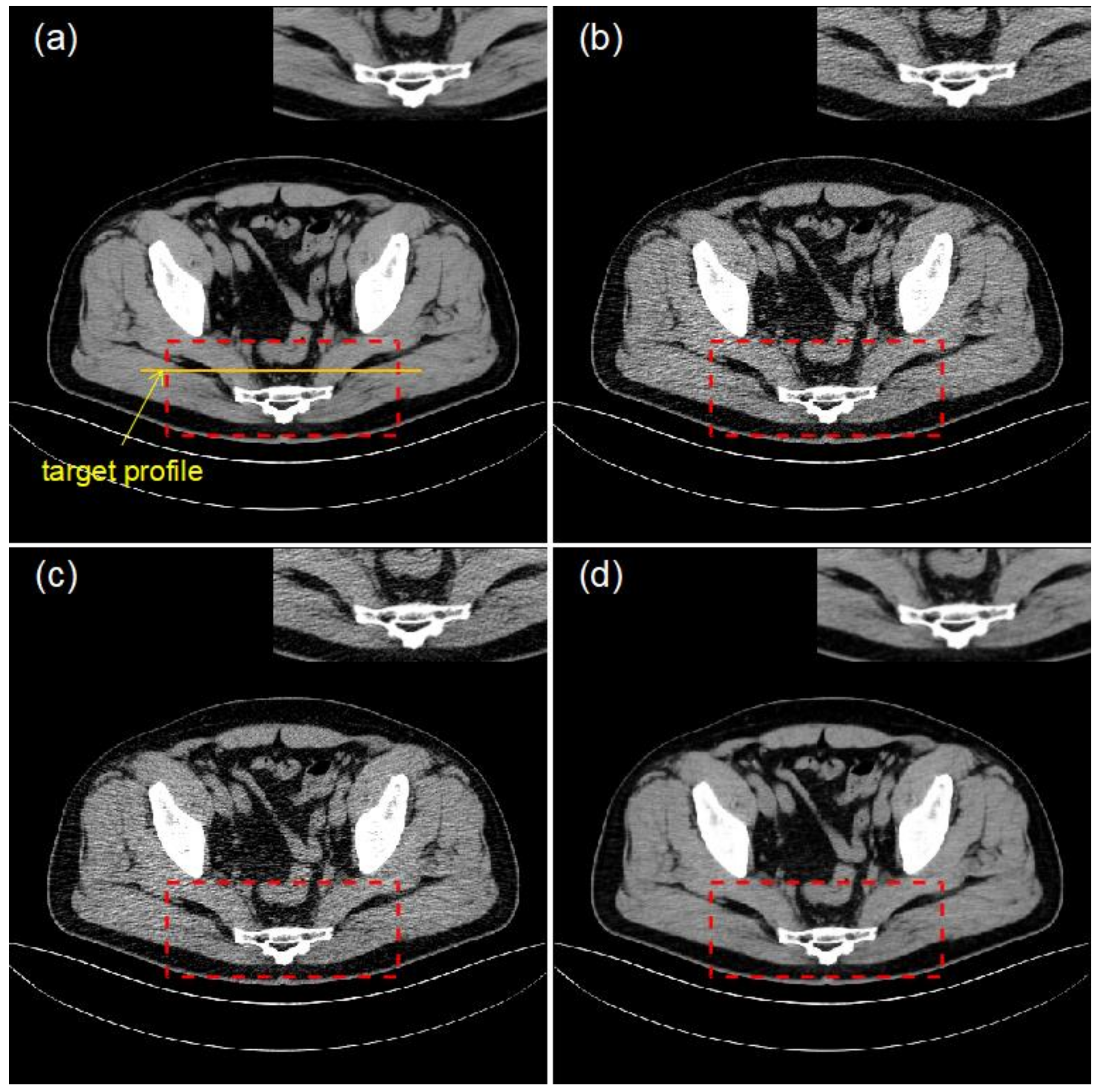
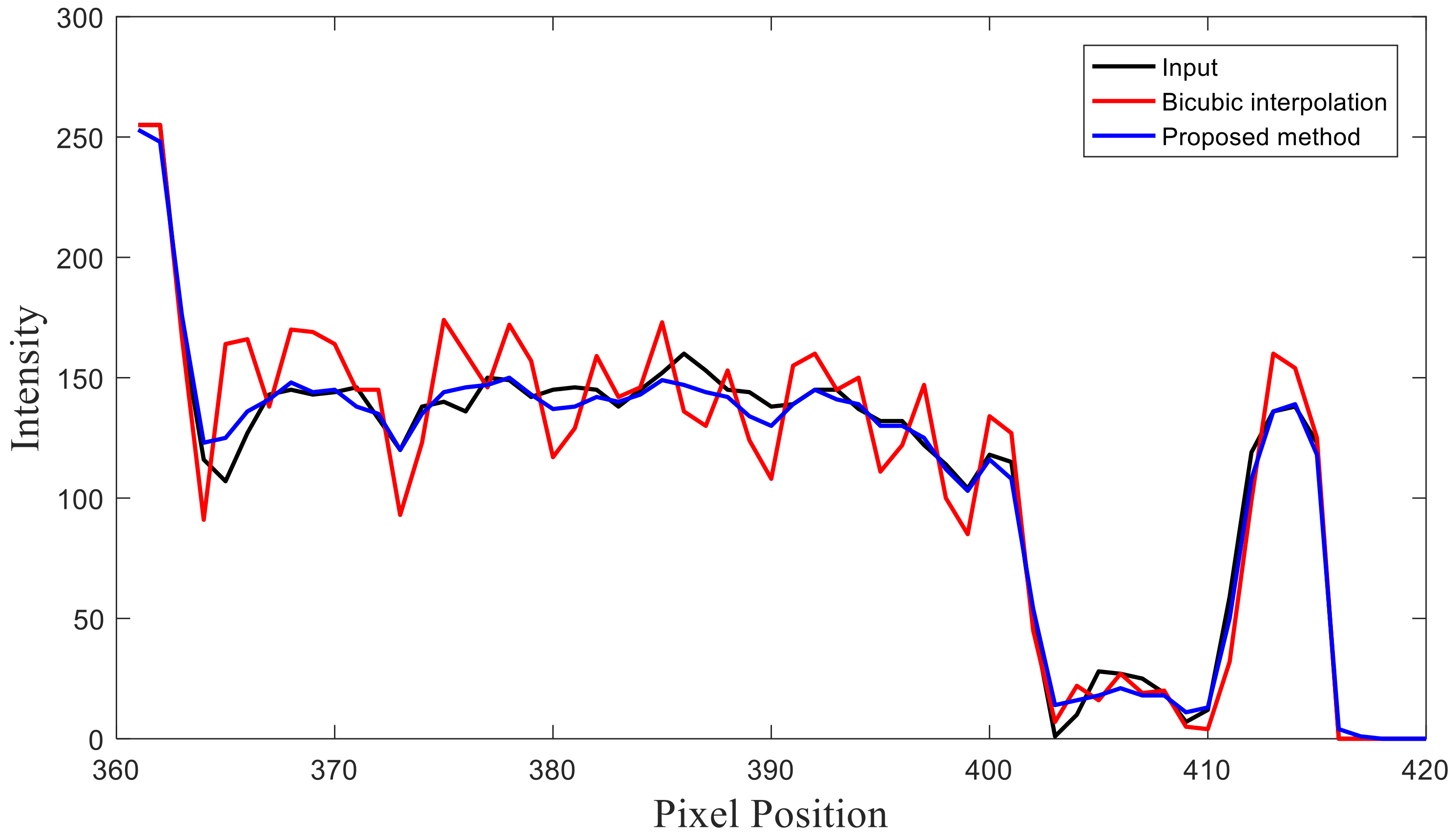
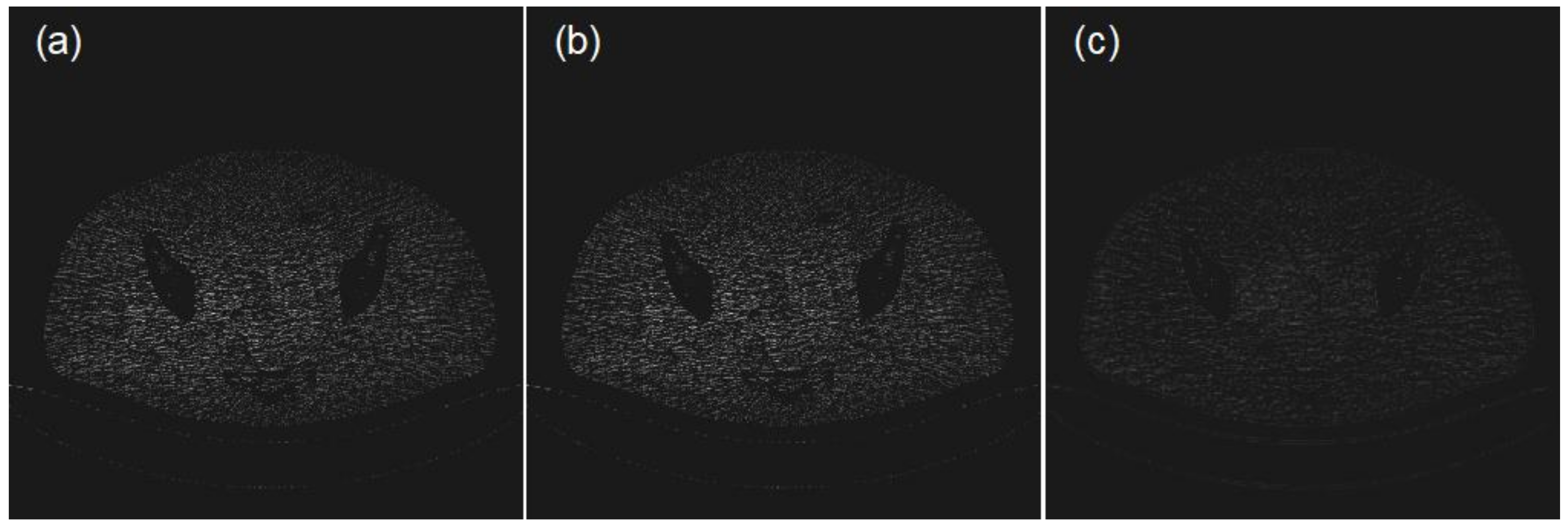
4.2. Clinical Data Experiments
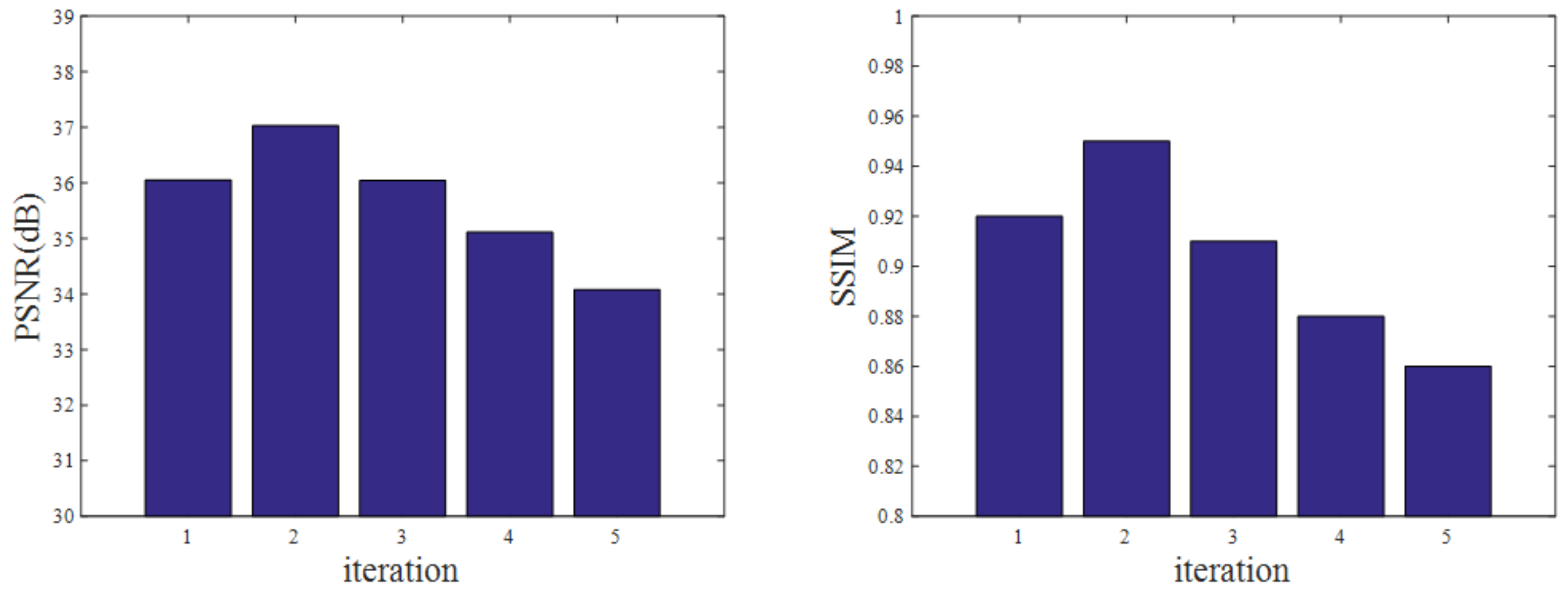
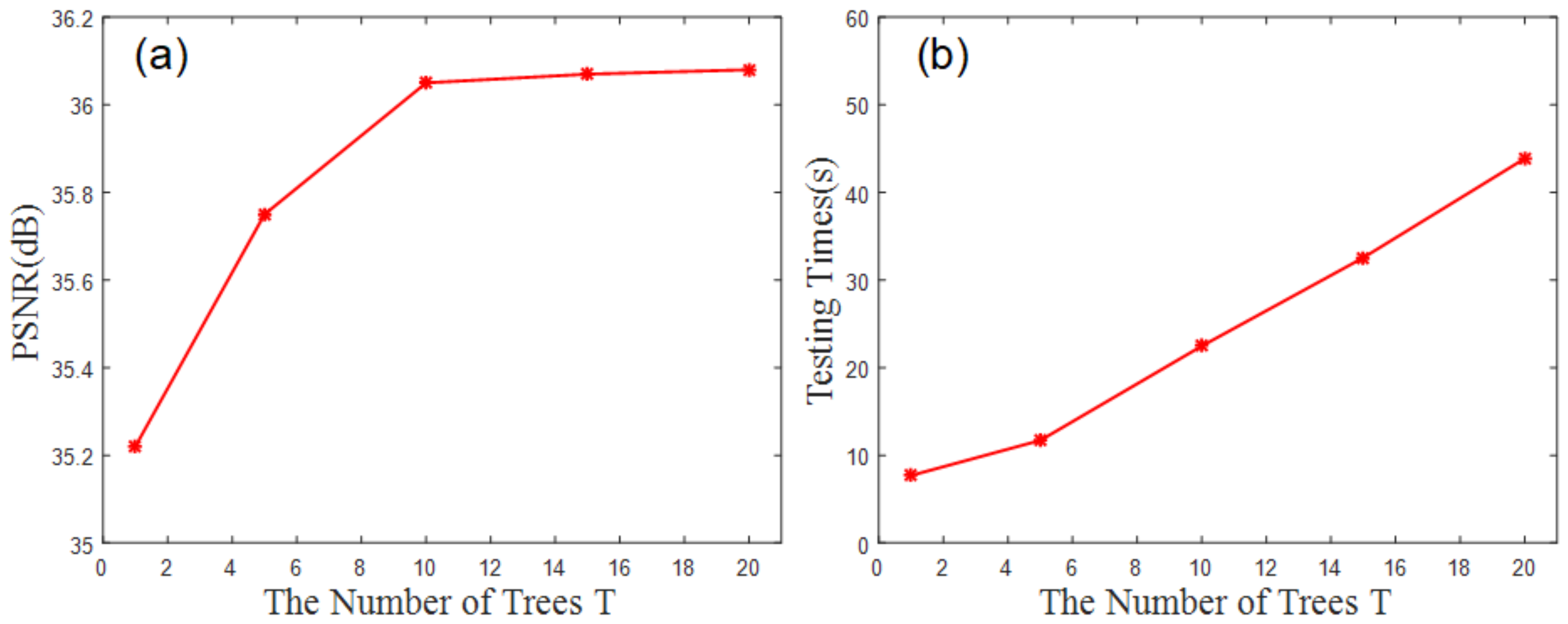
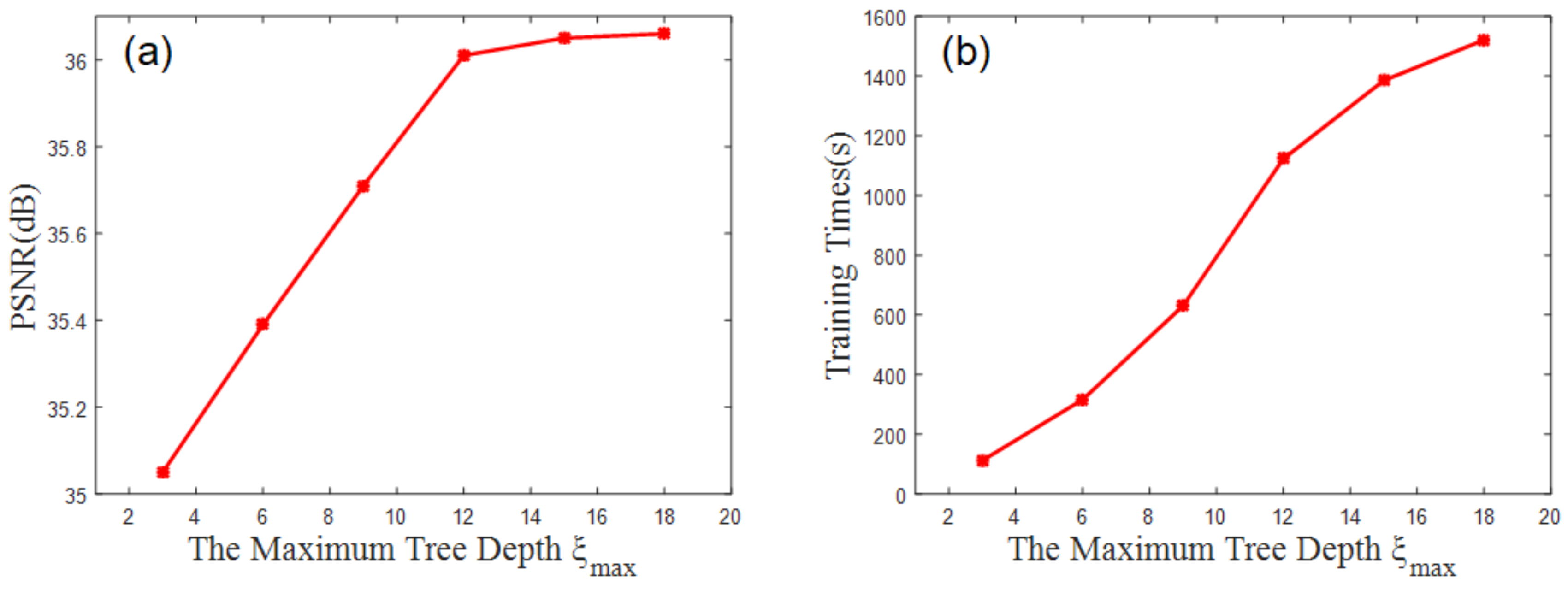
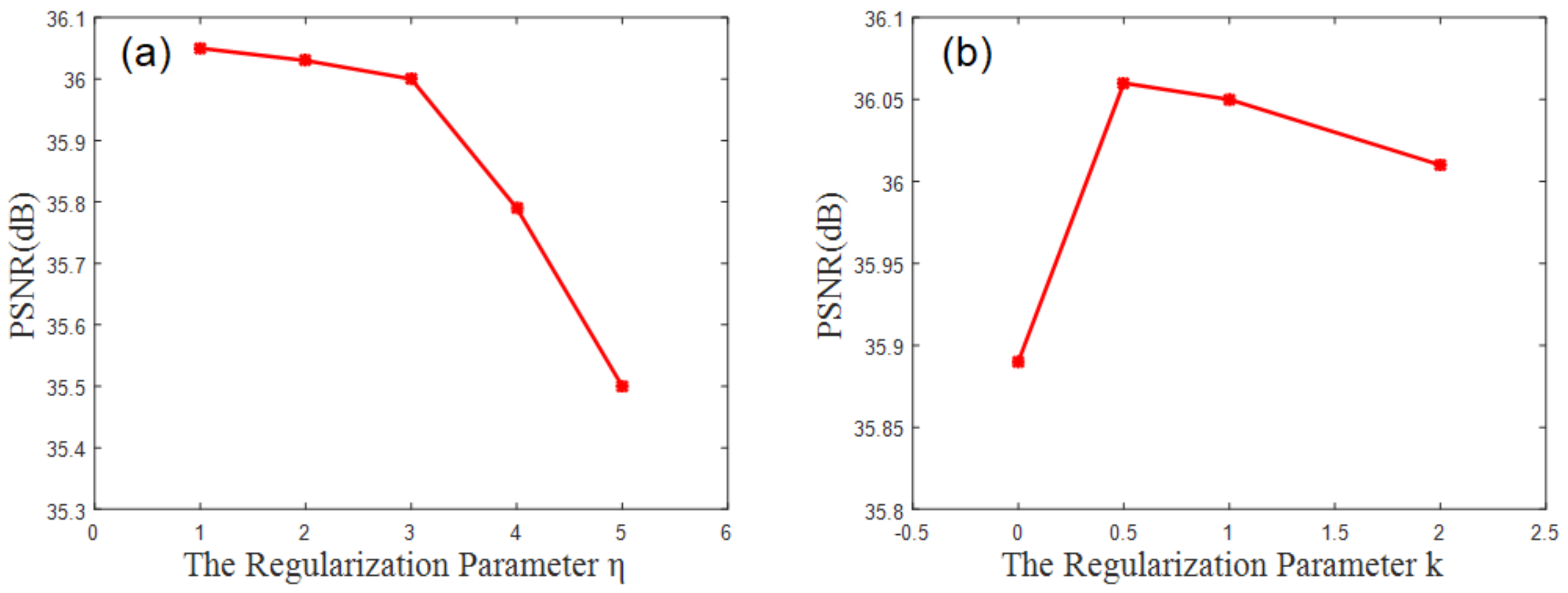
4.3. Parameter Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brenner, D.J.; Hall, E.J. Computer tomography-An increasing source of radiation exposure. N. Engl. J. Med. 2007, 357, 2277–2284. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, J. Adaptive streak artifact reduction in computed tomography resulting from excessive X-ray photon noise. Med. Phys. 1998, 25, 2139–2147. [Google Scholar] [CrossRef] [PubMed]
- Yun, S.J. Comparison of Low- and Standard-Dose CT for the Diagnosis of Acute Appendicitis: A Meta-Analysis. Am. J. Roentgenol. 2017, 208, W198–W207. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Liu, Q.; Zhang, N.; Zhang, Y.; Peng, X. Image Reconstruction from Few-view CT Data by Gradient-domain Dictionary Learning. J. X-Ray Sci. Technol. 2016, 24, 627–638. [Google Scholar] [CrossRef] [PubMed]
- Mouton, A.; Breckon, T.P. On the relevance of denoising and artefact reduction in 3d segmentation and classification within complex computed tomography imagery. J. X-Ray Sci. Technol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Qi, Z. A new adaptive-weighted total variation sparse-view computed tomography image reconstruction with local improved gradient information. J. X-Ray Sci. Technol. 2018, 26, 957–975. [Google Scholar] [CrossRef] [PubMed]
- Hou, H.S.; Andrews, H.C. Cubic spline for image interpolation and digital filtering. IEEE Trans. Signal Process. 1978, 26, 508–517. [Google Scholar]
- Sun, J.; Xu, Z.; Shum, H. Image super-resolution using gradient profile prior. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Dai, S.; Han, M.; Xu, W.; Wu, Y.; Gong, Y. Soft edge smoothness prior for alpha channel super resolution. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Zhang, R.; Thibault, J.-B.; Bouman, C.A.; Sauer, K.D.; Hsieh, J. Model-based iterative reconstruction for dual-energy x-ray ct using a joint quadratic likelihood model. IEEE Trans. Med. Imag. 2014, 33, 117–134. [Google Scholar] [CrossRef]
- Yu, G.; Sapiro, G.; Mallat, S. Solving inverse problems with piecewise linear estimators: From Gaussian mixture models to structured sparsity. IEEE Trans. Image Process. 2012, 21, 2481–2499. [Google Scholar]
- Peleg, T.; Elad, M. A Statistical Prediction Model Based on Sparese Representations for Single Image Super-Resolution. IEEE Trans. Image Process. 2014, 23, 2569–2582. [Google Scholar] [CrossRef]
- Yu, Z.; Thibault, J.-B.; Bouman, C.A.; Sauer, K.D.; Hsieh, J. Fast model-based x-ray ct reconstruction using spatially nonhomogeneous icd optimization. IEEE Trans. Image Process. 2011, 20, 161–175. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Pattern Recogntion and Machine Learning; Springer: Berlin, Germany, 2007. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sprase representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Z.; Lin, Z.; Cohen, S.; Huang, T.S. Couple dictionary training for image super-resolution. IEEE Trans. Image Process 2012, 21, 3467–3478. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yang, Y.; Wang, Z.; Chang, S.; Yang, J.; Huang, T.S. Learning super-resolution jointly from external and internal examples. IEEE Trans.Image Process. 2015, 24, 4359–4371. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Zhang, Q.; Fan, R.; Hu, Z. Super-resolution ct image reconstruction based on dictionary learning and sparse representation. Sci. Rep. 2018, 8, 8799. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Liang, D.; Xia, D.; Zheng, H. Compressive sampling in computed tomography: Method and application. Nucl. Instrum. Methods Phys. Res. A 2014, 748, 26–32. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, Y.; Liu, J.; Ma, J.; Zheng, H.; Liang, D. A feature refinement approach for statistical interior CT reconstruction. Phys. Med. Biol. 2016, 61, 5311–5334. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, T.; Jiang, C.; Gao, J.; Yang, Y.; Liang, D.; Liu, X.; Zheng, H.; Hu, Z. Low-count PET image restoration using sparse representation. Nucl. Instrum. Methods Phys. Res. A 2018, 888, 222–227. [Google Scholar] [CrossRef]
- Dong, W.S.; Zhang, L.; Shi, G.; Wu, X.L. Image deblurring and super-resolution by adaptive sparse domain selction and adaptive regularization. IEEE Trans.Image Process 2011, 20, 1838–1857. [Google Scholar] [CrossRef]
- Timofte, R.; Smet, V.D.; Gool, L.V. A+: Adjusted Anchored Neighborhood Regression for Fast Super-Resolution. In Proceedings of the Asian Conference on Computer Vision (ACCV 2014), Singapore, 1–5 November 2014. [Google Scholar]
- Timofte, R.; Smet, V.D.; Gool, L.V. Anchored Neighborhood Regression for Fast Example-Based Super-Resolution. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013. [Google Scholar]
- Schulter, S.; Leistner, C.; Bischof, H. Fast and Accurate Image Upscaling with Super-Resoltion Forests. In Proceedings of the IEEE Conference on Computer Vision and Pattern Classification (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3791–3799. [Google Scholar]
- Amit, Y.; Geman, D. Shape quantization and recongnition with randomized trees. NECO 1997, 9, 1545–1588. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Criminisi, A.; Shotton, J. Decision Forests for Computer Vision and Medical Image Analysis; Springer: London, UK, 2013; Volume 10, pp. 4471–4929. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J.; Wang, Z.; Chang, S.; Yang, Y.; Liu, D. Sparse Coding and Its Application in Computer Vision; World Scientific: Singapore, 2016. [Google Scholar]
- Freeman, W.T.; Jones, T.R.; Pasztor, E.C. Example-based super-resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
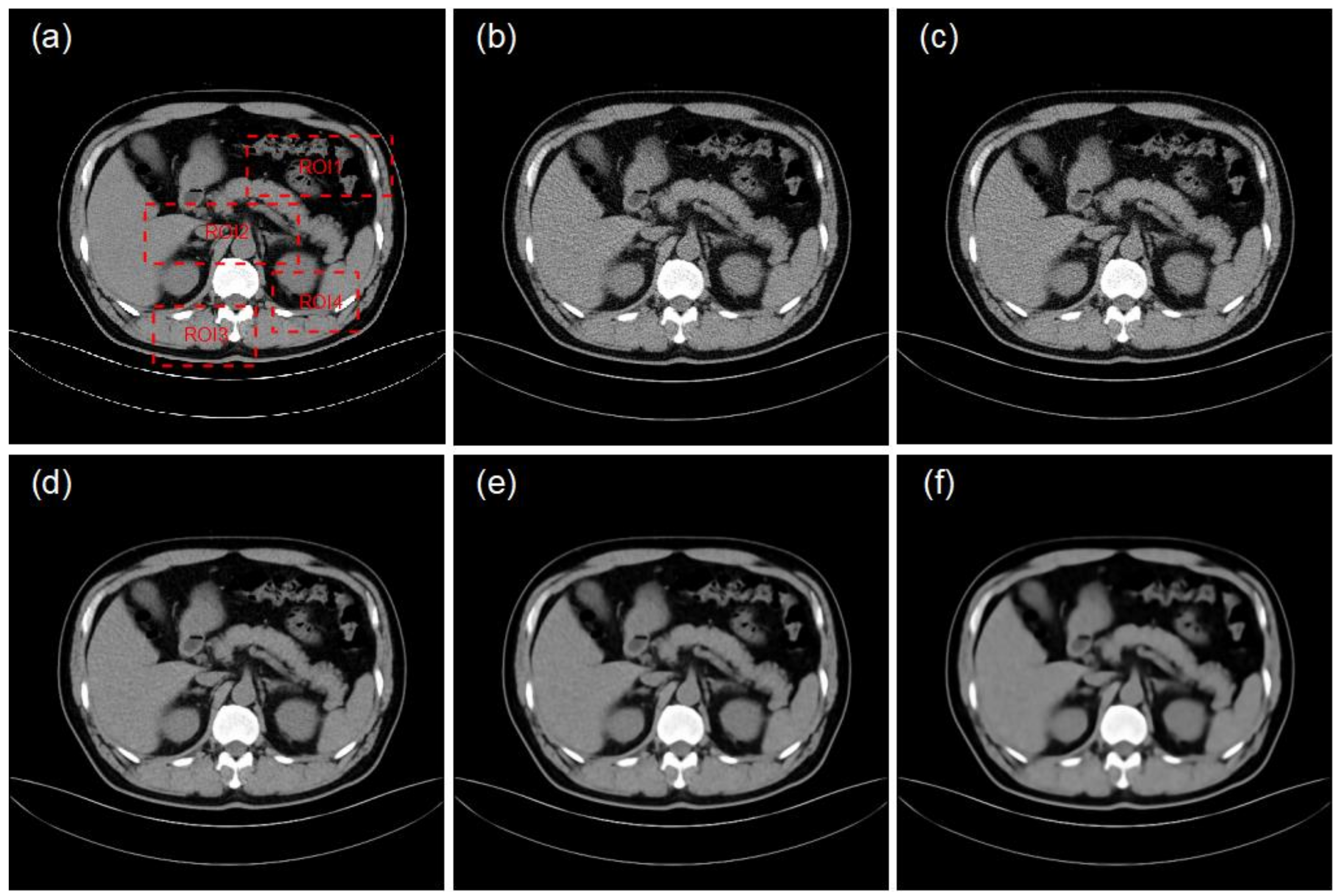
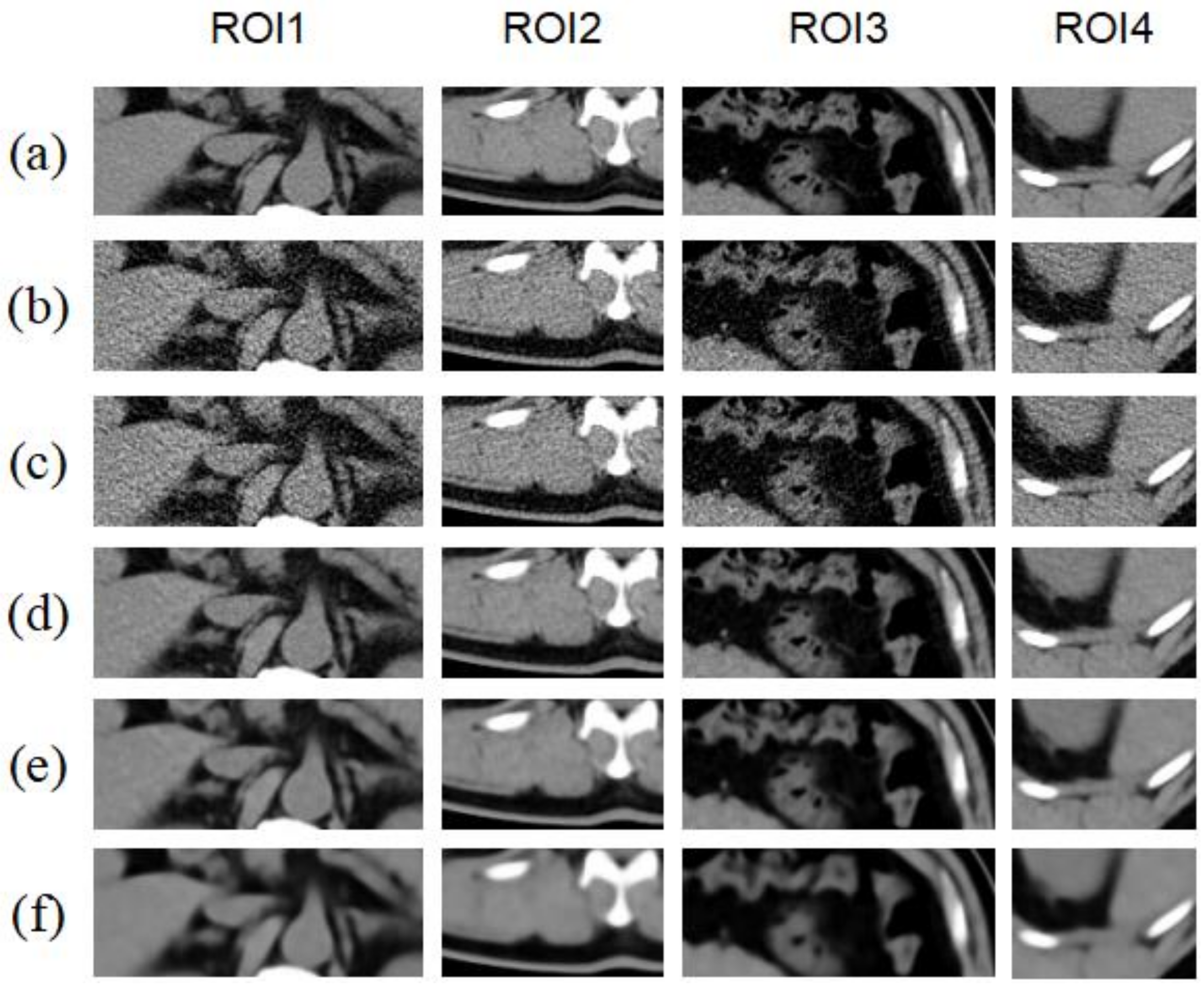
| 1 Input: an LDCT image x |
| 2 Output: the final processed image y |
| 3 LDCT image and HDCT image N-sample points in the training set |
| 4 Train individual random forest trees and then combine the trained trees into a random forest |
| 5 The dependence matrix function is obtained by Equation (10) |
| 6 Compute the mapping relationship function using Equations (7) and (8) |
| 7 The relationship between the data matrix of the HR is obtained by Equation (6) |
| 8 Coupling dictionary learning of the LR dictionary is completed by Equation (5) |
| 9 Implement the inverse of image down-sampling by Equation (4) and obtain the final image by Equation (3) |
| 1 for k = 1 to K |
| 2 Randomly extract N-samples to construct feature vector sets |
| 3 while (tree depth is below the minimum) |
| (1) randomly select n eigenvectors from the set of feature vectors |
| (2) select the optimal vector and the optimal split point from the feature vectors |
| (3) split the optimal split point into left and right child nodes |
| (4) update tree depth |
| 4 end while |
| 6 end for |
| LDCT | Bicubic | RFSR | RFSR 2nd | RFSR 5th | |
|---|---|---|---|---|---|
| PSNR(dB) | 21.65 | 26.23 | 36.05 | 37.03 | 34.08 |
| SSIM | 0.75 | 0.80 | 0.92 | 0.95 | 0.86 |
| ROI | LDCT | Bicubic | RFSR | RFSR 2nd | RFSR 5th |
|---|---|---|---|---|---|
| 1 | 20.55 | 25.76 | 35.89 | 36.97 | 34.01 |
| 2 | 21.33 | 26.13 | 35.97 | 37.01 | 34.03 |
| 3 | 22.31 | 27.43 | 36.12 | 37.09 | 34.09 |
| 4 | 22.06 | 26.54 | 36.45 | 37.63 | 34.61 |
| ROI | LDCT | Bicubic | RFSR | RFSR 2nd | RFSR 5th |
|---|---|---|---|---|---|
| 1 | 0.71 | 0.79 | 0.90 | 0.92 | 0.86 |
| 2 | 0.74 | 0.81 | 0.92 | 0.95 | 0.88 |
| 3 | 0.78 | 0.83 | 0.91 | 0.94 | 0.87 |
| 4 | 0.76 | 0.82 | 0.89 | 0.93 | 0.85 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, P.; Jiang, C.; Ji, M.; Zhang, Q.; Ge, Y.; Liang, D.; Liu, X.; Yang, Y.; Zheng, H.; Hu, Z. Low-Dose Computed Tomography Image Super-Resolution Reconstruction via Random Forests. Sensors 2019, 19, 207. https://doi.org/10.3390/s19010207
Gu P, Jiang C, Ji M, Zhang Q, Ge Y, Liang D, Liu X, Yang Y, Zheng H, Hu Z. Low-Dose Computed Tomography Image Super-Resolution Reconstruction via Random Forests. Sensors. 2019; 19(1):207. https://doi.org/10.3390/s19010207
Chicago/Turabian StyleGu, Peijian, Changhui Jiang, Min Ji, Qiyang Zhang, Yongshuai Ge, Dong Liang, Xin Liu, Yongfeng Yang, Hairong Zheng, and Zhanli Hu. 2019. "Low-Dose Computed Tomography Image Super-Resolution Reconstruction via Random Forests" Sensors 19, no. 1: 207. https://doi.org/10.3390/s19010207
APA StyleGu, P., Jiang, C., Ji, M., Zhang, Q., Ge, Y., Liang, D., Liu, X., Yang, Y., Zheng, H., & Hu, Z. (2019). Low-Dose Computed Tomography Image Super-Resolution Reconstruction via Random Forests. Sensors, 19(1), 207. https://doi.org/10.3390/s19010207






