In-Fiber Mach-Zehnder Interferometer Based on Three-Core Fiber for Measurement of Directional Bending
Abstract
1. Introduction
2. Experimental Procedures and Methods
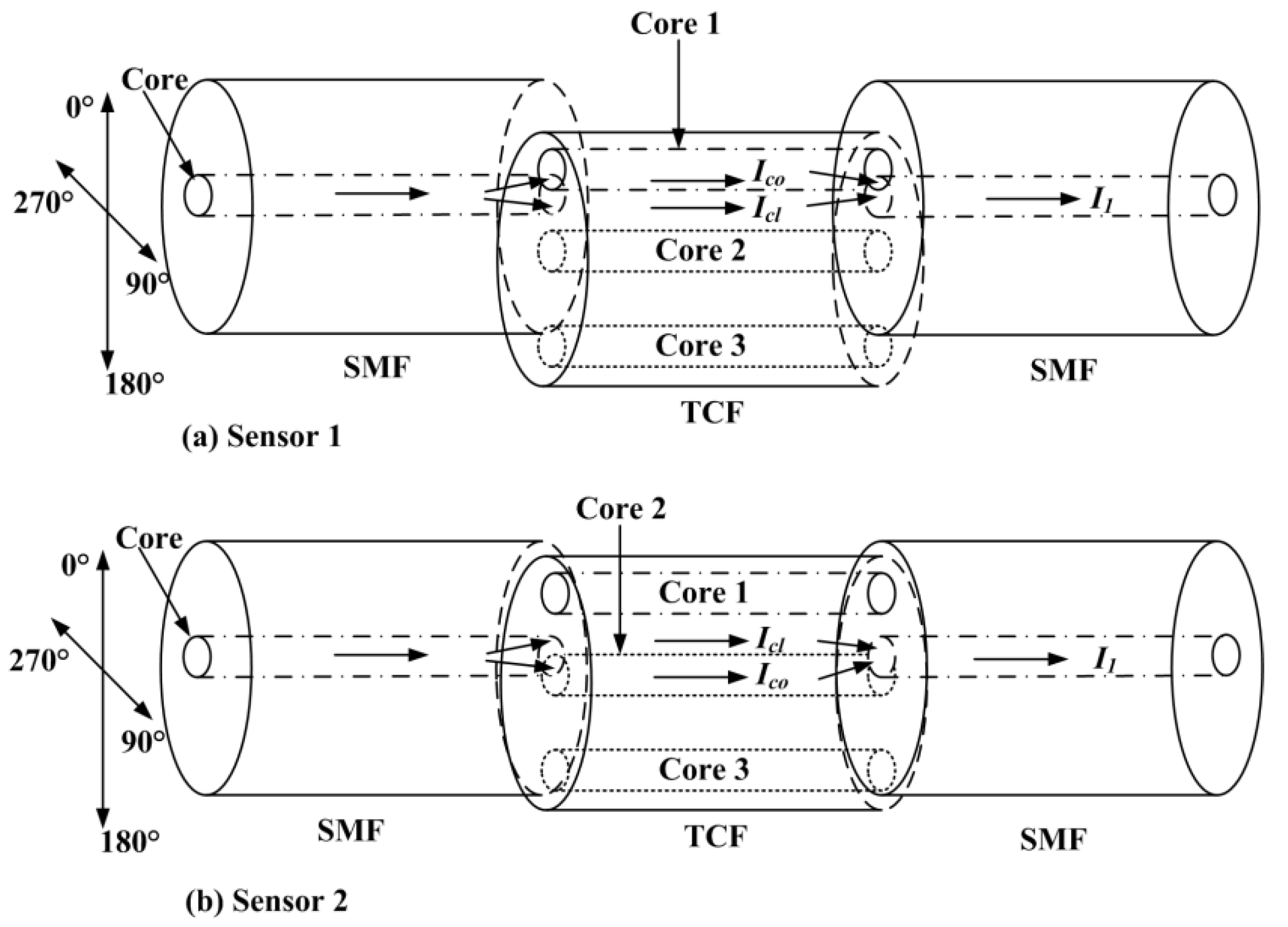
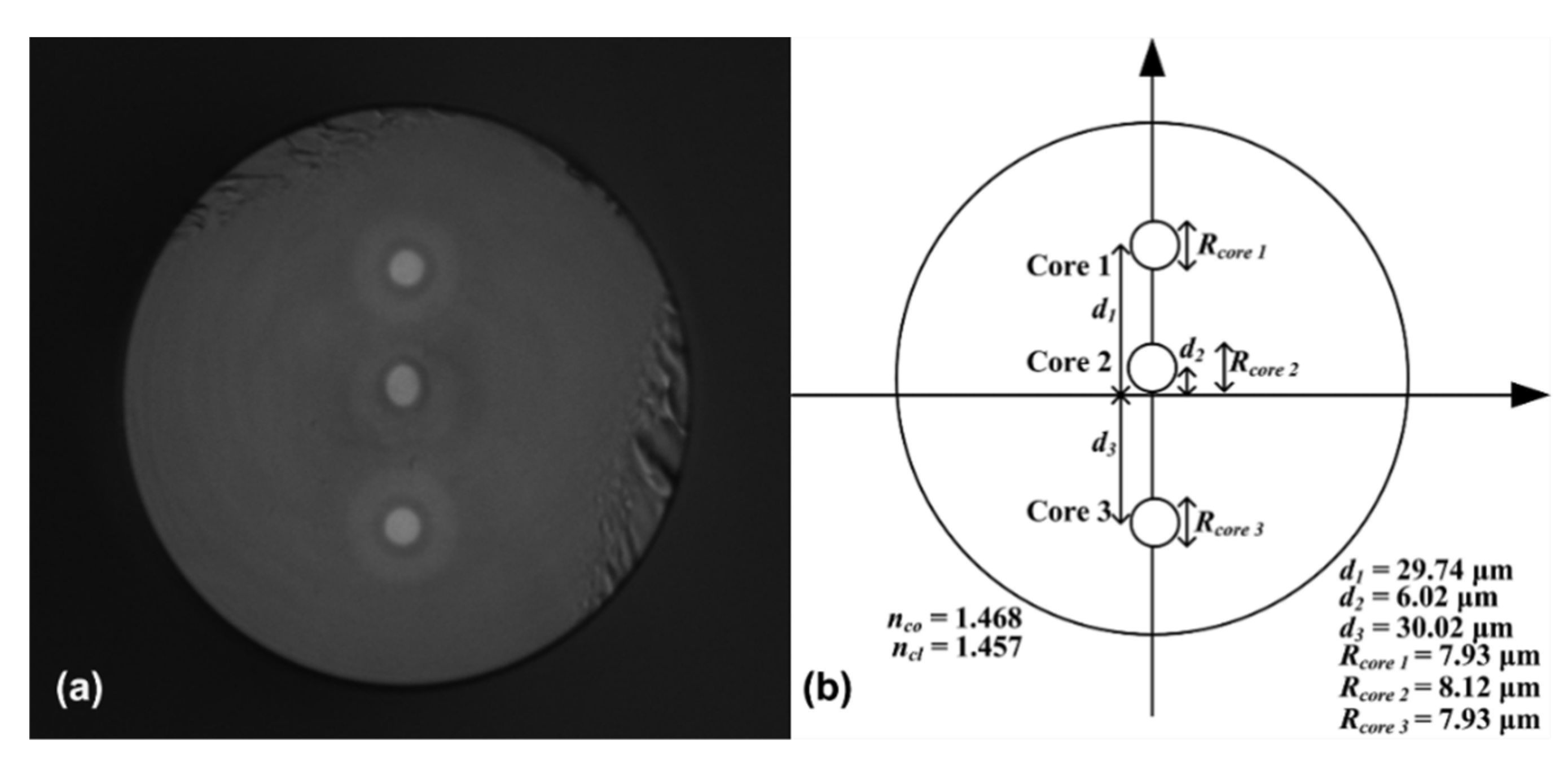
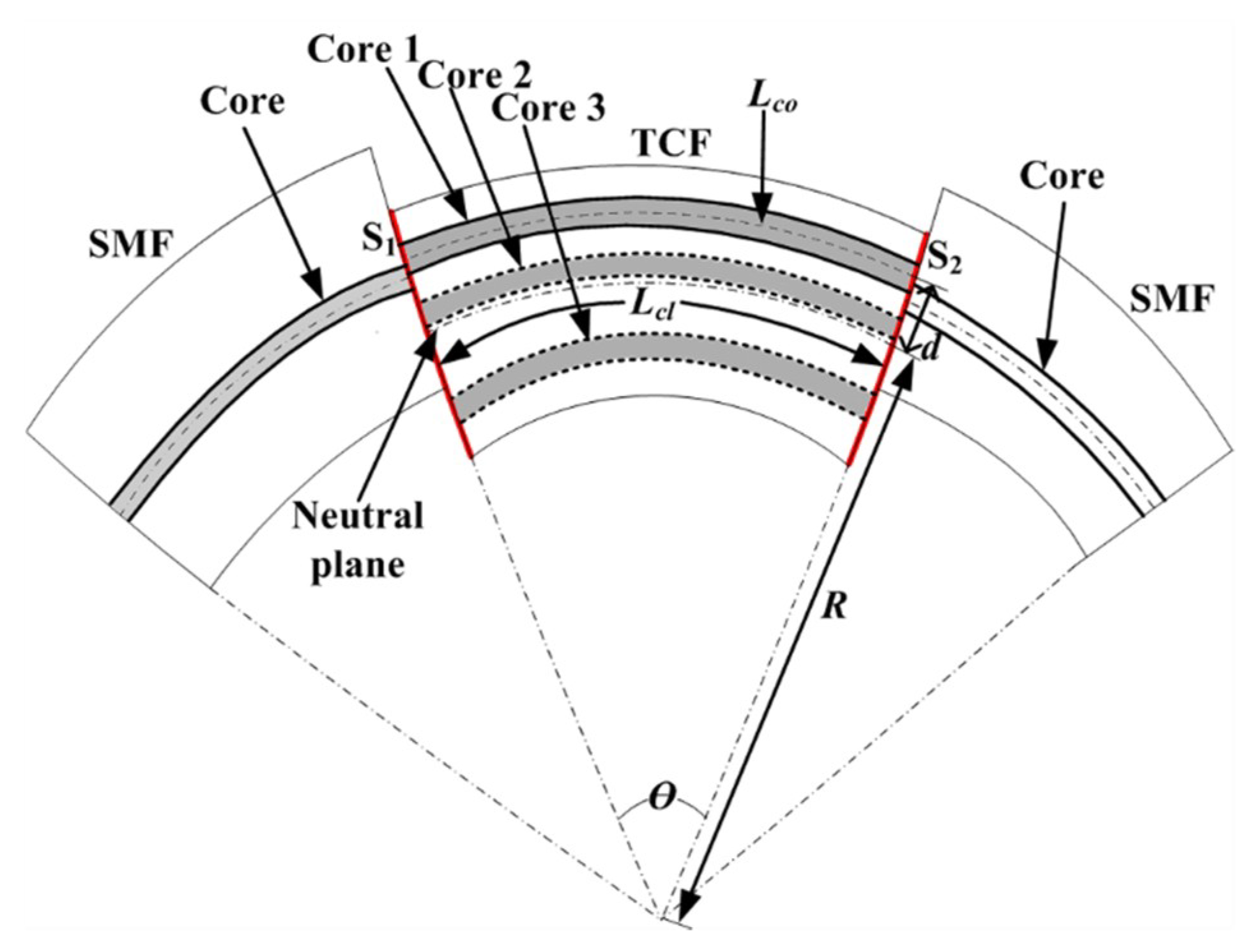
2.1. Sensor Fabrication and Principles
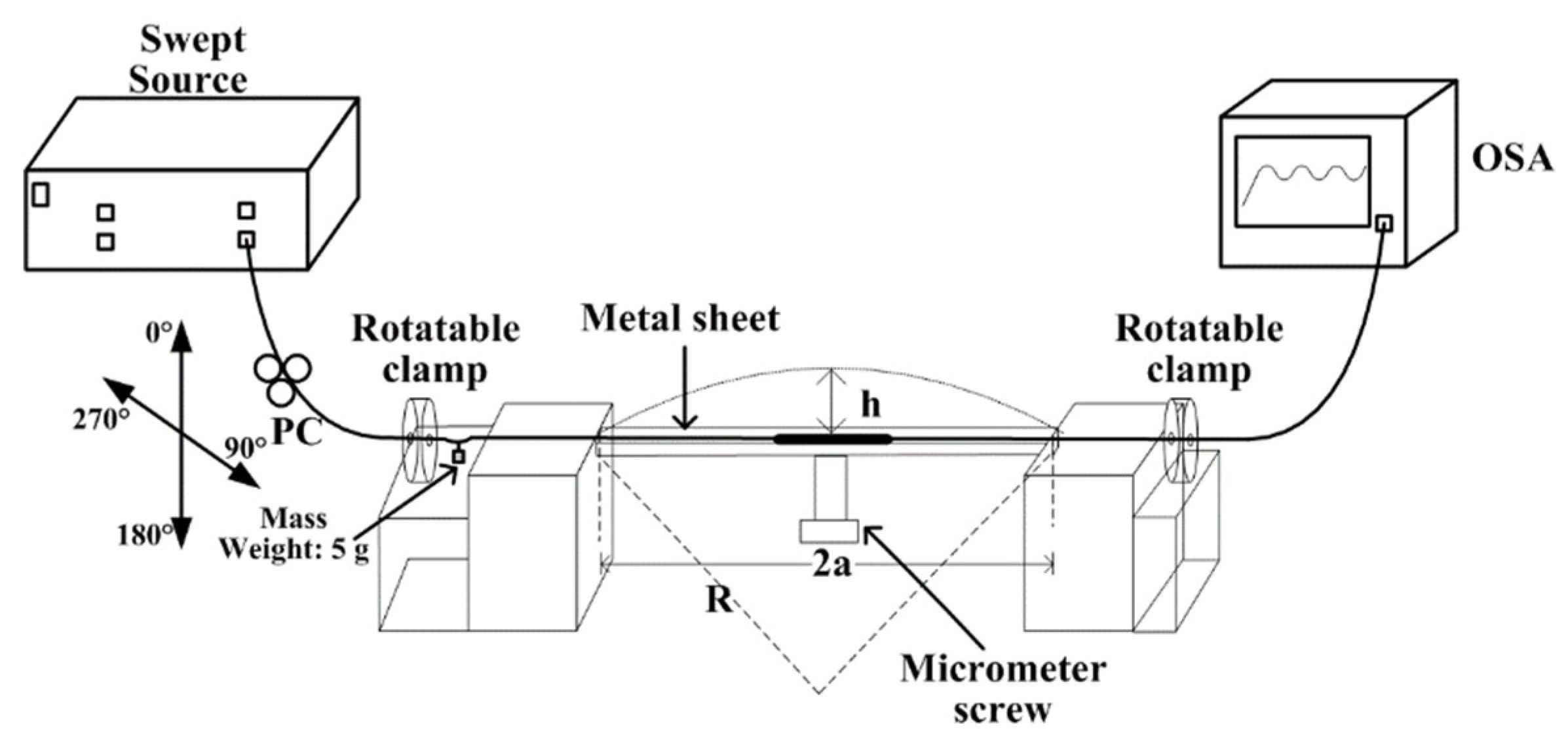
2.2. Experimental Setup
2.3. Bending Experiments
3. Results and Discussion
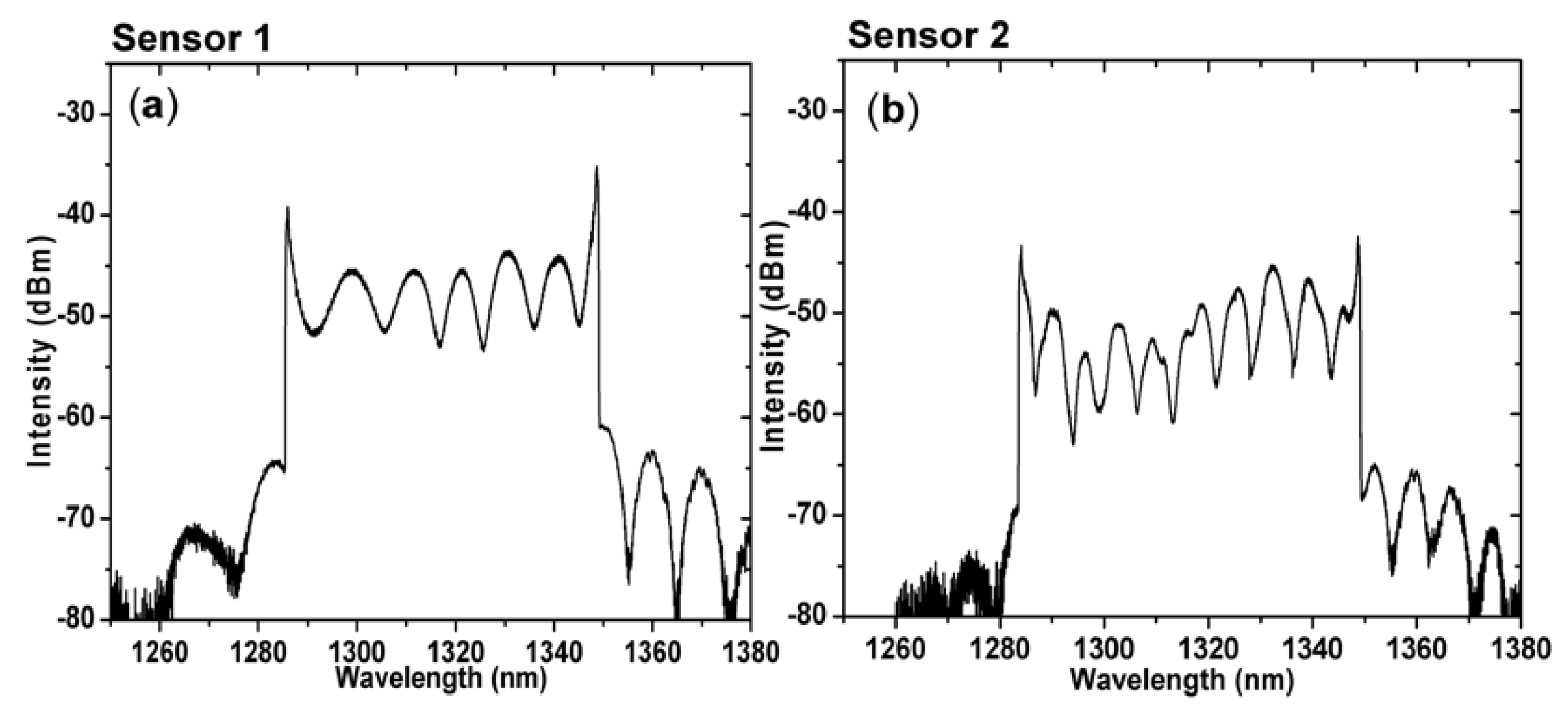
3.1. Transmission Spectra of the Sensors
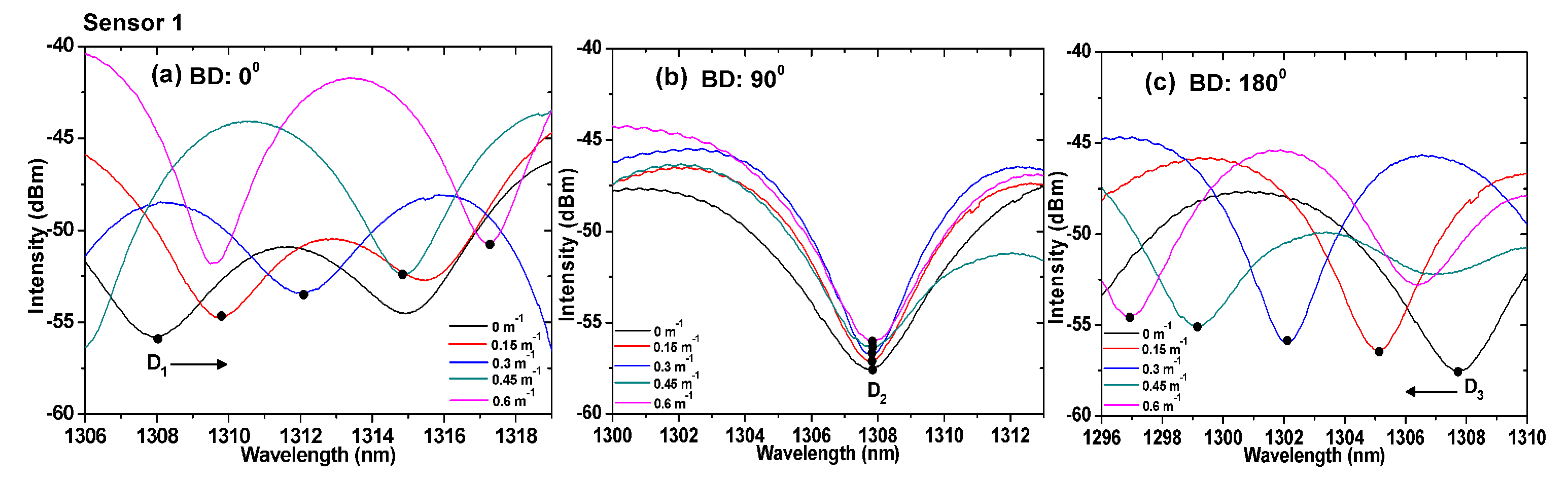
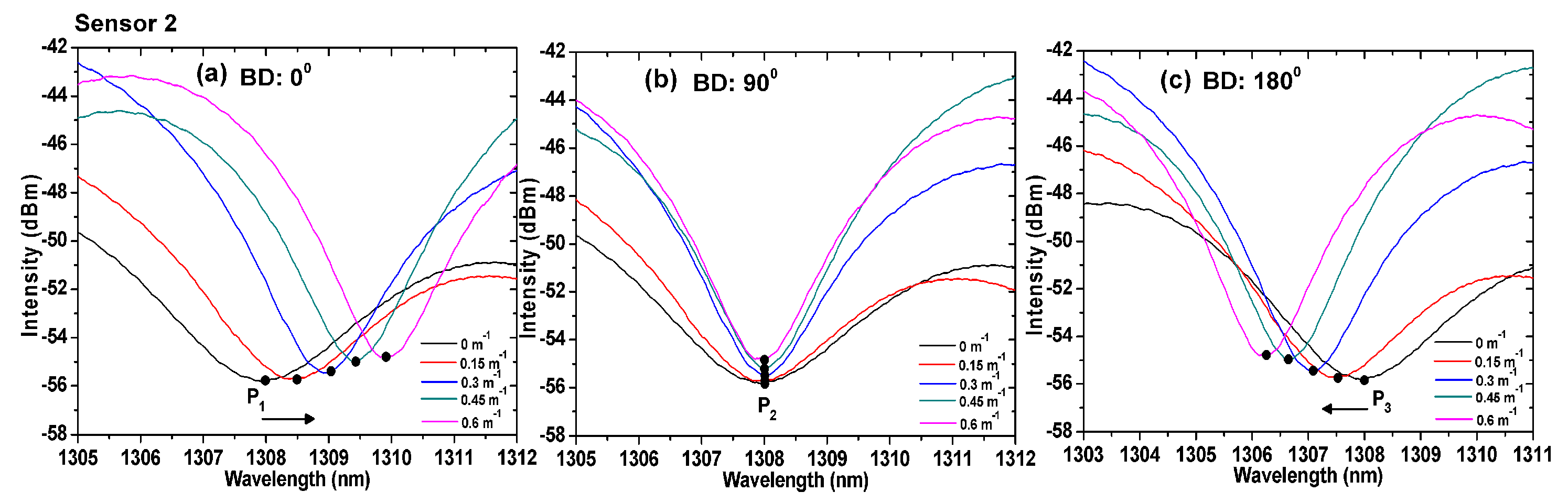
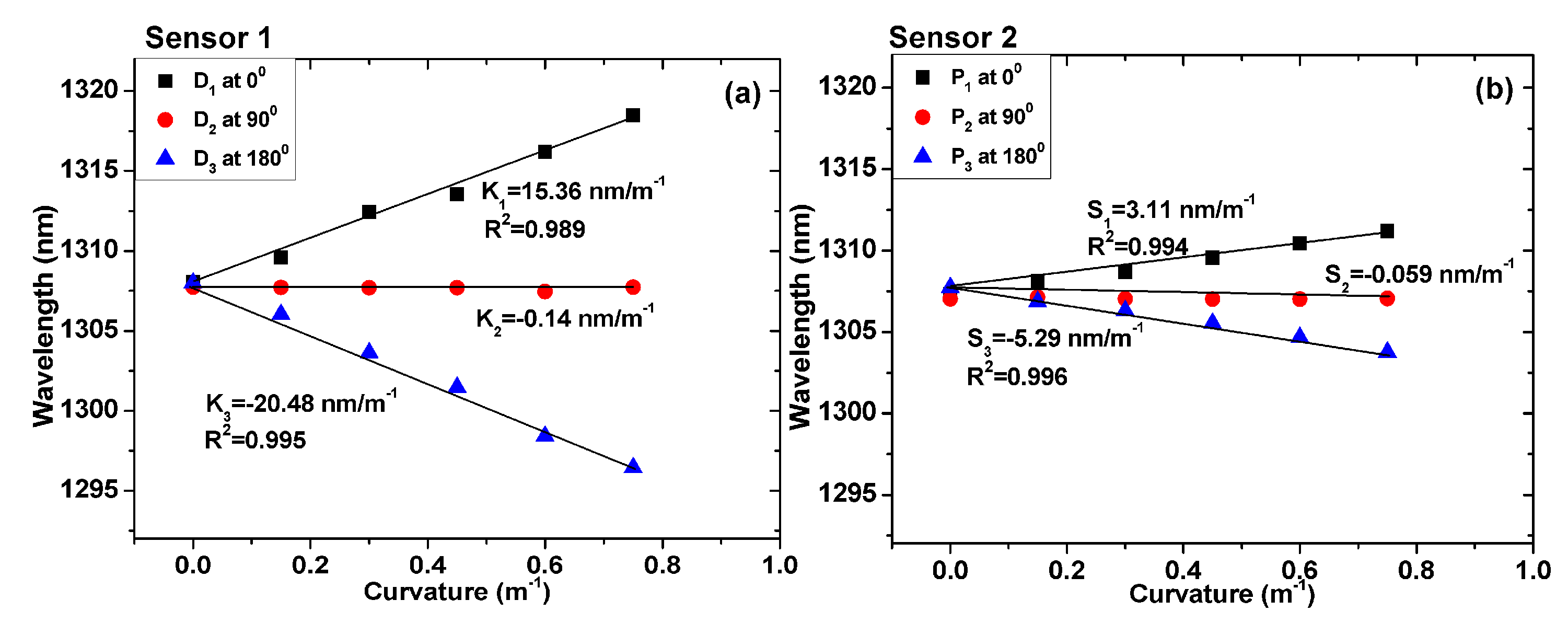
3.2. Wavelength Shift of the TCF-Based Sensor in Bending Experiments
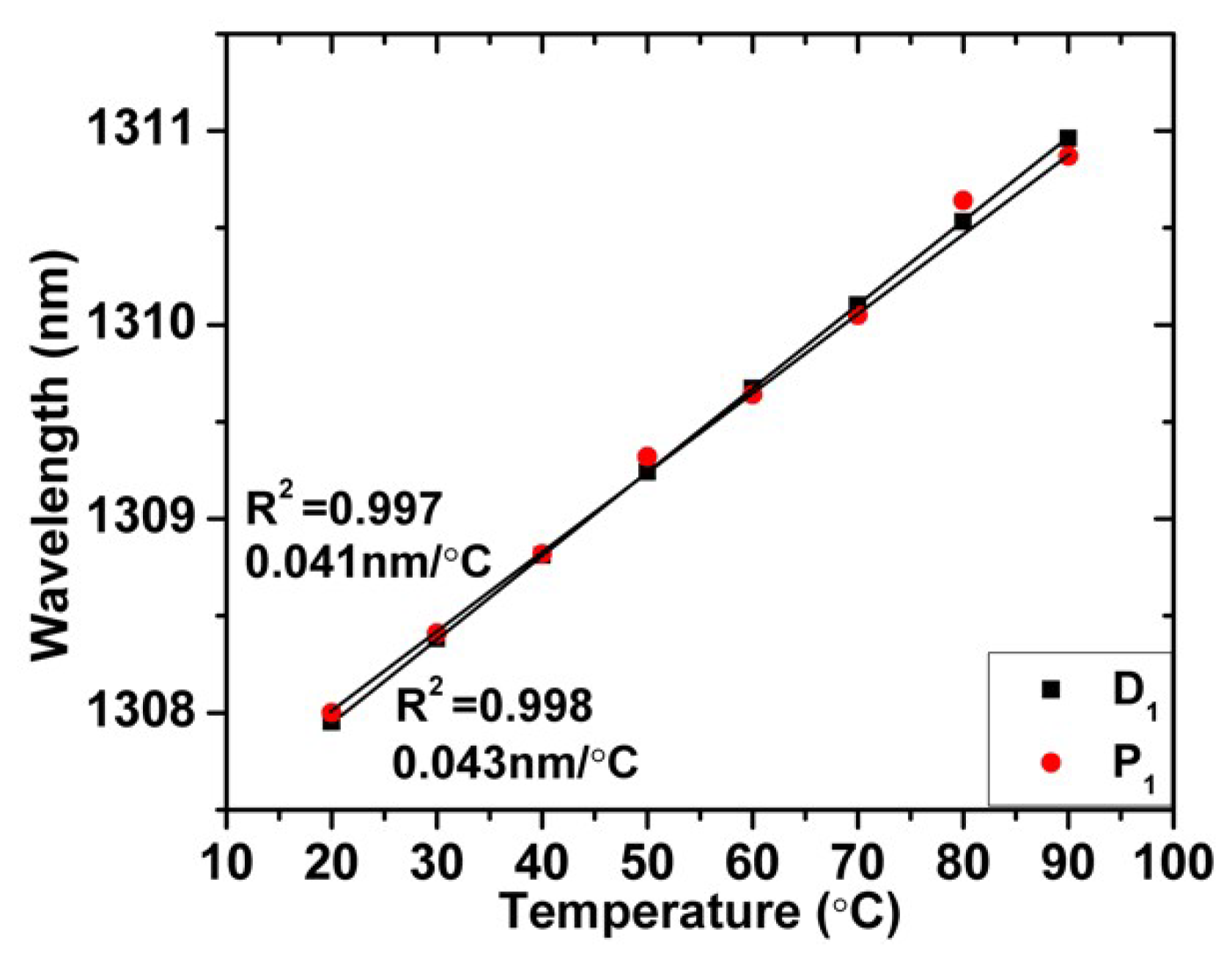
3.3. Wavelength Shift of the TCF-Based Sensor in Temperature Experiments
3.4. Limitations of the Research
3.5. Future Work
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ping, L.; Liqiu, M.; Kevin, S.; Qiying, C. Tapered fiber Mach–Zehnder interferometer for simultaneous measurement of refractive index and temperature. Appl. Phys. Lett. 2009, 94, 131110. [Google Scholar]
- Shangdong, D.; Bo, D.; Changyuan, Y.; Yongxin, G. High Sensitivity Optical Fiber Curvature Sensor Based on Cascaded Fiber Interferometer. J. Lightw. Technol. 2018, 36, 1125–1130. [Google Scholar]
- Dong, N.; Wang, S.; Jiang, L.; Jiang, Y.; Wang, P.; Zhang, L. Pressure and Temperature Sensor Based on Graphene Diaphragm and Fiber Bragg Gratings. IEEE Photonics Technol. Lett. 2018, 30, 431–434. [Google Scholar] [CrossRef]
- Bjorn, P.; Jung, H.; Jihyun, H.; Seongjin, H.; Sanghwa, L.; Jun, K.K.; Kyunghwan, O. High sensitivity temperature measurement via mask-free hybrid polymer long period fiber grating. Opt. Exp. 2018, 26, 16125–16137. [Google Scholar]
- Ding, L.; Tong, X.; Yu, L. Quantitative method for gait pattern detection based on fiber Bragg grating sensors. J. Biomed. Opt. 2017, 22, 037005. [Google Scholar] [CrossRef]
- Saffari, P.; Allsop, T.; Adebayo, A.; Webb, D.; Haynes, R.; Roth, M.M. Long period grating in multicore optical fiber: An ultra-sensitive vector bending sensor for low curvatures. Opt. Lett. 2014, 39, 3508–3511. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.; Si, J.; Chen, T.; Hou, X. Compact bending sensor based on a fiber Bragg grating in an abrupt biconical taper. Opt. Exp. 2015, 23, 11031–11036. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Huang, Y.; Liu, S.; Wang, C.; He, J.; Liao, C.; Yin, G.; Zhao, J.; Liu, Y.; Tang, J.; et al. Asymmetrical in-fiber Mach-Zehnder interferometer for curvature measurement. Opt. Exp. 2015, 23, 14596–14602. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Yu, Y.; Li, X.; Chen, X.; Zhang, Y.; Zhou, W.; Du, C. Micro-bending vector sensor based on six-airhole grapefruit microstructure fiber using lateral offset splicing. Opt. Exp. 2015, 23, 3010–3019. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, C.; Webb, D.J.; Kalli, K.; Peng, G.D. Compact assembly-free vector bend sensor based on all-in-fiber-core Mach-Zehnder interferometer. Opt. Lett. 2018, 43, 531–534. [Google Scholar] [CrossRef] [PubMed]
- Ou, Y.; Liu, J.; Xu, X.; Zhao, Y.; Zhou, A. Phase-Shifted Eccentric Core Fiber Bragg Grating Fabricated by Electric Arc Discharge for Directional Bending Measurement. Sensors 2018, 18, 1168–1176. [Google Scholar]
- Kong, J.; Zhou, A.; Cheng, C.; Yang, J.; Yuan, Y. Two-axis bending sensor based on cascaded eccentric core fiber Bragg gratings. IEEE Photonics Technol. Lett. 2016, 28, 1237–1240. [Google Scholar] [CrossRef]
- Flockhart, G.M.H.; MacPherson, W.N.; Barton, J.S.; Jones, J.D.C.; Zhang, L.; Bennion, I. Measurement uncertainty of Multicore Optical Fiber sensors used to sense curvature and bending direction. Measurement 2018, 18, 30861–30864. [Google Scholar]
- Han, Y.G.; Kim, G.; Lee, K.; Lee, S.; Chang, H.; Oh, C.; Hee, J. Bending sensitivity of long-period fiber gratings inscribed in holey fibers depending on an axial rotation angle. Opt. Exp. 2007, 15, 12866–12871. [Google Scholar] [CrossRef]
- Sun, A.; Wu, Z. Multimode interference in single mode–multimode FBG for simultaneous measurement of strain and bending. IEEE Sens. J. 2015, 15, 3390–3394. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, Y.; Wang, Z.; Jiang, M.; Ji, W.; Han, T.; Li, S.; Shao, X.; Dinh, X.Q.; Tjin, S.C.; et al. Simultaneous measurement of curvature and strain based on fiber Bragg grating in two-dimensional waveguide array fiber. Opt. Lett. 2013, 38, 4070–4073. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Zhao, D.; Chen, X.; Zhou, K.; Zhang, L.; Bennion, I.; MacPherson, W.N.; Barton, J.S.; Jones, D.C. Bend sensors with direction recognition based on long period gratings written in D-shaped fiber. Appl. Opt. 2004, 43, 5425–5428. [Google Scholar] [CrossRef] [PubMed]
- Yong, Z.; Zhan, C.; Lee, J.; Yin, S.; Ruffin, P. Multiple parameter vector bending and high-temperature sensors based on asymmetric multimode fiber Bragg gratings inscribed by an infrared femtosecond laser. Opt. Lett. 2006, 31, 1794–1796. [Google Scholar] [CrossRef]
- Wang, Y.P.; Rao, Y.J. A novel long period fiber grating sensor measuring curvature and determining bend-direction simultaneously. IEEE Sens. J. 2005, 5, 839–843. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, W.; Chen, L.; Bai, Z. Bending vector sensor based on a sector-shaped long period grating. IEEE Photonics Technol. Lett. 2015, 27, 713–716. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Chen, L.; Zhang, Y.; Wang, S.; Yu, L.; Li, Y.; Geng, P.; Kong, L. Concave-lens-like long-period fiber grating bidirectional high-sensitivity bending sensor. Opt. Lett. 2017, 42, 3892–3895. [Google Scholar] [CrossRef] [PubMed]
- Shao, L.Y.; Laronche, A.; Smietana, M.; Mikulic, P.; Bock, W.; Albert, J. Highly sensitive bend sensor with hybrid long-period and tilted fiber Bragg grating. Opt. Commun. 2010, 283, 2690–2694. [Google Scholar] [CrossRef]
- Zhang, J.H. Two-dimensional bending vector sensor based on Mach-Zehnder interferometer of two orthogonal lateral-offsets. Microw. Opt. Technol. Lett. 2015, 57, 709–713. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Wang, J.; Wang, L. A fiber bending vector sensor based on M-Z interferometer exploiting two hump-shaped tapers. IEEE Photonics Technol. Lett. 2015, 27, 1240–1243. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, B.; Miao, Y.; Zhang, H.; Liu, J. Effect of bending and orientation on the fiber modal Mach-Zehnder interferometer. Microw. Opt. Technol. Lett. 2012, 54, 136–139. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, W.; Geng, P.; Wang, L. A Mach-Zehnder interferometer constructed using lateral offset and a long period fiber grating for two-dimensional bending vector sensing. J. Opt. 2014, 16, 015501. [Google Scholar] [CrossRef]
- Andrews, C.; Ross, R.; Munzke, D.; Hoorn, C.; Brzezinski, A.; Barnes, J.; Reich, C.; Loock, H. In-fiber Mach-Zehnder interferometer for gas refractive index measurements based on a hollow-core photonic crystal fiber. Opt. Exp. 2016, 24, 14086–14099. [Google Scholar] [CrossRef] [PubMed]
- Ou, Y.; Guo, H. An In-Fiber Dual Air-Cavity Fabry–Perot Interferometer for Simultaneous Measurement of Strain and Direcstional Bend. IEEE Sens. J. 2017, 17, 3362–3366. [Google Scholar]
- Deng, M.; Tang, C.-P.; Zhu, T.; Rao, Y.-J. Highly sensitive bend sensor based on Mach–Zehnder interferometer using photonic crystal fiber. Opt. Commun. 2011, 284, 2849–2853. [Google Scholar] [CrossRef]
- Kong, J.; Xiao, W.; Ou, Y.; Zhou, A. Pure Directional Bending Measurement with a Fiber Bragg Grating at the Connection Joint of Eccentric-Core and Single-Mode Fibers. J. Lightw. Technol. 2016, 34, 3288–3292. [Google Scholar] [CrossRef]
| Subjects | Approach | Bending Sensitivities | |
|---|---|---|---|
| 0° | 180° | ||
| 1 | FPI | 242.5 pm/m−1 | −231.5 pm/m−1 |
| 2 | FBG based on ECF | 49.3 pm/m−1 | −50.3 pm/m−1 |
| 3 | PCF-based MZI | 5.129 nm/m−1 (No direction) | 5.129 nm/m−1 (No direction) |
| 4 | TCF-based MZI | 15.36 nm/m−1 | −20.48 nm/m−1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, L.; Li, Y.; Zhou, C.; Hu, M.; Xiong, Y.; Zeng, Z. In-Fiber Mach-Zehnder Interferometer Based on Three-Core Fiber for Measurement of Directional Bending. Sensors 2019, 19, 205. https://doi.org/10.3390/s19010205
Ding L, Li Y, Zhou C, Hu M, Xiong Y, Zeng Z. In-Fiber Mach-Zehnder Interferometer Based on Three-Core Fiber for Measurement of Directional Bending. Sensors. 2019; 19(1):205. https://doi.org/10.3390/s19010205
Chicago/Turabian StyleDing, Lei, Yu Li, Cai Zhou, Min Hu, Yuli Xiong, and Zhongliang Zeng. 2019. "In-Fiber Mach-Zehnder Interferometer Based on Three-Core Fiber for Measurement of Directional Bending" Sensors 19, no. 1: 205. https://doi.org/10.3390/s19010205
APA StyleDing, L., Li, Y., Zhou, C., Hu, M., Xiong, Y., & Zeng, Z. (2019). In-Fiber Mach-Zehnder Interferometer Based on Three-Core Fiber for Measurement of Directional Bending. Sensors, 19(1), 205. https://doi.org/10.3390/s19010205




