Highly Sensitive Diode-Based Micro-Pirani Vacuum Sensor with Low Power Consumption
Abstract
1. Introduction
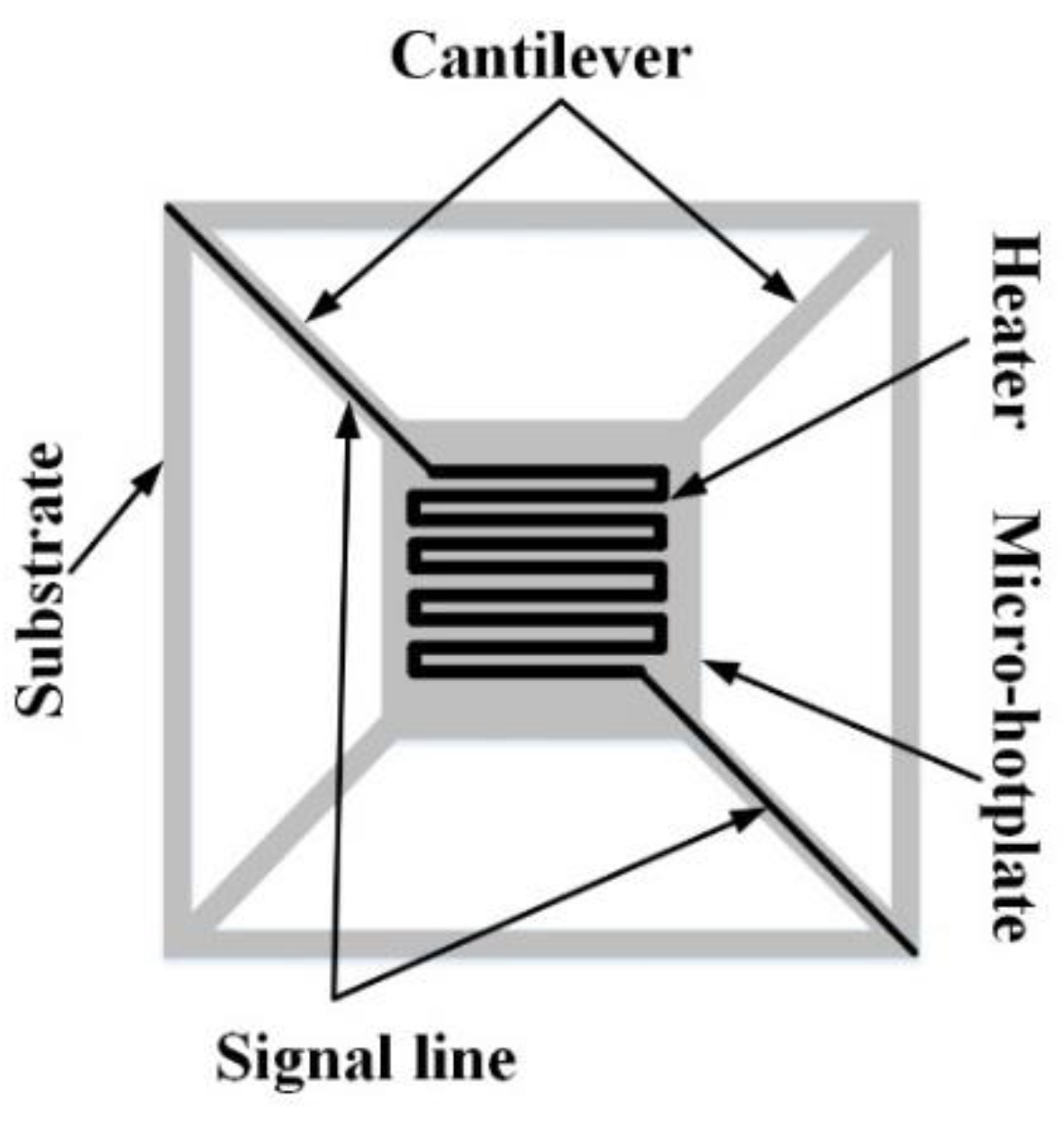
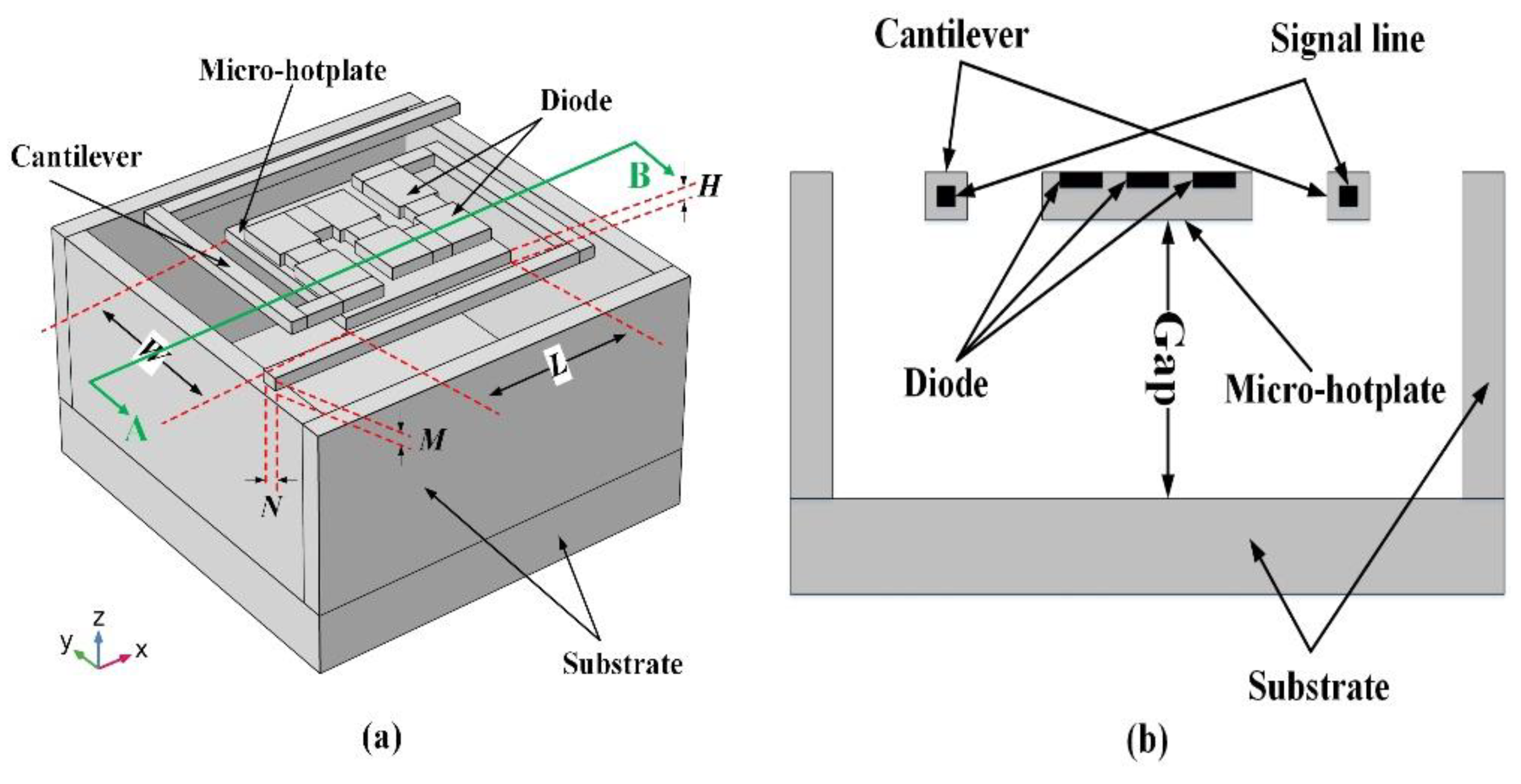
2. Basic Principle of the Diode-Based Micro-Pirani Vacuum Sensor
3. Simulation and Optimization of Micro-Pirani Vacuum Sensor
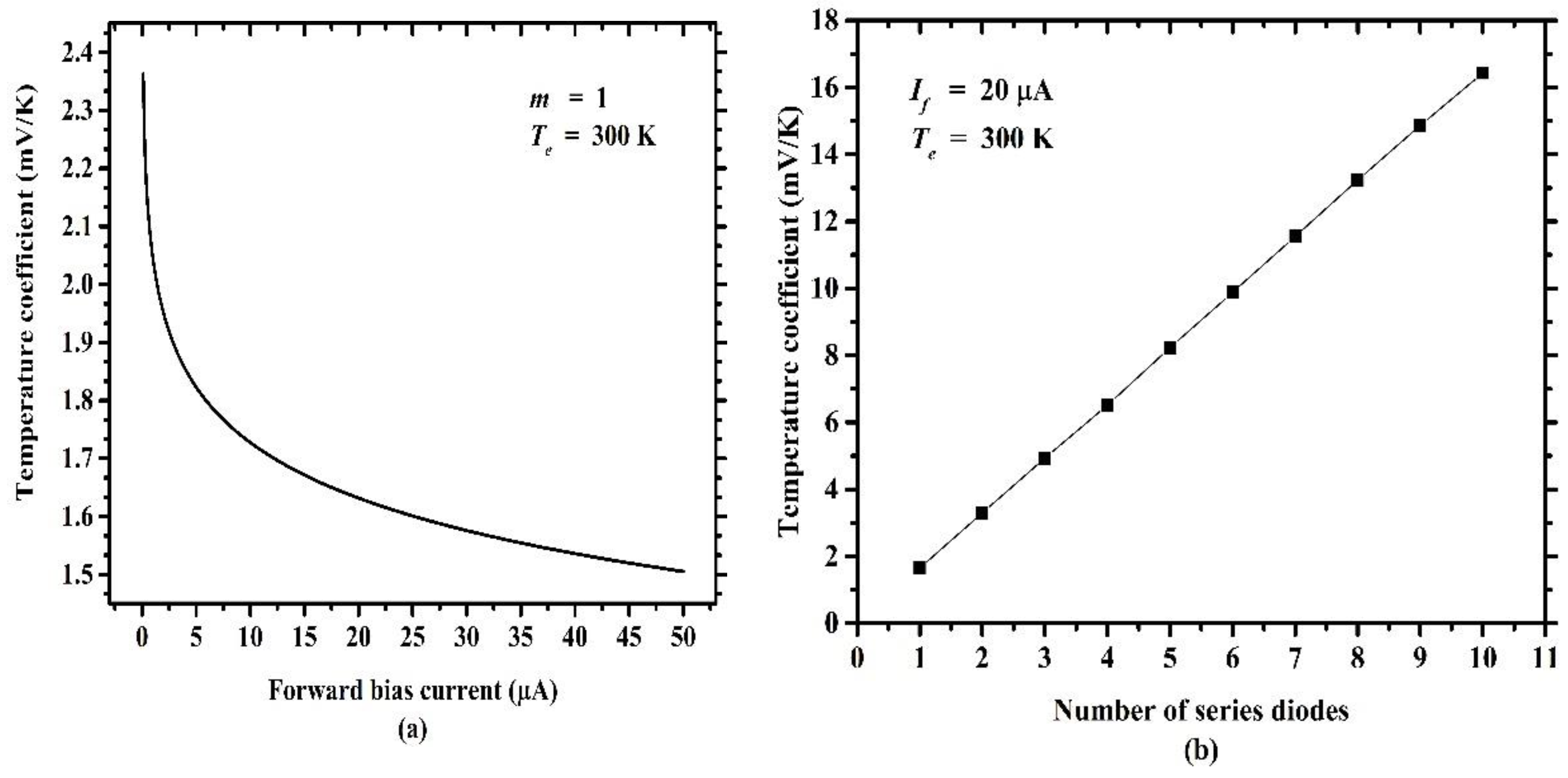
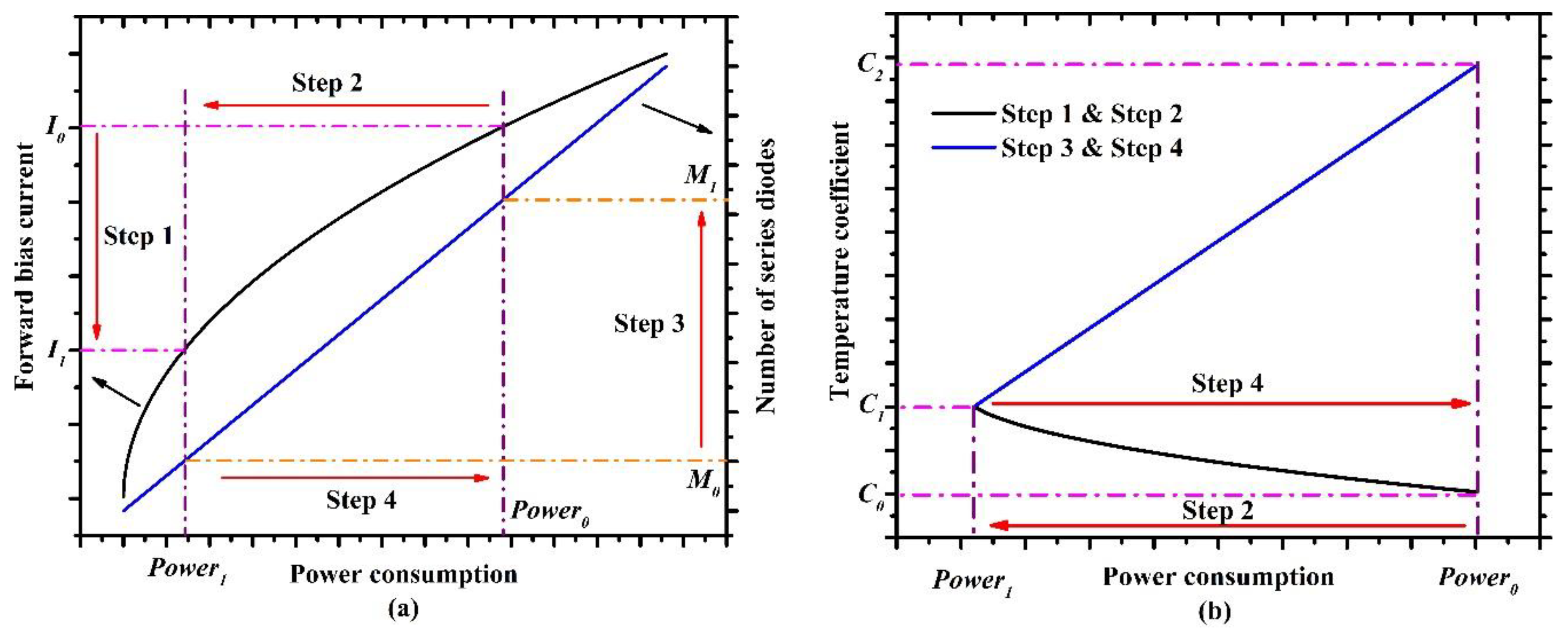
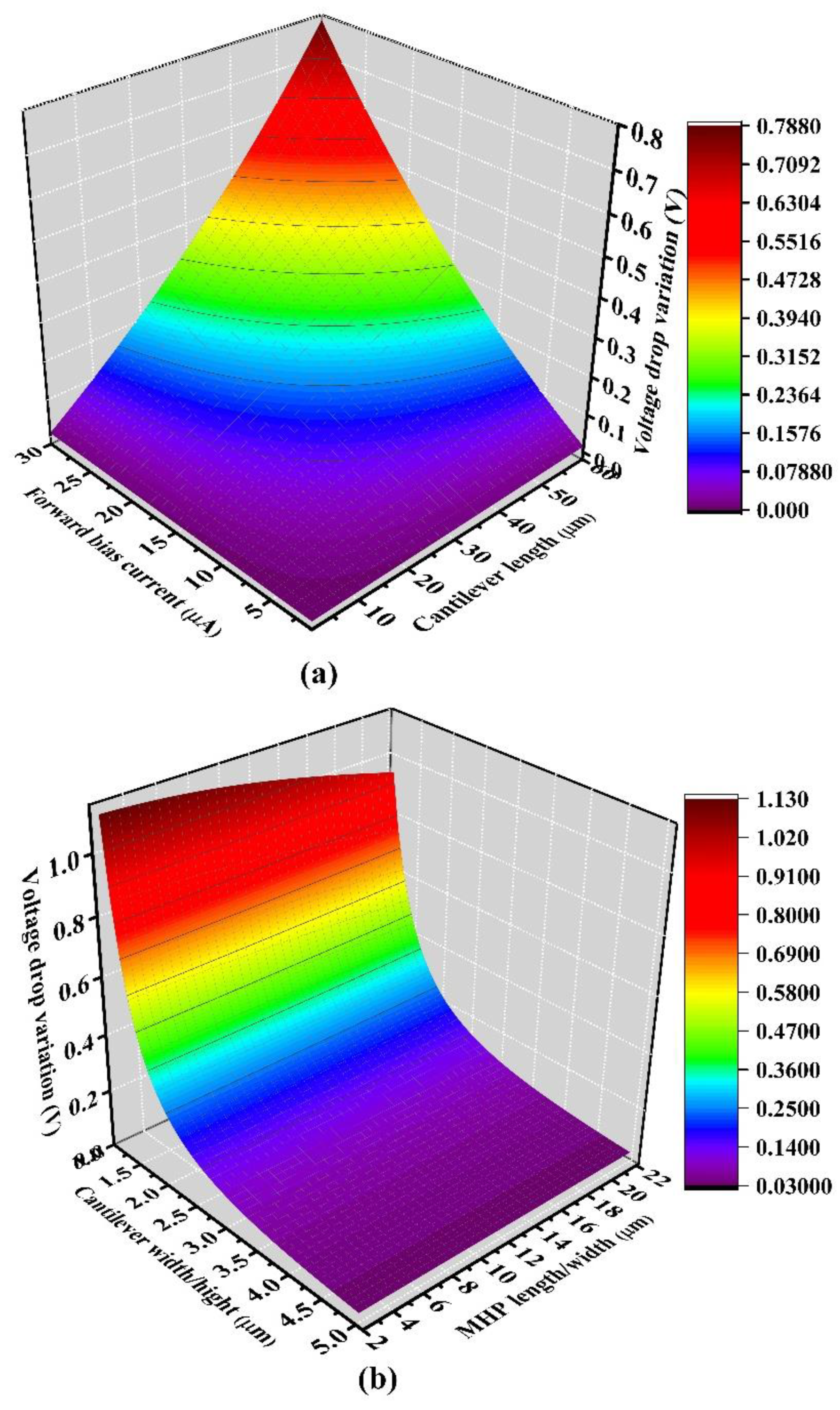
3.1. Greater Temperature Coefficient without Increasing Power Consumption
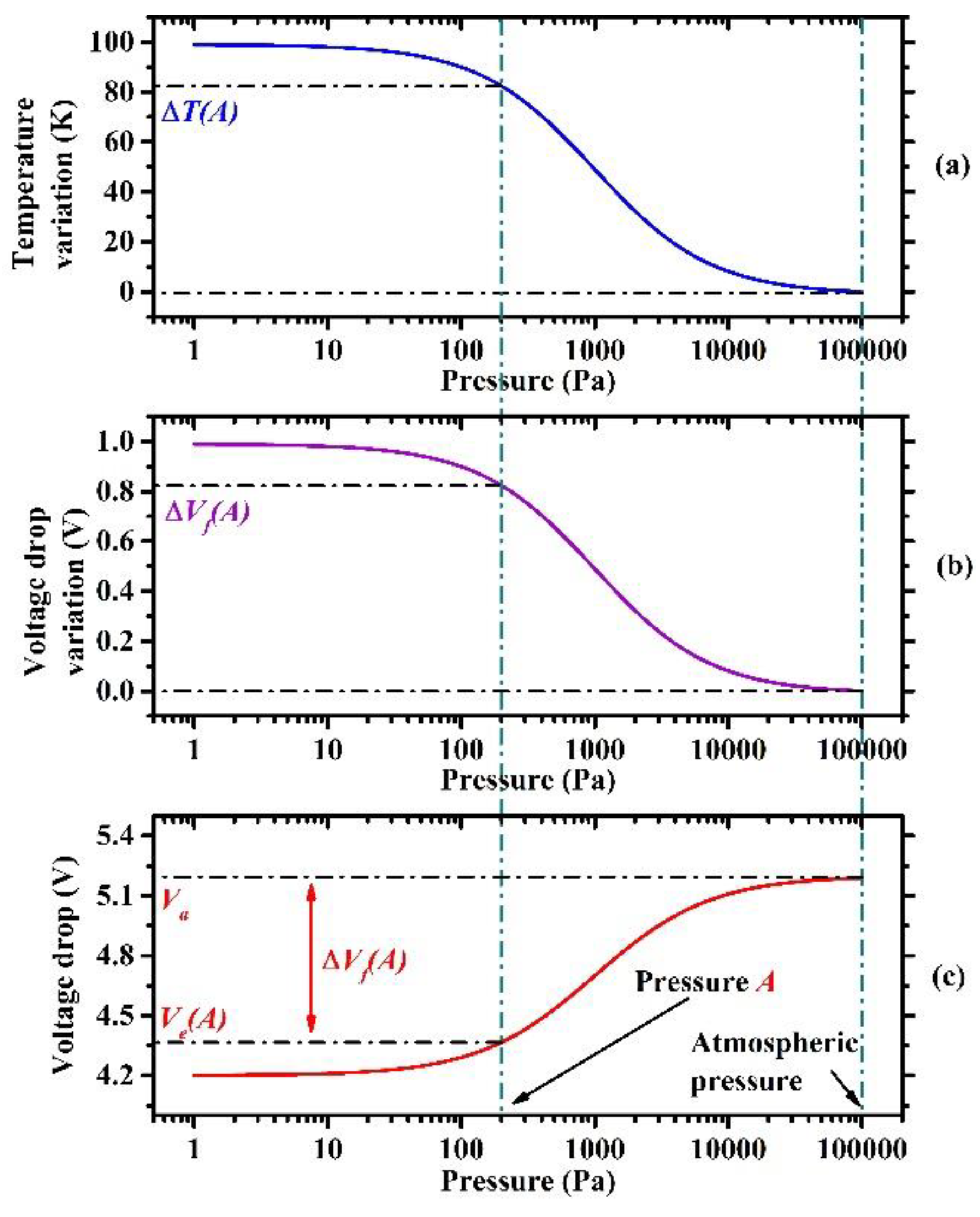
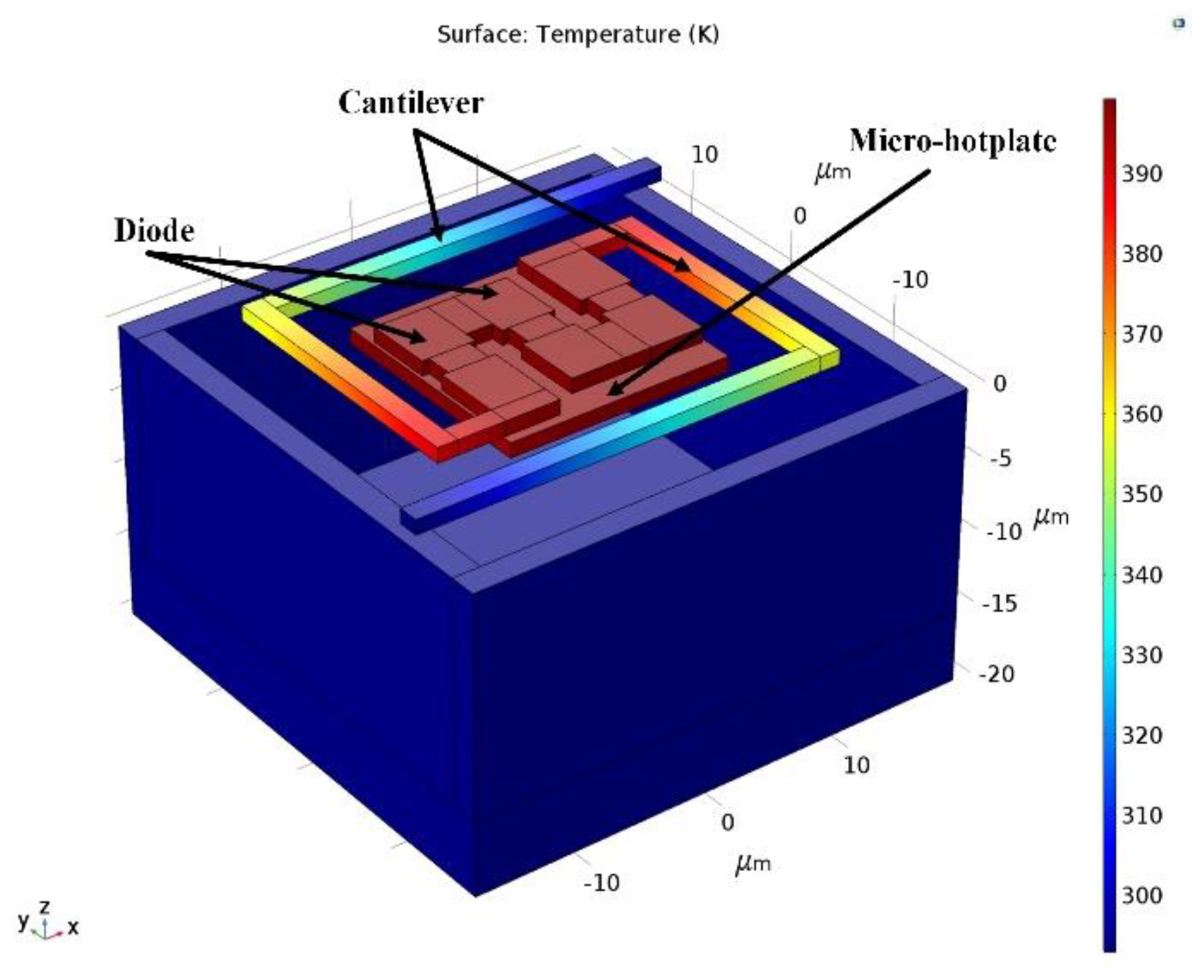
3.2. Larger Temperature Variation by Sensor Structure Optimization
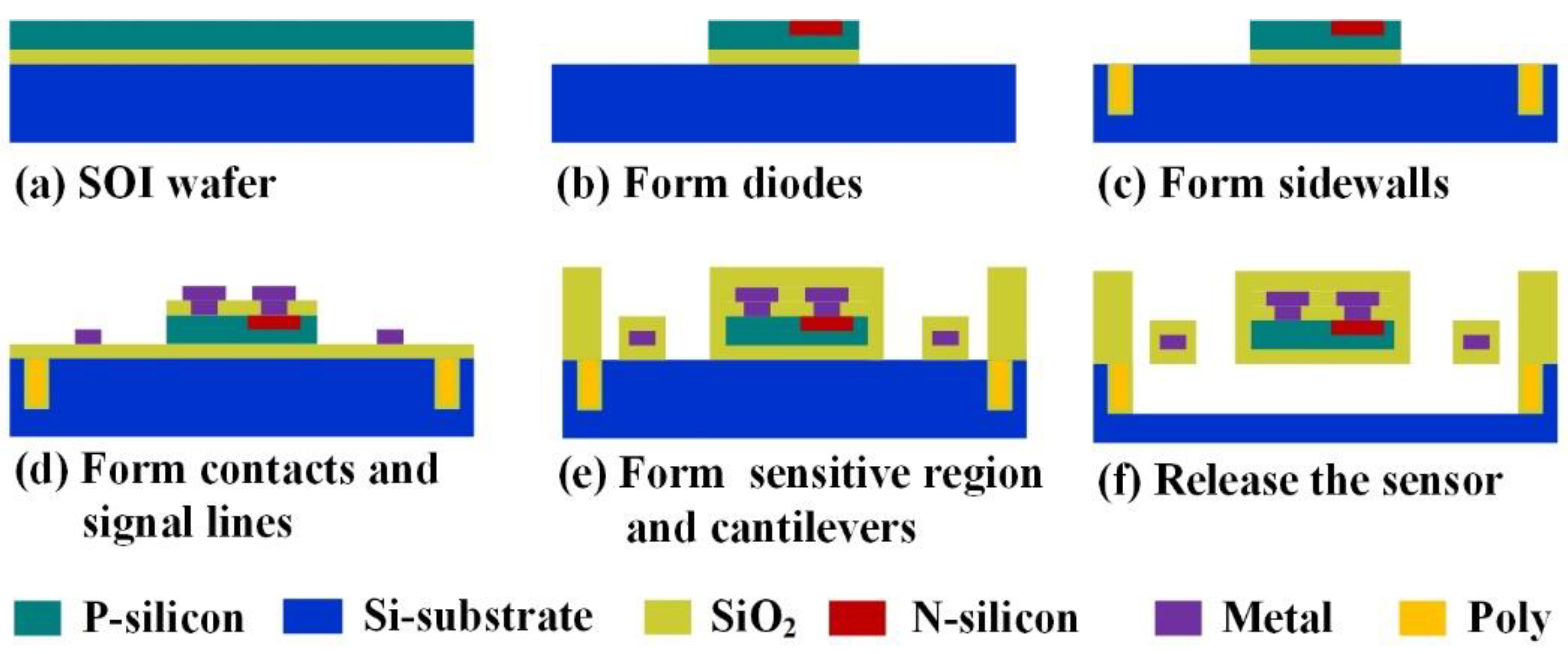
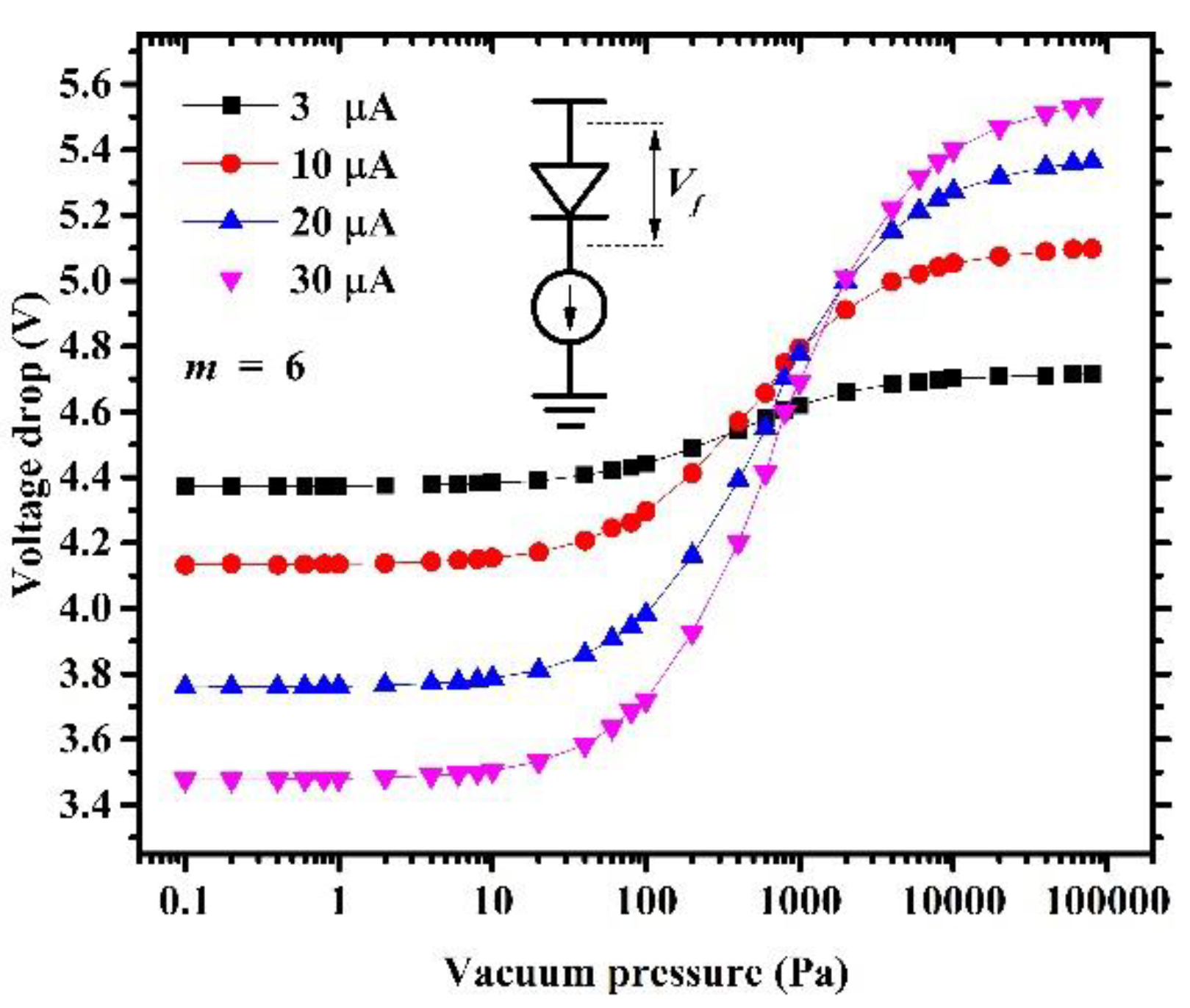
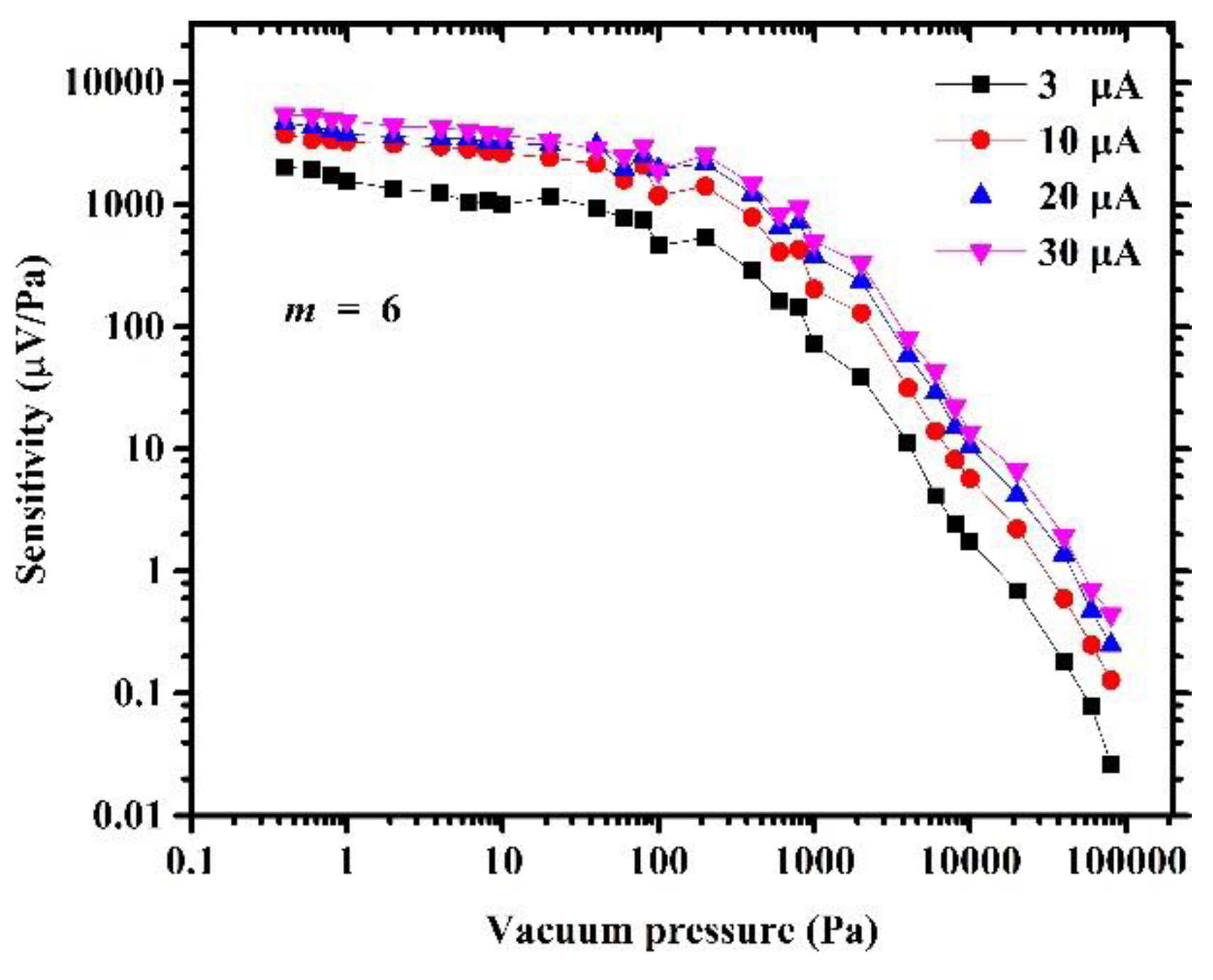
4. Fabrication and Experiments of the Micro-Pirani Vacuum Sensor
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schelcher, G.; Fabbri, F.; Lefeuvre, E.; Brault, S.; Coste, P.; Dufour-Gergam, E.; Parrain, F. Modeling and Characterization of MicroPirani Vacuum Gauges Manufactured by a Low-Temperature Film Transfer Process. J. Microelectromech. Syst. 2011, 20, 1184–1191. [Google Scholar] [CrossRef]
- Ghouila-Houri, C.; Talbi, A.; Viard, R.; Moutaouekkil, M.; Elmazria, O.; Gallas, Q.; Garnier, E.; Merlen, A.; Pernod, P. High temperature gradient nanogap-Pirani micro-sensor with maximum sensitivity around atmospheric pressure. Appl. Phys. Lett. 2017, 111, 113502. [Google Scholar] [CrossRef]
- Zhang, L.M.; Jiao, B.B.; Yun, S.C.; Kong, Y.M.; Ku, C.W.; Chen, D.P. A CMOS Compatible MEMS Pirani Vacuum Gauge with Monocrystal Silicon Heaters and Heat Sinks. Chin. Phys. Lett. 2017, 34, 025101. [Google Scholar] [CrossRef]
- Cao, H.; Li, H.; Kou, Z.; Shi, Y.; Tang, J.; Ma, Z.; Shen, C.; Liu, J. Optimization and Experiment of Dual-Mass MEMS Gyroscope Quadrature Error Correction Methods. Sensors 2016, 16, 71. [Google Scholar] [CrossRef]
- Huang, J.T.; Lee, C.H.; Yang, C.C.; Jeng, K.Y.; Lin, J.; Lee, K.Y. The 3-Axis CMOS-MEMS Accelerometer Include Accelerator Sensing Method of Z-Axis. In Proceedings of the 10th International Conference on Electronics Materials and Packaging, Taipei, Taiwan, 22–24 October 2008. [Google Scholar]
- Shen, C.; Song, R.; Li, J.; Zhang, X.; Tang, J.; Shi, Y.; Liu, J.; Cao, H. Temperature drift modeling of MEMS gyroscope based on genetic-Elman neural network. Mech. Syst. Signal Process. 2016, 72, 897–905. [Google Scholar] [CrossRef]
- Aydemir, A.; Terzioglu, Y.; Akin, T. A new design and a fabrication approach to realize a high performance three axes capacitive MEMS accelerometer. Sens. Actuators A Phys. 2016, 244, 324–333. [Google Scholar] [CrossRef]
- Junseok, C.; Joseph, M.G.; Khalil, N. Fabrication and characterization of a wafer-level MEMS vacuum package with vertical feedthroughs. J. Microelectromech. Syst. 2008, 17, 193–200. [Google Scholar] [CrossRef]
- Geiger, W.; Bartholomeyczik, J.; Breng, U.; Gutmann, W.; Hafen, M. MEMS IMU for AHRS Applications. In Proceedings of the 2008 IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008. [Google Scholar]
- Piotto, M.; Cesta, S.D.; Bruschi, P. A CMOS compatible micro-Pirani vacuum sensor based on mutual heat transfer with 5-decade operating range and 0.3 Pa detection limit. Sens. Actuators A Phys. 2017, 263, 718–726. [Google Scholar] [CrossRef]
- Li, Q.; Goosen, J.F.L.; Beek, J.T.M.; Keulen, F. A SOI sensor with triple heat sinks. Sens. Actuators A Phys. 2010, 162, 267–271. [Google Scholar] [CrossRef]
- Tatjana, D.; Kasun, A.G.P.; Evan, Z.; Sidra, F.; Payam, H.; Alan, F.; Heinz, B. Extension of operating range towards lower pressures of MEMS-based thermal vacuum gauges by laser-induced heating. In Proceedings of the 26th European Conference on Solid-State Transducers, Krakow, Poland, 9–12 September 2012. [Google Scholar]
- Khosraviani, K.; Ma, Y.; Leung, A.M. Low-Cost Surface Micromachined Pirani Pressure Sensor with Atmospheric pressure range. In Proceedings of the 20th Annual Canadian Conference on Electrical and Computer Engineering, Vancouver, BC, Canada, 22–26 April 2007. [Google Scholar]
- Zhang, M.; Nicolas, L. Exploiting a Micro Pirani Gauge for beyond Atmospheric Pressure Measurement. In Proceedings of the 1st International Symposium on Integrated Circuits and Systems, Taormina, Italy, 2–3 September 2018. [Google Scholar]
- Puers, R.; Reyntjens, S.; Bruyker, D.D. The NanoPirani-an extremely miniaturized pressure sensor fabricated by focused ion beam rapid prototyping. Sens. Actuators A Phys. 2002, 97, 208–214. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Zhang, J. Single-walled Carbon Nanotube Pirani vacuum Gauge. In Proceedings of the 10th IEEE International Conference on Solid-State and Integrated Circuit Technology, Shanghai, China, 1–4 November 2010. [Google Scholar]
- Sun, Y.C.; Liang, K.C.; Cheng, C.L.; Lin, M.Y.; Chen, R.; Fang, W. Performance improvement of CMOS-MEMS Pirani vacuum gauge with hollow heater design. In Proceedings of the 18th International Conference on Solid-State Sensors, Actuators and Microsystems, Anchorage, AK, USA, 21–25 June 2015. [Google Scholar]
- Jiang, W.; Wang, X.; Zhang, J. A single crystal silicon micro-Pirani vacuum gauge with high aspect ratio structure. Sens. Actuators A Phys. 2010, 163, 159–163. [Google Scholar] [CrossRef]
- Wang, J.; Tang, Z.; Li, J.; Zhang, F. A MicroPirani Pressure Sensor Based on the Tungsten Microhotplate in a standard CMOS process. IEEE Trans. Ind. Electron. 2009, 56, 1086–1091. [Google Scholar] [CrossRef]
- Santagata, F.; Iervolino, E.; Mele, L.; Herwaarden, A.W.; Creemer, J.F.; Sarro, P.M. An analytical model and verification for MEMS Pirani gauges. J. Micromech. Microeng. 2011, 21, 115007. [Google Scholar] [CrossRef]
- Volklein, F.; Meier, A. Microstructured vacuum gauges and their future perspectives. Vacuum 2007, 82, 420–430. [Google Scholar] [CrossRef]
- Volklein, F.; Grau, M.; Meier, A.; Hemer, G.; Breuer, L. Optimized MEMS Pirani sensor with increased pressure measurement sensitivity in the fine and high vacuum regime. J. Vac. Sci. Technol. A 2013, 31, 061604. [Google Scholar] [CrossRef]
- Weng, P.K.; Shie, J.S. Micro-Pirani vacuum gauge. Rev. Sci. Instrum. 1994, 65, 492–499. [Google Scholar] [CrossRef]
- Zhang, F.T.; Tang, Z.; Yu, J.; Jin, R.C. A micro-Pirani vacuum gauge based on micro-hotplate technology. Sens. Actuators A Phys. 2006, 126, 300–305. [Google Scholar] [CrossRef]
- Mastrangelo, C.H. Thermal Applications of Microbridges. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1991. [Google Scholar]
- Shie, J.S.; Chen, Y.M.; Ou-Yang, M.; Chou, B.C.S. Characterization and Modeling of Metal-Film Microbolometer. J. Microelectromech. Syst. 1996, 5, 298–306. [Google Scholar] [CrossRef]
- Kimura, M.; Toshima, K. Thermistor-like pn junction temperature sensor with variable sensitivity and its combination with a micro-air-bridge heater. Sens. Actuators A Phys. 2003, 108, 239–243. [Google Scholar] [CrossRef]
- Takashima, N.; Kimura, M. Diode temperature sensor with the output voltage proportional to the absolute temperature and its application to the thin film Pirani Vacuum Sensor. In Proceedings of the 33rd Annual Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 5–8 November 2007. [Google Scholar]
- Sun, X.; Xu, D.; Xiong, B.; Wu, G.; Wang, Y. A wide measurement pressure range CMOS-MEMS based integrated thermopile vacuum gauge with an XeF2 dry-etching process. Sens. Actuators A Phys. 2013, 201, 428–433. [Google Scholar] [CrossRef]
- Zhang, F.; Zhen, Y.; Tang, B.; Su, W.; Tang, Z. Design and Fabrication of High Vacuum Gauge Based on Micro Hotplate. Key Eng. Mater. 2015, 645, 698–705. [Google Scholar] [CrossRef]
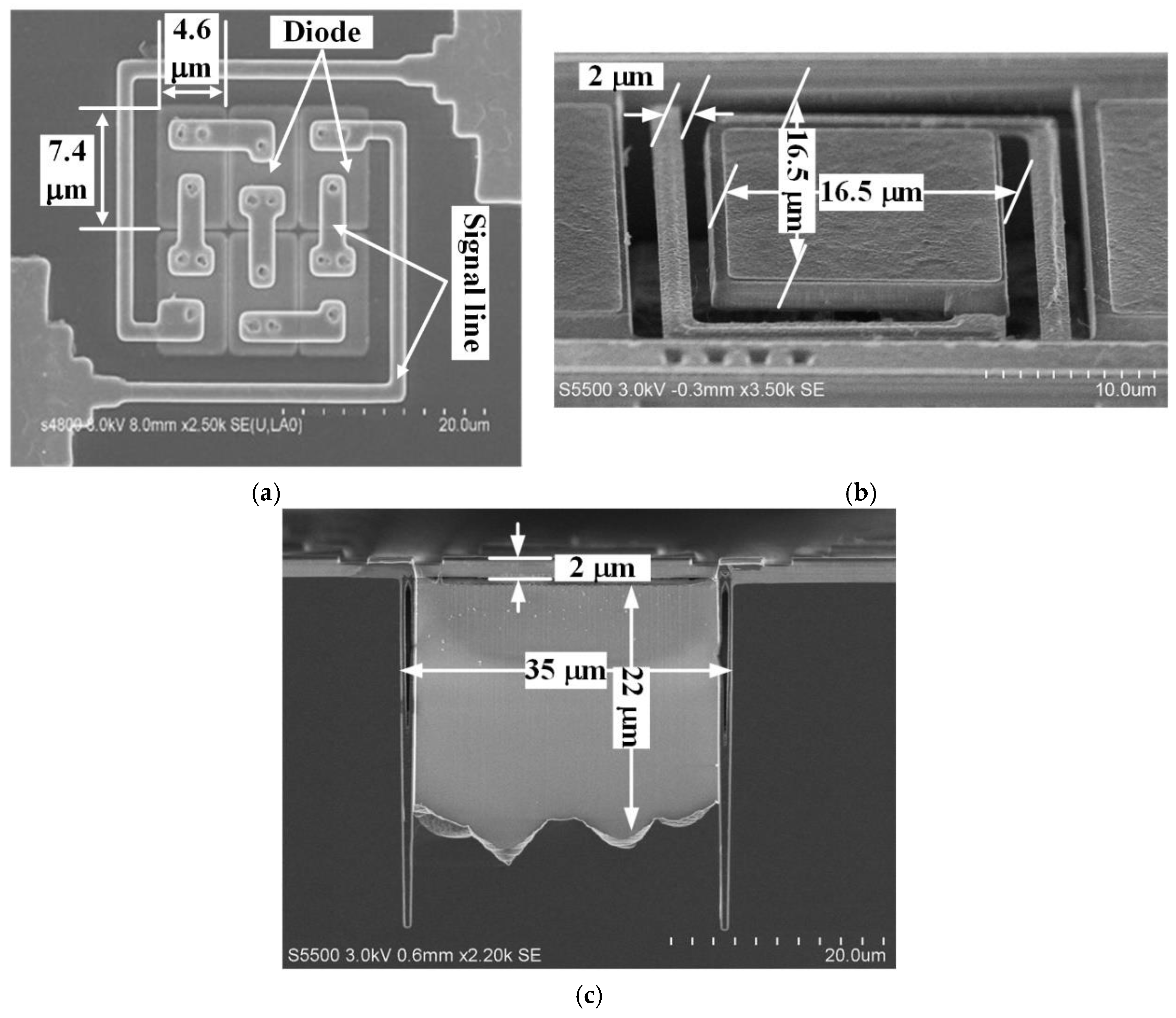

| Total Size | Microhotplate Size (L × W × H) | Cantilever Size (Lcan × N × M) | Gap between MHP and Substrate |
|---|---|---|---|
| 35 × 35 μm | 16.5 × 16.5 × 2 μm | 39 × 2 × 2 μm | 22 μm |
| Researcher | Average Sensitivity (μV/Pa) Sensitivity of Unit Power Consumption (V/W/Pa) | Dynamic Vacuum Pressure Range (Pa) | Sensor Power Consumption (μW) | Sensor Size (μm2) |
|---|---|---|---|---|
| J. Wang et al. [19] | 230 μV/Pa (0.02 V/W/Pa) | 1 to 1 × 102 | 4900 | 100 × 100 |
| Y. C. Sun et al. [17] | - | 26.6 to 2.66 × 104 | 127.59 | 206 × 82 |
| M. Piotto et al. [10] | 200 μV/Pa (0.18 V/W/Pa) | 3 × 10−1 to 1 × 105 | 1100 | 200 × 200 |
| X. Sun et al. [29] | 4.5 μV/Pa (0.001 V/W/Pa) | 5 × 10−3 to 1 × 105 | 4500 | 400 × 1500 |
| F. Zhang et al. [30] | 60 μV/Pa (0.43 V/W/Pa) | 5 × 10−3 to 1 × 103 | 140 | 500 × 500 |
| Presented | 90 μV/Pa (1.8 V/W/Pa) | 1 × 10−1 to 1 × 104 | 50 | 35 × 35 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, D.; Fu, J.; Liu, R.; Hou, Y.; Liu, C.; Wang, W.; Chen, D. Highly Sensitive Diode-Based Micro-Pirani Vacuum Sensor with Low Power Consumption. Sensors 2019, 19, 188. https://doi.org/10.3390/s19010188
Wei D, Fu J, Liu R, Hou Y, Liu C, Wang W, Chen D. Highly Sensitive Diode-Based Micro-Pirani Vacuum Sensor with Low Power Consumption. Sensors. 2019; 19(1):188. https://doi.org/10.3390/s19010188
Chicago/Turabian StyleWei, Debo, Jianyu Fu, Ruiwen Liu, Ying Hou, Chao Liu, Weibing Wang, and Dapeng Chen. 2019. "Highly Sensitive Diode-Based Micro-Pirani Vacuum Sensor with Low Power Consumption" Sensors 19, no. 1: 188. https://doi.org/10.3390/s19010188
APA StyleWei, D., Fu, J., Liu, R., Hou, Y., Liu, C., Wang, W., & Chen, D. (2019). Highly Sensitive Diode-Based Micro-Pirani Vacuum Sensor with Low Power Consumption. Sensors, 19(1), 188. https://doi.org/10.3390/s19010188





