Path Smoothing Techniques in Robot Navigation: State-of-the-Art, Current and Future Challenges
Abstract
1. Introduction
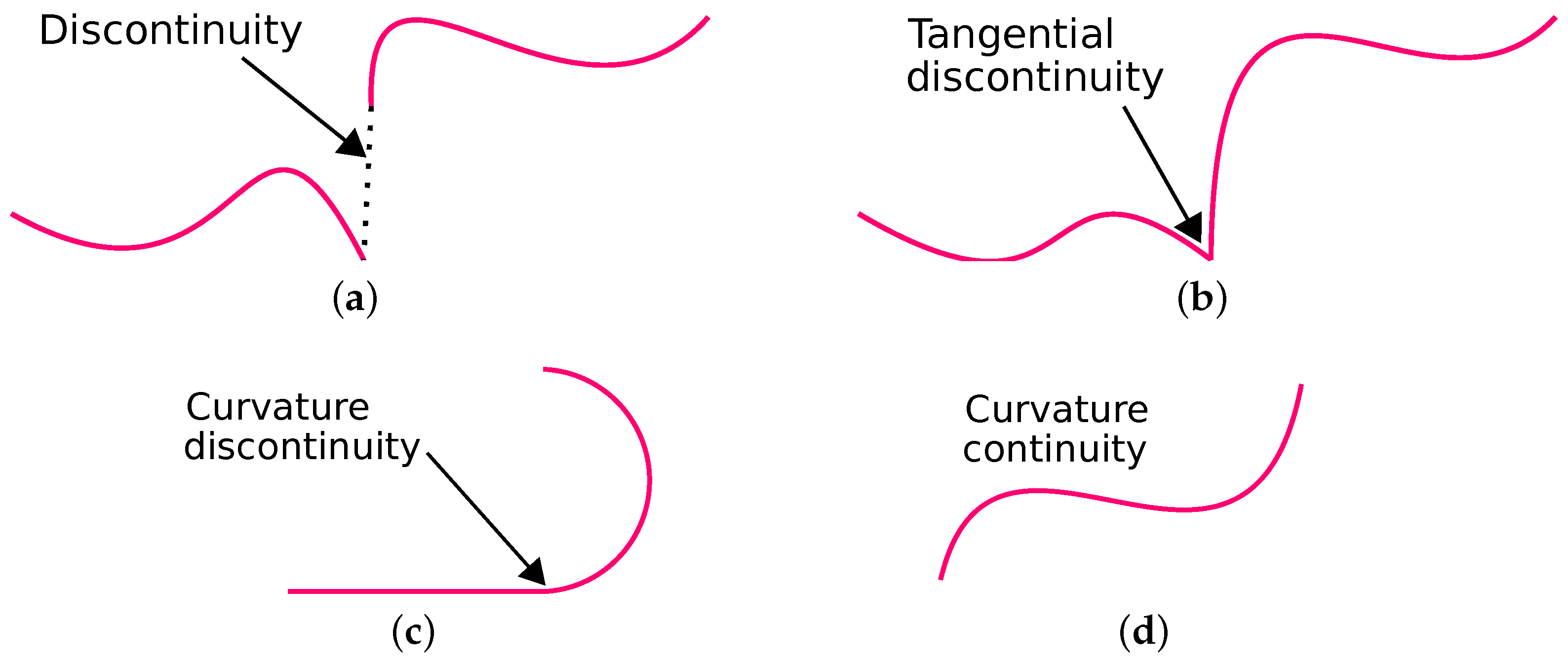
2. A Short Note on Path Continuity
3. Interpolation Based Path Smoothing
3.1. Polynomial Interpolation
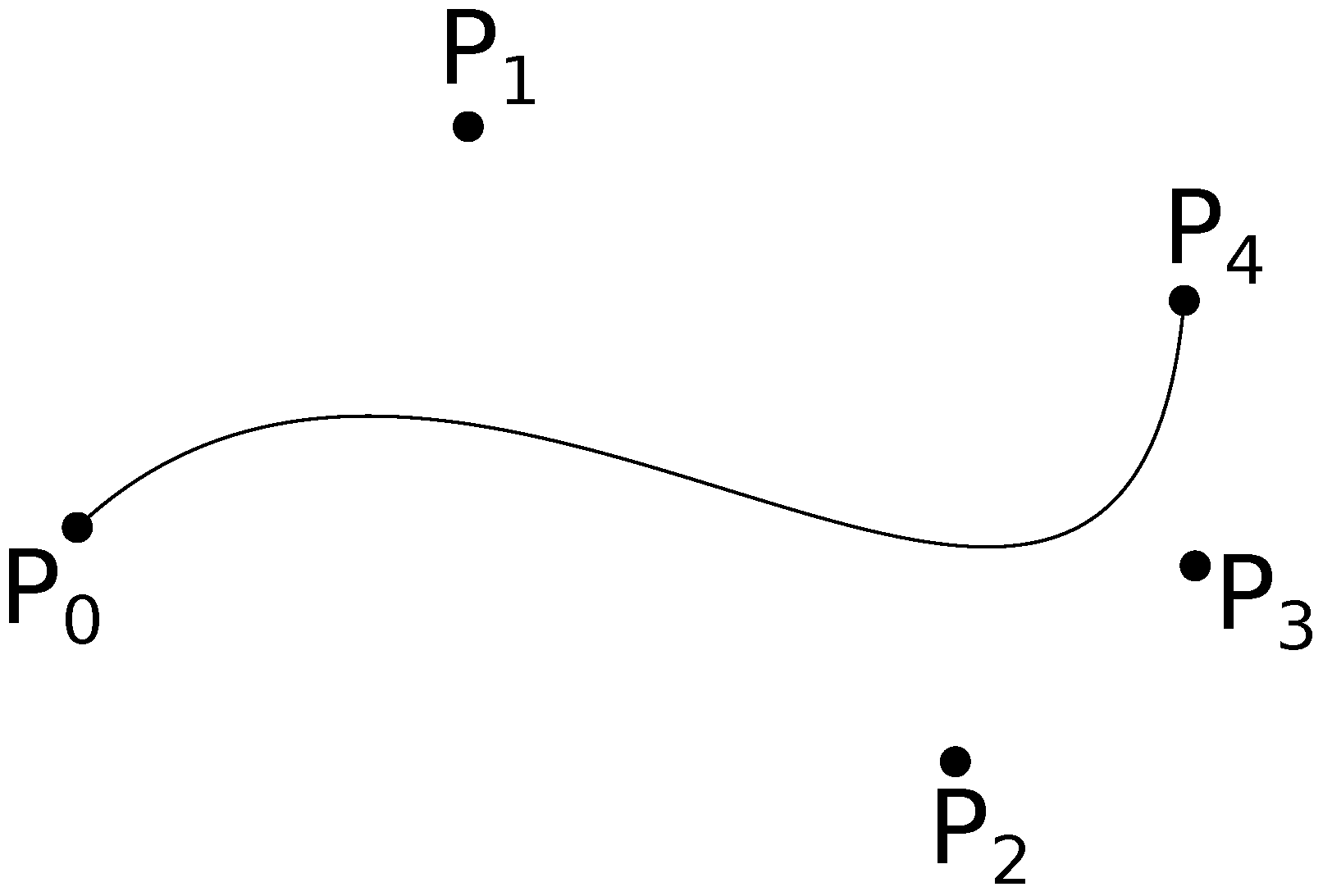
3.2. Bézier Curve
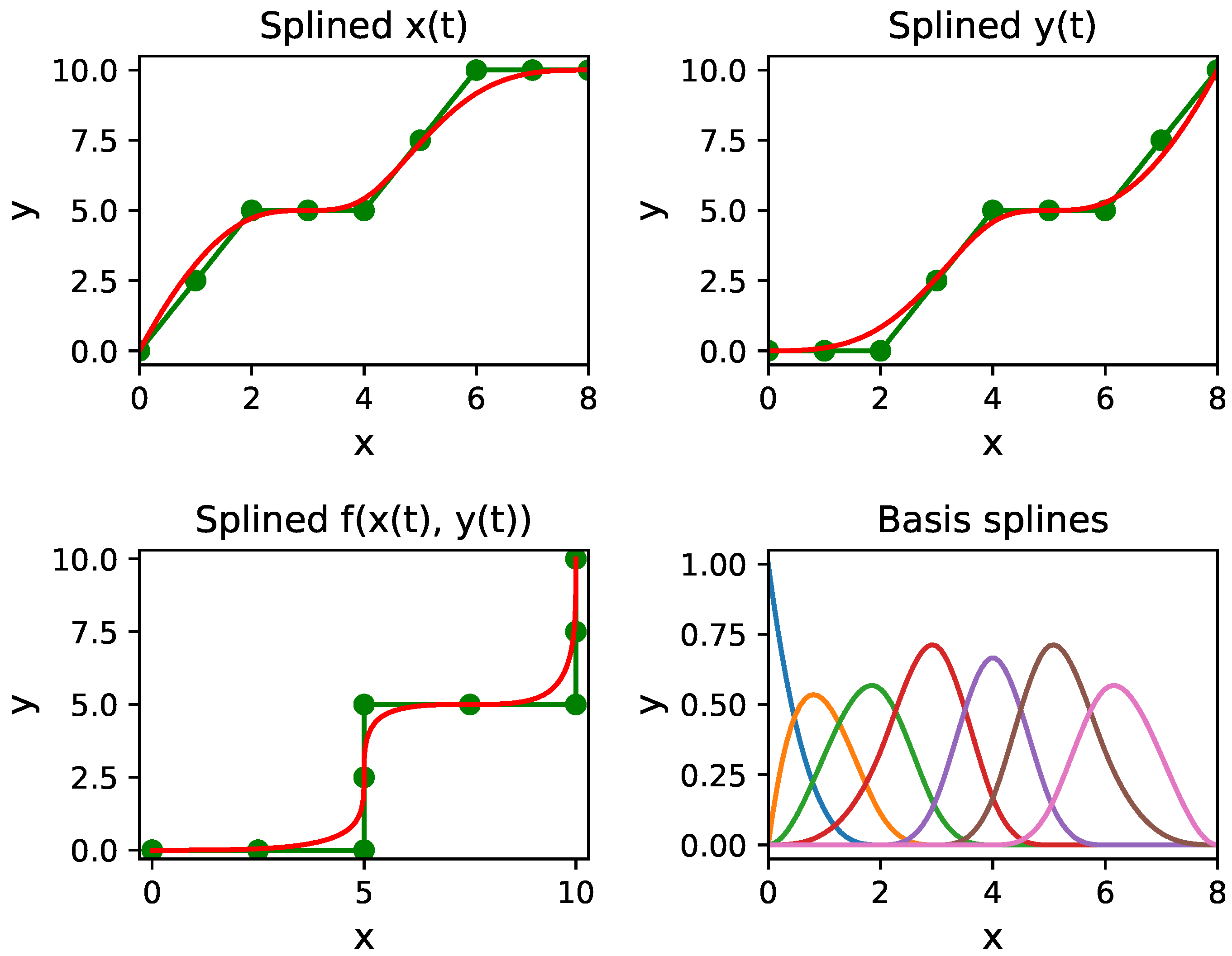
3.3. Cubic Splines
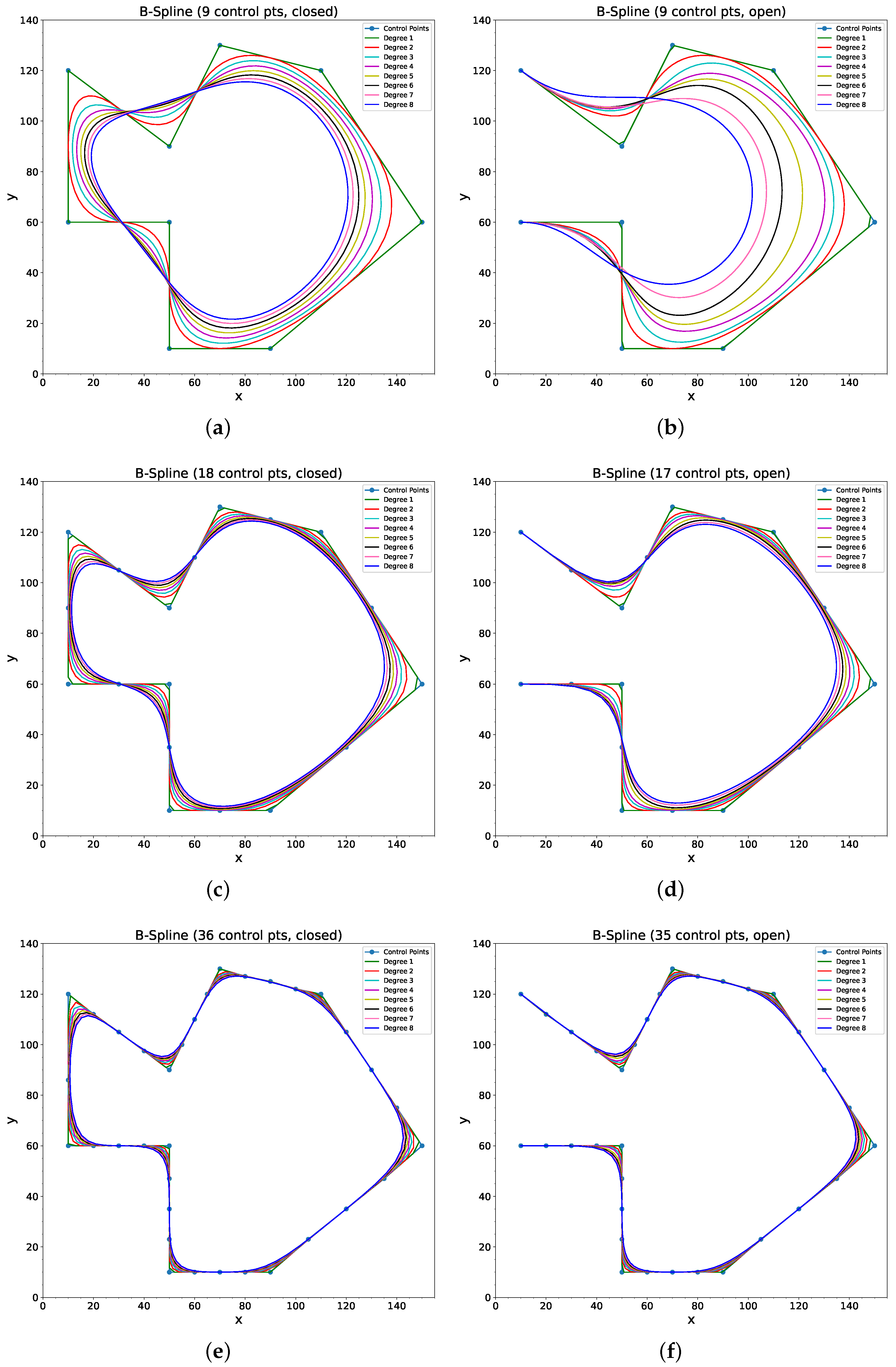
3.4. B-Spline
3.5. NURBS Curve
4. Path Smoothing Using Special Curves
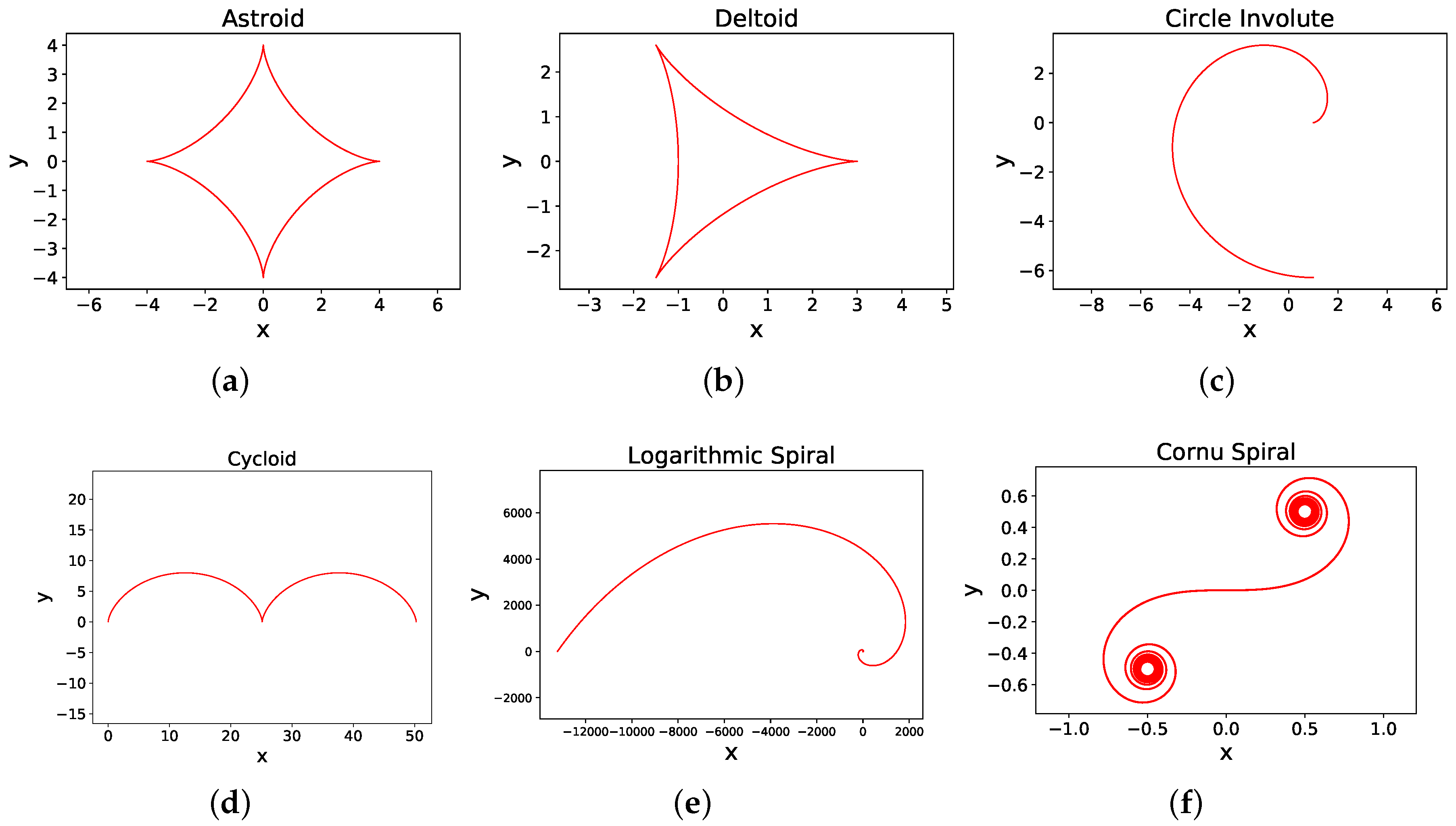
4.1. Dubin’s Curve
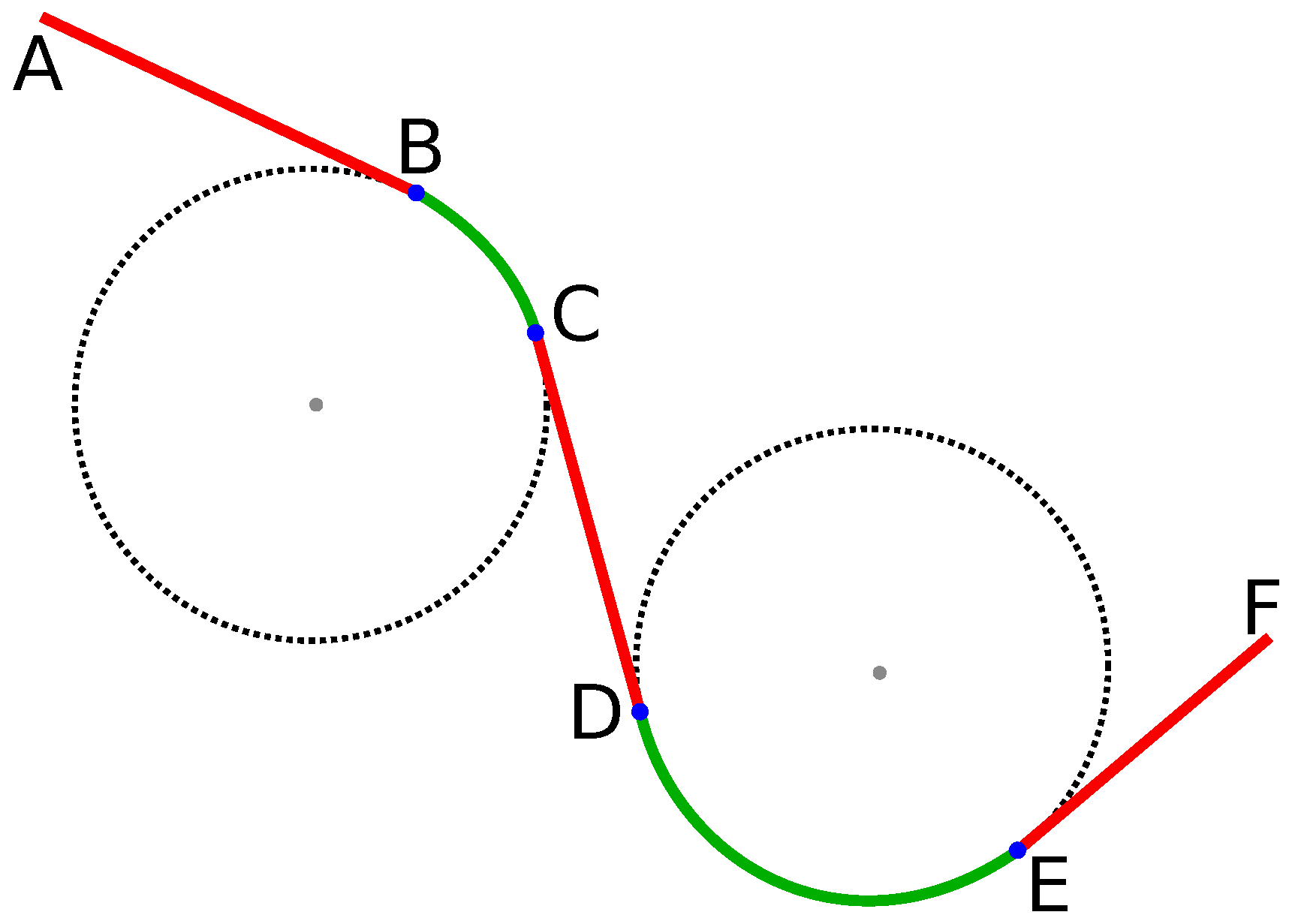
4.2. Clothoid
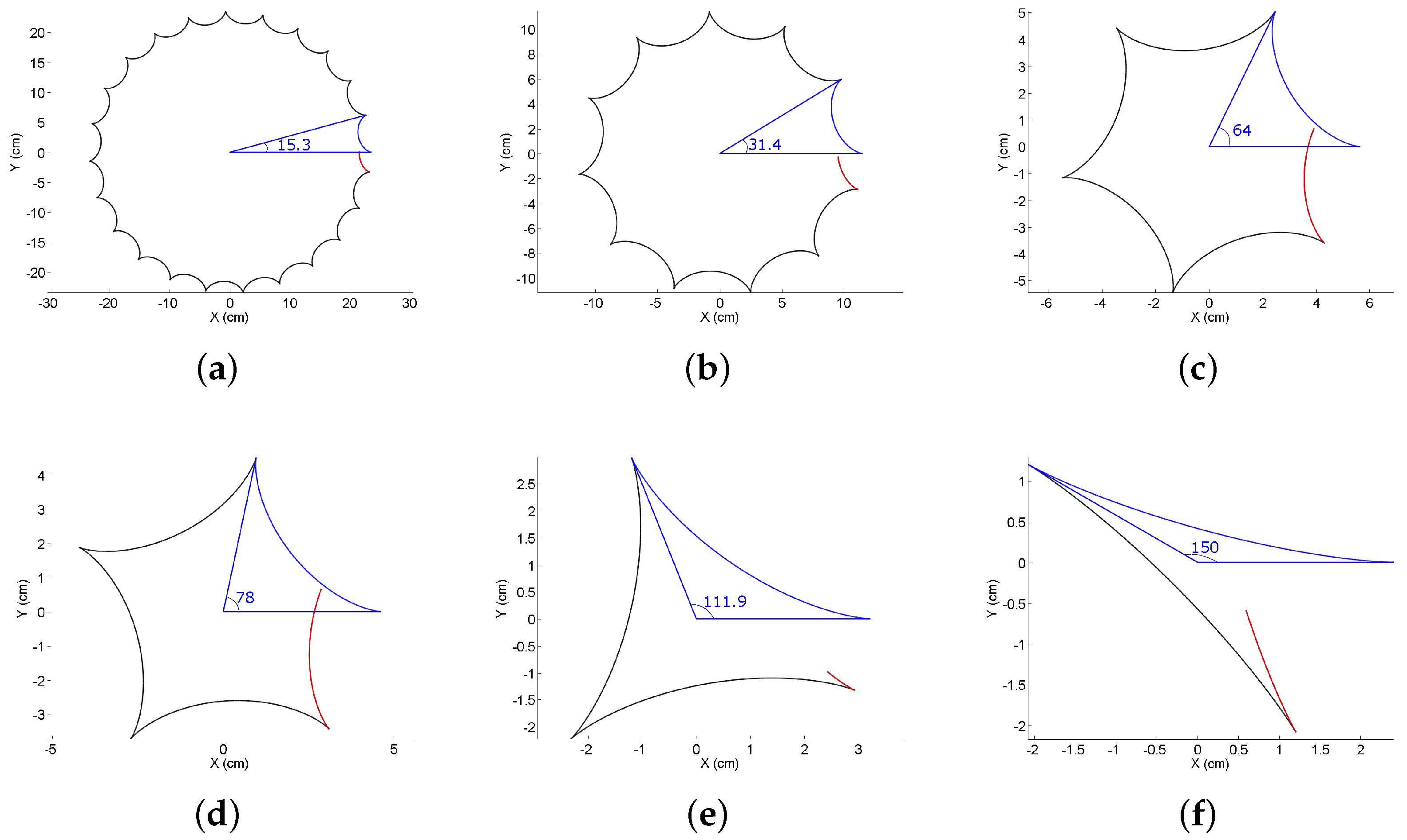
4.3. Hypocycloid
5. Optimization-Based Path Smoothing
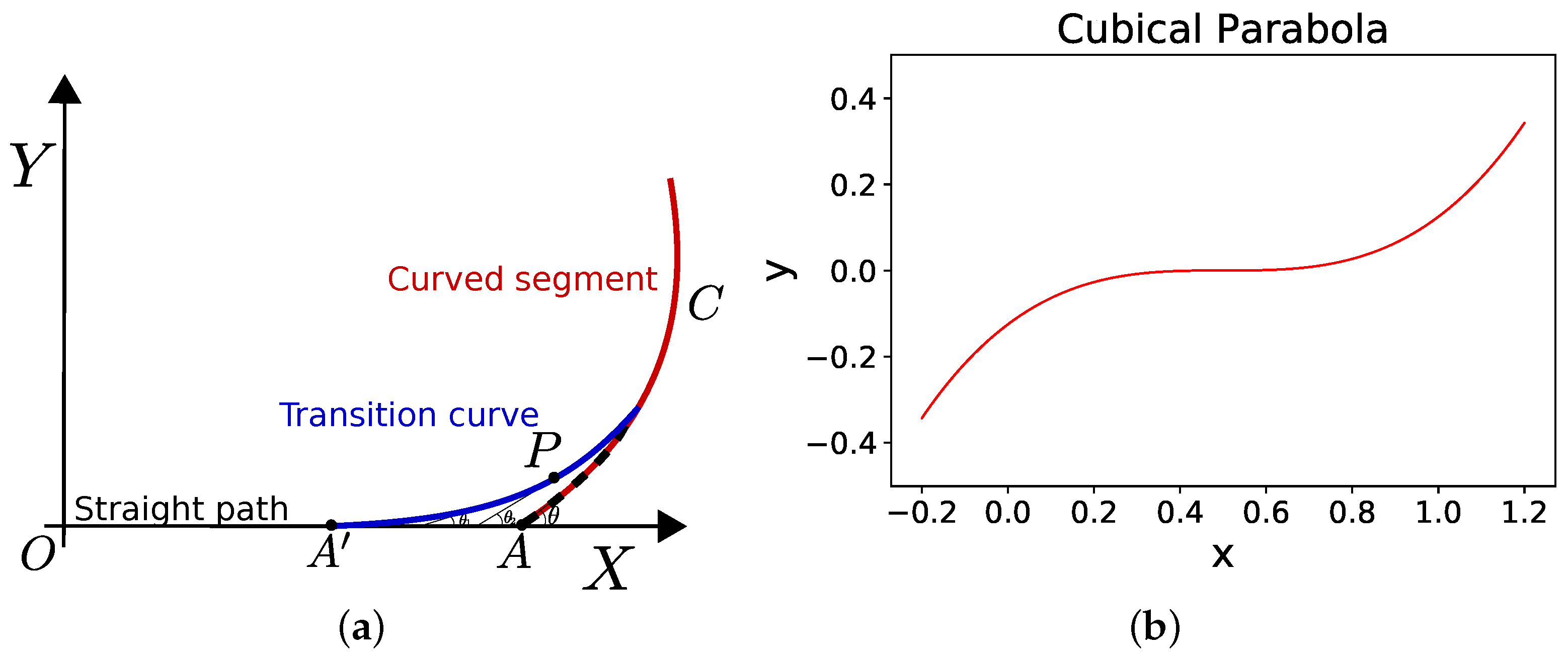
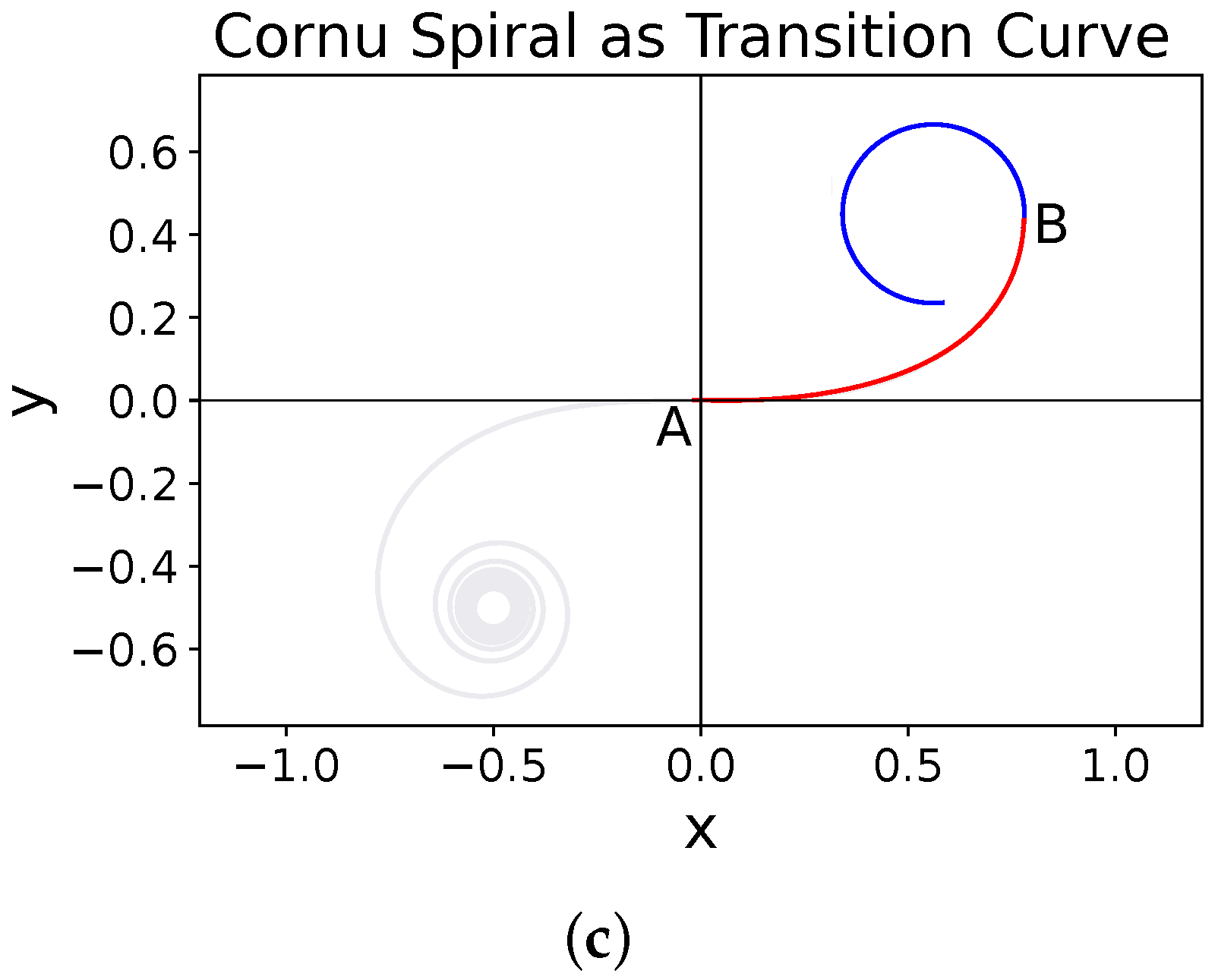
6. A Note on Transition Curves
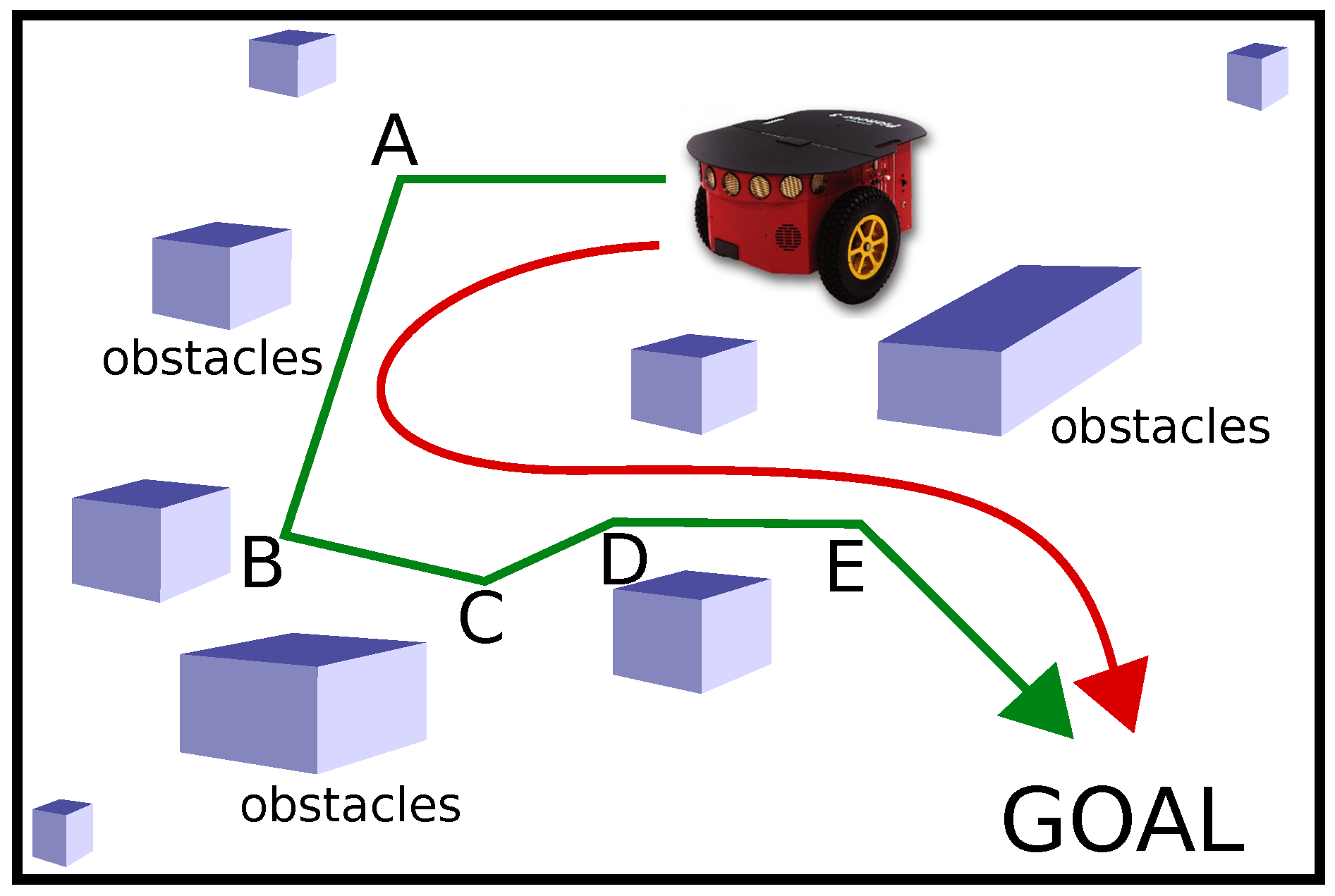
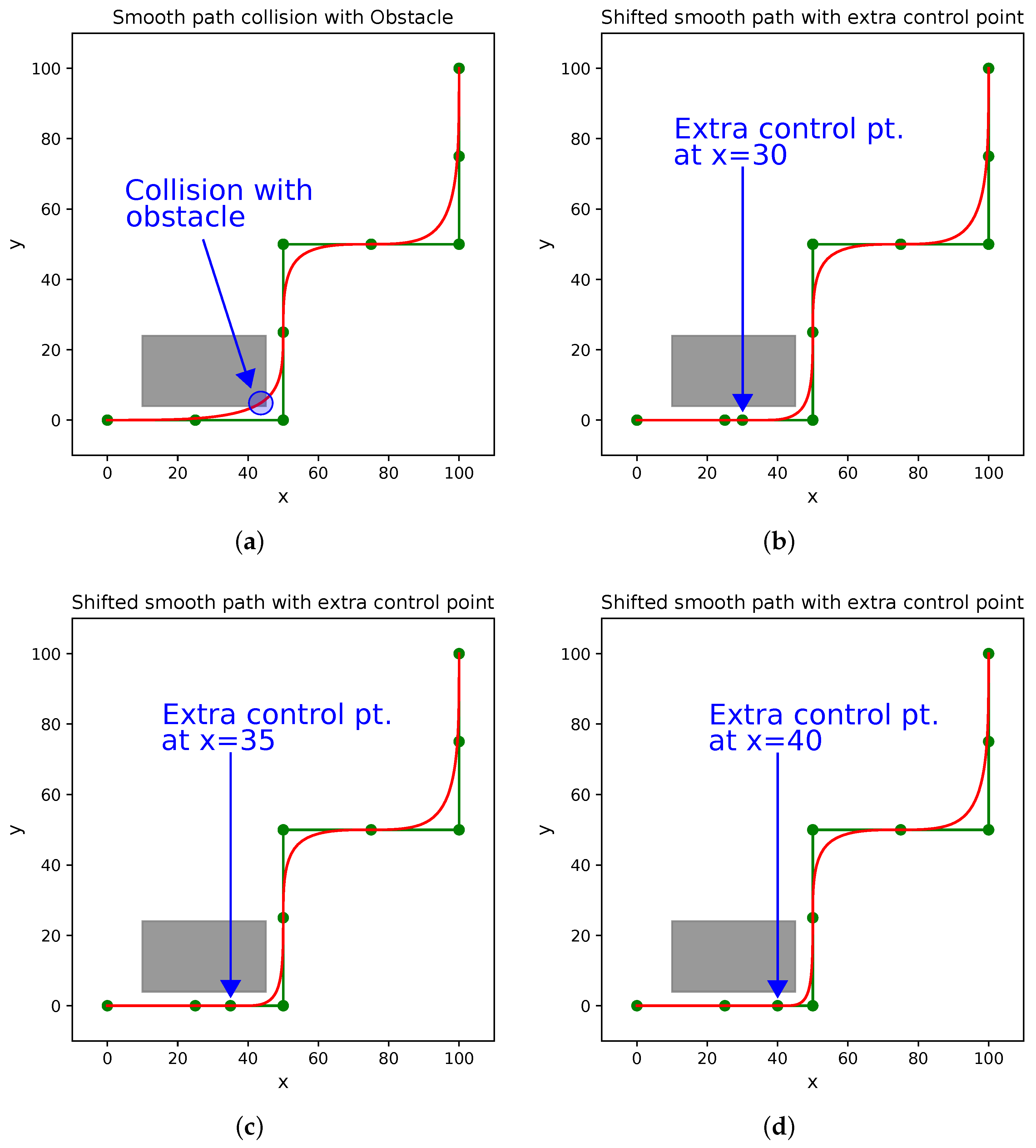
7. Robot Trajectories with Obstacle Avoidance
8. Challenges
- Trajectory smoothing in dynamic environments: One of the biggest constraint in these terms is the speed of detection of dynamic entities which is directly affected by the total number of entities tracked. Hence, in an environment like an open public space, there are a lot of dynamic entities for the mobile robot to track which consumes a lot of time. This has an adverse effect on the trajectory smoothing process as the robot ends up stopping suddenly or considerably reducing the speed while trying to select the best possible alternate trajectory among the potential candidates. It is important to accurately track these dynamic entities in conjunction to path smoothing. This is more challenging in autonomous self driving cars at high speeds. Work in [169] has succinctly summarized the challenges in pedestrian detection considering the resolution, range, and field-of-view of various on-borad sensors like radar, lidar, or omni-directional cameras with various types of hardwares. In addition, work in [170] has focused the survey of challenges of pedestrian detection with vision based sensors which are very prominent recently. In adverse conditions like low illumination, night, snowfall, and rain, it is further difficult to detect the dynamic entities while work has been done in this regards by using thermal images [171]. In both indoor and outdoor environments, occlusion is another big hindrance with dynamic entity detection and solutions have been proposed [172,173], although it still is an open problem.
- Fusing trajectory smoothing into SLAM process: SLAM in an indispensable module for any mobile robot. Even autonomous vehicles need to localize themselves in the environment and build or update their map using perceptive sensors like GPS, cameras, or range sensors. SLAM models the uncertainty of the robot motion and the sensor errors to come up with the most optimum state estimation [5,174]. Trajectory generation is directly linked with currently estimated state and perception and hence fusing it in the SLAM module is beneficial. Currently, it seems like SLAM module is decoupled from the trajectory smoothing module. However, the two modules must work side-by-side to update the map with the new obstacles or entities and generate real-time smooth trajectories on the fly. Work in [175] presents a motion planning algorithm considering both the uncertainty caused by robot and dynamic entities. The motion of dynamic entities are predicted using a local planner, and the uncertainty along the predicted trajectory is computed based on Gaussian propagation. In this regard, a relative continuous-time SLAM has been proposed by Anderson et al. [176] which uses weights on cubic B-splines to represent continuous state variables. Only the local weights are adjusted during optimization, while implicit trajectory prior is arbitrary. In [177], a Simultaneous Trajectory Estimation and Mapping (STEAM) is proposed which uses Gaussian Process (GP) regression instead of cubic B-splines. It interpolates between conventional state parameterizations at certain key times. When applied in SE3, this parameterization can represent realistic probabilistic trajectories obeying nonlinear, nonholonomic motion models. Although slow for dense kernels, a careful selection can result in realistic sparse GP kernels that are very fast. A non-uniform sampling of the trajectory representation over the sliding window with continuous correction is presented in [178]. In [179], a dense map-centric SLAM method based on a continuous-time trajectory is proposed which removes the need for global trajectory optimization by introducing map deformation. Some other recent significant works in continuous-time SLAM are [180,181,182,183], while a broad overview of challenges in SLAM can be found in [184].
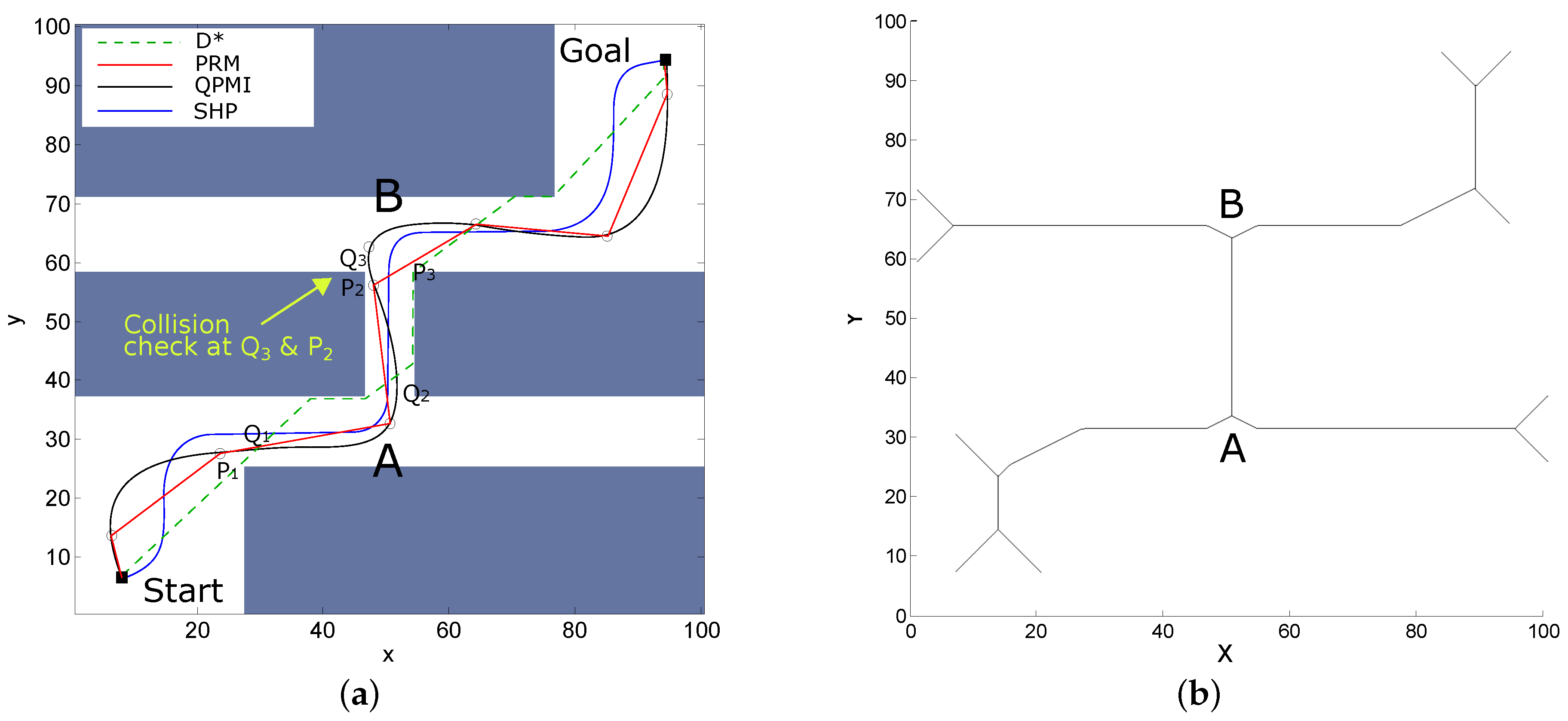
- Operator in the loop, Safety, and User Experience: In case of tele-operated robots, currently, the trajectory generation and control lacks the input from the operator. This is more important in case of autonomous vehicles to feedback the planned trajectory to the driver, and generate smooth trajectories based on driver’s intentions. This requires active feedback mechanisms and integration of human-robot integration [185,186,187]. Researchers have proposed work in this regard in [188,189] by proposing a trajectory planning algorithm that ‘adapts’ to traffic on a lane-structured infrastructure such as highways. In many researches, the emphasis has been on the mathematical completeness of the system while the user-experience seems to get ignored. For instance, in case of an autonomous robot wheelchair used in hospitals, safety is important and the wheelchair must not come close to either of the walls. Hence, in this particular scenario, it is important that the robot wheelchair moves in nearly a straight line in the center lane of the passage. However, aiming for or higher continuities, many algorithms generate a path which brings the robot close to either of the walls. For example, Figure 11a shows the results of paths generated by D* [19], PRM [25], QPMI [39], and SHP [117] in dotted green, red, black, and blue colors, respectively (results reproduced from [117]). The curve in black is continuous, however, it brings the robot too close to the obstacles at points and . On the other hand, SHP [117] curve in blue keeps the robot sufficiently far from the obstacles and keeps straight segments of the path straight considering the input from operators of robot wheelchair. Such safe paths are easy to generate particularly on grid-maps by using Voronoi paths [190], or using thinning algorithms [191,192] or skeleton maps [193,194]. Figure 11b shows the skeleton path of the environment shown in Figure 11a. In conjunction to the previous point, the feedback from the operator must be fused, and operator intentions must be anticipated to generate smooth paths. With the advent of autonomous cars and platforms like fully autonomous robotic wheelchair, the concept of user experience especially in terms of passenger comfort is being re-evaluated. This is a relatively new area of research with a strong correlation with smooth trajectory generation, and some promising research has been proposed in [195,196,197,198,199,200].
9. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- ITU. Ubiquitous Sensor Networks (USN). 2018. Available online: http://www.itu.int/dms_pub/itu-t/oth/23/01/T23010000040001PDFE.pdf (accessed on 1 June 2018).
- Cost of Computing. Wikipedia, 2016. Available online: https://en.wikipedia.org/wiki/FLOPS (accessed on 30 December 2016).
- Ortigoza, R.S.; Marcelino-Aranda, M.; Ortigoza, G.S.; Guzman, V.M.H.; Molina-Vilchis, M.A.; Saldana-Gonzalez, G.; Herrera-Lozada, J.C.; Olguin-Carbajal, M. Wheeled Mobile Robots: A review. IEEE Lat. Am. Trans. 2012, 10, 2209–2217. [Google Scholar] [CrossRef]
- Correll, N.; Bekris, K.E.; Berenson, D.; Brock, O.; Causo, A.; Hauser, K.; Okada, K.; Rodriguez, A.; Romano, J.M.; Wurman, P.R. Analysis and Observations from the First Amazon Picking Challenge. IEEE Trans. Autom. Sci. Eng. 2018, 15, 172–188. [Google Scholar] [CrossRef]
- Ravankar, A.A.; Hoshino, Y.; Ravankar, A.; Jixin, L.; Emaru, T.; Kobayashi, Y. Algorithms and a Framework for Indoor Robot Mapping in a Noisy Environment using Clustering in Spatial and Hough Domains. Int. J. Adv. Robot. Syst. 2015, 12, 27. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Hoshino, Y.; Emaru, T.; Kobayashi, Y. On a Hopping-points SVD and Hough Transform Based Line Detection Algorithm for Robot Localization and Mapping. Int. J. Adv. Robot. Syst. 2016, 13, 98. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D.; Hexmoor, H.; Mataric, M. A Probabilistic Approach to Concurrent Mapping and Localization for Mobile Robots. Mach. Learn. 1998, 31, 29–53. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. Avoiding blind leading the blind. Int. J. Adv. Robot. Syst. 2016, 13, 1729881416666088. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Emaru, T. Hitchhiking Robots: A Collaborative Approach for Efficient Multi-Robot Navigation in Indoor Environments. Sensors 2017, 17, 1878. [Google Scholar] [CrossRef] [PubMed]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Hoshino, Y.; Peng, C.C.; Watanabe, M. Hitchhiking Based Symbiotic Multi-Robot Navigation in Sensor Networks. Robotics 2018, 7, 37. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Emaru, T. Symbiotic Navigation in Multi-Robot Systems with Remote Obstacle Knowledge Sharing. Sensors 2017, 17, 1581. [Google Scholar] [CrossRef] [PubMed]
- Delling, D.; Sanders, P.; Schultes, D.; Wagner, D. Engineering Route Planning Algorithms. In Algorithmics of Large and Complex Networks; Lerner, J., Wagner, D., Zweig, K., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5515, pp. 117–139. [Google Scholar]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006; Available online: http://planning.cs.uiuc.edu/ (accessed on 11 February 2016).
- Latombe, J.C. Robot Motion Planning; Kluwer Academic Publishers: Norwell, MA, USA, 1991. [Google Scholar]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Shu-Xi, W. The Improved Dijkstra’s Shortest Path Algorithm and Its Application. 2012 International Workshop on Information and Electronics Engineering. Procedia Eng. 2012, 29, 1186–1190. [Google Scholar] [CrossRef]
- Fujita, Y.; Nakamura, Y.; Shiller, Z. Dual Dijkstra Search for paths with different topologies. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (ICRA ’03), Taipei, Taiwan, 14–19 September 2003; Volume 3, pp. 3359–3364. [Google Scholar]
- Hart, P.; Nilsson, N.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Stentz, A.; Mellon, I.C. Optimal and Efficient Path Planning for Unknown and Dynamic Environments. Int. J. Robot. Autom. 1993, 10, 89–100. [Google Scholar]
- Stentz, A. The Focussed D* Algorithm for Real-Time Replanning. In Proceedings of the International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1652–1659. [Google Scholar]
- Lavalle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Technical Report; Computer Science Department, Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- LaValle, S.M.; Kuffner, J.J. Randomized Kinodynamic Planning. Int. J. Robot. Res. 2001, 20, 378–400. Available online: http://journals.sagepub.com/doi/pdf/10.1177/02783640122067453 (accessed on 19 September 2018). [CrossRef]
- Lavalle, S.M.; Kuffner, J.J., Jr. Rapidly-Exploring Random Trees: Progress and Prospects. In Algorithmic and Computational Robotics: New Directions; CRC Press: Boca Raton, FL, USA, 2000; pp. 293–308. [Google Scholar]
- Hwang, Y.; Ahuja, N. A potential field approach to path planning. IEEE Trans. Robot. Autom. 1992, 8, 23–32. [Google Scholar] [CrossRef]
- Kavraki, L.; Svestka, P.; Latombe, J.C.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Shene, C.K. Continuity Issues. 2018. Available online: http://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/curves/continuity.html (accessed on 1 June 2018).
- Guibas, L. Geometric Modeling. 2018. Available online: http://graphics.stanford.edu/courses/cs348a-17-winter/ReaderNotes/handout27.pdf (accessed on 1 June 2018).
- Farin, G. Curves and Surfaces for CAGD: A Practical Guide, 5th ed.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2002. [Google Scholar]
- De Boor, C. A Practical Guide to Splines; Springer Verlag: New York, NY, USA, 1978. [Google Scholar]
- Waring, E. Problems concerning Interpolations. Philos. Trans. R. Soc. 1779, 69, 59–67. [Google Scholar] [CrossRef]
- Waring, E. Problems Concerning Interpolations; The Royal Society Publishing: London, UK, 2015; Available online: http://rstl.royalsocietypublishing.org/content/69/59.full.pdf+html (accessed on 15 January 2016).
- Weisstein, E.W. Lagrange Interpolating Polynomial from MathWorld—A Wolfram Web Resource. 2018. Available online: http://mathworld.wolfram.com/LagrangeInterpolatingPolynomial.html (accessed on 1 June 2018).
- Weisstein, E.W. Hermite’s Interpolating Polynomial from MathWorld—A Wolfram Web Resource. 2018. Available online: http://mathworld.wolfram.com/HermitesInterpolatingPolynomial.html (accessed on 1 June 2018).
- Song, B.; Tian, G.; Zhou, F. A comparison study on path smoothing algorithms for laser robot navigated mobile robot path planning in intelligent space. J. Inf. Comput. Sci. 2010, 7, 2943–2950. [Google Scholar]
- Mathematical Interpolation. Wikipedia, 2016. Available online: https://en.wikipedia.org/wiki/Interpolation (accessed on 11 February 2016).
- Epperson, J.F. On the Runge Example. Am. Math. Mon. 1987, 94, 329–341. [Google Scholar] [CrossRef]
- Huh, U.Y.; Chang, S.R. A G2 Continuous Path-smoothing Algorithm Using Modified Quadratic Polynomial Interpolation. Int. J. Adv. Robot. Syst. 2013, 11. [Google Scholar] [CrossRef]
- Chang, S.R.; Huh, U.Y. A Collision-Free G2 Continuous Path-Smoothing Algorithm Using Quadratic Polynomial Interpolation. Int. J. Adv. Robot. Syst. 2014, 11, 194. [Google Scholar] [CrossRef]
- Takahashi, A.; Hongo, T.; Ninomiya, Y.; Sugimoto, G. Local Path Planning and Motion Control for Agv in Positioning. In Proceedings of the Autonomous Mobile Robots and Its Applications, IEEE/RSJ International Workshop on Intelligent Robots and Systems (IROS ’89), Tsukuba, Japan, 4–6 September 1989; pp. 392–397. [Google Scholar]
- Weisstein, E.W. Bernstein Polynomial from MathWorld—A Wolfram Web Resource. 2018. Available online: http://mathworld.wolfram.com/BernsteinPolynomial.html (accessed on 1 June 2018).
- Choi, J.W.; Curry, R.; Elkaim, G. Path Planning Based on Bezier Curve for Autonomous Ground Vehicles. In Proceedings of the Advances in Electrical and Electronics Engineering—IAENG Special Edition of the World Congress on Engineering and Computer Science 2008 (WCECS ’08), San Francisco, CA, USA, 22–24 October 2008; pp. 158–166. [Google Scholar]
- Weisstein, E.W. Bezier Curve from MathWorld—A Wolfram Web Resource. 2018. Available online: http://mathworld.wolfram.com/BezierCurve.html (accessed on 1 June 2018).
- Kawabata, K.; Ma, L.; Xue, J.; Zhu, C.; Zheng, N. A Path Generation for Automated Vehicle Based on Bezier Curve and Via-points. Robot. Auton. Syst. 2015, 74, 243–252. [Google Scholar] [CrossRef]
- Rastelli, J.P.; Lattarulo, R.; Nashashibi, F. Dynamic trajectory generation using continuous-curvature algorithms for door to door assistance vehicles. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 510–515. [Google Scholar]
- Walton, D.; Meek, D.; Ali, J. Planar G2 transition curves composed of cubic Bézier spiral segments. J. Comput. Appl. Math. 2003, 157, 453–476. [Google Scholar] [CrossRef]
- Montes, N.; Herraez, A.; Armesto, L.; Tornero, J. Real-time clothoid approximation by Rational Bezier curves. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 2246–2251. [Google Scholar]
- Montes, N.; Mora, M.C.; Tornero, J. Trajectory Generation based on Rational Bezier Curves as Clothoids. In Proceedings of the 2007 IEEE Intelligent Vehicles Symposium, Istanbul, Turkey, 13–15 June 2007; pp. 505–510. [Google Scholar]
- Han, L.; Yashiro, H.; Nejad, H.T.N.; Do, Q.H.; Mita, S. Bezier curve based path planning for autonomous vehicle in urban environment. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, San Diego, CA, USA, 21–24 June 2010; pp. 1036–1042. [Google Scholar]
- Pérez, J.; Godoy, J.; Villagrá, J.; Onieva, E. Trajectory generator for autonomous vehicles in urban environments. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 409–414. [Google Scholar]
- González, D.; Pérez, J.; Lattarulo, R.; Milanés, V.; Nashashibi, F. Continuous curvature planning with obstacle avoidance capabilities in urban scenarios. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1430–1435. [Google Scholar]
- Liang, Z.; Zheng, G.; Li, J. Automatic parking path optimization based on Bezier curve fitting. In Proceedings of the 2012 IEEE International Conference on Automation and Logistics, Zhengzhou, China, 15–17 August 2012; pp. 583–587. [Google Scholar]
- Weisstein, E.W. Spline from MathWorld—A Wolfram Web Resource. 2018. Available online: http://mathworld.wolfram.com/Spline.html (accessed on 1 June 2018).
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics (Texts in Applied Mathematics); Springer-Verlag: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Komoriya, K.; Tanie, K. Trajectory Design and Control of a Wheel-type Mobile Robot Using B-spline Curve. In Proceedings of the Autonomous Mobile Robots and Its Applications, IEEE/RSJ International Workshop on Intelligent Robots and Systems (IROS ’89), Tsukuba, Japan, 4–6 September 1989; pp. 398–405. [Google Scholar]
- Trepagnier, P.G.; Nagel, J.; Kinney, P.M.; Koutsougeras, C.; Dooner, M. KAT-5: Robust Systems for Autonomous Vehicle Navigation in Challenging and Unknown Terrain. In The 2005 DARPA Grand Challenge: The Great Robot Race; Springer: Berlin/Heidelberg, Germany, 2007; pp. 103–128. [Google Scholar]
- Nagel, J.; Trepagnier, P.G.; Koutsougeras, C.; Kinney, P.M.; Dooner, M. The Culebra Algorithm for Path Planning and Obstacle Avoidance in Kat-5. In Proceedings of the 2006 18th IEEE International Conference on Tools with Artificial Intelligence (ICTAI ’06), Arlington, VA, USA, 13–15 November 2006; pp. 247–253. [Google Scholar]
- DARPA Grand Challenge. Wikipedia, 2018. Available online: https://en.wikipedia.org/wiki/DARPA_Grand_Challenge (accessed on 5 May 2018).
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The Robot That Won the DARPA Grand Challenge: Research Articles. J. Robot. Syst. 2006, 23, 661–692. [Google Scholar]
- Bacha, A.; Bauman, C.; Faruque, R.; Fleming, M.; Terwelp, C.; Reinholtz, C.; Hong, D.; Wicks, A.; Alberi, T.; Anderson, D.; et al. Odin: Team VictorTango’s Entry in the DARPA Urban Challenge. J. Field Robot. 2008, 25, 467–492. [Google Scholar] [CrossRef]
- Berglund, T.; Brodnik, A.; Jonsson, H.; Staffanson, M.; Soderkvist, I. Planning Smooth and Obstacle-Avoiding B-Spline Paths for Autonomous Mining Vehicles. IEEE Trans. Autom. Sci. Eng. 2010, 7, 167–172. [Google Scholar] [CrossRef]
- Piazzi, A.; Bianco, C.G.L.; Bertozzi, M.; Fascioli, A.; Broggi, A. Quintic G2-splines for the iterative steering of vision-based autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2002, 3, 27–36. [Google Scholar] [CrossRef]
- Delingette, H.; Hebert, M.; Ikeuchi, K. Trajectory generation with curvature constraint based on energy minimization. In Proceedings of the IEEE/RSJ International Workshop on Intelligent Robots and Systems ’91, Intelligence for Mechanical Systems (IROS ’91), Osaka, Japan, 3–5 November 1991; Volume 1, pp. 206–211. [Google Scholar]
- Yang, K.; Sukkarieh, S. An Analytical Continuous-Curvature Path-Smoothing Algorithm. IEEE Trans. Robot. 2010, 26, 561–568. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M.; Jazar, R. Randomized Bidirectional B-Spline Parameterization Motion Planning. IEEE Trans. Intell. Transp. Syst. 2016, 17, 406–419. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book, 2nd ed.; Springer-Verlag: New York, NY, USA, 1996. [Google Scholar]
- Weisstein, E.W. NURBS from MathWorld—A Wolfram Web Resource. 2018. Available online: http://mathworld.wolfram.com/NURBSCurve.html (accessed on 1 June 2018).
- Bingol, O.R. NURBS-Python. 2016. Available online: https://nurbs-python.readthedocs.io/en/latest/ (accessed on 19 September 2018).
- Piegl, L. On NURBS: A Survey. IEEE Comput. Graph. Appl. 1991, 11, 55–71. [Google Scholar] [CrossRef]
- Herrmann, P.; Gerngroß, M.; Endisch, C. NURBS based trajectory generation for an industrial five axis needle winding robot. In Proceedings of the 2018 4th International Conference on Control, Automation and Robotics (ICCAR), Auckland, New Zealand, 20–23 April 2018; pp. 31–36. [Google Scholar]
- Ravari, A.N.; Taghirad, H.D. NURBS-based representation of urban environments for mobile robots. In Proceedings of the 2016 4th International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 26–28 October 2016; pp. 20–25. [Google Scholar]
- Lai, T.C.; Xiao, S.R.; Aoyama, H.; Wong, C.C. Path planning and obstacle avoidance approaches for robot arm. In Proceedings of the 2017 56th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Kanazawa, Japan, 19–22 September 2017; pp. 334–337. [Google Scholar]
- Shi, X.; Fang, H.; Guo, L. Multi-objective optimal trajectory planning of manipulators based on quintic NURBS. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; pp. 759–765. [Google Scholar]
- Belaidi, H.; Hentout, A.; Bouzouia, B.; Bentarzi, H.; Belaidi, A. NURBs trajectory generation and following by an autonomous mobile robot navigating in 3D environment. In Proceedings of the 4th Annual IEEE International Conference on Cyber Technology in Automation, Control and Intelligent, Hong Kong, China, 4–7 June 2014; pp. 168–173. [Google Scholar]
- Tatematsu, N.; Ohnishi, K. Tracking motion of mobile robot for moving target using NURBS curve. In Proceedings of the IEEE International Conference on Industrial Technology, Maribor, Slovenia, 10–12 December 2003; Volume 1, pp. 245–249. [Google Scholar]
- Aleotti, J.; Caselli, S.; Maccherozzi, G. Trajectory reconstruction with NURBS curves for robot programming by demonstration. In Proceedings of the 2005 International Symposium on Computational Intelligence in Robotics and Automation, Espoo, Finland, 27–30 June 2005; pp. 73–78. [Google Scholar]
- Guo, H.; Meng, Y.; Jin, Y. Swarm robot pattern formation using a morphogenetic multi-cellular based self-organizing algorithm. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3205–3210. [Google Scholar]
- Schmid, A.J.; Woern, H. Path planning for a humanoid using NURBS curves. In Proceedings of the IEEE International Conference on Automation Science and Engineering, Edmonton, AB, Canada, 1–2 August 2005; pp. 351–356. [Google Scholar]
- Richtsfeld, A.; Mörwald, T.; Prankl, J.; Zillich, M.; Vincze, M. Segmentation of unknown objects in indoor environments. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 4791–4796. [Google Scholar]
- Farin, G. From conics to NURBS: A tutorial and survey. IEEE Comput. Graph. Appl. 1992, 12, 78–86. [Google Scholar] [CrossRef]
- Lockwood, E.H. Book of Curves; Cambridge Books; Cambridge University Press: Cambridge, UK, 1961. [Google Scholar]
- Dubins, L.E. On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Reeds, J.A.; Shepp, L.A. Optimal paths for a car that goes both forwards and backwards. Pac. J. Math. 1990, 145, 367–393. [Google Scholar] [CrossRef]
- Yang, D.; Li, D.; Sun, H. 2D Dubins Path in Environments with Obstacle. Math. Probl. Eng. 2013, 2013, 291372. [Google Scholar] [CrossRef]
- Gerlach, A.R.; Kingston, D.; Walker, B.K. UAV navigation using predictive vector field control. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 4907–4912. [Google Scholar]
- Lin, Y.; Saripalli, S. Path planning using 3D Dubins Curve for Unmanned Aerial Vehicles. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 296–304. [Google Scholar]
- Hwangbo, M.; Kuffner, J.; Kanade, T. Efficient Two-phase 3D Motion Planning for Small Fixed-wing UAVs. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 1035–1041. [Google Scholar]
- Lugo-Cárdenas, I.; Flores, G.; Salazar, S.; Lozano, R. Dubins path generation for a fixed wing UAV. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 339–346. [Google Scholar]
- Parlangeli, G.; Ostuni, L.; Mancarella, L.; Indiveri, G. A motion planning algorithm for smooth paths of bounded curvature and curvature derivative. In Proceedings of the 2009 17th Mediterranean Conference on Control and Automation, Thessaloniki, Greece, 24–26 June 2009; pp. 73–78. [Google Scholar]
- Klein, M.; Klos, A.; Lenhardt, J.; Schiffmann, W. Wind-Aware Emergency Landing Assistant Based on Dubins Curves. In Proceedings of the 2017 5th International Symposium on Computing and Networking (CANDAR), Aomori, Japan, 19–22 November 2017; pp. 546–550. [Google Scholar]
- Hameed, I.A. Coverage path planning software for autonomous robotic lawn mower using Dubins’ curve. In Proceedings of the 2017 IEEE International Conference on Real-time Computing and Robotics (RCAR), Okinawa, Japan, 14–18 July 2017; pp. 517–522. [Google Scholar]
- Fermat’s Spiral. Wikipedia, 2018. Available online: https://en.wikipedia.org/wiki/Fermat’s_spiral (accessed on 1 May 2018).
- Chen, X.; Zhang, J.; Yang, M.; Zhong, L.; Dong, J. Continuous-Curvature Path Generation Using Fermat’s Spiral for Unmanned Marine and Aerial Vehicles. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 4911–4916. [Google Scholar]
- Weisstein, E.W. Cornu Spiral from MathWorld—A Wolfram Web Resource. 2018. Available online: http://mathworld.wolfram.com/CornuSpiral.html (accessed on 1 June 2018).
- Weisstein, E.W. Fresnel Integrals from MathWorld—A Wolfram Web Resource. 2018. Available online: http://mathworld.wolfram.com/FresnelIntegrals.html (accessed on 1 June 2018).
- Gim, S.; Adouane, L.; Lee, S.; Dérutin, J.P. Clothoids Composition Method for Smooth Path Generation of Car-Like Vehicle Navigation. J. Intell. Robot. Syst. 2017, 88, 129–146. [Google Scholar] [CrossRef]
- Fraichard, T.; Scheuer, A. From Reeds and Shepp’s to continuous-curvature paths. IEEE Trans. Robot. 2004, 20, 1025–1035. [Google Scholar] [CrossRef]
- Liscano, R.; Green, D. Design and Implementation of a Trajectory Generator for an Indoor Mobile Robot. In Proceedings of the Autonomous Mobile Robots and Its Applications, IEEE/RSJ International Workshop on Intelligent Robots and Systems (IROS ’89), Tsukuba, Japan, 4–6 September 1989; pp. 380–385. [Google Scholar]
- Dai, J.; Wang, Y.; Bortoff, S.A.; Burns, D.J. From reeds-shepp’s paths to continuous curvature paths-Part I: Transition schemes algorithms. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Mauna Lani, HI, USA, 27–30 August 2017; pp. 355–362. [Google Scholar]
- Behringer, R.; Muller, N. Autonomous road vehicle guidance from autobahnen to narrow curves. IEEE Trans. Robot. Autom. 1998, 14, 810–815. [Google Scholar] [CrossRef]
- Kim, C.H.; Jeong, K.M.; Jeong, T.W. Semi-autonomous navigation of an unmanned ground vehicle for bird expellant in an airport. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems, JeJu Island, Korea, 17–21 October 2012; pp. 2063–2067. [Google Scholar]
- Funke, J.; Theodosis, P.; Hindiyeh, R.; Stanek, G.; Kritatakirana, K.; Gerdes, C.; Langer, D.; Hernandez, M.; Müller-Bessler, B.; Huhnke, B. Up to the limits: Autonomous Audi TTS. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Alcala de Henares, Spain, 3–7 June 2012; pp. 541–547. [Google Scholar]
- Broggi, A.; Medici, P.; Zani, P.; Coati, A.; Panciroli, M. Autonomous vehicles control in the VisLab Intercontinental Autonomous Challenge. Annu. Rev. Control 2012, 36, 161–171. [Google Scholar] [CrossRef]
- Vorobieva, H.; Minoiu-Enache, N.; Glaser, S.; Mammar, S. Geometric continuous-curvature path planning for automatic parallel parking. In Proceedings of the 2013 10th IEEE International Conference on Networking, Sensing and Control (ICNSC), Evry, France, 10–12 April 2013; pp. 418–423. [Google Scholar]
- Vorobieva, H.; Glaser, S.; Minoiu-Enache, N.; Mammar, S. Automatic parallel parking with geometric continuous-curvature path planning. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 465–471. [Google Scholar]
- Fuji, H.; Xiang, J.; Tazaki, Y.; Levedahl, B.; Suzuki, T. Trajectory planning for automated parking using multi-resolution state roadmap considering non-holonomic constraints. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 407–413. [Google Scholar]
- Brezak, M.; Petrović, I. Real-time Approximation of Clothoids With Bounded Error for Path Planning Applications. IEEE Trans. Robot. 2014, 30, 507–515. [Google Scholar] [CrossRef]
- Coombs, D.; Murphy, K.; Lacaze, A.; Legowik, S. Driving autonomously off-road up to 35 km/h. In Proceedings of the IEEE Intelligent Vehicles Symposium 2000 (Cat. No.00TH8511), Dearborn, MI, USA, 5 October 2000; pp. 186–191. [Google Scholar]
- Bevilacqua, P.; Frego, M.; Fontanelli, D.; Palopoli, L. Reactive Planning for Assistive Robots. IEEE Robot. Autom. Lett. 2018, 3, 1276–1283. [Google Scholar] [CrossRef]
- Kim, Y.H.; Park, J.B.; Son, W.S.; Yoon, T.S. Modified turn algorithm for motion planning based on clothoid curve. Electron. Lett. 2017, 53, 1574–1576. [Google Scholar] [CrossRef]
- Kim, K.B.; Kim, B.K. Minimum-Time Trajectory for Three-Wheeled Omnidirectional Mobile Robots Following a Bounded-Curvature Path With a Referenced Heading Profile. IEEE Trans. Robot. 2011, 27, 800–808. [Google Scholar] [CrossRef]
- Liu, C.A.; Cheng, W.G.; Hong, Z. A Trajectory Generator for a Mobile Robot in 3D Pathplanning. In Proceedings of the 2007 IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; pp. 1247–1251. [Google Scholar]
- Alia, C.; Reine, T.; Ali, C. Maneuver planning for autonomous vehicles, with clothoid tentacles for local trajectory planning. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–6. [Google Scholar]
- Otto, M.; Kramer, M. Implementation of a clothoid based trajectory into the ROS framework. In Proceedings of the 2016 International Conference on Control, Decision and Information Technologies (CoDIT), St. Julian’s, Malta, 6–8 April 2016; pp. 345–348. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.P.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009. [Google Scholar]
- Weisstein, E.W. Hypocycloid from MathWorld—A Wolfram Web Resource. 2016. Available online: http://mathworld.wolfram.com/Hypocycloid.html (accessed on 3 March 2016).
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. SHP: Smooth Hypocycloidal Paths with Collision-Free and Decoupled Multi-Robot Path Planning. Int. J. Adv. Robot. Syst. 2016, 13, 133. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. Path Smoothing Extension for Various Robot Path Planners. In Proceedings of the 16th IEEE International Conference on Control. Automation and Systems, Gyeongju, Korea, 16–19 October 2016. [Google Scholar]
- Campana, M.; Lamiraux, F.; Laumond, J.P. A Simple Path Optimization Method for Motion Planning. Working Paper or Preprint. HAL Archives; Rapport LAAS n° 15108. 2015. <hal-01137844v2>. Available online: https://hal.archives-ouvertes.fr/hal-01137844/file/paper_icra2016_hal.pdf (accessed on 19 September 2018).
- Park, C.; Pan, J.; Manocha, D. ITOMP: Incremental trajectory optimization for real-time replanning in dynamic environments. In Proceedings of the 22nd International Conference on Automated Planning and Scheduling (ICAPS 2012), Atibaia, Sao Paulo, Brazil, 25–29 June 2012; pp. 207–215. [Google Scholar]
- Garber, M.; Lin, M.C. Constraint-Based Motion Planning Using Voronoi Diagrams. In Algorithmic Foundations of Robotics V; Boissonnat, J.D., Burdick, J., Goldberg, K., Hutchinson, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 541–558. [Google Scholar]
- Richardson, A.; Olson, E. Iterative path optimization for practical robot planning. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 3881–3886. [Google Scholar]
- Zhu, Z.; Schmerling, E.; Pavone, M. A convex optimization approach to smooth trajectories for motion planning with car-like robots. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 835–842. [Google Scholar]
- Choi, J.; Huhtala, K. Constrained path optimization with Bézier curve primitives. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 246–251. [Google Scholar]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Integrated online trajectory planning and optimization in distinctive topologies. Robot. Auton. Syst. 2017, 88, 142–153. [Google Scholar] [CrossRef]
- Roesmann, C.; Feiten, W.; Woesch, T.; Hoffmann, F.; Bertram, T. Trajectory modification considering dynamic constraints of autonomous robots. In Proceedings of the 7th German Conference on Robotics (ROBOTIK 2012), Munich, Germany, 21–22 May 2012; pp. 1–6. [Google Scholar]
- Rösmann, C.; Feiten, W.; Wösch, T.; Hoffmann, F.; Bertram, T. Efficient trajectory optimization using a sparse model. In Proceedings of the 2013 European Conference on Mobile Robots, Barcelona, Spain, 25–27 September 2013; pp. 138–143. [Google Scholar]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Planning of multiple robot trajectories in distinctive topologies. In Proceedings of the 2015 European Conference on Mobile Robots (ECMR), Lincoln, UK, 2–4 September 2015; pp. 1–6. [Google Scholar]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Kinodynamic trajectory optimization and control for car-like robots. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 5681–5686. [Google Scholar]
- Rösmann, C. TEB Planner. 2018. Available online: http://wiki.ros.org/teb_local_planner (accessed on 1 May 2018).
- Rösmann, C. TEB Planner. 2018. Available online: https://github.com/rst-tu-dortmund/teb_local_planner (accessed on 1 May 2018).
- Kogan, D.; Murray, R.M. Optimization-Based Navigation for the DARPA Grand Challenge. In Proceedings of the 2006 Conference on Decision and Control (CDC), San Diego, CA, USA, 13–15 December 2006. [Google Scholar]
- Cremean, L.B.; Foote, T.B.; Gillula, J.H.; Hines, G.H.; Kogan, D.; Kriechbaum, K.L.; Lamb, J.C.; Leibs, J.; Lindzey, L.; Rasmussen, C.E.; et al. Alice: An Information-Rich Autonomous Vehicle for High-Speed Desert Navigation. In The 2005 DARPA Grand Challenge: The Great Robot Race; Buehler, M., Iagnemma, K., Singh, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 437–482. [Google Scholar]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- Ziegler, J.; Bender, P.; Schreiber, M.; Lategahn, H.; Strauss, T.; Stiller, C.; Dang, T.; Franke, U.; Appenrodt, N.; Keller, C.G.; et al. Making Bertha Drive;An Autonomous Journey on a Historic Route. IEEE Intell. Transp. Syst. Mag. 2014, 6, 8–20. [Google Scholar] [CrossRef]
- Ziegler, J.; Bender, P.; Dang, T.; Stiller, C. Trajectory planning for Bertha—A local, continuous method. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 450–457. [Google Scholar]
- Gu, T.; Dolan, J.M. On-Road Motion Planning for Autonomous Vehicles. In Intelligent Robotics and Applications; Su, C.Y., Rakheja, S., Liu, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 588–597. [Google Scholar]
- Howard, C.R. The Transition-Curve Field-Book; Palala Press: Warsaw, Poland, 2015; ISBN 1347030956. [Google Scholar]
- Habib, Z.; Sakai, M. Family of G2 cubic transition curves. In Proceedings of the 2003 International Conference on Geometric Modeling and Graphics, London, UK, 16–18 July 2003; pp. 117–122. [Google Scholar]
- Ahmad, A.; Gobithasan, R.; Ali, J.M. G2 Transition curve using Quartic Bezier Curve. In Proceedings of the Computer Graphics, Imaging and Visualisation (CGIV ’07), Bangkok, Thailand, 14–17 August 2007; pp. 223–228. [Google Scholar]
- Ahmad, A.; Ali, J.M. G3 Transition Curve Between Two Straight Lines. In Proceedings of the 5th International Conference on Computer Graphics, Imaging and Visualisation, (CGIV ’08), Penang, Malaysia, 26–28 August 2008; pp. 154–159. [Google Scholar]
- Srivastava, S.; Roychowdhury, J. Independent and Interdependent Latch Setup/Hold Time Characterization via Newton Raphson Solution and Euler Curve Tracking of State-Transition Equations. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2008, 27, 817–830. [Google Scholar] [CrossRef]
- Quinlan, S.; Khatib, O. Elastic bands: Connecting path planning and control. In Proceedings of the IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; Volume 2, pp. 802–807. [Google Scholar]
- Quinlan, S. Real-Time Modification of Collision-Free Paths. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1995. [Google Scholar]
- Khatib, M. Sensor-Based Motion Control for Mobile Robots; LAAS-CNRS: Toulouse, France, 1996; Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.37.668&rep=rep1&type=pdf (accessed on 19 September 2018).
- Khatib, M.; Jaouni, H.; Chatila, R.; Laumond, J.P. Dynamic path modification for car-like nonholonomic mobile robots. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; Volume 4, pp. 2920–2925. [Google Scholar]
- Graf, B.; Manuel Hostalet, W.J.; Schaeffer, C. Flexible Path Planning for Nonholonomic Mobile Robots. In Proceedings of the Fourth European Workshop on Advanced Mobile Robots, Lund, Sweden, 19–21 September 2001. [Google Scholar]
- Brock, O.; Khatib, O. Executing motion plans for robots with many degrees of freedom in dynamic environments. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20–20 May 1998; Volume 1, pp. 1–6. [Google Scholar]
- Fiorini, P.; Shiller, Z. Motion Planning in Dynamic Environments Using Velocity Obstacles. Int. J. Robot. Res. 1998, 17, 760–772. [Google Scholar] [CrossRef]
- Wray, K.H.; Ruiken, D.; Grupen, R.A.; Zilberstein, S. Log-space harmonic function path planning. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 1511–1516. [Google Scholar]
- Hong, R.; DeSouza, G.N. A real-time path planner for a smart wheelchair using harmonic potentials and a rubber band model. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 3282–3287. [Google Scholar]
- Garrido, S.; Moreno, L.; Blanco, D. Exploration and Mapping Using the VFM Motion Planner. IEEE Trans. Instrum. Meas. 2009, 58, 2880–2892. [Google Scholar] [CrossRef]
- Minguez, J.; Montano, L. Extending Collision Avoidance Methods to Consider the Vehicle Shape. Kinematics, and Dynamics of a Mobile Robot. IEEE Trans. Robot. 2009, 25, 367–381. [Google Scholar] [CrossRef]
- Borenstein, J.; Koren, Y. Real-time obstacle avoidance for fast mobile robots. IEEE Trans. Syst. Man Cybern. 1989, 19, 1179–1187. [Google Scholar] [CrossRef]
- Borenstein, J.; Koren, Y. The vector field histogram-fast obstacle avoidance for mobile robots. IEEE Trans. Robot. Autom. 1991, 7, 278–288. [Google Scholar] [CrossRef]
- Ulrich, I.; Borenstein, J. VFH+: Reliable obstacle avoidance for fast mobile robots. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20 May 1998; Volume 2, pp. 1572–1577. [Google Scholar]
- Ulrich, I.; Borenstein, J. VFH/sup*/: Local obstacle avoidance with look-ahead verification. In Proceedings of the IEEE International Conference on Robotics and Automation, Millennium Conference (2000 ICRA) (Cat.No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 3, pp. 2505–2511. [Google Scholar]
- Jie, D.; Xueming, M.; Kaixiang, P. IVFH*: Real-time dynamic obstacle avoidance for mobile robots. In Proceedings of the 2010 11th International Conference on Control Automation Robotics Vision, Singapore, 7–10 December 2010; pp. 844–847. [Google Scholar]
- Babinec, A.; Duchoň, F.; Dekan, M.; Pásztó, P.; Kelemen, M. VFH*TDT (VFH* with Time Dependent Tree). Robot. Auton. Syst. 2014, 62, 1098–1115. [Google Scholar] [CrossRef]
- Molinos, E.; Llamazares, A.; Ocana, M.; Herranz, F. Dynamic obstacle avoidance based on curvature arcs. In Proceedings of the 2014 IEEE/SICE International Symposium on System Integration, Tokyo, Japan, 13–15 December 2014; pp. 186–191. [Google Scholar]
- Brock, O.; Khatib, O. High-speed navigation using the global dynamic window approach. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No.99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 1, pp. 341–346. [Google Scholar]
- Ogren, P.; Leonard, N.E. A convergent dynamic window approach to obstacle avoidance. IEEE Trans. Robot. 2005, 21, 188–195. [Google Scholar] [CrossRef]
- Minguez, J.; Montano, L. Nearness diagram (ND) navigation: Collision avoidance in troublesome scenarios. IEEE Trans. Robot. Autom. 2004, 20, 45–59. [Google Scholar] [CrossRef]
- Minguez, J.; Montano, L. Nearness diagram navigation (ND): A new real time collision avoidance approach. In Proceedings of the 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2000) (Cat. No.00CH37113), Takamatsu, Japan, 31 October–5 November 2000; Volume 3, pp. 2094–2100. [Google Scholar]
- Minguez, J.; Montano, L.; Simeon, T.; Alami, R. Global nearness diagram navigation (GND). In Proceedings of the IEEE International Conference on Robotics and Automation (2001 ICRA) (Cat. No.01CH37164), Seoul, Korea, 21–26 May 2001; Volume 1, pp. 33–39. [Google Scholar]
- Li, G.; Wu, G.; Wei, W. ND-DWA: A Reactive Method for Collision Avoidance in Troublesome Scenarios. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; Volume 2, pp. 9307–9311. [Google Scholar]
- Durham, J.W.; Bullo, F. Smooth Nearness-Diagram Navigation. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 690–695. [Google Scholar]
- Kamil, F.; Tang, S.; Khaksar, W.; Zulkifli, N.; Ahmad, S.A. A Review on Motion Planning and Obstacle Avoidance Approaches in Dynamic Environments. Adv. Robot. Autom. 2015, 4, 134–142. [Google Scholar]
- Gandhi, T.; Trivedi, M.M. Pedestrian Protection Systems: Issues, Survey, and Challenges. IEEE Trans. Intell. Transp. Syst. 2007, 8, 413–430. [Google Scholar] [CrossRef]
- Zheng, G.; Chen, Y. A review on vision-based pedestrian detection. In Proceedings of the 2012 IEEE Global High Tech Congress on Electronics, Shenzhen, China, 18–20 November 2012; pp. 49–54. [Google Scholar]
- Ko, B.C.; Kwak, J.; Nam, J. Online learning based multiple pedestrians tracking in thermal imagery for safe driving at night. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 78–79. [Google Scholar]
- Zhu, C.; Peng, Y. A Boosted Multi-Task Model for Pedestrian Detection with Occlusion Handling. IEEE Trans. Image Process. 2015, 24, 5619–5629. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Amon, P.; Hutter, A.; Kaup, A. Detecting closely spaced and occluded pedestrians using specialized deep models for counting. In Proceedings of the 2017 IEEE Visual Communications and Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Ravankar, A.A.; Hoshino, Y.; Emaru, T.; Kobayashi, Y. Map building from laser range sensor information using mixed data clustering and singular value decomposition in noisy environment. In Proceedings of the 2011 IEEE/SICE International Symposium on System Integration (SII), Kyoto, Japan, 20–22 December 2011; pp. 1232–1238. [Google Scholar]
- Xu, W.; Pan, J.; Wei, J.; Dolan, J.M. Motion planning under uncertainty for on-road autonomous driving. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2507–2512. [Google Scholar]
- Anderson, S.; MacTavish, K.; Barfoot, T.D. Relative Continuous-time SLAM. Int. J. Robot. Res. 2015, 34, 1453–1479. [Google Scholar] [CrossRef]
- Anderson, S.; Barfoot, T.D. Full STEAM ahead: Exactly sparse gaussian process regression for batch continuous-time trajectory estimation on SE(3). In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 157–164. [Google Scholar]
- Dubé, R.; Sommer, H.; Gawel, A.; Bosse, M.; Siegwart, R. Non-uniform sampling strategies for continuous correction based trajectory estimation. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4792–4798. [Google Scholar]
- Park, C.; Moghadam, P.; Kim, S.; Elfes, A.; Fookes, C.; Sridharan, S. Elastic LiDAR Fusion: Dense Map-Centric Continuous-Time SLAM. arXiv, 2017; arXiv:1711.01691. [Google Scholar]
- Anderson, S.W. Batch Continuous-Time Trajectory Estimation. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2017. [Google Scholar]
- Anderson, S.; Barfoot, T.D.; Tong, C.H.; Särkkä, S. Batch Nonlinear Continuous-Time Trajectory Estimation as Exactly Sparse Gaussian Process Regression. arXiv, 2014; arXiv:1412.0630. [Google Scholar]
- Droeschel, D.; Schwarz, M.; Behnke, S. Continuous mapping and localization for autonomous navigation in rough terrain using a 3D laser scanner. Robot. Auton. Syst. 2017, 88, 104–115. [Google Scholar] [CrossRef]
- Nüchter, A.; Bleier, M.; Schauer, J.; Janotta, P. Continuous-Time SLAM—Improving Google’s Cartographer 3D Mapping. In Latest Developments in Reality-Based 3D Surveying and Modelling; Chapter Continuous-Time SLAM—Improving Google’s Cartographer 3D Mapping; Remondino, F., Georgopoulos, A., Gonzalez-Aguilera, D., Agrafiotis, P., Eds.; MDPI: Basel, Switzerland, 2018; pp. 53–73. [Google Scholar]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- González, D.; Pérez, J.; Milanés, V.; Nashashibi, F. A Review of Motion Planning Techniques for Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- Robla-Gómez, S.; Becerra, V.M.; Llata, J.R.; González-Sarabia, E.; Torre-Ferrero, C.; Pérez-Oria, J. Working Together: A Review on Safe Human-Robot Collaboration in Industrial Environments. IEEE Access 2017, 5, 26754–26773. [Google Scholar] [CrossRef]
- Lisetti, C.L.; Brown, S.M.; Alvarez, K.; Marpaung, A.H. A social informatics approach to human-robot interaction with a service social robot. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2004, 34, 195–209. [Google Scholar] [CrossRef]
- Vanholme, B.; Glaser, S.; Mammar, S.; Gruyer, D. Manoeuvre-based trajectory planning for highly autonomous vehicles on real road with traffic. In Proceedings of the 2009 European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 3281–3286. [Google Scholar]
- Glaser, S.; Vanholme, B.; Mammar, S.; Gruyer, D.; Nouveliere, L. Maneuver-Based Trajectory Planning for Highly Autonomous Vehicles on Real Road With Traffic and Driver Interaction. IEEE Trans. Intell. Transp. Syst. 2010, 11, 589–606. [Google Scholar] [CrossRef]
- Bhattacharya, P.; Gavrilova, M. Roadmap-Based Path Planning—Using the Voronoi Diagram for a Clearance-Based Shortest Path. IEEE Robot. Autom. Mag. 2008, 15, 58–66. [Google Scholar] [CrossRef]
- Arcelli, C.; Di Baja, G.S. A Width-Independent Fast Thinning Algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1985, PAMI-7, 463–474. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Suen, C.Y. A Fast Parallel Algorithm for Thinning Digital Patterns. Commun. ACM 1984, 27, 236–239. [Google Scholar] [CrossRef]
- Sakellariou, G.; Shanahan, M.; Kuipers, B. Skeletonisation as mobile robot navigation. In Proceedings of the Towards Autonomous Robotic Systems (TAROS-04), Essex, UK, 6–8 September 2004; pp. 149–155. [Google Scholar]
- Bai, X.; Latecki, L.; Liu, W.Y. Skeleton Pruning by Contour Partitioning with Discrete Curve Evolution. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 449–462. [Google Scholar] [CrossRef] [PubMed]
- Elbanhawi, M.; Simic, M.; Jazar, R. In the Passenger Seat: Investigating Ride Comfort Measures in Autonomous Cars. IEEE Intell. Transp. Syst. Mag. 2015, 7, 4–17. [Google Scholar] [CrossRef]
- Morales, Y.; Abdur-Rahim, J.; Watanabe, A.; Even, J. Analysis of navigational habituation. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 3056–3062. [Google Scholar]
- Sawabe, T.; Okajima, T.; Kanbara, M.; Hagita, N. Evaluating passenger characteristics for ride comfort in autonomous wheelchairs. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 102–107. [Google Scholar]
- Chang, C.; Lv, C.; Wang, H.; Wang, H.; Cao, D.; Velenis, E.; Wang, F. Multi-point turn decision making framework for human-like automated driving. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–6. [Google Scholar]
- Nagasaka, N.; Harada, M. Towards safe, smooth, and stable path planning for on-road autonomous driving under uncertainty. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 795–801. [Google Scholar]
- Sawabe, T.; Kanbara, M.; Hagita, N. Diminished Reality for Acceleration—Motion Sickness Reduction with Vection for Autonomous Driving. In Proceedings of the 2016 IEEE International Symposium on Mixed and Augmented Reality (ISMAR-Adjunct), Merida, Mexico, 19–23 September 2016; pp. 297–299. [Google Scholar]
| Classification | Main Advantages (+) and Disadvantages (−) |
|---|---|
| Dubins Curve | + Fast to compute for given configuration of obstacles. |
| + Dubin’s curves are easy to compute even on low spec hardware. | |
| + Shortest paths are assured. | |
| − These curves do not have curvature continuity. | |
| − Robot will experience a jerk at the point of transition of straight line and circle. | |
| Bezier Curve | + Bezier curves have low computational cost. |
| + Control points can generate curve of desired characteristic. | |
| + Bezier curves can be connected with each other to get desired shape. | |
| − With increasing degree of curves, computation costs increase. | |
| − Difficult to adjust for curves with higher degrees. | |
| − Global waypoints affect the entire curve | |
| − It might be difficult to place control points. | |
| Splines | + Splines have low computational cost. |
| + They can easily provide continuity desired for robots. | |
| + Knots can easily control the shape of splines. | |
| − It might be difficult to balance the trade-off between continuity and desired shape. | |
| NURBS | + NURBS are easy to compute, with fast and stable computation. |
| + They can be very flexible to generate desired trajectories. | |
| + They are invariant under shear, translation, rotation, or scaling. | |
| + They are powerful tools used in CAD/CAM applications. | |
| − NURBS require more memory storage. | |
| − Improper initialization of weights can lead to bad parametrization. | |
| Clothoids | + Clothoids curvature changes linearly. |
| + Curvature continuity is easy to obtain. | |
| + Clothoids can be used as transition curves in conjunction to other curves. | |
| + Heavily used in railway track and highway road designs. | |
| − Fresnel’s integral might be difficult to compute. | |
| − Clothoid based planning uses global waypoints. | |
| Interpolation Methods | + Generally easy to compute. |
| + Curves can be concatenated to get desired shape. | |
| + Fit for local planning for safety. | |
| − Difficult to control coefficients of curves of higher order (). | |
| − Curves of higher order are time consuming and not suitable for high speeds. | |
| Hypocycloids | + Easy to compute. |
| + Can be generated for desired angles. | |
| − continuity is not guaranteed. | |
| − Requires using transition curves (clothoids) for curvature continuity. | |
| − Not suitable for robots at high speeds. | |
| Optimization Methods | + Various constraints can be taken into account while optimizing. |
| + Can be combined with other approaches. | |
| − Depends on global pathways. | |
| − Optimization is time consuming and might not necessarily converge. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Hoshino, Y.; Peng, C.-C. Path Smoothing Techniques in Robot Navigation: State-of-the-Art, Current and Future Challenges. Sensors 2018, 18, 3170. https://doi.org/10.3390/s18093170
Ravankar A, Ravankar AA, Kobayashi Y, Hoshino Y, Peng C-C. Path Smoothing Techniques in Robot Navigation: State-of-the-Art, Current and Future Challenges. Sensors. 2018; 18(9):3170. https://doi.org/10.3390/s18093170
Chicago/Turabian StyleRavankar, Abhijeet, Ankit A. Ravankar, Yukinori Kobayashi, Yohei Hoshino, and Chao-Chung Peng. 2018. "Path Smoothing Techniques in Robot Navigation: State-of-the-Art, Current and Future Challenges" Sensors 18, no. 9: 3170. https://doi.org/10.3390/s18093170
APA StyleRavankar, A., Ravankar, A. A., Kobayashi, Y., Hoshino, Y., & Peng, C.-C. (2018). Path Smoothing Techniques in Robot Navigation: State-of-the-Art, Current and Future Challenges. Sensors, 18(9), 3170. https://doi.org/10.3390/s18093170






