Hyperspectral Image Classification with Capsule Network Using Limited Training Samples
Abstract
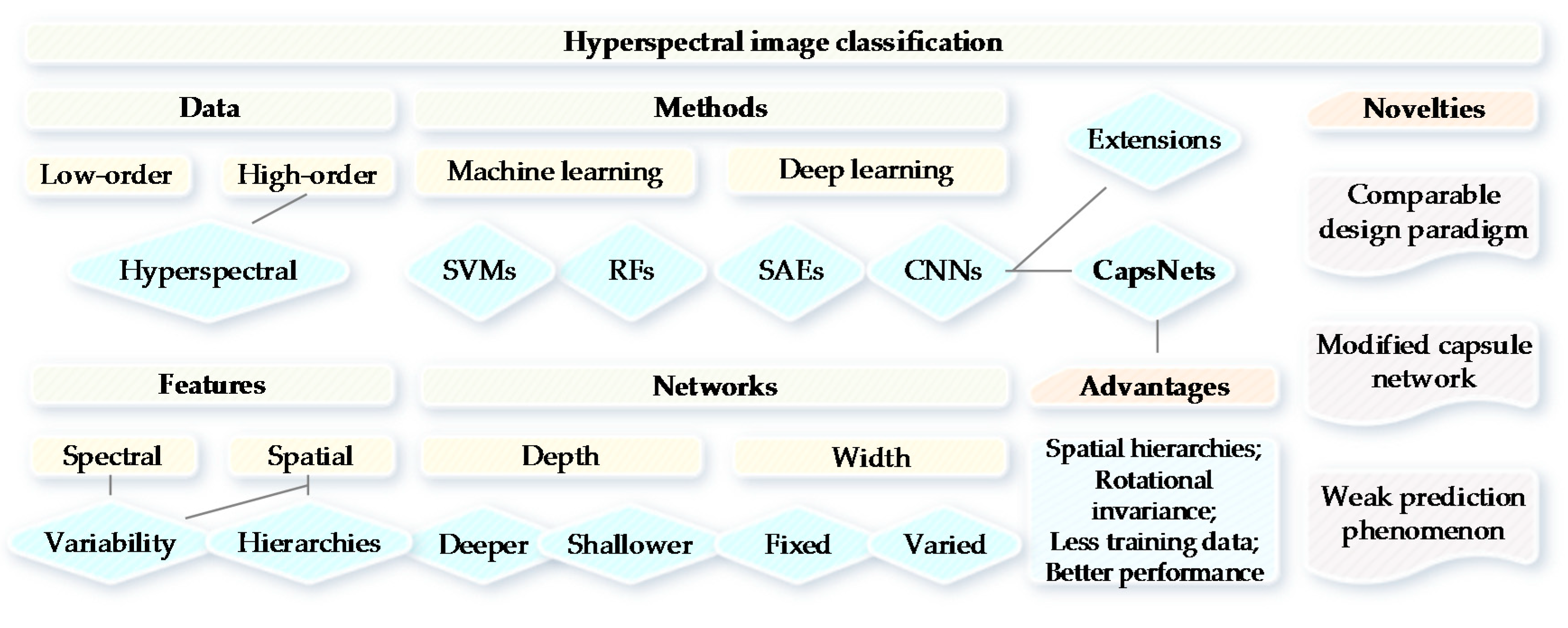
1. Introduction
2. Related Work
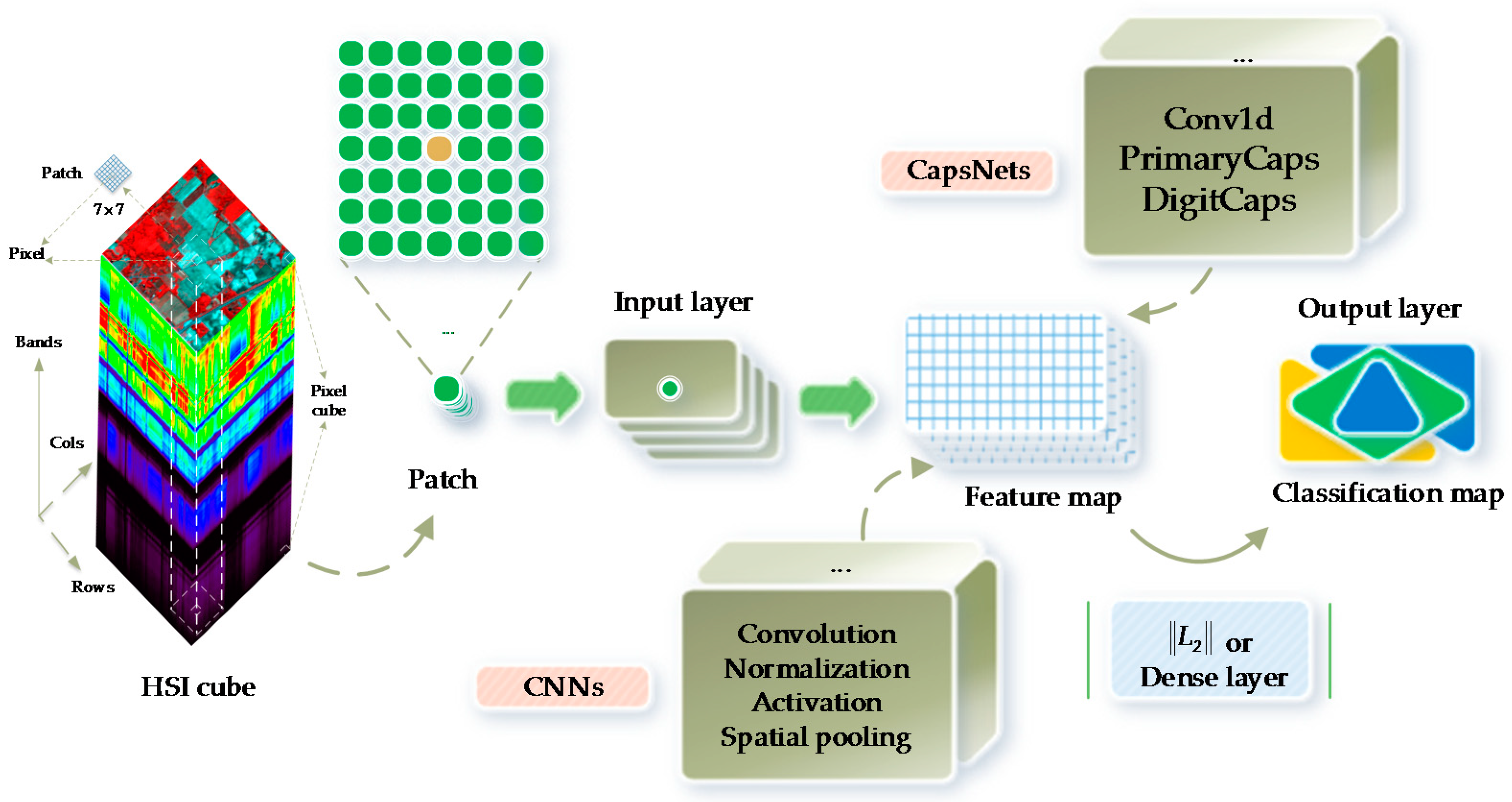
2.1. CNNs
2.2. CapsNets
3. Proposed Approach
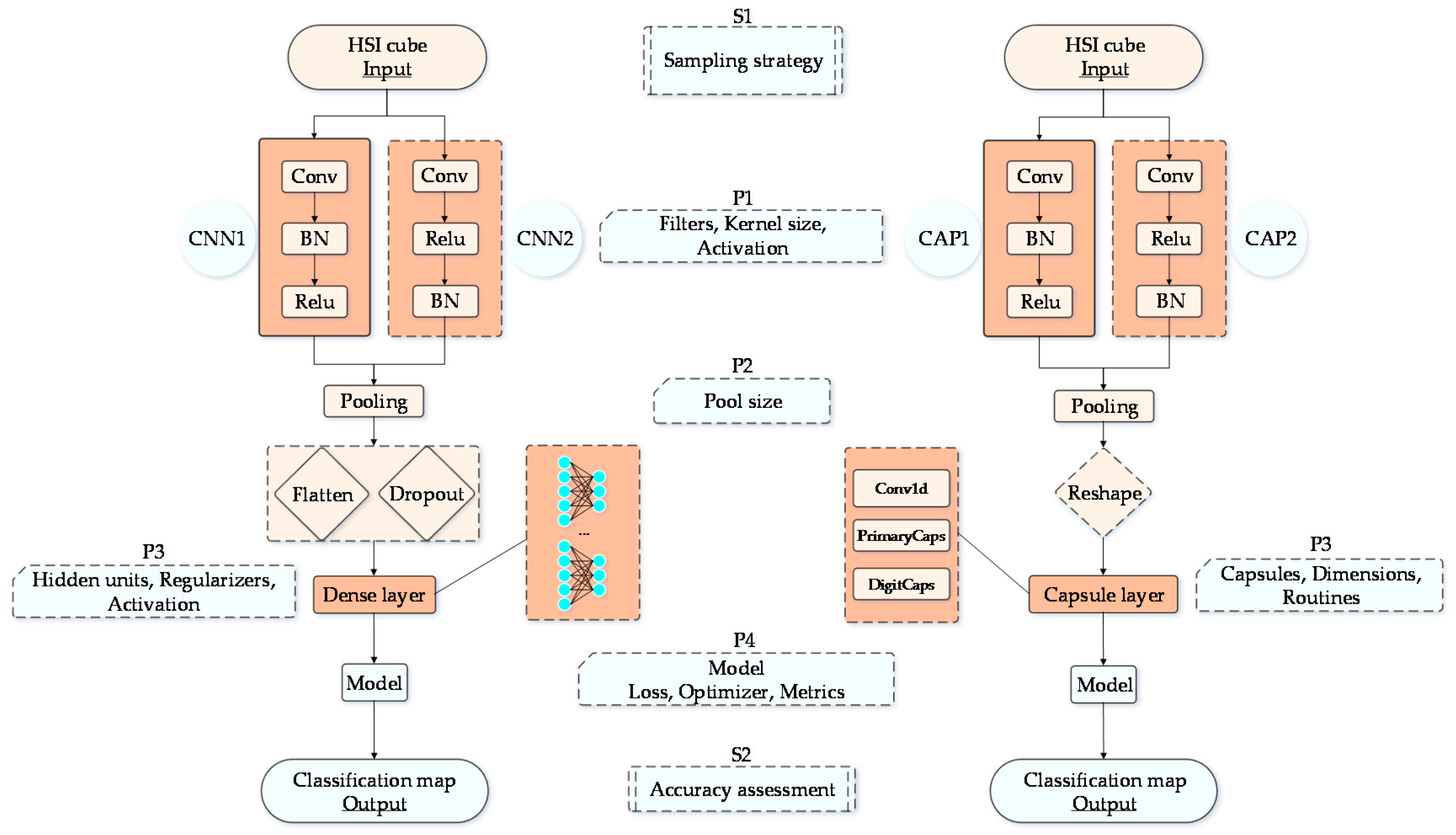
3.1. Network Design
3.2. Parameter Learning
3.3. Sampling Strategy
4. Results and Analysis
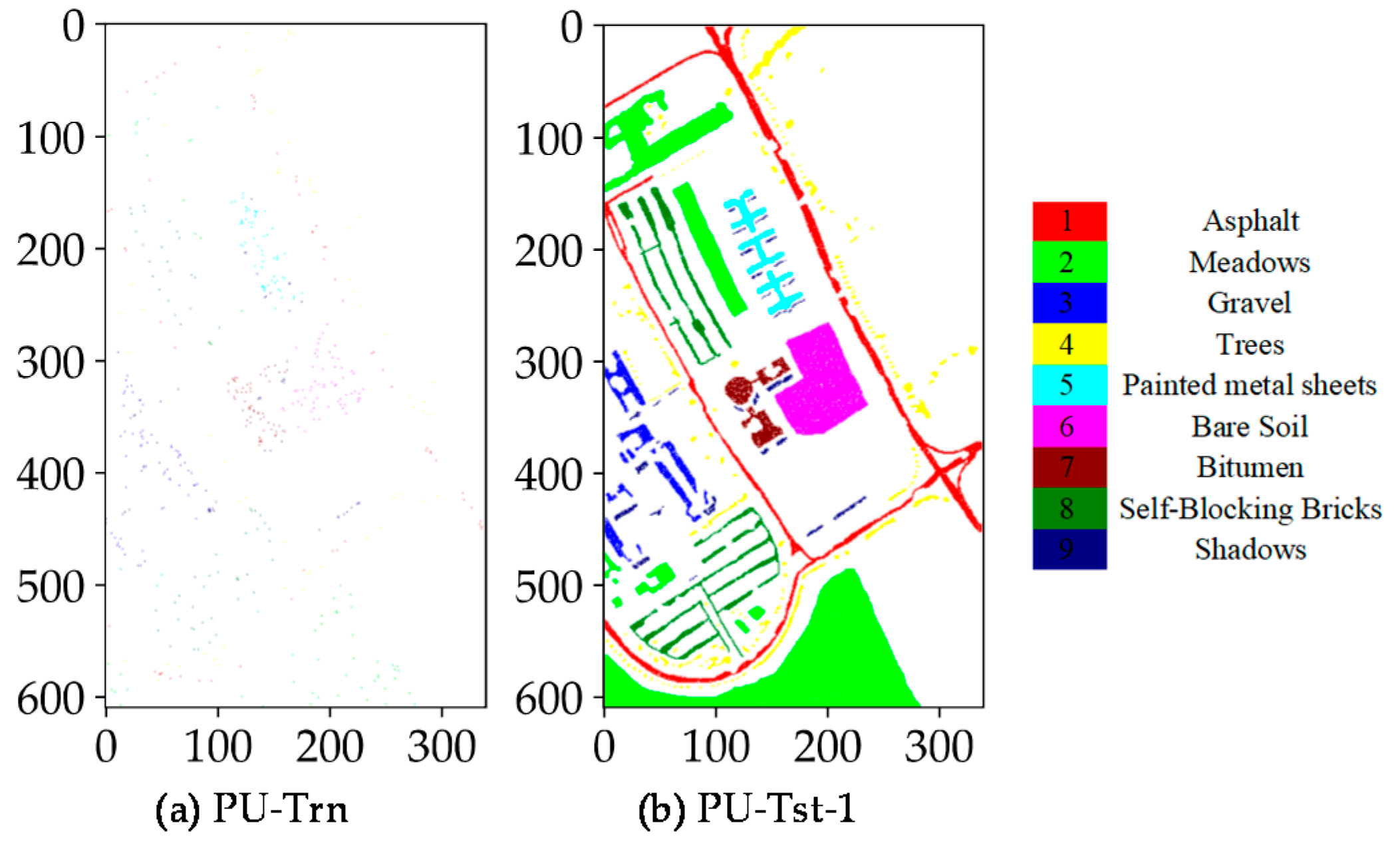
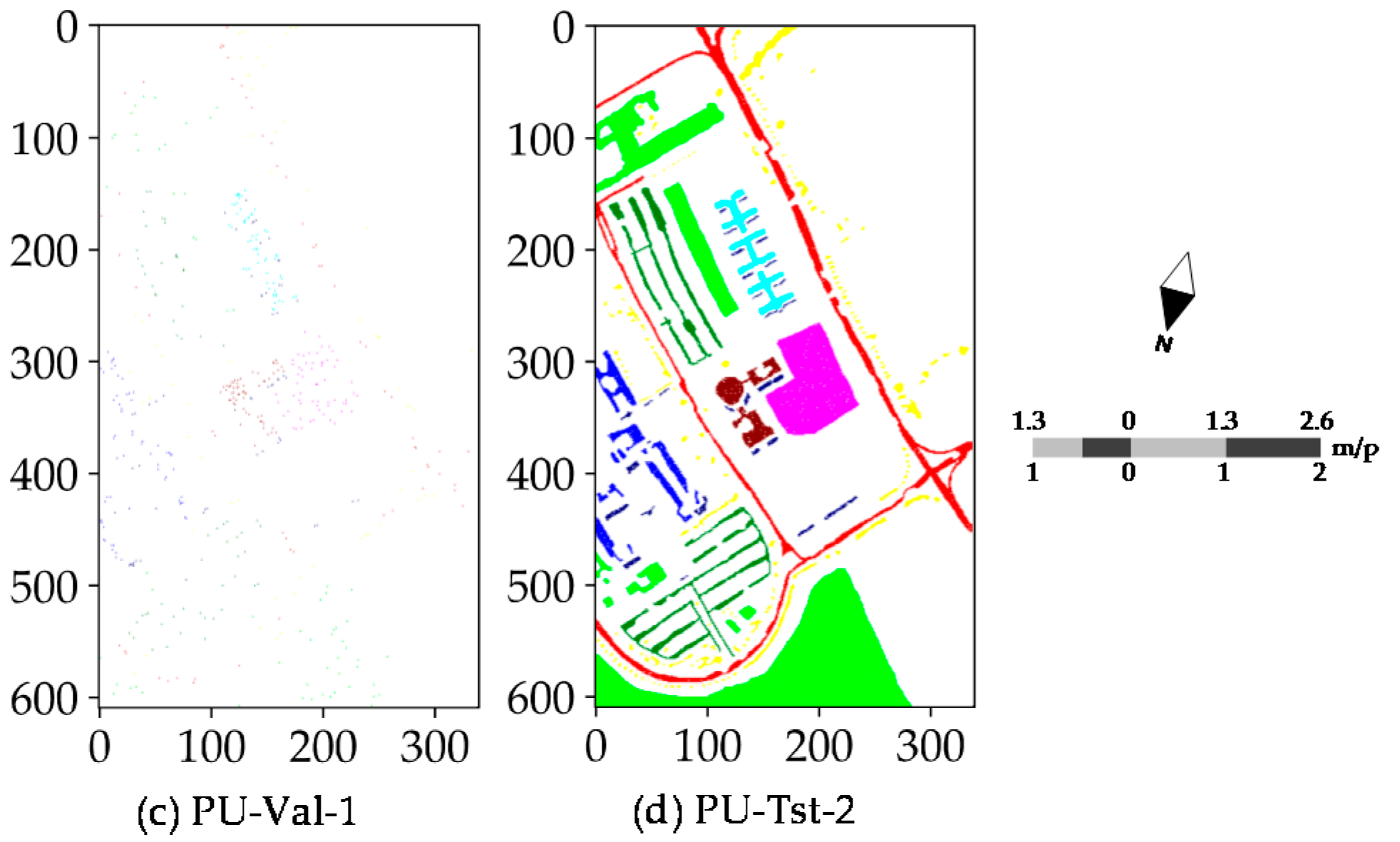
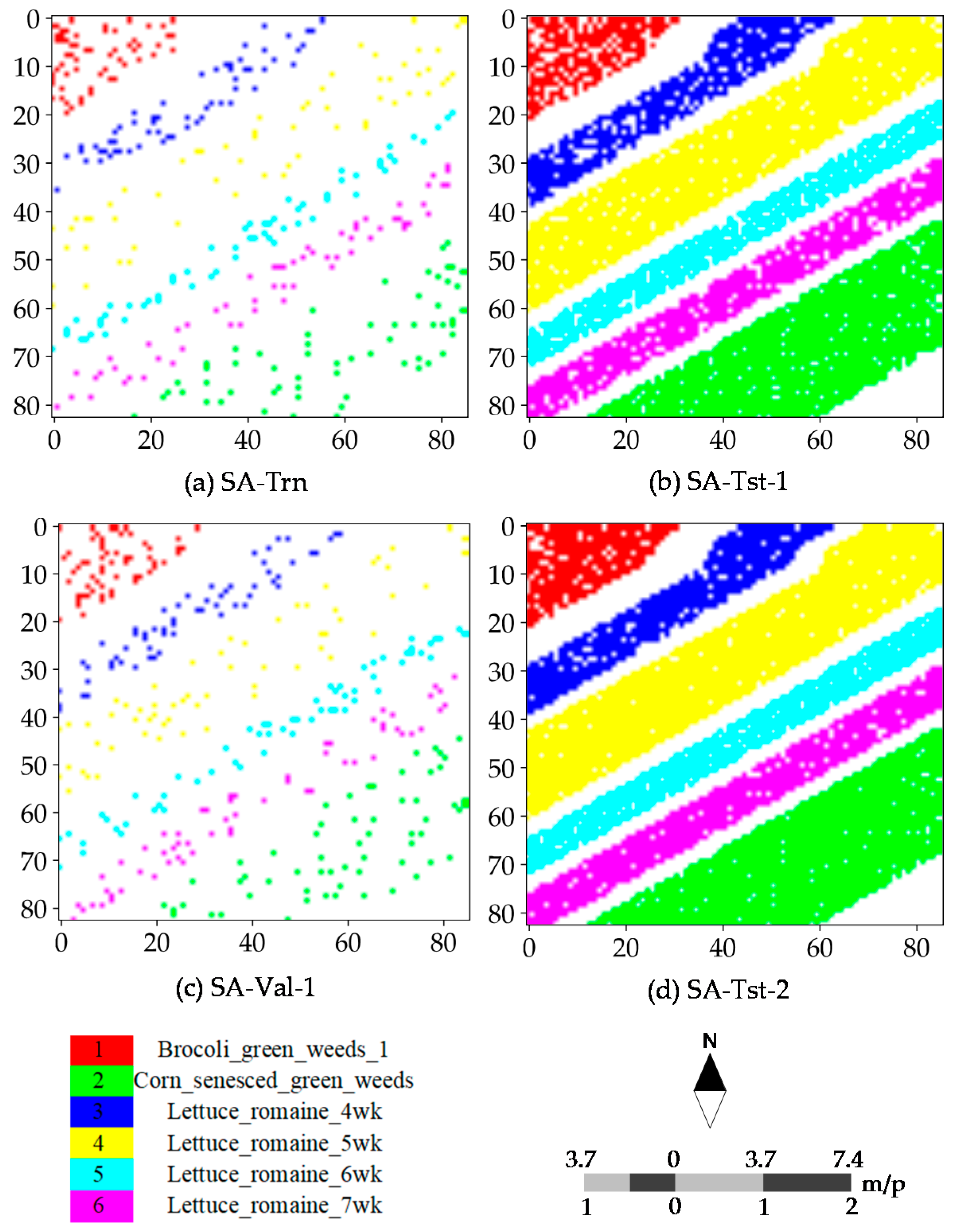
4.1. Dataset Description
4.2. Experimental Setup
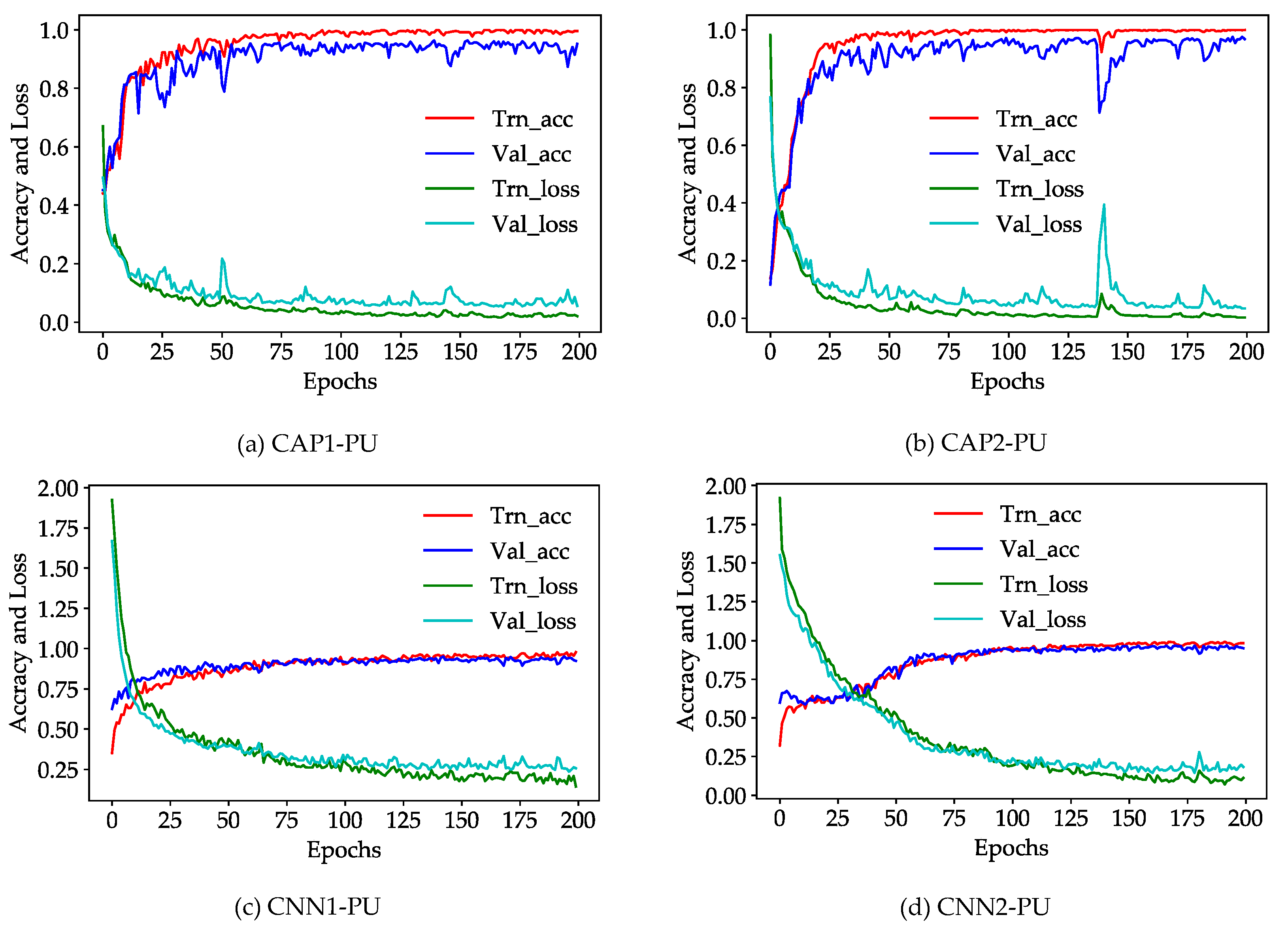
4.3. Training Details
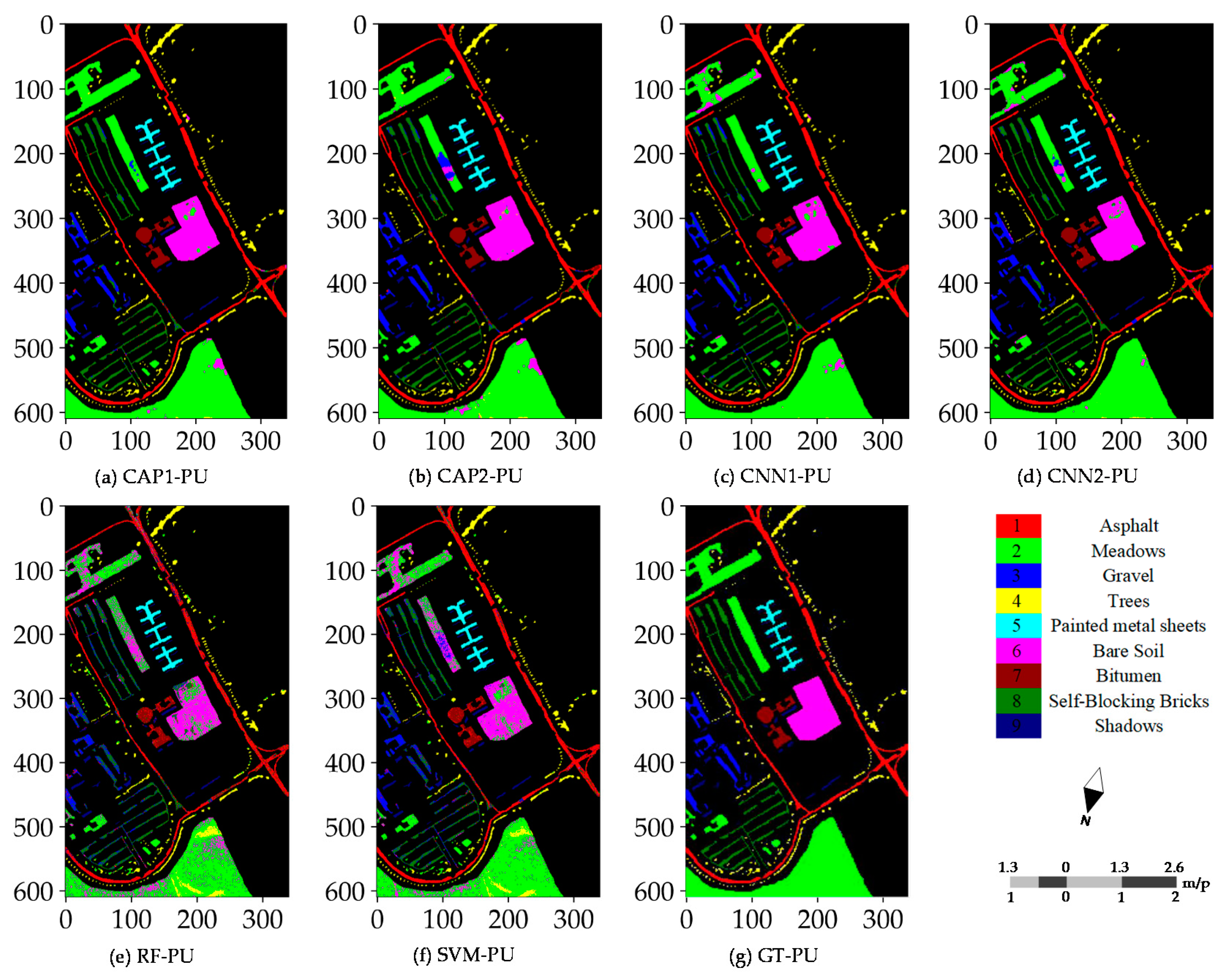
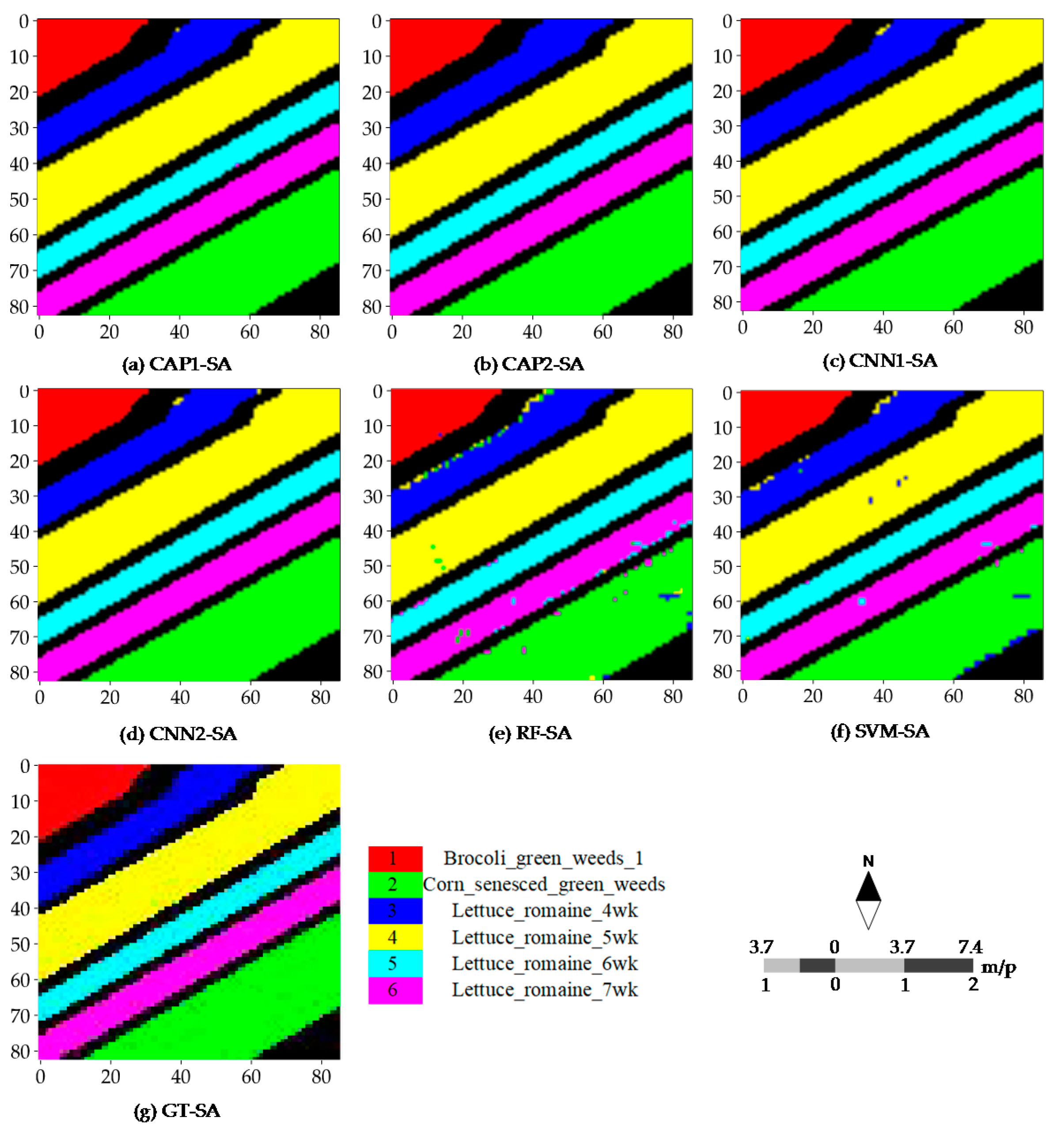
4.4. Classification Maps
4.5. Classification Accuracies
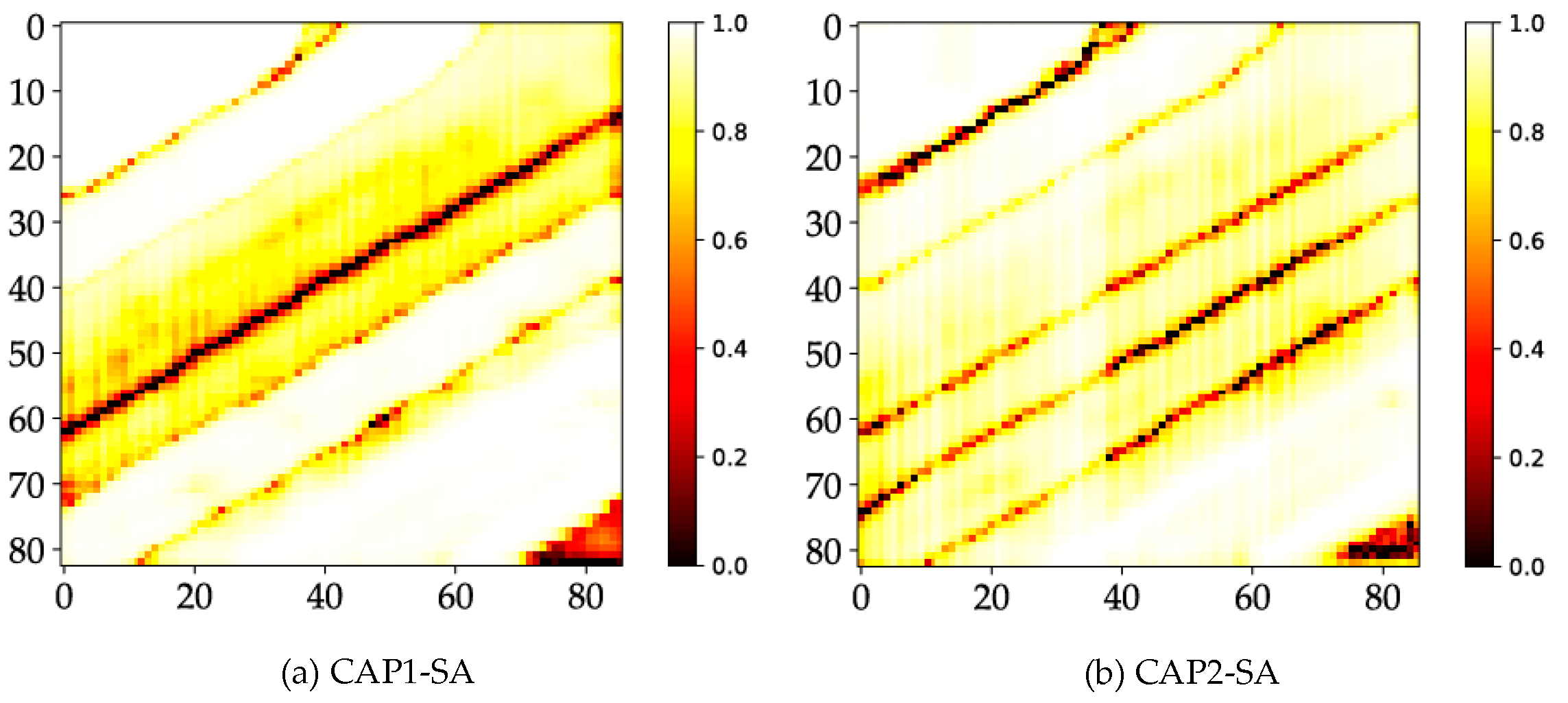
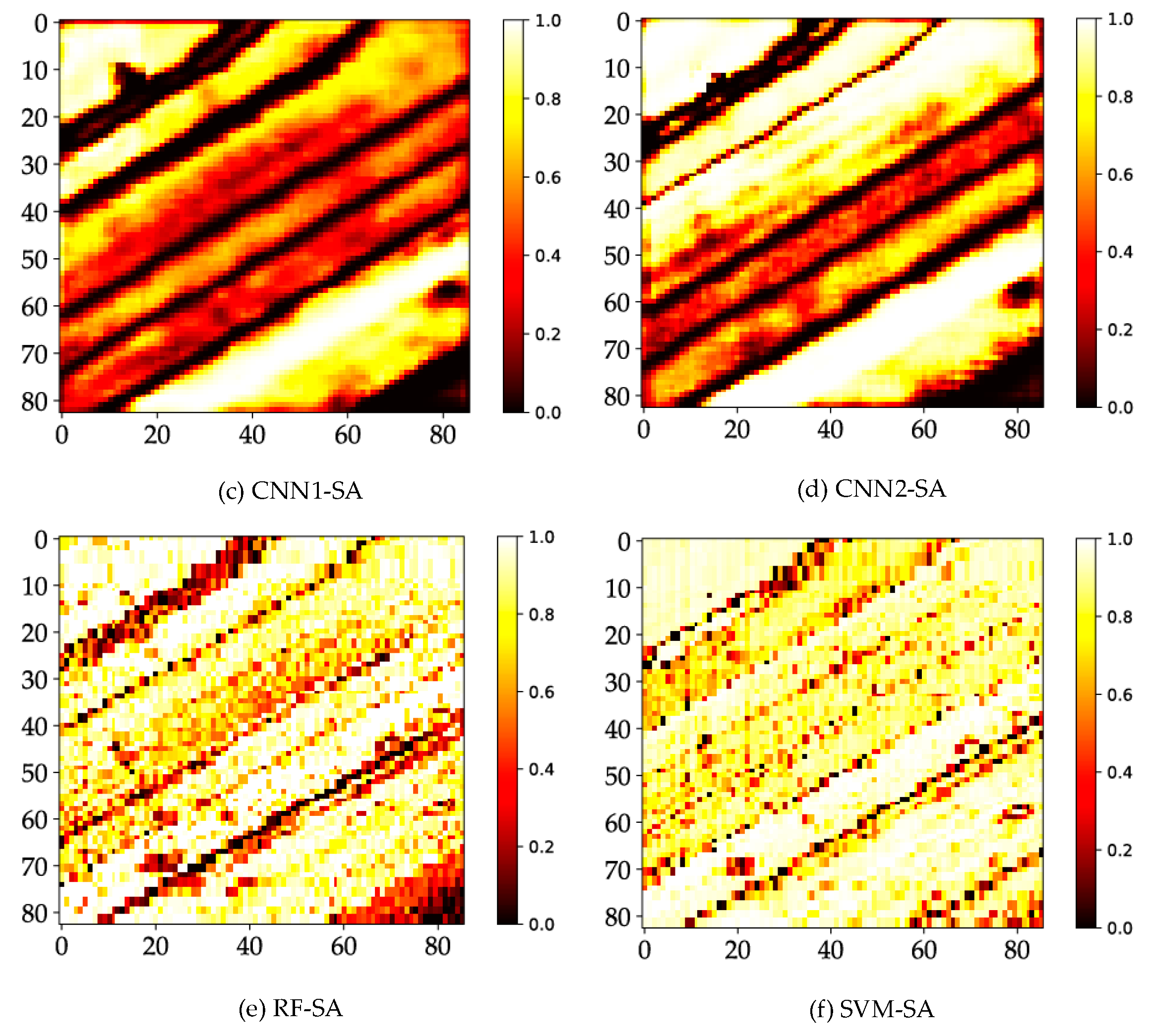
4.6. Probability Maps
5. Discussion
5.1. Parameters Determination
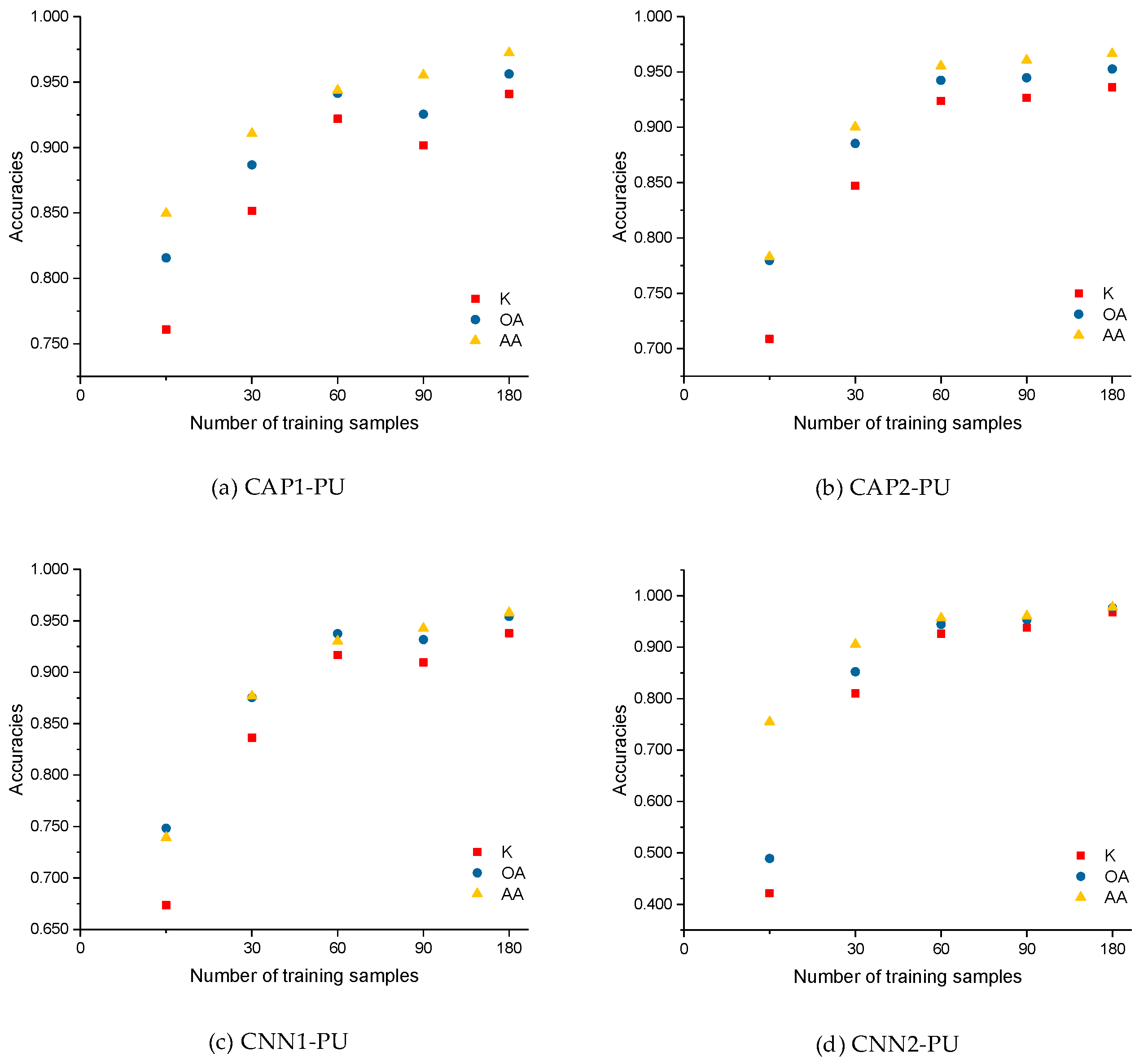
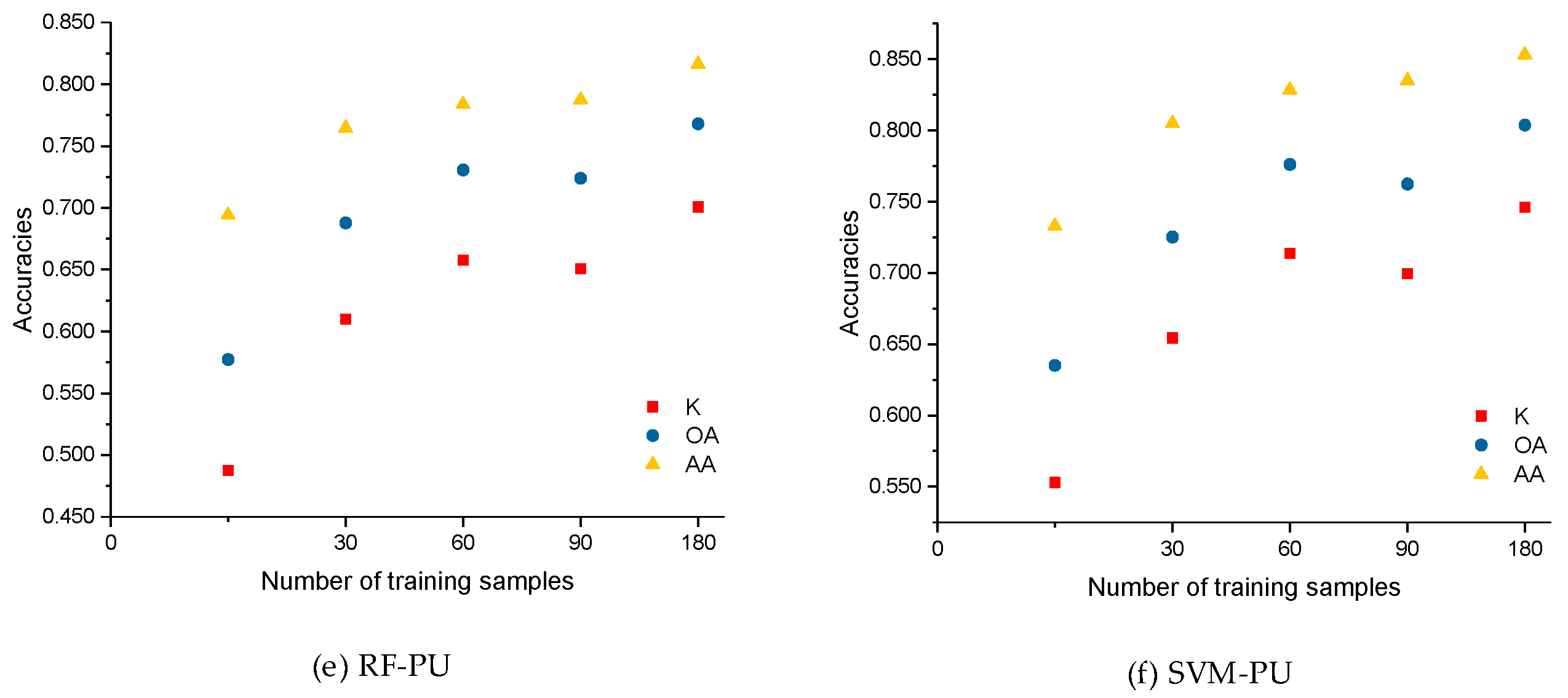
5.2. Impact of Training Size
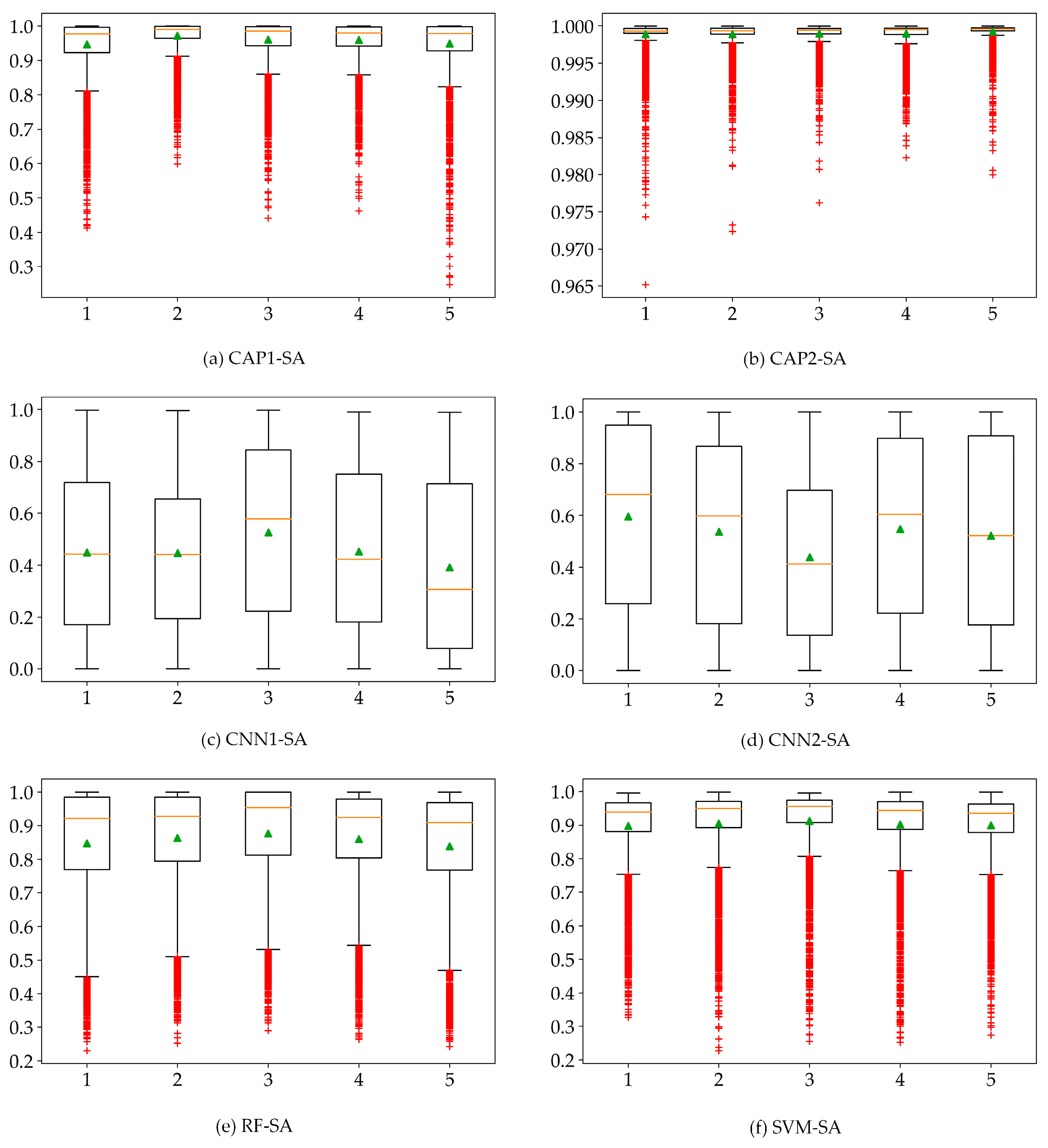
5.3. Uncertainty Analysis
5.4. Time Consumption
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Du, Q.; Zhang, L.; Zhang, B.; Tong, X.; Du, P.; Chanussot, J. Foreword to the special issue on hyperspectral remote sensing: Theory, methods, and applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 459–465. [Google Scholar] [CrossRef]
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- Zhang, L.; Du, B. Recent advances in hyperspectral image processing. Geo-Spat. Inf. Sci. 2012, 15, 143–156. [Google Scholar] [CrossRef]
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Yan, W.Y.; Shaker, A.; El-Ashmawy, N. Urban land cover classification using airborne LiDAR data: A review. Remote Sens. Environ. 2015, 158, 295–310. [Google Scholar] [CrossRef]
- Eslami, M.; Mohammadzadeh, A. Developing a spectral-based strategy for urban object detection from airborne hyperspectral TIR and visible data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1808–1816. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of Spectral–Temporal Response Surfaces by Combining Multispectral Satellite and Hyperspectral UAV Imagery for Precision Agriculture Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Govender, M.; Chetty, K.; Bulcock, H. A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water SA 2007, 33, 145–151. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral-Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Lein, J.K. Environmental Sensing: Analytical Techniques for Earth Observation; Springer: New York, NY, USA, 2011. [Google Scholar]
- Luo, Y.; Zou, J.; Yao, C.; Li, T.; Bai, G. HSI-CNN: A Novel Convolution Neural Network for Hyperspectral Image. arXiv, 2018; arXiv:1802.10478. [Google Scholar]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Ho, T.K. The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Gualtieri, J.A.; Chettri, S. Support vector machines for classification of hyperspectral data. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS 2000), Honolulu, HI, USA, 24–28 July 2000; pp. 813–815. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Chutia, D.; Bhattacharyya, D.K.; Sarma, K.K.; Kalita, R.; Sudhakar, S. Hyperspectral Remote Sensing Classifications: A Perspective Survey. Trans. GIS 2016, 20, 463–490. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 7, 2094–2107. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Makantasis, K.; Doulamis, A.; Doulamis, N.; Nikitakis, A.; Voulodimos, A. Tensor-based Nonlinear Classifier for High-Order Data Analysis. arXiv, 2018; arXiv:1802.05981. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; p. 1. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y. LeNet-5, Convolutional Neural Networks. 2015, p. 20. Available online: http://yann.lecun.com/exdb/lenet (accessed on 17 August 2018).
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Yu, S.; Jia, S.; Xu, C. Convolutional neural networks for hyperspectral image classification. Neurocomputing 2017, 219, 88–98. [Google Scholar] [CrossRef]
- Zhong, Z.; Fan, B.; Duan, J.; Wang, L.; Ding, K.; Xiang, S.; Pan, C. Discriminant tensor spectral-spatial feature extraction for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1028–1032. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3859–3869. [Google Scholar]
- Xi, E.; Bing, S.; Jin, Y. Capsule Network Performance on Complex Data. arXiv, 2017; arXiv:1712.03480. [Google Scholar]
- Wei, W.; Zhang, J.; Zhang, L.; Tian, C.; Zhang, Y. Deep Cube-Pair Network for Hyperspectral Imagery Classification. Remote Sens. 2018, 10, 783. [Google Scholar] [CrossRef]
- Makantasis, K.; Doulamis, A.D.; Doulamis, N.D.; Nikitakis, A. Tensor-Based Classification Models for Hyperspectral Data Analysis. IEEE Trans. Geosci. Remote Sens. 2018, 99, 1–15. [Google Scholar] [CrossRef]
- Afshar, P.; Mohammadi, A.; Plataniotis, K.N. Brain Tumor Type Classification via Capsule Networks. arXiv, 2018; arXiv:1802.10200. [Google Scholar]
- Jaiswal, A.; AbdAlmageed, W.; Natarajan, P. CapsuleGAN: Generative Adversarial Capsule Network. arXiv, 2018; arXiv:1802.06167. [Google Scholar]
- Kumar, A.D. Novel Deep Learning Model for Traffic Sign Detection Using Capsule Networks. arXiv, 2018; arXiv:1805.04424. [Google Scholar]
- LaLonde, R.; Bagci, U. Capsules for Object Segmentation. arXiv, 2018; arXiv:1804.04241. [Google Scholar]
- Li, Y.; Qian, M.; Liu, P.; Cai, Q.; Li, X.; Guo, J.; Yan, H.; Yu, F.; Yuan, K.; Yu, J.; et al. The recognition of rice images by UAV based on capsule network. Clust. Comput. 2018, 1–10. [Google Scholar] [CrossRef]
- Qiao, K.; Zhang, C.; Wang, L.; Yan, B.; Chen, J.; Zeng, L.; Tong, L. Accurate reconstruction of image stimuli from human fMRI based on the decoding model with capsule network architecture. arXiv, 2018; arXiv:1801.00602. [Google Scholar]
- Wang, Y.; Sun, A.; Han, J.; Liu, Y.; Zhu, X. Sentiment Analysis by Capsules. In Proceedings of the 2018 World Wide Web Conference on World Wide Web, Lyon, France, 23–27 April 2018; pp. 1165–1174. [Google Scholar]
- Zhao, W.; Ye, J.; Yang, M.; Lei, Z.; Zhang, S.; Zhao, Z. Investigating Capsule Networks with Dynamic Routing for Text Classification. arXiv, 2018; arXiv:1804.00538. [Google Scholar]
- Andersen, P. Deep Reinforcement Learning using Capsules in Advanced Game Environments. arXiv, 2018; arXiv:1801.09597. [Google Scholar]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral-Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Guidici, D.; Clark, M.L. One-Dimensional convolutional neural network land-cover classification of multi-seasonal hyperspectral imagery in the San Francisco Bay Area, California. Remote Sens. 2017, 9, 629. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.; Hu, J.; Zhang, L. Transferring deep convolutional neural networks for the scene classification of high-resolution remote sensing imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep learning classification of land cover and crop types using remote sensing data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 778–782. [Google Scholar] [CrossRef]
- Gao, Q.; Lim, S.; Jia, X. Hyperspectral Image Classification Using Convolutional Neural Networks and Multiple Feature Learning. Remote Sens. 2018, 10, 299. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Ma, L.; Jiang, H.; Zhao, H. Deep Residual Networks for Hyperspectral Image Classification. In Proceedings of the Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Camps-Valls, G.; Bruzzone, L. Kernel-based methods for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1351–1362. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Cui, X.; Chen, J. Change vector analysis in posterior probability space: A new method for land cover change detection. IEEE Geosci. Remote Sens. Lett. 2011, 8, 317–321. [Google Scholar] [CrossRef]
- Schneider, A.; Friedl, M.A.; Potere, D. Mapping global urban areas using MODIS 500-m data: New methods and datasets based on ‘urban ecoregions’. Remote Sens. Environ. 2010, 114, 1733–1746. [Google Scholar] [CrossRef]
- Sexton, J.O.; Noojipady, P.; Anand, A.; Song, X.; McMahon, S.; Huang, C.; Feng, M.; Channan, S.; Townshend, J.R. A model for the propagation of uncertainty from continuous estimates of tree cover to categorical forest cover and change. Remote Sens. Environ. 2015, 156, 418–425. [Google Scholar] [CrossRef]
- Yang, D.; Chen, X.; Chen, J.; Cao, X. Multiscale integration approach for land cover classification based on minimal entropy of posterior probability. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1105–1116. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]

| Dt | Cn | Class | Samples | Train | Test | Val |
|---|---|---|---|---|---|---|
| PU | C0 | Non-ground truth | 164,624 | 0 | 0 | 0 |
| C1 | Asphalt | 6631 | 60 | 6511 | 60 | |
| C2 | Meadows | 18,649 | 60 | 18,529 | 60 | |
| C3 | Gravel | 2099 | 60 | 1979 | 60 | |
| C4 | Trees | 3064 | 60 | 2944 | 60 | |
| C5 | Painted metal sheets | 1345 | 60 | 1225 | 60 | |
| C6 | Bare Soil | 5029 | 60 | 4909 | 60 | |
| C7 | Bitumen | 1330 | 60 | 1210 | 60 | |
| C8 | Self-Blocking Bricks | 3682 | 60 | 3562 | 60 | |
| C9 | Shadows | 947 | 60 | 827 | 60 | |
| SA | C0 | Non-ground truth | 1790 | 0 | 0 | 0 |
| C1 | Brocoli_green_weeds_1 | 391 | 60 | 271 | 60 | |
| C2 | Corn_senesced_green_weeds | 1343 | 60 | 1223 | 60 | |
| C3 | Lettuce_romaine_4wk | 616 | 60 | 496 | 60 | |
| C4 | Lettuce_romaine_5wk | 1525 | 60 | 1405 | 60 | |
| C5 | Lettuce_romaine_6wk | 674 | 60 | 554 | 60 | |
| C6 | Lettuce_romaine_7wk | 799 | 60 | 679 | 60 |
| CAP1-PU | CAP2-PU | CNN1-PU | CNN2-PU | RF-PU | SVM-PU | |
|---|---|---|---|---|---|---|
| K | 0.9324 ± 0.0242 | 0.9456 ± 0.0181 | 0.9345 ± 0.0130 | 0.9332 ± 0.0221 | 0.6450 ± 0.0147 | 0.7070 ± 0.0094 |
| OA | 0.9490 ± 0.0185 | 0.9590 ± 0.0138 | 0.9511 ± 0.0097 | 0.9496 ± 0.0169 | 0.7189 ± 0.0124 | 0.7703 ± 0.0071 |
| AA | 0.9542 ± 0.0112 | 0.9627 ± 0.0138 | 0.9367 ± 0.0174 | 0.9563 ± 0.0089 | 0.7869 ± 0.0098 | 0.8273 ± 0.0096 |
| C1 | 0.8943 ± 0.0545 | 0.9277 ± 0.0264 | 0.9468 ± 0.0279 | 0.9382 ± 0.0407 | 0.6604 ± 0.0143 | 0.7629 ± 0.0248 |
| C2 | 0.9686 ± 0.0278 | 0.9659 ± 0.0210 | 0.9807 ± 0.0070 | 0.9507 ± 0.0272 | 0.6892 ± 0.0237 | 0.7374 ± 0.0082 |
| C3 | 0.9229 ± 0.0312 | 0.8882 ± 0.1190 | 0.8518 ± 0.0782 | 0.8851 ± 0.0404 | 0.6364 ± 0.0284 | 0.7171 ± 0.0438 |
| C4 | 0.9797 ± 0.0096 | 0.9761 ± 0.0121 | 0.9724 ± 0.0178 | 0.9720 ± 0.0124 | 0.9142 ± 0.0250 | 0.9042 ± 0.0259 |
| C5 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 0.9928 ± 0.0052 | 0.9969 ± 0.0016 |
| C6 | 0.9609 ± 0.0338 | 0.9781 ± 0.0284 | 0.9212 ± 0.0241 | 0.9483 ± 0.0321 | 0.7191 ± 0.0334 | 0.7738 ± 0.0324 |
| C7 | 0.9831 ± 0.0137 | 0.9800 ± 0.0085 | 0.8783 ± 0.1855 | 0.9620 ± 0.0125 | 0.8296 ± 0.0205 | 0.8537 ± 0.0288 |
| C8 | 0.8796 ± 0.0806 | 0.9483 ± 0.0224 | 0.8799 ± 0.0649 | 0.9504 ± 0.0196 | 0.6612 ± 0.0332 | 0.7015 ± 0.0380 |
| C9 | 0.9985 ± 0.0009 | 0.9998 ± 0.0005 | 0.9993 ± 0.0006 | 1.0000 ± 0.0000 | 0.9793 ± 0.0072 | 0.9986 ± 0.0013 |
| CAP1-SA | CAP2-SA | CNN1-SA | CNN2-SA | RF-SA | SVM-SA | |
|---|---|---|---|---|---|---|
| K | 0.9992 ± 0.0007 | 0.9991 ± 0.0004 | 0.9994 ± 0.0004 | 0.9991 ± 0.0003 | 0.9647 ± 0.0073 | 0.9845 ± 0.0035 |
| OA | 0.9994 ± 0.0005 | 0.9993 ± 0.0003 | 0.9995 ± 0.0003 | 0.9993 ± 0.0002 | 0.9720 ± 0.0058 | 0.9877 ± 0.0028 |
| AA | 0.9995 ± 0.0002 | 0.9992 ± 0.0003 | 0.9993 ± 0.0004 | 0.9989 ± 0.0003 | 0.9704 ± 0.0051 | 0.9883 ± 0.0025 |
| C1 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 0.9940 ± 0.0019 | 0.9952 ± 0.0024 |
| C2 | 0.9990 ± 0.0020 | 0.9987 ± 0.0019 | 1.0000 ± 0.0000 | 0.9997 ± 0.0007 | 0.9574 ± 0.0170 | 0.9782 ± 0.0056 |
| C3 | 0.9984 ± 0.0008 | 0.9968 ± 0.0027 | 0.9956 ± 0.0027 | 0.9940 ± 0.0022 | 0.9266 ± 0.0070 | 0.9763 ± 0.0082 |
| C4 | 0.9994 ± 0.0008 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 0.9974 ± 0.0008 | 0.9944 ± 0.0041 |
| C5 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 0.9954 ± 0.0052 | 0.9971 ± 0.0030 |
| C6 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 1.0000 ± 0.0000 | 0.9518 ± 0.0199 | 0.9886 ± 0.0055 |
| Models | PU (610 × 340 × 103) | SA (83 × 86 × 204) | ||
|---|---|---|---|---|
| Total Parameters | Training Time (s) | Total Parameters | Training Time (s) | |
| CAP1 | 1.42 × 105 | 35 | 2.33 × 105 | 27 |
| CAP2 | 37 | 27 | ||
| CNN1 | 1.08 × 105 | 21 | 2.10 × 105 | 20 |
| CNN2 | 21 | 20 | ||
| RF | - | 51 | - | 52 |
| SVM | - | 13 | - | 5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, F.; Pu, S.; Chen, X.; Shi, Y.; Yuan, T.; Pu, S. Hyperspectral Image Classification with Capsule Network Using Limited Training Samples. Sensors 2018, 18, 3153. https://doi.org/10.3390/s18093153
Deng F, Pu S, Chen X, Shi Y, Yuan T, Pu S. Hyperspectral Image Classification with Capsule Network Using Limited Training Samples. Sensors. 2018; 18(9):3153. https://doi.org/10.3390/s18093153
Chicago/Turabian StyleDeng, Fei, Shengliang Pu, Xuehong Chen, Yusheng Shi, Ting Yuan, and Shengyan Pu. 2018. "Hyperspectral Image Classification with Capsule Network Using Limited Training Samples" Sensors 18, no. 9: 3153. https://doi.org/10.3390/s18093153
APA StyleDeng, F., Pu, S., Chen, X., Shi, Y., Yuan, T., & Pu, S. (2018). Hyperspectral Image Classification with Capsule Network Using Limited Training Samples. Sensors, 18(9), 3153. https://doi.org/10.3390/s18093153







