Smartphone-Based Traveled Distance Estimation Using Individual Walking Patterns for Indoor Localization
Abstract
:1. Introduction
- (1)
- Outdoor walking patterns are learned and then applied to indoor localization. To learn the individual user’s walking patterns, the trajectory with a GPS error was corrected for the user, and along with the IMU sensor signal was mapped on the available GPS area using the user’s own smartphone. Indeed, our proposed approach is more effective in terms of the device, user, and walking pattern diversities compared to conventional manually-designed feature extraction.
- (2)
- Estimation of the average moving speed for segmented IMU sensor signal frames. In the case of conventional PDR, the traveled distance is estimated by calculating the step count and stride length using the handcrafted features of the IMU signal. However, we proposed a scheme to estimate the traveled distance by calculating the average moving speed and duration of the signal frame.
- (3)
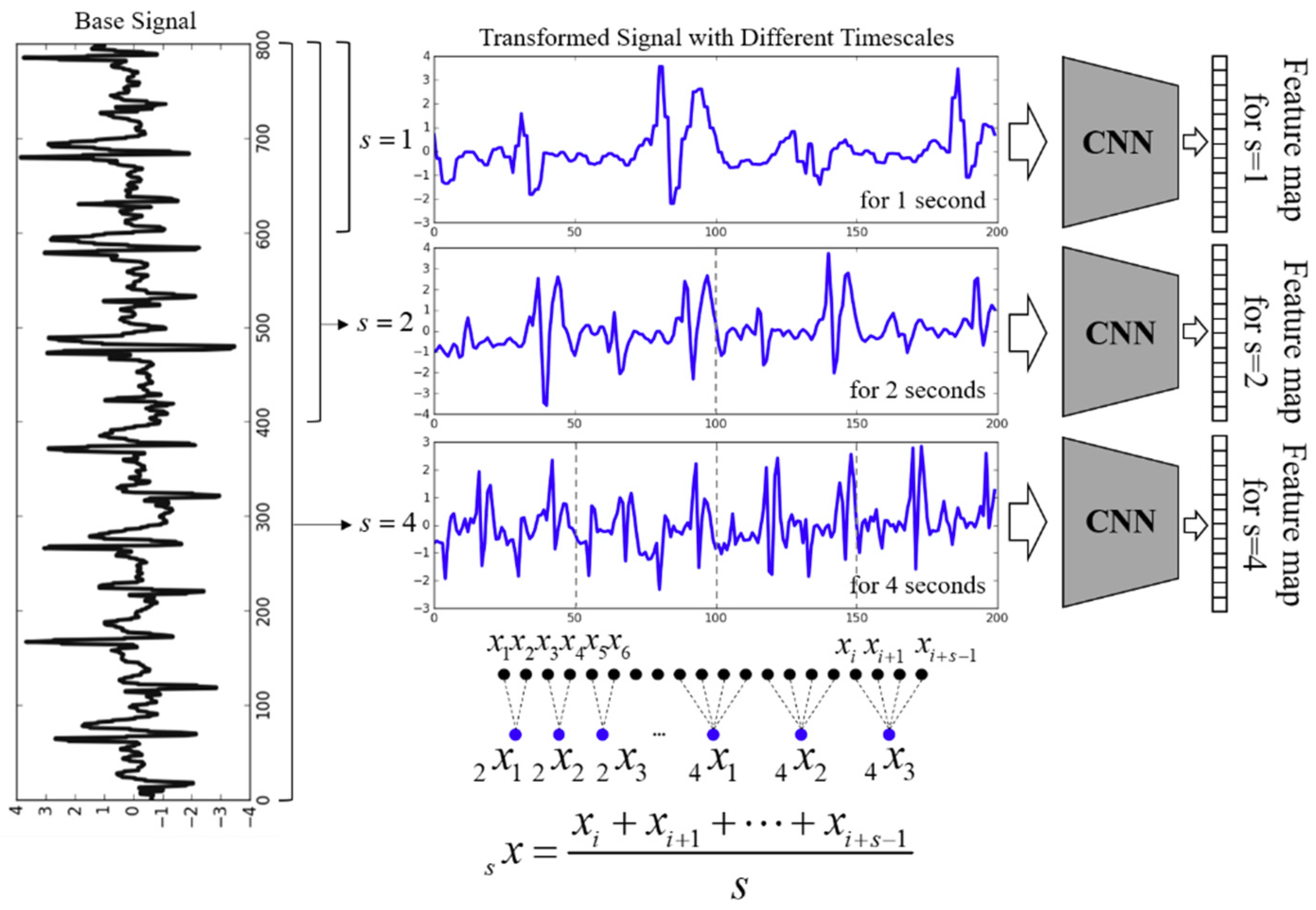
- Combination of multiscaling for automatic pre-processing at different time scales and CNNs for nonlinear feature extraction and RNNs for temporal information along the walking patterns. Multi-scaling makes the overall trend for different time series input signals. Several stacked convolutional operations create feature vectors from the input signal automatically, and a recurrent neural network model deals with the sequence problems.
- (4)
- End-to-end time series classification model without any handcraft feature extractions as well as requiring any signal or application specific analysis. Many of the existing methods are time-consuming and labor-intensive for feature extraction and classification, and these are limited in their domain-specific application. However, our proposed framework is a general-purpose approach, and it can be easily applied to more kinds of time-series signal classification, regression, and forecasting.
2. Related Works
2.1. Indoor Localization
2.2. Deep Learning for Time-Series Sensory Signal Analysis
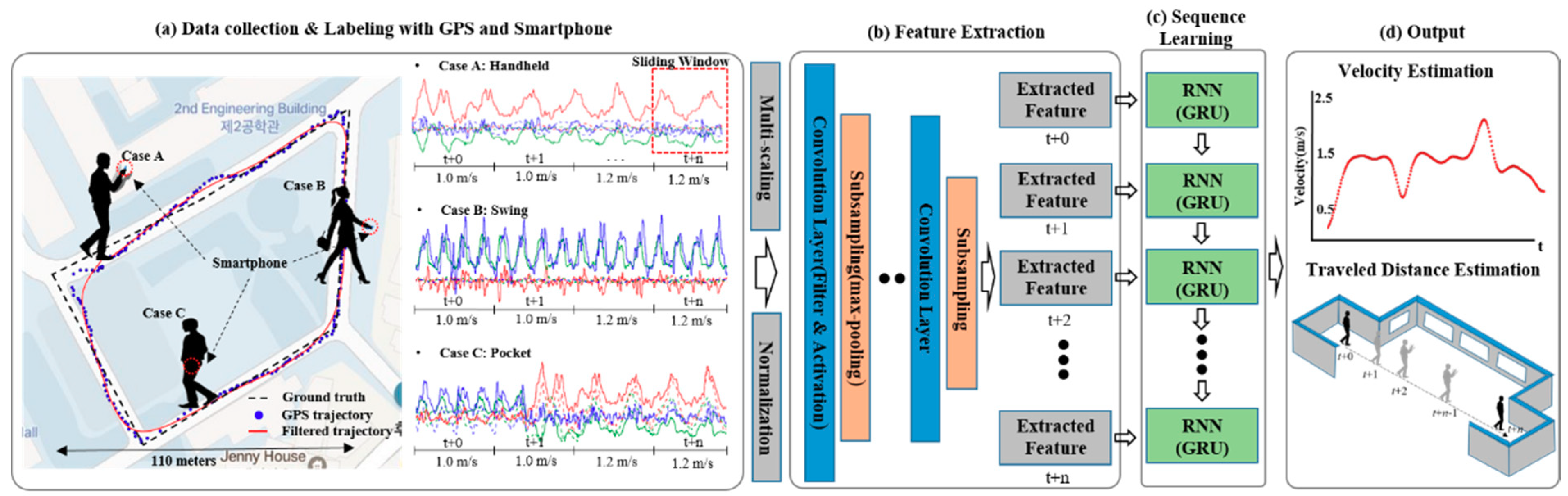
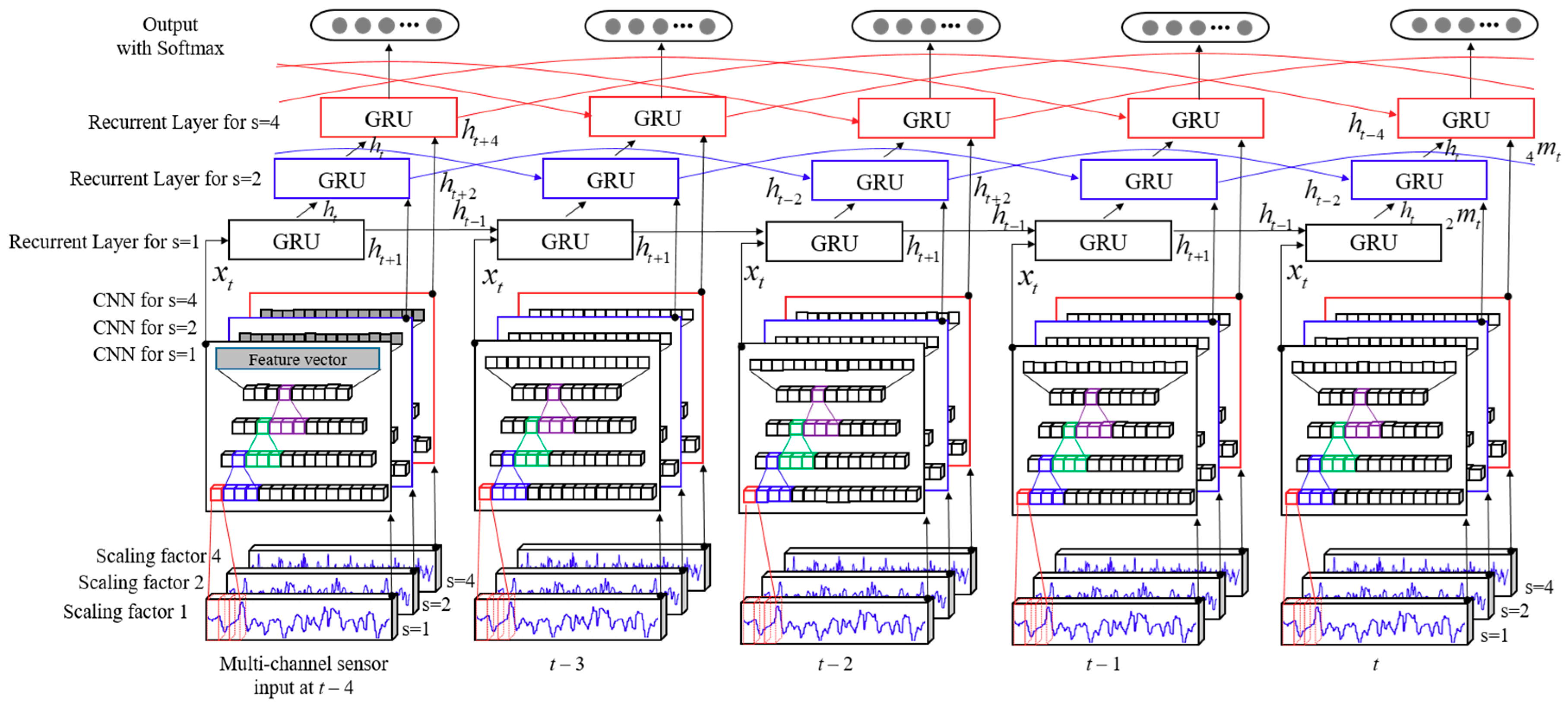
3. The Proposed System Design
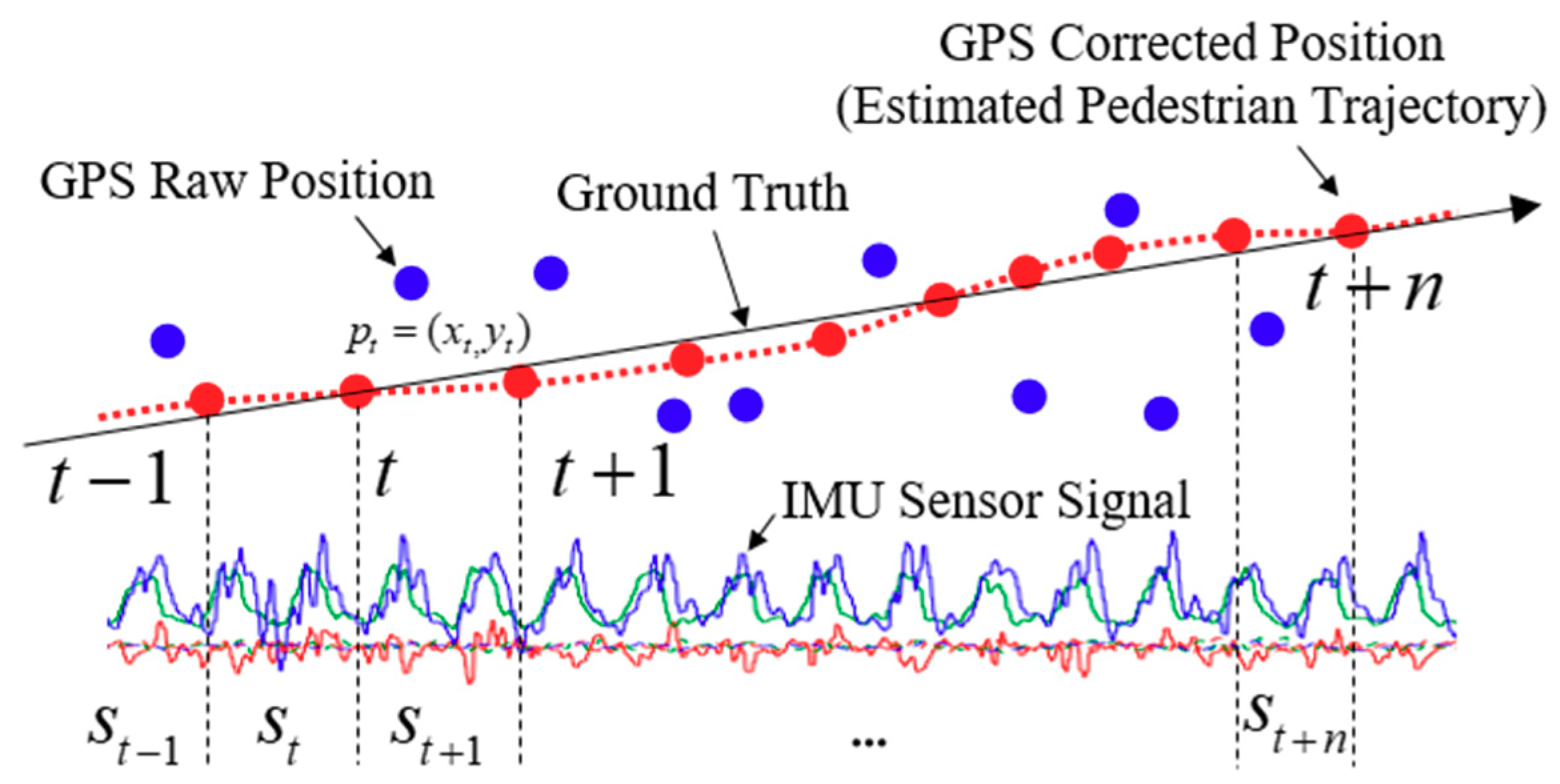
3.1. Automatic Dataset Collection Using the Corrected Pedestrian Trajectory with Kalman Filter
3.2. Multiscale and Multiple 1D-CNN for Feature Extraction
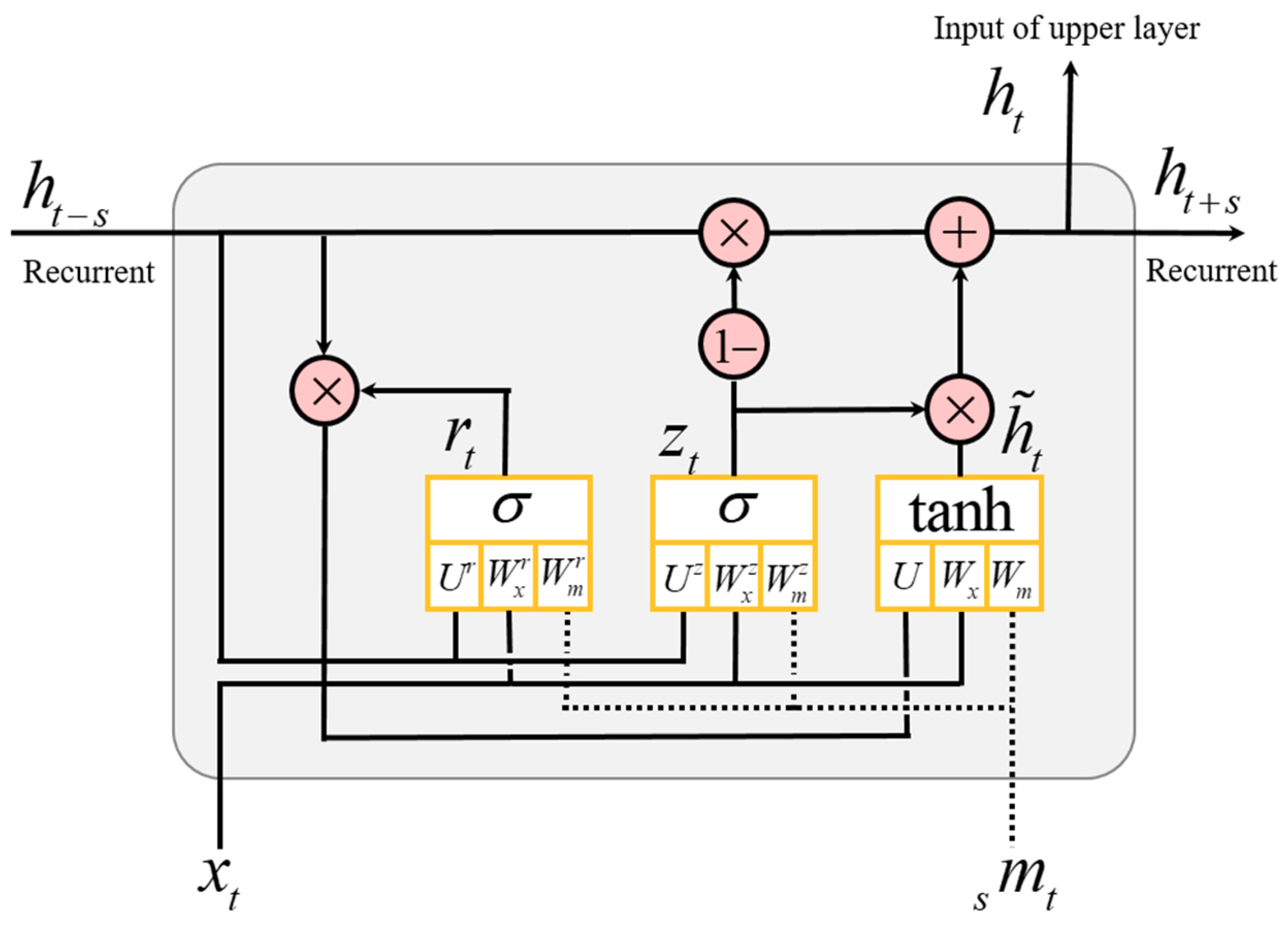
3.3. Hierarchical Multiscale Recurrent Neural Networks
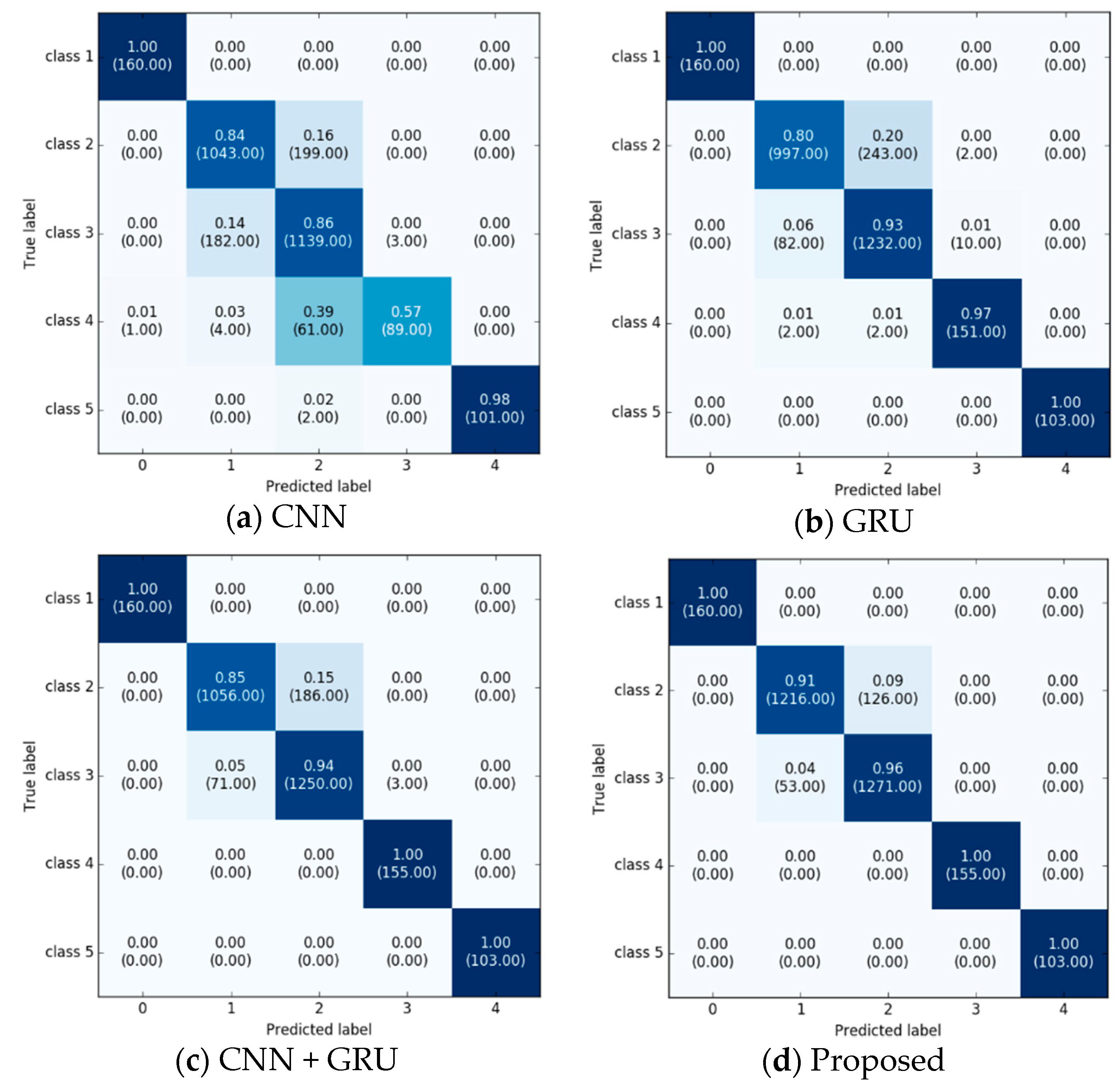
4. Experimental Results
4.1. Experimental Setup
4.2. Performance Evaluation
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brena, R.F.; García-Vázquez, J.P.; Galván-Tejada, C.E.; Muñoz-Rodriguez, D.; Vargas-Rosales, C.; Fangmeyer, J. Evolution of Indoor Positioning Technologies: A Survey. J. Sens. 2017, 2017, 2630413. [Google Scholar] [CrossRef]
- Pavel, D.; Robert, P. A survey of selected indoor positioning methods for smartphones. IEEE Common. Surv. Tutor. 2017, 19, 1347–1370. [Google Scholar] [CrossRef]
- Hui, L.; Houshang, D.; Pat, B.; Jing, L. Survey of wireless indoor positioning techniques and systems. IEEE Trans. Syst. Man Cybern. 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Xiaohua, T.; Ruofei, S.; Duowen, L.; Yutian, W.; Xinbing, W. Performance analysis of RSS fingerprinting based indoor localization. IEEE Trans. Mobile Comput. 2017, 16, 2847–2861. [Google Scholar] [CrossRef]
- Luo, H.; Zhao, F.; Jiang, M.; Ma, H.; Zhang, Y. Constructing an indoor floor plan using crowdsourcing based on magnetic fingerprinting. Sensors 2017, 17, 2678. [Google Scholar] [CrossRef] [PubMed]
- Sabet, M.T.; Daniali, H.R.M.; Fathi, A.R.; Alizadeh, E. Experimental analysis of a low-cost dead reckoning navigation system for a land vehicle using a robust AHRS. Robot. Auton. Syst. 2017, 95, 37–51. [Google Scholar] [CrossRef]
- Kang, W.; Han, Y. SmartPDR: Smartphone-based pedestrian dead reckoning for indoor localization. IEEE Sens. J. 2015, 15, 2906–2916. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Wei, D.; Ji, X.; Yuan, H. A Foot-Mounted PDR System Based on IMU/EKF + HMM + ZUPT + ZARU + HDR + Compass Algorithm. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017. [Google Scholar]
- Yu, N.; Zhan, X.; Zhao, S.; Wu, Y.; Feng, R. A precise dead reckoning algorithm based on bluetooth and multiple sensors. IEEE Internet Things J. 2018, 5, 336–351. [Google Scholar] [CrossRef]
- Kang, X.; Huang, B.; Qi, G. A novel walking detection and step counting algorithm using unconstrained smartphones. Sensors 2018, 18, 297. [Google Scholar] [CrossRef] [PubMed]
- Ho, N.-H.; Truong, P.H.; Jeong, G.-M. Step-detection and adaptive step-length estimation for pedestrian dead-reckoning at various walking speeds using a smartphone. Sensors 2016, 16, 1432. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, H. Using the ADXL202 in Pedometer and Personal Navigation Application; Analog Devices AN-602 Application Note: Norwood, MA, USA, 2002. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. In Proceedings of the Deep Learning and Representation Learning Workshop: NIPS, Montreal, QC, Canada, 12 December 2014. [Google Scholar]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.A.; Al-Khalifa, H.S. Ultra wideband indoor positioning technologies: Analysis and recent advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Gao, L.; Man, S.; Pandey, S. CSI-based fingerprinting for indoor localization: A deep learning approach. IEEE Trans. Veh. Technol. 2017, 66, 763–776. [Google Scholar] [CrossRef]
- Li, J.; Guo, M.; Li, S. Smartphone-Based Indoor Localization with Bluetooth Low Energy Beacons. In Proceedings of the 2nd International Conference on Frontieres of Science and Technology (ICFST-18), Shenzhen, China, 21–22 July 2017. [Google Scholar]
- Luo, J.; Fu, L. A smartphone indoor localization algorithm based on WLAN location fingerprinting with feature extraction and clustering. Sensors 2017, 17, 1339. [Google Scholar] [CrossRef]
- Shu, Y.; Bo, C.; Shen, G.; Zhao, C.; Li, L.; Zhao, F. Magicol: Indoor localization using pervasive magnetic field and opportunistic WiFi sensing. IEEE J. Sel. Areas Commun. 2015, 33, 1443–1457. [Google Scholar] [CrossRef]
- Xie, H.; Gu, T.; Tao, X.; Ye, H.; Lu, J. A reliablility-augmented particle filter for magnetic fingerprinting based indoor localization on smartphone. IEEE Trans. Mobile Comput. 2016, 15, 1877–1892. [Google Scholar] [CrossRef]
- Yang, Z.; Wu, C.; Zhou, Z.; Zhang, X.; Wang, X.; Liu, Y. Mobility increases localizability: A survey on wireless indoor localization using inertial sensors. ACM Comput. Surv. 2015, 47. [Google Scholar] [CrossRef]
- Wu, C.; Yang, Z.; Liu, Y.; Xi, W. WILL: Wireless indoor localization without site survey. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 839–848. [Google Scholar] [CrossRef]
- Goyal, P.; Ribeiro, V.J.; Saran, H.; Kumar, A. Strap-down Pedestrian Dead-Reckoning System. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011. [Google Scholar]
- Huang, B.; Qi, G.; Yang, X.; Zhao, L.; Zou, H. Exploiting cyclic features of walking for pedestrian dead reckoning with unconstrained smartphones. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Heidelberg, Germany, 12–16 September 2016; pp. 374–385. [Google Scholar]
- Kang, W.; Nam, S.; Han, Y.; Lee, S. Improved Heading Estimation for Smartphone-Based Indoor Positioning Systems. In Proceedings of the 2012 IEEE 23rd International Symposium on Personal, Indoor and Mobile Radio Communications—(PIMRC), Sydney, Australia, 9–12 September 2012; pp. 2449–2453. [Google Scholar]
- Bao, H.; Wong, W.-C. A Indoor Dead-Reckoning Algorithm with Map Matching. In Proceedings of the 9th International Wireless Communications and Mobile Computing Conference (IWCMC), Sardinia, Italy, 1–5 July 2013. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 63, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their application. Neurocomputing 2017, 203, 11–26. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Gabbouj, M. Real-time patient-specific ECG classification by 1D convolutional neural networks. IEEE Trans. Biomed. Eng. 2015, 63, 664–675. [Google Scholar] [CrossRef] [PubMed]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-time motor fault detection by 1-D convolutional neural networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 338, 154–170. [Google Scholar] [CrossRef]
- Ha, S.; Choi, S. Convolutional Neural Networks for Human Activity Recognition Using Multiple Accelerometer and Gyroscope Sensors. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 381–388. [Google Scholar]
- Ordonez, F.J.; Roggen, D. Deep convolutional and LSTM recurrent neural network for multimodal wearable activity recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.; Hu, S.; Zhao, Y.; Zhang, A.; Abdelzaher, T. Deepsense: A Unified Deep Learning Framework for Time-Series Mobile Sensing Data Processing. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 351–360. [Google Scholar]
- Edel, M.; Koppe, E. An Advanced Method for Pedestrian Dead Reckoning Using Blstm-Rnns. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015. [Google Scholar]
- Xing, H.; Li, J.; Hou, B.; Zhang, Y.; Guo, M. Pedestrian Stride Length Estimation from IMU measurements and ANN based algorithm. J. Sens. 2017, 2017, 6091261. [Google Scholar] [CrossRef]
- Hannink, J.; Kautz, T.; Pasluosta, C.F.; Barth, J.; Schulein, S.; GaBmann, K.G.; Klucken, J.; Eskofier, B.M. Mobile stride length estimation with deep convolutional neural network. IEEE J. Biomed. Health Inf. 2018, 22, 354–362. [Google Scholar] [CrossRef] [PubMed]
- Hannink, J.; Kautz, T.; Pasuosta, C.F.; Gabmann, K.-G.; Kluchen, J.; Eskofier, B.M. Sensor-based gait parameter extraction with deep convolutional network. IEEE J. Biomed. Health Inf. 2017, 21, 85–93. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Chen, W.; Chen, Y. Multi-scale convolutional neural networks for time series classification. arXiv, 2016; arXiv:1603.06995v4. [Google Scholar]
- Lecun, Y.; Bottou, L.; Orr, G.B.; Muller, K.-R. Efficient backprop. In Neural Networks: Tricks of the Trade LNCS; Springer: Berlin, Germany, 2012; pp. 9–48. [Google Scholar]
- Kang, J.; Park, Y.-J.; Lee, J.; Wang, S.-H.; Eom, D.-S. Novel leakage detection by ensemble CNN-SVM and graph-based localization in water distribution systems. IEEE Trans. Ind. Electron. 2018, 65, 4279–4289. [Google Scholar] [CrossRef]
- Hak, L.; Houdijk, H.; Beek, P.J.; Dieen, J.H.V. Steps to take to enhance gait stability: The effect of stride frequency, stride length, and walking speed on local dynamic stability and margins of stability. PLoS ONE 2013, 8, e082842. [Google Scholar] [CrossRef] [PubMed]
- Sutherland, D. The development of mature gait. Gait Posture 1997, 6, 163–170. [Google Scholar] [CrossRef]
- Parisi, G.I.; Tani, J.; Weber, C.; Wermter, S. Lifelong learning of human actions with deep neural network self-organization. Neural Netw. 2017, 96, 137–149. [Google Scholar] [CrossRef] [PubMed]
| Structure | Input (I) | Filter | Depth | Stride | Output (O) | Number of Parameters |
|---|---|---|---|---|---|---|
| Conv1 + Relu | 200 × 1 × 3 | 4 × 1 | 64 | 1 | 197 × 1 × 64 | (4 × 1 × 3 + 1) × 64 = 832 |
| Max Pooling (dropout 0.2) | 197 × 1 × 64 | 2 × 1 | 98 × 1 × 64 | |||
| Conv2 + Relu | 98 × 1 × 64 | 4 × 1 | 64 | 1 | 95 × 1 × 64 | (4 × 1 × 64 + 1) × 64 = 16,448 |
| Max Pooling (dropout 0.2) | 95 × 1 × 64 | 2 × 1 | 47 × 1 × 64 | |||
| Conv3 + Relu | 47 × 1 × 64 | 4 × 1 | 64 | 1 | 44 × 1 × 64 | (4 × 1 × 64 + 1) × 64 = 16,448 |
| GRU | 44 × 1 × 64 | 128 | 2 × 3(I2 + I × O + I) = 49,758,720 | |||
| Output Classes | 128 | 5 | 128 × 5 = 640 | |||
| Overall | 49,793,088 |
| Type | Distance (m)/Mean ± Std | ||||
|---|---|---|---|---|---|
| 25 m | 50 m | 75 m | 100 m | Average | |
| Handheld | 1.53 ± 0.45 | 0.83 ± 0.27 | 1.29 ± 0.22 | 2.44 ± 0.56 | 1.52 |
| Swing | 2.55 ± 0.49 | 2.25 ± 0.20 | 1.23 ± 0.28 | 1.94 ± 0.32 | 1.99 |
| 2.28 ± 0.82 | 2.88 ± 0.49 | 1.64 ± 0.68 | 2.05 ± 0.88 | 1.96 | |
| Mix | 2.57 ± 0.55 | 0.87 ± 0.26 | 1.26 ± 0.48 | 1.61 ± 0.45 | 1.58 |
| Average | 1.79 m | 1.28 m | 1.50 m | 2.08 m | 1.66 m |
| Models | Evaluation Parameters | ||||
|---|---|---|---|---|---|
| Distance Error (%) | Accuracy | Precision | Recall | F − 1 Score | |
| ANN | 6.466 | 0.668 | 0.564 | 0.536 | 0.538 |
| CNN | 3.599 | 0.878 | 0.852 | 0.848 | 0.87 |
| Vanilla RNN | 5.676 | 0.714 | 0.643 | 0.633 | 0.629 |
| LSTM | 2.441 | 0.904 | 0.895 | 0.888 | 0.887 |
| GRU | 2.379 | 0.903 | 0.890 | 0.885 | 0.885 |
| CNN + GRU | 1.860 | 0.925 | 0.915 | 0.913 | 0.912 |
| Multiscale CNN + GRU with classification (Proposed) | 1.278 | 0.949 | 0.943 | 0.942 | 0.942 |
| Multiscale CNN + GRU with regression | 1.572 | - | |||
| Types | Subject 1 | Subject 2 | Subject 3 | Subject 4 | Subject 5 | Subject 6 | Subject 7 | Subject 8 | Subject 9 |
|---|---|---|---|---|---|---|---|---|---|
| Smartphone | Samsung Galaxy Note 7 | Samsung Galaxy S8 | LG V30 | Samsung Galaxy S7 | LG G6 | LG V30 | Samsung Galaxy Note 7 | Samsung Galaxy S8+ | Samsung Galaxy S7 |
| Dataset configuration for training | 14.4 h, 41 km | 11.1 h, 34 km | 10.1 h, 31 km | 4.0 h, 22 km | 4.9 h, 16 km | 4.3 h, 14 km | 2.2 h, 10 km | 2.4 h, 7 km | 1.3 h, 3.6 km |
| Pedestrian properties | 181 cm, 85 kg, 38 age, male | 175 cm, 68 kg, 30 age, male | 179 cm, 78 kg 30 age, male | 173 cm, 75 kg, 28 age, male | 163 cm, 53 kg, 24 age, female | 177 cm, 79 kg, 35 age, male | 172 cm, 70 kg, 27 age, male | 160 cm, 55 kg, 21 age, female | 161 cm, 48 kg, 28 age, female |
| Models | Subject 1 | Subject 2 | Subject 3 | Subject 4 | Subject 5 | Subject 6 | Subject 7 | Subject 8 | Subject 9 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Proposed Method | Handheld | 1.12 ± 0.14 | 1.01 ± 0.34 | 1.66 ± 0.49 | 2.02 ± 0.33 | 0.89 ± 0.07 | 1.51 ± 0.17 | 1.42 ± 0.14 | 1.98 ± 0.38 | 3.02 ± 0.75 | 1.63 m |
| Swing | 1.05 ± 0.27 | 1.16 ± 0.29 | 1.03 ± 0.15 | 1.99 ± 0.24 | 1.12 ± 0.37 | 1.60 ± 0.40 | 1.45 ± 0.61 | 2.63 ± 0.63 | 3.55 ± 0.64 | 1.74 m | |
| 0.78 ± 0.07 | 0.65 ± 0.15 | 0.87 ± 0.21 | 1.18 ± 0.19 | 1.04 ± 0.21 | 2.37 ± 0.27 | 1.40 ± 0.41 | 2.73 ± 0.35 | 3.42 ± 0.67 | 1.60 m | ||
| Weinberg [12] | Handheld | 12.7 ± 0.74 | 13.8 ± 0.29 | 8.12 ± 1.15 | 12.4 ± 0.67 | 12.3 ± 1.36 | 8.73 ± 1.57 | 4.27 ± 2.71 | 3.67 ± 0.86 | 3.95 ± 0.97 | 8.90 m |
| Swing | 25.26 ± 3.78 | 22.16 ± 4.14 | 29.58 ± 2.70 | 27.05 ± 2.01 | 20.46 ± 2.16 | 25.12 ± 2.21 | 20.88 ± 5.39 | 17.44 ± 3.12 | 16.64 ± 3.17 | 22.73 m | |
| 16.20 ± 0.95 | 18.23 ± 2.09 | 20.30 ± 1.94 | 17.02 ± 2.21 | 25.91 ± 3.29 | 18.18 ± 4.92 | 13.75 ± 2.70 | 12.37 ± 0.94 | 14.20 ± 1.58 | 17.35 m | ||
| Ho et al. [11] | Handheld | 6.30 ± 3.82 | 3.01 ± 3.81 | 4.49 ± 3.00 | 3.48 ± 1.61 | 3.18 ± 1.88 | 3.46 ± 1.22 | 2.43 ± 2.55 | 6.39 ± 3.46 | 4.93 ± 4.25 | 4.19 m |
| Swing | 13.73 ± 2.66 | 18.26 ± 3.40 | 21.65 ± 3.84 | 17.65 ± 3.61 | 20.26 ± 2.62 | 22.14 ± 1.79 | 18.67 ± 3.22 | 20.57 ± 3.71 | 16.39 ± 2.58 | 18.81 m | |
| 17.37 ± 3.89 | 12.63 ± 5.15 | 14.11 ± 1.48 | 15.13 ± 2.19 | 16.35 ± 2.18 | 15.72 ± 5.74 | 10.82 ± 1.07 | 13.63 ± 2.22 | 10.33 ± 2.26 | 14.01 m | ||
| Huang et al. [23] | Handheld | - | - | - | - | - | - | - | - | - | - |
| Swing | 3.24 ± 1.10 | 4.22 ± 2.27 | 11.39 ± 1.90 | 3.38 ± 3.00 | 16.03 ± 6.14 | 15.31 ± 6.14 | 7.25 ± 4.23 | 12.21 ± 3.90 | 4.24 ± 1.81 | 8.58 m | |
| - | - | - | - | - | - | - | - | - | - | ||
| Xing et al. [35] | Handheld | 2.50 ± 0.52 | 2.75 ± 0.26 | 3.19 ± 0.70 | 3.61 ± 1.68 | 4.28 ± 0.97 | 5.93 ± 0.40 | 3.98 ± 2.13 | 5.53 ± 0.94 | 5.76 ± 1.06 | 4.17 m |
| Swing | 4.17 ± 0.95 | 3.94 ± 1.92 | 5.93 ± 0.38 | 4.08 ± 0.41 | 5.69 ± 2.17 | 6.13 ± 0.68 | 7.54 ± 0.81 | 6.57 ± 1.00 | 7.48 ± 0.66 | 5.73 m | |
| 5.21 ± 0.98 | 4.94 ± 0.97 | 7.64 ± 1.11 | 6.42 ± 1.76 | 7.14 ± 1.15 | 8.02 ± 1.62 | 8.83 ± 0.43 | 9.29 ± 2.52 | 8.28 ± 1.12 | 7.31 m | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.; Lee, J.; Eom, D.-S. Smartphone-Based Traveled Distance Estimation Using Individual Walking Patterns for Indoor Localization. Sensors 2018, 18, 3149. https://doi.org/10.3390/s18093149
Kang J, Lee J, Eom D-S. Smartphone-Based Traveled Distance Estimation Using Individual Walking Patterns for Indoor Localization. Sensors. 2018; 18(9):3149. https://doi.org/10.3390/s18093149
Chicago/Turabian StyleKang, Jiheon, Joonbeom Lee, and Doo-Seop Eom. 2018. "Smartphone-Based Traveled Distance Estimation Using Individual Walking Patterns for Indoor Localization" Sensors 18, no. 9: 3149. https://doi.org/10.3390/s18093149
APA StyleKang, J., Lee, J., & Eom, D.-S. (2018). Smartphone-Based Traveled Distance Estimation Using Individual Walking Patterns for Indoor Localization. Sensors, 18(9), 3149. https://doi.org/10.3390/s18093149





