A Novel Tri-Axial MEMS Gyroscope Calibration Method over a Full Temperature Range
Abstract
:1. Introduction
2. Lagrange Interpolation
3. Calibration Method
3.1. Error Model
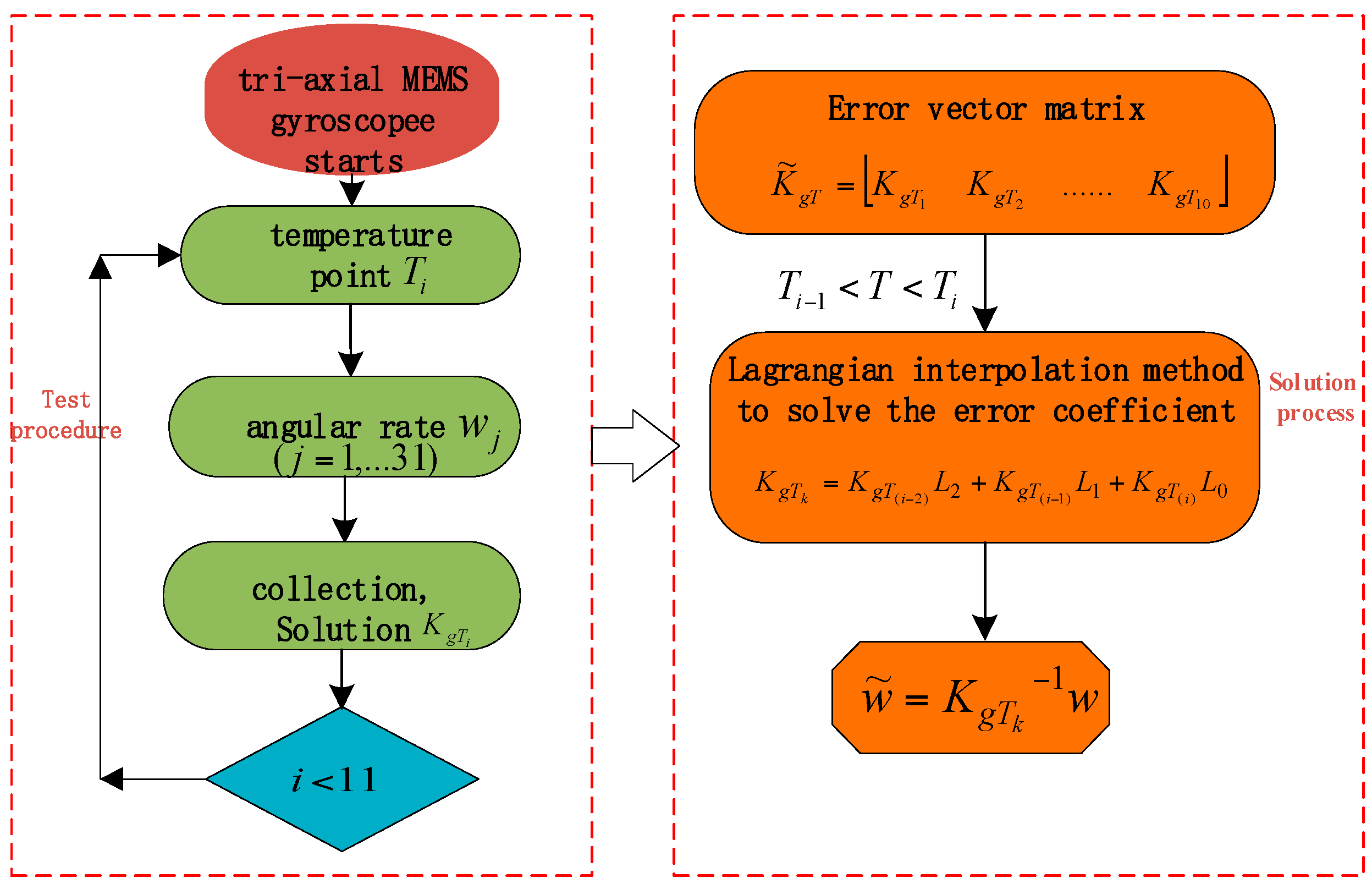
3.2. Calibration Scheme
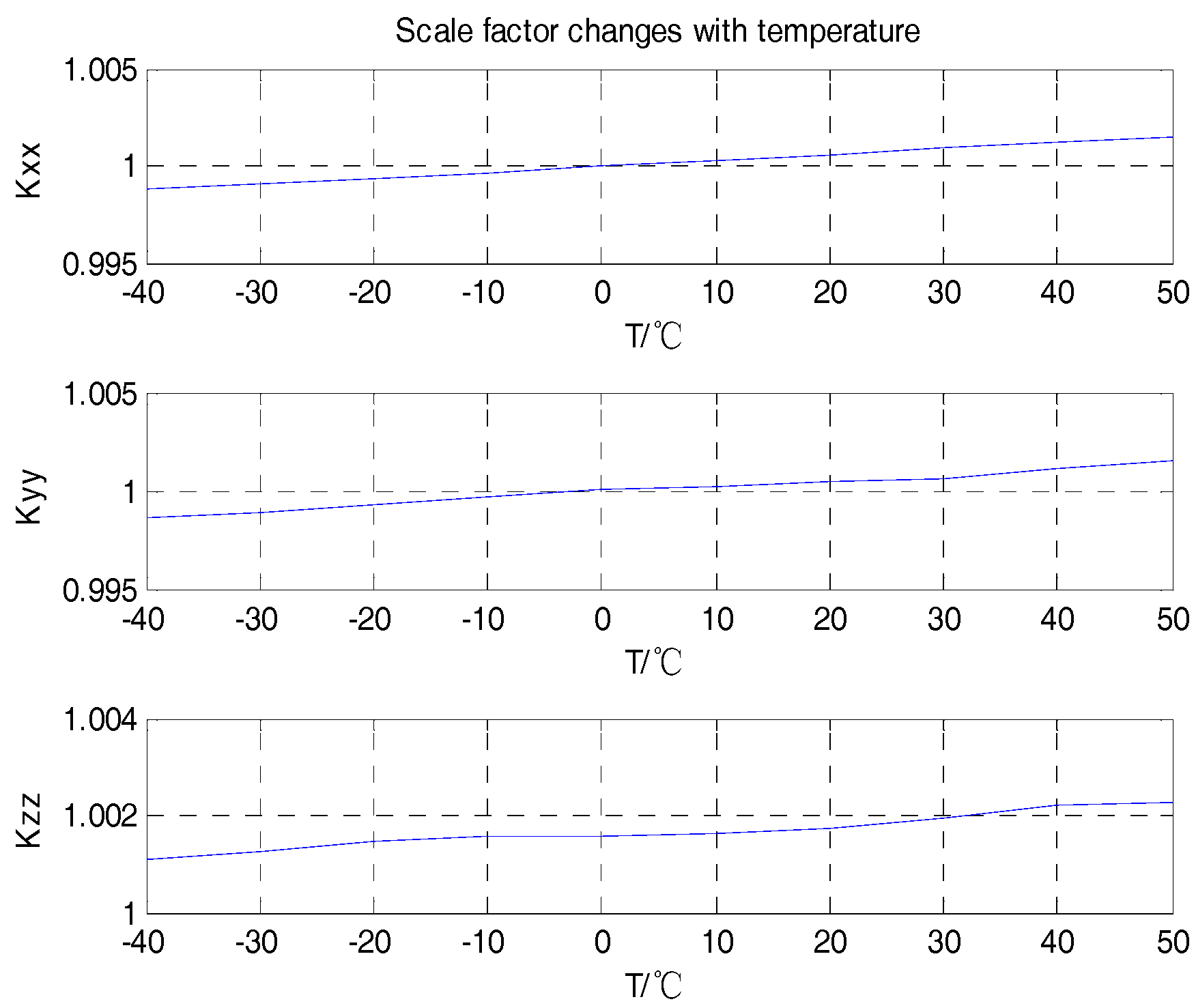
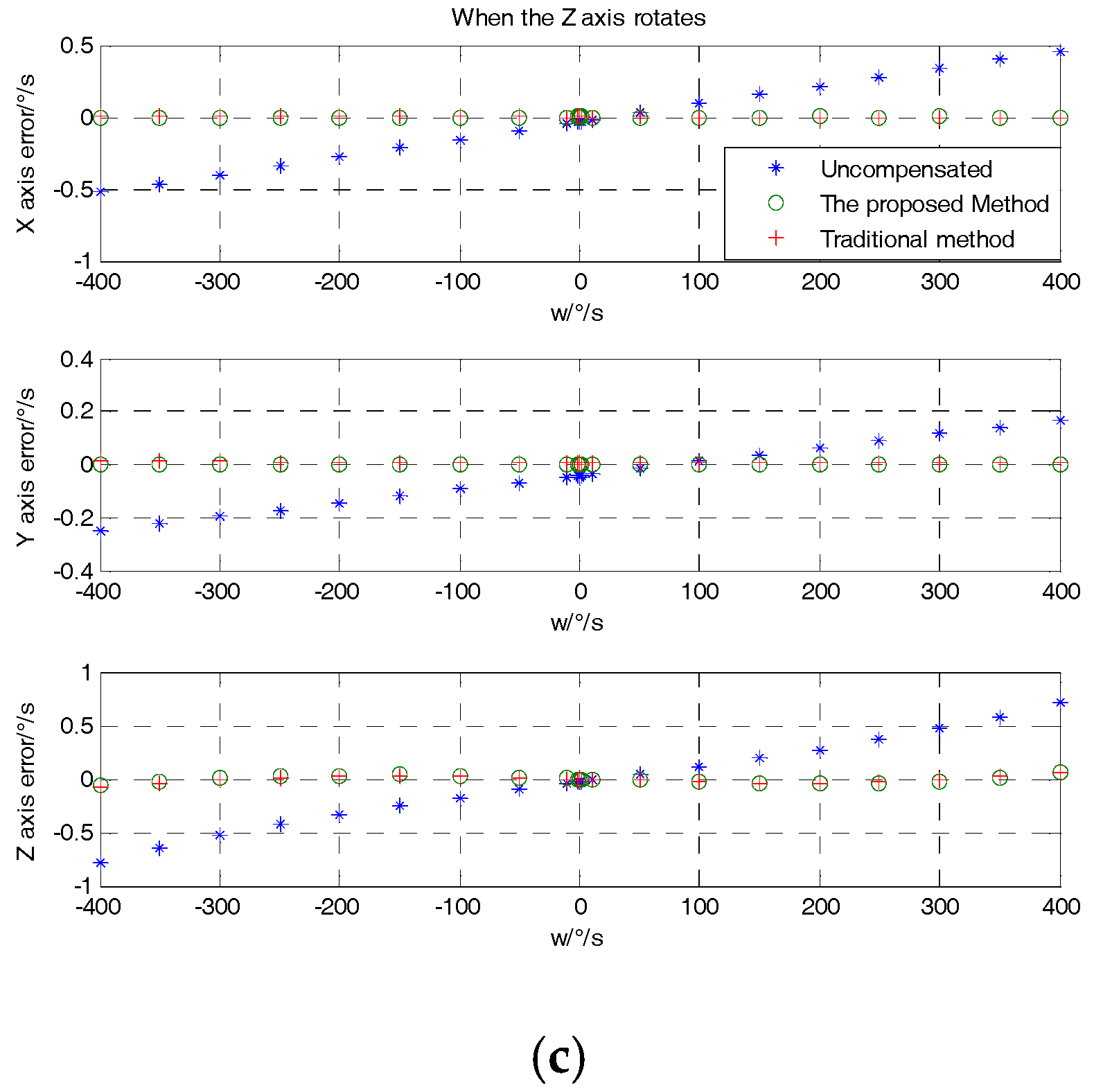
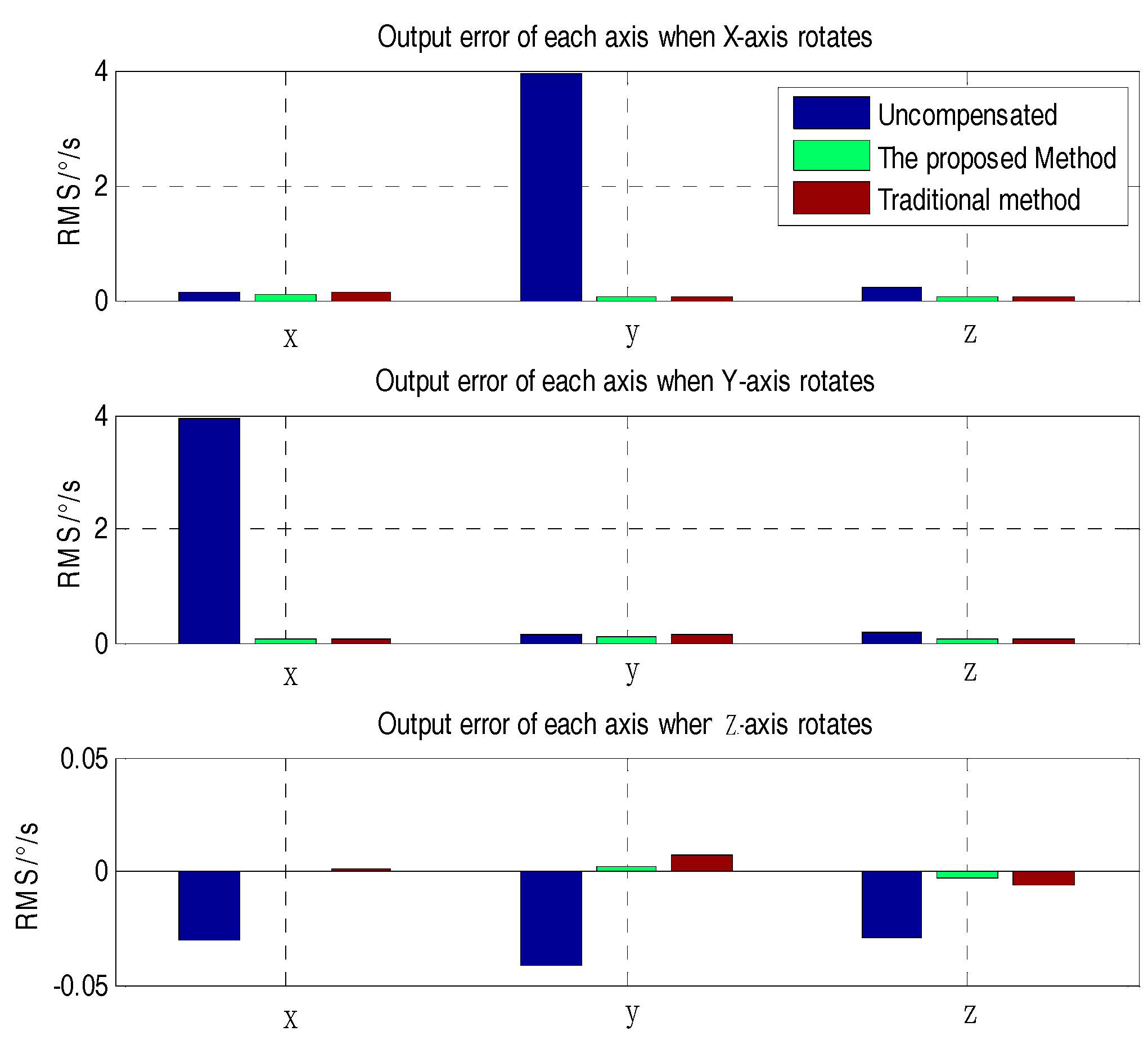
4. Test Results and Analysis
5. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- El-Sheimy, N.; Hou, H.; Niu, X. Analysis and modeling of inertial sensors using Allan variance. IEEE Trans. Instrum. Meas. 2008, 57, 140–149. [Google Scholar] [CrossRef]
- Delgado, J.V.; Silva, P.; Quiroz, C. Automatic calibration of low cost inertial gyroscopes with a PTU. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 121–125. [Google Scholar]
- Zeng, M.; Zou, Z.; Yu, Z. An investigation on the second-order drift error coefficient calibration of gyroscope by vibration table. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 5374–5380. [Google Scholar]
- Golovan, A.; Kozlov, A.; Tarygin, I. Calibration of a 3-axis hemispherical resonator gyro assembly. In Proceedings of the 2017 8th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 19–22 June 2017; pp. 393–396. [Google Scholar]
- Wang, Q.; Wang, L.X.; Qin, W.W. Continuous Self-Calibration of Inertial Platform Based on Dual Extended Kalman Filter. J. Astronaut. 2017, 38, 621–629. [Google Scholar] [CrossRef]
- Li, R.B.; Liu, J.Y.; Sun, Y.R. MEMS-IMU configuration and its inertial sensors’ calibration for installation errors. J. Chin. Inert. Technol. 2007, 15, 526–529. [Google Scholar] [CrossRef]
- Eminoglu, B.; Kline, M.H.; Izyumin, I. Background calibrated MEMS gyroscope. In Proceedings of the 2014 IEEE Sensors, Valencia, Spain, 2–5 November 2014; pp. 922–925. [Google Scholar]
- Prikhodko, P.; Gregory, J.A.; Merritt, C. In-run bias self-calibration for low-cost MEMS vibratory gyroscopes. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014; pp. 515–518. [Google Scholar]
- Shen, S.C.; Chen, C.J.; Huang, H.J. A new calibration method for MEMS inertial sensor module. In Proceedings of the 2010 11th IEEE International Workshop on Advanced Motion Control (AMC), Nagaoka, Japan, 22–24 March 2010; pp. 106–111. [Google Scholar]
- Jia, Y.; Li, S.; Qin, Y. Error Analysis and Compensation of MEMS Rotation Modulation Inertial Navigation System. IEEE. Sens. J. 2018, 18, 2023–2030. [Google Scholar] [CrossRef]
- Han, X.; Hu, S.M.; Luo, H. A new method for bias calibration of laser gyros using a single-axis turning table. Optik 2013, 124, 5588–5590. [Google Scholar] [CrossRef]
- Zhu, Y.Q.; Wang, L.L.; Wang, X.L. A D-optimal Multi-position Calibration Method for Dynamically Tuned Gyroscopes. Chin. J. Aeronaut. 2011, 24, 210–218. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Y.; Su, Y. Research on the Calibration Method of Micro Inertial Measurement Unit for Engineering Application. J. Sens. 2016, 1, 1–11. [Google Scholar] [CrossRef]
- Wang, S.M.; Meng, N. A new Multi-position calibration method for gyroscope’s drift coefficients on centrifuge. Aerosp. Sci. Technol. 2017, 68, 104–108. [Google Scholar] [CrossRef]
- Li, J.; Min, D. Fuzzy Modeling and Compensation of Scale Factor for MEMS Gyroscope. In Proceedings of the 2010 International Conference on Digital Manufacturing & Automation, Changsha, China, 18–20 December 2010; IEEE Computer Society: Washington, DC, USA, 2010; pp. 766–771. [Google Scholar]
- Secer, G.; Barshan, B. Improvements in deterministic error modeling and calibration of inertial sensors and magnetometers. Sens. Actuators A Phys. 2016, 247, 522–538. [Google Scholar] [CrossRef] [Green Version]
- Tedaldi, D.; Pretto, A.; Menegatti, E. A robust and easy to implement method for IMU calibration without external equipments. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 3042–3049. [Google Scholar]
- Kim, M.S.; Yu, S.B.; Lee, K.S. Development of a high-precision calibration method for inertial measurement unit. Int. J. Precis. Eng. Man. 2014, 15, 567–575. [Google Scholar] [CrossRef]
- Lee, D.; Lee, S.; Park, S. Test and error parameter estimation for MEMS-based low cost IMU calibration. Int. J. Precis. Eng. Man. 2011, 12, 597–603. [Google Scholar] [CrossRef]
- Eldiasty, M.; Elrabbany, A.; Pagiatakis, S. Temperature variation effects on stochastic characteristics for low-cost MEMS-based inertial sensor error. Meas. Sci. Technol. 2007, 18, 3321–3332. [Google Scholar] [CrossRef]
- Aggarwal, P.; Syed, Z.; Niu, X. A Standard Testing and Calibration Procedure for Low Cost MEMS Inertial Sensors and Units. J. Navig. 2008, 61, 323–336. [Google Scholar] [CrossRef]
- Sasani, S.; Asgari, J.; Amiri-Simkooei, A.R. Improving MEMS-IMU/GPS integrated systems for land vehicle navigation applications. GPS Solut. 2016, 20, 89–100. [Google Scholar] [CrossRef]
- Li, W.H.; Li, J.; Yang, W.Q. A Compentation Method for Temperature Drift Error of MEMS Gyroscopes. Micronanoelectron. Technol. 2017, 54, 533–538. [Google Scholar] [CrossRef]
- Julius, O.S. Lagrange_Interpolation. In Interpolation of Functions; Center for Computer Research in Music and Acoustics (CCRMA), Stanford University: Stanford, CA, USA, 1990; Volume 4, pp. 5–36. [Google Scholar]
- Mofdi, E.A.; Mohammed, S. A finite element semi-Lagrange method with L2 interpolation. Int. J Numer. Methods Eng. 2012, 90, 1485–1507. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, X.X.; Ellero, M. Analysis of interpolation schemes for the accurate estimation of energy spectrum in Lagrange methods. Comput. Fluids 2013, 82, 122–131. [Google Scholar] [CrossRef]
- Labanda, N.A.; Giusti, S.M.; Luccioni, B.M. A path-following technique implemented in a Lagrange formulation to model quasi-brittle fracture. Eng. Fract. Mech. 2018, 194, 319–336. [Google Scholar] [CrossRef]
- Zhou, J.W.; Zhang, J. Lagrange Interpolation Model and Statistical Data Inspection and Application. Stat. Dec. 2016, 5, 78–80. [Google Scholar] [CrossRef]
- He, Y.J.; Yang, L. Analysis of interpolation results on GPS/IGS precise ephemeris based on Lagrange interpolation. Eng. Surv. Mapp. 2011, 20, 60–66. [Google Scholar] [CrossRef]
- Ye, S.; Ding, Y.; Wang, X. Adaptive Image Scaling with Third-order Lagrange Interpolation. J. Chin. Comput. Syst. 2012, 33, 1278–1283. [Google Scholar] [CrossRef]
- Chatfield, A.B. Fundamentals of High Accuracy Inertial Navigation; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1997; Volume 5, pp. 79–107. [Google Scholar]
- Arriaga, C.; Muñiz, E.; Morilla, A. A chronology of interpolation: From ancient astronomy to modern signal and image processing. Proc. IEEE 2002, 90, 319–342. [Google Scholar] [CrossRef]
- Syed, Z.F.; Aggarwal, P.; Goodall, C.; Niu, X.; El-Sheimy, N. A new multi-position calibration method for MEMS inertial navigation systems. Meas. Sci. Technol. 2007, 18, 1897–1907. [Google Scholar] [CrossRef]
- Lai, Y.C.; Jan, S.S.; Hsiao, F.B. Development of a Low-Cost Attitude and Heading Reference System Using a Three-Axis Rotating Platform. Sensors 2010, 10, 2472–2491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fong, W.T.; Ong, S.K.; Nee, A.Y.C. Methods for in-field user calibration of an inertial measurement unit without external equipment. Meas. Sci. Technol. 2008, 19, 817–822. [Google Scholar] [CrossRef]
- Jurman, D.; Jankovec, M.; Kamnik, R.; Marko, T. Calibration and data fusion solution for the miniature attitude and heading reference system. Sens. Actuators A Phys. 2007, 138, 411–420. [Google Scholar] [CrossRef]
- Hwangbo, M.; Kanade, T. Factorization-based calibration method for MEMS inertial measurement unit. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation (ICRA), Pasadena, CA, USA, 19–23 May 2008; pp. 1306–1311. [Google Scholar]
- Qin, Y.Y. Inertial Navigation; Science Press: Xi’an, China, 2014; pp. 288–289. [Google Scholar]

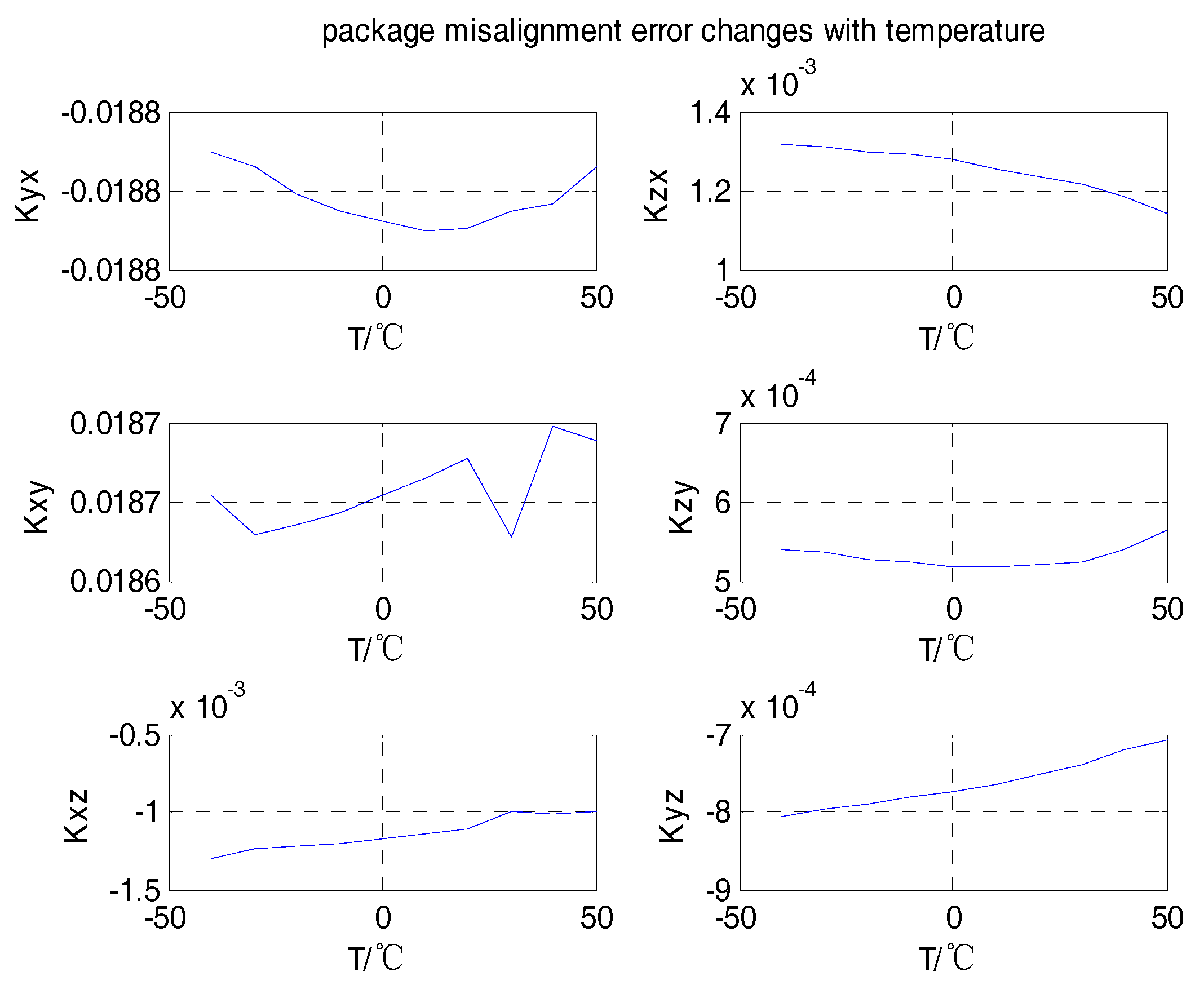
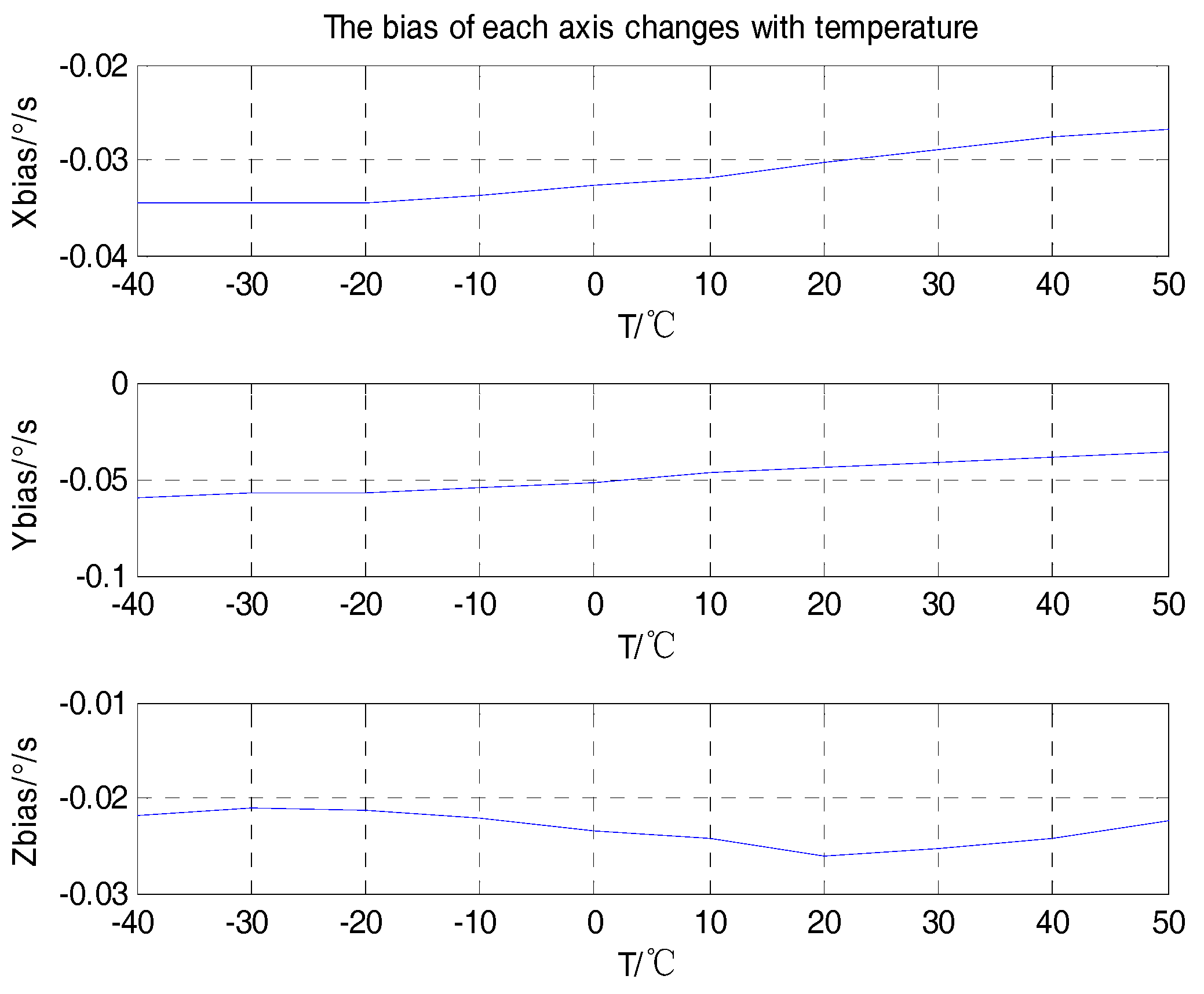
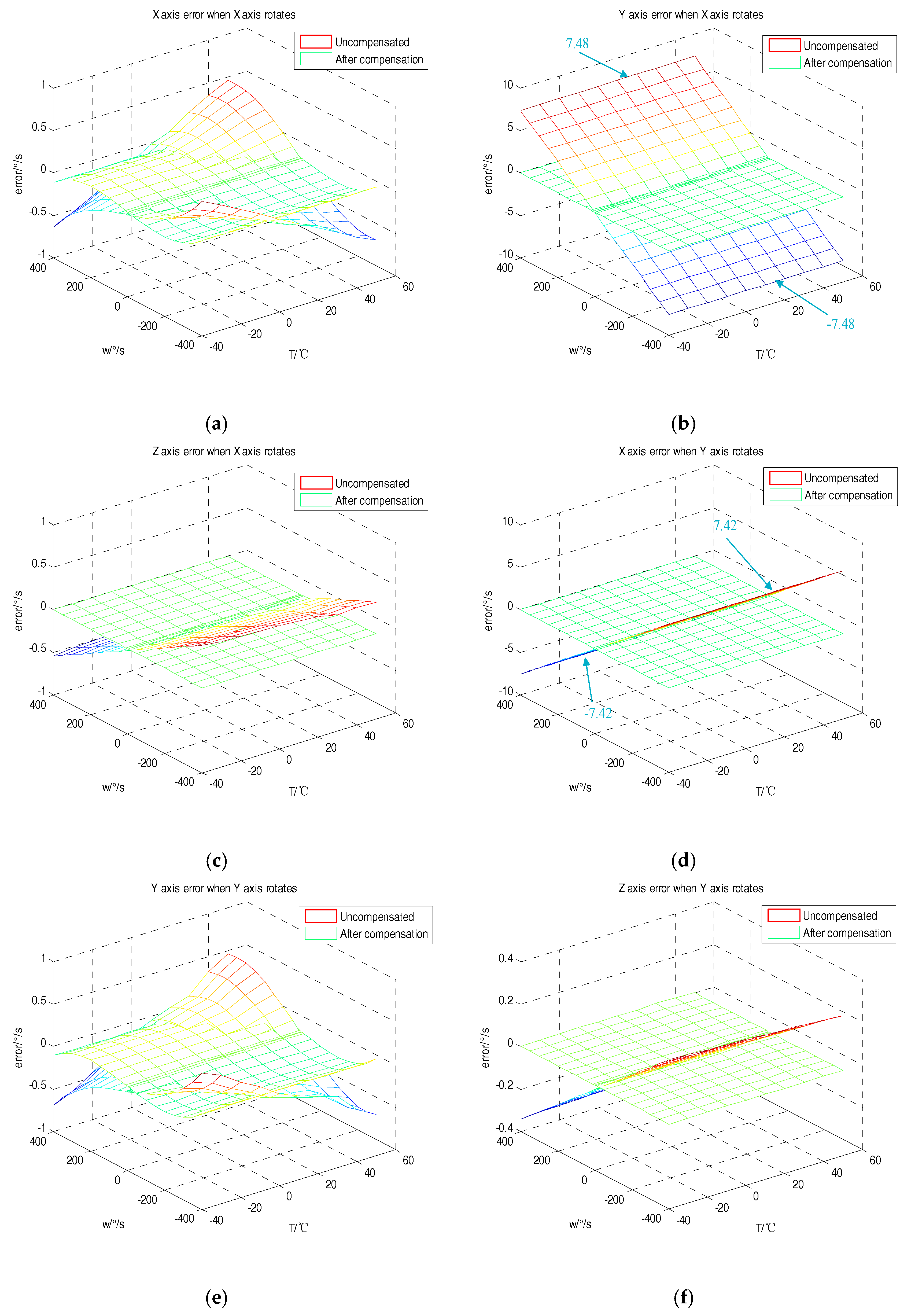
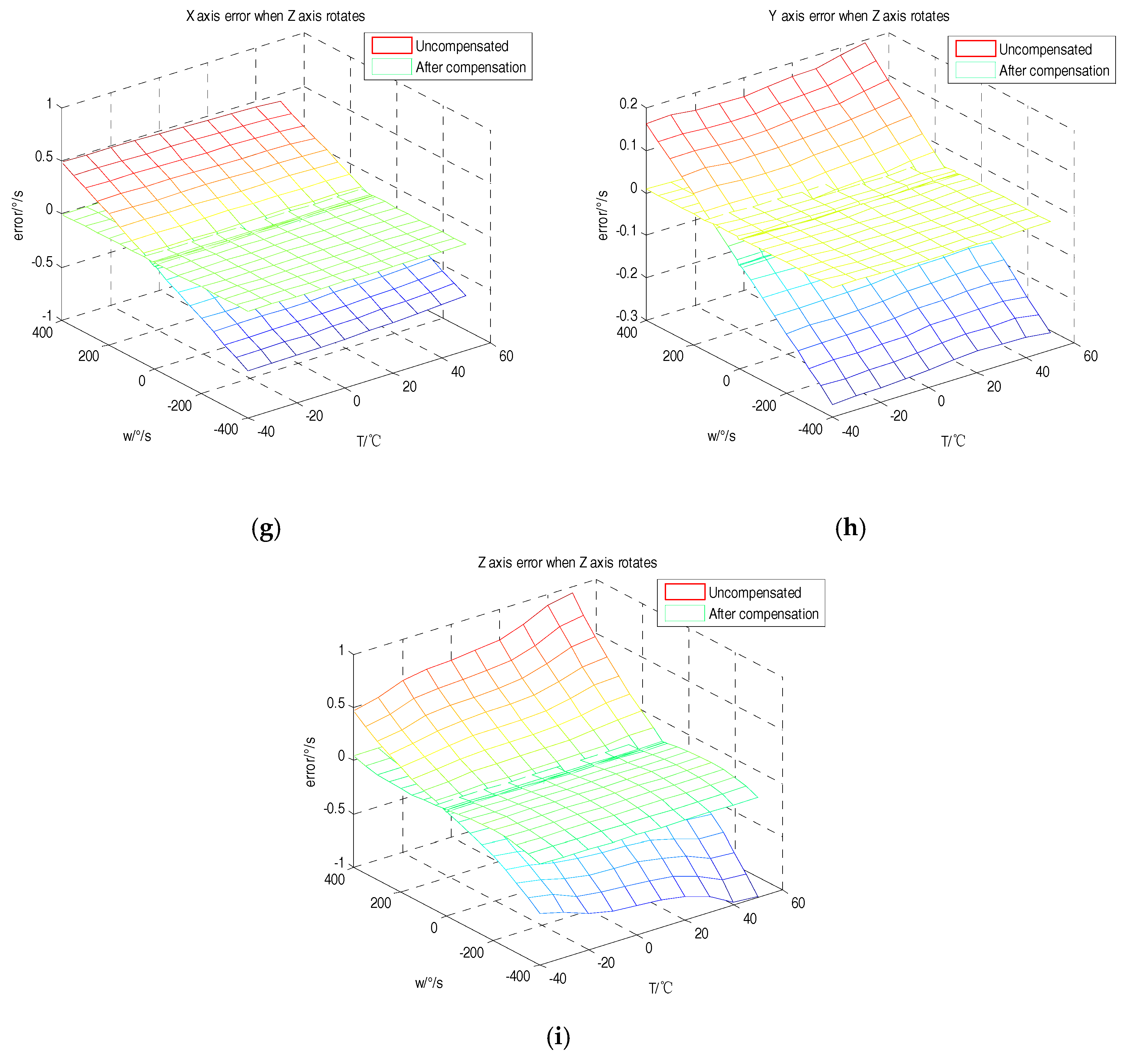
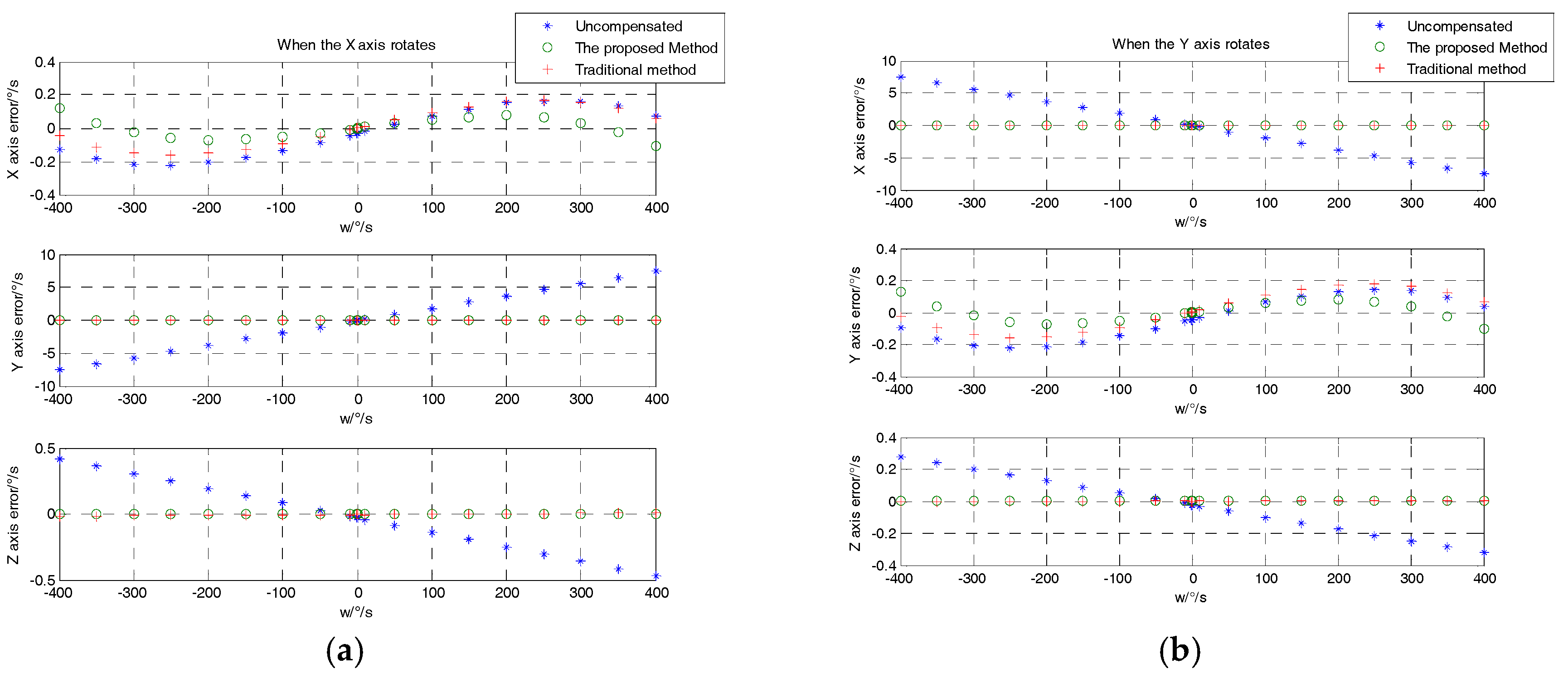
| Number | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Value | −40 | −30 | −20 | −10 | 0 | 10 | 20 | 30 | 40 | 50 |
| 0 | ±0.1 | ±1 | ±10 | ±50 | ±100 | ±150 | ±200 | ±250 | ±300 | ±400 |
| Uncompensated (°/s) | Proposed Method (°/s) | |||
|---|---|---|---|---|
| X-axis rotates | X-axis | Mean | −0.0302 | 0.0013 |
| RMS | 0.1783 | 0.0532 | ||
| Y-axis | Mean | −0.0538 | −0.0050 | |
| RMS | 4.0177 | 0.0011 | ||
| Z-axis | Mean | −0.0242 | −9.9029 × 10−3 | |
| RMS | 0.2459 | 0.0015 | ||
| Y-axis rotates | X-axis | Mean | −0.0330 | −0.0014 |
| RMS | 4.0446 | 0.0018 | ||
| Y-axis | Mean | −0.0471 | 0.0017 | |
| RMS | 0.1789 | 0.0568 | ||
| Z-axis | Mean | −0.0197 | 0.0035 | |
| RMS | 0.1644 | 0.0011 | ||
| Z-axis rotates | X-axis | Mean | −0.0315 | 1.260 × 10−4 |
| RMS | 0.2695 | 9.253 × 10−4 | ||
| Y-axis | Mean | −0.0455 | 0.0033 | |
| RMS | 0.1143 | 0.0016 | ||
| Z-axis | Mean | −0.0257 | −0.0025 | |
| RMS | 0.3621 | 0.0263 | ||
| Uncompensated Method (°/s) | Traditional Method (°/s) | The Proposed Method (°/s) | Compared to Uncompensated Method (%) | Compared to Traditional Method (%) | ||
|---|---|---|---|---|---|---|
| X-axis rotates | X-axis | 0.1453 | 0.1271 | 0.0931 | 35.93 | 26.75 |
| Y-axis | 3.9339 | 0.0474 | 0.0473 | 98.78 | 2.110 | |
| Z-axis | 0.2391 | 0.0492 | 0.0488 | 79.59 | 8.130 | |
| Y-axis rotates | X-axis | 3.9576 | 0.0467 | 0.0467 | 98.82 | 0 |
| Y-axis | 0.1374 | 0.1287 | 0.0957 | 30.35 | 25.64 | |
| Z-axis | 0.1656 | 0.0486 | 0.0486 | 70.65 | 0 | |
| Z-axis rotates | X-axis | −0.0307 | 9.8550 × 10−4 | −4.3855 × 10−4 | 98.57 | 55.50 |
| Y-axis | −0.0418 | 0.0069 | 0.0017 | 95.93 | 75.36 | |
| Z-axis | −0.0292 | −0.0060 | −0.0031 | 89.38 | 48.33 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Zhou, B.; Wang, L.; Xing, H.; Zhang, R. A Novel Tri-Axial MEMS Gyroscope Calibration Method over a Full Temperature Range. Sensors 2018, 18, 3004. https://doi.org/10.3390/s18093004
Yang H, Zhou B, Wang L, Xing H, Zhang R. A Novel Tri-Axial MEMS Gyroscope Calibration Method over a Full Temperature Range. Sensors. 2018; 18(9):3004. https://doi.org/10.3390/s18093004
Chicago/Turabian StyleYang, Haotian, Bin Zhou, Lixin Wang, Haifeng Xing, and Rong Zhang. 2018. "A Novel Tri-Axial MEMS Gyroscope Calibration Method over a Full Temperature Range" Sensors 18, no. 9: 3004. https://doi.org/10.3390/s18093004
APA StyleYang, H., Zhou, B., Wang, L., Xing, H., & Zhang, R. (2018). A Novel Tri-Axial MEMS Gyroscope Calibration Method over a Full Temperature Range. Sensors, 18(9), 3004. https://doi.org/10.3390/s18093004






