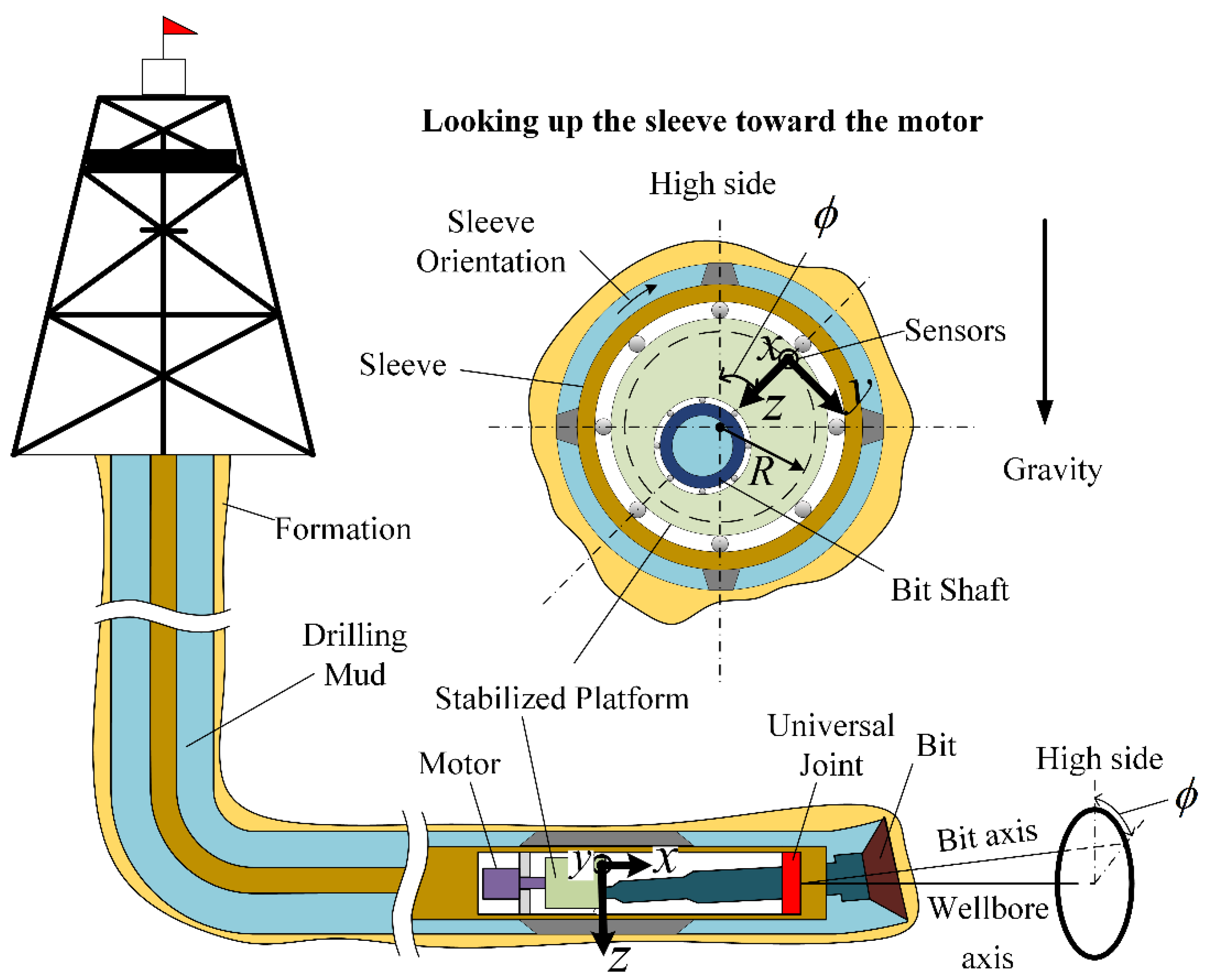
Dynamic Toolface Estimation for Rotary Steerable Drilling System
Abstract
1. Introduction
2. Preliminaries
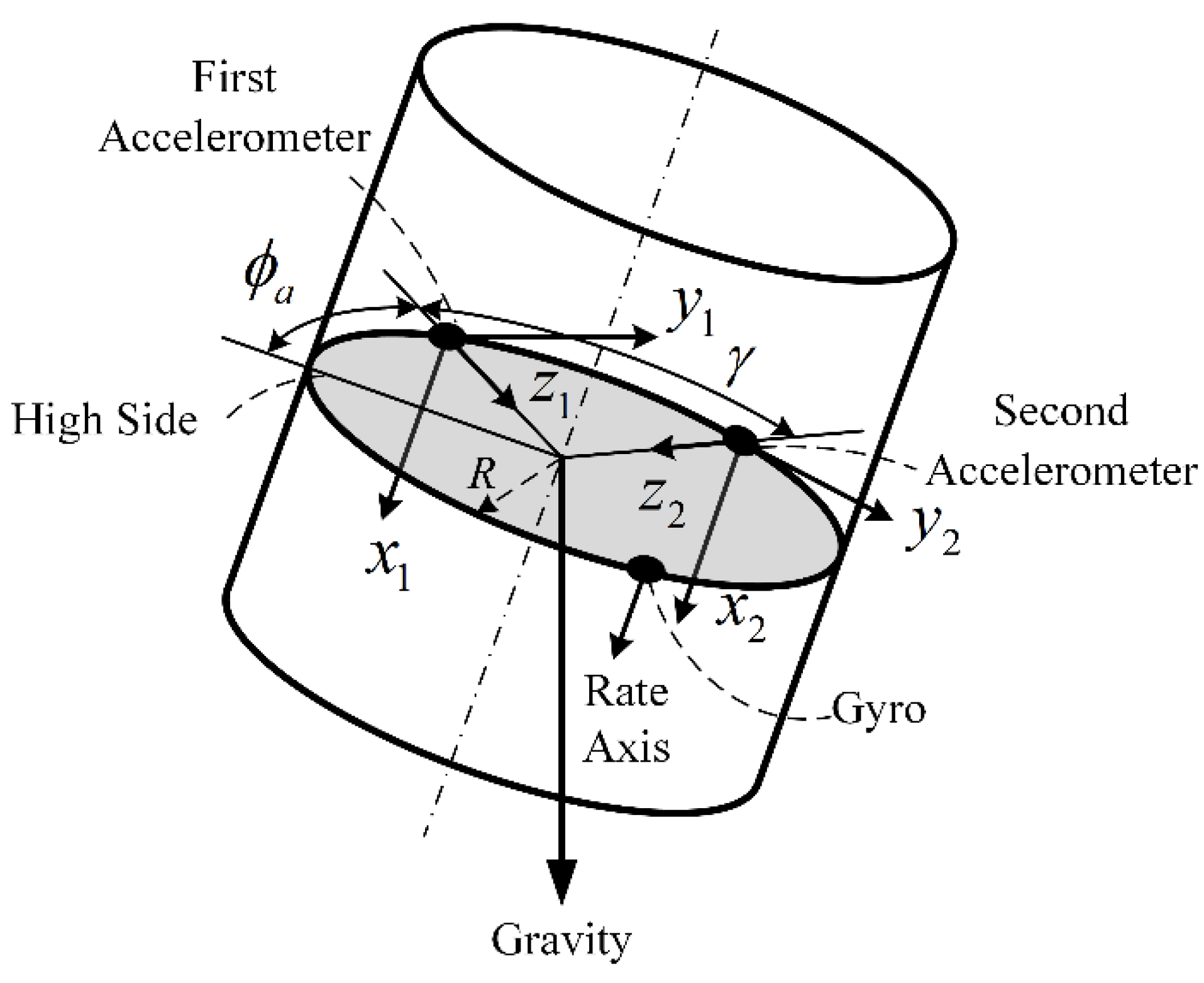
2.1. Toolface Estimation from Tri-Axial Accelerometer
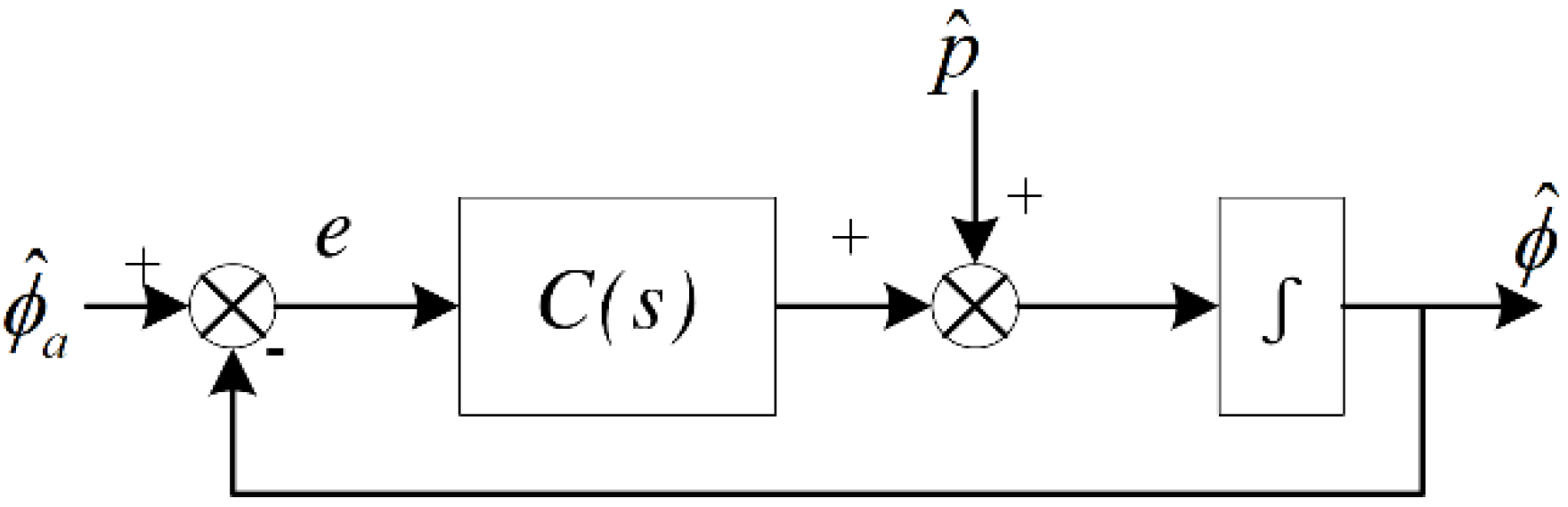
2.2. Toolface Estimation from Gyro
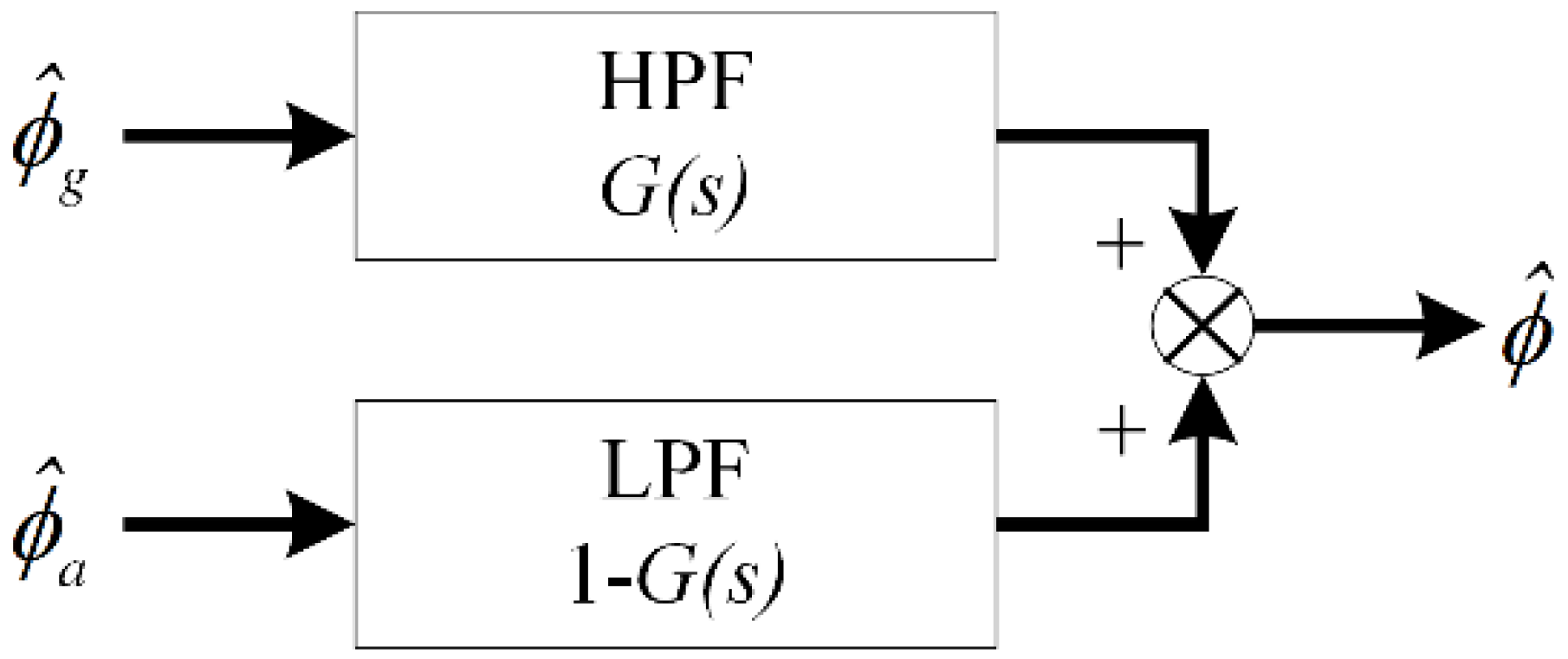
2.3. Complementary Filter
3. Toolface Estimation Method
3.1. Dual-Accelerometer Toolface Measurement
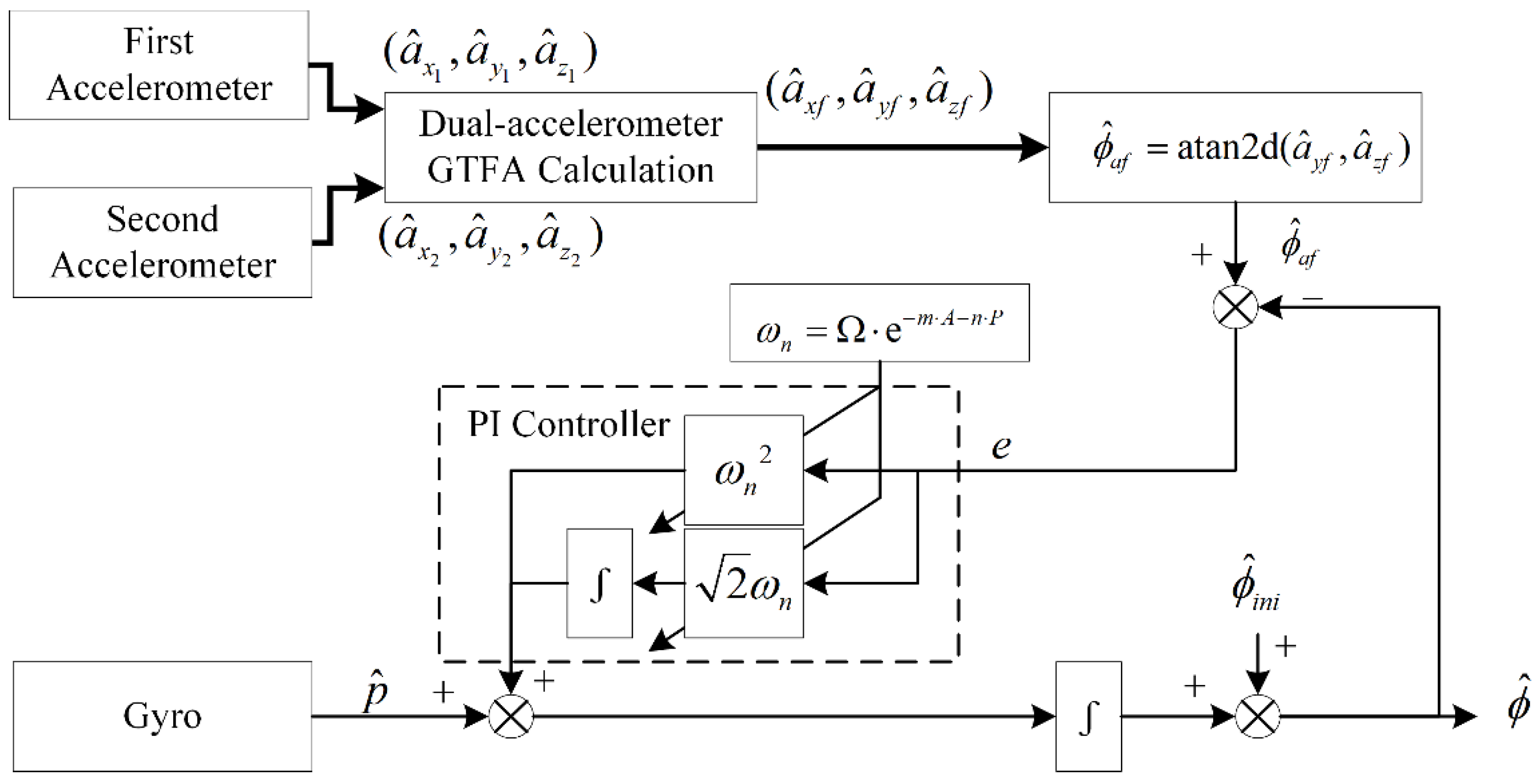
3.2. Toolface Adaptive Nonlinear CF Scheme
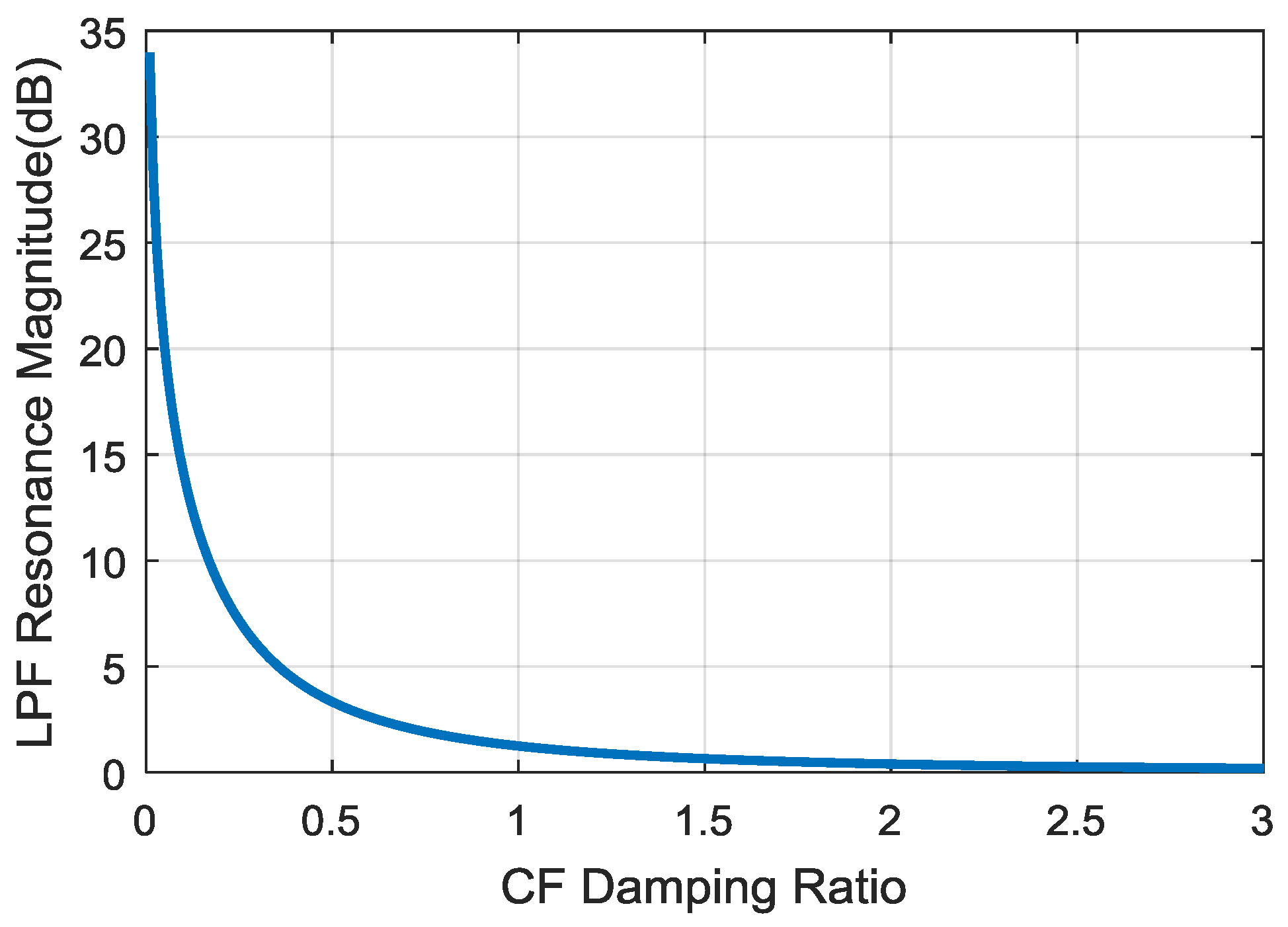
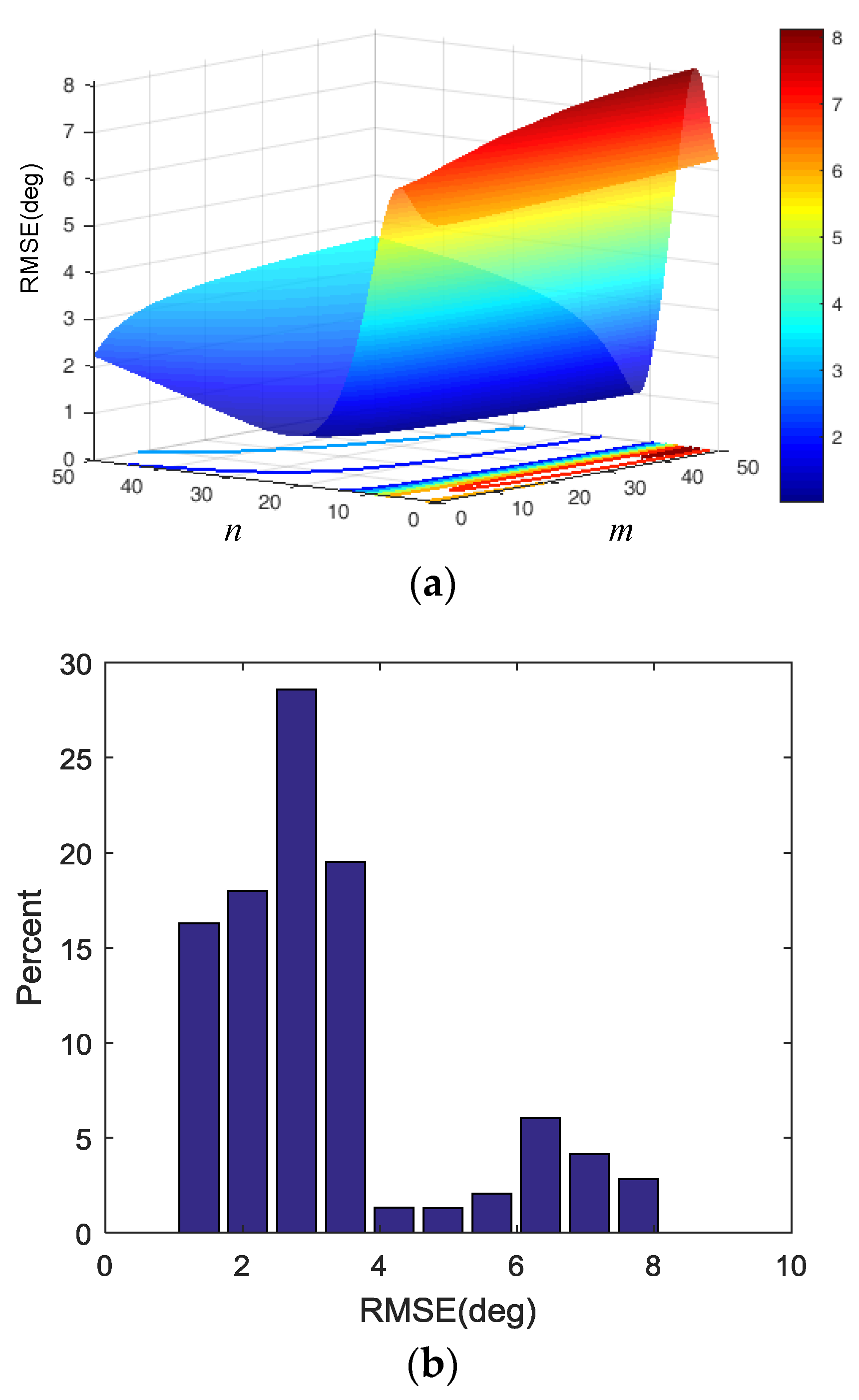
3.2.1. Frequency-Domain Characteristics of Nonlinear CF
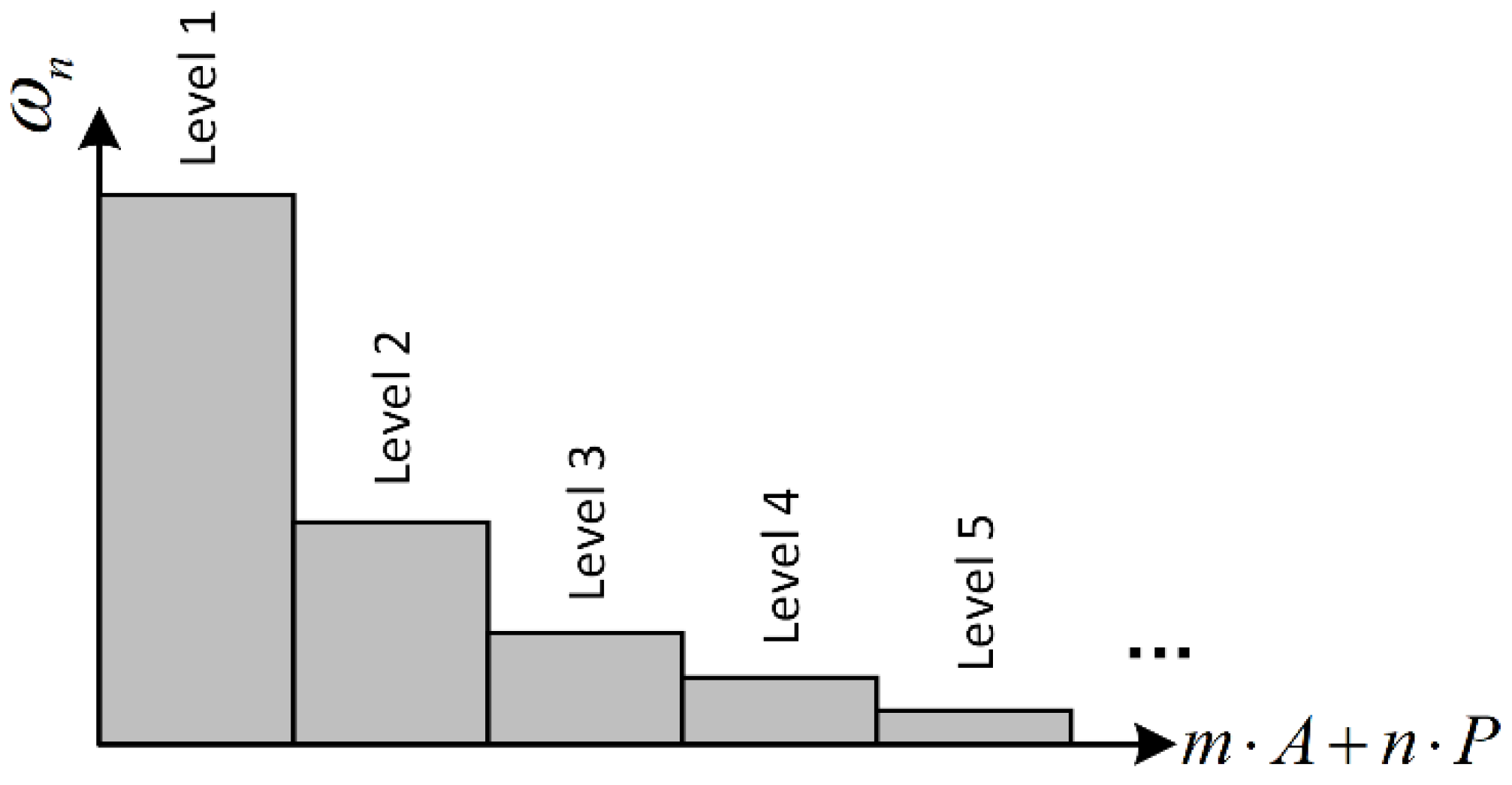
3.2.2. Adaptive Nonlinear CF Scheme
- Step 1:
- Initialization: Acquire data from dual-accelerometer in steady state, calculate by Equation (15), let and ;
- Step 2:
- Start estimation: Calculate and by Equation (15) and Equation (16), respectively;
- Step 3:
- Calculate and by Equation (22), then obtain from Equation (23);
- Step 4:
- Calculate by Equation (24), GOTO step 2 for next instant.
4. Experiments and Results
4.1. DPRSS Prototype for Experiments
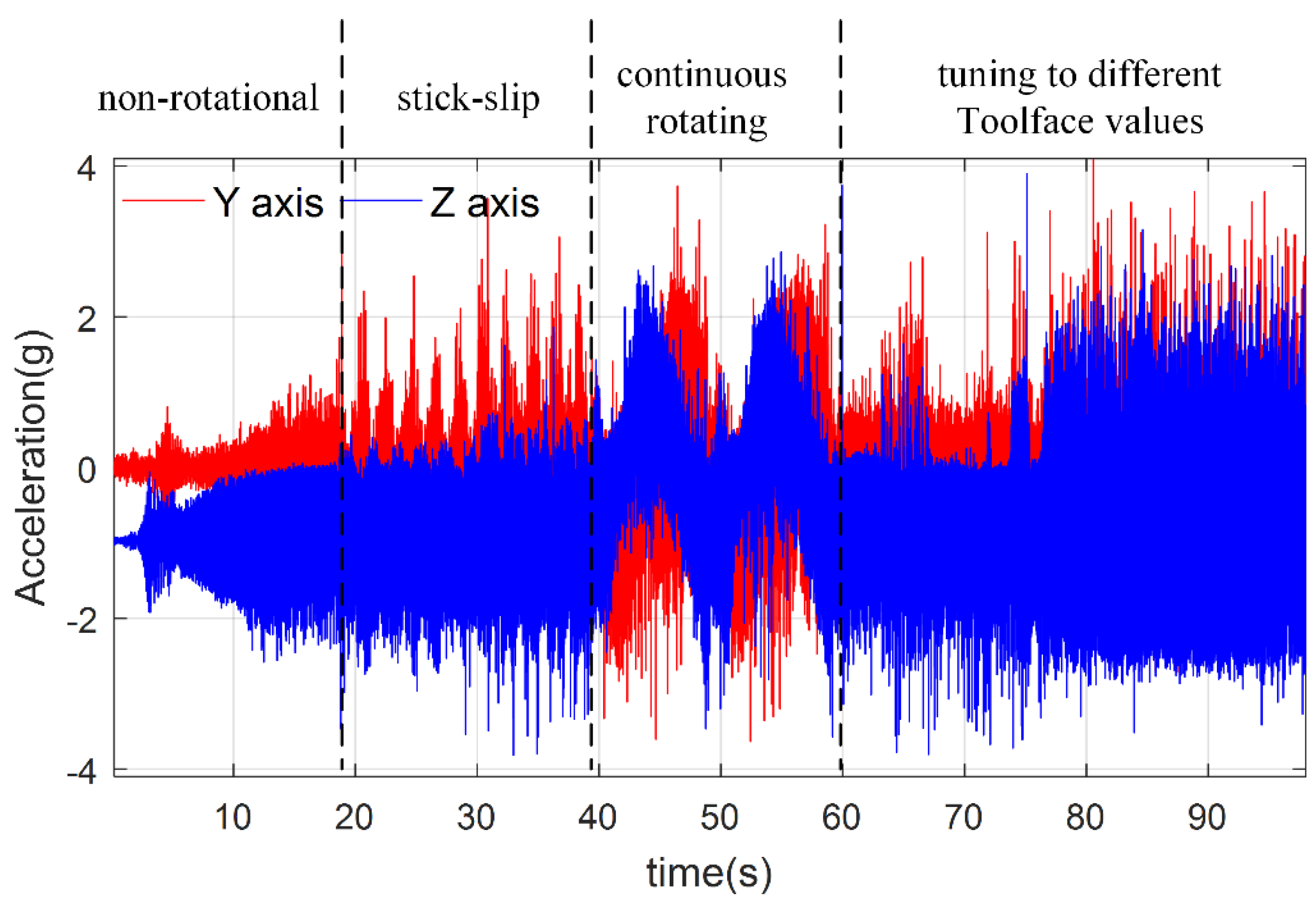
4.2. Dual-Accelerometer Toolface Measurement Test
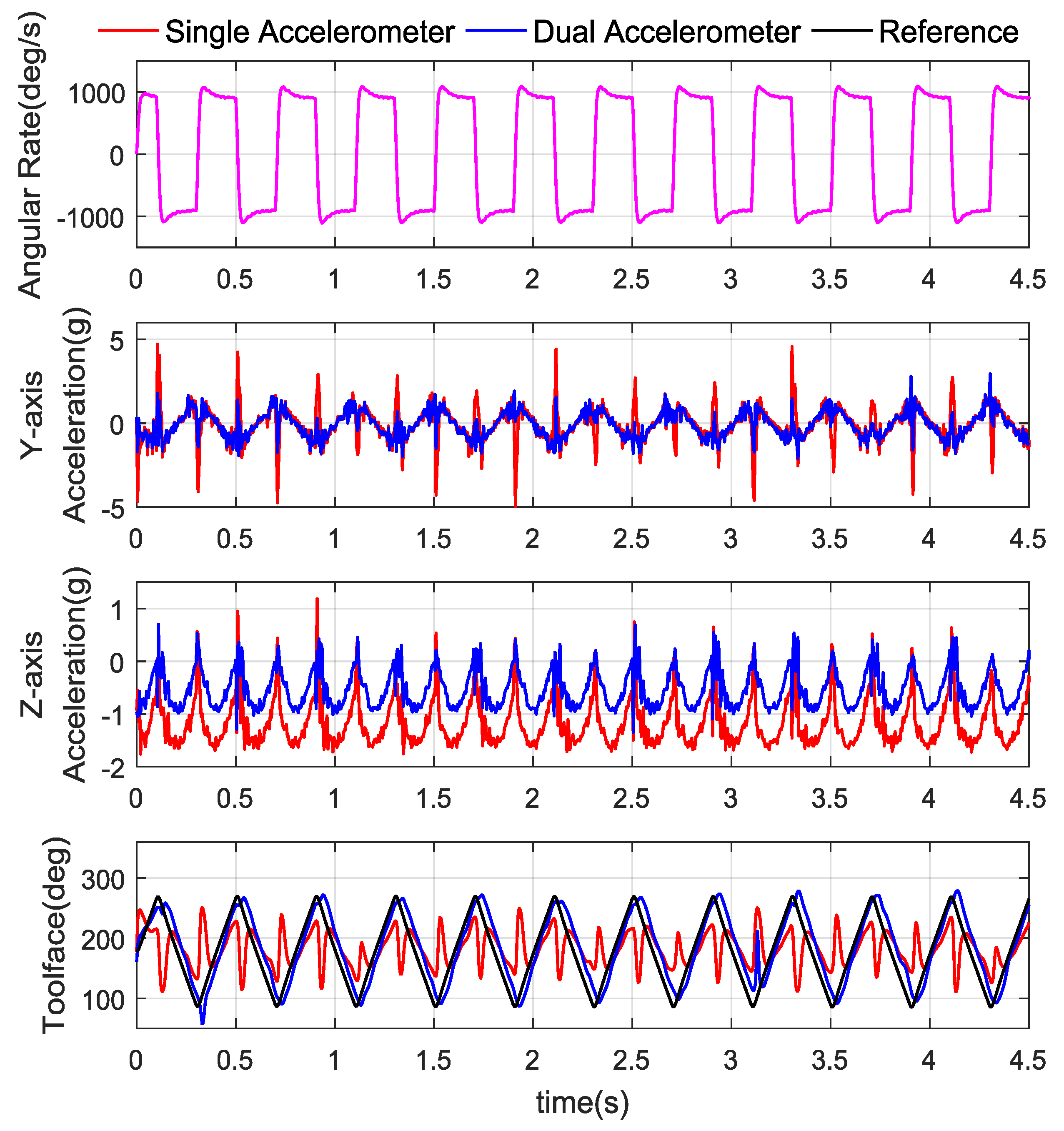
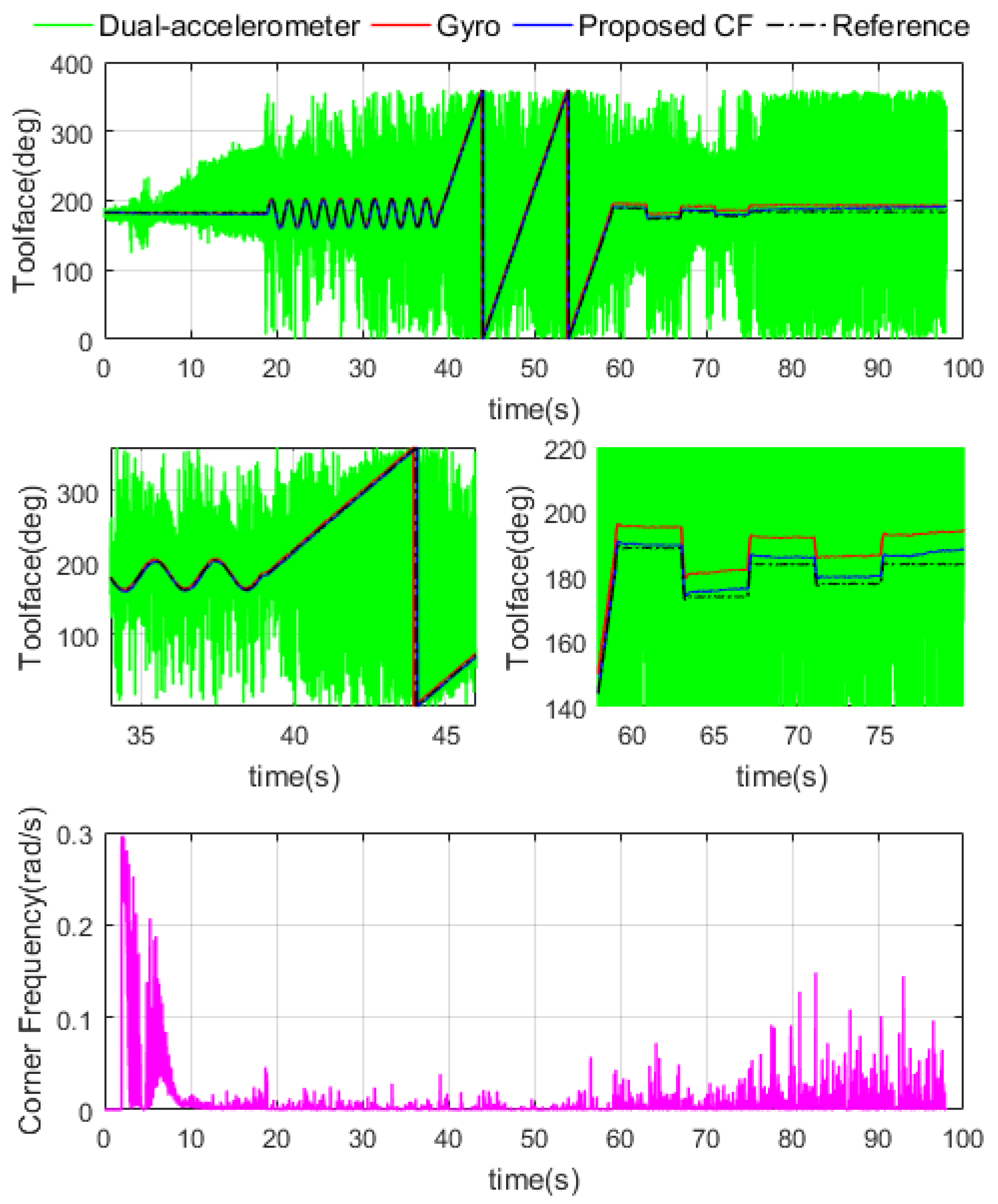
4.3. Dynamic Toolface Estimator Performance Test
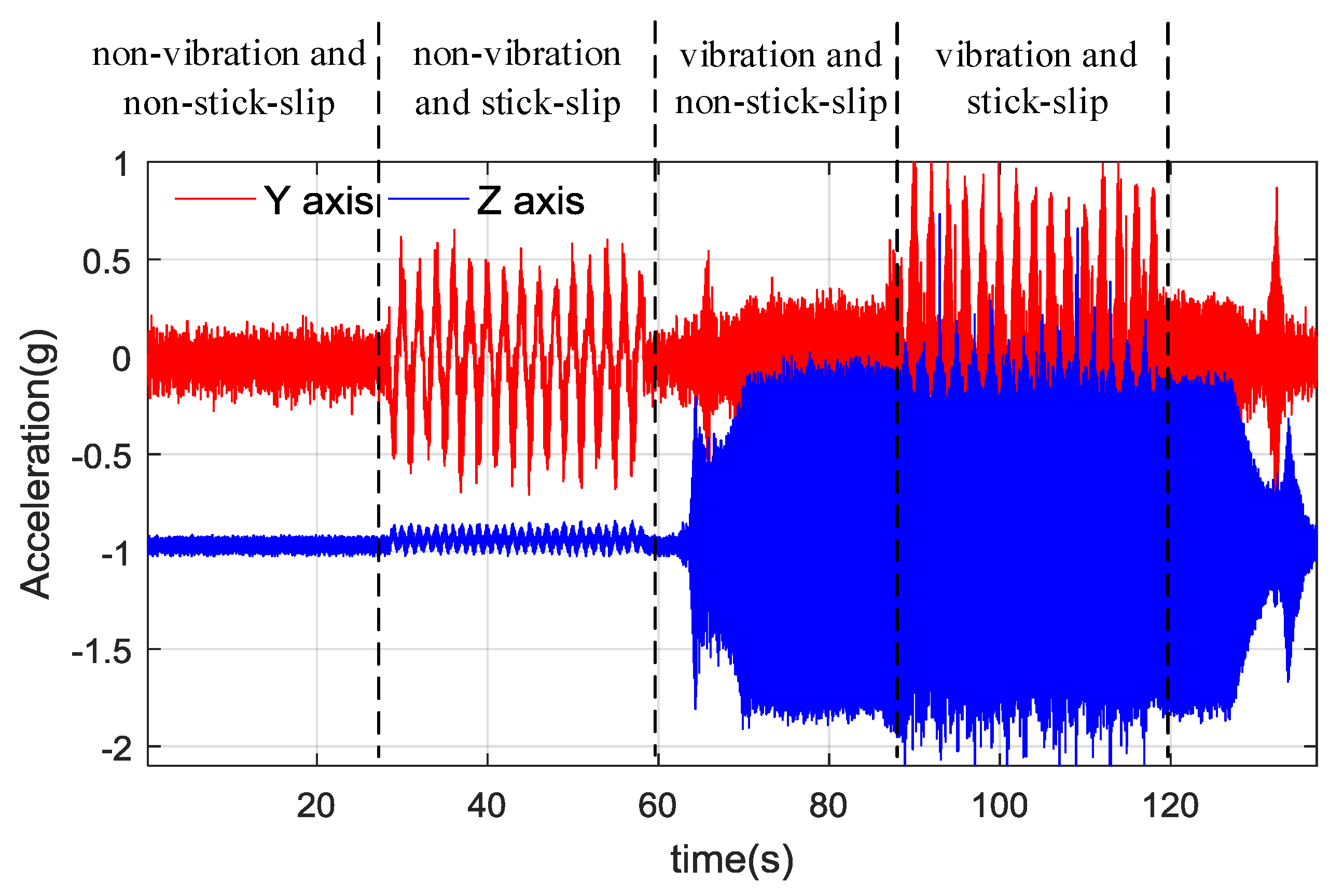
4.3.1. Stick-Slip Dynamic Toolface Estimator Test and Parameters Tuning
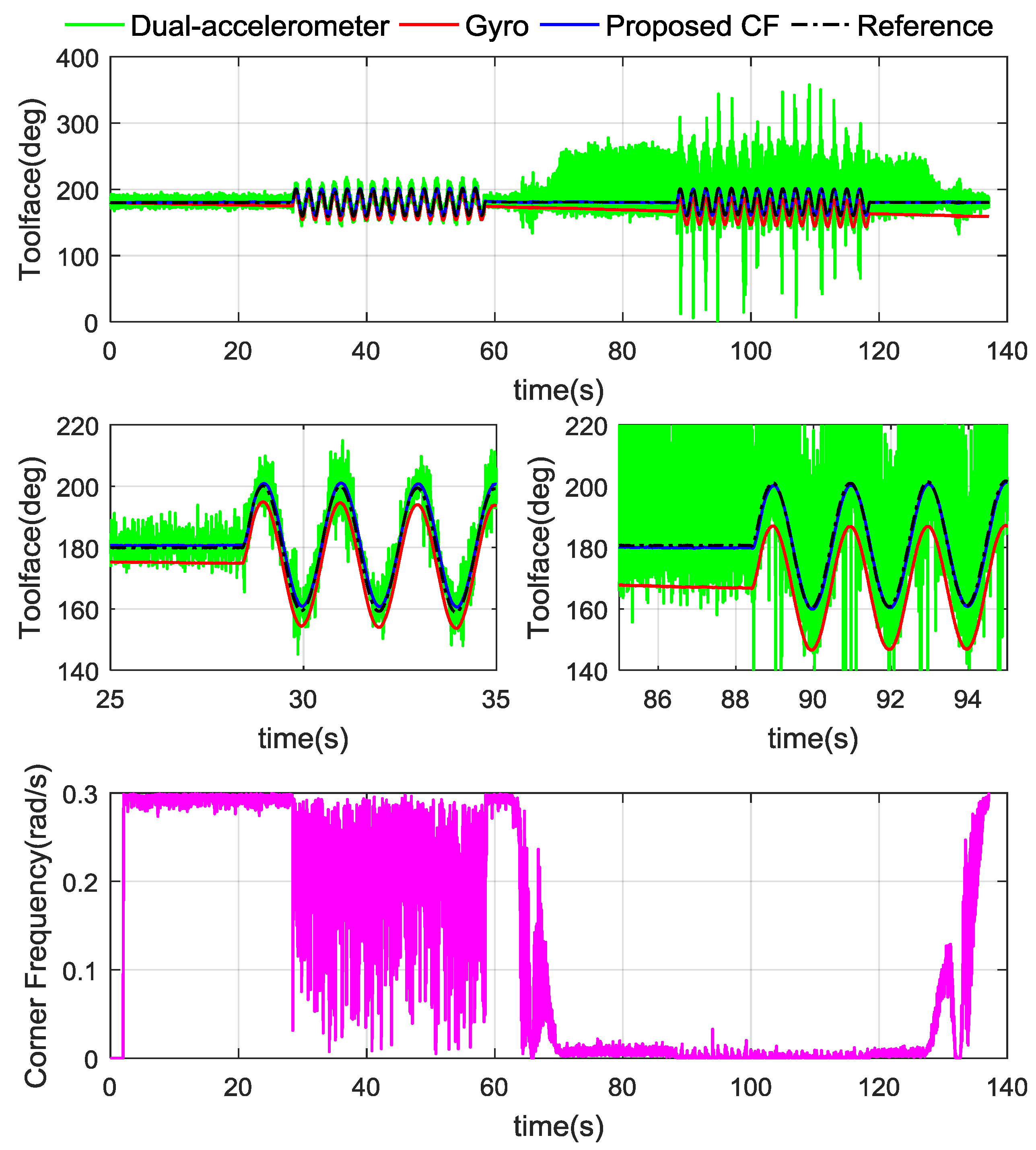
4.3.2. Multi Processes Dynamic Toolface Estimator Test
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schaaf, S.; Mallary, C.; Pafitis, D. Point-the-bit rotary steerable system: Theory and field results. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000; Society of Petroleum Engineers: Richardson, TX, USA, 2000. [Google Scholar]
- Zhang, C.; Zou, W.; Cheng, N. Overview of rotary steerable system and its control methods. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation (ICMA), Harbin, China, 7–10 August 2016; pp. 1559–1565. [Google Scholar]
- Yan, Z.D.; Geng, Y.F.; Wang, Z.F.; Wang, W.L. Design of Offsetting Steerable Mechanism for Rotary Steerable Drilling Tool Based on Double Eccentric Rings. Appl. Mech. Mater. 2013, 288, 13–18. [Google Scholar] [CrossRef]
- Wang, W.; Geng, Y.; Yan, Z. Dynamic Point-The-Bit Rotary Steerable Drilling Tool and Measuring Method Thereof. U.S. Patent 9,587,440, 7 March 2017. [Google Scholar]
- Qilong, X.; Ruihe, W.; Feng, S.; Leilei, H.; Laiju, H. Continuous measurement-while-drilling utilizing strap-down multi-model surveying system. IEEE Trans. Instrum. Meas. 2014, 63, 650–657. [Google Scholar] [CrossRef]
- Elgizawy, M.; Noureldin, A.M.; El-Sheimy, N. Continuous wellbore surveying while drilling utilizing MEMS gyroscopes based on Kalman filtering. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010; Society of Petroleum Engineers: Richardson, TX, USA, 2010. [Google Scholar]
- Heinisch, D.; Oueslati, H.; Popp, T.M.; Meyer-Heye, B.; Schepelmann, C.; Reckmann, H. Testing and Characterization of Shock and Vibration Loads to Enhance Drilling Tool Reliability and Efficiency. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 7–10 November 2016; Society of Petroleum Engineers: Richardson, TX, USA, 2016. [Google Scholar]
- Ledgerwood, L.W.; Hoffmann, O.J.-M.; Jain, J.R.; El Hakam, C.; Herbig, C.; Spencer, R. Downhole vibration measurement, monitoring, and modeling reveal stick/slip as a primary cause of PDC-bit damage in today. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010; Society of Petroleum Engineers: Richardson, TX, USA, 2010. [Google Scholar]
- Sugiura, J. The use of the near-bit vibration sensor while drilling lead to optimized rotary-steerable drilling in push-and point-the-bit configurations. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, 20–22 October 2008; Society of Petroleum Engineers: Richardson, TX, USA, 2008. [Google Scholar]
- ADXRS645 Datasheet. Available online: http://www.analog.com/media/en/technical-documentation/data-sheets/ADXRS645.pdf (accessed on 4 September 2018).
- Yang, Q.J.; Zuo, X.; Lin, E.H. A New Method for Dynamic Position Measurement While Drilling String Rotating. Appl. Mech. Mater. 2012, 152–154, 1102–1105. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, Z.; Chen, J.; Fourati, H.; Li, R. Fast Complementary Filter for Attitude Estimation Using Low-Cost MARG Sensors. IEEE Sens. J. 2016, 16, 6997–7007. [Google Scholar] [CrossRef]
- Higgins, W. A Comparison of Complementary and Kalman Filtering. IEEE Trans. Aerosp. Electron. Syst. 1975, AES-11, 321–325. [Google Scholar] [CrossRef]
- Brown, R.G. Integrated navigation systems and Kalman filtering: A perspective. Navigation 1972, 19, 355–362. [Google Scholar] [CrossRef]
- Xue, Q.; Leung, H.; Wang, R.; Liu, B.; Wu, Y. Continuous Real-Time Measurement of Drilling Trajectory with New State-Space Models of Kalman Filter. IEEE Trans. Instrum. Meas. 2016, 65, 144–154. [Google Scholar] [CrossRef]
- Chao, D.; El-Sheimy, N. Continuous Measurement-While-Drilling Surveying System Utilizing Low-Cost SINS. In Proceedings of the SPE/IADC Middle East Drilling Technology Conference and Exhibition, Abu Dhabi, UAE, 26–28 January 2016; Society of Petroleum Engineers: Richardson, TX, USA, 2016. [Google Scholar]
- Benziane, L.; El Hadri, A.; Seba, A.; Benallegue, A.; Chitour, Y. Attitude Estimation and Control Using Linearlike Complementary Filters: Theory and Experiment. IEEE Trans. Control Syst. Technol. 2016, 24, 2133–2140. [Google Scholar] [CrossRef]
- Yoo, T.S.; Hong, S.K.; Yoon, H.M.; Park, S. Gain-scheduled complementary filter design for a MEMS based attitude and heading reference system. Sensors 2011, 11, 3816–3830. [Google Scholar] [CrossRef] [PubMed]
- Close, D.; Owens, S.; Macpherson, J. Measurement of BHA vibration using MWD. In Proceedings of the SPE/IADC Drilling Conference, Dallas, TX, USA, 28 February–2 March 1988; Society of Petroleum Engineers: Richardson, TX, USA, 1988. [Google Scholar]
- Tian, Y.; Wei, H.; Tan, J. An Adaptive-Gain Complementary Filter for Real-Time Human Motion Tracking with MARG Sensors in Free-Living Environments. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 21, 254–264. [Google Scholar] [CrossRef] [PubMed]
- Mahony, R.; Hamel, T.; Pflimlin, J.-M. Nonlinear Complementary Filters on the Special Orthogonal Group. IEEE Trans. Autom. Control 2008, 53, 1203–1218. [Google Scholar] [CrossRef]
- Poddar, S.; Narkhede, P.; Kumar, V.; Kumar, A. PSO Aided Adaptive Complementary Filter for Attitude Estimation. J. Intell. Robot. Syst. 2017, 87, 531–543. [Google Scholar] [CrossRef]
- Safa, A.; Baradarannia, M.; Kharrati, H.; Khanmohammadi, S. Global attitude stabilization of rigid spacecraft with unknown input delay. Nonlinear Dyn. 2015, 82, 1623–1640. [Google Scholar] [CrossRef]
- Hong, S.K. Fuzzy logic based closed-loop strapdown attitude system for unmanned aerial vehicle (UAV). Sens. Actuators Phys. 2003, 107, 109–118. [Google Scholar] [CrossRef]
- Shen, X.; Yao, M.; Jia, W.; Yuan, D. Adaptive complementary filter using fuzzy logic and simultaneous perturbation stochastic approximation algorithm. Measurement 2012, 45, 1257–1265. [Google Scholar] [CrossRef]
- Narkhede, P.; Joseph Raj, A.N.; Kumar, V.; Karar, V.; Poddar, S. Least square estimation-based adaptive complimentary filter for attitude estimation. Trans. Inst. Meas. Control 2018. [Google Scholar] [CrossRef]
- Duong, D.Q.; Sun, J.; Nguyen, T.P.; Luo, L. Attitude estimation by using MEMS IMU with Fuzzy Tuned Complementary Filter. In Proceedings of the IEEE International Conference on Electronic Information and Communication Technology (ICEICT), Harbin, China, 20–22 August 2016; pp. 372–378. [Google Scholar]
- Kang, C.H.; Park, C.G.; Song, J.W. An Adaptive Complementary Kalman Filter Using Fuzzy Logic for a Hybrid Head Tracker System. IEEE Trans. Instrum. Meas. 2016, 65, 2163–2173. [Google Scholar] [CrossRef]
- Jieru, S. Research on Measurement Method of Dynamic Point-the-Bit Rotary Steerable Drilling Tool; China University of Petroleum (East China): Qingdao, China, 2018. (In Chinese) [Google Scholar]
- Jing, Z.; Yi, Z.; Xing, L.; XIao, C.; Yingjun, J. Method of Eliminating Vibrational Acceleration in Rotary Steerable Drilling System. Oil Drill. Prod. Technol. 2010, 32, 19–22. (In Chinese) [Google Scholar]
- Baiyan, L.; Yi nao, S.; Xinyuan, C.; Jiangang, X.; Liangcai, Z. Theoretical and experimental investigation on dynamic measurements of hole inclination in automatic vertical drilling process. Acta Pet. Sin. 2006, 27, 105. (In Chinese) [Google Scholar]


| Parameters | Accelerometer | Gyro |
|---|---|---|
| Range | ±8 g | ±1200°/s |
| Sensitivity | 1024 counts/g | 0.83 mV/°/s |
| Bandwidth | 400 Hz | 40 Hz |
| Sources | Dual-Accelerometer | Gyro | Proposed CF |
|---|---|---|---|
| RMSE (°) | 18.022 | 11.6306 | 1.0069 |
| Sources | Dual-Accelerometer | Gyro | Proposed CF |
|---|---|---|---|
| RMSE (°) | 61.032 | 5.872 | 3.017 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Geng, Y.; Wang, K.; Si, J.; Fiaux, J.D.O. Dynamic Toolface Estimation for Rotary Steerable Drilling System. Sensors 2018, 18, 2944. https://doi.org/10.3390/s18092944
Wang W, Geng Y, Wang K, Si J, Fiaux JDO. Dynamic Toolface Estimation for Rotary Steerable Drilling System. Sensors. 2018; 18(9):2944. https://doi.org/10.3390/s18092944
Chicago/Turabian StyleWang, Weiliang, Yanfeng Geng, Kai Wang, Jieru Si, and Joice De Oliveira Fiaux. 2018. "Dynamic Toolface Estimation for Rotary Steerable Drilling System" Sensors 18, no. 9: 2944. https://doi.org/10.3390/s18092944
APA StyleWang, W., Geng, Y., Wang, K., Si, J., & Fiaux, J. D. O. (2018). Dynamic Toolface Estimation for Rotary Steerable Drilling System. Sensors, 18(9), 2944. https://doi.org/10.3390/s18092944




