GNSS-Assisted Integrated Sensor Orientation with Sensor Pre-Calibration for Accurate Corridor Mapping †
Abstract
1. Introduction
1.1. Related Work
1.2. Paper Structure
2. System Design
2.1. UAV
2.2. Camera
2.3. GNSS Module
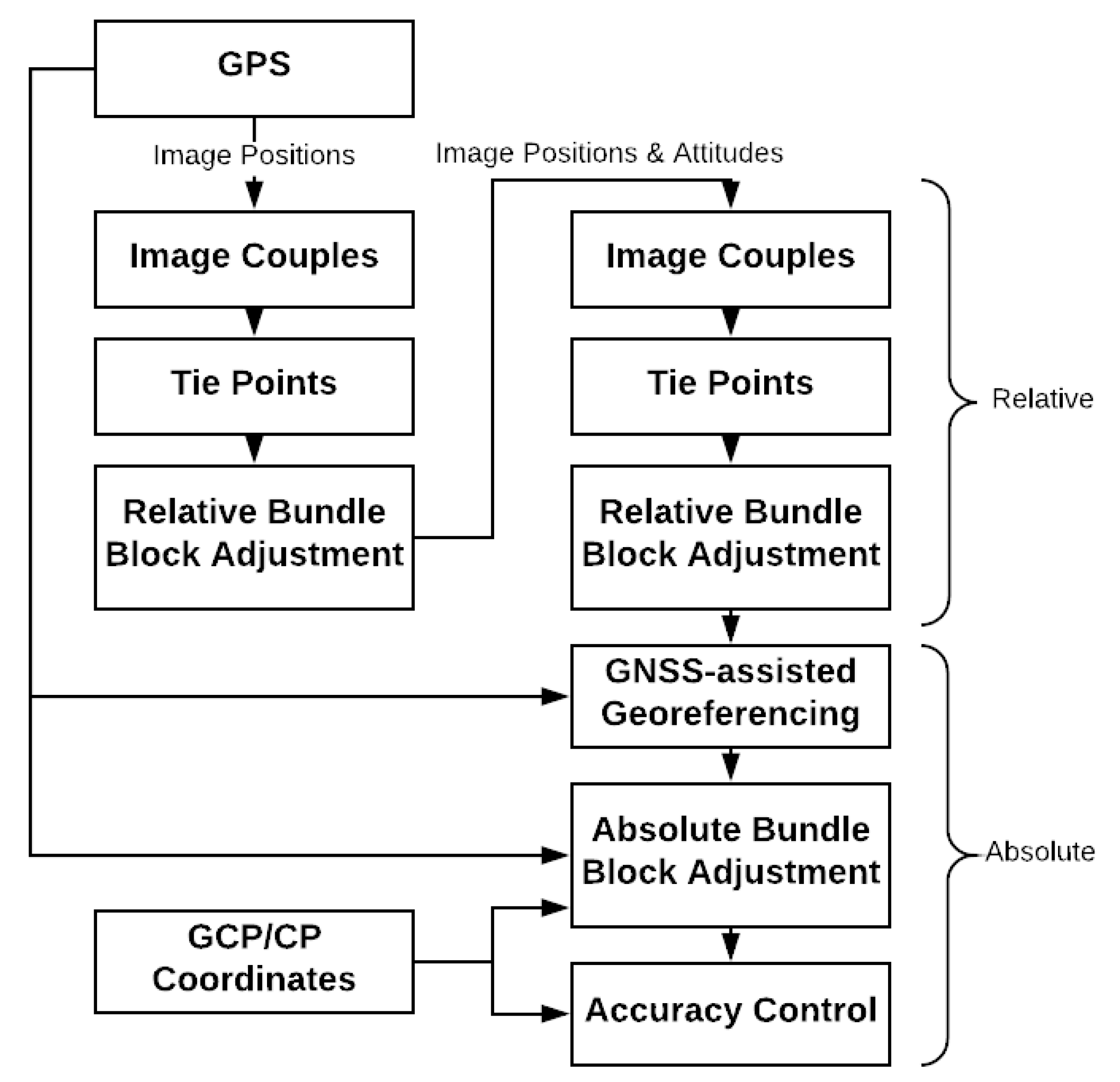
3. Methodology
- l is the index of tie points;
- m is the image index;
- z is the index of image blocks assorted by lever-arm;
- k is the index of images with GNSS measurements;
- n is the index of GCPs;
- ζ is the camera model;
- π is the projection function;
- pl,m is the 2D position of tie point l in image m;
- (Rm, Cm) is the pose of image m;
- Pl is the 3D position of tie point l;
- Ck is the camera projection center of image k;
- Cgnss,k is the phase center of GNSS antenna of image k;
- Rk is the world to camera rotation;
- is the lever-arm of image block z;
- Pn is the pseudo-intersection position of GCP n;
- Pgcp,n is the ground measurement of GCP n;
- pn,m is the image measurement of GCP n in image m;
- is the weight of tie points in images;
- is the weight of GNSS measurements;
- is the weight of GCPs; and
- is the weight of image measurements of GCPs.
4. Data Acquisition
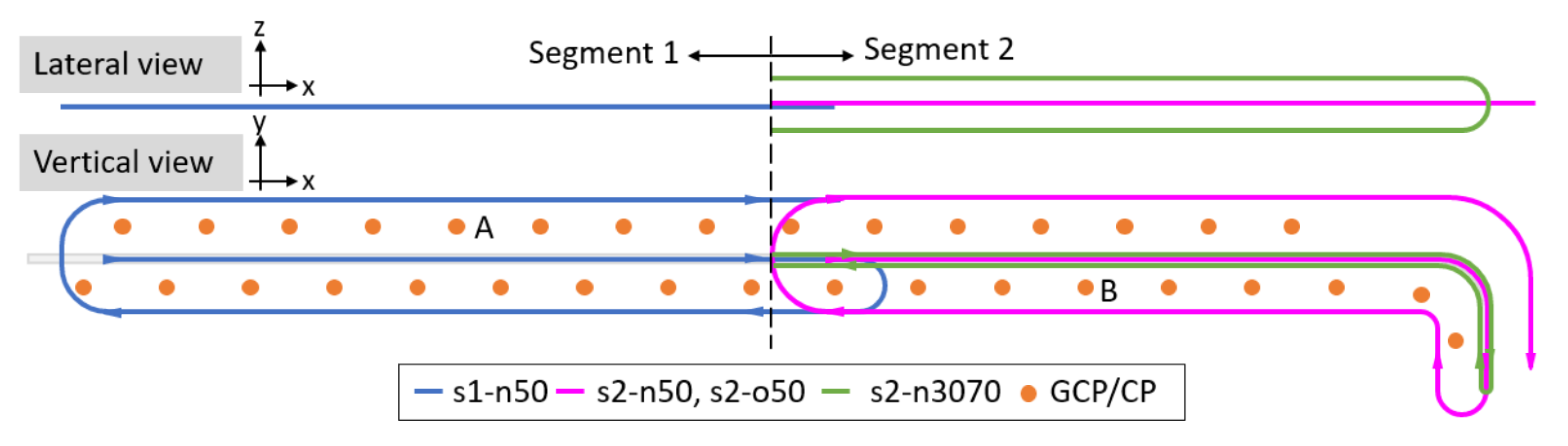
4.1. Acquisition Field
4.2. Flight Design
5. Data Processing
5.1. Topographic Data Processing
5.2. GNSS Data Processing
5.3. Synchronization of GNSS and Camera Modules
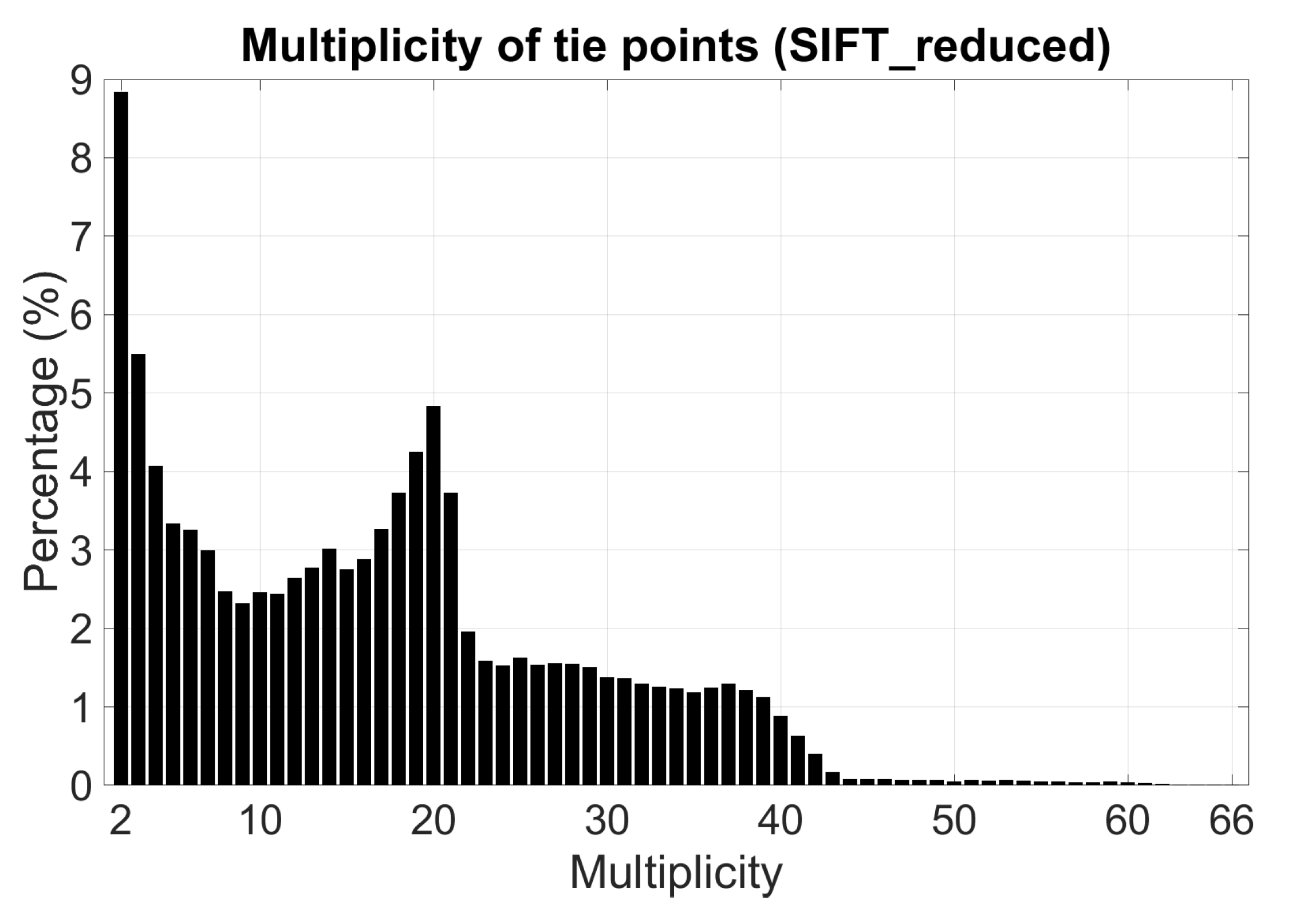
5.4. Photogrammetric Data Processing
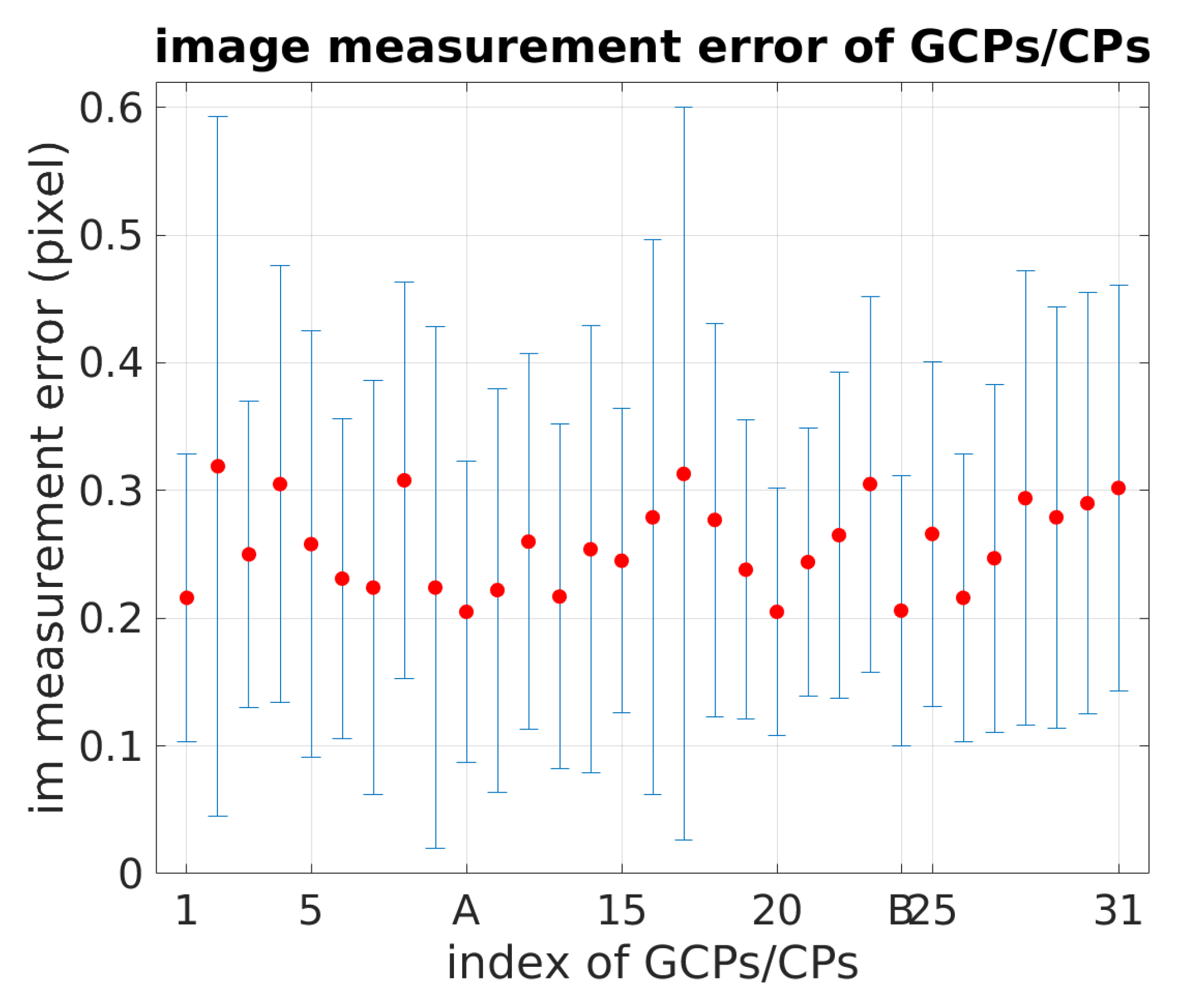
6. Results
6.1. Influence of Oblique Images
6.2. Influence of Multiple Flight Heights
6.3. Basic Flight Configuration
7. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global navigation satellite system |
| BBA | Bundle block adjustment |
| ISO | Integrated sensor orientation |
| UAV | Unmanned aerial vehicles |
| GCP | Ground control points |
| INS | Inertial navigation system |
| IMU | Inertial measurement unit |
| CP | Check point |
| Loemi | Laboratoire d’opto-éléctrique de métrologie et d’instrumentation |
| IGN | Institut national de l’information géographique et forestière |
| SIFT | Scale Invariant Feature Transform |
| DGAC | Direction générale de l’aviation civil |
| ENSG | Ecole Nationale des Sciences Géographiques |
| RMS | Root mean square |
References
- Remondino, F.; Barazzetti, L.; Nex, F.; Scaioni, M.; Sarazzi, D. UAV photogrammetry for mapping and 3d modeling-current status and future perspectives. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, C22. [Google Scholar] [CrossRef]
- Vallet, J.; Panissod, F.; Strecha, C.; Tracol, M. Photogrammetric performance of an ultra light weight swinglet UAV. In Proceedings of the Unmanned Aerial Vehicle in Geomatics Conference, Zürich, Switzerland, 14–16 September 2011. [Google Scholar]
- Tournadre, V.; Pierrot-Deseilligny, M.; Faure, P.H. UAV photogrammetry to monitor dykes-calibration and comparison to terrestrial lidar. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 143. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Rehak, M.; Skaloud, J. Fixed-wing micro aerial vehicle for accurate corridor mapping. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 23. [Google Scholar] [CrossRef]
- Skaloud, J.; Rehak, M.; Lichti, D. Mapping with MAV: Experimental Study on the Contribution of Absolute and Relative Aerial Position Control. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 123. [Google Scholar] [CrossRef]
- Ackermann, F. Operational rules and accuracy models for GPS-aerotriangulation. Arch. ISPRS 1992, 1, 691–700. [Google Scholar]
- Heipke, C.; Jacobsen, K.; Wegmann, H. Integrated Sensor Orientation: Test Report and Workshop Proceedings; Bundesamt für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2002. [Google Scholar]
- Ellum, C.; EL-SHEIMY, N. Inexpensive Kinematic Attitude Determination from MEMS-Based Accelerometers and GPS-Derived Accelerations. Navigation 2002, 49, 117–126. [Google Scholar] [CrossRef]
- Skaloud, J.; Vallet, J. High accuracy handheld mapping system for fast helicopter deployment. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 614–619. [Google Scholar]
- Lichti, D.; Skaloud, J.; Schaer, P. On the calibration strategy of medium format cameras for direct georeferencing. In Proceedings of the International Calibration and Orientation Workshop EuroCOW, Castelldefels, Spain, 30 January–1 February 2008. [Google Scholar]
- Daakir, M.; Pierrot-Deseilligny, M.; Bosser, P.; Pichard, F.; Thom, C.; Rabot, Y.; Martin, O. Lightweight UAV with on-board photogrammetry and single-frequency GPS positioning for metrology applications. ISPRS J. Photogramm. Remote Sens. 2017, 127, 115–126. [Google Scholar] [CrossRef]
- Skaloud, J.; Cramer, M.; Schwarz, K. Exterior orientation by direct measurement of camera position and attitude. Int. Arch. Photogramm. Remote Sens. 1996, 31, 125–130. [Google Scholar]
- Kruck, E. Combined IMU and sensor calibration with BINGO-F. In Proceedings of the OEEPE Workshop Integrated Sensor Orientation, Hannover, Germany, 17–18 September 2001. [Google Scholar]
- Cramer, M.; Stallmann, D. System calibration for direct georeferencing. Int. Arch. Photogramm. Remote Sens. 2002, 34, 79–84. [Google Scholar]
- Mostafa, M. Camera/IMU boresight calibration: New advances and performance analysis. In Proceedings of the ASPRS Annual Meeting, Washington, DC, USA, 19–26 April 2002; pp. 21–26. [Google Scholar]
- Skaloud, J.; Schaer, P. Towards A More Rigorous Boresight Determination: Theory, Technology and Realities of Inertial/GPS Sensor Orientation. In Proceedings of the ISPRS, WG 1/5 Platform and Sensor Integration Conference, Munich, Germany, 17–19 September 2003. [Google Scholar]
- Heipke, C.; Jacobsen, K.; Wegmann, H. Analysis of the results of the OEEPE test Integrated Sensor Orientation. In OEEPE Integrated Sensor Orientation Test Report and Workshop Proceedings; Citeseer: State College, PA, USA, 2002. [Google Scholar]
- Mian, O.; Lutes, J.; Lipa, G.; Hutton, J.; Gavelle, E.; Borghini, S. Direct georeferencing on small unmanned aerial platforms for improved reliability and accuracy of mapping without the need for ground control points. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 397. [Google Scholar] [CrossRef]
- Jozkow, G.; Toth, C. Georeferencing experiments with UAS imagery. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 25. [Google Scholar] [CrossRef]
- Blázquez, M.; Colomina, I. Relative INS/GNSS aerial control in integrated sensor orientation: Models and performance. ISPRS J. Photogramm. Remote Sens. 2012, 67, 120–133. [Google Scholar] [CrossRef]
- Cucci, D.A.; Rehak, M.; Skaloud, J. Bundle adjustment with raw inertial observations in UAV applications. ISPRS J. Photogramm. Remote Sens. 2017, 130, 1–12. [Google Scholar] [CrossRef]
- Martin, O.; Meynard, C.; Pierrot Deseilligny, M.; Souchon, J.P.; Thom, C. Réalisation d’une caméra photogrammétrique ultralégère et de haute résolution. In Proceedings of the Colloque Drones et Moyens Légers Aéroportés D’observation, Montpellier, France, 24–26 June 2014; pp. 24–26. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Corfu, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar]
- Rupnik, E.; Daakir, M.; Deseilligny, M.P. MicMac—A free, open-source solution for photogrammetry. Open Geospat. Data Softw. Stand. 2017, 2, 14. [Google Scholar] [CrossRef]
- Tournadre, V. Métrologie par Photogrammétrie Aéroportée Légère: Application au Suivi D’évolution de Digues. Ph.D. Thesis, Université Paris-Est, Saint-Mande, France, 2015. [Google Scholar]
- Wright, S.; Nocedal, J. Numerical Optimization; Springer: Berlin, Germany, 1999; Volume 35, p. 7. [Google Scholar]
- Martinez-Rubi, O. Improving Open-Source Photogrammetric Workflows for Processing Big Datasets; Netherlands eScience Center: Amsterdam, The Netherlands, 2016. [Google Scholar]




| Flight | s1-n50 | s2-n50 | s2-n3070 | s2-o50 | |
|---|---|---|---|---|---|
| Nb of images | 395 | 315 | 200 | 323 | |
| Height (m) | 50 | 50 | 30, 70 | 50 | |
| Orientation | nadir | nadir | nadir | oblique | |
| Nb of strips | 3 | 3 | 2 | 3 | |
| Overlap (%) | forward | 80 | |||
| side | 70 | ||||
| GCP accuracy (mm) | horizontal | 1.3 | |||
| vertical | 1 | ||||
| Camera focal length (mm) | 35 | ||||
| GSD (mm) | 10 | 10 | 6, 14 | 10 | |
| Positioning Mode | Kinematic | Troposphere Correction | Saastamoinen |
| Frequencies | L1 | Satellite Ephemeris | Broadcast |
| Filter type | Combined | Navigation System | GPS |
| Elevation Mask | 15° | Integer Ambiguity Resolution | Fix and Hold |
| Ionosphere Correction | Broadcast | Min Ratio to Fix Ambiguity | 3.0 |
| GCP | Parameter Liberation | [] | RMS [] | Lever-Arm [] | Correlation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| xy | z | 3D | xy | z | 3D | ||||||||
| Calibration | |||||||||||||
| s2-n50 + s2-o50 | 0 | camera model, lever-arm | 5.2 | 1.9 | 8.3 | 8.5 | na: | 51.4 | 34.8 | 62.1 | 0.18 | 0.99 ± 0.00 | 0.18 ± 0.00 |
| ob: | 63.2 | 12.7 | 64.5 | ||||||||||
| 1 (pt B) | camera model, lever-arm | 4.9 | 0.9 | 0.6 | 1.1 | na: | 51.0 | 41.8 | 65.9 | 0.84 | 0.80 ± 0.06 | 0.68 ± 0.05 | |
| ob: | 66.2 | 18.8 | 68.8 | ||||||||||
| s2-n50 + s2-o50 + s2-n3070 | 0 | camera model, lever-arm | 5.0 | 1.9 | 5.9 | 6.2 | na: | 51.9 | 36.8 | 63.7 | 0.07 | 0.99 ± 0.00 | 0.07 ± 0.00 |
| ob: | 64.8 | 14.6 | 66.4 | ||||||||||
| 1 (pt B) | camera model, lever-arm | 4.7 | 0.7 | 0.8 | 1.0 | na: | 51.7 | 42.3 | 66.8 | 0.55 | 0.62 ± 0.09 | 0.33 ± 0.06 | |
| ob: | 66.5 | 19.4 | 69.3 | ||||||||||
| 14 (all) | camera model, lever-arm | 4.7 | / | / | / | na: | 51.7 | 42.8 | 67.2 | 0.85 | 0.44 ± 0.09 | 0.39 ± 0.08 | |
| ob: | 66.6 | 19.9 | 69.5 | ||||||||||
| Acquisition | |||||||||||||
| s1-n50 | 0 | camera model, lever-arm | 4.8 | 3.3 | 15.0 | 15.3 | na: | 53.8 | 47.7 | 71.9 | 0.28 | 0.99 ± 0.00 | 0.28 ± 0.00 |
| 1 (pt A) | camera model, lever-arm | 4.8 | 3.3 | 0.9 | 3.4 | na: | 54.1 | 33.0 | 63.4 | 0.92 | 0.98 ± 0.02 | 0.91 ± 0.01 | |
| 0 | N/A, given | 5.2 | 3.3 | 2.1 | 3.9 | na: | 51.7 | 42.8 | 67.2 | / | / | / | |
| 1 (pt A) | N/A, given | 5.1 | 3.4 | 2.1 | 4.0 | na: | 51.7 | 42.8 | 67.2 | / | / | / | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Rupnik, E.; Faure, P.-H.; Pierrot-Deseilligny, M. GNSS-Assisted Integrated Sensor Orientation with Sensor Pre-Calibration for Accurate Corridor Mapping. Sensors 2018, 18, 2783. https://doi.org/10.3390/s18092783
Zhou Y, Rupnik E, Faure P-H, Pierrot-Deseilligny M. GNSS-Assisted Integrated Sensor Orientation with Sensor Pre-Calibration for Accurate Corridor Mapping. Sensors. 2018; 18(9):2783. https://doi.org/10.3390/s18092783
Chicago/Turabian StyleZhou, Yilin, Ewelina Rupnik, Paul-Henri Faure, and Marc Pierrot-Deseilligny. 2018. "GNSS-Assisted Integrated Sensor Orientation with Sensor Pre-Calibration for Accurate Corridor Mapping" Sensors 18, no. 9: 2783. https://doi.org/10.3390/s18092783
APA StyleZhou, Y., Rupnik, E., Faure, P.-H., & Pierrot-Deseilligny, M. (2018). GNSS-Assisted Integrated Sensor Orientation with Sensor Pre-Calibration for Accurate Corridor Mapping. Sensors, 18(9), 2783. https://doi.org/10.3390/s18092783




