A Framework of Joint Energy Provisioning and Manufacturing Scheduling in Smart Industrial Wireless Rechargeable Sensor Networks
Abstract
1. Introduction
2. Related Work
3. Preliminaries
3.1. Problem Statement
- The first problem is how to reasonably replenish energy for sensor nodes under the condition of insuring continuous machining and avoiding sensors failure, based on actively predicting the available electricity of wireless sensor nodes.
- The second problem is how to effectively assign production tasks to the optional machines under the constraint of operational relationships, and further minimize the processing time of the entire production tasks on the basis of separation between nodes charging and machines processing.
3.2. Model Assumptions
- Each machine can only process one workstage at most in synchronization.Each workstage can only be processed by one machine at most in synchronization.
- The processing sequence of each workpiece must satisfy the requirements of production, and the different workstages of a workpiece cannot coincide.
- Once the workstage starts processing, it cannot be interrupted until processing is completed.
- The workpieces are independent from each other, there is no sequence constraint, and there is no difference between priorities.
- At the beginning, the initial state of all machines is idle.
- At the beginning, all the workpieces arrive at the factory to be processed.
- The transfer time between the different workstages of a workpiece is negligible.
- The working output current of wireless sensors is constant by default.
- The charging input current of wireless sensors is constant by default.
- When the machine is not working, wireless sensors can enter low-power mode, regardless of the energy consumption during this period.
- At the beginning, all the wireless sensors are at full charge.
- Charging for wireless sensors starts with the associated machine finishing one workstage and has stopped working.
- When wireless sensors are charging, the associated machine must shut down.
- Regardless of the capacity loss of the battery, the maximum battery capacity of the wireless sensor is constant.
- The wireless sensor adopts greedy charging such that it charges until it is full.
- The maximum battery capacity of wireless sensors is sufficient to support any workstage.
- The uncertainty of communication and operations on the sensor nodes is negligible.
4. Joint Energy Provisioning and Manufacturing Scheduling (J-EPMS)
4.1. Symbol Definition
4.2. Decision Variables
4.3. Model Establishment
4.4. Solution Algorithm
| Algorithm 1. Presents the detailed procedures of DCQGA-TS for J-EPMS. |
|
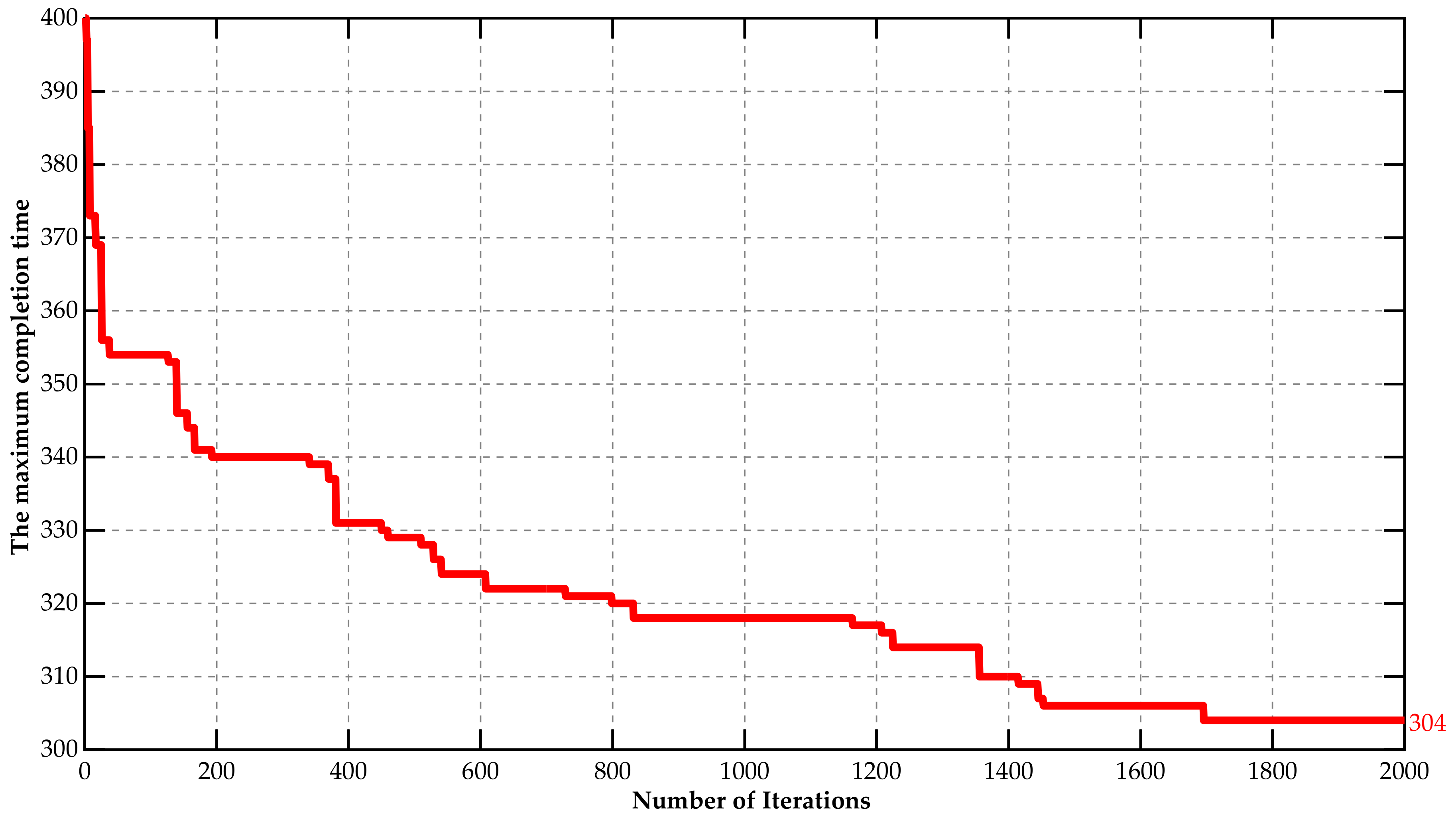
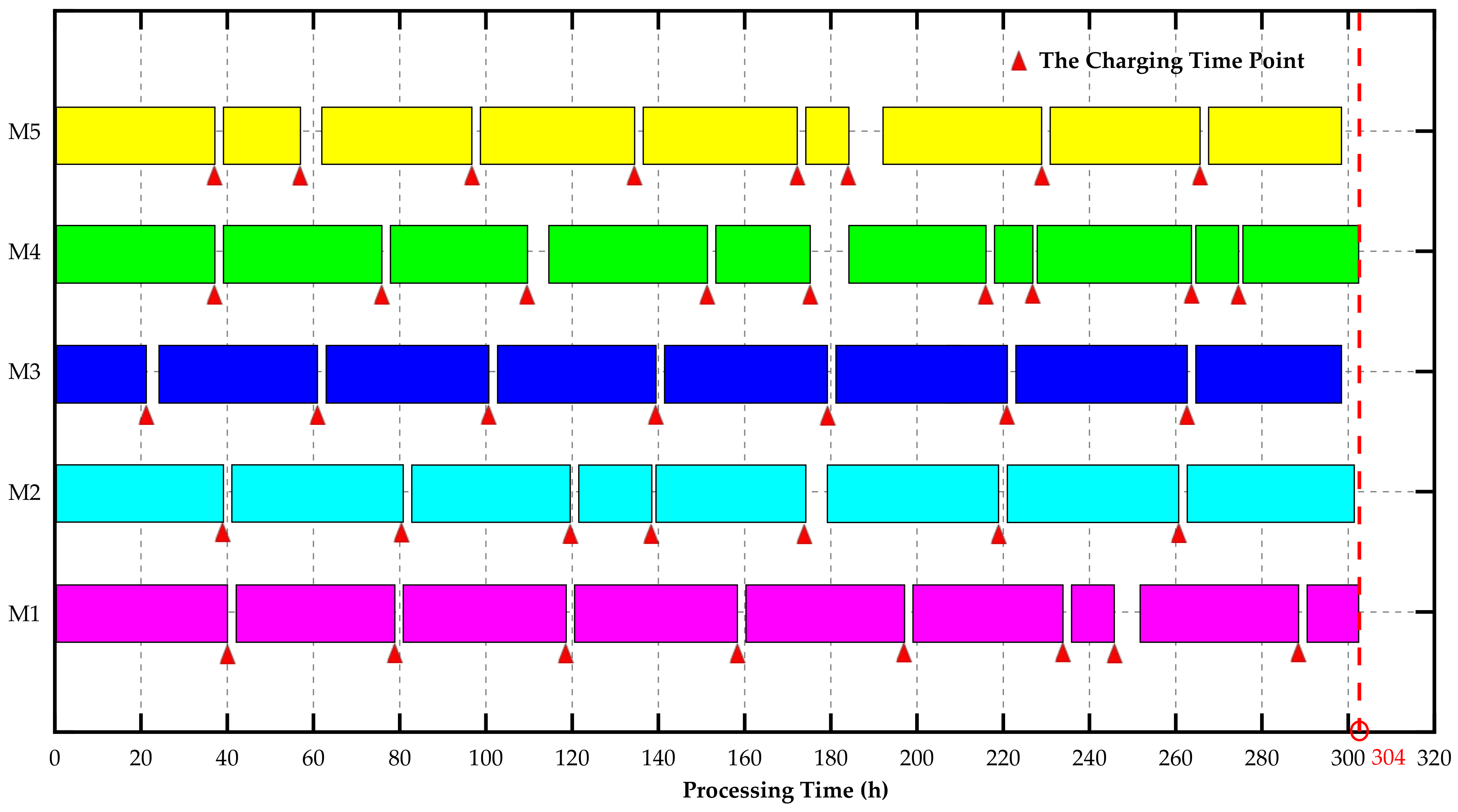
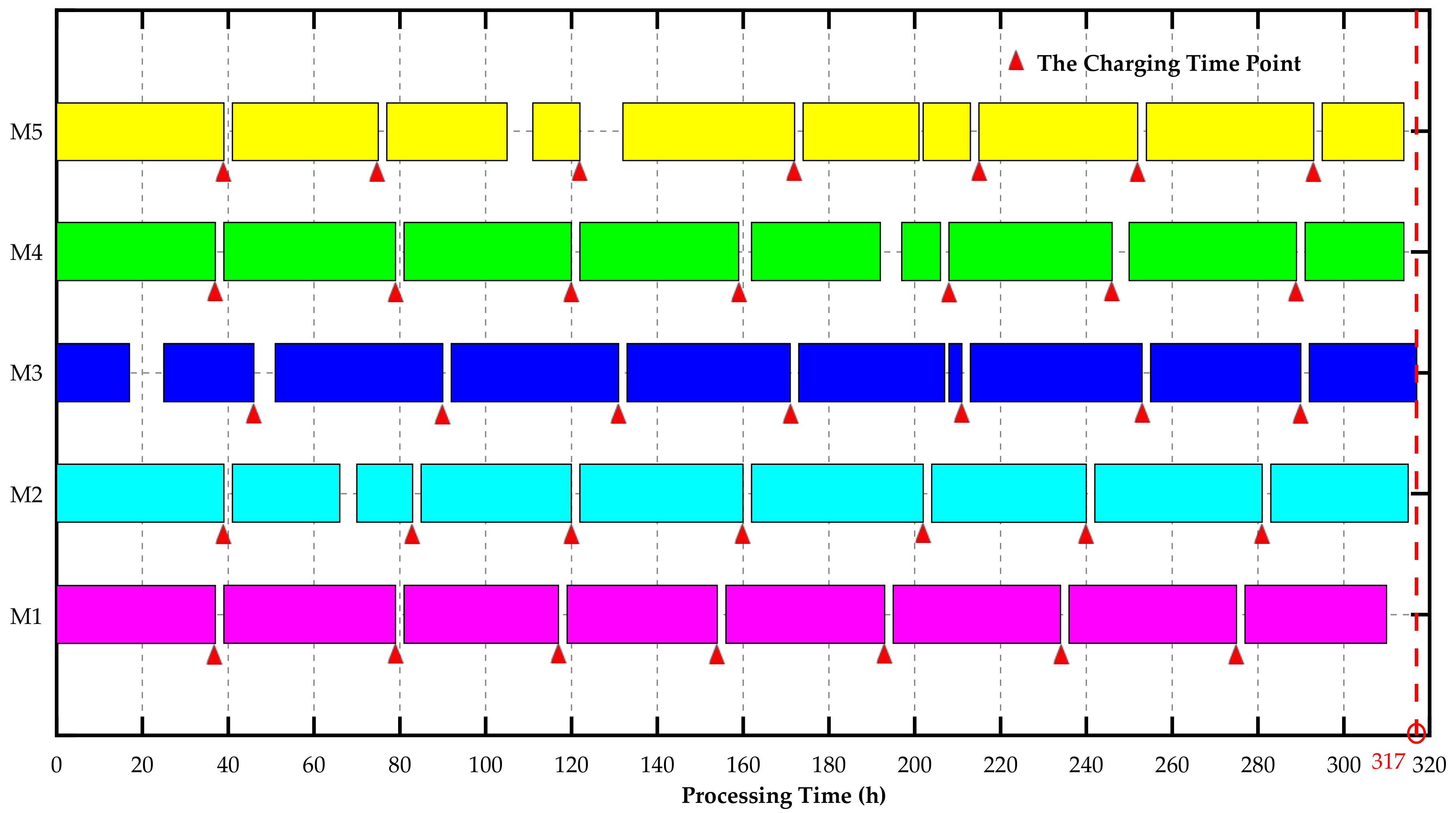
5. Simulations
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, S.C.; Jeon, T.G.; Hwang, H.; Kim, C. Design and Implementation of Wireless Sensor Based-Monitoring System for Smart Factory; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Ilyas, M.; Mahgoub, I. Handbook of Sensor Networks: Compact Wireless and Wired Sensing Systems; CRC Press: Boca Raton, FL, USA, 2005; pp. 5–15. ISBN 9780849319686. [Google Scholar]
- Gungor, V.C.; Hancke, G.P. Industrial Wireless Sensor Networks: Challenges, Design Principles, and Technical Approaches. IEEE Trans. Ind. Electron. 2009, 10, 4258–4265. [Google Scholar] [CrossRef]
- Zoppi, S.; Van Bemten, A.; Gursu, H.M.; Vilgelm, M.; Guck, J.; Kellerer, W. Achieving Hybrid Wired/Wireless Industrial Networks with WDetServ: Reliability-Based Scheduling for Delay Guarantees. IEEE Trans. Ind. Inform. 2018, 5, 2307–2319. [Google Scholar] [CrossRef]
- Flammini, A.; Ferrari, P.; Marioli, D.; Sisinni, E.; Taroni, A. Wired and wireless sensor networks for industrial applications. Microelectron. J. 2009, 9, 1322–1336. [Google Scholar] [CrossRef]
- Willig, A.; Matheus, K.; Wolisz, A. Wireless Technology in Industrial Networks. Proc. IEEE 2005, 6, 1130–1151. [Google Scholar] [CrossRef]
- Wang, K.; Li, H.; Feng, Y.; Tian, G. Big Data Analytics for System Stability Evaluation Strategy in the Energy Internet. IEEE Trans. Ind. Inform. 2017, 4, 1969–1978. [Google Scholar] [CrossRef]
- Sheng, Z.; Mahapatra, C.; Zhu, C.; Leung, V.C.M. Recent Advances in Industrial Wireless Sensor Networks toward Efficient Management in IoT. IEEE Access 2015, 622–637. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Z.; Tian, S.; Tian, G.; Lv, Z.; Jia, H. Data-driven accurate design of variable blank holder force in sheet forming under interval uncertainty using sequential approximate multi-objective optimization. Future Gener. Comput. Syst. 2018, 1242–1250. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, Y.; Zhang, Z.; Tan, J. An optimal dynamic interval preventive maintenance scheduling for series systems. Reliab. Eng. Syst. Safe 2015, 19–30. [Google Scholar] [CrossRef]
- Wan, J.; Chen, B.; Wang, S.; Xia, M.; Li, D.; Liu, C. Fog Computing for Energy-aware Load Balancing and Scheduling in Smart Factory. IEEE Trans. Ind. Inform. 2018. [Google Scholar] [CrossRef]
- Feng, Y.; Hu, B.; Hao, H.; Gao, Y.; Li, Z.; Tan, J. Design of Distributed Cyber-Physical Systems for Connected and Automated Vehicles with Implementing Methodologies. IEEE Trans. Ind. Inform. 2018, 1. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, C. Wireless Rechargeable Sensor Networks; Springer: Cham, Switzerland, 2015; ISBN 9783319176550. [Google Scholar]
- He, S.; Chen, J.; Jiang, F.; Yau, D.K.Y.; Xing, G.; Sun, Y. Energy Provisioning in Wireless Rechargeable Sensor Networks. IEEE Trans. Mobile Comput. 2013, 10, 1931–1942. [Google Scholar] [CrossRef]
- Gao, D.; Liu, Y.; Zhang, F.; Song, J. Anycast Routing Protocol for Forest Monitoring in Rechargeable Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2013, 12, 239860. [Google Scholar] [CrossRef]
- Lu, X.; Niyato, D.; Wang, P.; Kim, D.I.; Han, Z. Wireless charger networking for mobile devices: Fundamentals, standards, and applications. IEEE Wirel. Commun. 2015, 2, 126–135. [Google Scholar] [CrossRef]
- Cecilio, J.; Pedro, N.S.F. Wireless Sensors in Industrial Time-Critical Environments; Springer: Cham, Switzerland, 2014; ISBN 9783319028880. [Google Scholar]
- Radziwon, A.; Bilberg, A.; Bogers, M.; Madsen, E.S. The Smart Factory: Exploring Adaptive and Flexible Manufacturing Solutions. Procedia Eng. 2014, 1184–1190. [Google Scholar] [CrossRef]
- Ding, X.; Shi, L.; Han, J.; Lu, J. The study of cross-layer optimization for wireless rechargeable sensor networks implemented in coal mines. Sensors 2016, 16, 171. [Google Scholar] [CrossRef] [PubMed]
- Zou, Z.; Nagayama, T.; Fujino, Y. Efficient multihop communication for static wireless sensor networks in the application to civil infrastructure monitoring. Struct. Control Health Monit. 2014, 4, 603–619. [Google Scholar] [CrossRef]
- Erol-Kantarci, M.; Mouftah, H.T. Suresense: Sustainable wireless rechargeable sensor networks for the smart grid. IEEE Wirel. Commun. 2012, 3, 30–36. [Google Scholar] [CrossRef]
- Xu, C.; Cheng, R.; Wu, T. Wireless rechargeable sensor networks with separable charger array. Int. J. Distrib. Sens. Netw. 2018, 4. [Google Scholar] [CrossRef]
- Dai, H.; Wu, X.; Chen, G.; Xu, L.; Lin, S. Minimizing the number of mobile chargers for large-scale wireless rechargeable sensor networks. Comput. Commun. 2014, 54–65. [Google Scholar] [CrossRef]
- Porta, T.; Petrioli, C.; Phillips, C.; Spenza, D. Sensor Mission Assignment in Rechargeable Wireless Sensor Networks. ACM Trans. Sens. Netw. (TOSN) 2014, 4, 1–39. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, X.; Zhang, D.; Zeng, F. Collaborative mobile charging policy for perpetual operation in large-scale wireless rechargeable sensor networks. Neurocomputing 2017, 137–144. [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, M.; Tian, G.; Li, Z.; Zhang, Z.; Zhang, Qin.; Tan, J. Target disassembly sequencing and scheme evaluation for CNC machine tools using improved multiobjective ant colony algorithm and fuzzy integral. IEEE Trans. Syst. Man Cybern. Syst. 2018. [Google Scholar] [CrossRef]
- Ye, X.; Liang, W. Charging utility maximization in wireless rechargeable sensor networks. Wirel. Netw. 2017, 7, 2069–2081. [Google Scholar] [CrossRef]
- Gao, Y.C.; Wang, Q.R.; Feng, Y.X.; Zheng, H.; Zheng, B.; Tan, J.R. An Energy-Saving Optimization Method of Dynamic Scheduling for Disassembly Line. Energies 2018, 5, 1261. [Google Scholar] [CrossRef]
- Lin, C.; Wu, G.; Obaidat, M.S.; Yu, C.W. Clustering and splitting charging algorithms for large scaled wireless rechargeable sensor networks. J. Syst. Softw. 2016, 381–394. [Google Scholar] [CrossRef]
- Zhong, P.; Zhang, Y.; Ma, S.; Kui, X.; Gao, J. RCSS: A Real-Time On-Demand Charging Scheduling Scheme for Wireless Rechargeable Sensor Networks. Sensors 2018, 18, 1601. [Google Scholar] [CrossRef] [PubMed]
- Shih, K.; Yang, C. A coverage-aware energy replenishment scheme for wireless rechargeable sensor networks. EURASIP J. Wirel. Commun. Netw. 2017, 1, 1–11. [Google Scholar] [CrossRef]
- Shu, Y.; Shin, K.G.; Chen, J.; Sun, Y. Joint Energy Replenishment and Operation Scheduling in Wireless Rechargeable Sensor Networks. IEEE Trans. Ind. Inform. 2017, 1, 125–134. [Google Scholar] [CrossRef]
- Chang, H.; Lin, J.; Wu, Y.; Huang, S. MMCS: Multi-module charging strategy for increasing the lifetime of wireless rechargeable sensor networks. Energies 2016, 9, 664. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Ye, F.; Yang, Y. A Mobile Data Gathering Framework for Wireless Rechargeable Sensor Networks with Vehicle Movement Costs and Capacity Constraints. IEEE Trans. Comput. 2016, 8, 2411–2427. [Google Scholar] [CrossRef]
- Arivudainambi, D.; Balaji, S. Optimal Placement of Wireless Chargers in Rechargeable Sensor Networks. IEEE Sens. J. 2018, 10, 4212–4222. [Google Scholar] [CrossRef]
- Li, S.; Fu, L.; He, S.; Sun, Y. Near-Optimal Co-Deployment of Chargers and Sink Stations in Rechargeable Sensor Networks. ACM Trans. Embed. Comput. Syst. 2018, 1, 1–19. [Google Scholar] [CrossRef]
- Shu, Y.; Yousefi, H.; Cheng, P.; Chen, J.; Gu, Y.J.; He, T.; Shin, K.G. Near-Optimal Velocity Control for Mobile Charging in Wireless Rechargeable Sensor Networks. IEEE Trans. Mob. Comput. 2016, 7, 1699–1713. [Google Scholar] [CrossRef]
- Yang, X.; Han, G.; Liu, L.; Qian, A.; Zhang, W. IGRC: An improved grid-based joint routing and charging algorithm for wireless rechargeable sensor networks. Future Gener. Comput. Syst. 2017. [Google Scholar] [CrossRef]
- Fu, L.; He, L.; Cheng, P.; Gu, Y.; Pan, J.; Chen, J. ESync: Energy Synchronized Mobile Charging in Rechargeable Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2016, 9, 7415–7431. [Google Scholar] [CrossRef]
- Jiang, J.R.; Liao, J.H. Efficient Wireless Charger Deployment for Wireless Rechargeable Sensor Networks. Energies 2016, 9, 696. [Google Scholar] [CrossRef]
- Rao, X.; Yang, P.; Yan, Y.; Zhou, H.; Wu, X. Optimal Recharging With Practical Considerations in Wireless Rechargeable Sensor Network. IEEE Access 2017, 4401–4409. [Google Scholar] [CrossRef]
- Feng, Y.; Gao, Y.; Tian, G.; Li, Z.; Hu, H.; Zheng, H. Dynamic process planning and End-of-life decision making for product recovery optimization based on hybrid disassembly. IEEE Trans. Autom. Sci. Eng. 2018. [Google Scholar] [CrossRef]
- Li, X.; Tang, Q.; Sun, C. Energy efficient dispatch strategy for the dual-functional mobile sink in wireless rechargeable sensor networks. Wirel. Netw. 2018, 3, 671–681. [Google Scholar] [CrossRef]
- Lin, T.L.; Li, S.L.; Chang, H.Y. A Power Balance Aware Wireless Charger Deployment Method for Complete Coverage in Wireless Rechargeable Sensor Networks. Energies 2016, 9, 695. [Google Scholar] [CrossRef]
- Rout, R.R.; Krishna, M.S.; Gupta, S. Markov Decision Process-Based Switching Algorithm for Sustainable Rechargeable Wireless Sensor Networks. IEEE Sens. J. 2016, 8, 2788–2797. [Google Scholar] [CrossRef]
- Shu, Y.; Cheng, P.; Gu, Y.; Chen, J.; He, T. TOC: Localizing Wireless Rechargeable Sensors with Time of Charge. ACM Trans. Sens. Netw. 2015, 3, 1–22. [Google Scholar] [CrossRef]
- Najeeb, N.W.; Detweiler, C. Extending Wireless Rechargeable Sensor Network Life without Full Knowledge. Sensors 2017, 17, 1642. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Cheng, P.; Gu, Y.; Chen, J.; He, T. Optimal Charging in Wireless Rechargeable Sensor Networks. IEEE Trans. Veh. Technol. 2016, 1, 278–291. [Google Scholar] [CrossRef]
- Kaswan, A.; Tomar, A.; Jana, P.K. An efficient scheduling scheme for mobile charger in on-demand wireless rechargeable sensor networks. J. Netw. Comput. Appl. 2018, 123–134. [Google Scholar] [CrossRef]
- Wei, Y.K.; Ma, X.H.; Yang, N.; Chen, Y.J. Energy-Saving Traffic Scheduling in Hybrid Software Defined Wireless Rechargeable Sensor Networks. Sensors 2017, 17, 2126. [Google Scholar] [CrossRef]
- Feng, Y.; Hong, Z.; Tian, G.; Li, Z.; Tan, J.; Hu, H. Environmentally friendly MCDM of reliability-based product optimisation combining DEMATEL-based ANP, interval uncertainty and Vlse Kriterijumska Optimizacija Kompromisno Resenje (VIKOR). Inform. Sci. 2018, 128–144. [Google Scholar] [CrossRef]
- Ding, X.; Han, J.; Shi, L. The optimization based dynamic and cyclic working strategies for rechargeable wireless sensor networks with multiple base stations and wireless energy transfer devices. Sensors 2015, 15, 6270–6305. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Zhou, J.; Guo, C.; Song, H.; Wu, G.; Obaidat, M.S. TSCA: A Temporal-Spatial Real-Time Charging Scheduling Algorithm for On-Demand Architecture in Wireless Rechargeable Sensor Networks. IEEE Trans. Mobile Comput. 2018, 1, 211–224. [Google Scholar] [CrossRef]
- Han, G.; Qian, A.; Jiang, J.; Sun, N.; Liu, L. A grid-based joint routing and charging algorithm for industrial wireless rechargeable sensor networks. Comput. Netw. 2016, 19–28. [Google Scholar] [CrossRef]
- Jia, J.; Chen, J.; Deng, Y.S.; Wang, X.W.; Aghvami, A.H. Joint Power Charging and Routing in Wireless Rechargeable Sensor Networks. Sensors 2017, 17, 2290. [Google Scholar] [CrossRef] [PubMed]
- Zhong, P.; Li, Y.T.; Liu, W.R.; Duan, G.H.; Chen, Y.W.; Xiong, N. Joint Mobile Data Collection and Wireless Energy Transfer in Wireless Rechargeable Sensor Networks. Sensors 2017, 17, 1881. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Wang, C.; Yang, Y. Joint Mobile Data Gathering and Energy Provisioning in Wireless Rechargeable Sensor Networks. IEEE Trans. Mob. Comput. 2014, 12, 2836–2852. [Google Scholar] [CrossRef]
- Zhao, M.; Li, J.; Yang, Y. A Framework of Joint Mobile Energy Replenishment and Data Gathering in Wireless Rechargeable Sensor Networks. IEEE Trans. Mob. Comput. 2014, 12, 2689–2705. [Google Scholar] [CrossRef]
- Pezzella, F.; Morganti, G.; Ciaschetti, G. A genetic algorithm for the Flexible Job-shop Scheduling Problem. Comput. Oper. Res. 2008, 10, 3202–3212. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, Z.; Liu, M. A preference-inspired multi-objective soft scheduling algorithm for the practical steelmaking-continuous casting production. Comput. Ind. Eng. 2018, 582–594. [Google Scholar] [CrossRef]
- Liu, L.; Hu, R.; Hu, X.; Zhao, G.; Wang, S. A hybrid PSO-GA algorithm for job shop scheduling in machine tool production. Int. J. Prod. Res. 2015, 19, 5755–5781. [Google Scholar] [CrossRef]
- Aydemir, E.; Koruca, H.I. A new production scheduling module using priority-rule based genetic algorithm. Int. J. Simul. Model. 2015, 3, 450–462. [Google Scholar] [CrossRef]
- Xu, W.; Wang, R.; Yang, J. An improved league championship algorithm with free search and its application on production scheduling. J. Intell. Manuf. 2018, 1, 165–174. [Google Scholar] [CrossRef]
- Zhang, R. Sustainable Scheduling of Cloth Production Processes by Multi-Objective Genetic Algorithm with Tabu-Enhanced Local Search. Sustainability 2017, 10, 1754. [Google Scholar] [CrossRef]
- Tian, G.; Zhang, H.; Feng, Y.; Wang, D.; Peng, Y.; Jia, H. Green decoration materials selection under interior environment characteristics: A grey-correlation based hybrid MCDM method. Renew. Sustain. Energy Rev. 2018, 682–692. [Google Scholar] [CrossRef]
- Boscaino, V.; Pellitteri, F.; Rosa, L.; Capponi, G. Wireless battery chargers for portable applications: Design and test of a high-efficiency power receiver. IET Power Electron. 2013, 1, 20–29. [Google Scholar] [CrossRef]
- Framinan, J.M.; Ruiz, R. Guidelines for the deployment and implementation of manufacturing scheduling systems. Int. J. Prod. Res. 2012, 7, 1799–1812. [Google Scholar] [CrossRef]
- Bensten, A. Genetic Algorithms in Applications; Scitus Academics LLC: Valley Cottage, NY, USA, 2017; ISBN 9781681172637. [Google Scholar]
- Narayanan, A.; Moore, M. Quantum-inspired genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996. [Google Scholar]
- Kuk-Hyun, H.; Jong-Hwan, K. Genetic quantum algorithm and its application to combinatorial optimization problem. In Proceedings of the 2000 Congress on Evolutionary Computation, CEC00 (Cat. No. 00TH8512), La Jolla, CA, USA, 16–19 July 2000. [Google Scholar]
- Kong, H.; Li, N.; Shen, Y. Adaptive double chain quantum genetic algorithm for constrained optimization problems. Chin. J. Aeronaut. 2015, 1, 214–228. [Google Scholar] [CrossRef]
- Chen, P.; Yuan, L.; He, Y.; Luo, S. An improved SVM classifier based on double chains quantum genetic algorithm and its application in analogue circuit diagnosis. Neurocomputing 2016, 202–211. [Google Scholar] [CrossRef]

| Notation | Definition |
|---|---|
| n | The total number of workpieces |
| The ith workpiece, i = 1, 2, …, n | |
| The number of workstages for the workpiece | |
| m | The total number of machines |
| The kth machine, k = 1, 2, …, m | |
| q | The total number of wireless sensors |
| The rth wireless sensor, r = 1, 2, …, q | |
| The jth workstage of the workpiece , j = 1, 2, …, | |
| The processing time of the workstage on the machine | |
| The beginning time of the workstage | |
| The finishing time of the workstage | |
| The completion time of the workpieces , i = 1, 2, …, n | |
| The battery capacity of the wireless sensor, r = 1, 2, …, q | |
| The working output current of the wireless sensor , r = 1, 2, …, q | |
| The charging input current of the wireless sensor , r = 1, 2, …, q | |
| The maximum completion time of the entire production tasks |
| Variables | Definitions |
|---|---|
| If the workstage is processed on the machine , then ; otherwise | |
| The sequence number of the workstage processed on the machine | |
| The processing sequence of the workstage processed on the machine | |
| The vth value of the processing sequence indicates the workstage is processed on machine , where | |
| If the wireless sensor is mounted on the machine , then ; otherwise | |
| If the vth workstage of machine finishes and the associated wireless sensor starts charging at once, then ; otherwise |
| Workpieces | Workstages | M1 | M2 | M3 | M4 | M5 |
|---|---|---|---|---|---|---|
| W1 | O11 | 1 | 3 | 4 | 1 | 3 |
| O12 | 3 | 8 | 2 | 1 | 10 | |
| O13 | 3 | 5 | 4 | 7 | 4 | |
| O14 | 4 | 1 | 1 | 3 | 1 | |
| W2 | O21 | 2 | 3 | 9 | 3 | 6 |
| O12 | 9 | 1 | 2 | 5 | 7 | |
| O13 | 8 | 6 | 3 | 5 | 6 | |
| W3 | O31 | 4 | 5 | 8 | 1 | 2 |
| O32 | 10 | 7 | 3 | 5 | 9 | |
| O33 | 6 | 5 | 6 | 10 | 7 | |
| O34 | 2 | 2 | 5 | 8 | 4 | |
| O35 | 8 | 3 | 7 | 4 | 5 | |
| W4 | O41 | 7 | 6 | 4 | 7 | 3 |
| O42 | 5 | 3 | 7 | 9 | 2 | |
| O43 | 4 | 5 | 9 | 3 | 6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Wang, Y.; Zheng, H.; Mi, S.; Tan, J. A Framework of Joint Energy Provisioning and Manufacturing Scheduling in Smart Industrial Wireless Rechargeable Sensor Networks. Sensors 2018, 18, 2591. https://doi.org/10.3390/s18082591
Feng Y, Wang Y, Zheng H, Mi S, Tan J. A Framework of Joint Energy Provisioning and Manufacturing Scheduling in Smart Industrial Wireless Rechargeable Sensor Networks. Sensors. 2018; 18(8):2591. https://doi.org/10.3390/s18082591
Chicago/Turabian StyleFeng, Yixiong, Yong Wang, Hao Zheng, Shanghua Mi, and Jianrong Tan. 2018. "A Framework of Joint Energy Provisioning and Manufacturing Scheduling in Smart Industrial Wireless Rechargeable Sensor Networks" Sensors 18, no. 8: 2591. https://doi.org/10.3390/s18082591
APA StyleFeng, Y., Wang, Y., Zheng, H., Mi, S., & Tan, J. (2018). A Framework of Joint Energy Provisioning and Manufacturing Scheduling in Smart Industrial Wireless Rechargeable Sensor Networks. Sensors, 18(8), 2591. https://doi.org/10.3390/s18082591






