Temperature Sensing Performance of Microsphere Resonators
Abstract
1. Introduction
- Amorphous silicone microsphere resonators
- Silica glass microsphere resonators with different structure
- Compound glass microsphere resonators
- Droplet microsphere resonators
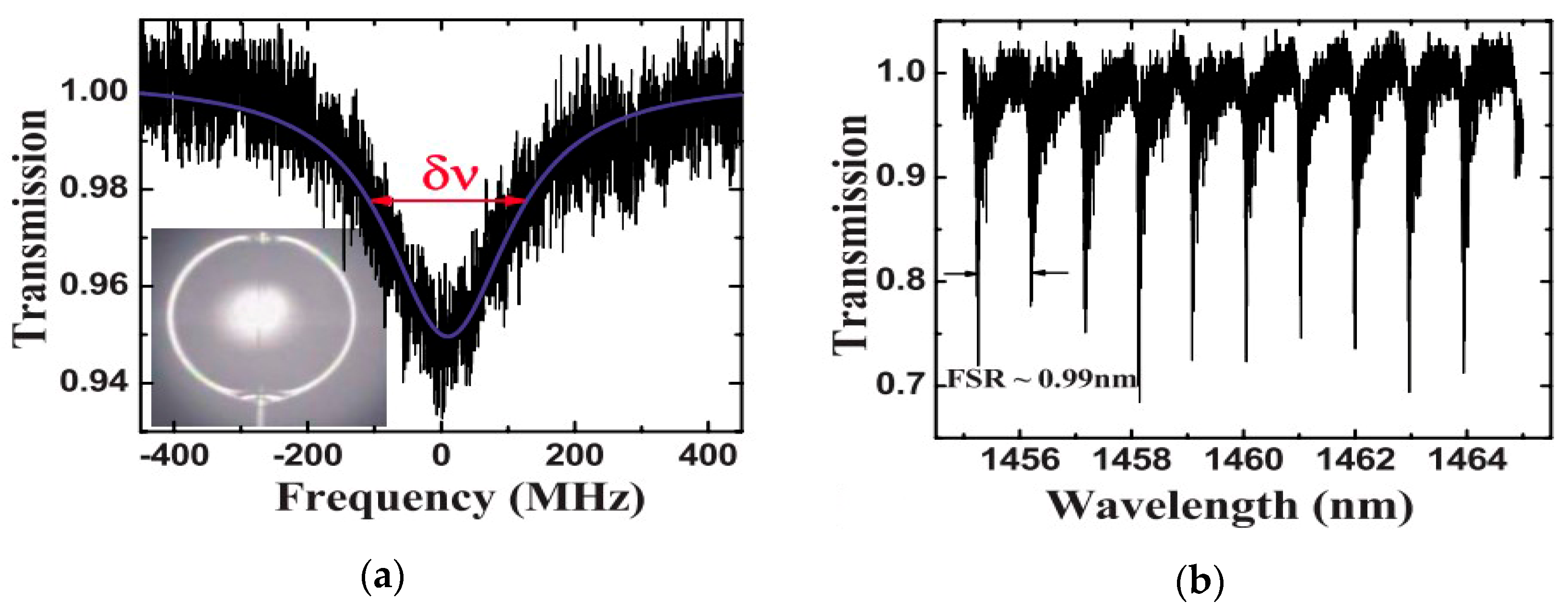
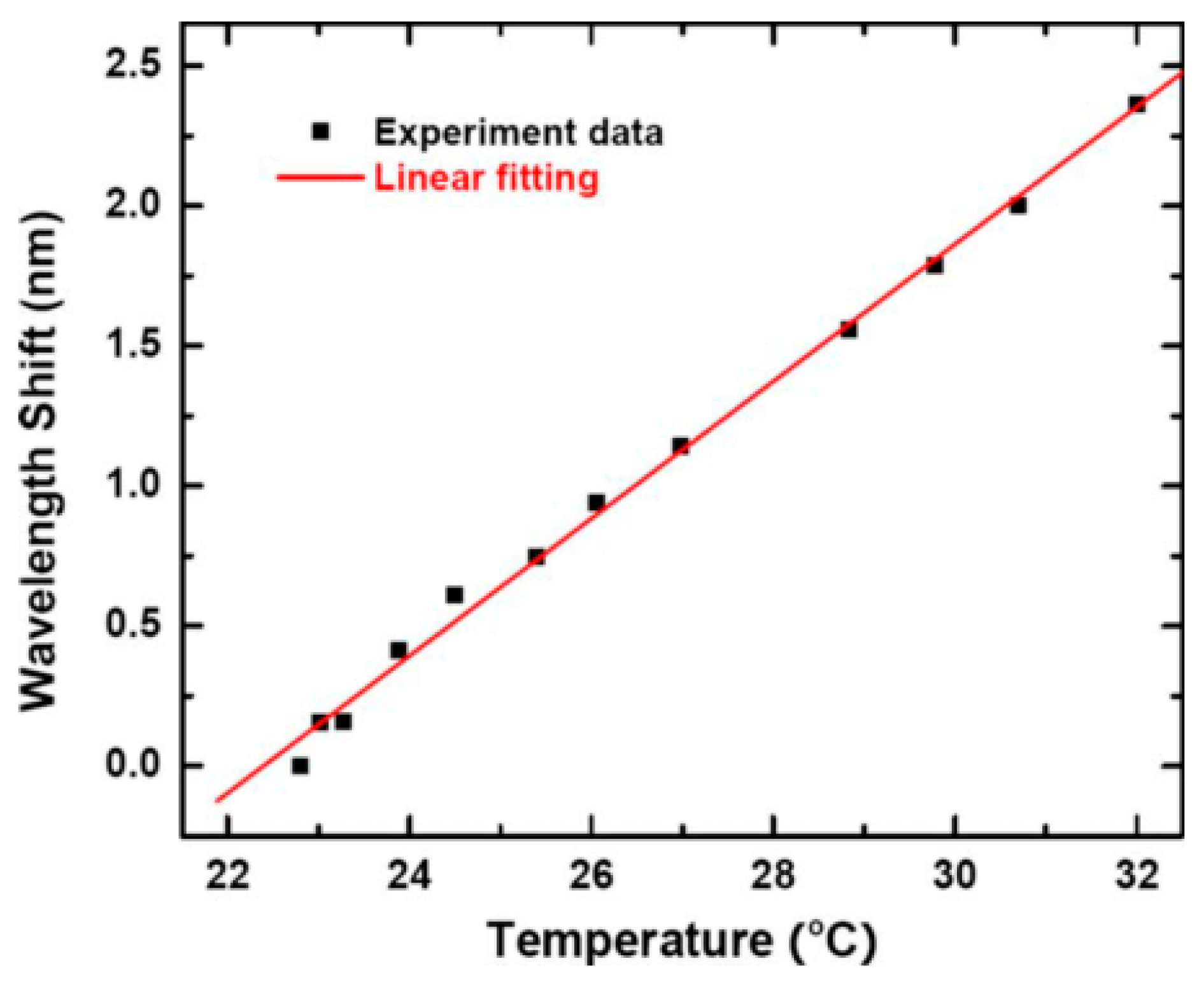
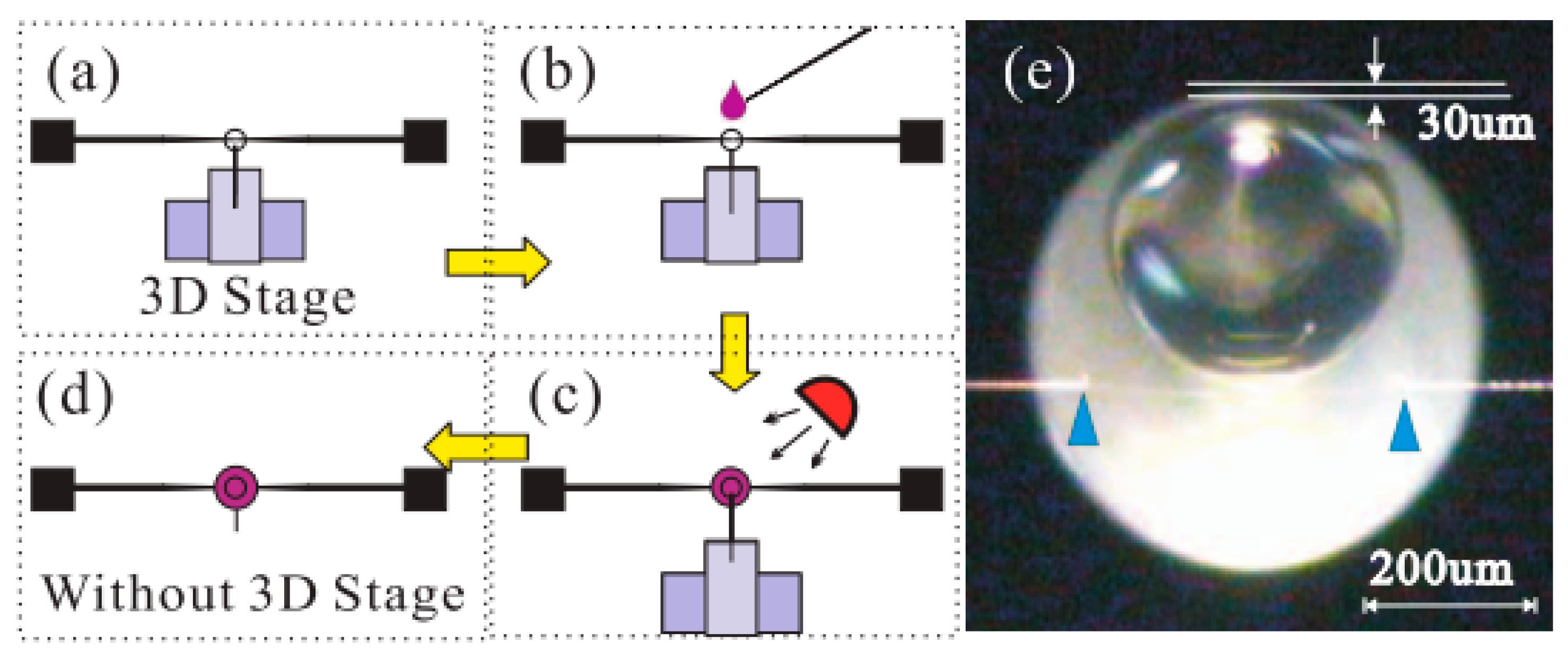
2. Silicone Glass Microsphere Resonators
3. Silica Glass Microsphere Resonators
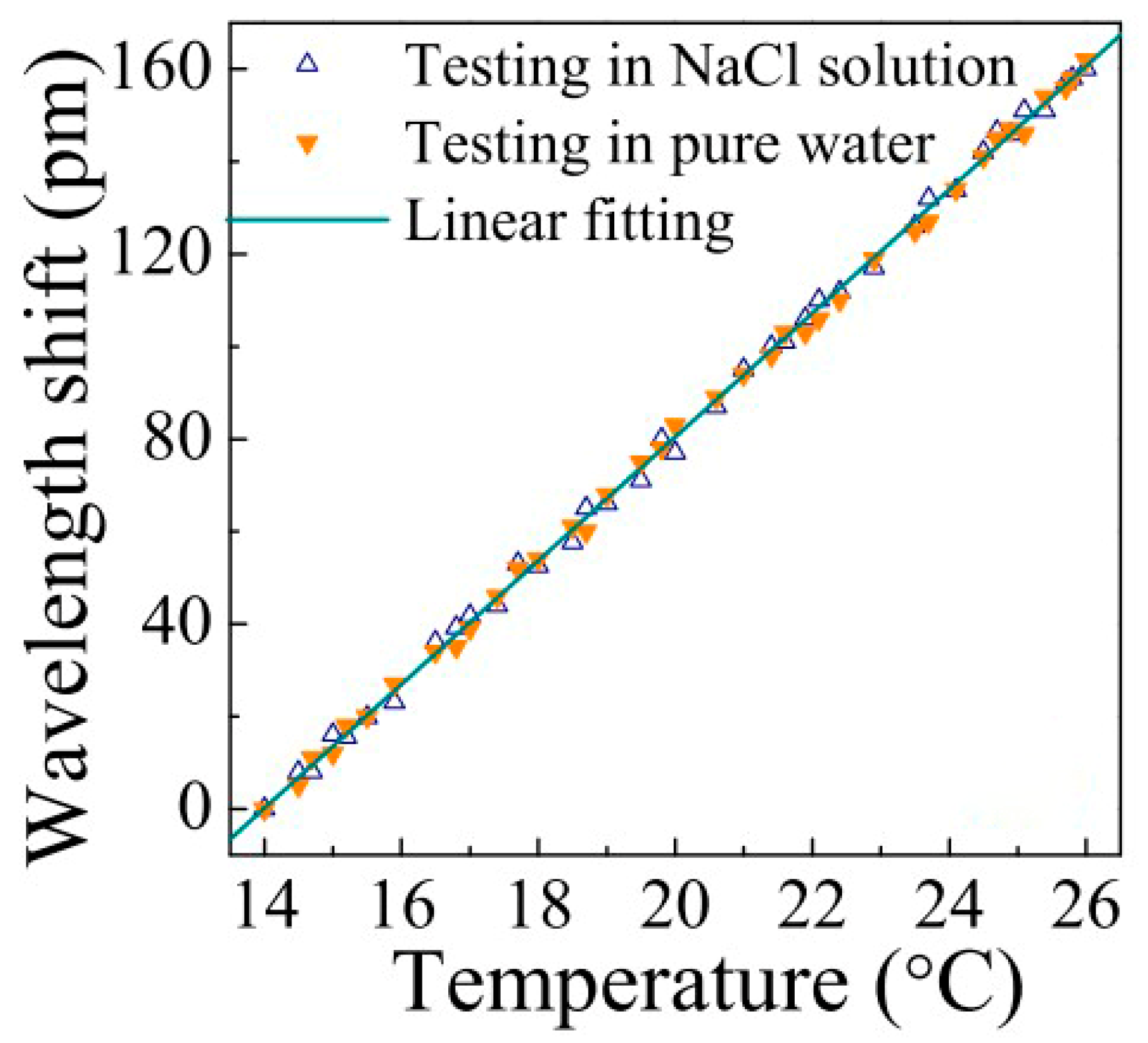
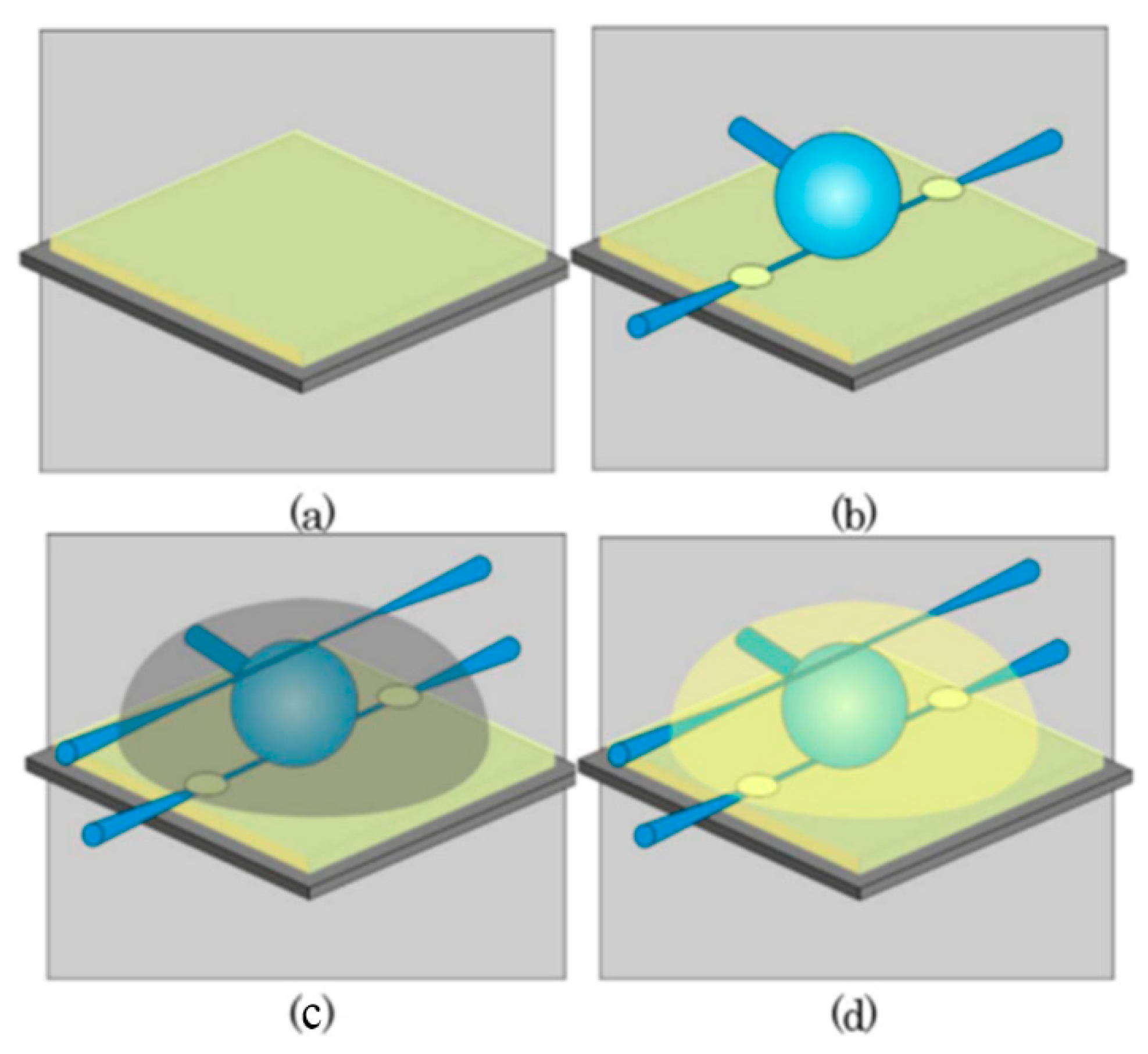
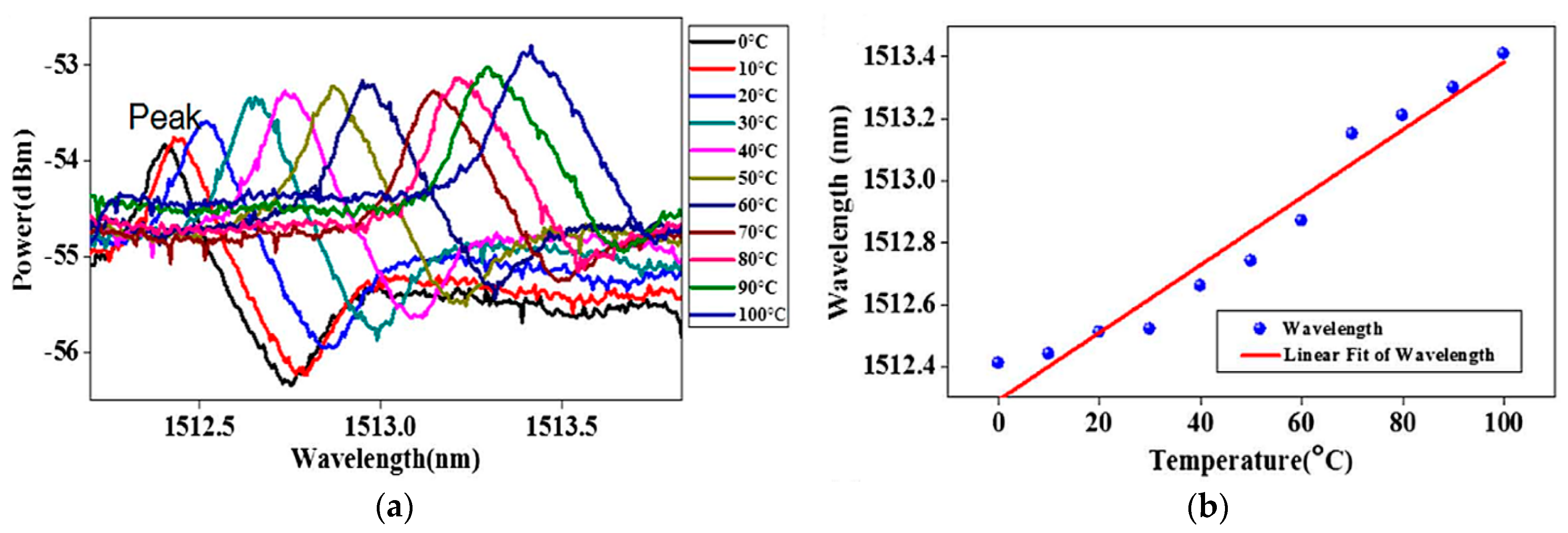
3.1. Conventional Silica Glass Microsphere Resonators
3.2. Packaged Silica Glass Microsphere Resonators
4. Compound Glass Microsphere Resonators
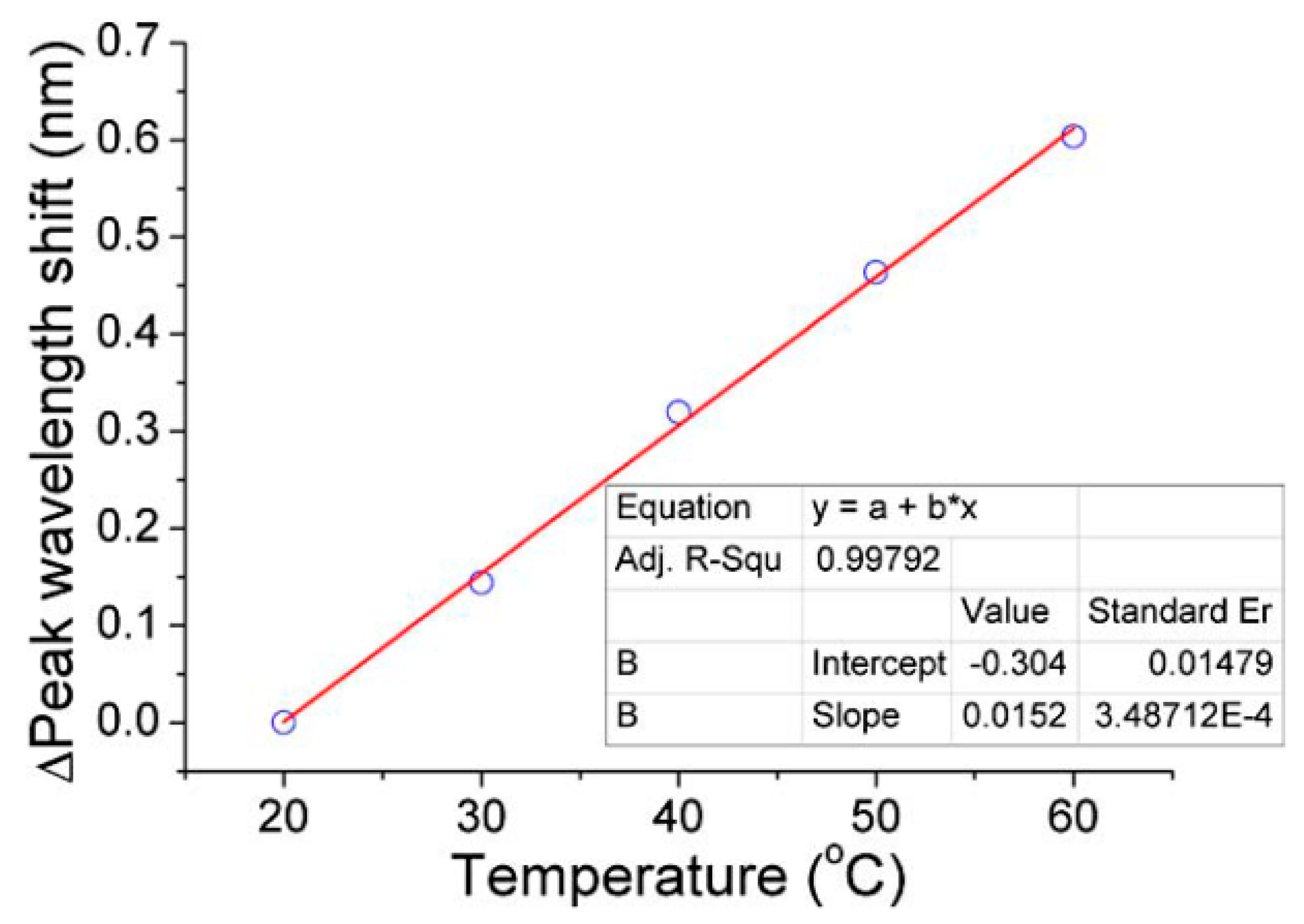
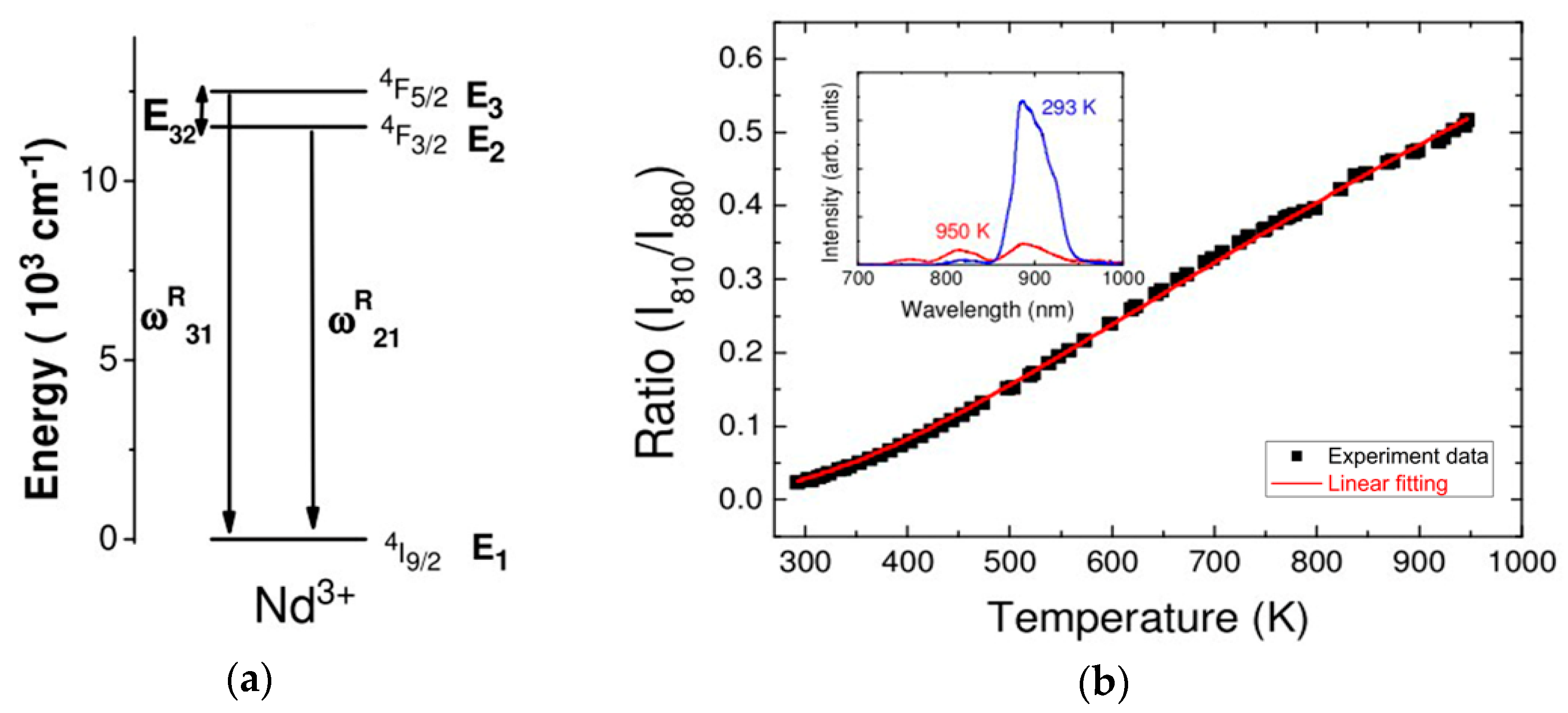
4.1. Nd3+ Doped BaTiO3 Glass Microsphere Resonators
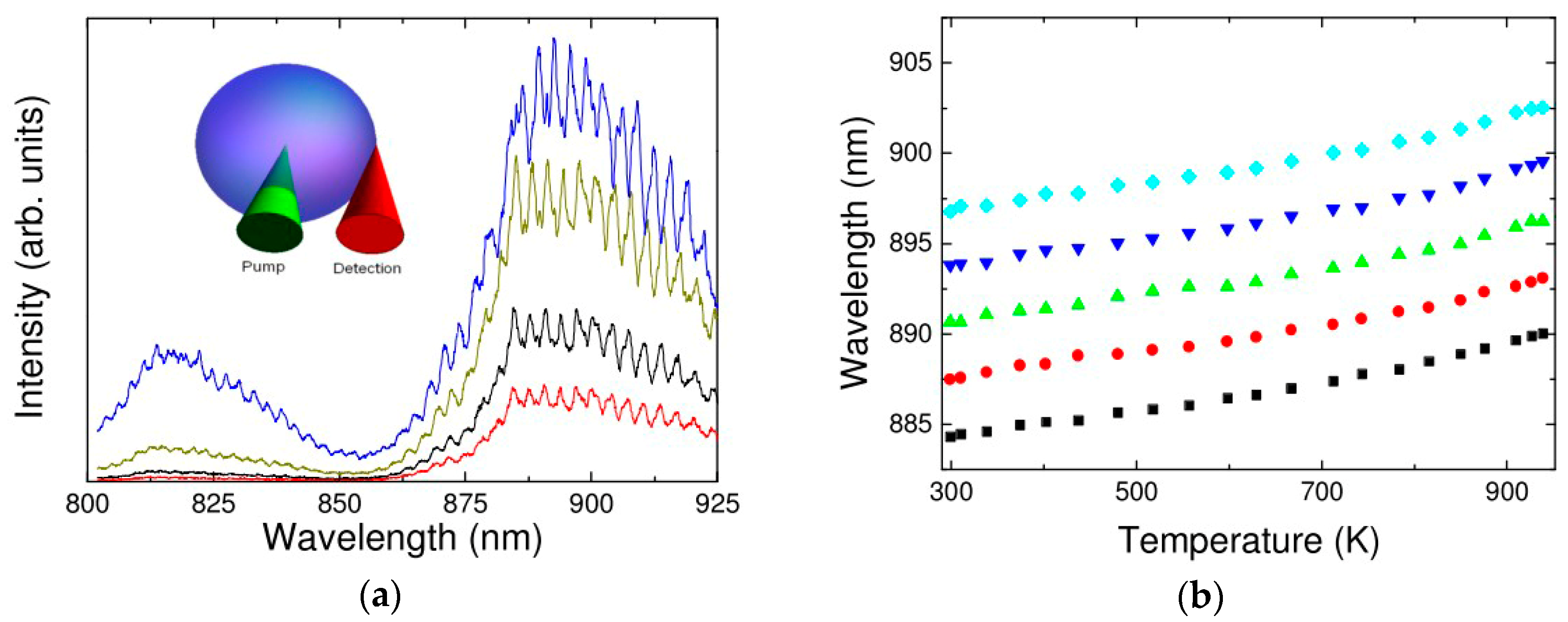
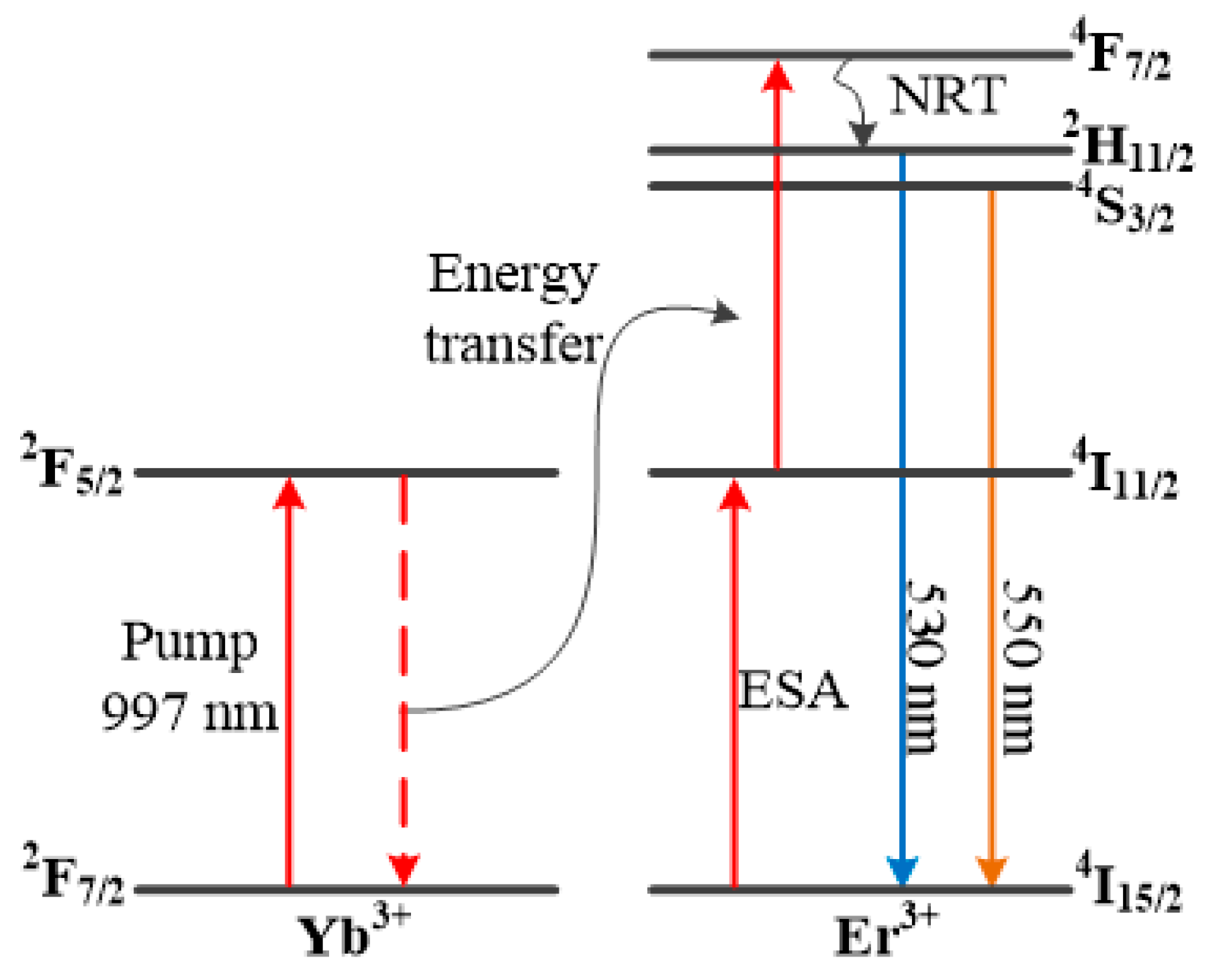
4.2. Er3+-Yb3+ Co-Doped Strontium Barium Niobate Glass Microsphere Resonators
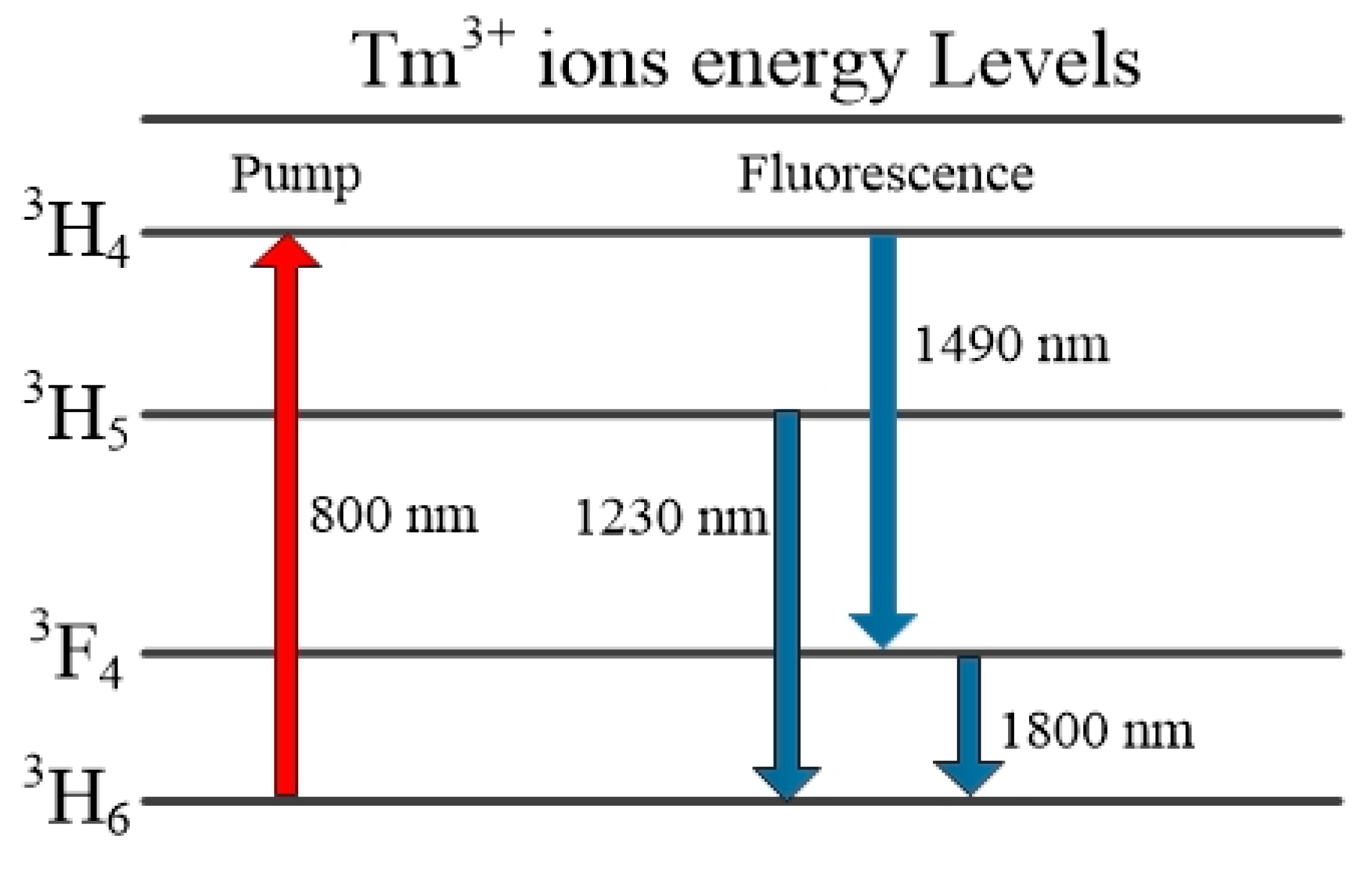
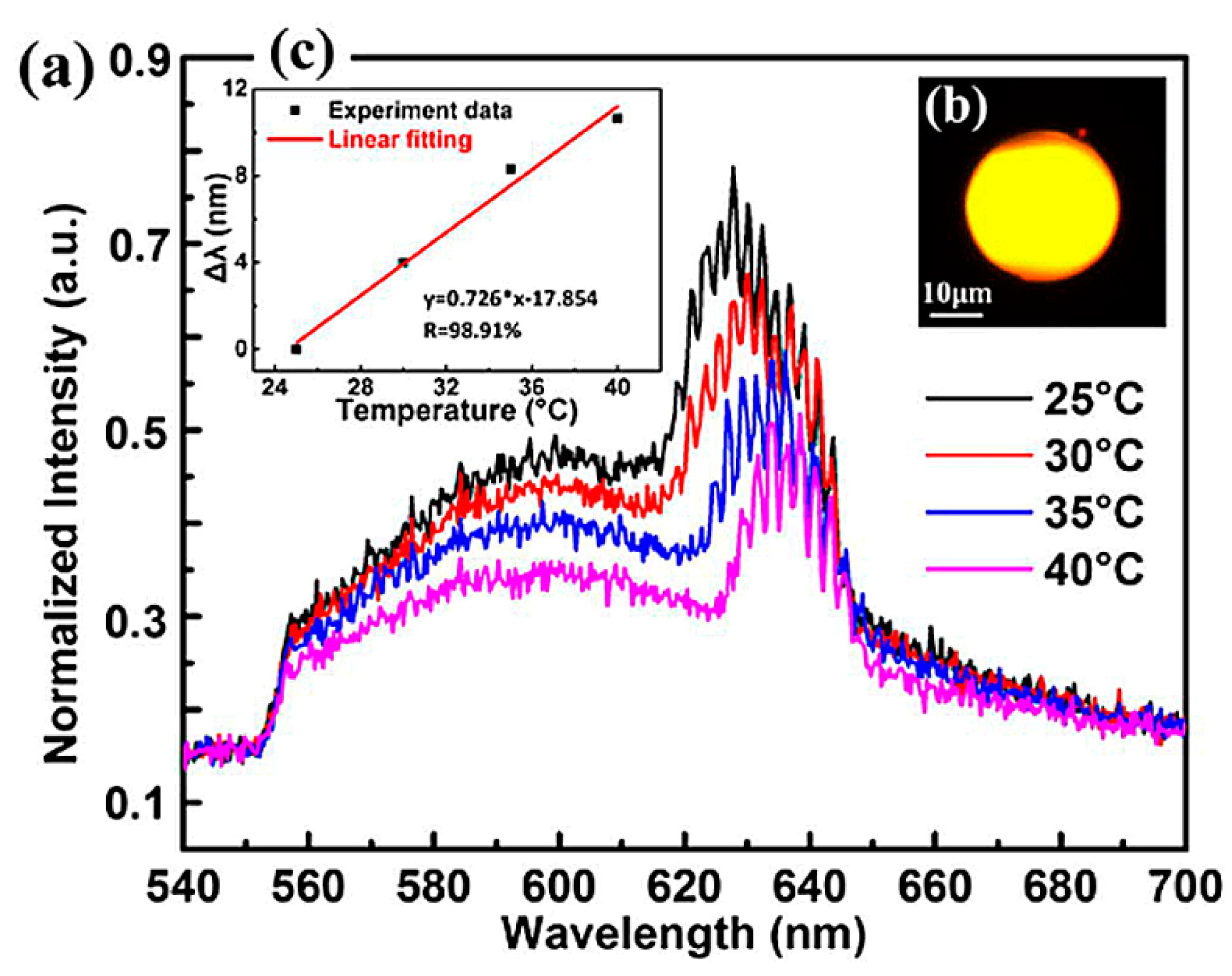
4.3. Chalcogenide Glass Microsphere Resonators
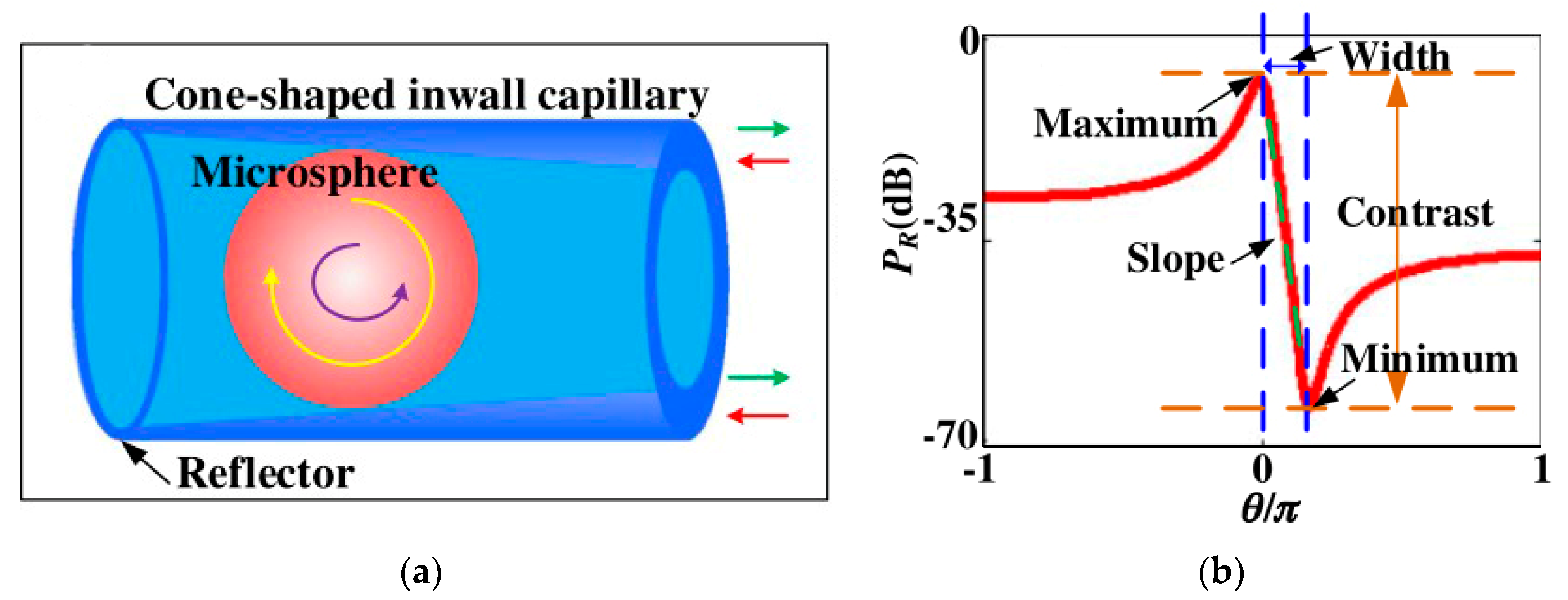
4.4. BaTiO3 Microsphere Resonators Based on Inwall Capillary
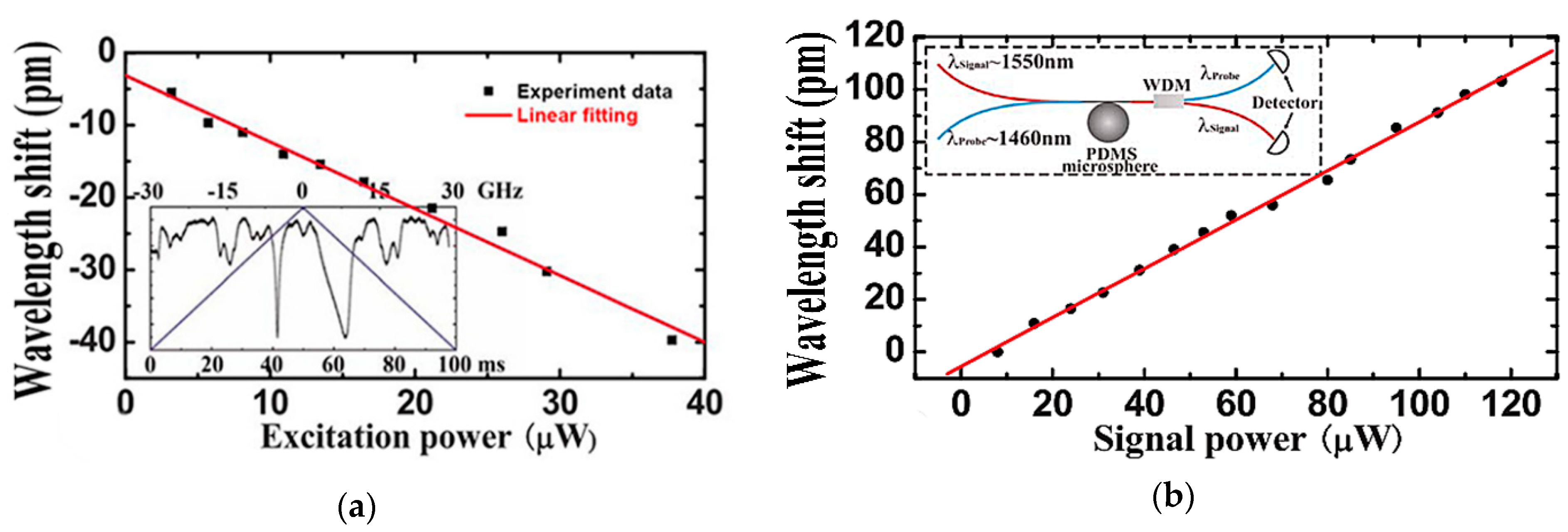
5. Droplet Microsphere Resonators
5.1. Dichloromethane Dye Doped Droplet Microsphere Resonators
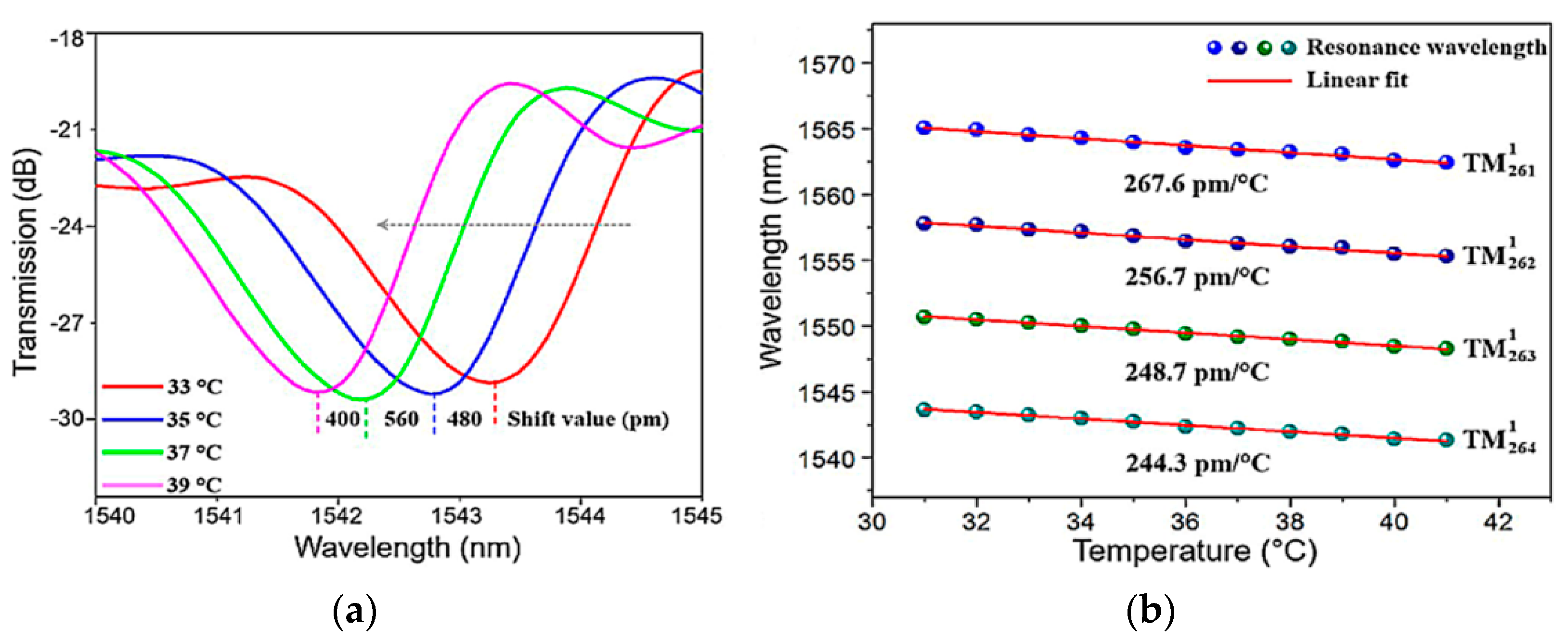
5.2. Liquid Crystal Microsphere Resonators
6. Comparison between Different Types of Microsphere Resonators
7. Conclusions and Outlook
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Moodera, J.S.; Kinder, L.R.; Wong, T.M.; Meservey, R. Large magnetoresistance at room temperature in ferromagnetic thin film tunnel junctions. Phys. Rev. Lett. 1995, 74, 3273–3276. [Google Scholar] [CrossRef] [PubMed]
- Lange, R.A.; Frey, H.M.; Hector, J. A thermodynamic model for the plagioclase-liquid hygrometer/thermometer. Am. Mineral. 2009, 94, 494–506. [Google Scholar] [CrossRef]
- David, R.; Hunter, I.W. A liquid-in-glass thermometer read by an interferometer. Sens. Actuators A Phys. 2005, 121, 31–34. [Google Scholar] [CrossRef]
- De Leeuw, A.A.C.; Crezee, J.; Lagendijk, J.J.W. Temperature and SAR measurements in deep-body hyperthermia with thermocouple thermometry. Int. J. Hyperth. 1993, 9, 685–697. [Google Scholar] [CrossRef]
- Carnochan, P.; Dickinson, R.J.; Joiner, M.C. The practical use of thermocouples for temperature measurement in clinical hyperthermia. Int. J. Hyperth. 1986, 2, 1–19. [Google Scholar] [CrossRef]
- Venkatasubramanian, R.; Siivola, E.; Colpitts, T.; O’Quinn, B. Thin-film thermoelectric devices with high room- temperature figures of merit. Nature 2001, 413, 597–602. [Google Scholar] [CrossRef] [PubMed]
- Childs, P.R.N.; Greenwood, J.R.; Long, C.A. Review of temperature measurement. Rev. Sci. Instrum. 2000, 71, 2959–2978. [Google Scholar] [CrossRef]
- Reindl, L.; Shrena, I.; Kenshil, S.; Peter, R. Wireless measurement of temperature using surface acoustic waves sensors. In Proceedings of the 2003 IEEE International Frequency Control Symposium, PDA Exhibition Jointly with the 17th European Frequency and Time Forum, Tampa, FL, USA, 4–8 May 2003; pp. 935–941. [Google Scholar]
- Moldover, M.R.; Tew, W.L.; Yoon, H.W. Advances in thermometry. Nat. Phys. 2016, 12, 7–11. [Google Scholar] [CrossRef] [PubMed]
- Khuri-Yakub, B.T.; Saraswat, K. Temperature measurement in rapid thermal processing using the acoustic temperature sensor. IEEE Trans. Semicond. Manuf. 1996, 9, 115–121. [Google Scholar] [CrossRef]
- Rempe, J.L.; Knudson, D.L.; Condie, K.G.; Crepeau, J.C.; Daw, J.E.; Wilkins, S.C. Options Extending the Applicability of High-Temperature Irradiation-Resistant Thermocouples. Nucl. Technol. 2009, 167, 169–177. [Google Scholar] [CrossRef]
- Beresna, M.; Gecevičius, M.; Kazansky, P.G. Ultrafast laser direct writing and nanostructuring in transparent materials. Adv. Opt. Photonics 2014, 6, 293–339. [Google Scholar] [CrossRef]
- Murphy, A.; Farmer, A. Temperature measurement in thermal plasmas by Rayleigh scattering. J. Phys. D Appl. Phys. 2000, 25, 634–643. [Google Scholar] [CrossRef]
- Fujishima, H. Corneal temperature in patients with dry eye evaluated by infrared radiation thermometry. Br. J. Ophthalmol. 1996, 80, 29–32. [Google Scholar] [CrossRef] [PubMed]
- Barrera, D.; Finazzi, V.; Villatoro, J.; Sales, S.; Pruneri, V. Packaged optical sensors based on regenerated fiber bragg gratings for high temperature applications. IEEE Sens. J. 2012, 12, 107–112. [Google Scholar] [CrossRef]
- Mihailov, S.J. Fiber bragg grating sensors for harsh environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.B.; Amtmann, K.; Ristein, J.; Ley, L. Noncontact temperature measurements of diamond by Raman scattering spectroscopy. J. Appl. Phys. 1998, 83, 7929–7933. [Google Scholar] [CrossRef]
- Dakin, J.P.; Pratt, D.J.; Bibby, G.W.; Ross, J.N. Distributed optical fibre Raman temperature sensor using a semiconductor light source and detector. Electron. Lett. 1985, 21, 569–570. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, L.; Zhu, Z.; Zhang, Y.; Wei, Y.; Zhang, X.; Zhao, E.; Zhang, Y.; Yang, J.; Yuan, L. Whispering gallery mode temperature sensor of liquid microresonastor. Opt. Lett. 2016, 41, 4649. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Wu, Y.; Zhang, X.; Zhang, W.; Xu, P.; Dai, S. Low temperature fabrication of chalcogenide microsphere resonators for thermal sensing. IEEE Photonics Technol. Lett. 2017, 29, 66–69. [Google Scholar] [CrossRef]
- Cai, Z.P.; Xiao, L.; Xu, H.Y.; Mortier, M. Point temperature sensor based on green decay in an Er:ZBLALiP microsphere. J. Lumin. 2009, 129, 1994–1996. [Google Scholar] [CrossRef]
- Martín, L.L.; Pérez-Rodríguez, C.; Haro-González, P.; Martín, I.R. Whispering gallery modes in a glass microsphere as a function of temperature. Opt. Express 2011, 19, 25792–25798. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.-H.; He, L.; Xiao, Y.-F.; Gaddam, V.R.; Ozdemir, S.K.; Han, Z.-F.; Guo, G.-C.; Yang, L. Fabrication of high-Q polydimethylsiloxane optical microspheres for thermal sensing. Appl. Phys. Lett. 2009, 94, 231119. [Google Scholar] [CrossRef]
- Teraoka, I.; Arnold, S. Whispering-gallery modes in a microsphere coated with a high-refractive index layer: Polarization-dependent sensitivity enhancement of the resonance-shift sensor and TE-TM resonance matching. J. Opt. Soc. Am. B 2007, 24, 653. [Google Scholar] [CrossRef]
- Tapalian, H.C.; Laine, J.P.; Lane, P.A. Thermooptical switches using coated microsphere resonators. IEEE Photonics Technol. Lett. 2002, 14, 1118–1120. [Google Scholar] [CrossRef]
- Maznev, A.A.; Hohlfeld, J.; Güdde, J. Surface thermal expansion of metal under femtosecond laser irradiation. J. Appl. Phys. 1997, 82, 5082–5085. [Google Scholar] [CrossRef]
- Gensch, T.; Viappiani, C. Time-resolved photothermal methods: Accessing time-resolved thermodynamics of photoinduced processes in chemistry and biologyDedicated to Professor Silvia Braslavsky, to mark her great contribution to photochemistry and photobiology particularly in the fi. Photochem. Photobiol. Sci. 2003, 2, 699–721. [Google Scholar] [CrossRef]
- Guo, Z.; Ma, Q. Erratum: Whispering-gallery mode silica microsensors for cryogenic to room temperature measurement (Measurement Science and Technology (2010) 21 (025310)). Meas. Sci. Technol. 2012, 23. [Google Scholar] [CrossRef]
- Wang, P.; Ding, M.; Murugan, G.S.; Bo, L.; Guan, C.; Semenova, Y.; Wu, Q.; Farrell, G.; Brambilla, G. Packaged, high-Q, microsphere-resonator-based add–drop filter. Opt. Lett. 2014, 39, 5208–5211. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.-Z.; Zou, C.-L.; Yan, S.-B.; Sun, F.-W.; Ji, Z.; Liu, J.; Zhang, Y.-G.; Wang, L.; Xue, C.-Y.; Zhang, W.-D.; et al. Packaged silica microsphere-taper coupling system for robust thermal sensing application. Opt. Express 2011, 19, 5753–5759. [Google Scholar] [CrossRef] [PubMed]
- Wade, S.A.; Collins, S.F.; Baxter, G.W. Fluorescence intensity ratio technique for optical fiber point temperature sensing. J. Appl. Phys. 2003, 94, 4743–4756. [Google Scholar] [CrossRef]
- Dos Santos, P.V.; De Araujo, M.T.; Gouveia-Neto, A.S.; Medeiros Neto, J.A.; Sombra, A.S.B. Optical temperature sensing using upconversion fluorescence emission in Er3+/Yb3+-codoped chalcogenide glass. Appl. Phys. Lett. 1998, 73, 578–580. [Google Scholar] [CrossRef]
- Alencar, M.A.R.C.; Maciel, G.S.; de Araújo, C.B.; Patra, A. Er3+-doped BaTiO3 nanocrystals for thermometry: Influence of nanoenvironment on the sensitivity of a fluorescence based temperature sensor. Appl. Phys. Lett. 2004, 84, 4753–4755. [Google Scholar] [CrossRef]
- Collins, S.F.; Baxter, G.W.; Wade, S.A.; Sun, T.; Grattan, K.T.V.; Zhang, Z.Y.; Palmer, A.W. Comparison of fluorescence-based temperature sensor schemes: Theoretical analysis and experimental validation. J. Appl. Phys. 1998, 84, 4649–4654. [Google Scholar] [CrossRef]
- Pérez-Rodríguez, C.; Labrador-Páez, L.; Martín, I.R.; Ríos, S. Temperature response of the whispering gallery mode resonances from the green upconversion emission of an Er3+-Yb3+ co-doped microsphere. Laser Phys. Lett. 2015, 12, 046003. [Google Scholar] [CrossRef]
- Martín, L.L.; Martín, I.R.; Haro-González, P. Transfer and backtransfer processes in Yb3+-Er3+ codoped Strontium Barium Niobate glass-ceramics. J. Lumin. 2011, 131, 2446–2450. [Google Scholar] [CrossRef]
- Li, B.B.; Xiao, Y.F.; Zou, C.L.; Jiang, X.F.; Liu, Y.C.; Sun, F.W.; Li, Y.; Gong, Q. Experimental controlling of Fano resonance in indirectly coupled whispering-gallery microresonators. Appl. Phys. Lett. 2012, 100, 021108. [Google Scholar] [CrossRef]
- Fan, S. Sharp asymmetric line shapes in side-coupled waveguide-cavity systems. Appl. Phys. Lett. 2002, 80, 908–910. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Y.; Bai, H.; Wang, J.; Yan, M.; Xiao, H.; Wang, T. Theoretical aspects and sensing demonstrations of cone-shaped inwall capillary-based microsphere resonators. Photonics Res. 2017, 5, 516–520. [Google Scholar] [CrossRef]
- Constable, A.; Kim, J.; Mervis, J.; Zarinetchi, F.; Prentiss, M. Demonstration of a fiber-optical light-force trap. Opt. Lett. 1993, 18, 1867–1869. [Google Scholar] [CrossRef] [PubMed]
- Kresge, C.T.; Leonowicz, M.E.; Roth, W.J.; Vartuli, J.C.; Beck, J.S. Ordered mesoporous molecular sieves synthesized by a liquid-crystal template mechanism. Nature 1992, 359, 710–712. [Google Scholar] [CrossRef]
- Ikeda, T.; Tsutsumi, O. Optical Switching and Image Storage by Means of Azobenzene Liquid-Crystal Films. Science 1995, 268, 1873–1875. [Google Scholar] [CrossRef] [PubMed]
- Humar, M.; Muševič, I. Surfactant sensing based on whispering-gallery-mode lasing in liquid-crystal microdroplets. Opt. Express 2011, 19, 19836–19844. [Google Scholar] [CrossRef] [PubMed]
- Humar, M.; Muševič, I. 3D microlasers from self-assembled cholesteric liquid-crystal microdroplets. Opt. Express 2010, 18, 26995–27003. [Google Scholar] [CrossRef] [PubMed]
- Humar, M.; Ravnik, M.; Pajk, S.; Muševič, I. Electrically tunable liquid crystal optical microresonators. Nat. Photonics 2009, 3, 595–600. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Zhao, L.; Liu, Y.; Liu, S.; Yang, J. Tapered optical fiber waveguide coupling to whispering gallery modes of liquid crystal microdroplet for thermal sensing application. Opt. Express 2017, 25, 918–926. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Gauza, S.; Wu, S.-T. Temperature effect on liquid crystal refractive indices. J. Appl. Phys. 2004, 96, 19–24. [Google Scholar] [CrossRef]
| Type | Structure | Coupling Method | Range | Maximum Sensitivity | Highest Resolution |
|---|---|---|---|---|---|
| 1. Silicone glass | PDMS microsphere [23] | Tapered fiber coupling | 295–305 K | 285 pm/°C | 0.2 mK |
| 2. Silica glass | Silica microsphere [28] | Tapered fiber coupling | 100–300 K | 11 pm/°C | 1.4 mK |
| UV packaged silica microsphere [30] | Tapered fiber coupling | 287–299 K | 13.37 pm/°C | 1.1 mK | |
| UV packaged add-drop silica microsphere [29] | Tapered fiber coupling | 293–333 K | 15.1 pm/°C | ||
| 3. Compound glass | Nd3+ doped BaTiO3 glass microsphere [22] | Free-space coupling | 300–950 K | 10 pm/°C | 0.1 K |
| Er3+-Yb3+ co-doped SBN glass microsphere [35] | Free-space coupling | 290–380 K | 4.7 pm/°C | 8 mK | |
| Tm3+ doped chalcogenide glass mcirosphere [20] | Tapered fiber coupling | 299–373 K | 28 pm/°C | ||
| Cone-shaped inwall BaTiO3 microsphere [39] | Capillary coupling | 273–373 K | 10.9 pm/°C | ||
| 4. Microdroplet | DCM doped droplet mcirosphere [19] | Free-sapce coupling | 298–313 K | 726 pm/°C | |
| LC droplet microsphere [46] | Tapered fiber coupling | 306–312 K | 267.6 pm/°C | 75 mK |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Lewis, E.; Brambilla, G.; Wang, P. Temperature Sensing Performance of Microsphere Resonators. Sensors 2018, 18, 2515. https://doi.org/10.3390/s18082515
Yu J, Lewis E, Brambilla G, Wang P. Temperature Sensing Performance of Microsphere Resonators. Sensors. 2018; 18(8):2515. https://doi.org/10.3390/s18082515
Chicago/Turabian StyleYu, Jibo, Elfed Lewis, Gilberto Brambilla, and Pengfei Wang. 2018. "Temperature Sensing Performance of Microsphere Resonators" Sensors 18, no. 8: 2515. https://doi.org/10.3390/s18082515
APA StyleYu, J., Lewis, E., Brambilla, G., & Wang, P. (2018). Temperature Sensing Performance of Microsphere Resonators. Sensors, 18(8), 2515. https://doi.org/10.3390/s18082515






