A Collaborative Data Collection Scheme Based on Optimal Clustering for Wireless Sensor Networks
Abstract
1. Introduction
- (1)
- We model the optimal clustering problem as a separable convex optimization problem and solve it analytically to obtain the optimal clustering size and the optimal transmission radius.
- (2)
- We design a cluster heads-linking algorithm based on the pseudo Hilbert curve to collect the compressed sensed data among cluster heads in a collaborative and accumulative manner.
- (3)
- We design a distributed cluster-constructing algorithm to construct the inter-cluster data collection structure around virtual cluster heads in a wireless sensor network.
2. Related Work
3. System Model and Clustering Analysis
3.1. Overview of the Compressed Sensing Theory
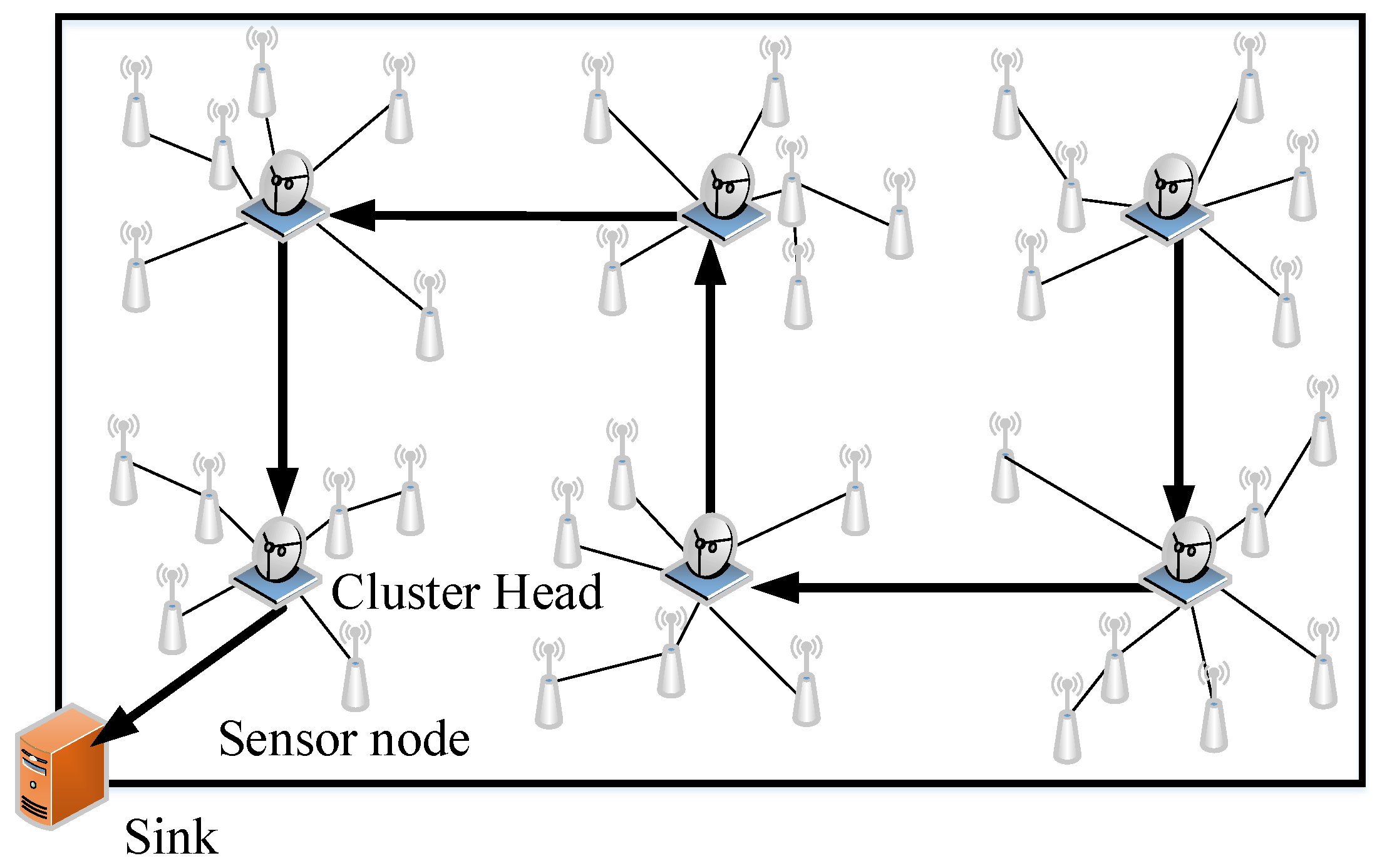
3.2. System Model
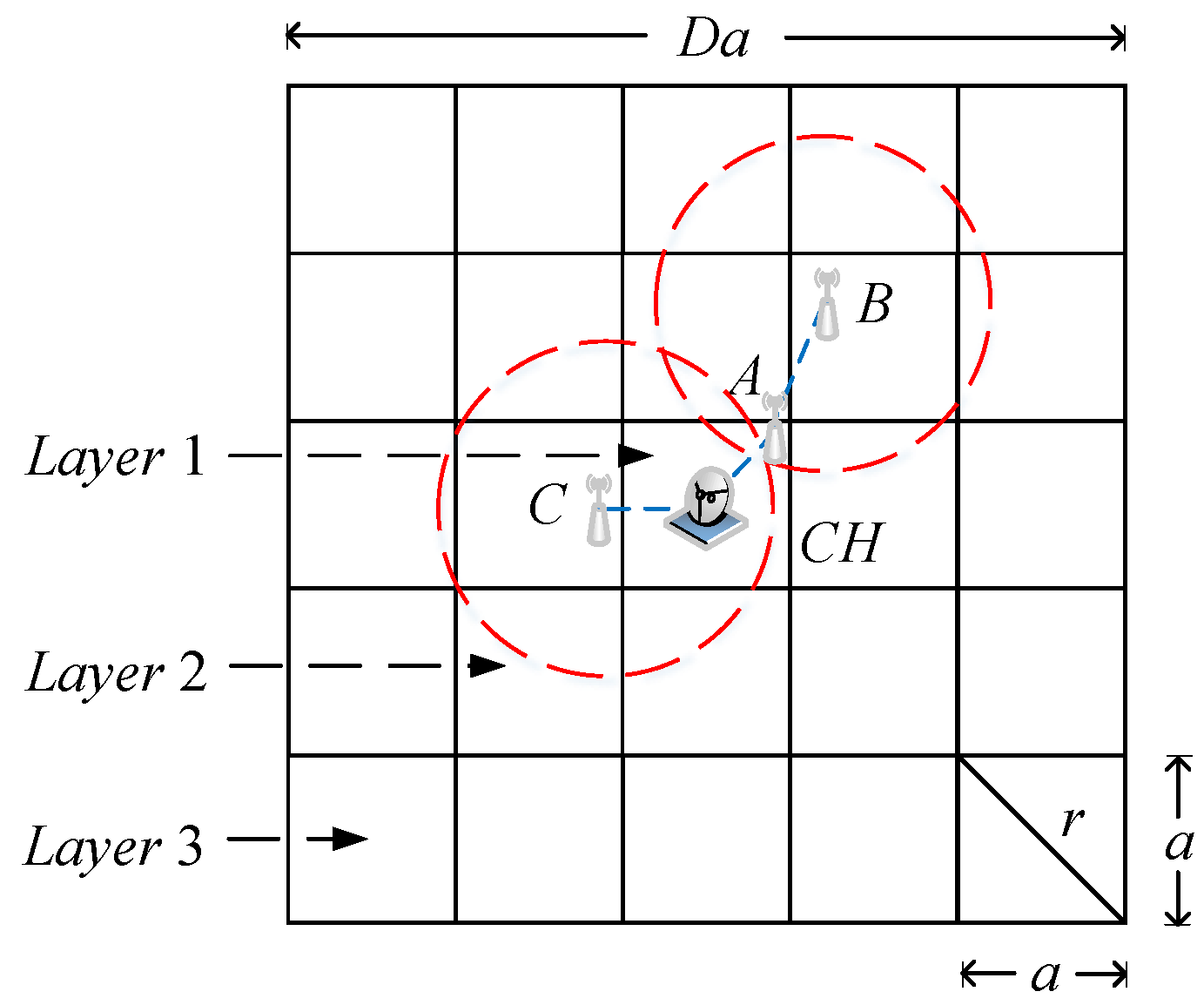
3.3. Clustering Analysis
- (1)
- All sensor nodes are randomly distributed in the surveillance area with an independent and identical distribution, which can be modelled as a Poisson point process with parameter .
- (2)
- All sensor nodes are set to the same level of data transmission power and data transmission rate. Therefore, the data transmission range of all sensor nodes is identical.
- (3)
- Every sensor node is aware of its location. A number of sensor localization algorithms for WSNs can be used for this purpose [32].
4. The Collaborative Data Collection Scheme
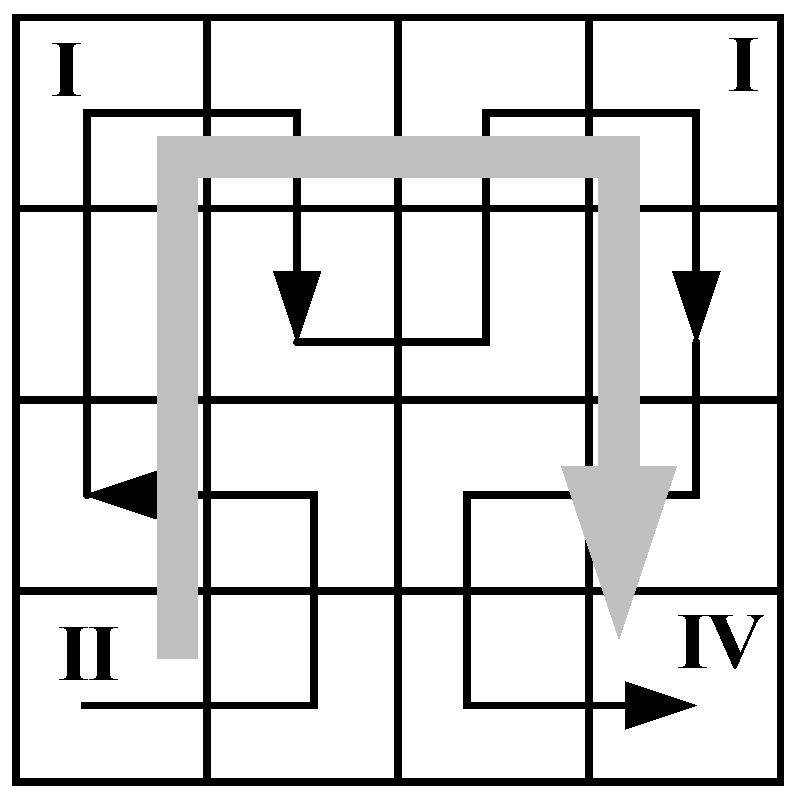
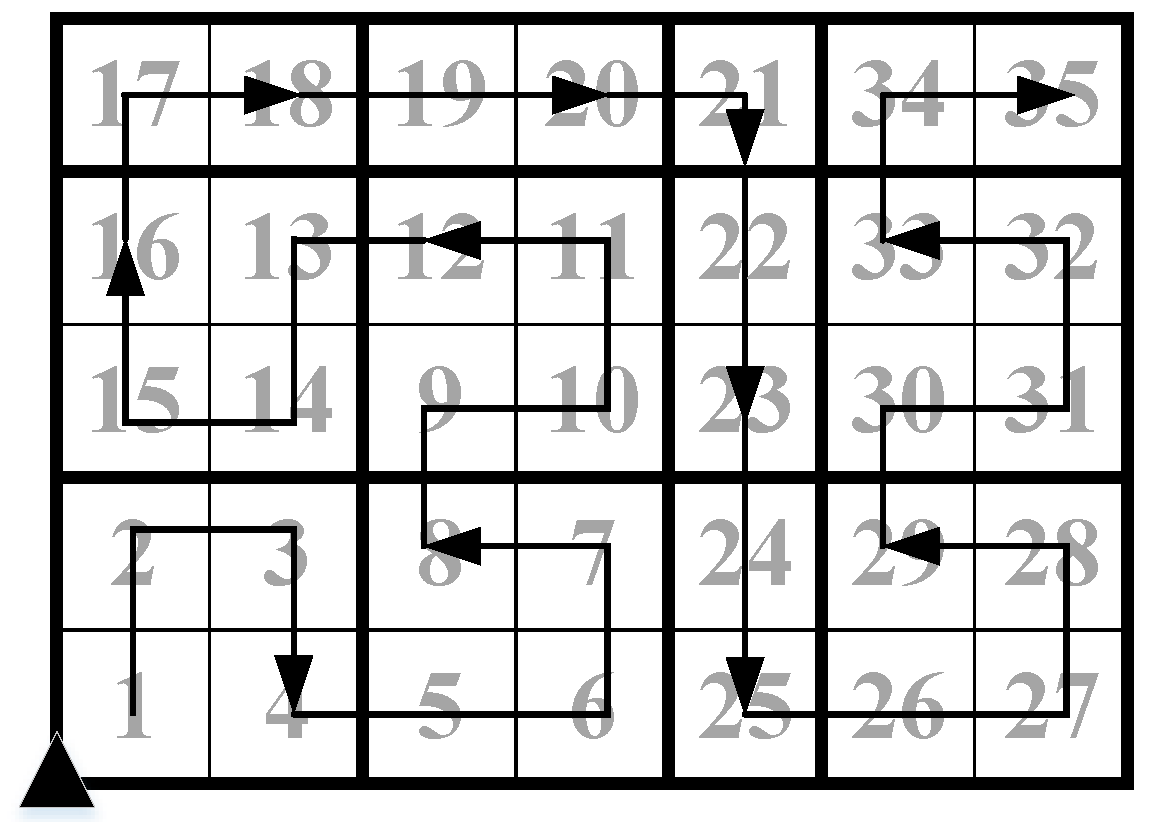
4.1. The Cluster Heads-Linking Algorithm Based on the Pseudo Hilbert Curve
| Algorithm 1 Cluster heads-linking algorithm based on the pseudo Hilbert curve. |
|
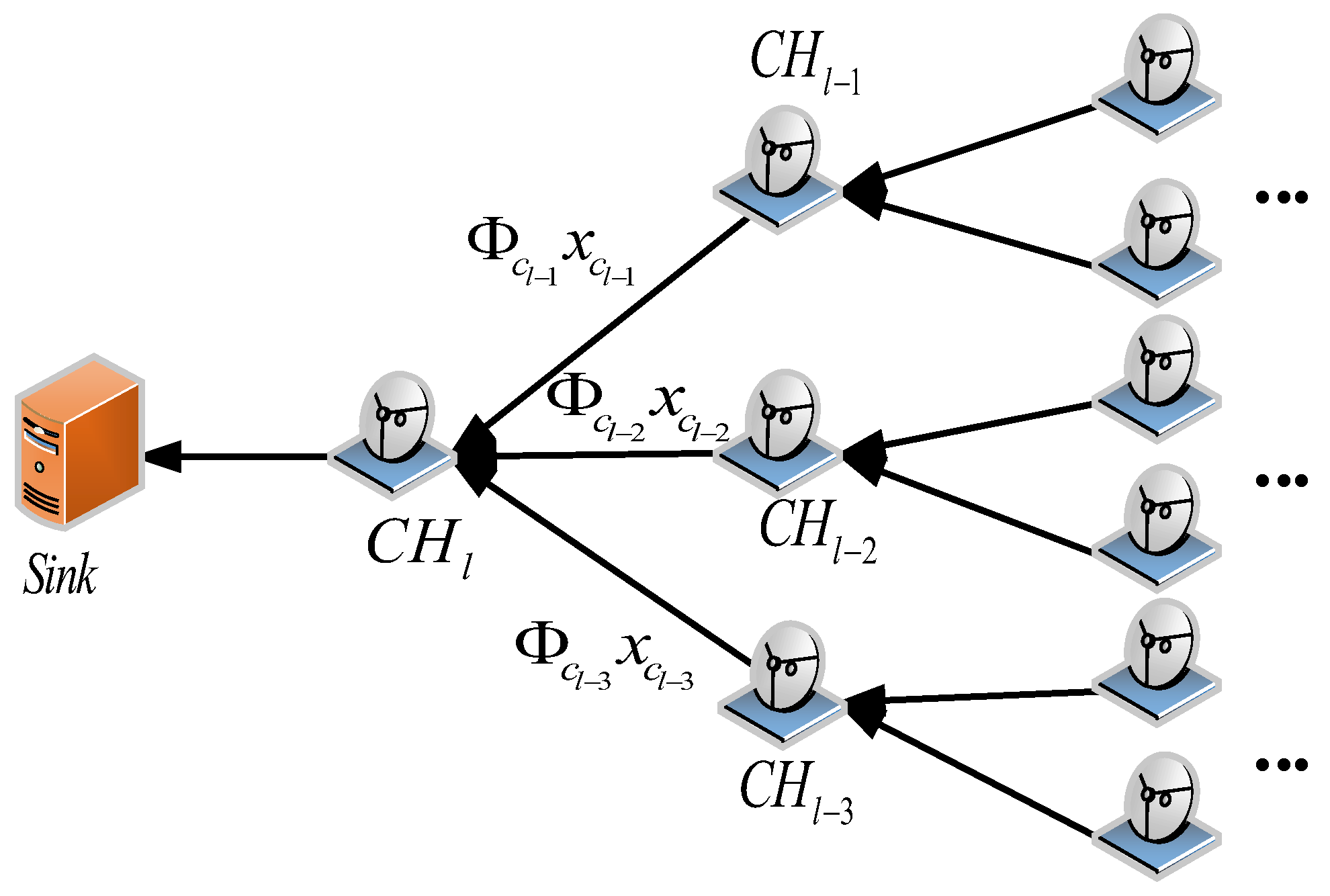
4.2. The Distributed Cluster Constructing Algorithm
| Algorithm 2 Distributed cluster-constructing algorithm. |
|
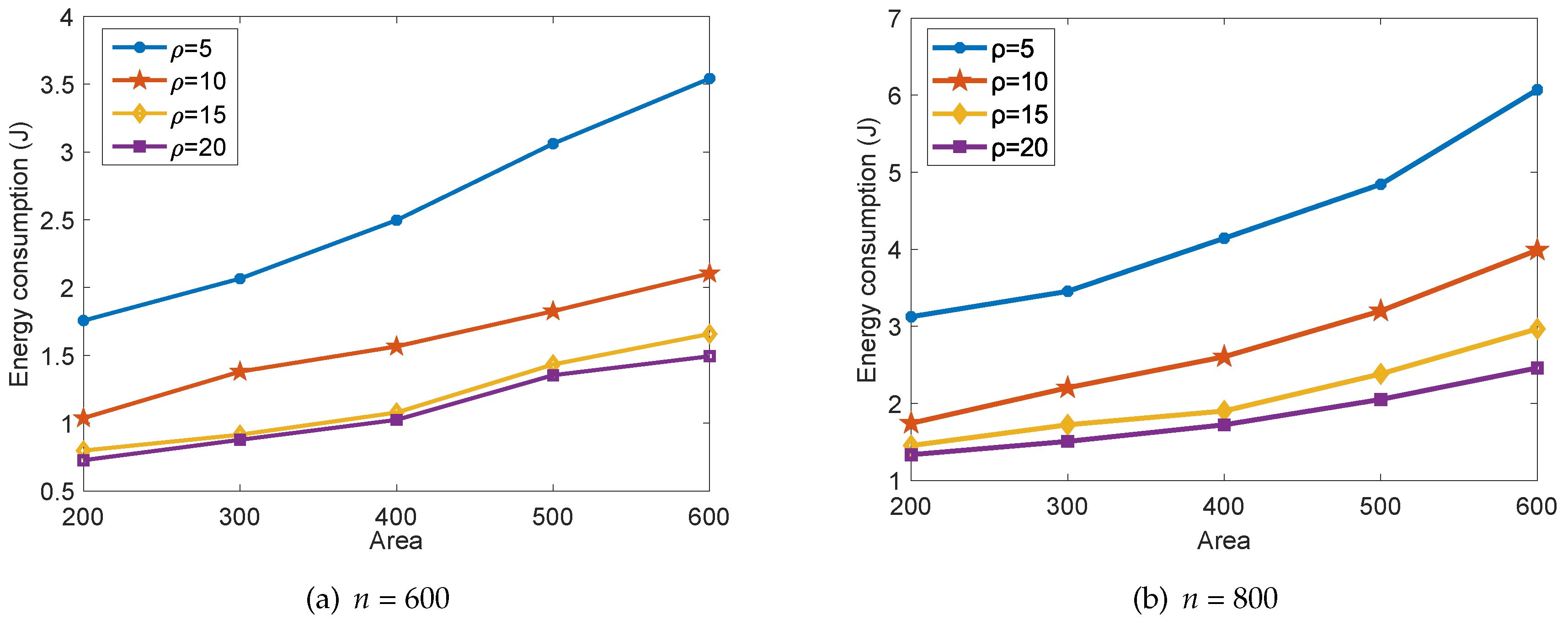
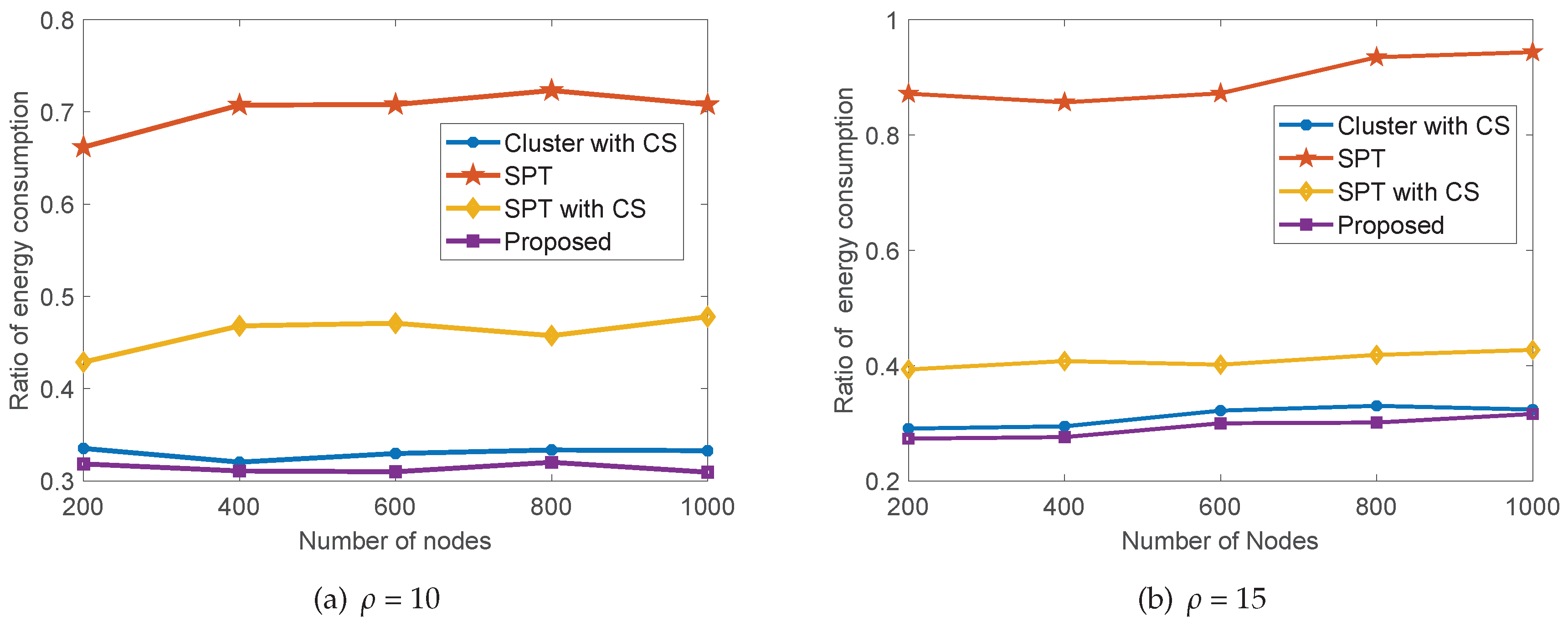
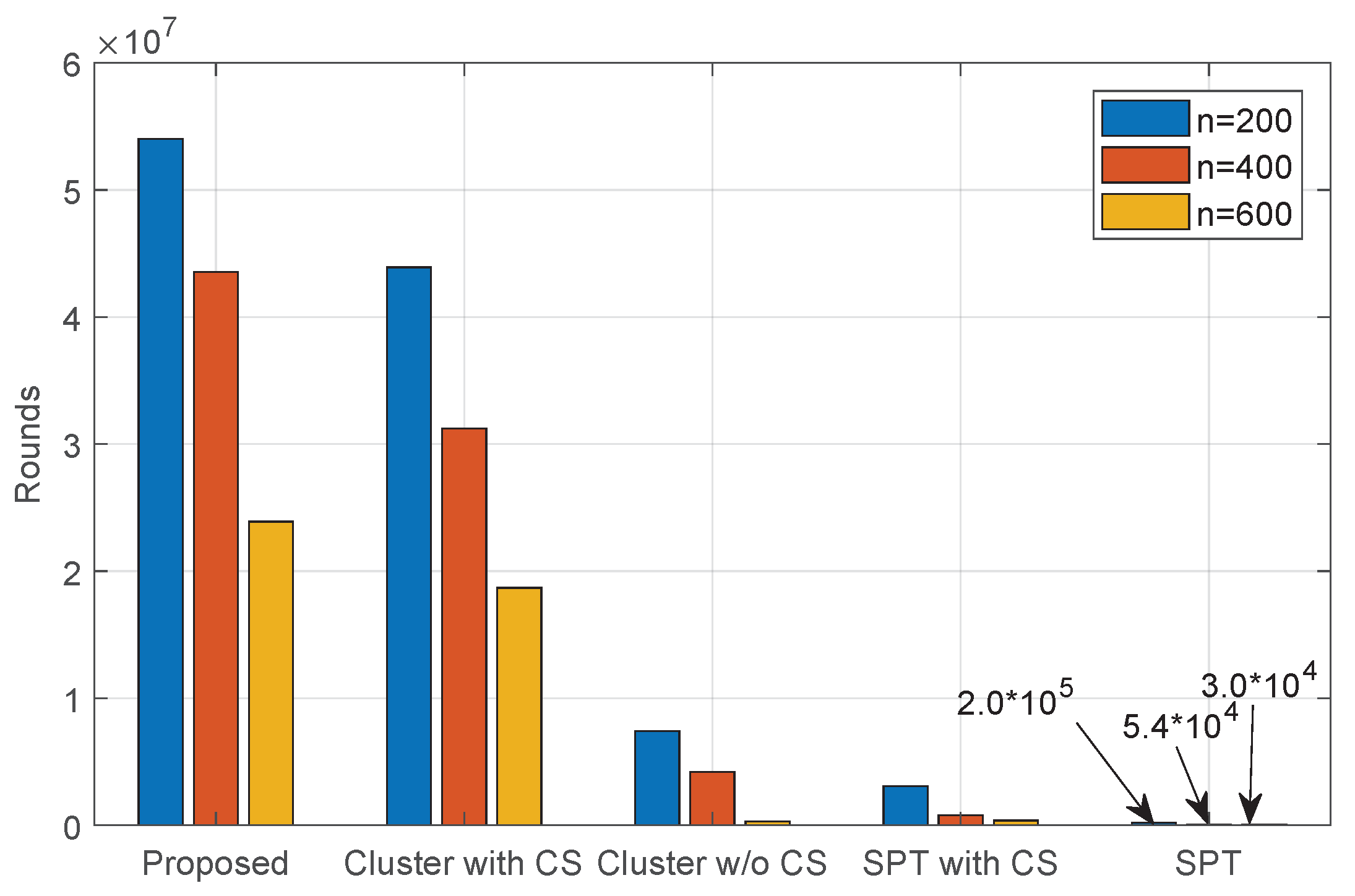
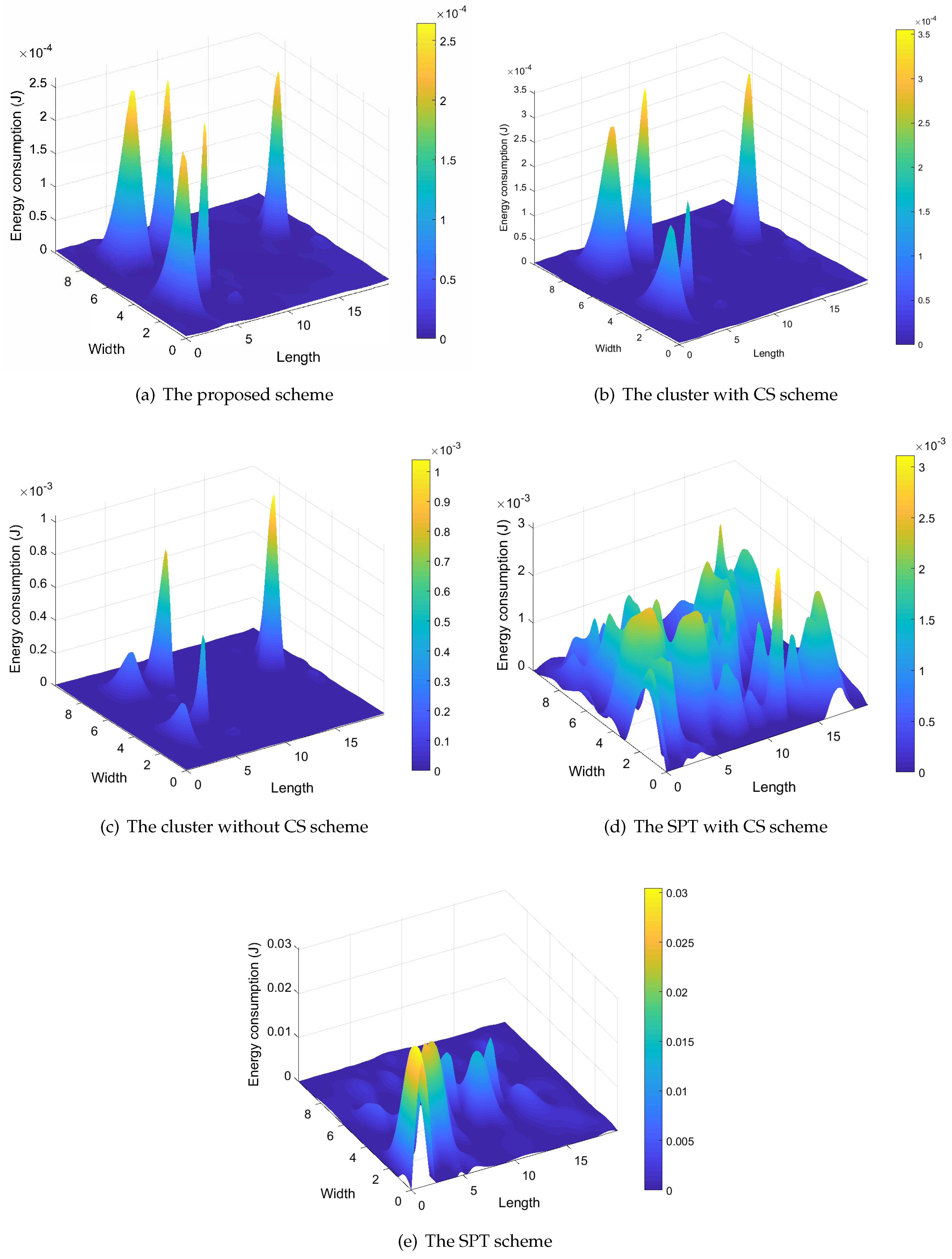
5. Performance Evaluations
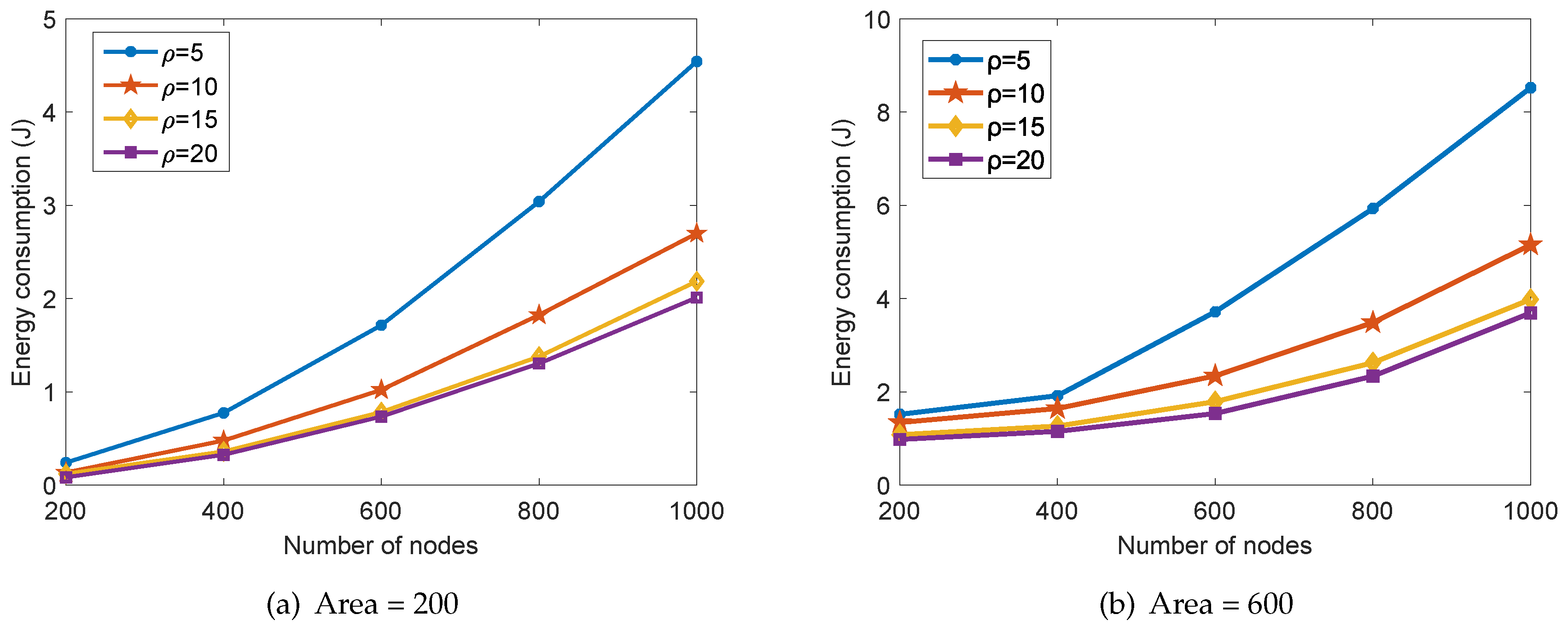
5.1. Performance Analysis
5.2. Performance Comparison
6. Conclusions and Future Research
Author Contributions
Funding
Conflicts of Interest
References
- Rawat, P.; Singh, K.D.; Chaouchi, H.; Bonnin, J.M. Wireless sensor networks: A survey on recent developments and potential synergies. J. Supercomput. 2014, 68, 1–48. [Google Scholar] [CrossRef]
- Borges, L.M.; Velez, F.J.; Lebres, A.S. Survey on the characterization and classification of wireless sensor network applications. IEEE Commun. Surv. Tutor. 2014, 16, 1860–1890. [Google Scholar] [CrossRef]
- Yong, W.; Yang, Z.; Zhang, J.; Feng, L.; Wen, H.; Shen, Y. CS2-Collector: A new approach for data collection in wireless sensor networks based on two-dimensional compressive sensing. Sensors 2016, 16, 1318. [Google Scholar]
- Abdul-Salaam, G.; Abdullah, A.H.; Anisi, M.H.; Gani, A.; Alelaiwi, A. A comparative analysis of energy conservation approaches in hybrid wireless sensor networks data collection protocols. Telecommun. Syst. 2016, 61, 159–179. [Google Scholar] [CrossRef]
- Middya, R.; Chakravarty, N.; Naskar, M.K. Compressive sensing in wireless sensor networks—A survey. IETE Tech. Rev. 2016, 33, 1–13. [Google Scholar] [CrossRef]
- Luo, J.; Xiang, L.; Rosenberg, C. Does compressed sensing improve the throughput of wireless sensor networks? In Proceedings of the IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010; pp. 1–6. [Google Scholar]
- Sucasas, V.; Radwan, A.; Marques, H.; Rodriguez, J.; Vahid, S.; Tafazolli, R. A survey on clustering techniques for cooperative wireless networks. Ad Hoc Netw. 2016, 47, 53–81. [Google Scholar] [CrossRef]
- Jan, B.; Farman, H.; Javed, H.; Montrucchio, B.; Khan, M.; Ali, S. Energy efficient hierarchical clustering approaches in wireless sensor networks: A survey. Wirel. Commun. Mobile Comput. 2017, 2017, 1–14. [Google Scholar] [CrossRef]
- Singh, V.K.; Kumar, M. A compressed sensing approach to resolve the energy hole problem in large scale WSNs. Wirel. Pers. Commun. 2018, 99, 185–201. [Google Scholar] [CrossRef]
- Singh, V.K.; Kumar, M. In-network data processing in wireless sensor networks using compressed sensing. Int. J. Sens. Netw. 2018, 26, 174–189. [Google Scholar] [CrossRef]
- Lan, K.C.; Wei, M.Z. A compressibility-based clustering algorithm for hierarchical compressive data gathering. IEEE Sens. J. 2017, 17, 2550–2562. [Google Scholar] [CrossRef]
- Qiao, J.; Zhang, X. Compressive data gathering based on even clustering for wireless sensor networks. IEEE Access 2018, 6, 24391–24410. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, W.; Yang, Y.; Yao, S. Treelet-based clustered compressive data aggregation for wireless sensor networks. IEEE Trans. Veh. Technol. 2015, 64, 4257–4267. [Google Scholar] [CrossRef]
- Li, X.; Tao, X.; Mao, G. Unbalanced expander based compressive data gathering in clustered wireless sensor networks. IEEE Access 2017, 5, 7553–7566. [Google Scholar] [CrossRef]
- Bajwa, W.; Haupt, J.; Sayeed, A.; Nowak, R. Joint source-channel communication for distributed estimation in sensor networks. IEEE Trans. Inf. Theory 2007, 53, 3629–3653. [Google Scholar] [CrossRef]
- Luo, C.; Wu, F.; Sun, J.; Chen, C.W. Compressive data gathering for large-scale wireless sensor networks. In Proceedings of the International Conference on Mobile Computing and Networking, Beijing, China, 20–25 September 2009; pp. 145–156. [Google Scholar]
- Xiang, L.; Luo, J.; Rosenberg, C. Compressed data aggregation: energy-efficient and high-fidelity data collection. IEEE/ACM Trans. Netw. 2013, 21, 1722–1735. [Google Scholar] [CrossRef]
- Zheng, H.; Yang, F.; Tian, X.; Gan, X.; Wang, X.; Xiao, S. Data gathering with compressive sensing in wireless sensor networks: A random walk based approach. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 35–44. [Google Scholar] [CrossRef]
- Hammoudeh, M.; Newman, R. Information extraction from sensor networks using the Watershed transform algorithm. Inf. Fusion 2015, 22, 39–49. [Google Scholar] [CrossRef]
- Quan, L.; Xiao, S.; Xue, X.; Lu, C. Neighbor-aided spatial-temporal compressive data gathering in wireless sensor networks. IEEE Commun. Lett. 2016, 20, 578–581. [Google Scholar] [CrossRef]
- Cheng, J.; Ye, Q.; Jiang, H.; Wang, D. STCDG: An efficient data gathering algorithm based on matrix completion for wireless sensor networks. IEEE Trans. Wirel. Commun. 2013, 12, 850–861. [Google Scholar] [CrossRef]
- Piao, X.; Hu, Y.; Sun, Y.; Yin, B.; Gao, J. Correlated spatio-temporal data collection in wireless sensor networks based on low rank matrix approximation and optimized node sampling. Sensors 2014, 14, 23137–23158. [Google Scholar] [CrossRef] [PubMed]
- Xie, K.; Ning, X.; Wang, X.; Xie, D.; Cao, J.; Xie, G.; Wen, J. Recover corrupted data in sensor networks: A matrix completion solution. IEEE Trans. Mobile Comput. 2017, 16, 1434–1448. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Qaisar, S.; Bilal, R.M.; Iqbal, W.; Naureen, M. Compressive sensing: From theory to applications, a survey. J. Commun. Netw. 2013, 15, 443–456. [Google Scholar] [CrossRef]
- Campobello, G.; Segreto, A.; Serrano, S. Data gathering techniques for wireless sensor networks: A comparison. Int. J. Distrib. Sens. Netw. 2016, 12, 1–17. [Google Scholar] [CrossRef]
- Candes, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2008, 1, 586–597. [Google Scholar] [CrossRef]
- Soussen, C.; Idier, J.; Duan, J.; Brie, D. Homotopy based algorithms for l0-regularized least-squares. IEEE Trans. Signal Process. 2014, 63, 3301–3316. [Google Scholar] [CrossRef]
- Jain, P.; Tewari, A.; Dhillon, I.S. Partial hard thresholding. IEEE Trans. Inf. Theory 2017, 63, 3029–3038. [Google Scholar] [CrossRef]
- Han, G.; Xu, H.; Duong, T.Q.; Jiang, J.; Hara, T. Localization algorithms of wireless sensor networks: A survey. Telecommun. Syst. 2013, 52, 2419–2436. [Google Scholar] [CrossRef]
- Xu, G.; Zhu, M.; Luo, X.; Wu, M.; Ren, F. An unequal clustering algorithm based on energy balance for wireless sensor networks. IEEJ Trans. Electr. Electron. Eng. 2012, 7, 402–407. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Chen, W.; Jia, W.; Li, B.; Xiong, J. COCA: Constructing optimal clustering architecture to maximize sensor network lifetime. Comput. Commun. 2013, 36, 256–268. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, X.; Liu, Z. A grid-based clustering algorithm via load analysis for industrial Internet of things. IEEE Access 2018, 6, 13117–13128. [Google Scholar] [CrossRef]
- Wu, C.; Chang, Y. Approximately even partition algorithm for coding the Hilbert curve of arbitrary-sized image. IET Image Process. 2012, 6, 746–755. [Google Scholar] [CrossRef]
- Xie, R.; Jia, X. Transmission-efficient clustering method for wireless sensor networks using compressive sensing. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 806–815. [Google Scholar]
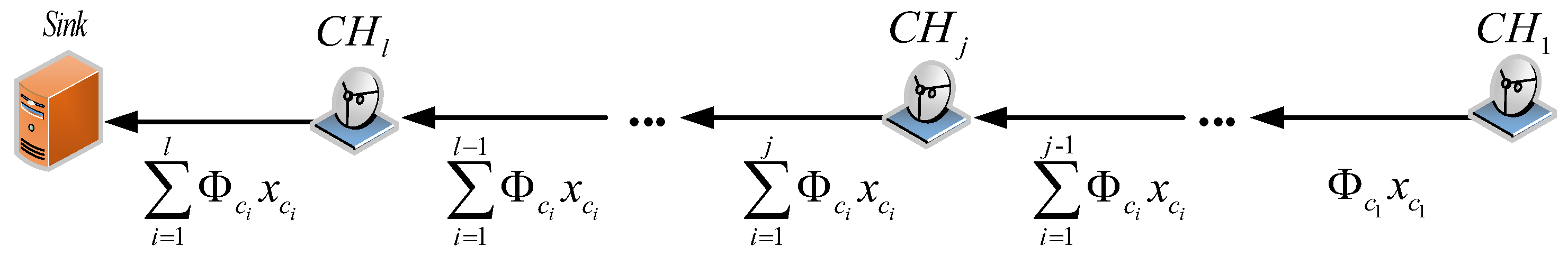
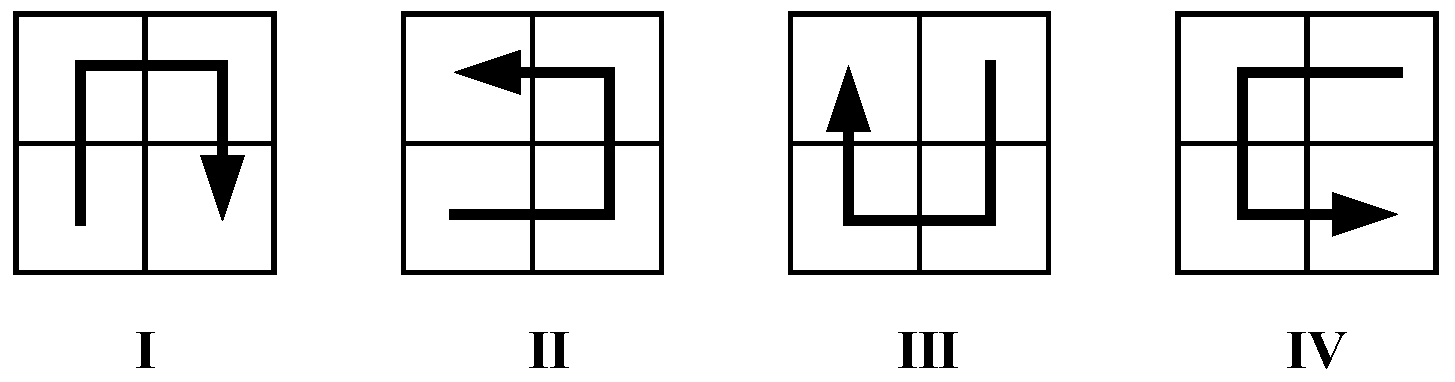

| Parent Orientation | ||||
|---|---|---|---|---|
| I | II | IV | I | I |
| II | I | II | III | II |
| III | III | III | II | IV |
| IV | IV | I | IV | III |
| Scheme | Number of Nodes | ||||
|---|---|---|---|---|---|
| 200 | 400 | 600 | 800 | 1000 | |
| Proposed | 0.1012 | 0.3536 | 0.7777 | 1.43234 | 2.0637 |
| Cluster with CS | 0.1065 | 0.3557 | 0.8078 | 1.4724 | 2.1138 |
| Cluster w/oCS | 0.3663 | 1.2067 | 2.5087 | 4.4584 | 6.5277 |
| SPT with CS | 0.1441 | 0.4922 | 1.2334 | 2.0445 | 3.4418 |
| SPT | 0.3571 | 1.0301 | 2.3671 | 3.8858 | 5.6929 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Chen, H.; Peng, S.; Li, X.; Wang, C.; Yu, S.; Yin, P. A Collaborative Data Collection Scheme Based on Optimal Clustering for Wireless Sensor Networks. Sensors 2018, 18, 2487. https://doi.org/10.3390/s18082487
Li G, Chen H, Peng S, Li X, Wang C, Yu S, Yin P. A Collaborative Data Collection Scheme Based on Optimal Clustering for Wireless Sensor Networks. Sensors. 2018; 18(8):2487. https://doi.org/10.3390/s18082487
Chicago/Turabian StyleLi, Guorui, Haobo Chen, Sancheng Peng, Xinguang Li, Cong Wang, Shui Yu, and Pengfei Yin. 2018. "A Collaborative Data Collection Scheme Based on Optimal Clustering for Wireless Sensor Networks" Sensors 18, no. 8: 2487. https://doi.org/10.3390/s18082487
APA StyleLi, G., Chen, H., Peng, S., Li, X., Wang, C., Yu, S., & Yin, P. (2018). A Collaborative Data Collection Scheme Based on Optimal Clustering for Wireless Sensor Networks. Sensors, 18(8), 2487. https://doi.org/10.3390/s18082487





