Modeling and Analysis of a Novel Ultrasensitive Differential Resonant Graphene Micro-Accelerometer with Wide Measurement Range
Abstract
1. Introduction
2. Modeling the Designed Accelerometer
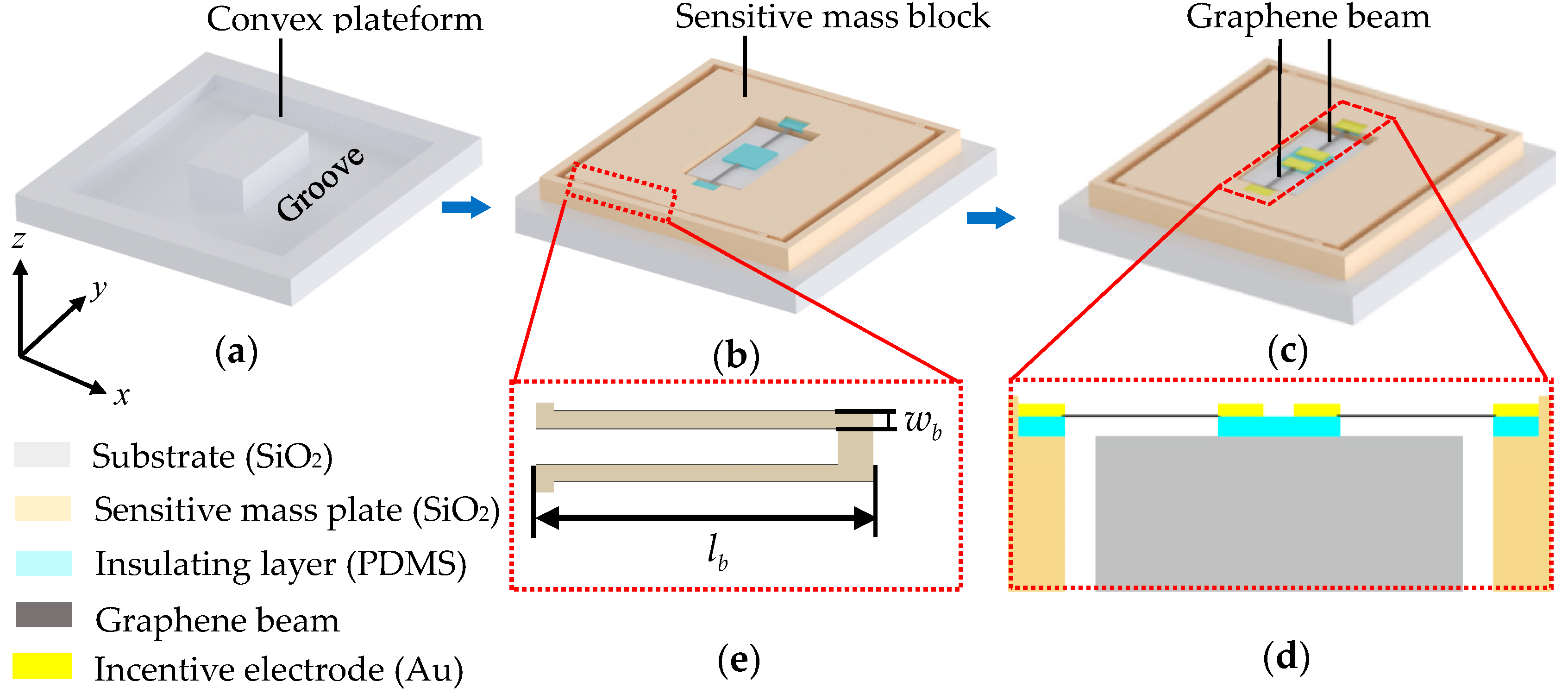
2.1. Design of Resonant Graphene Accelerometer
2.2. Working Principle
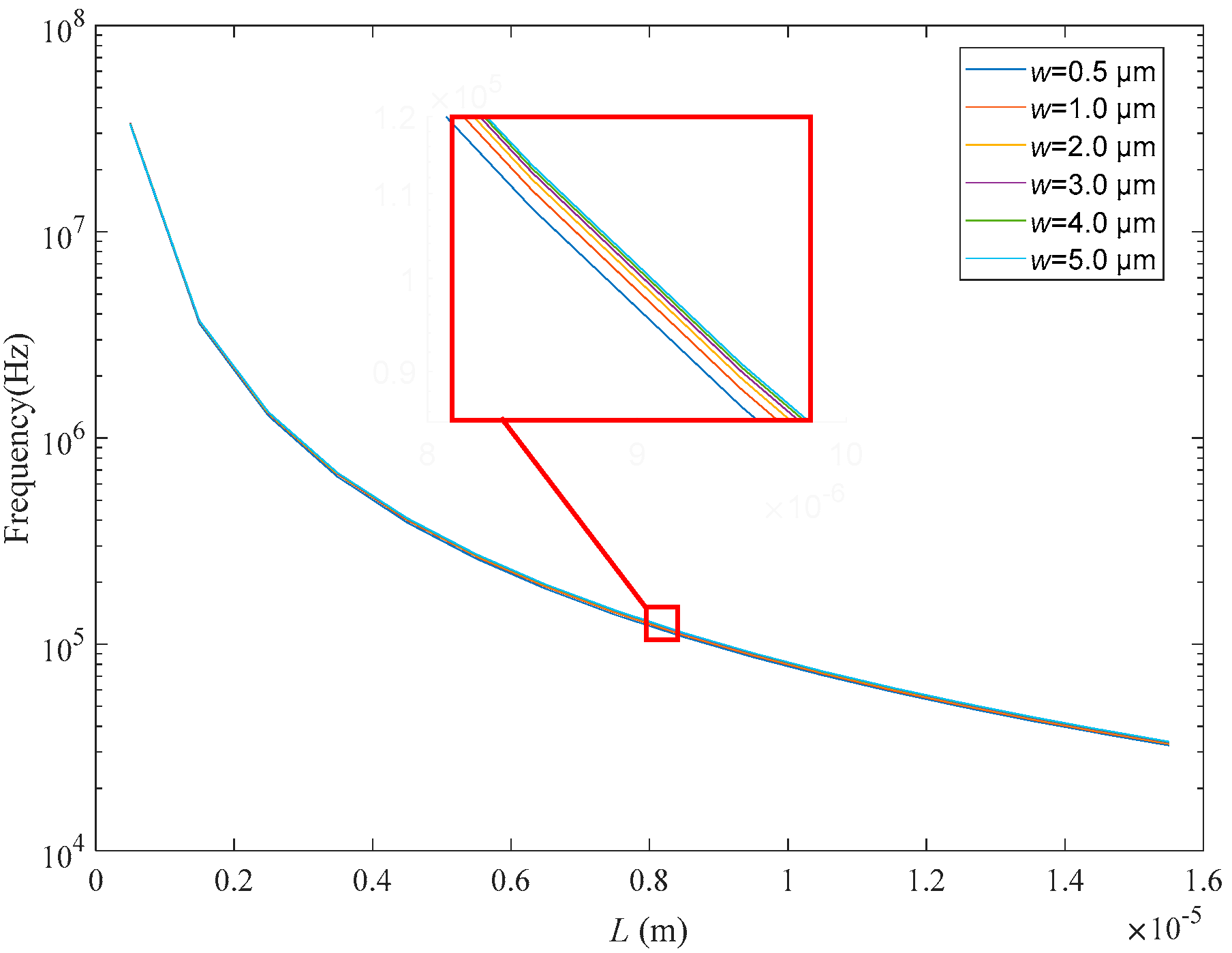
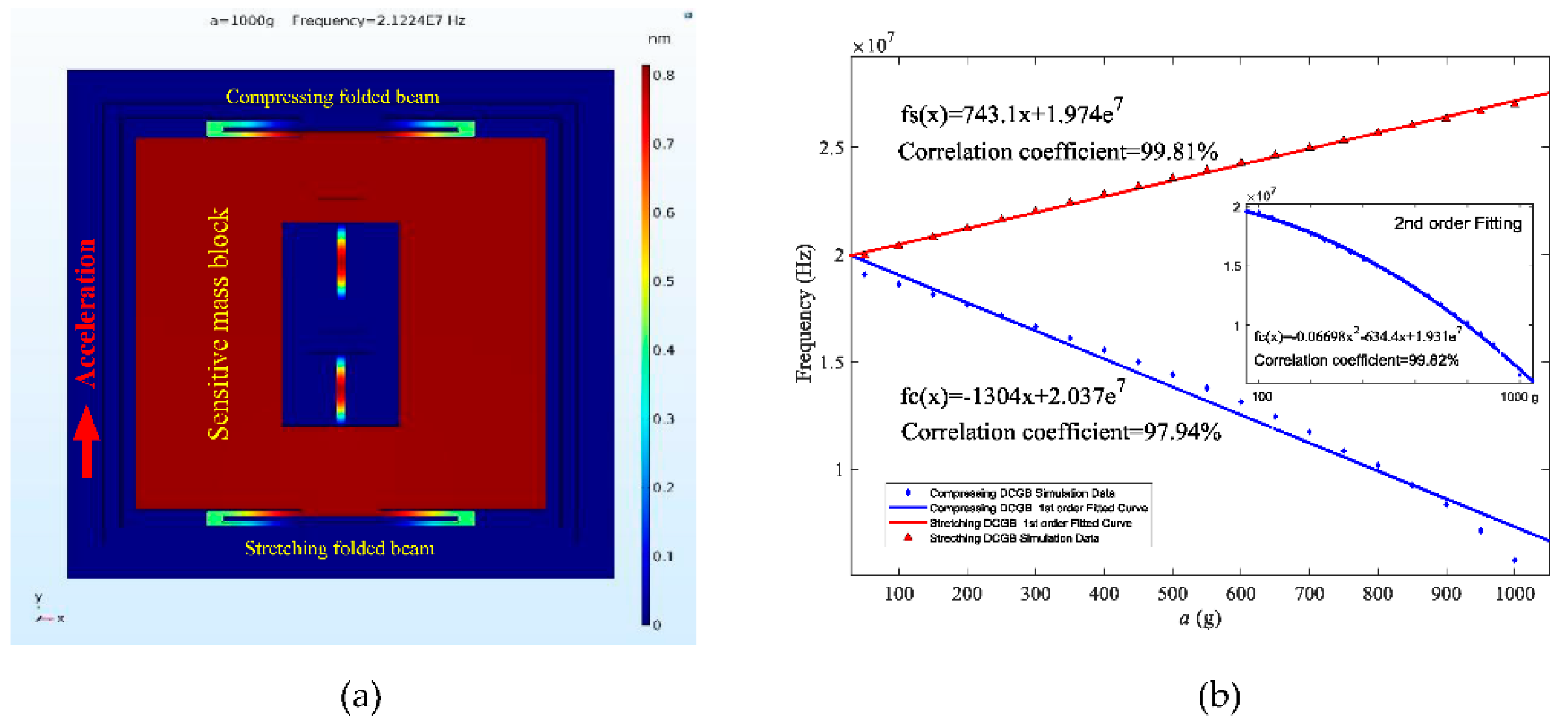
3. Structural Optimization and Simulation
4. Performance Analysis and Discussion
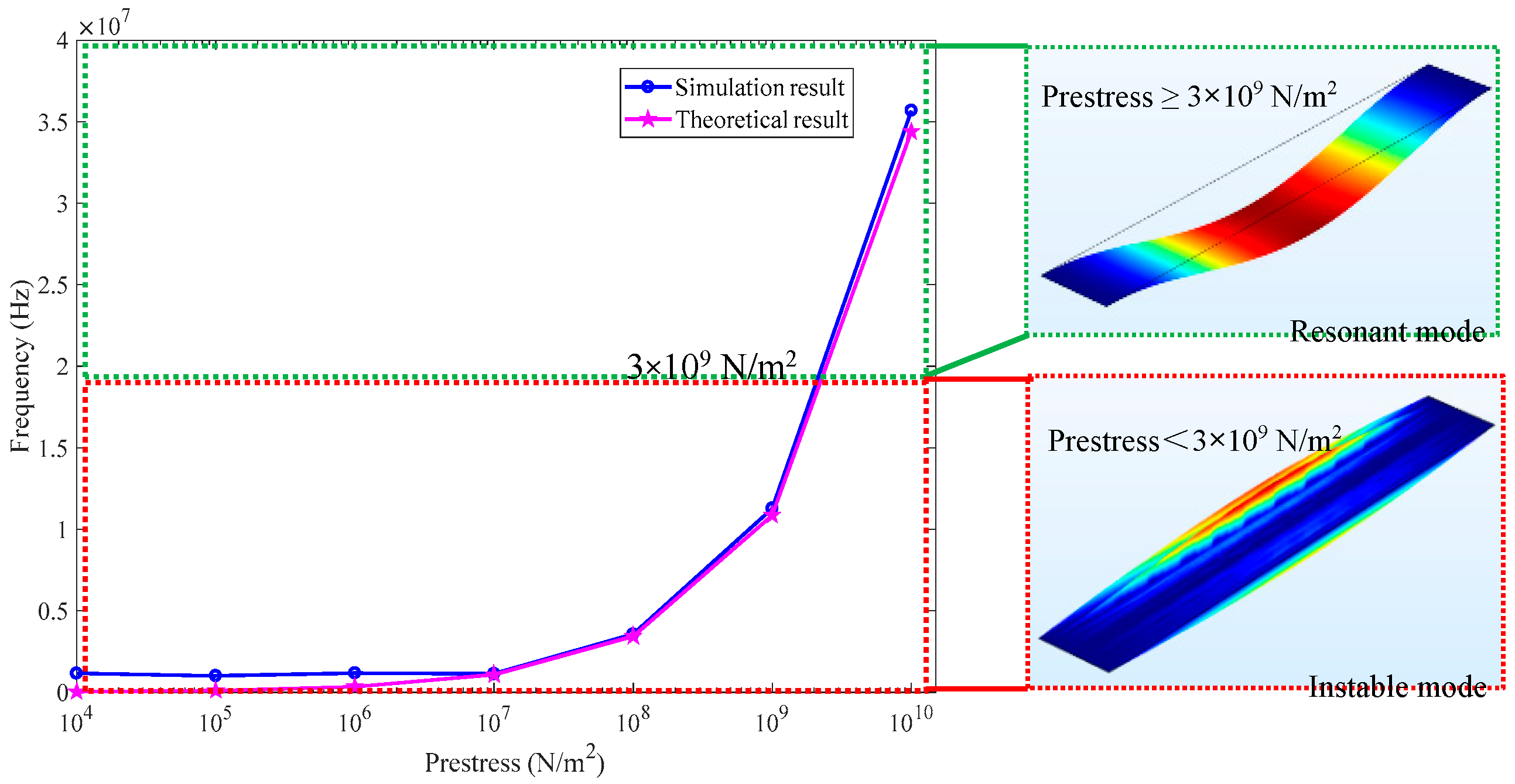
4.1. Effect of Prestress
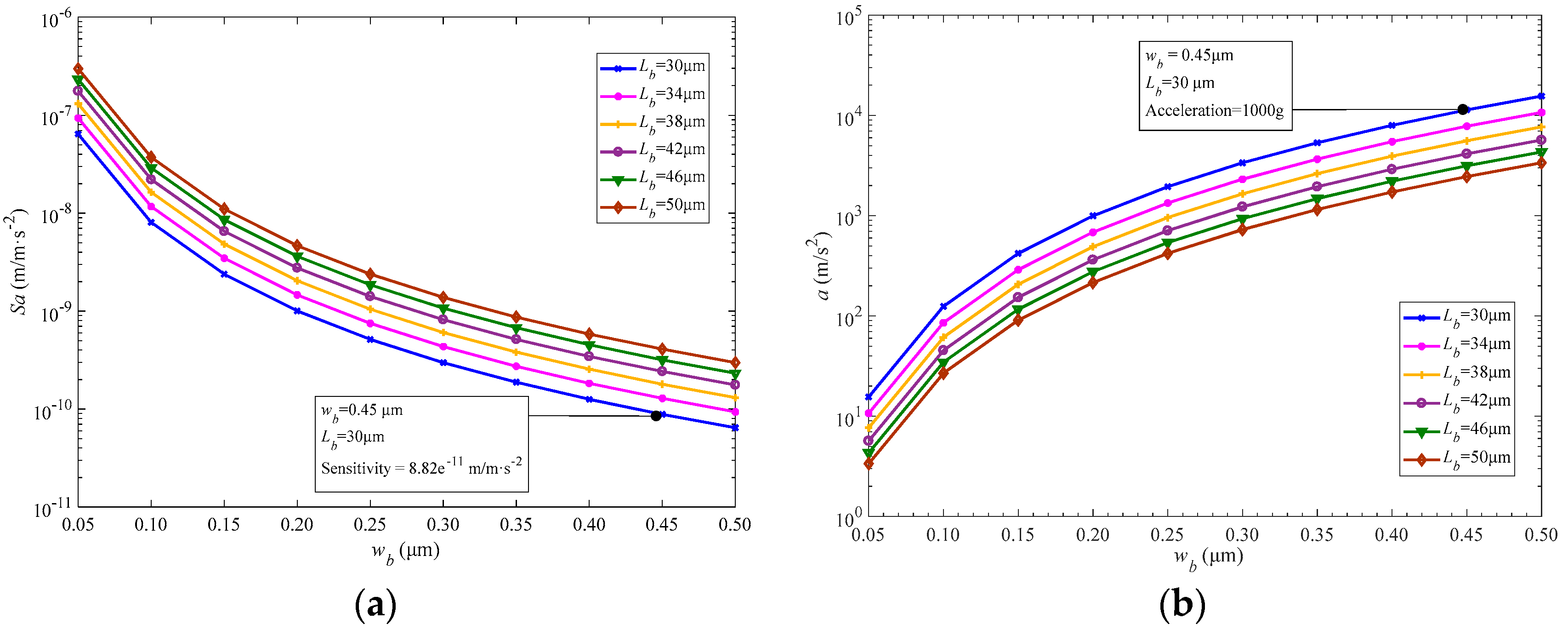
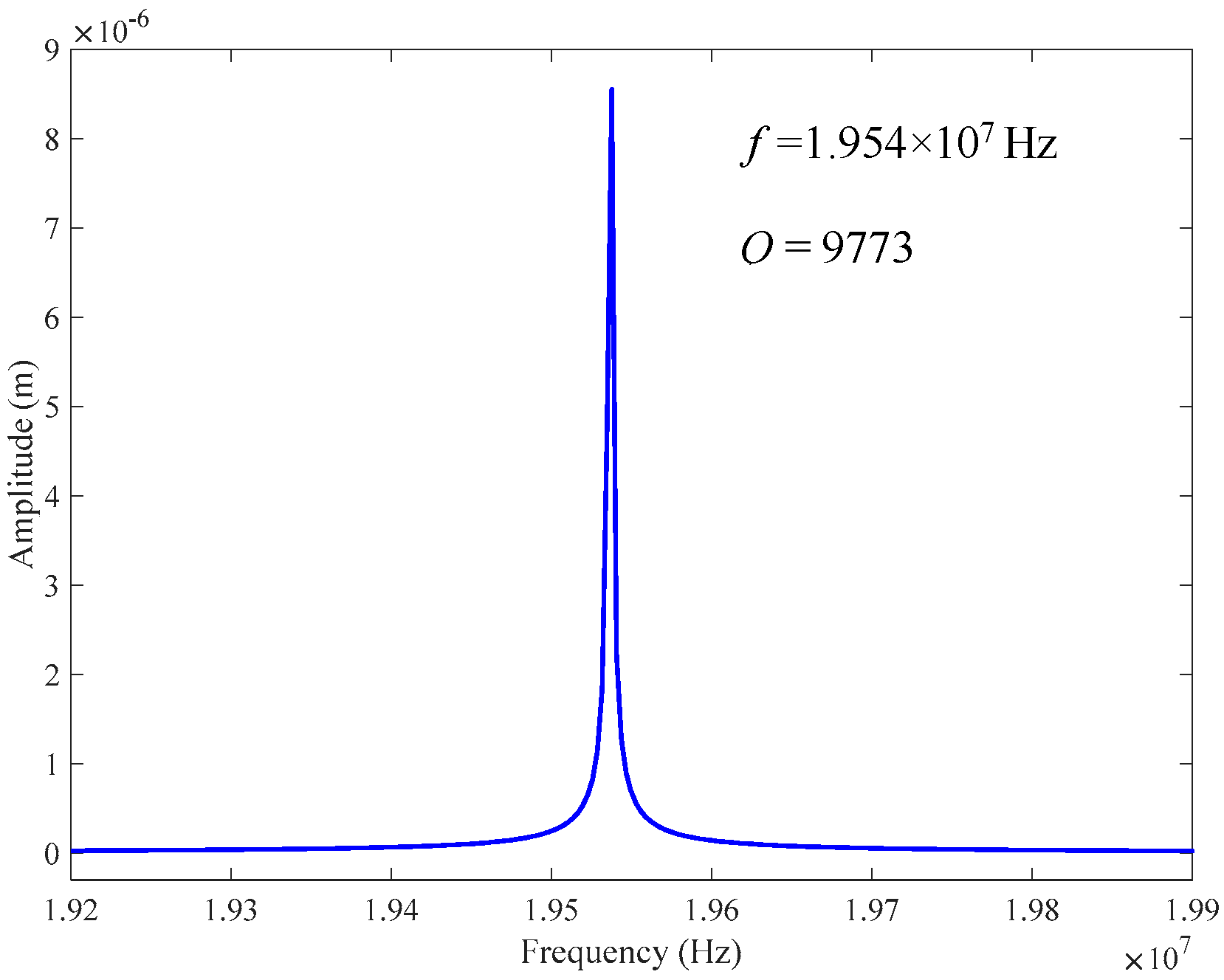
4.2. Performance and Analyses
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mohd, H.M.; Qu, P.; Qu, H. A low-cost CMOS-MEMS piezoresistive accelerometer with large proof mass. Sensors 2011, 11, 7892–7907. [Google Scholar]
- Tian, W.; Wu, S.; Zhou, Z. High resolution space quartz-flexure accelerometer based on capacitive sensing and electrostatic control technology. Rev. Sci. Instrum. 2012, 83, 095002. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Li, M.; Qin, L.; Liu, J. Flip chip bonding of a quartz MEMS-based vibrating beam accelerometer. Sensors 2013, 13, 10844–10855. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Fan, S.; Jin, W. Graphene diaphragm analysis for pressure or acoustic sensor applications. Microsyst. Technol. 2013, 21, 117–122. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Pereira, V.M.; Neto, A.H.C. Strain engineering of graphene’s electronic structure. Phys. Rev. Lett. 2009, 103, 046801. [Google Scholar] [CrossRef] [PubMed]
- Bonaccorso, F.; Sun, Z.; Hasan, T. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611–622. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.S.; Zha, Y.; Jang, H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Hu, K.; Peng, Z.; Meng, G. Tunable micro- and nanomechanical resonators. Sensors 2015, 15, 26478–26566. [Google Scholar] [CrossRef] [PubMed]
- Bunch, J.S.; Van, A.M.; Verbridge, S.S. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Rosenblatt, S.; Bolotin, K.I. Performance of monolayer graphene nanomechanical resonators with electrical readout. Nat. Nanotechnol. 2009, 4, 861–867. [Google Scholar] [CrossRef] [PubMed]
- Oshidari, Y.; Hatakeyama, T.; Kometani, R. High quality factor graphene resonator fabrication using resist shrinkage-induced strain. Appl. Phys. Express 2012, 5, 117201. [Google Scholar] [CrossRef]
- Kwon, O.K.; Lee, G.Y.; Hwang, H.J. Molecular dynamics modeling and simulations to understand gate-tunable graphene-nanoribbon-resonator. Phys. E 2012, 45, 194–200. [Google Scholar] [CrossRef]
- Kwon, O.K.; Lee, J.H.; Park, J. Molecular dynamics simulation study on graphene nanoribbon resonators tuned by adjusting axial strain. Curr. Appl. Phys. 2013, 13, 360–365. [Google Scholar] [CrossRef]
- Li, C.; Lan, T.; Yu, X. Room-temperature pressure-induced optically-actuated fabry-perot nanomechanical resonator with multilayer graphene diaphragm in Air. Nanomaterials 2017, 7, 366. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.W.; Lee, J.H.; Hwang, H.J. Developing accelerometer based on graphene nanoribbon resonators. Phys. Lett. A 2012, 376, 3248–3255. [Google Scholar] [CrossRef]
- Byun, K.R.; Kim, K.S.; Hwang, H.J. Sensitivity of graphene-nanoribbon-based accelerometer with attached mass. Comput. Theor. Nanosci. 2013, 10, 1886–1891. [Google Scholar] [CrossRef]
- Lee, S.; Chen, C.; Deshpande, V.V. Electrically integrated SU-8 clamped graphene drum resonators for strain engineering. Appl. Phys. Lett. 2013, 102, 153101. [Google Scholar] [CrossRef]
- Hurst, A.M.; Lee, S.; Cha, W. A graphene accelerometer. In Proceedings of the IEEE International Conference on MICRO Electro Mechanical Systems, Estoril, Portugal, 18–22 January 2015; pp. 865–868. [Google Scholar]
- Kang, J.W.; Park, J.H.; Lee, G.Y. Molecular dynamics simulation on crossroad-type graphene-resonator accelerometer. Comput. Theor. Nanosci. 2015, 12, 4186–4190. [Google Scholar] [CrossRef]
- Jie, W.; Hu, F.; Wang, X.; Qin, S. Acceleration sensing based on graphene resonator. In Proceedings of the International Conference on Photonics and Optical Engineering, Xi’an, China, 14–17 October 2016. [Google Scholar] [CrossRef]
- Shivaraman, S.; Barton, R.A.; Yu, X. Free-standing epitaxial graphene. Nano Lett. 2009, 9, 3100–3105. [Google Scholar] [CrossRef] [PubMed]
- Barton, R.A.; Ilic, B.; Zande, A.M. High, size-dependent quality factor in an array of graphene mechanical resonators. Nano Lett. 2011, 11, 1232–1236. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhu, K. Graphene-based nanoresonator with applications in optical transistor and mass sensing. Sensors 2014, 14, 16740–16753. [Google Scholar] [CrossRef] [PubMed]
- Radtke, C.; Baumvol, I.J.R.; Stedile, F.C. Thermal growth of SiO2, on SiC investigated by isotopic tracing and subnanometric depth profiling. Appl. Surf. Sci. 2003, 10, 570–574. [Google Scholar] [CrossRef]
- Iikawa, H.; Izumi, M.N.K. Dose-window dependence on Si crystal orientation in separation by implanted oxygen substrate formation. J. Mater. Res. 2004, 19, 3607–3613. [Google Scholar] [CrossRef]
- Dai, G.; Li, M.; He, X. Thermal drift analysis using a multiphysics model of bulk silicon MEMS capacitive accelerometer. Sens. Actuators A Phys. 2011, 172, 369–378. [Google Scholar] [CrossRef]
- Benmessaoud, M.; Nasreddine, M.M. Optimization of MEMS capacitive accelerometer. Microsyst. Technol. 2013, 19, 713–720. [Google Scholar] [CrossRef]
- Smith, A.D.; Vazirs, S.; Delin, A. Strain engineering in suspended graphene devices for pressure sensor application. In Proceedings of the 13th IEEE International Conference on Ultimate Integration on Silicon, Grenoble, France, 6–7 March 2012; pp. 21–24. [Google Scholar]
- Xing, R.; Jian, S.S. Numerical analysis on the multilayer nanoring waveguide pair. IEEE Photonics Technol. Lett. 2016, 28, 2779–2782. [Google Scholar] [CrossRef]
- Wang, H.; Kurata, K.; Fukunaga, T. In-situ measurement of the heat transport in defect-engineered free-standing single-layer graphene. Sci. Rep. 2016, 6, 21823. [Google Scholar] [CrossRef] [PubMed]
- Bu, H.; Chen, Y.; Zou, M. Atomistic simulations of mechanical properties of graphene nanoribbons. Phys. Lett. A 2009, 373, 3359–3362. [Google Scholar] [CrossRef]
- Georgantzinos, S.K.; Giannopoulos, G.I.; Katsareas, D.E. Size-dependent non-linear mechanical properties of graphene nanoribbons. Comput. Mater. Sci. 2011, 50, 2057–2062. [Google Scholar] [CrossRef]
- Zhao, L.; Dai, B.; Yang, B. Design and simulations of a new biaxial silicon resonant micro-accelerometer. Microsyst. Technol. 2015, 22, 1–6. [Google Scholar] [CrossRef]
- Zande, A.M.; Barton, R.A.; Alden, J.S. Large-scale arrays of single layer graphene resonators. Nano Lett. 2010, 10, 4869–4873. [Google Scholar] [CrossRef] [PubMed]
| Description | Length (μm) | Width (μm) | Thickness (or Height) (μm) |
|---|---|---|---|
| Substrate | 70 | 70 | 6 |
| Convex platform | 24 | 14 | 7 |
| Sensitive mass plate | 60 | 60 | 5 |
| Sensitive mass block | 53 | 53 | 5 |
| Folded support beams | 46 | 0.2 | 5 |
| Graphene resonant beams | 10 | 1 | 0.335 × 10−3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, F.-T.; Fan, S.-C.; Li, C.; Peng, X.-B. Modeling and Analysis of a Novel Ultrasensitive Differential Resonant Graphene Micro-Accelerometer with Wide Measurement Range. Sensors 2018, 18, 2266. https://doi.org/10.3390/s18072266
Shi F-T, Fan S-C, Li C, Peng X-B. Modeling and Analysis of a Novel Ultrasensitive Differential Resonant Graphene Micro-Accelerometer with Wide Measurement Range. Sensors. 2018; 18(7):2266. https://doi.org/10.3390/s18072266
Chicago/Turabian StyleShi, Fu-Tao, Shang-Chun Fan, Cheng Li, and Xiao-Bin Peng. 2018. "Modeling and Analysis of a Novel Ultrasensitive Differential Resonant Graphene Micro-Accelerometer with Wide Measurement Range" Sensors 18, no. 7: 2266. https://doi.org/10.3390/s18072266
APA StyleShi, F.-T., Fan, S.-C., Li, C., & Peng, X.-B. (2018). Modeling and Analysis of a Novel Ultrasensitive Differential Resonant Graphene Micro-Accelerometer with Wide Measurement Range. Sensors, 18(7), 2266. https://doi.org/10.3390/s18072266






