Second Iteration of Photogrammetric Processing to Refine Image Orientation with Improved Tie-Points †
Abstract
1. Introduction
1.1. Related Works
1.2. Contributions
- contrary to [30], our algorithm is not constrained by the presence of dominant 3D planes in the scene, therefore is not constrained to urban reconstructions;
- our initial structure is represented in form of a triangulated mesh, and the re-projection to images of each mesh entity is rectified to a pre-selected geometry; as the perspective deformations are removed, the algorithm is apt to handle wide baseline acquisitions;
2. Materials and Methods
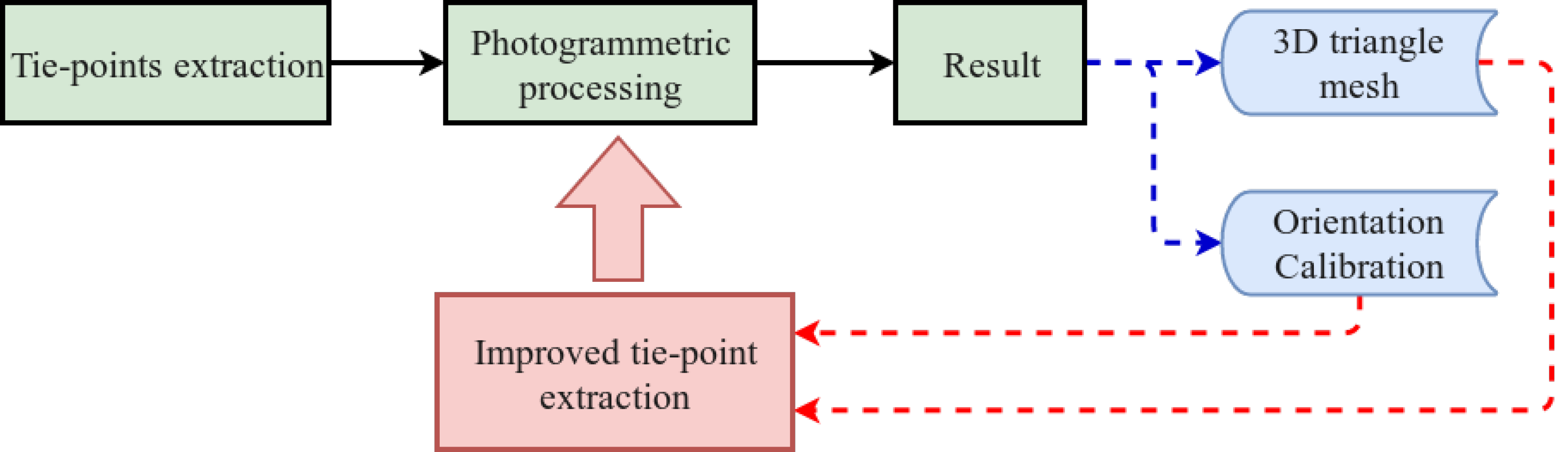
2.1. An Overview
- Image selection and scene partition.
- Detection of interest points (keypoints).
- Matching by correlation and LSM.
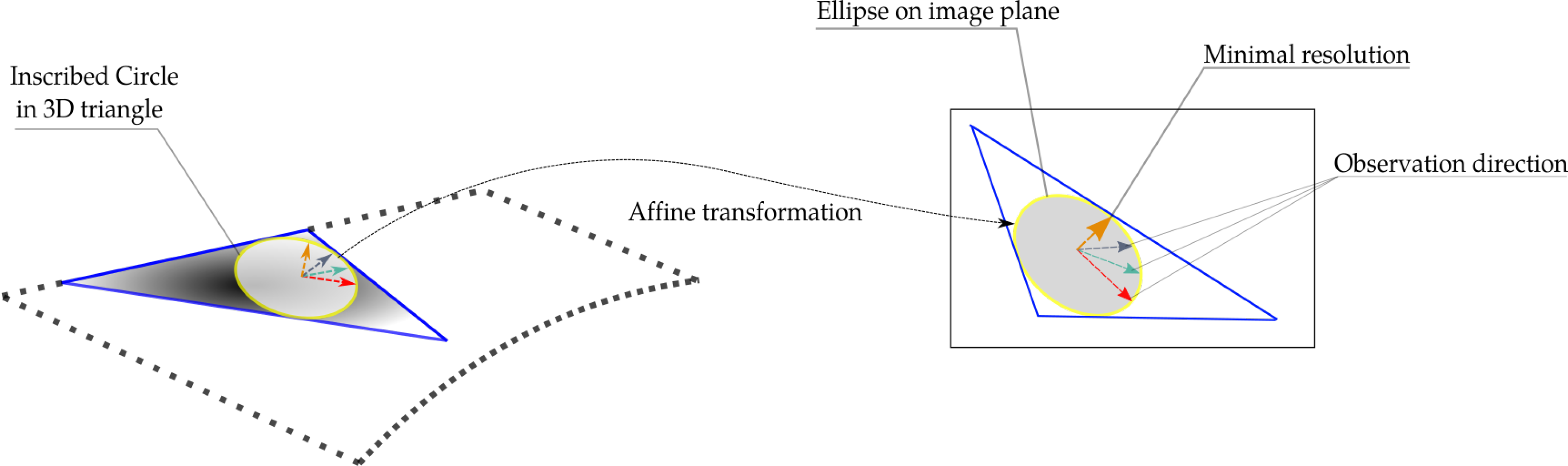
2.2. Image Selection and Scene Partition
- visibility (here implemented by a Z-buffer filter), and
- minimum resolution (triangles with surface area below 100 pixels will be filtered-out).
- fronto-parallel with respect to the 3D triangle in question, which results in least deformed triangle back-projections, and
- nearer to the triangle in question, which is equivalent of higher resolution.
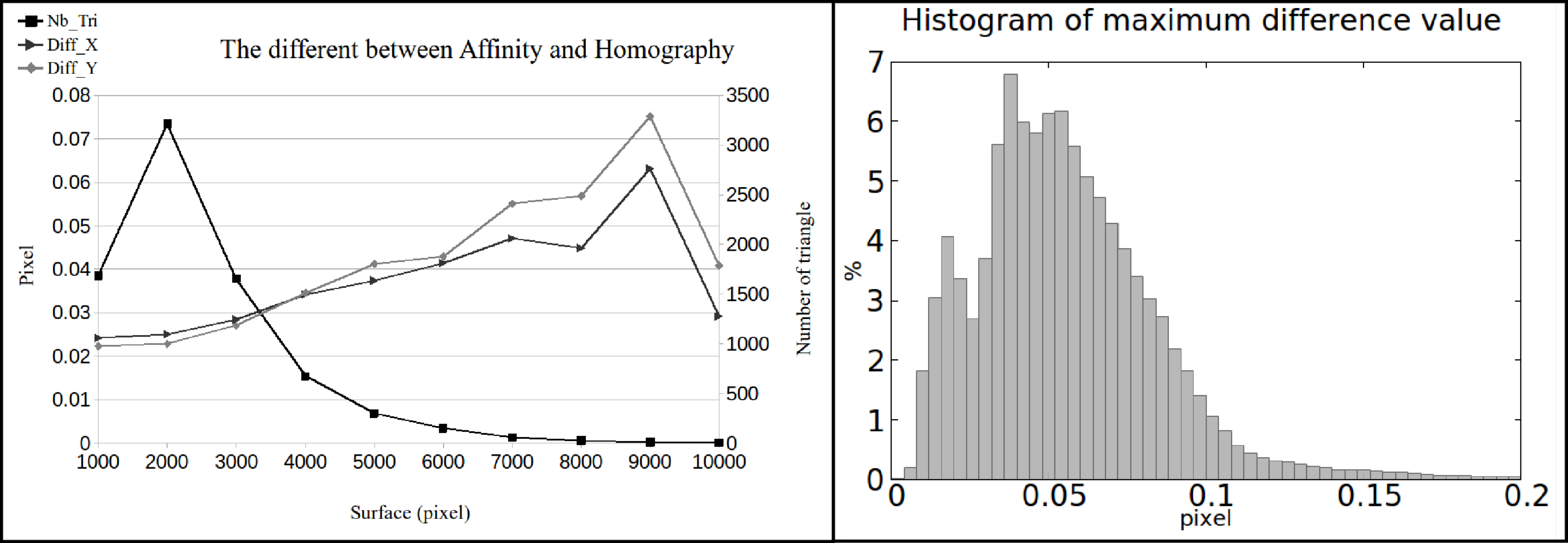
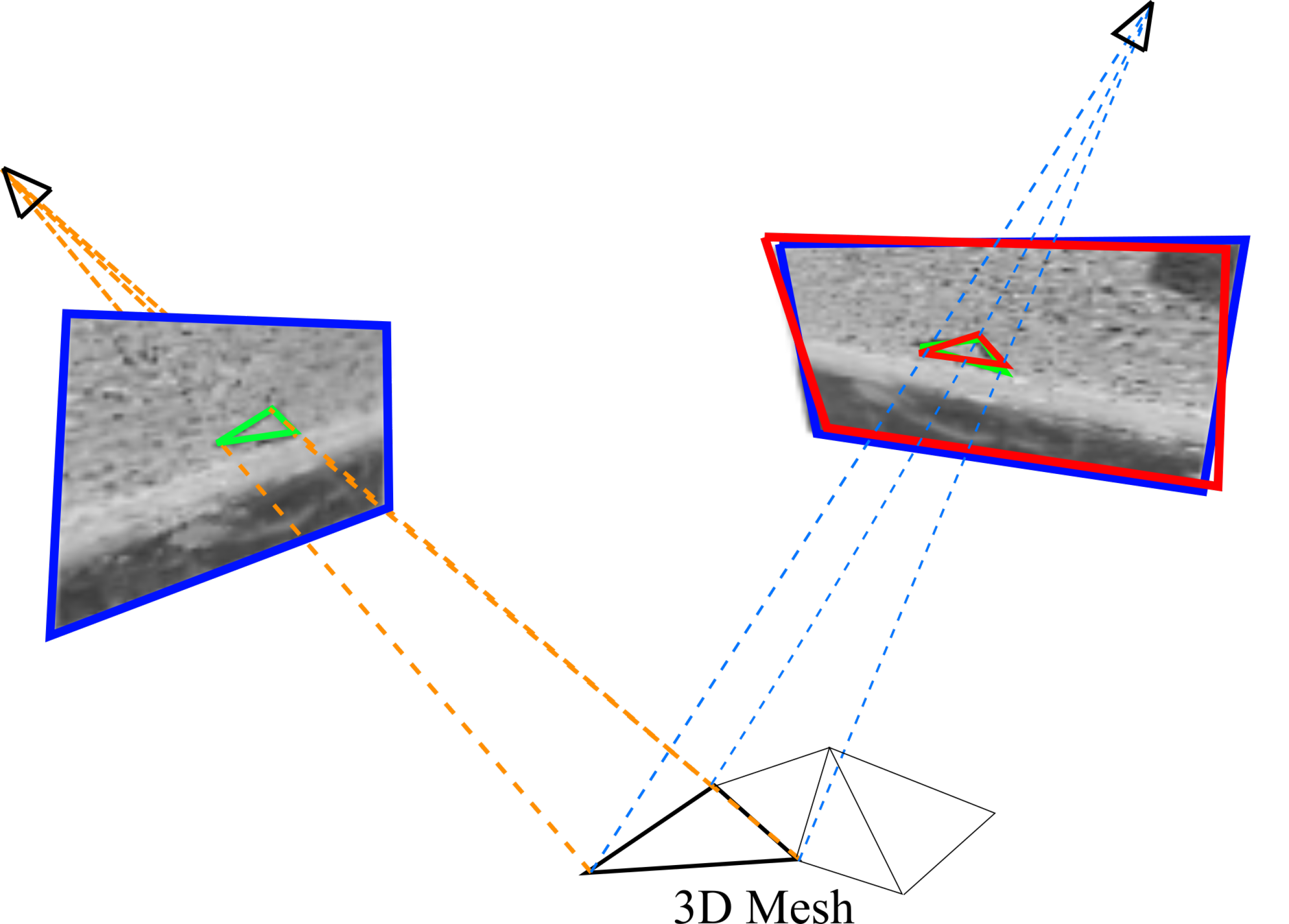
2.2.1. Region of Interest Rectification
2.3. Detection of Interest Points
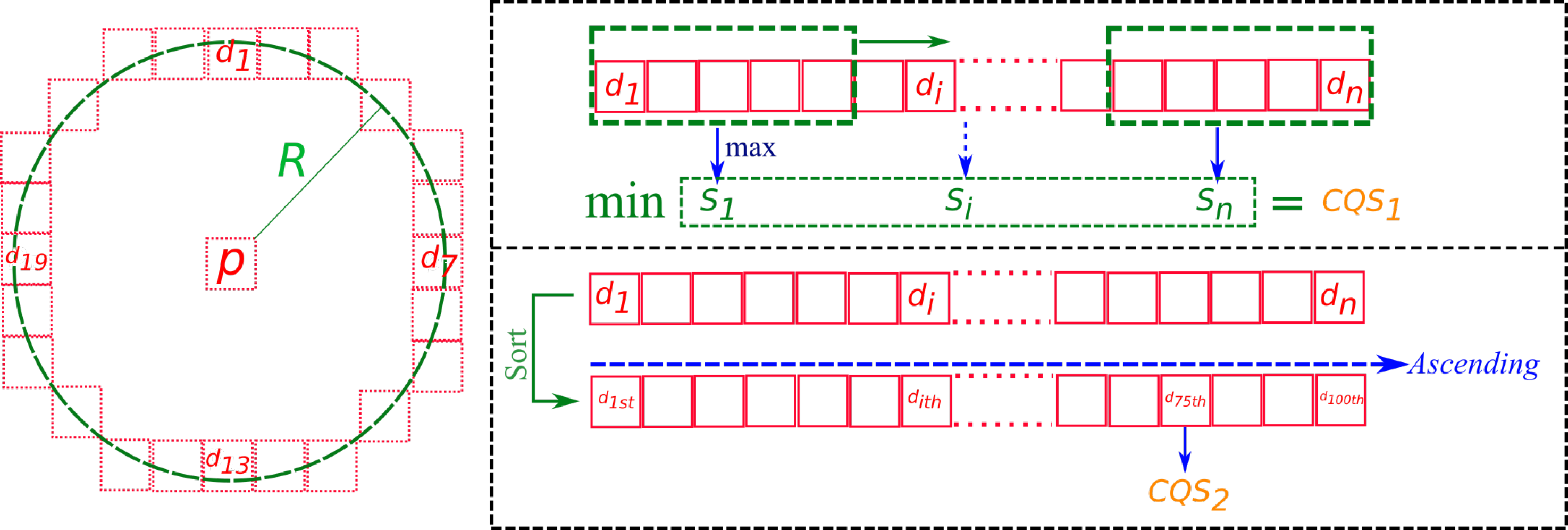
2.3.1. Contrast Quality Filter
- Fast processing speed: in comparing to Difference of Gaussian approach detector such as SIFT.
- Perform on non-perspective ROI: as presented in Section 2.2.1, perspective in ROI is eliminated. Therefore, a scale rotation invariant approach is unnecessary.
- Interest point localization: interest points are detected at pixel exact and FAST filter-based approach work on pixel exact also. Therefore, we avoid the sub-pixel point localization problem in SIFT approach [36]. Region-based matching method by correlation and Least Square Matching in matching step will localize tie-point at sub-pixel precision.
- contiguous priority contrast score , and
- global contrast score .
2.3.2. Non-Repetitive Pattern Filter
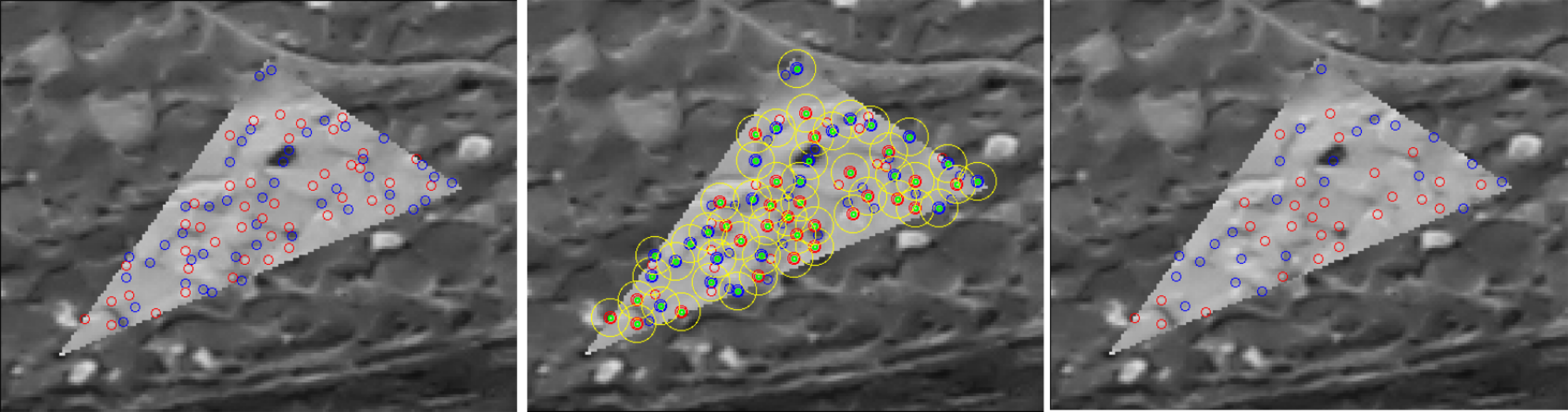
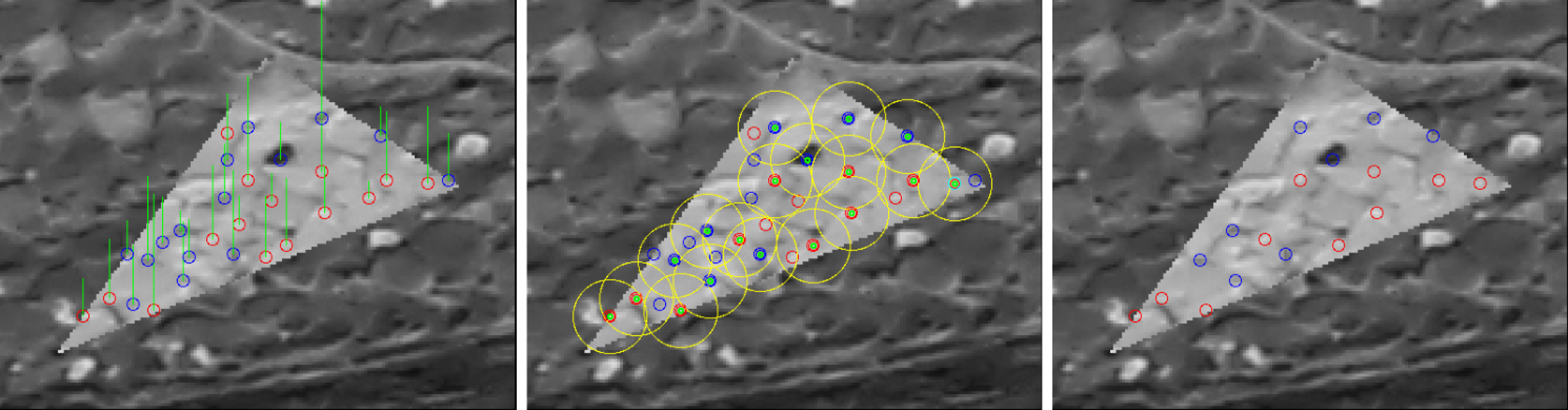
2.3.3. Interest Point Reduction
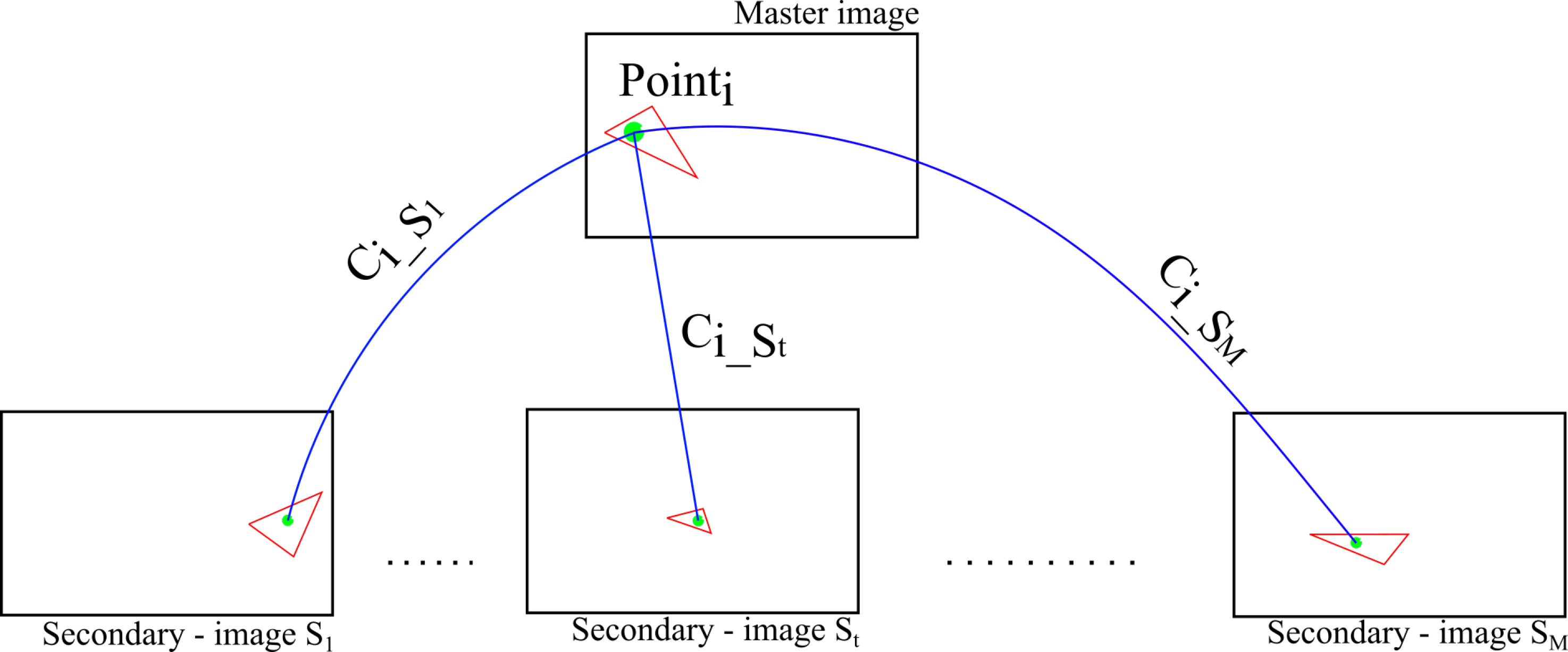
2.4. Matching
2.4.1. Matching by Correlation
- at 2-times down-sampled resolution (every other pixel is discarded),
- at the nominal resolution, and
- at sub-pixel resolution (up to 0.1 pixel).
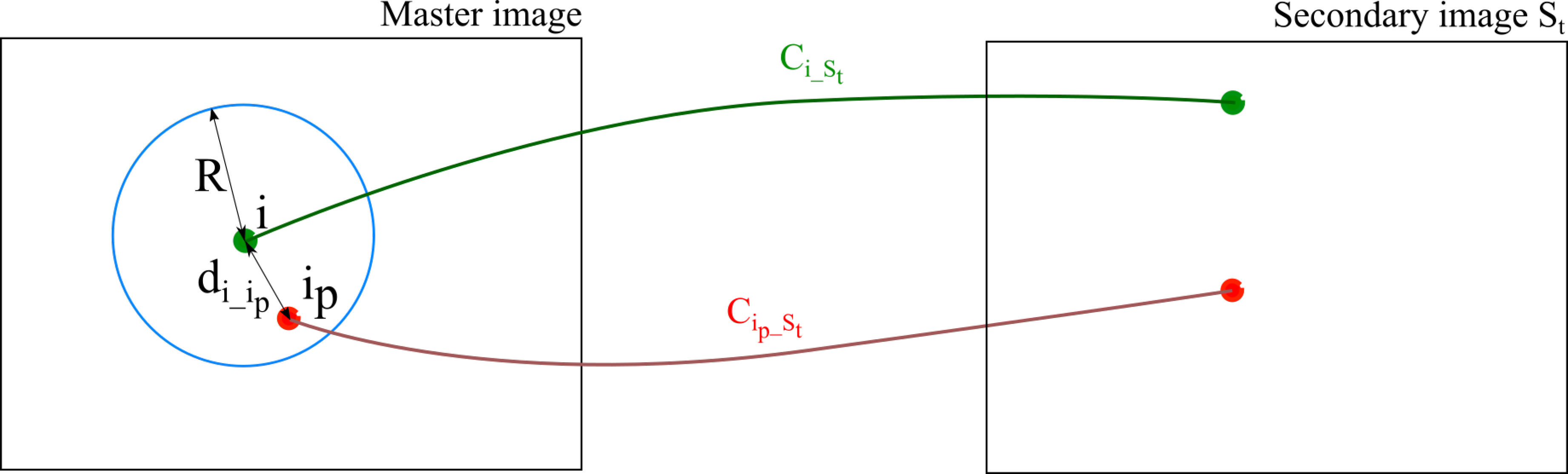
2.4.2. The Tie-Point Spatial Filter
- prioritisation of points with high ZNCC scores,
- prioritisation of points with with high manifold,
- even distribution of points in both master and secondary images.
| Algorithm 1: Tie-point spatial filter |
 |
2.4.3. Matching Refinement by Least Square Matching
3. Experiments and Results
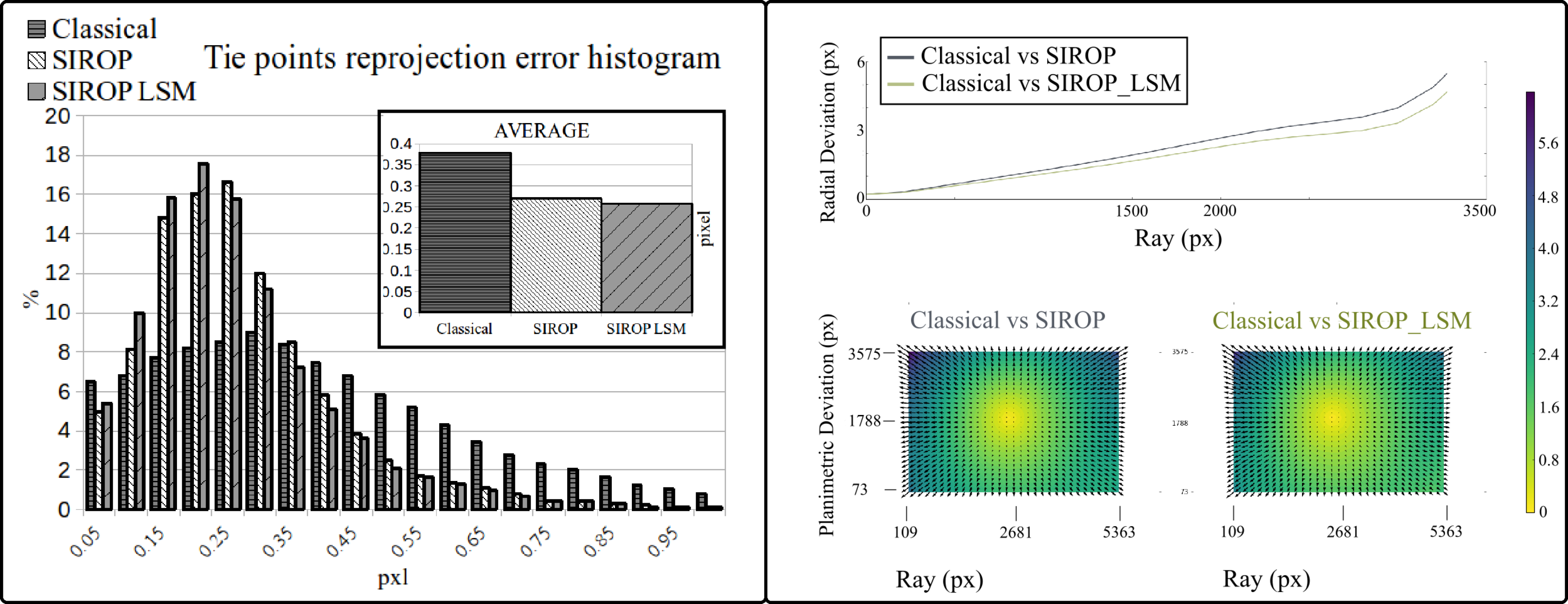
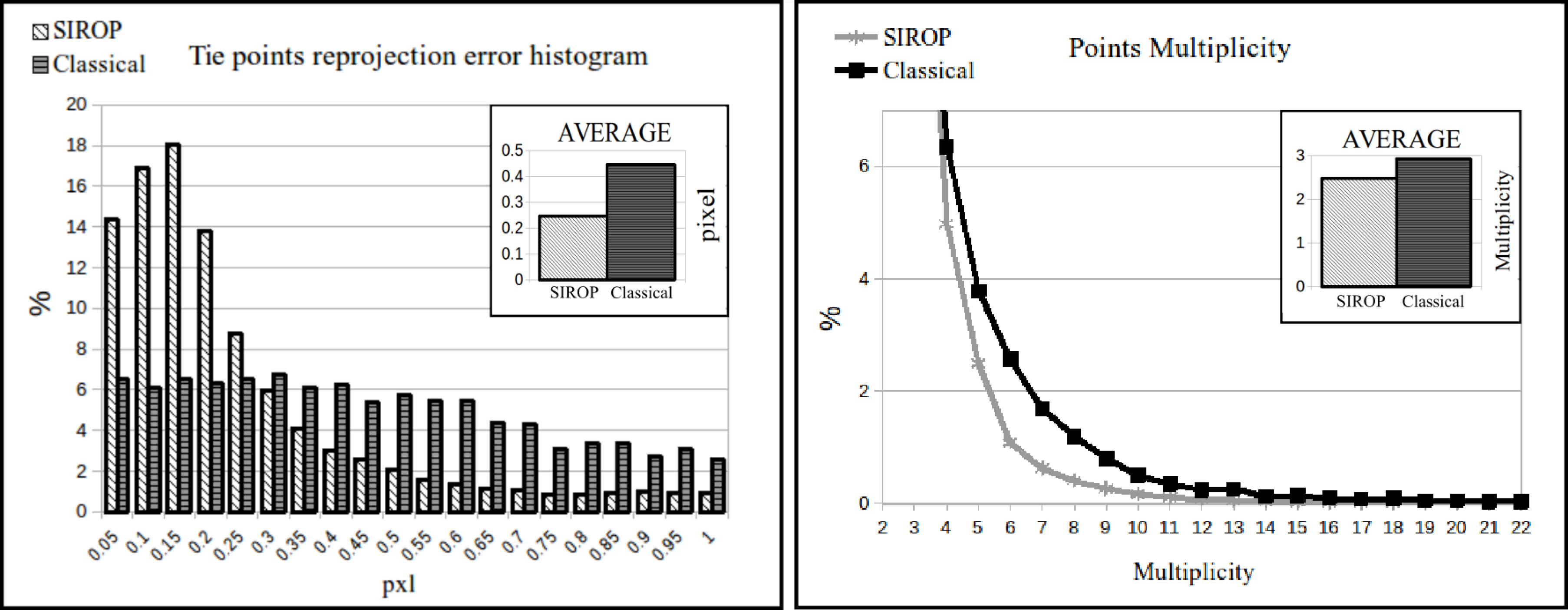
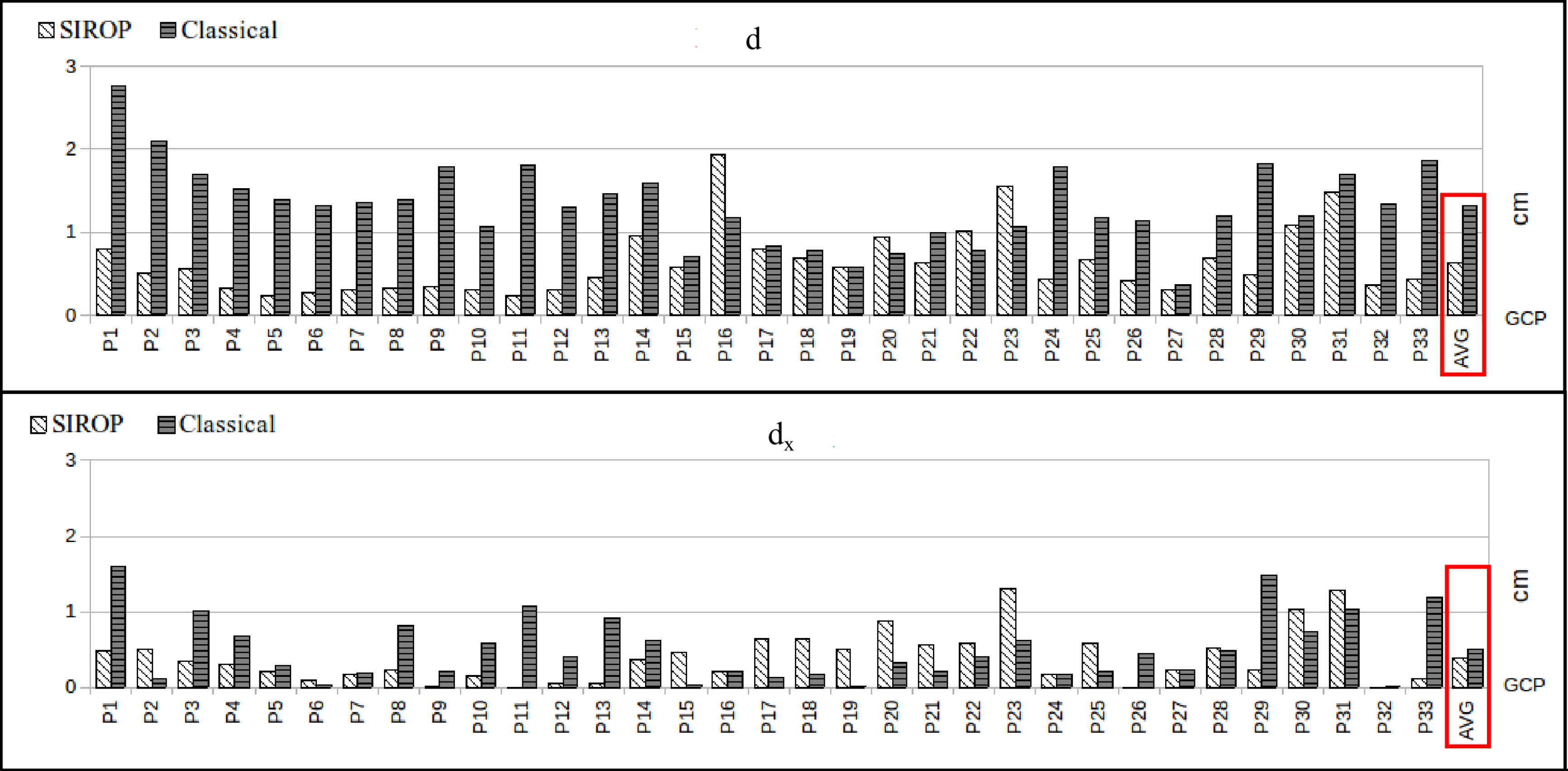
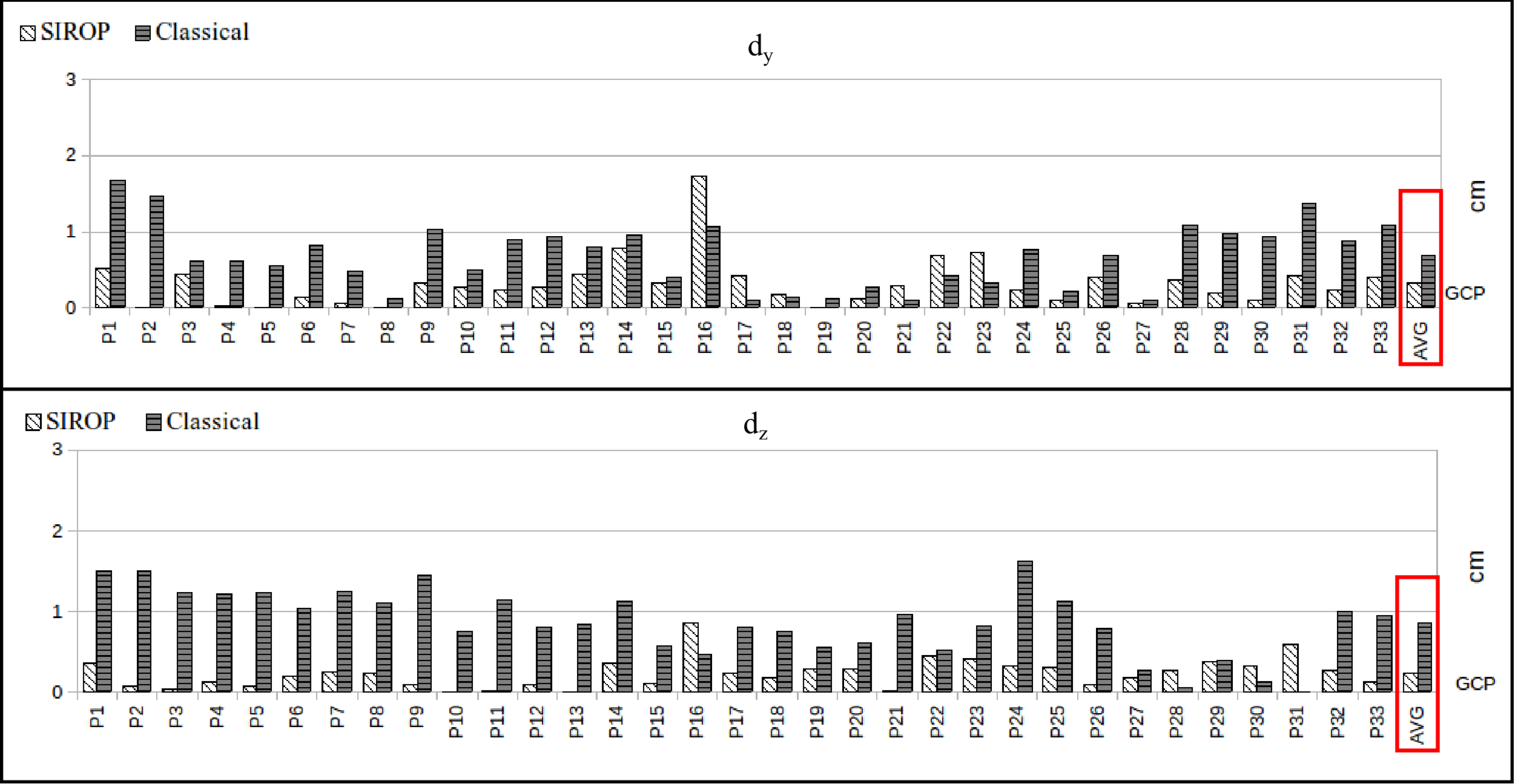
3.1. The Evaluation Procedure
- euclidean distance between GCPs resulting from image triangulation and their true values (d).
- the BBA standard deviation.
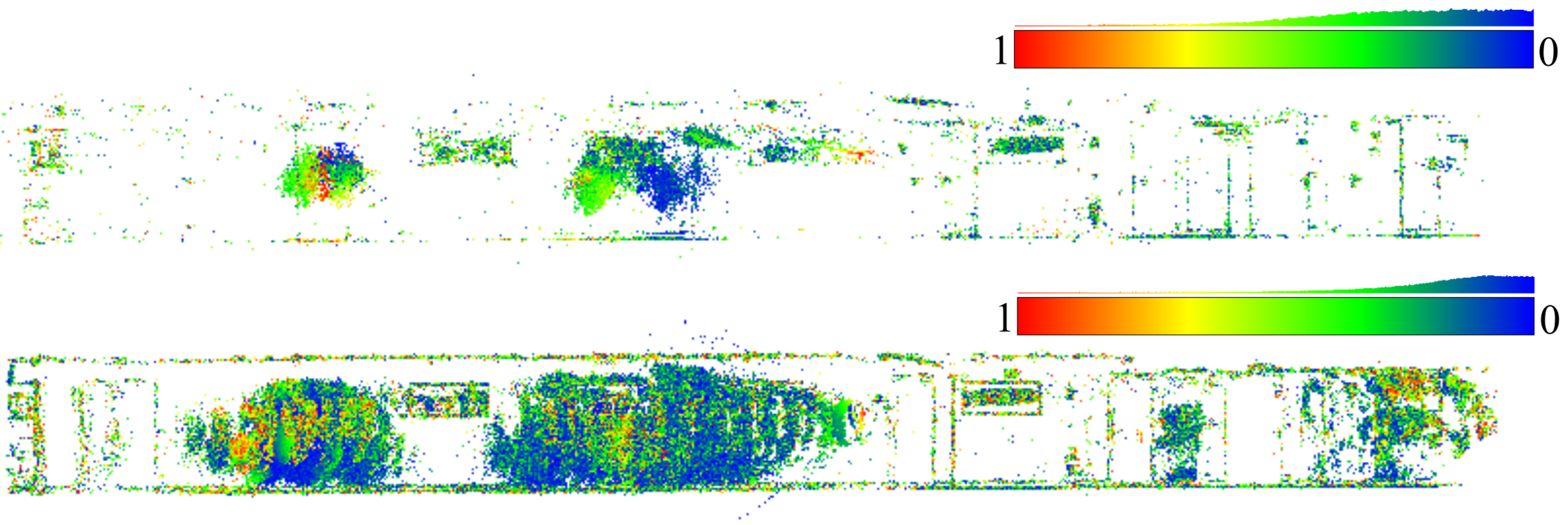
- color-coded error map of tie-points residuals.
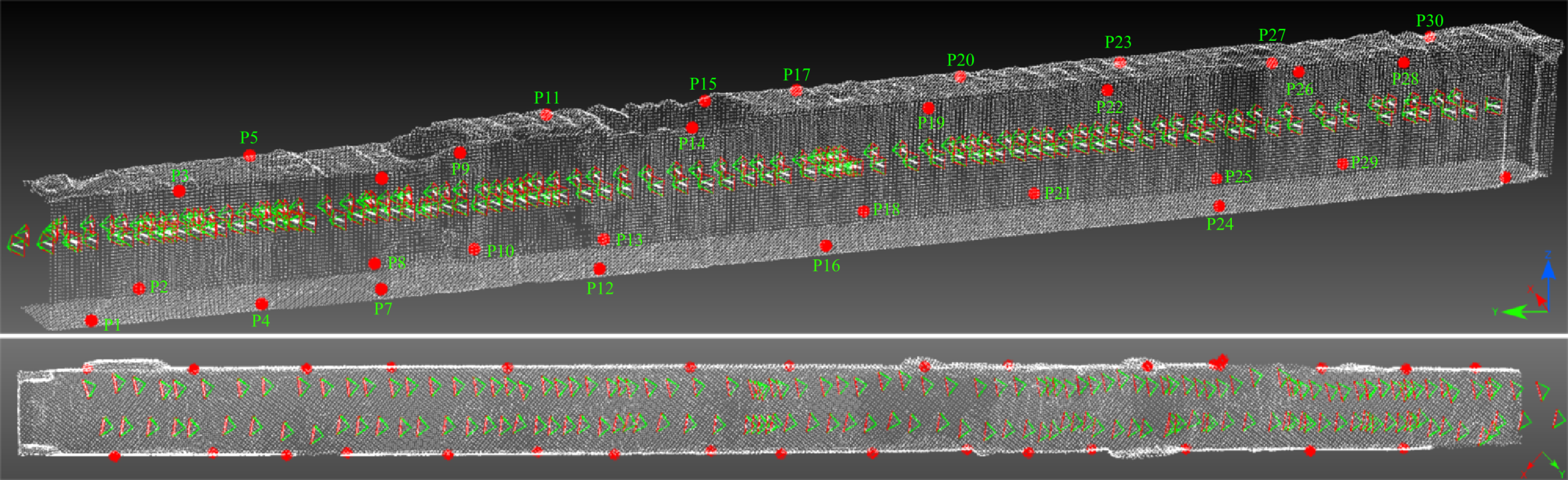
3.2. The Hallway Dataset
3.3. UAV Datasets
4. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SIROP | Second Iteration to Refine image Orientation with improved Tie-Point |
| ICP | Iterative Closest Point |
| LSM | Least Square Matching |
| ROI | Region of interest |
| CQS | Contrast Quality Score |
| ZNCC | Zero Mean Normalized Cross-Correlation |
| BBA | Bundle Block Adjustment |
| GCP | Ground Control Point |
| UAV | Unmanned aerial vehicle |
References
- Luhmann, T. Close range photogrammetry for industrial applications. ISPRS J. Photogramm. Remote Sens. 2010, 65, 558–569. [Google Scholar] [CrossRef]
- Mautz, R.; Tilch, S. Survey of optical indoor positioning systems. In Proceedings of the 2011 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Guimaraes, Portugal, 21–23 September 2011; pp. 1–7. [Google Scholar]
- Barazzetti, L.; Remondino, F.; Scaioni, M. Extraction of accurate tie points for automated pose estimation of close-range blocks. In ISPRS Technical Commission III Symposium on Photogrammetric Computer Vision and Image Analysis; ISPRS Archives: Saint-Mandé, France, 2010; Volume XXXVIII, Part 3A. [Google Scholar]
- Paparoditis, N.; Papelard, J.P.; Cannelle, B.; Devaux, A.; Soheilian, B.; David, N.; Houzay, E. Stereopolis II: A multi-purpose and multi-sensor 3D mobile mapping system for street visualisation and 3D metrology. Revue Française de Photogrammétrie et de Télédétection 2012, 200, 69–79. [Google Scholar]
- Daakir, M.; Pierrot-Deseilligny, M.; Bosser, P.; Pichard, F.; Thom, C.; Rabot, Y.; Martin, O. Lightweight UAV with on-board photogrammetry and single-frequency GPS positioning for metrology applications. ISPRS J. Photogramm. Remote Sens. 2017, 127, 115–126. [Google Scholar] [CrossRef]
- Kedzierski, M.; Fryskowska, A.; Wierzbicki, D.; Nerc, P. Chosen aspects of the production of the basic map using UAV imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2016, 41, 873. [Google Scholar] [CrossRef]
- Jacobsen, K.; Cramer, M.; Ladstädter, R.; Ressl, C.; Spreckels, V. DGPF-project: Evaluation of digital photogrammetric camera systems–geometric performance. Photogramm. Fernerkund. Geoinform. 2010, 2010, 83–97. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surface Proc. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Tournadre, V.; Pierrot-Deseilligny, M.; Faure, P. UAV linear photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2015, 40, 327. [Google Scholar] [CrossRef]
- Apollonio, F.; Ballabeni, A.; Gaiani, M.; Remondino, F. Evaluation of feature-based methods for automated network orientation. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2014, 40, 47. [Google Scholar] [CrossRef]
- Karel, W.; Ressl, C.; Pfeifer, N. Efficient Orientation and Calibtaion of Large Aerial Blocks of Multi-Camera Platforms. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; Volume XLI-B1. [Google Scholar]
- Martinez-Rubi, O.; Nex, F.; Pierrot-Deseilligny, M.; Rupnik, E. Improving FOSS photogrammetric workflows for processing large image datasets. Open Geospat. Data Softw. Stand. 2017, 2, 12. [Google Scholar] [CrossRef]
- Schmid, C.; Mohr, R.; Bauckhage, C. Evaluation of interest point detectors. Int. J. Comput. Vis. 2000, 37, 151–172. [Google Scholar] [CrossRef]
- Moravec, H.P. Obstacle Avoidance and Navigation in the Real World by A Seeing Robot Rover. Technical Report; Stanford University: Stanford, CA, USA, 1980. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Fourth Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; Volume 15, pp. 10–5244. [Google Scholar]
- Förstner, W.; Gülch, E. A fast operator for detection and precise location of distinct points, corners and centres of circular features. In Proceedings of the Intercommission Conference on Fast Processing of Photogrammetric Data, Interlaken, Switzerland, 2–4 June 1987; ISPRS: Christian Heipke, Germany, 1987; pp. 281–305. [Google Scholar]
- Smith, S.M.; Brady, J.M. SUSAN—A new approach to low level image processing. Int. J. Comput. Vis. 1997, 23, 45–78. [Google Scholar] [CrossRef]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin, Germany, 2006; pp. 430–443. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Crowley, J.L.; Parker, A.C. A representation for shape based on peaks and ridges in the difference of low-pass transform. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 156–170. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. Scale & affine invariant interest point detectors. Int. J. Comput. Vis. 2004, 60, 63–86. [Google Scholar]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In European Conference on Computer Vision; Springer: Berlin, Germany, 2006; pp. 404–417. [Google Scholar]
- Tuytelaars, T.; Van Gool, L.J. Wide Baseline Stereo Matching based on Local, Affinely Invariant Regions. In Proceedings of the 11th British Machine Vision Conference (BMVC 2000), Bristol, UK, 11–14 September 2000; pp. 412–422. [Google Scholar]
- Matas, J.; Bilek, P.; Chum, O. Rotational Invariants for Wide-Baseline Stereo. Available online: https://pdfs.semanticscholar.org/062c/935007c9498d3e3b502edb0be66080527f20.pdf?_ga=2.235926401.1832659476.1530501990-1875454276.1513739194 (accessed on 2 June 2018).
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust wide-baseline stereo from maximally stable extremal regions. Image Vis. Comput. 2004, 22, 761–767. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Tuytelaars, T.; Schmid, C.; Zisserman, A.; Matas, J.; Schaffalitzky, F.; Kadir, T.; Van Gool, L. A comparison of affine region detectors. Int. J. Comput. Vis. 2005, 65, 43–72. [Google Scholar] [CrossRef]
- Morel, J.M.; Yu, G. ASIFT: A new framework for fully affine invariant image comparison. SIAM J. Imag. Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Gruen, A.; Baltsavias, E.P. Geometrically constrained multiphoto matching. Photogramm. Eng. Remote Sens. 1988, 54, 633–641. [Google Scholar]
- Li, Z.; Wang, J. Least squares image matching: A comparison of the performance of robust estimators. ISPRS Annl. Photogramm. Remote Sensi. Spat. Inform. Sci. 2014, 2, 37. [Google Scholar] [CrossRef]
- Yang, M.Y.; Cao, Y.; Förstner, W.; McDonald, J. Robust wide baseline scene alignment based on 3d viewpoint normalization. In International Symposium on Visual Computing; Springer: Berlin, Germany, 2010; pp. 654–665. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Sensor Fusion IV: Control Paradigms and Data Structures. International Society for Optics and Photonics; SPIE: Bellingham, WA, USA, 1992; Volume 1611, pp. 586–607. [Google Scholar]
- Rupnik, E.; Daakir, M.; Deseilligny, M.P. MicMac—A free, open-source solution for photogrammetry. Open Geospat. Data Softw. Stand. 2017, 2, 14. [Google Scholar] [CrossRef]
- Deseilligny, M.P.; Clery, I. Apero, an open source bundle adjusment software for automatic calibration and orientation of set of images. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, ISPRS Trento 2011 Workshop, Trento, Italy, 2–4 March 2011; Volume XXXVIII-5/W16. [Google Scholar]
- Nguyen, T.G.; Pierrot-Deseilligny, M.; Muller, J.M.; Thom, C. Second Iteration of Photogrammetric Pipeline to Enhance The Accuracy of Image Pose Estimation. In Proceedings of the EuroCOW 2017 High-Resolution Earth Imaging for Geospatial Information, Hannover, Germany, 6–9 June 2017; pp. 225–230. [Google Scholar] [CrossRef]
- Rosten, E. FAST corner detection. Engineering Department, Machine Intelligence Laboratory, University of Cambridge. Available online: https://www.edwardrosten.com/work/fast.html (accessed on 2 July 2018).
- Remondino, F. Detectors and descriptors for photogrammetric applications. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2006, 36, 49–54. [Google Scholar]
- Pierrot-Deseilligny, M.; Paparoditis, N. A multiresolution and optimization-based image matching approach: An application to surface reconstruction from SPOT5-HRS stereo imagery. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2006, 36. [Google Scholar]
- Vedaldi, A. An Open Implementation of the SIFT Detector and Descriptor; Technical Report 070012; Department of Engineering Science The University of Oxford: Oxford, UK, 2007. [Google Scholar]
- Fraser, C.S. Digital camera self-calibration. ISPRS J. Photogramm. Remote sens. 1997, 52, 149–159. [Google Scholar] [CrossRef]
- Martin, O.; Meynard, C.; Pierrot Deseilligny, M.; Souchon, J.P.; Thom, C. Réalisation d’une caméra photogrammétrique ultralégère et de haute résolution. In Proceedings of the colloque drones et moyens légers aéroportés d’observation, Montpellier, France, 24–26 June 2014; pp. 24–26. (In French). [Google Scholar]
- Nocerino, E.; Menna, F.; Remondino, F.; Saleri, R. Accuracy and block deformation analysis in automatic UAV and terrestrial photogrammetry-Lesson learnt. ISPRS Anna. Photogramm. Remote Sens. Spat. Inform. Sci. 2013, 2, 5. [Google Scholar] [CrossRef]
- Nocerino, E.; Menna, F.; Remondino, F. Accuracy of typical photogrammetric networks in cultural heritage 3D modeling projects. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2014, 40, 465. [Google Scholar] [CrossRef]

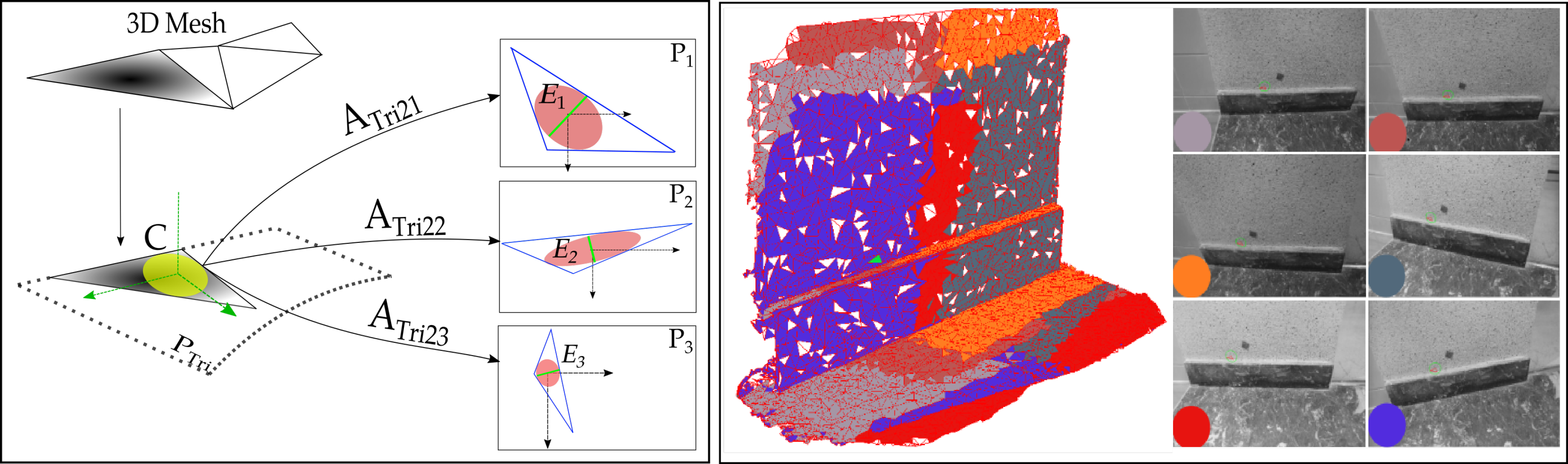










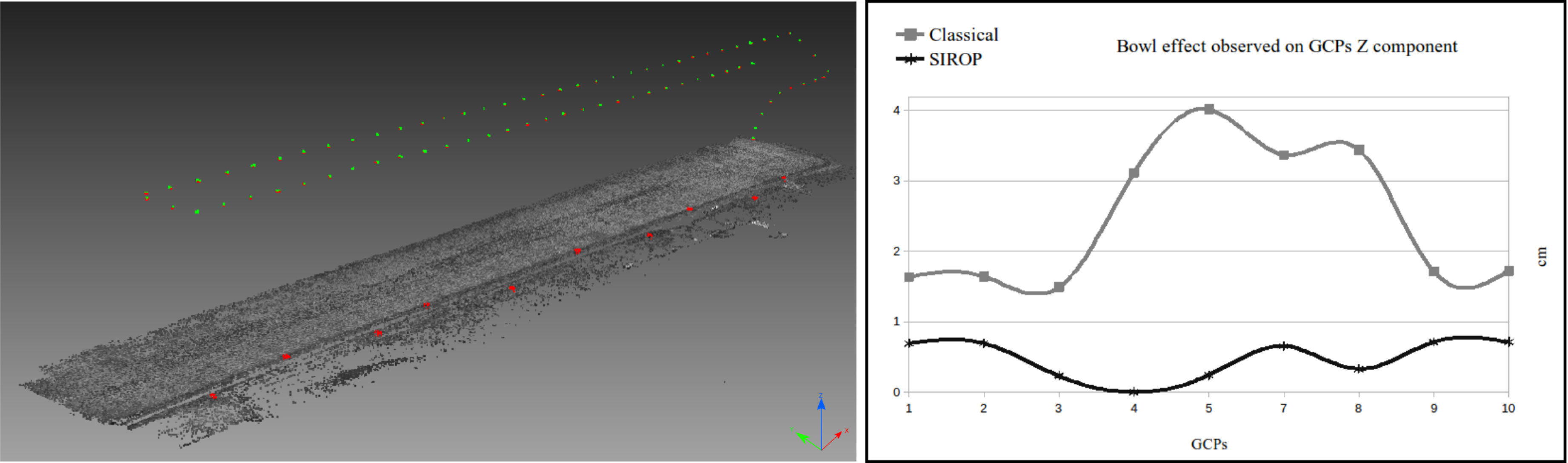
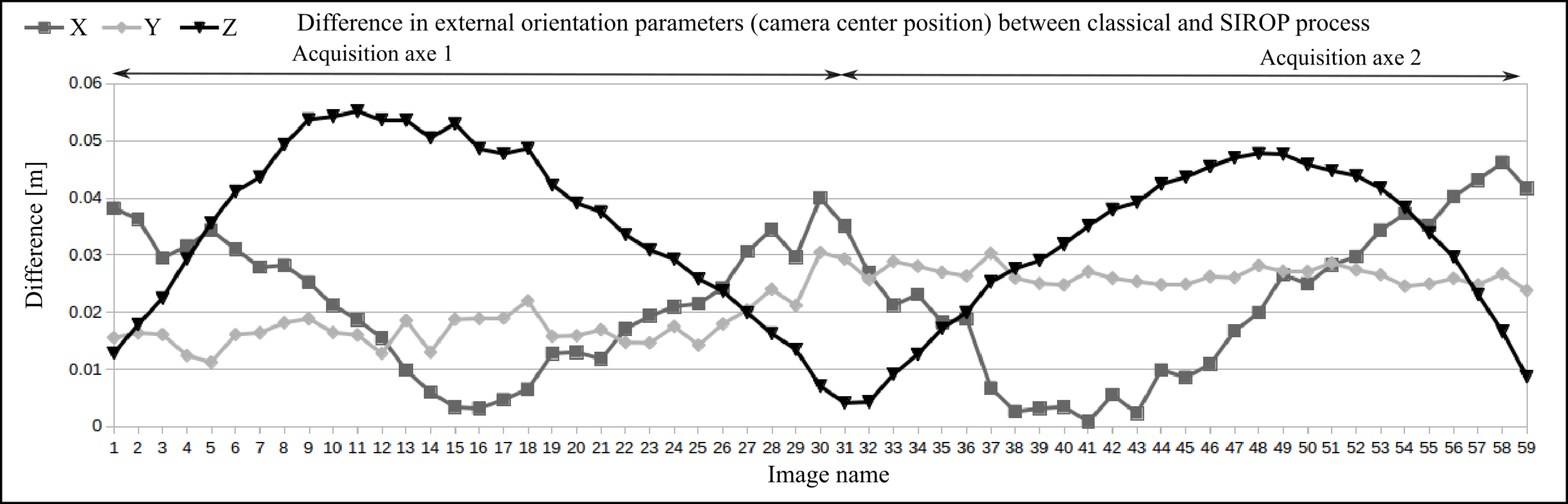
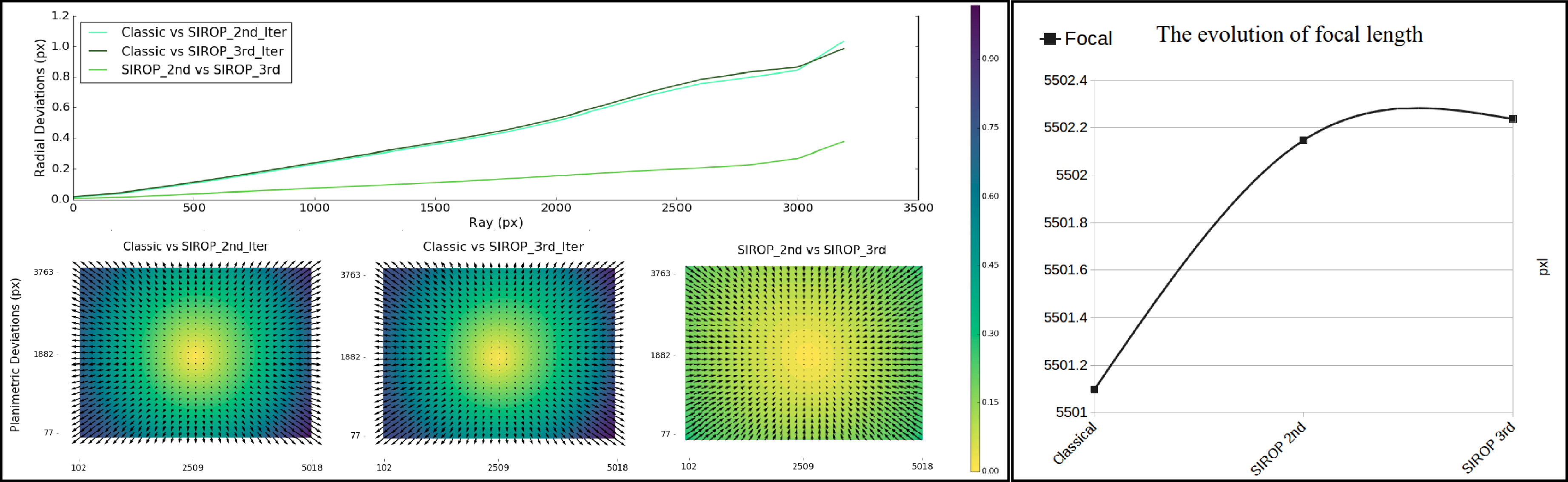

| Dataset Name | Hallway | Viabon 1 | Corridor |
|---|---|---|---|
| Type | Terrestrial/Indoor | Drone/Outdoor | Drone/Outdoor |
| Camera | IGN Camlight | IGN Camlight | IGN Camlight |
| Focal Length | 18 mm | 35 mm | 35 mm |
| Images | 179 | 118 | 77 |
| Scene Size • | 30 × 1.5 | 140 × 140 | 437 × 65 |
| Nb GCP • • | 33 Tophography mm | 7 GPS RTK cm | 10 GPS RTK cm |
| Datatset | Method | Value | |||||
|---|---|---|---|---|---|---|---|
| d [cm] | d_x [cm] | d_y [cm] | d_z [cm] | Rep_Err [pxl] | Multiplicity [Points] | ||
| Viabon 1 | Classical | 3.43 | 0.71 | 0.71 | 3.17 | 0.59 | 5.2 |
| SIROP | 1.21 | 0.64 | 0.69 | 0.52 | 0.31 | 5.6 | |
| Corridor | Classical | 2.13 | 0.86 | 0.8 | 1.44 | 0.29 | 3.2 |
| SIROP | 1.45 | 0.66 | 0.75 | 0.82 | 0.13 | 4.2 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Truong Giang, N.; Muller, J.-M.; Rupnik, E.; Thom, C.; Pierrot-Deseilligny, M. Second Iteration of Photogrammetric Processing to Refine Image Orientation with Improved Tie-Points †. Sensors 2018, 18, 2150. https://doi.org/10.3390/s18072150
Truong Giang N, Muller J-M, Rupnik E, Thom C, Pierrot-Deseilligny M. Second Iteration of Photogrammetric Processing to Refine Image Orientation with Improved Tie-Points †. Sensors. 2018; 18(7):2150. https://doi.org/10.3390/s18072150
Chicago/Turabian StyleTruong Giang, Nguyen, Jean-Michaël Muller, Ewelina Rupnik, Christian Thom, and Marc Pierrot-Deseilligny. 2018. "Second Iteration of Photogrammetric Processing to Refine Image Orientation with Improved Tie-Points †" Sensors 18, no. 7: 2150. https://doi.org/10.3390/s18072150
APA StyleTruong Giang, N., Muller, J.-M., Rupnik, E., Thom, C., & Pierrot-Deseilligny, M. (2018). Second Iteration of Photogrammetric Processing to Refine Image Orientation with Improved Tie-Points †. Sensors, 18(7), 2150. https://doi.org/10.3390/s18072150





