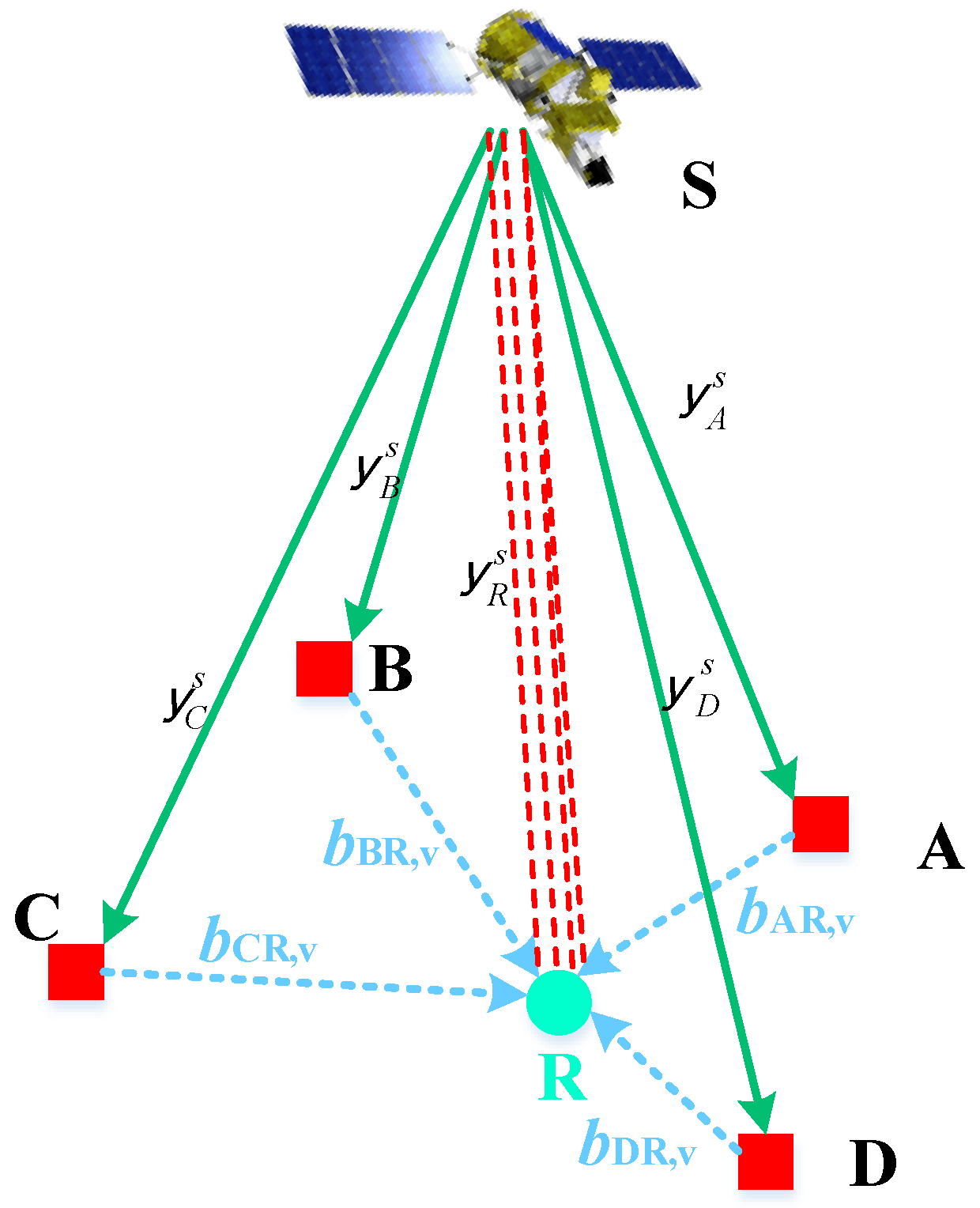
We have verified the proposed method by conducting the static and kinematic experiments. We extensively compared the ambiguity resolution and the positioning accuracy performance of the single receiver-antenna (SA) solution and multiple moving receiver-antenna (MA) solution. The SA solution means using a single antenna and receiver as the base station. Both experiments use dual-frequency code and phase GPS measurements. The standard deviation of un-differenced code and phase measurement is 30 cm and 3 mm respectively, by keeping measurement type weighting. It has been widely proven that the LAMBDA algorithm has the best success rate among the different integer aperture estimation methods [
33]. We therefore used the LAMBDA for ambiguity resolution. Since the proposed method can mitigate the effect of measurement noise from the combination of multiple reference receivers, an optimistic threshold is preferable to prove the edge of our proposed method. The threshold for ratio test is set up to 1/2 [
34,
35]. The ambiguity success rates are computed by comparing the single-epoch estimated ambiguities to the reference ambiguities obtained from the whole span of data. To evaluate position estimation accuracy, the horizontal and vertical position error (HPE/VPE) are:
where Δ
xE, Δ
xN, Δ
xU is the relative position estimation error of east, north and up component respectively. To quantify relative position estimation precision, assuming Rayleigh and Gaussian distribution of horizontal and vertical error, Equations (23) and (24) are used to compute the 95% horizontal and vertical error bounds, where operator std() denotes standard deviation operator [
36].
3.1. Static Experiment
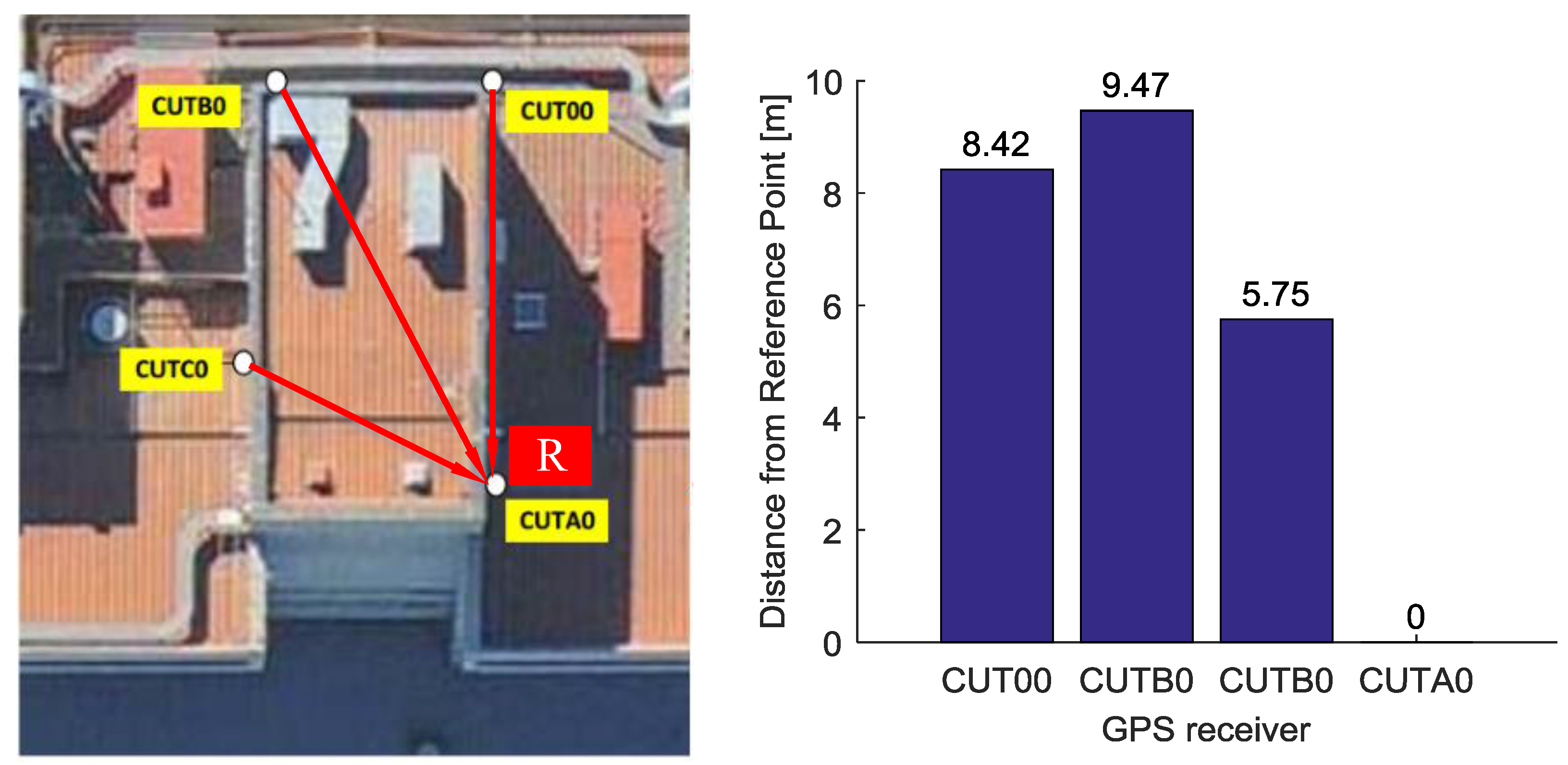
In the experiment, the performance of real-time relative positioning using MA solution are compared with commonly used SA solutions. The data from Curtin GNSS Research Centre was used as multiple reference receiver data in the static experiment. There are four stations marked CUTB0, CUTC0, CUT00, CUTA0 on the roof of the building of Curtin University in Perth, Australia, whose locations are precisely known. Each station is equipped with a TRM59800.00-SCIS antenna (Trimble Inc., Sunnyvale, CA, USA) which is connected with TRIMBLE NETR9 receiver (Trimble Inc., Sunnyvale, CA, USA). We assumed that entire roof would act as a base station; the receivers of CUTB0, CUTC0, CUT00 are used as reference receivers. We selected the location of station CUTA0 as the virtual point. Given the coordinates of each antenna in ECEF frame, we calculated the baseline length between the multiple reference receiver antennas and the virtual point. The distribution of CUTB0, CUTC0, CUT00, CUTA0 and the calculated baseline lengths are shown in
Figure 2. The details of the data used including baseline length between each reference receiver and the virtual point, the time of data collection, and the sampling rate are given in
Table 1.
To simulate the moving base station scenario, we assume that the absolute position of CUT00, CUTB0, CUTC0, CUTA0 are unknown, given the baseline lengths. We set CUT00 as the rover.
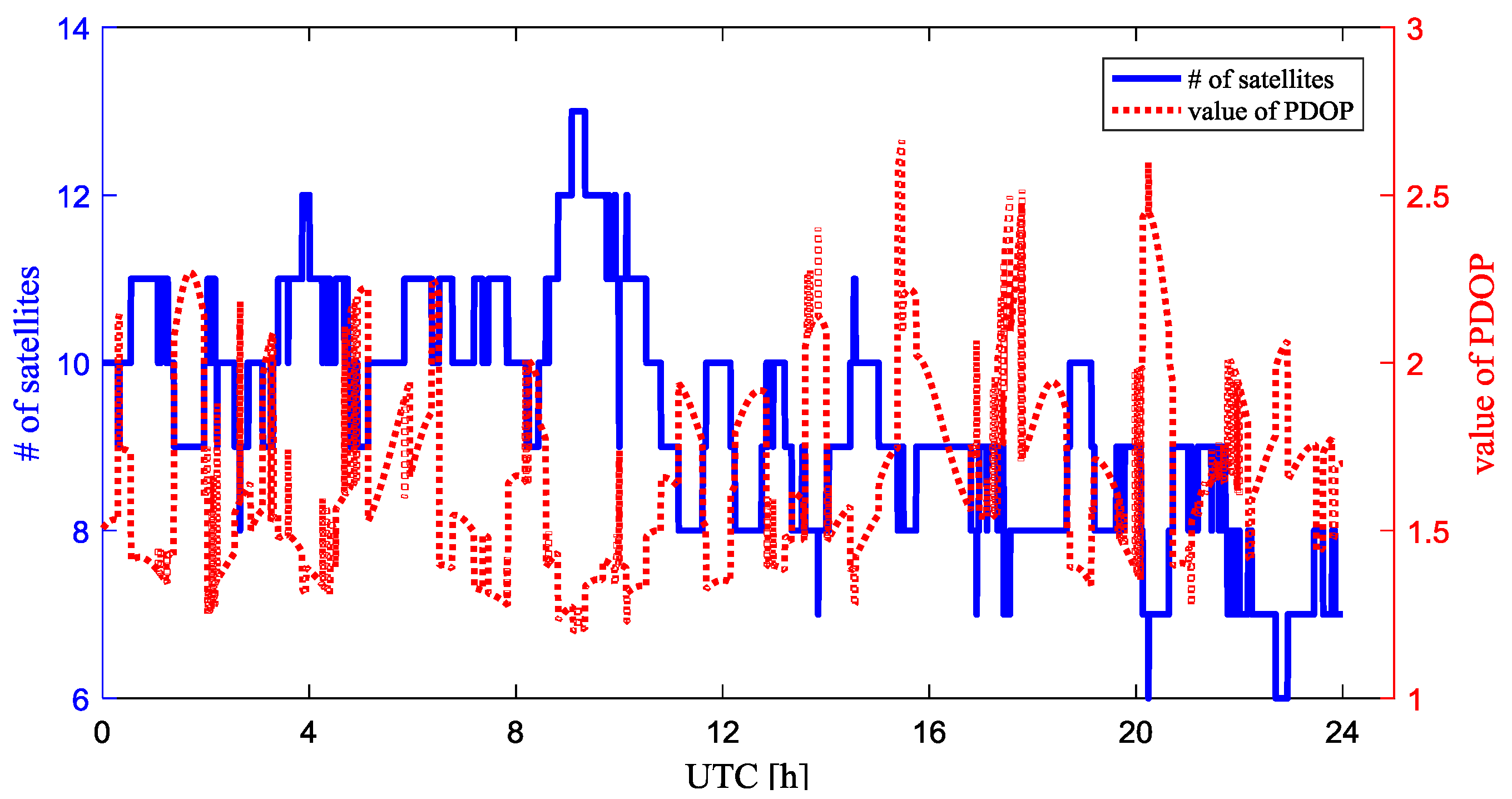
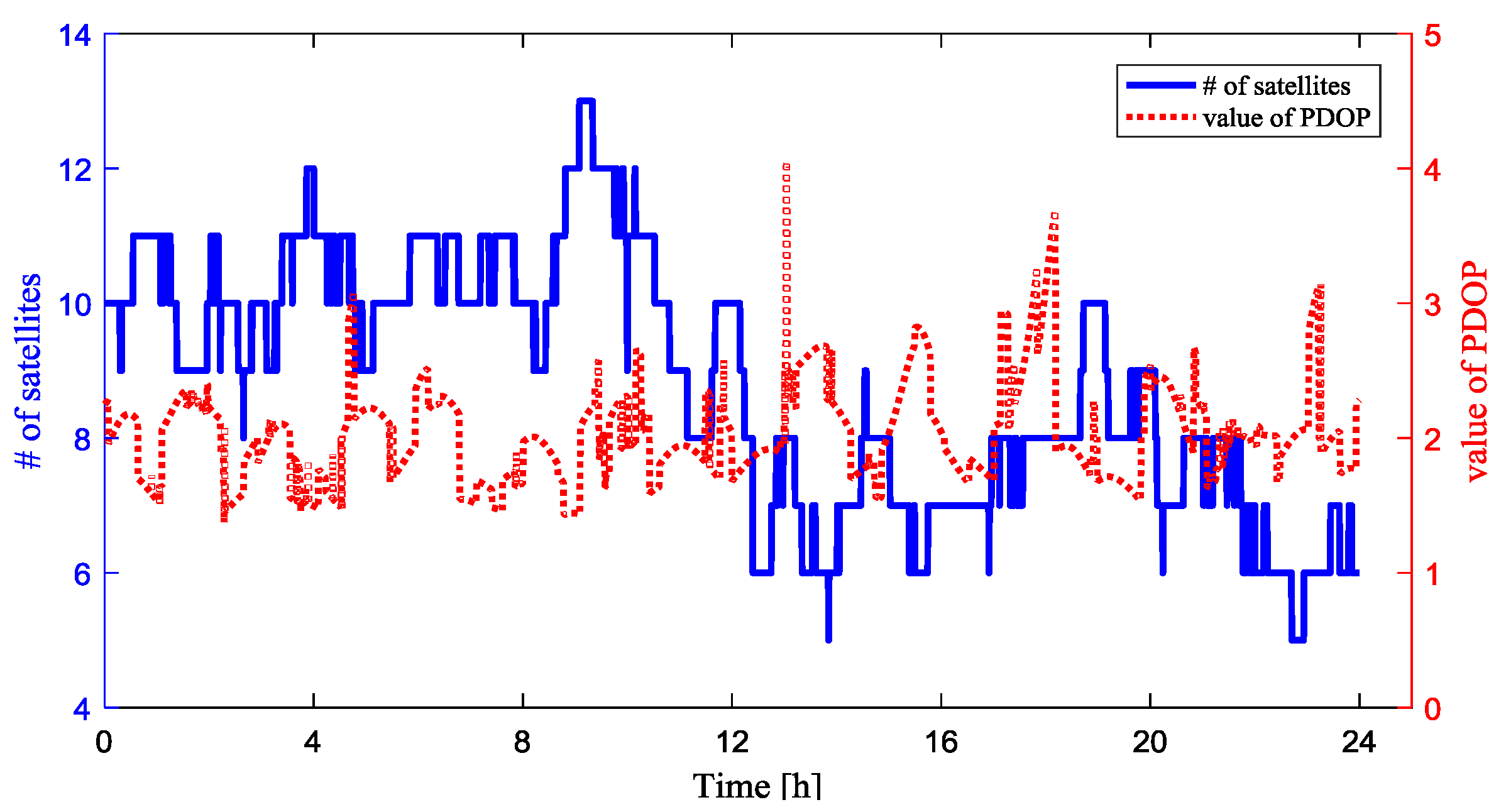
Figure 3 shows the number of the visible GPS satellites and the positional dilution of precision (PDOP) value for baseline between rover and the base station during the experiment, which helps to evaluate the observing conditions. The cutoff elevation angle is 5 degree. The number of visible GPS satellites varies from 7 to 13, while the PDOP values were smaller than 2 at most times.
With the baseline lengths shown in
Table 1, the fused code and phase measurements at the virtual point can be calculated as the measurements of base station. We can get the GPS double difference (DD) relative position estimation between the virtual point and the rover. The estimation accuracy and precision are shown in
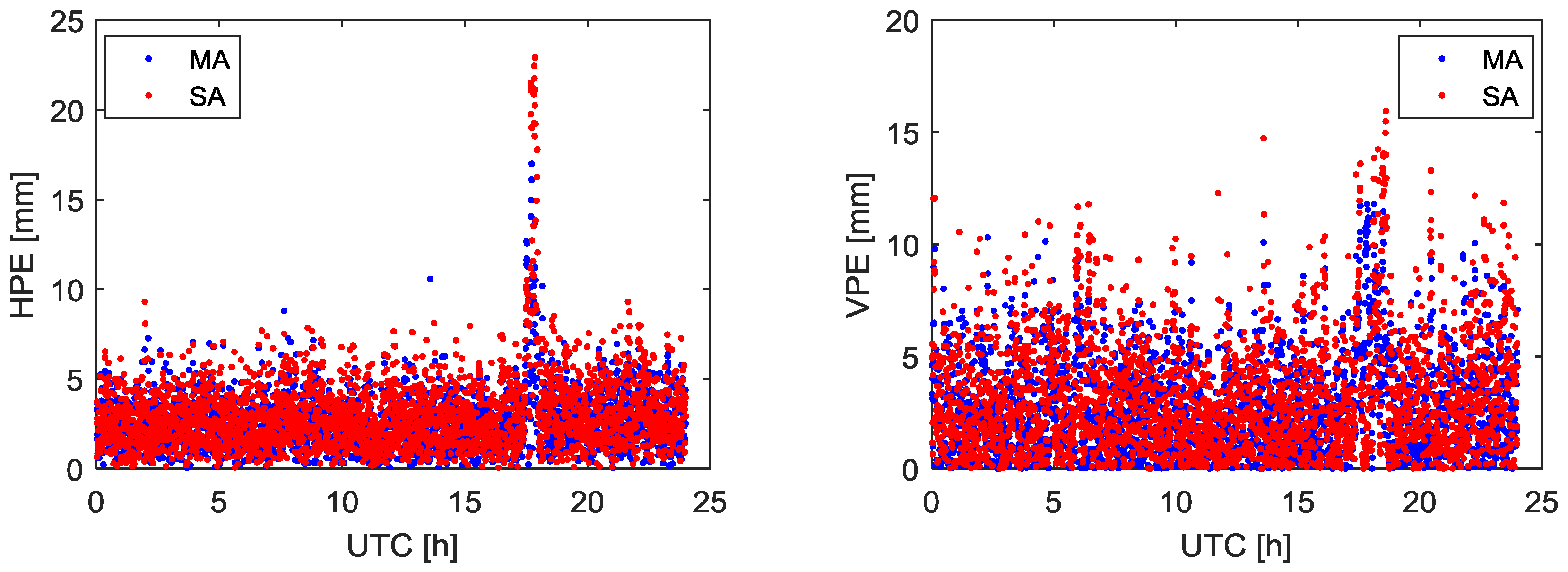
Figure 4 and
Table 2.
The experiment initially demonstrates the feasibility of the multiple moving receiver data fusion method. Considering all receivers of the base station and rover used in this experiment are installed at the top of the building in an open field of vision, the number of GPS satellites received and satellite geometry is appropriate. In addition, the baseline between the reference point and rover can be considered a short baseline. Therefore, in
Figure 4, the difference in position estimation accuracy obtained by using MA and the SA is not obvious. In
Table 2, the position estimation precision using MA and the SA is at the same level, and the ambiguity resolution success rates are all 100%.
To test the relative positioning performance with a longer baseline distance, we use PERT as the rover instead of CUT00. PERT is a permanent GNSS reference station in Australia in the IGS network, which is equipped with a TRM59800.00 antenna and TRIMBLE NETR9 receiver. The distance between PERT and the virtual point is about 22.4 km. To mitigate the effect of DD measurement residual errors, we increased the elevation angle to 10 degrees for the long baseline test. The visible GPS satellites and the PDOP value for baseline between rover and the base station are shown in
Figure 5, with a cutoff elevation angle of 10 degrees. During the experiment, 5 to 13 satellites were observed at the rover station. The PDOP values were oscillating near the value of 2 most of the time.
With the same fused code and phase measurements at the virtual point, the relative position estimation accuracy and precision are shown in
Figure 6 and
Table 3.
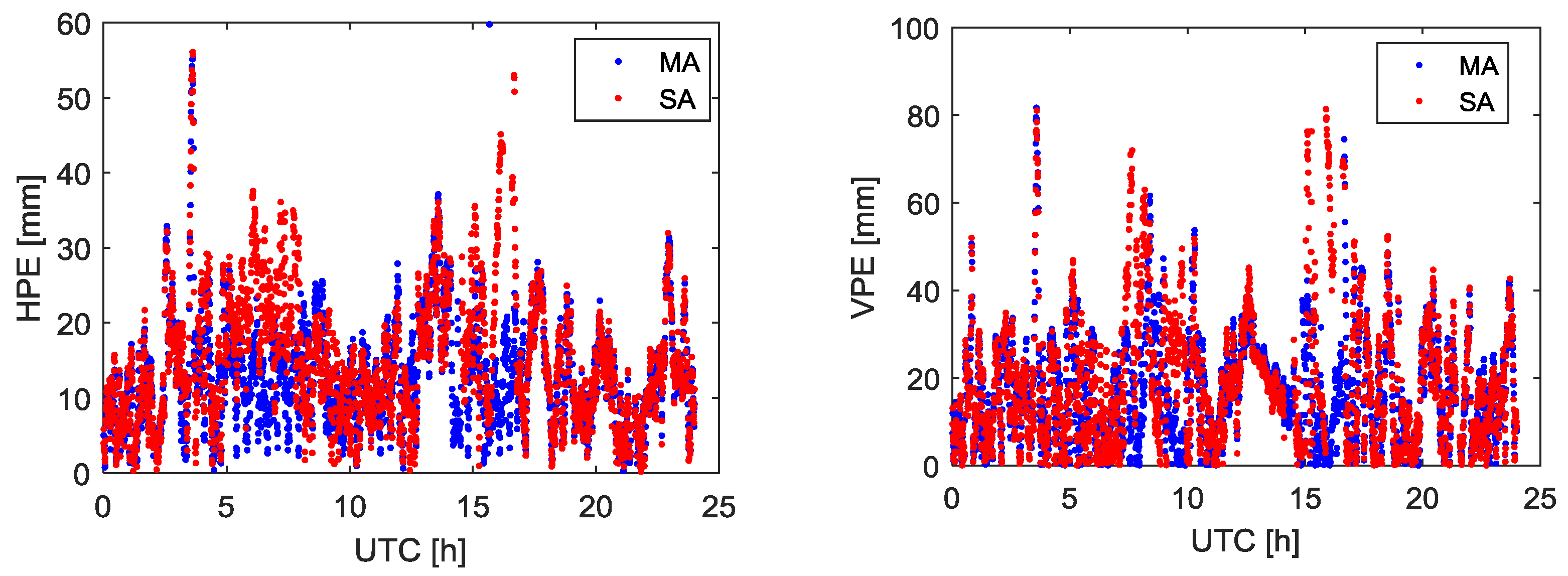
The relative position estimation errors in
Figure 6 are increased compared with
Figure 4 for both horizontal and vertical components. The position accuracy of MA solution is comparable with the SA solution. When compared with the SA, it can found that the ambiguity resolution success rate of MA is increased by 3.06%. Furthermore, the relative position estimation precision can be reduced by 15.9% for the horizontal component and 15.7% for the vertical component, compared with SA solution shown in
Table 3. The relative position estimation accuracy decreases mainly due to the de-correlation of the ionospheric and tropospheric delays with growing rover to reference point distance. MA solution can obtain better quality measurements and then have better ambiguity resolution success rate and position estimation precision compared with the SA solution. This is mainly because the MA solution pulls down the errors and generates higher precision fused measurements than the individual measurement used in SA solution.
The fused measurements obtained using baseline length in ECEF frame directly are not affected by the platform baseline errors and the attitude errors. However, if the baseline length in ECEF frame is unknown, it needs to be calculated by baseline length in body frame and attitude in navigation frame. In this case, the uncertainty of fused measurements is influenced by platform baseline errors and attitude errors, as shown in Equation (15). We use the static experiment data to evaluate the effect of attitude errors and baseline errors on relative position estimation results. As all the reference receivers are static to simplify simulation, the body frame and the navigation frame are assumed to be coincident. Different error models including baseline errors and attitude errors are used in the simulation.
is estimated as the baseline vector in the body frame, which can be obtained by platform survey or estimation in real time. Any estimation process for baseline vector cannot have a perfect solution. Therefore, there will be a residual uncertainty of
. We assume the uncertainty of baseline has a standard deviation of 1 cm [
37] in the simulation.
Figure 7 and
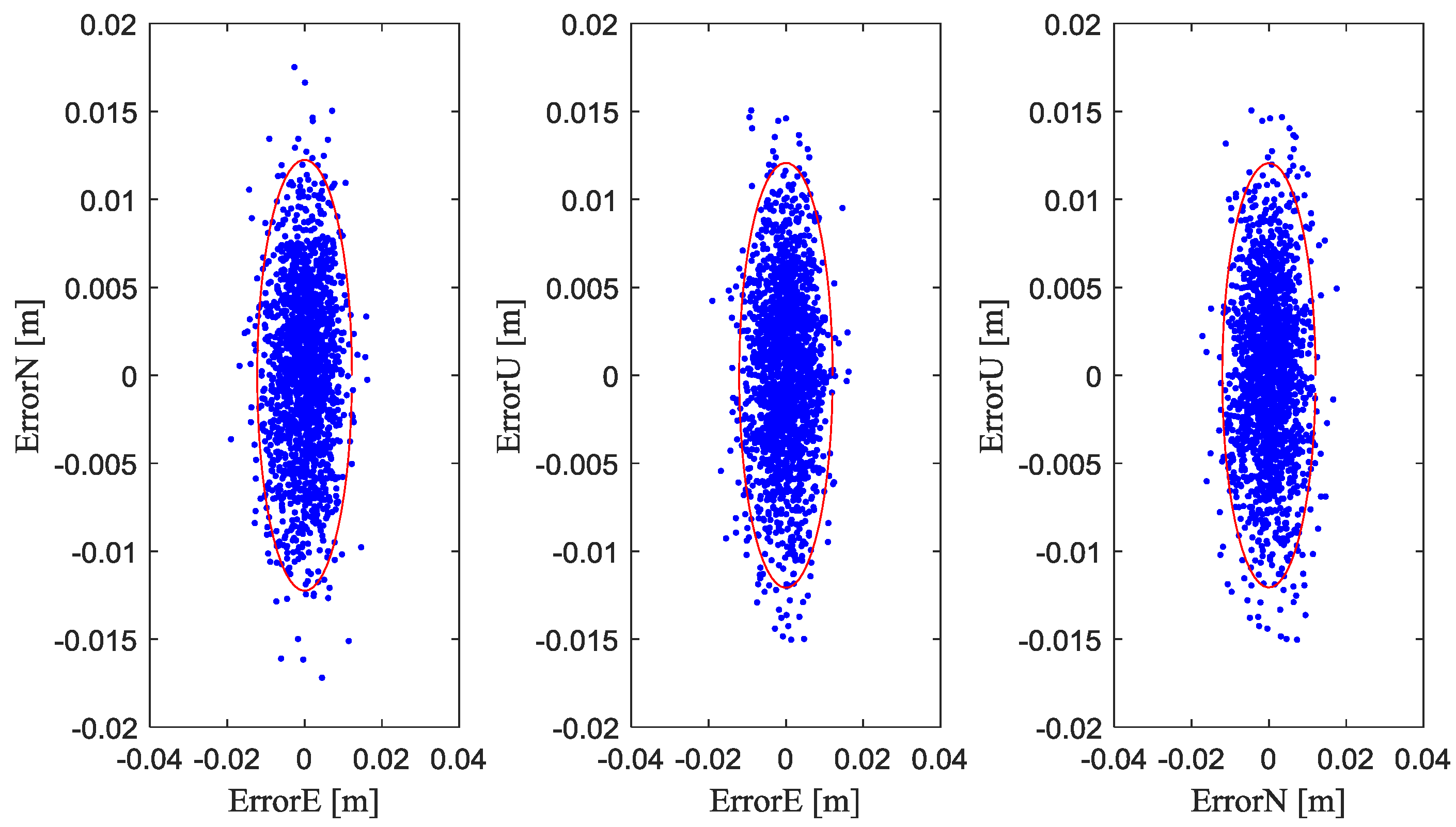
Table 4 shows the baseline-induced extra position estimation errors with fused measurements. In
Figure 7, the cloud of points represents the position estimation errors caused by baseline errors. The red ellipses represent 95% of position estimation errors. From
Figure 7 and
Table 4, it is seen that baseline uncertainty with a standard deviation of 1 cm causes centimeter-level accuracy changes in position estimation accuracy.
For attitude errors, it is also difficult to specify values as the expected errors in the simulation. This is because the attitude errors mainly depend on grade of attitude sensors. To show the effect of attitude errors on the final position estimation result, we assume that the standard deviation of attitude errors is approximately 0.05° to 0.3° in the simulation [
38,
39,
40,
41].
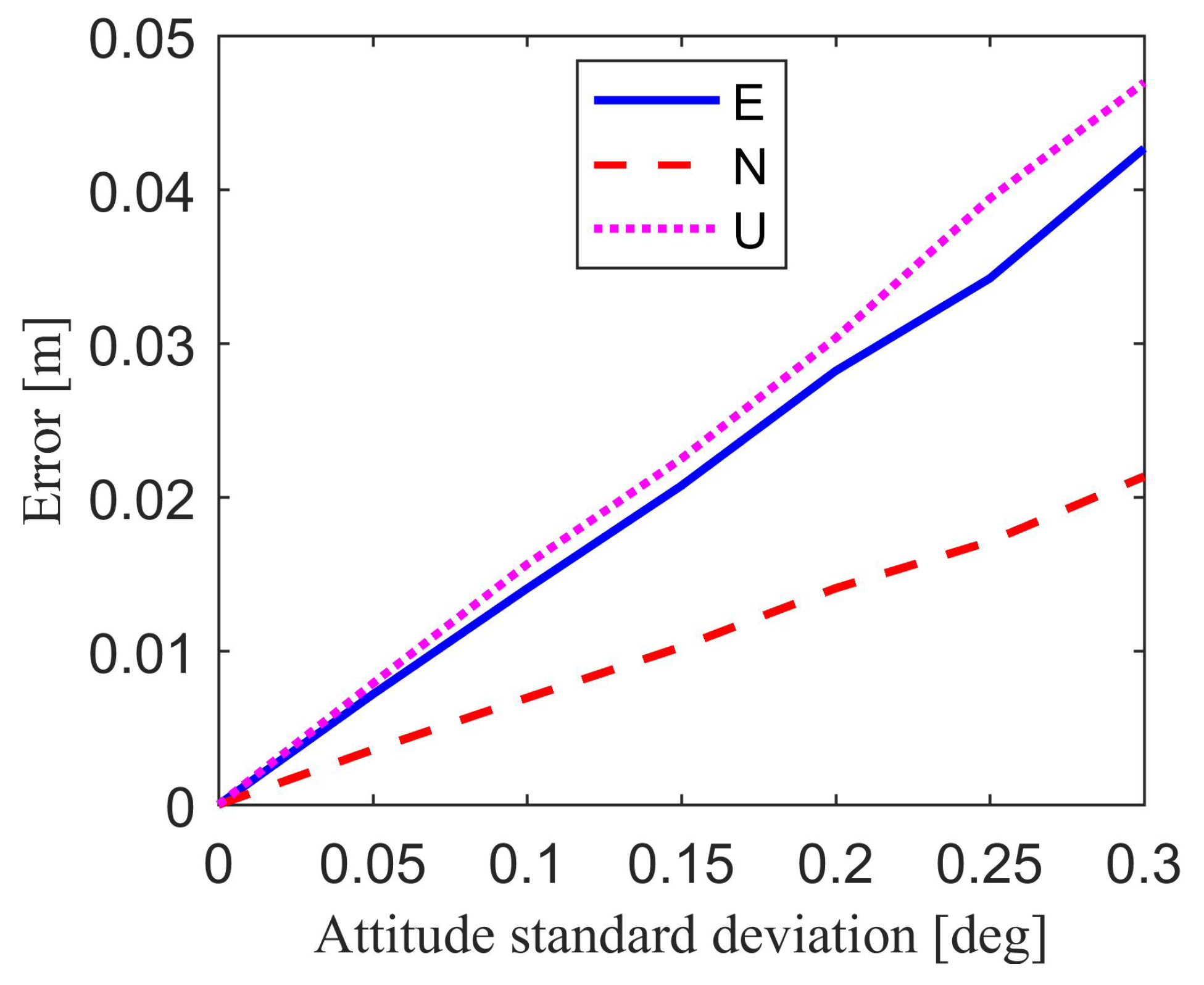
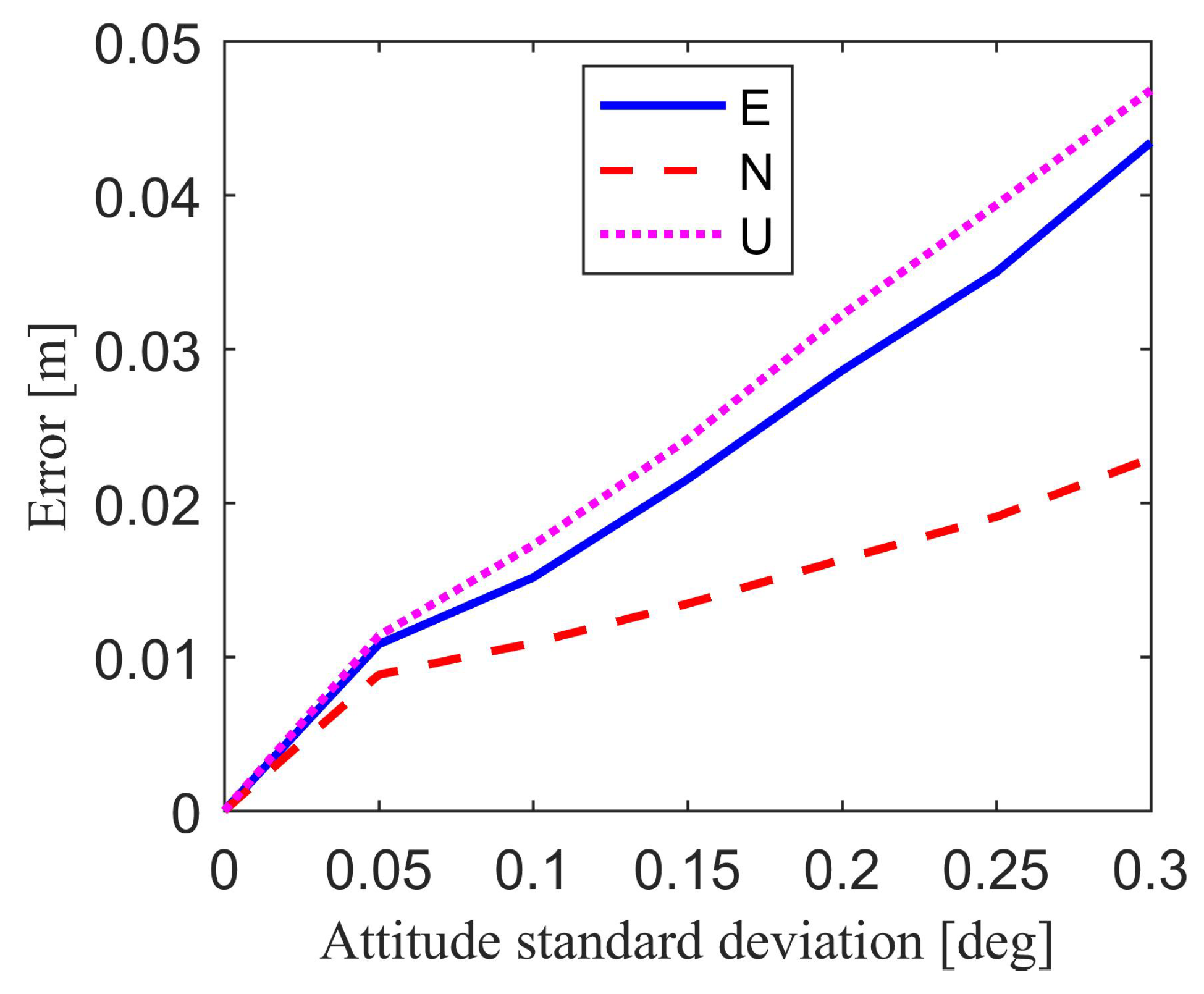
Figure 8 and
Table 5 show the relative position estimation errors in east, north, up component, and position estimation precision caused by attitude errors. It is clear that if the attitude standard deviation is small enough, for example smaller than 0.05°, the attitude-induced relative position estimation errors will change in millimeter-level compared with the results without attitude error.
Figure 9 and
Table 5 show the position estimation error due to the combined effect of baseline errors and attitude errors. The baseline standard deviation is set to 1 cm, while the attitude standard deviation ranges from 0.05° to 0.3°. If the baseline standard deviation is restricted to 1 cm, the combined baseline and attitude-induced position estimation errors have far less difference compared with attitude-induced position estimation errors. This means that the baseline length error with the standard deviation of 1 cm has little effect on the position estimation errors compared with the attitude errors. These figures and tables show the influence of the attitude errors and baseline errors on the position estimation results, thereby providing a reference for the accuracy of baseline and attitude.
3.2. Kinematic Experiment
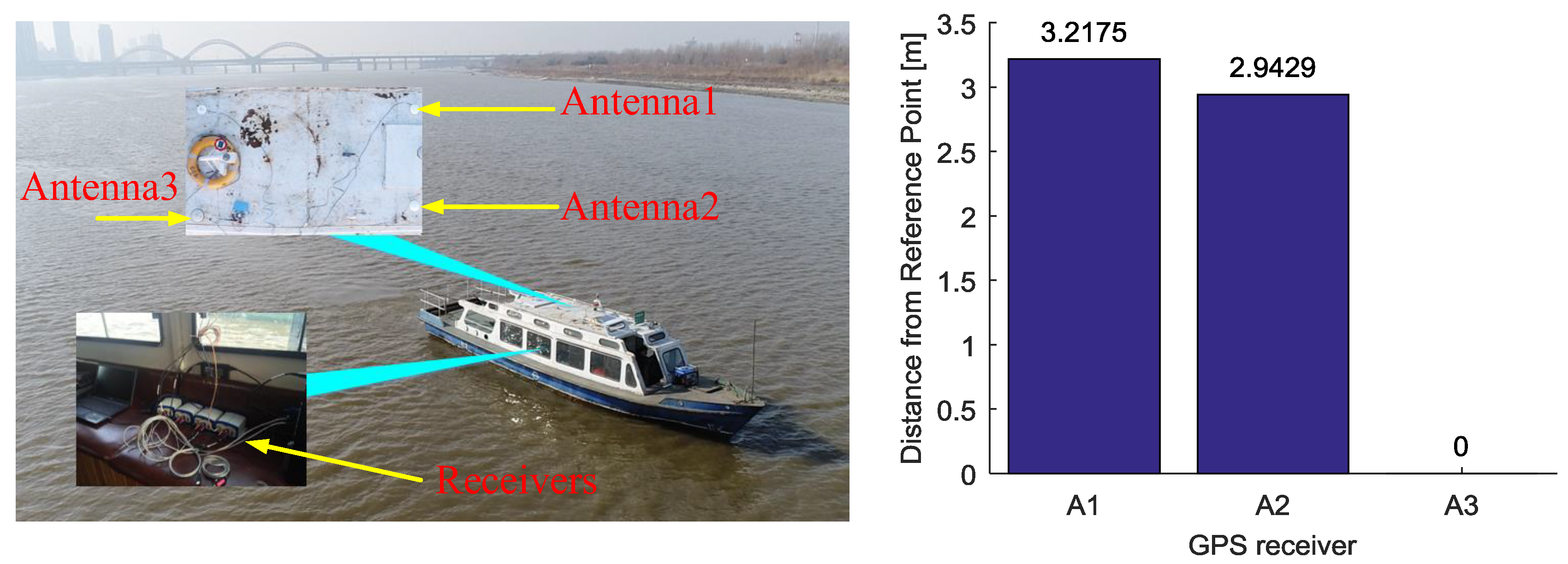
The kinematic experiment was conducted on the Songhua River of Harbin, China. The receiver antennas are mounted on the roof of the ship, as shown by
Figure 10. Three reference receivers (BDM683, Unicorecomm, Beijing, China) are placed in the cabin and connect with two CHCNAV A230GRB antennas and a Novatel GPS-703-GGG antenna, marked as A1, A2, A3, respectively. We use the post-processing software to obtain the coordinate of antennas A1~A3 as the benchmark. We set the receivers RCV1, RCV2, RCV3, which are connected with three antennas A1, A2, A3 respectively, as the reference receivers and set the location of antennas A3 as the reference point (R). The details of the data are given in
Table 6. The cutoff elevation angle is set up to 5 degrees.
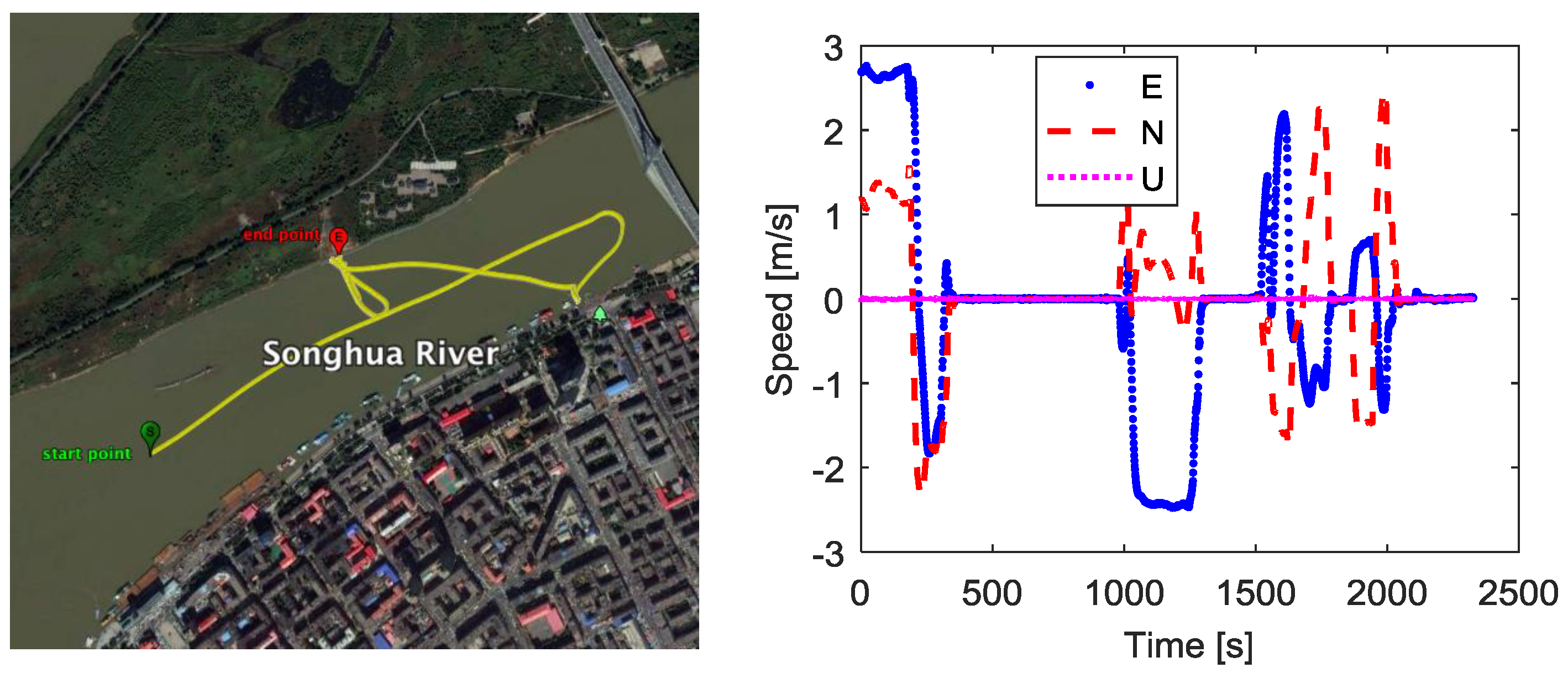
In the kinematic experiment, the ship sailed on the river for about 39 min. The horizontal trajectory is shown in
Figure 11, and the velocity of the ship are shown in the right part of
Figure 11. The ship moved irregularly during the experiment, and the three-dimensional velocity ranged from 0 m/s to 3 m/s.
We use the fused measurements at virtual R as the measurements of the base station. The fused measurements are obtained by the measurements from three moving receivers RCV1, RCV2, RCV3 which are connected with three antennas A1, A2, A3 respectively. One receiver located at Harbin Engineering University, China, is used as the rover. The distance between the rover and start point in
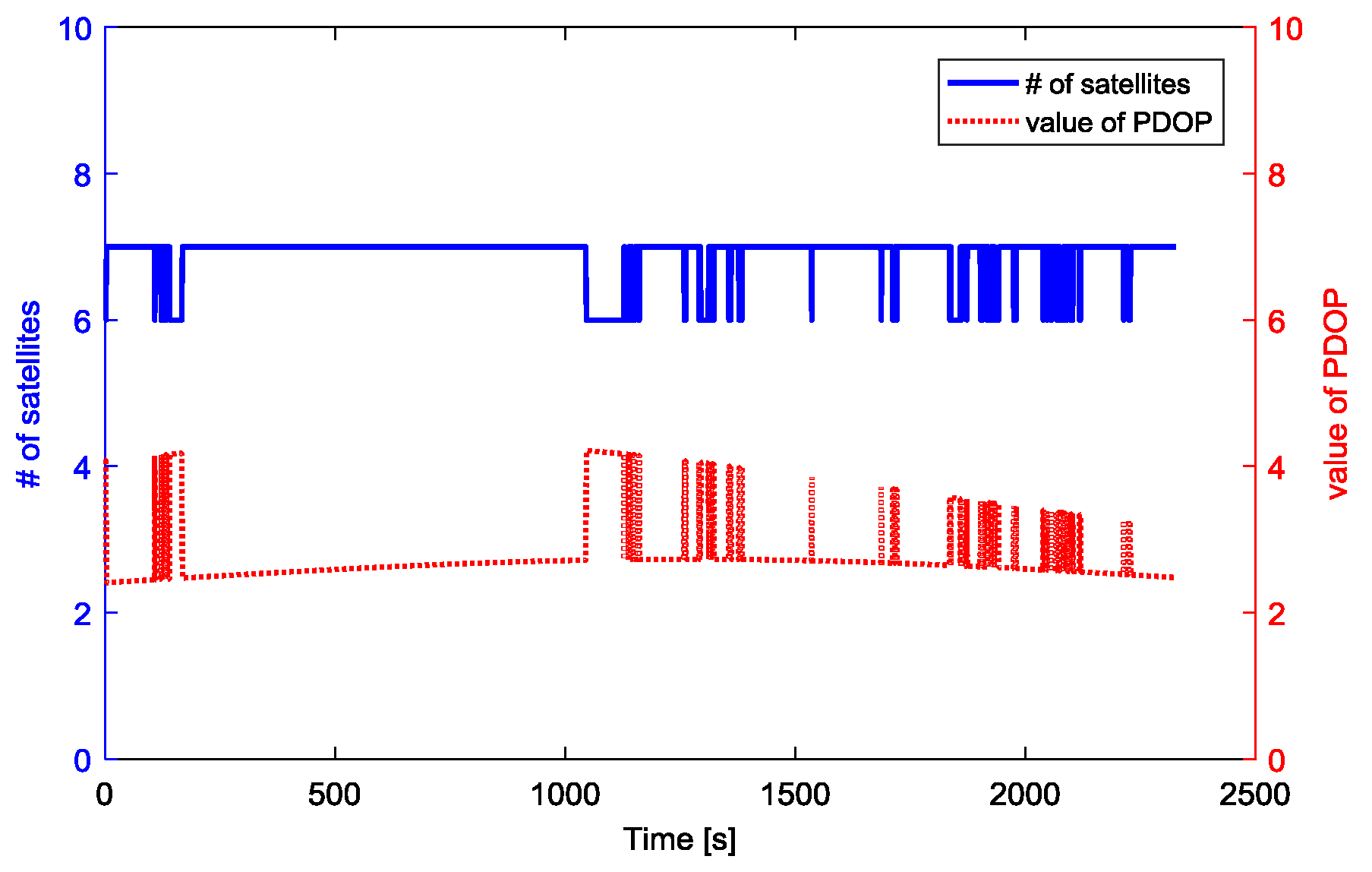
Figure 11 is about 4.1 km. During the kinematic experiment, the number of visible GPS satellites and PDOP values for baseline between rover and the base station are shown as
Figure 12. The visible GPS satellites number varied from 6 to 7, while the PDOP values were lager than 2. With the fused code and phase measurements at virtual point, the GPS DD relative position estimation accuracy and precision are shown in
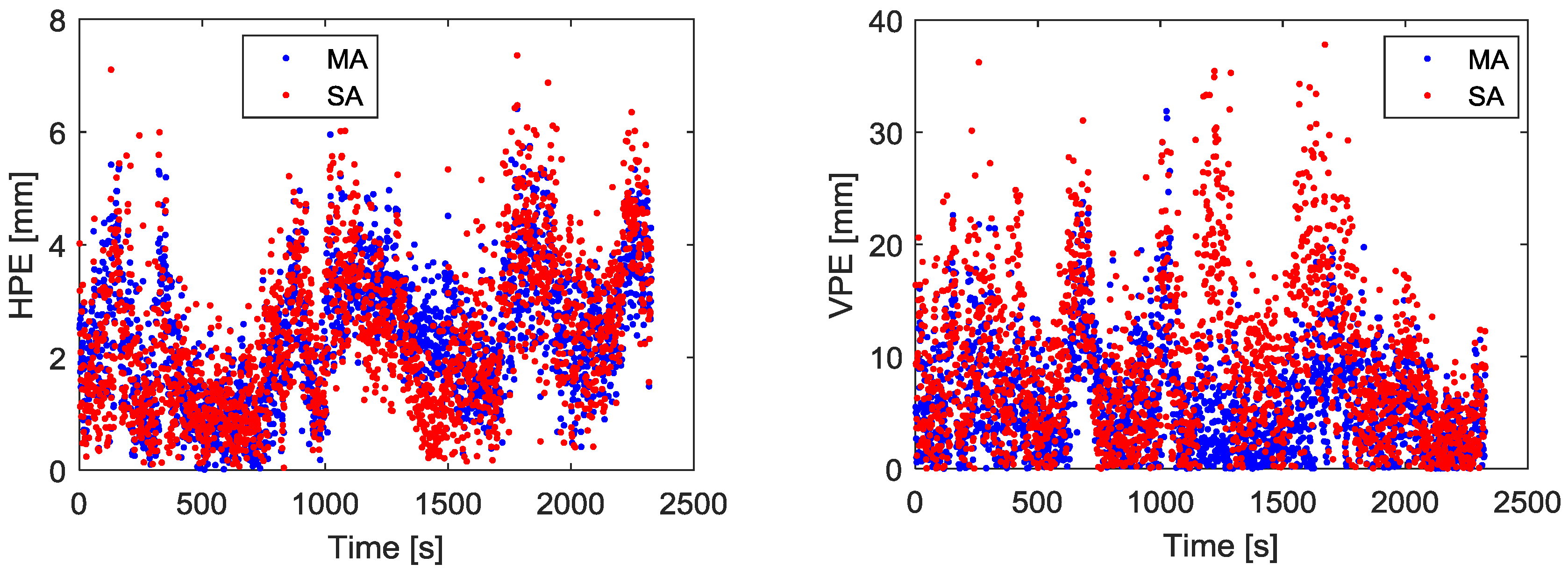
Figure 13 and
Table 7.
Figure 13 gives the final relative position estimation accuracy of the kinematic experiment, from which we can see that the position estimation accuracy using MA and the SA is at the same level after ambiguity resolution. However, the ambiguity resolution success rate using MA is increased by 1.33%, which is obtained with a cutoff elevation angle of 5; the position error can be reduced by 26.9% for vertical component when compared with SA solution, as shown in
Table 7. Compared with SA solution, the MA solution can reduce the errors of the measurement. Multipath is the dominant error in short-baseline differential GPS systems. The observation data at low elevation angle is more severely affected by multipath noise. MA can mitigate multipath noise to some extent, so it got a better ambiguity resolution rate than SA.