Enhancing Received Signal Strength-Based Localization through Coverage Hole Detection and Recovery †
Abstract
1. Introduction
- To the best of our knowledge, this is the first paper to detect and recover coverage holes of WSNs based on RSSI-based localization techniques, and we will enhance RSSI-based localization through coverage hole recovery.
- We systematically investigate the coverage model of RSSI-based localization techniques, and ellipse coverage model is derived from theoretical analysis and experimental verification.
- An approximation algorithm is proposed to recover coverage holes in WSNs with ellipse coverage model. Simulation results show that our algorithm can recover all holes and can reach any set coverage rate, up to 100% coverage.
2. Related Work
2.1. RSSI-Based Localization Techniques
2.2. Coverage Hole Detection and Recovery
3. Background
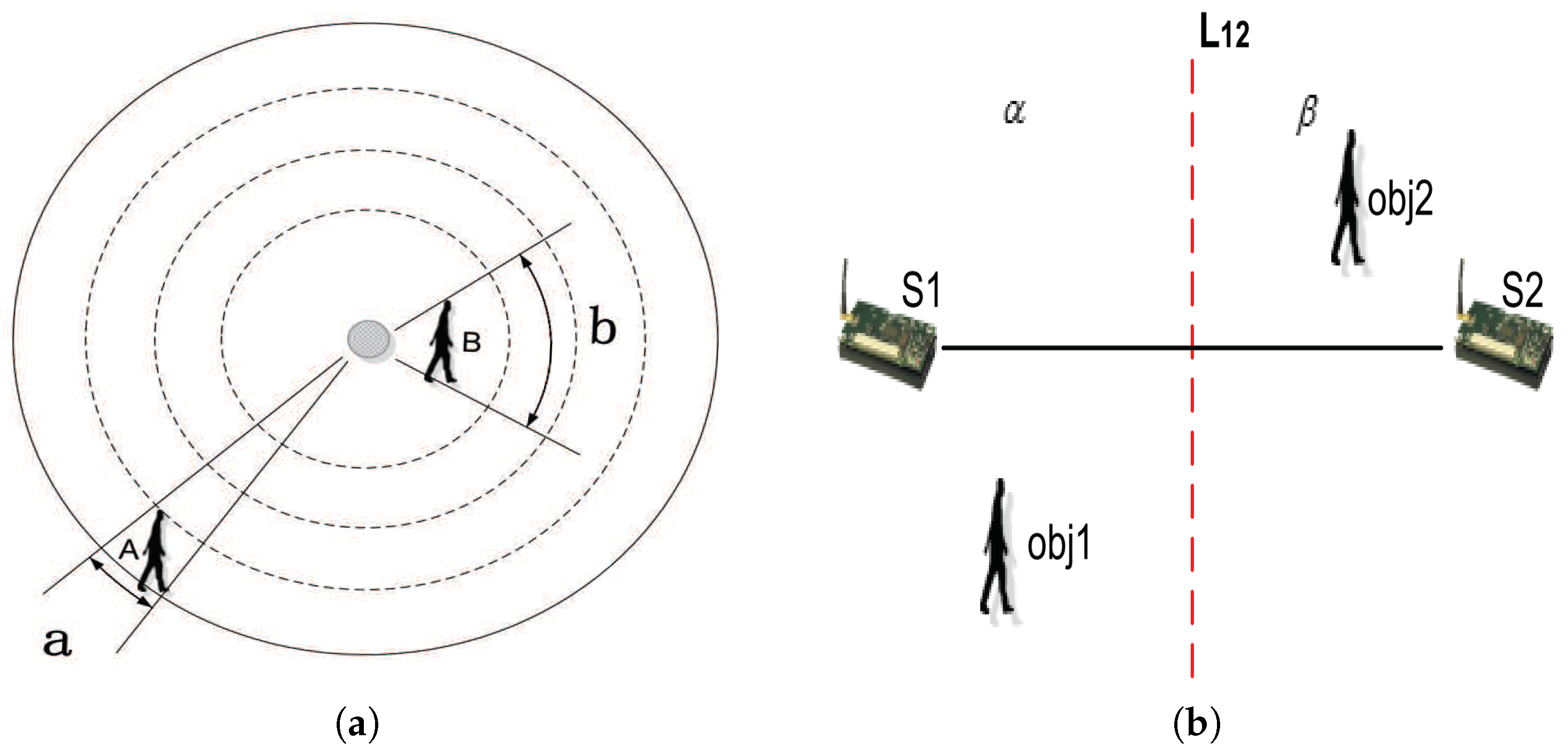
4. The Ellipse Coverage Model
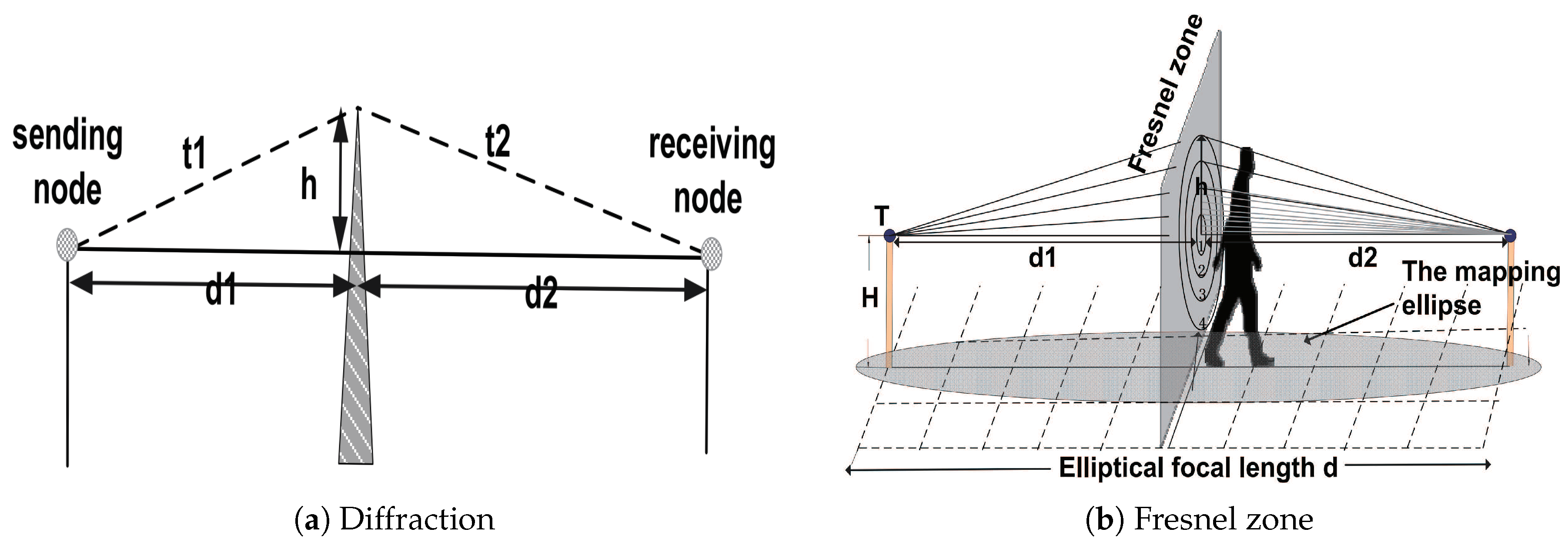
4.1. Theoretical Model
4.2. Mathematic Model
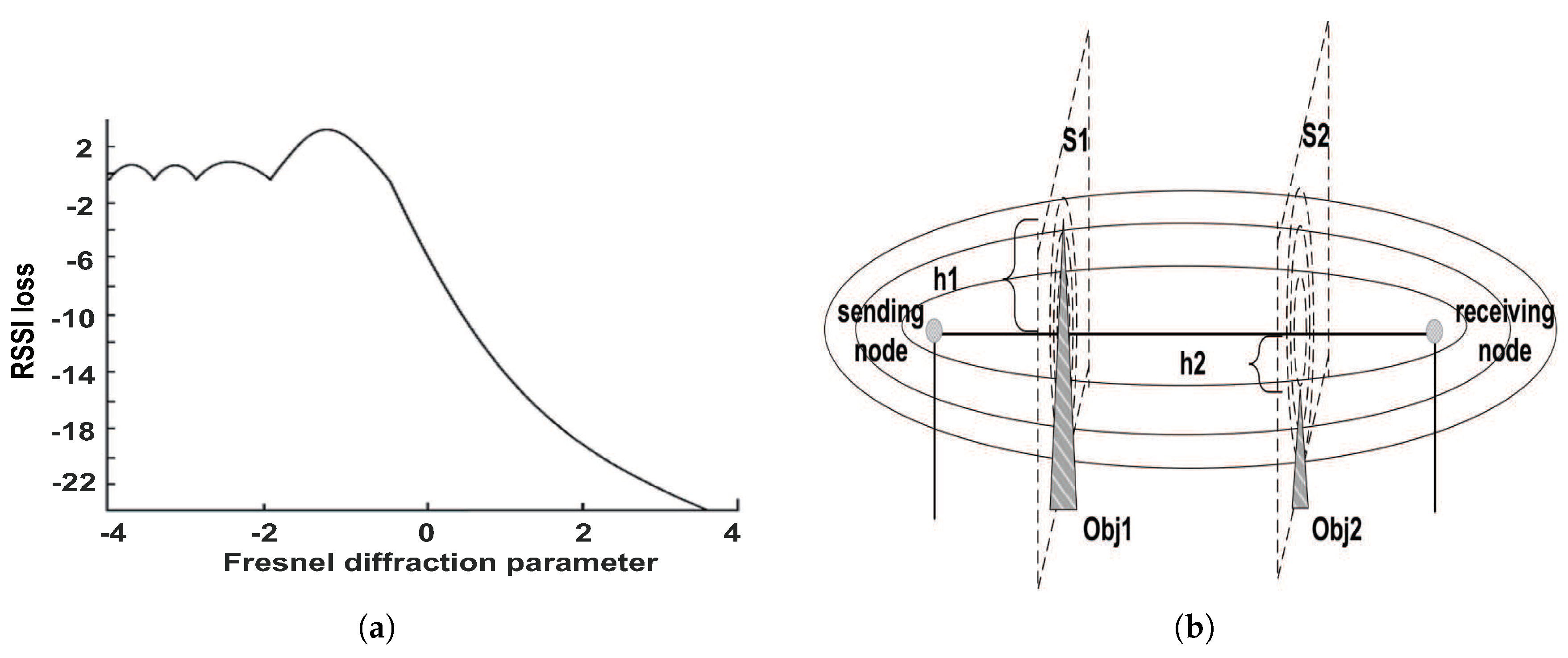
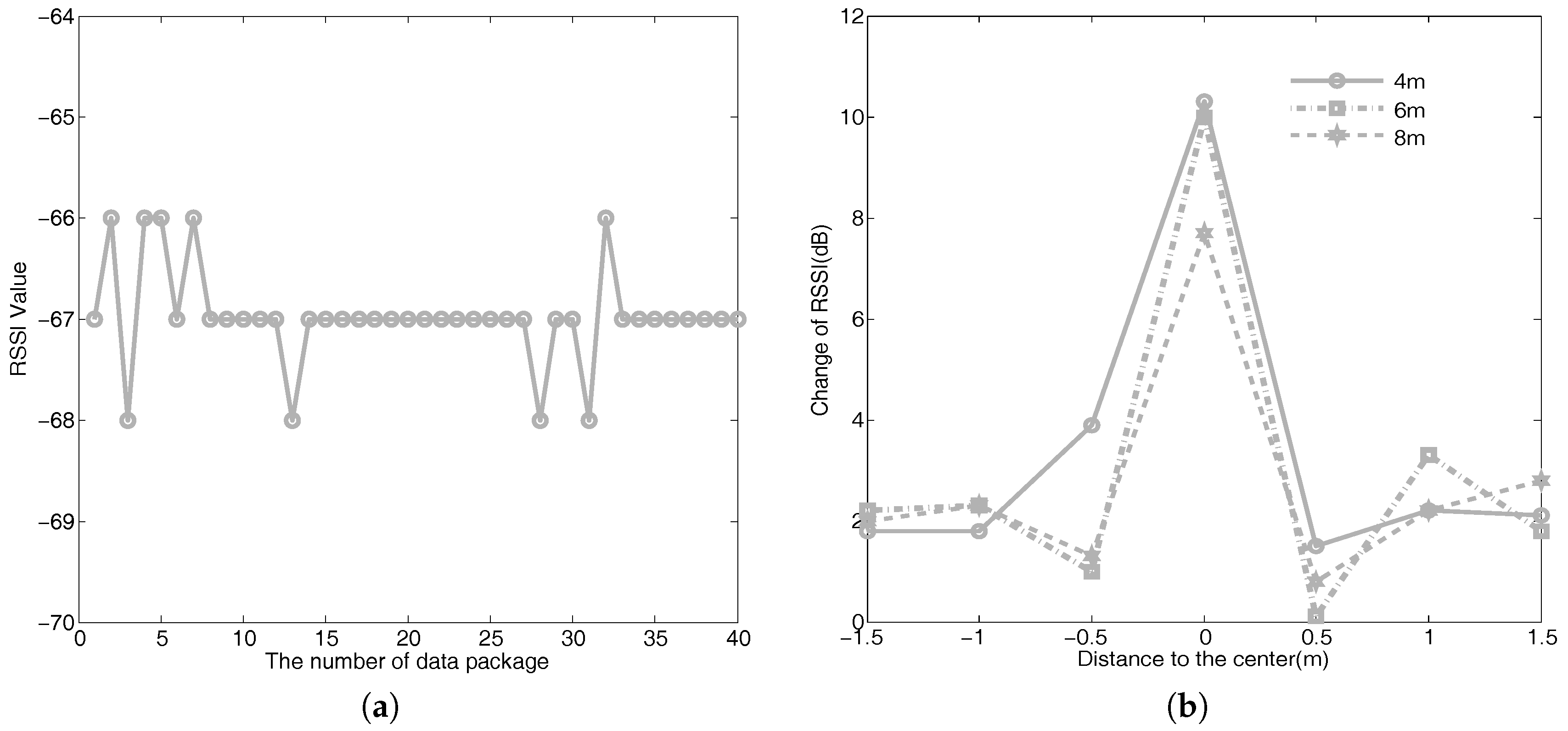
4.3. Experimental Verification
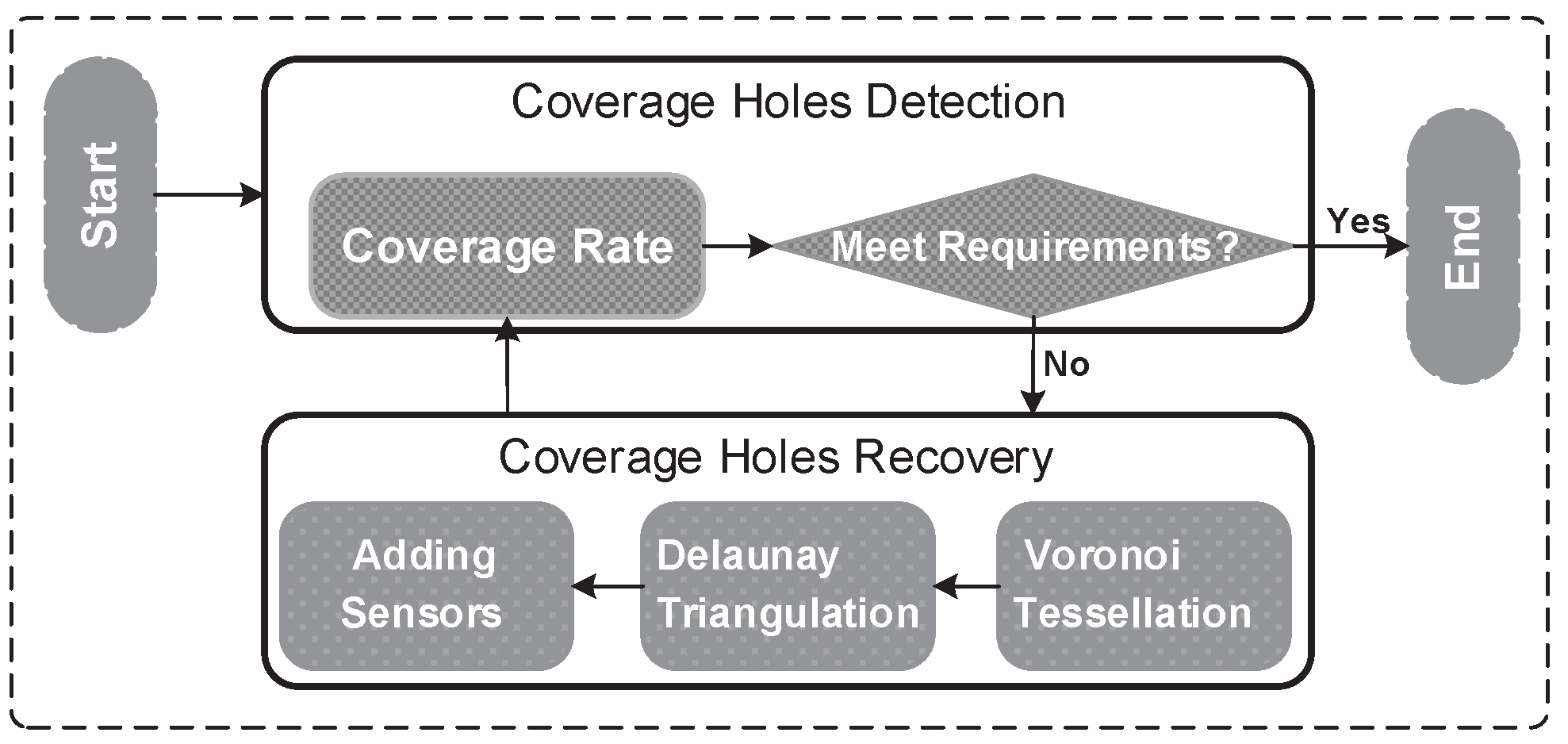
5. Detecting and Recovering Coverage Holes
5.1. Detecting Coverage Holes
| Algorithm 1: Procedure of Detecting Coverage Holes |
Input:
|
5.2. Recovering Coverage Holes
5.2.1. The Optimum Increase Coverage Problem (OICP) is NP-Complete
5.2.2. Voronoi Tessellation
5.2.3. Delaunay Triangulation
| Algorithm 2: Procedure of Recovering Coverage Holes |
Input:
|
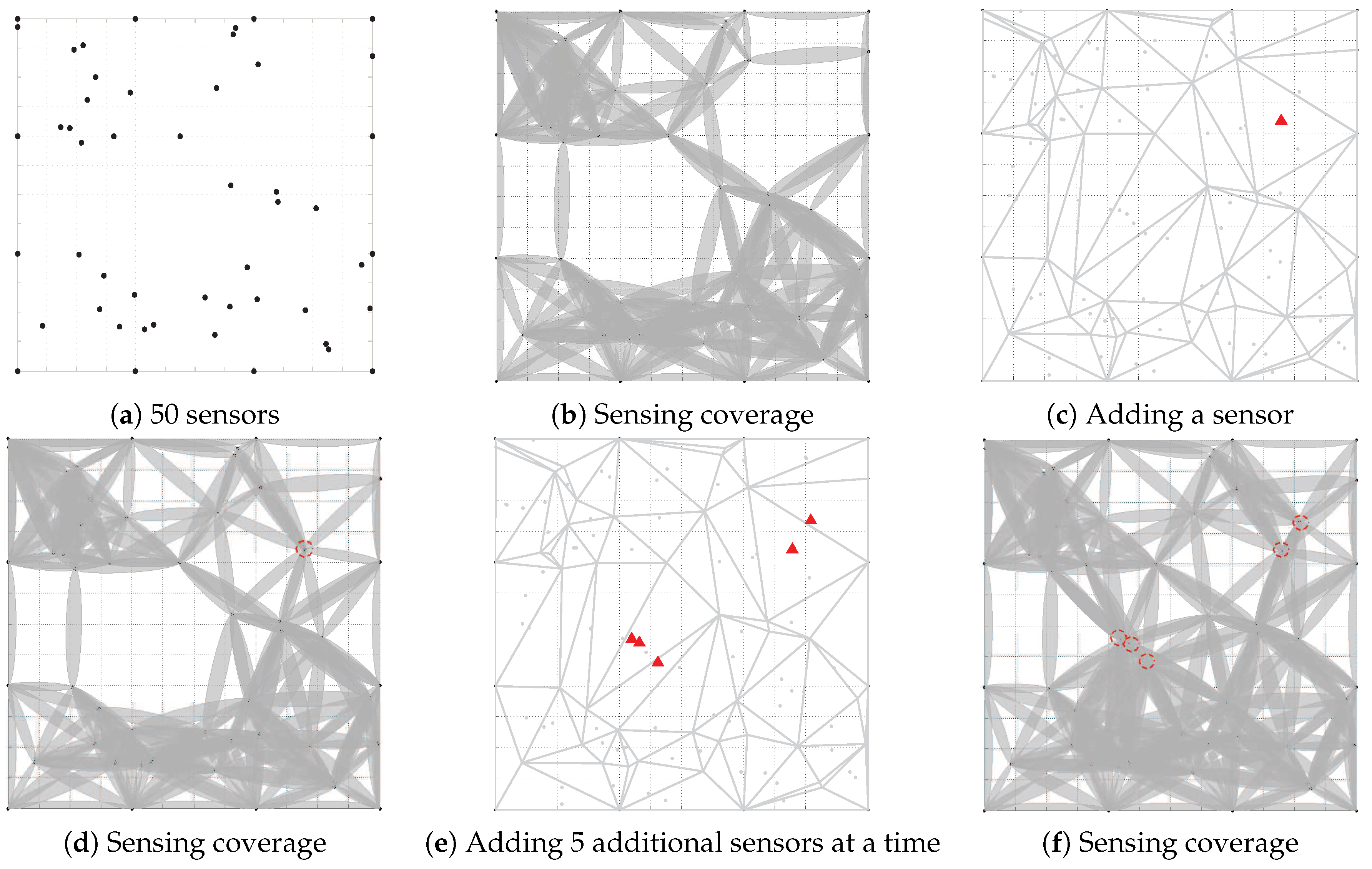
5.2.4. Algorithm Description and Analysis
- Firstly, we divide the regions into several small enough cells and verify whether these small cells are covered one by one. Then the total area of covered regions can be calculated by adding up all covered small cells in the target regions. The time complexity of this step is , where n is the number of small cells, which is determined by the size of small cells.
- We then calculate the coverage rate of the target regions by calculating the ratio of the total area of covered regions with the area of the target regions. If the coverage rate achieves the requirement of the corresponding systems, then exit; if not, then continue.
- Partitioning the regions by Voronoi tessellation. According to the optimization proposed in [44], the worst case time complexity is , where n is the number of sensors deployed in the target regions.
- According to the dual graph of Voronoi tessellation, we can obtain Delaunay triangle . Because the common border of adjacent Voronoi cells can be obtained in the process of Voronoi tessellation, the time complexity of the Delaunay triangle is , where n is the number of Delaunay triangles.
- We will next calculate the total area of all triangles of Delaunay triangulation and find the triangle with the largest area. The time complexity is determined by the sort algorithm, and it is , where n is the number of Delaunay triangles.
- Finally, the new sensors will be deployed. Go back to Step 2.
6. Experiment and Evaluation
6.1. Experimental Setup
6.1.1. Single-Link Setup
6.1.2. Multi-Link Setup
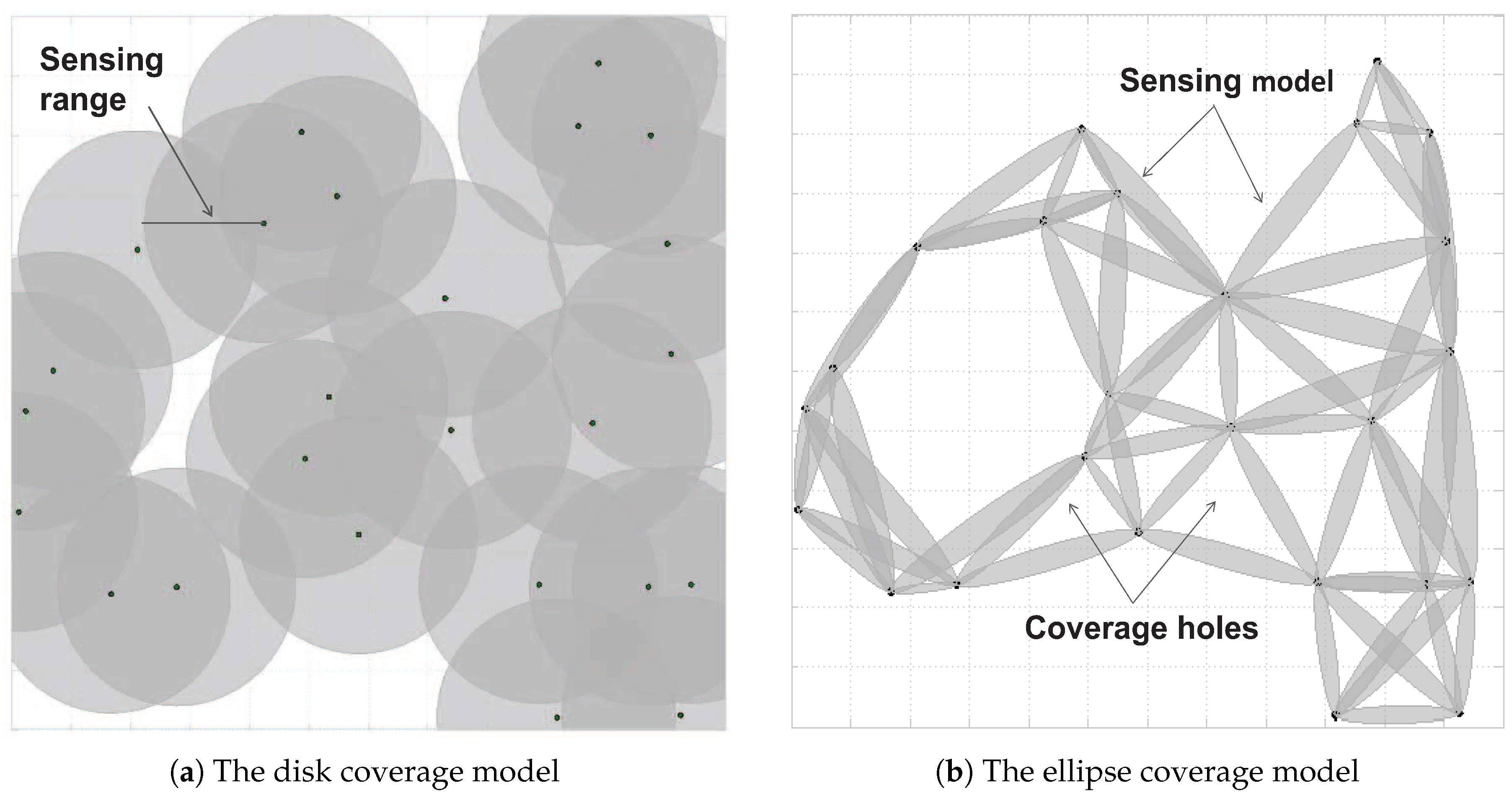
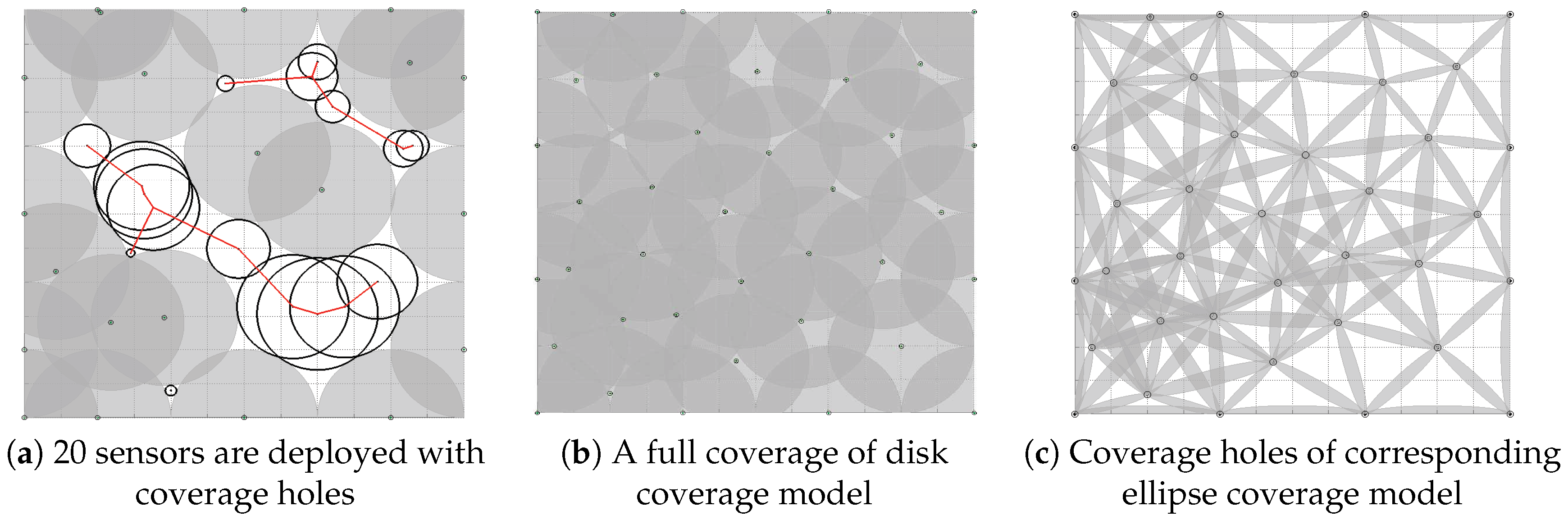
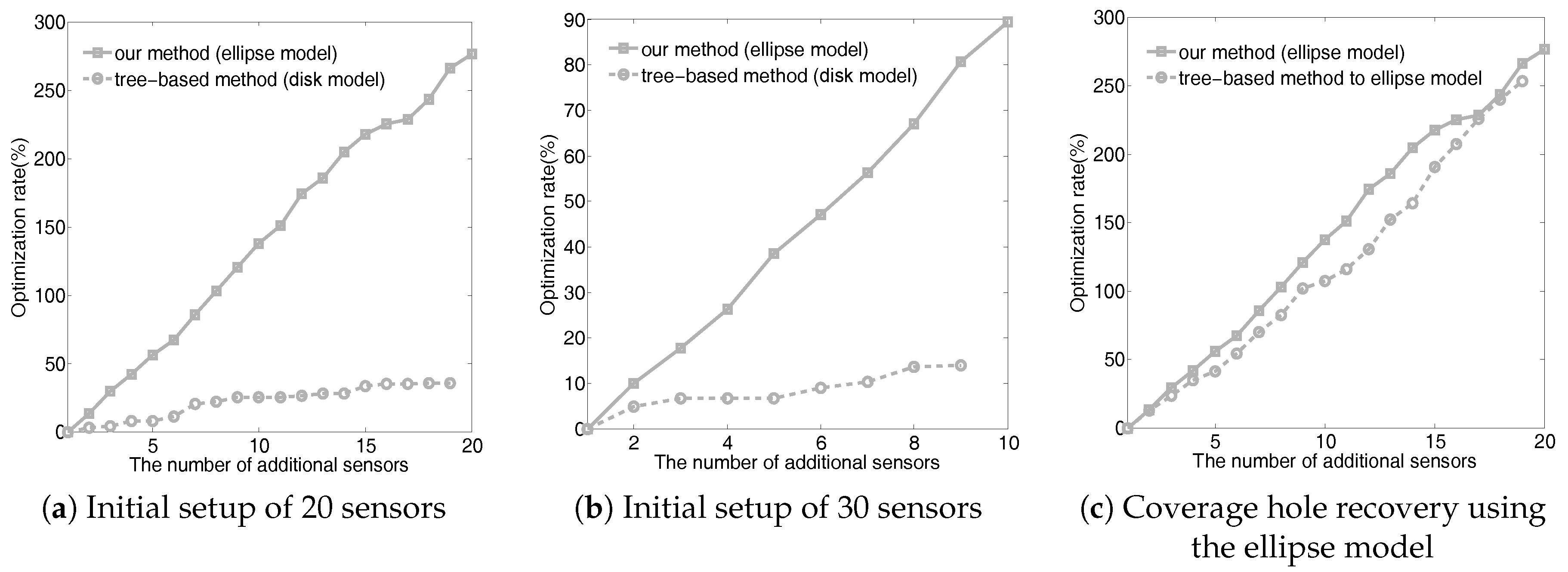
6.2. The Ellipse Coverage Model vs. the Disk Coverage Model
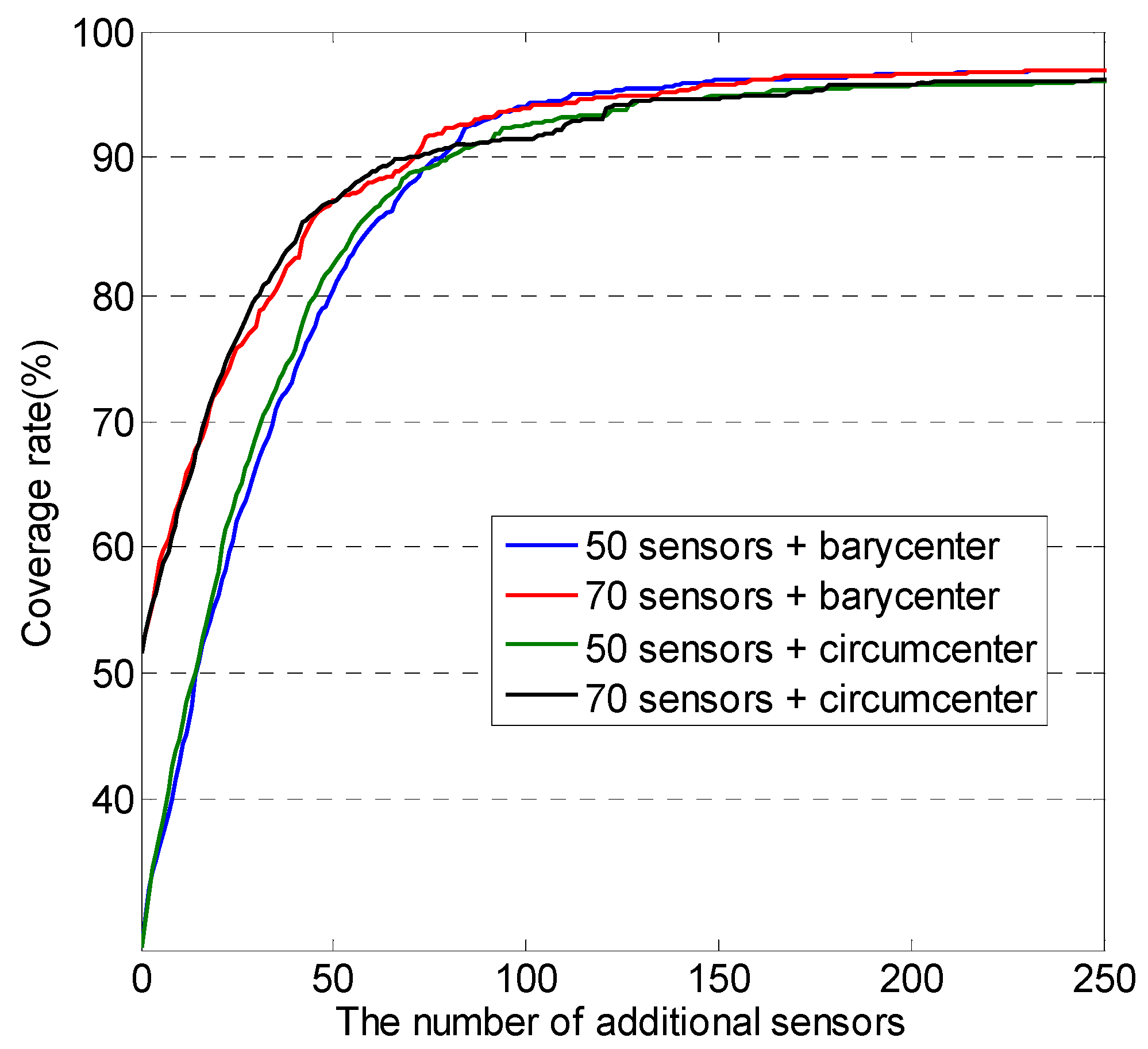
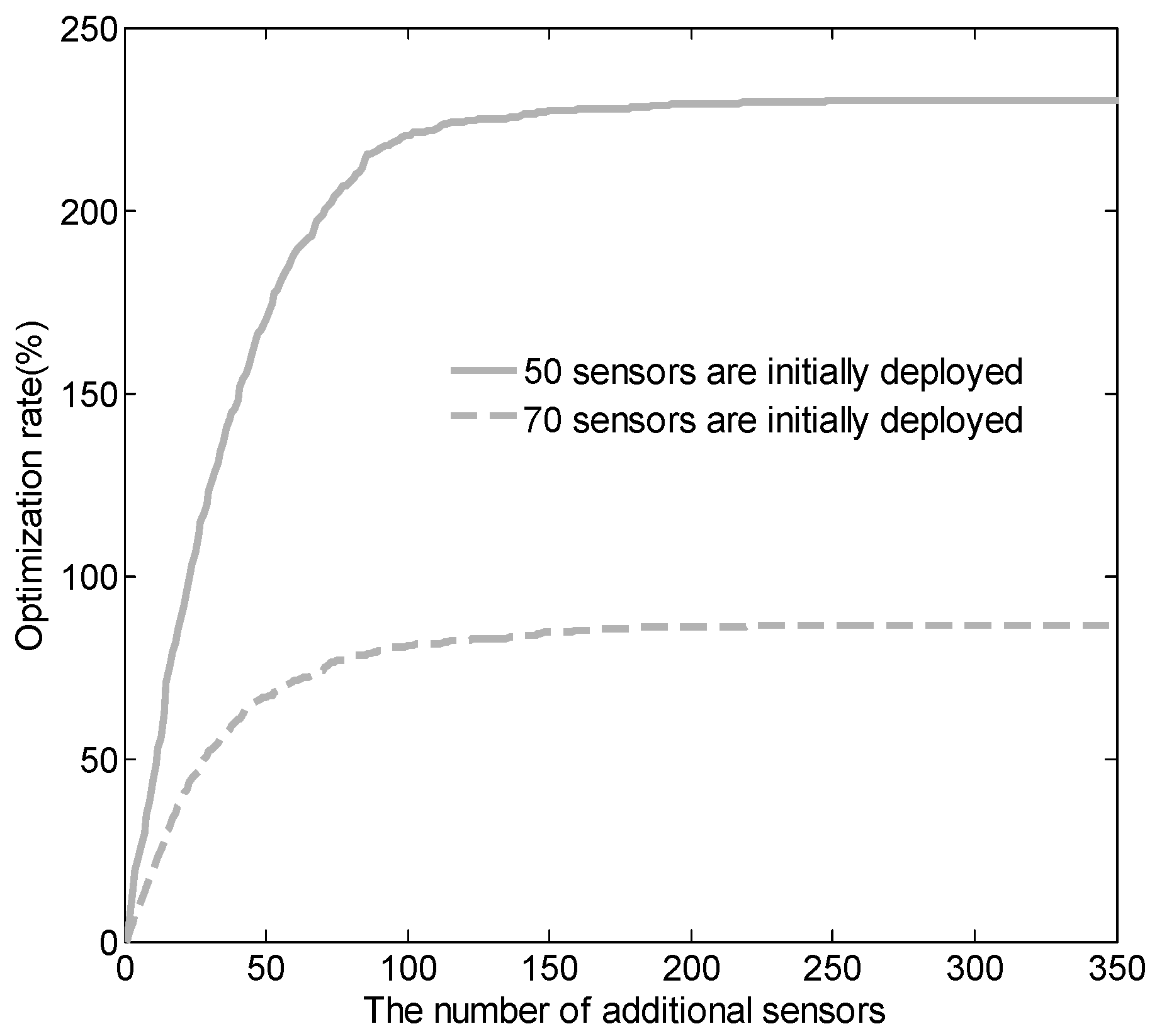
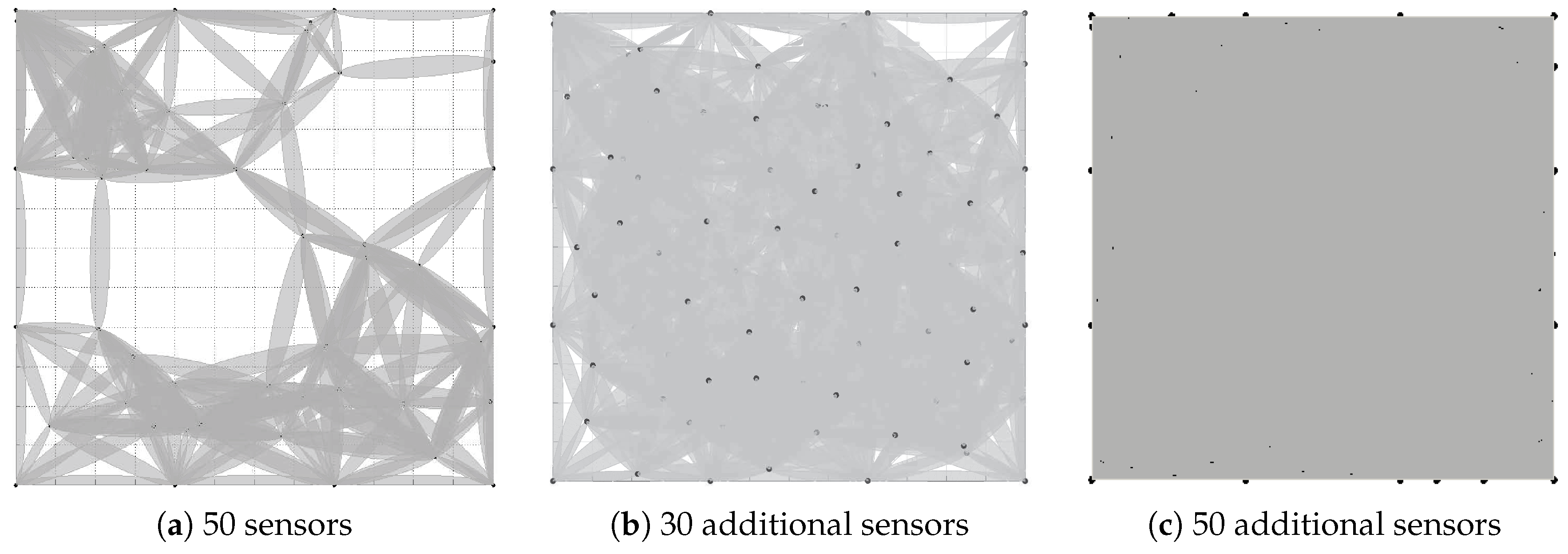
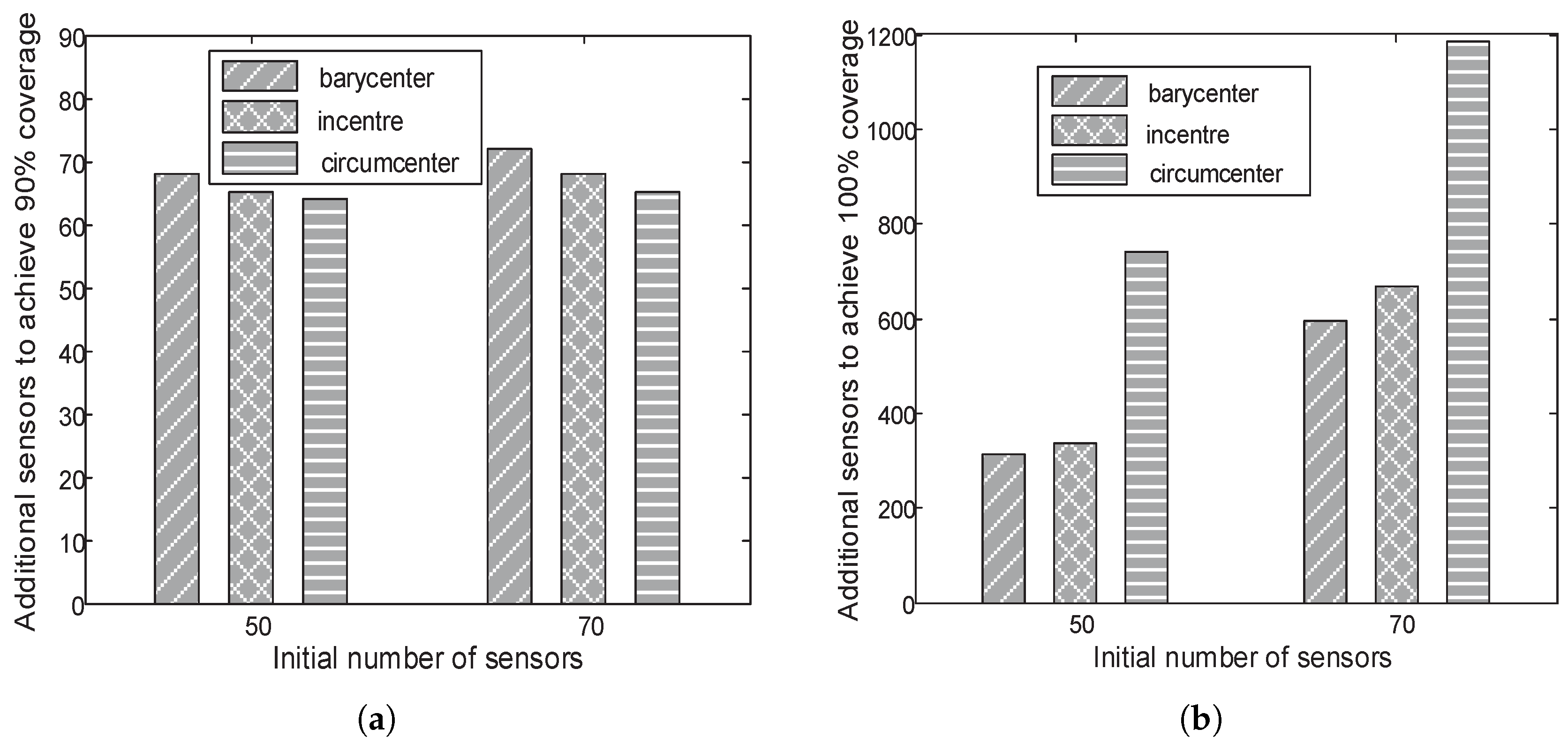
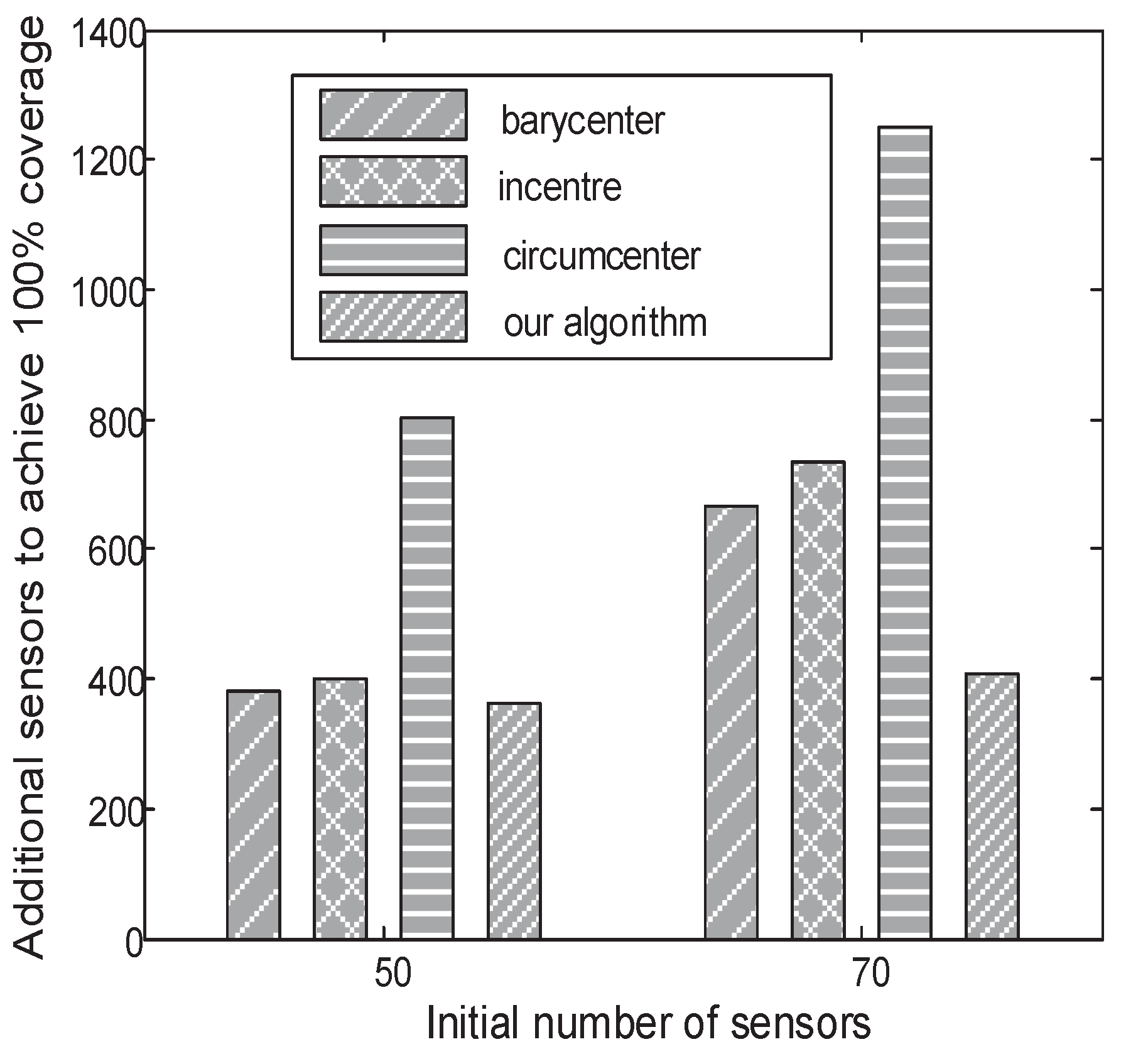
6.3. Results of Coverage Hole Recovery
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Wang, B. Coverage problems in sensor networks: A Survey. ACM Comput. Surv. 2011, 43, 32. [Google Scholar] [CrossRef]
- Li, X.; Hunter, D.K.; Yang, K. Distributed Coordinate-free Hole Detection and Recovery. In Proceedings of the IEEE Global Telecommunications Conference, San Francisco, CA, USA, 27 November–1 December 2006; pp. 1–5. [Google Scholar]
- Meguerdichian, S.; Koushanfar, F.; Potkonjak, M.; Srivastava, M.B. Coverage Problems in Wireless Ad-hoc Sensor Networks. In Proceedings of the IEEE INFOCOM, Anchorage, AK, USA, 22–26 April 2001; Volume 3, pp. 1380–1387. [Google Scholar]
- Huang, C.; Tseng, Y. The Coverage Problem in a Wireless Sensor Network. Mob. Netw. Appl. 2005, 10, 518–528. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, G. Barrier Coverage in Camera Sensor Networks. In Proceedings of the Twelfth ACM International Symposium on Mobile Ad Hoc Networking and Computing, Paris, France, 17–19 May 2011; Volume 10, pp. 3967–3974. [Google Scholar]
- Tan, R.; Xing, G.; Liu, B. Exploiting Data Fusion to Improve the Coverage of Wireless Sensor Networks. IEEE ACM Trans. Netw. 2012, 20, 450–462. [Google Scholar] [CrossRef]
- Senouci, M.R.; Mellouk, A.; Assnoune, K. Localized Movement-Assisted Sensor Deployment Algorithm for Hole Detection and Healing. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1267–1277. [Google Scholar] [CrossRef]
- Li, W.; Zhang, W. Coverage hole and boundary nodes detection in wireless sensor networks. J. Netw. Comput. Appl. 2015, 48, 35–43. [Google Scholar] [CrossRef]
- Tian, J.; Liang, X.; Wang, G. Deployment and reallocation in mobile survivability-heterogeneous wireless sensor networks for barrier coverage. Ad Hoc Netw. 2016, 36, 321–331. [Google Scholar] [CrossRef]
- Liang, J.; Liu, M.; Kui, X. A Survey of Coverage Problems in Wireless Sensor Networks. Sens. Transducers 2014, 163, 240–246. [Google Scholar]
- Abolhasan, M.; Maali, Y.; Rafiei, A.; Wei, N. Distributed Hybrid Coverage Hole Recovery in Wireless Sensor Networks. IEEE Sens. J. 2016, 16, 8640–8648. [Google Scholar] [CrossRef]
- Khalifa, B.; Aghbari, Z.A.; Khedr, A.M.; Abawajy, J.H. Coverage Hole Repair in WSNs Using Cascaded Neighbor Intervention. IEEE Sens. J. 2017, 17, 7209–7216. [Google Scholar] [CrossRef]
- Rafiei, A.; Abolhasan, M.; Franklin, D.R.; Safaei, F.; Smith, S.; Ni, W. Effect of the Number of Participating Nodes on Recovery of WSN Coverage Holes. In Proceedings of the 27th International Telecommunication Networks and Applications Conference (ITNAC), Melbourne, VIC, Australia, 22–24 November 2017; pp. 1–8. [Google Scholar]
- Li, W. A Novel Graphic Coverage Hole Description in Wireless Sensor Networks. IEEE Commun. Lett. 2014, 18, 2205–2208. [Google Scholar] [CrossRef]
- Xue, L.; Chen, C.; Zhao, J.; Li, A.; Guan, X. A Minimal Rigid Topology Control Algorithm Based on Voronoi Coverage and Delaunay Triangulation in Wireless Sensor Networks. Acta Autom. Sin. 2016, 42, 1570–1584. [Google Scholar]
- Bi, K.; Tu, K.; Gu, N.; Dong, W.L.; Liu, X. Topological Hole Detection in Sensor Networks with Cooperative Neighbors. In Proceedings of the International Conference on Systems and Networks Communications (ICSNC’06), Tahiti, French Polynesia, 29 October–3 November 2006; p. 31. [Google Scholar]
- Ghrist, R.; Muhammad, A. Coverage and Hole-Detection in Sensor Networks via Homology. In Proceedings of the Fourth International Symposium on Information Processing in Sensor Networks, (IPSN 2005), Boise, ID, USA, 15 April 2005; pp. 254–260. [Google Scholar]
- Silva, V.D.; Ghrist, R.; Muhammad, A. Blind Swarms for Coverage in 2-D. In Proceedings of the Robotics: Science and Systems, Cambridge, MA, USA, 8–11 June 2005; pp. 335–342. [Google Scholar]
- Stefan, F.; Christian, K. Hole Detection or: How Much Geometry Hides In Connectivity? In Proceedings of the 22nd Annual Symposium on Computational Geometry (SCG’06), Sedona, AZ, USA, 5–7 June 2006; pp. 377–385. [Google Scholar]
- Wang, Y.; Gao, J.; Mitchell, J.S. Boundary Recognition in Sensor Networks by Topological Methods. In Proceedings of the 12th Annual International Conference on Mobile Computing and Networking (MobiCom’06), Los Angeles, CA, USA, 23–29 September 2006; pp. 122–133. [Google Scholar]
- Fang, Q.; Gao, J.; Guibas, L.J. Locating and Bypassing Holes in Sensor Networks. Mob. Netw. Appl. 2006, 11, 187–200. [Google Scholar] [CrossRef]
- Kröller, A.; Fekete, S.P.; Pfisterer, D.; Fischer, S. Deterministic Boundary Recognition and Topology Extraction for Large Sensor Networks. In Proceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithm, Miami, FL, USA, 22–26 January 2006; pp. 1000–1009. [Google Scholar]
- Zhang, D.; Ma, J.; Chen, Q.; Ni, L.M. An RF-based system for tracking transceiver-free objects. In Proceedings of the Fifth Annual IEEE International Conference on Pervasive Computing and Communications, White Plains, NY, USA, 19–23 March 2007; pp. 135–144. [Google Scholar]
- Xie, B.; Fang, D.; Xing, T.; Zhang, L.; Chen, X.; Tang, Z.; Wang, A. FISCP: Fine-grained device-free positioning system for multiple targets working in sparse deployments. Wirel. Netw. 2016, 22, 1751–1766. [Google Scholar] [CrossRef]
- Liu, C.; Fang, D.; Yang, Z.; Chen, X.; Wang, W.; Xing, T.; An, N.; Cai, L. RDL: A Novel Approach for Passive Object Localization in WSN Based on RSSI. In Proceedings of the IEEE International Conference on Communications, Ottawa, ON, Canada, 10–15 June 2012; Volume 11, pp. 586–590. [Google Scholar]
- Zhang, D.; Ni, L.M. Dynamic clustering for tracking multiple transceiver-free objects. In Proceedings of the 2009 IEEE International Conference on Pervasive Computing and Communications, Galveston, TX, USA, 9–13 March 2009; pp. 1–8. [Google Scholar]
- Zhang, D.; Yang, Y.; Cheng, D.; Liu, S.; Ni, L.M. Cocktail: An RF-based hybrid approach for indoor localization. In Proceedings of the 2010 IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010; pp. 1–5. [Google Scholar]
- Kaltiokallio, O.; Bocca, M.; Eriksson, L.M. Distributed RSSI processing for intrusion detection in indoor environments. In Proceedings of the 9th ACM/IEEE International Conference on Information Processing in Sensor Networks, Stockholm, Sweden, 12–16 April 2010; pp. 404–405. [Google Scholar]
- Adewumi, O.G.; Djouani, K.; Kurien, A.M. RSSI based indoor and outdoor distance estimation for localization in WSN. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25–28 February 2013. [Google Scholar]
- Garcia-Sanchez, A.J.; Garcia-Sanchez, F.; Losilla, F.; Kulakowski, P.; Garcia-Haro, J.; Rodríguez, A.; López-Bao, J.V.; Palomares, F. Wireless Sensor Network Deployment for Monitoring Wildlife Passages. Sensors 2010, 10, 7236–7262. [Google Scholar] [CrossRef] [PubMed]
- Mistry, H.P.; Mistry, N.H. RSSI Based Localization Scheme in Wireless Sensor Networks: A Survey. In Proceedings of the 2015 Fifth International Conference on Advanced Computing & Communication Technologies (ACCT), Haryana, India, 21–22 February 2015; Volume 7, pp. 647–652. [Google Scholar]
- Yaghoubi, F.; Abbasfar, A.A.; Maham, B. Energy-Efficient RSSI-Based Localization for Wireless Sensor Networks. IEEE Commun. Lett. 2014, 18, 973–976. [Google Scholar] [CrossRef]
- Luo, Q.; Peng, Y.; Li, J.; Peng, X. RSSI-Based Localization Through Uncertain Data Mapping for Wireless Sensor Networks. IEEE Sens. J. 2016, 16, 3155–3162. [Google Scholar] [CrossRef]
- Abouzar, P.; Michelson, D.G.; Hamdi, M. RSSI-Based Distributed Self-Localization for Wireless Sensor Networks Used in Precision Agriculture. IEEE Trans. Wirel. Commun. 2016, 15, 6638–6650. [Google Scholar] [CrossRef]
- Ahmadi, H.; Viani, F.; Bouallegue, R. An accurate prediction method for moving target localization and tracking in wireless sensor networks. Ad Hoc Netw. 2018, 70, 14–22. [Google Scholar] [CrossRef]
- Liu, C.; Li, B.; Fang, D.; Guo, S.; Chen, X.; Xing, T. Demo: Rhinopithecus roxellana monitoring and identification using wireless sensor networks. In Proceedings of the 9th ACM Conference on Embedded Networked Sensor Systems (SenSys ’11), Seattle, WA, USA, 1–4 November 2011; pp. 427–428. [Google Scholar]
- Dyo, V.; Ellwood, S.A.; Macdonald, D.W.; Markham, A. Poster Abstract: Wildlife and Environmental Monitoring using RFID and WSN Technology. In Proceedings of the 7th ACM Conference on Embedded Networked Sensor Systems (SenSys ’09), Berkeley, CA, USA, 4–6 November 2009; pp. 371–372. [Google Scholar]
- Patwari, N.; Wilson, J. RF sensor networks for device-free localization: Measurements, models, and algorithms. Proc. IEEE 2010, 98, 1961–1973. [Google Scholar] [CrossRef]
- Wu, C.H.; Lee, K.C.; Chung, Y.C. A Delaunay Triangulation Based Method for Wireless Sensor Network Deployment. In Proceedings of the International Conference on Parallel & Distributed Systems, Minneapolis, MN, USA, 12–15 July 2006; Volume 30, pp. 253–260. [Google Scholar]
- Li, W.; Wu, Y. Tree-based coverage hole detection and healing method in wireless sensor networks. Comput. Netw. 2016, 103, 33–43. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications Principles and Practice; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Lee, W.C. Mobile Communications Engineering; McGraw-Hill: New York, NY, USA, 1982. [Google Scholar]
- Zhao, M.; Lei, J.; Wu, M.; Liu, Y.; Shu, W. Surface Coverage in Wireless Sensor Networks. In Proceedings of the IEEE INFOCOM, Rio de Janeiro, Brazil, 19–25 April 2009; Volume 39, pp. 109–117. [Google Scholar]
- Fortune, S. A Sweepline Algorithm for Voronoi Diagrams. Algorithmica 1987, 2, 153–157. [Google Scholar] [CrossRef]
- Krause, A.; Guestrin, C. Near-optimal Observation Selection using Submodular Functions. In Proceedings of the 22nd national conference on Artificial Intelligence, Vancouver, BC, Canada, 22–26 July 2007; pp. 1650–1654. [Google Scholar]
- Zhai, S.; Tang, Z.; Wang, D.; Li, Z.; Chen, X.; Fang, D.; Chen, F. Coverage Hole Detection and Recovery in Wireless Sensor Networks Based on RSSI-Based Localization. In Proceedings of the 2017 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC), Guangzhou, China, 21–24 July 2017; pp. 250–257. [Google Scholar]





| The target regions | |
| The transmission range of sensors | |
| (, ) | The coordinate of sensor |
| S = { , , , …, } | The set of sensors in the target regions |
| The Euclidean distance of sensor and sensor | |
| The ellipse coverage model determined by sensor and sensor | |
| The set of ellipse coverage model in the target regions | |
| The set of square elements dividing the target regions | |
| The square element is covered | |
| The set of covered square elements |
| Parameter Name | Parameter Value |
|---|---|
| Node type | Micaz |
| Distance between nodes | 4 m |
| Height of nodes | 1.5 m |
| Frequency of sending packets | one second every packet |
| Sampling distance | 0.5 m |
| Initial number of sensors | 20 | 30 | 40 | 50 | 60 |
| Additional sensors | 17 | 10 | 7 | 5 | 2 |
| Coverage rate of ellipse model | 23.75% | 21.05% | 32.69% | 41.3% | 44.83% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, S.; Tang, Z.; Wang, D.; Li, Q.; Li, Z.; Chen, X.; Fang, D.; Chen, F.; Wang, Z. Enhancing Received Signal Strength-Based Localization through Coverage Hole Detection and Recovery. Sensors 2018, 18, 2075. https://doi.org/10.3390/s18072075
Zhai S, Tang Z, Wang D, Li Q, Li Z, Chen X, Fang D, Chen F, Wang Z. Enhancing Received Signal Strength-Based Localization through Coverage Hole Detection and Recovery. Sensors. 2018; 18(7):2075. https://doi.org/10.3390/s18072075
Chicago/Turabian StyleZhai, Shuangjiao, Zhanyong Tang, Dajin Wang, Qingpei Li, Zhanglei Li, Xiaojiang Chen, Dingyi Fang, Feng Chen, and Zheng Wang. 2018. "Enhancing Received Signal Strength-Based Localization through Coverage Hole Detection and Recovery" Sensors 18, no. 7: 2075. https://doi.org/10.3390/s18072075
APA StyleZhai, S., Tang, Z., Wang, D., Li, Q., Li, Z., Chen, X., Fang, D., Chen, F., & Wang, Z. (2018). Enhancing Received Signal Strength-Based Localization through Coverage Hole Detection and Recovery. Sensors, 18(7), 2075. https://doi.org/10.3390/s18072075






