Shear Elasticity of Magnetic Gels with Internal Structures
Abstract
:1. Introduction
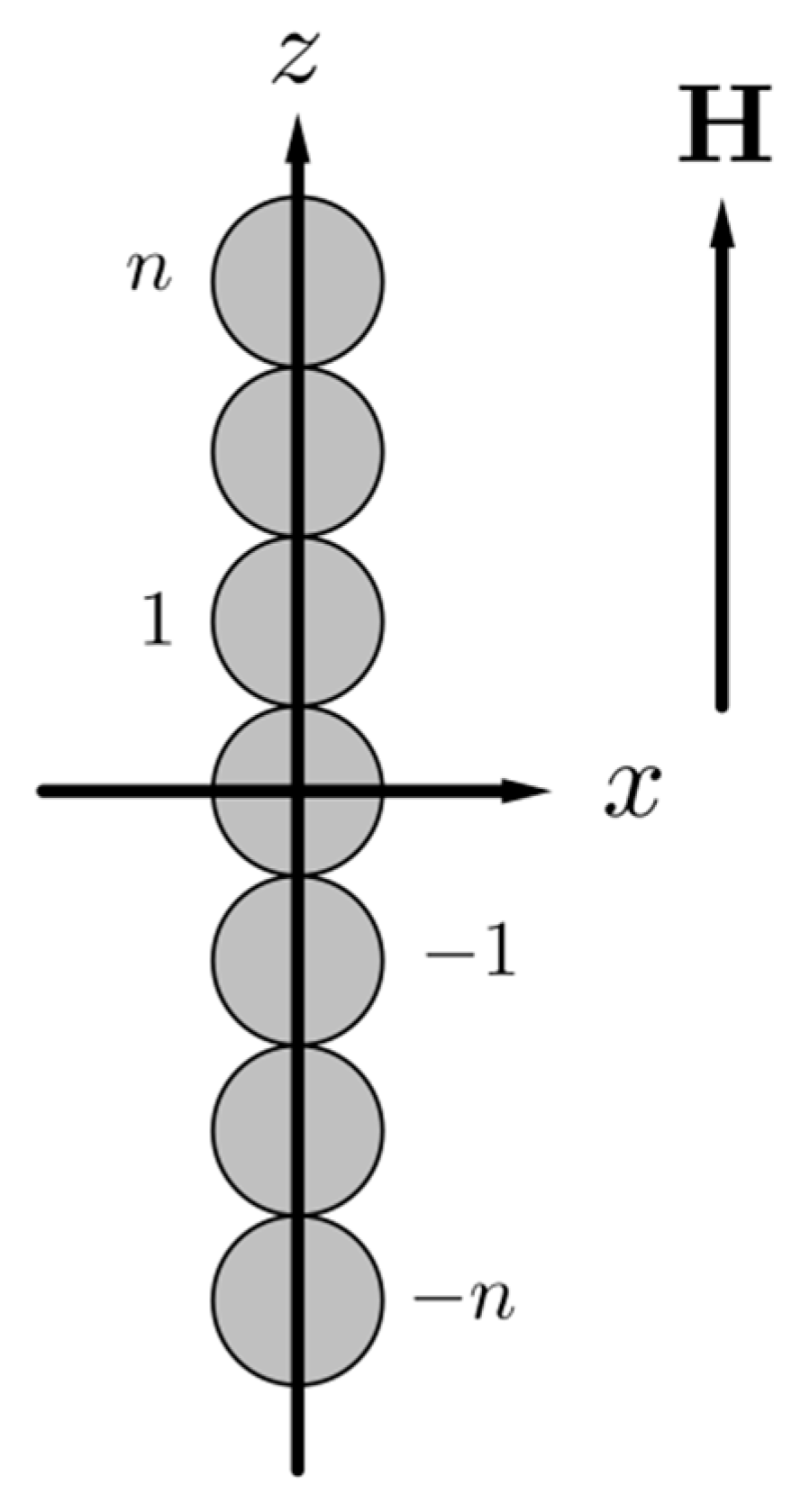
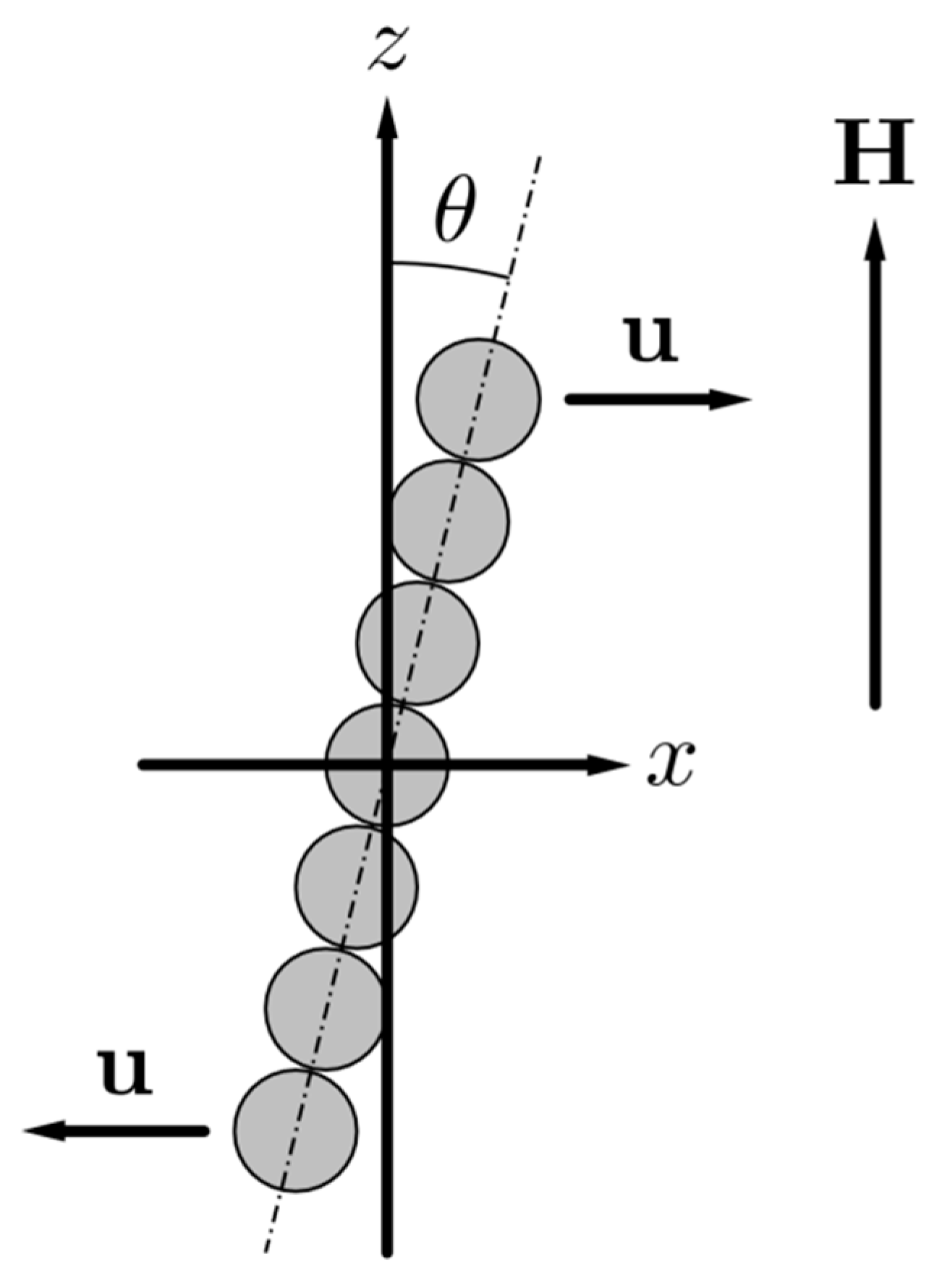
2. Physical and Mathematical Model
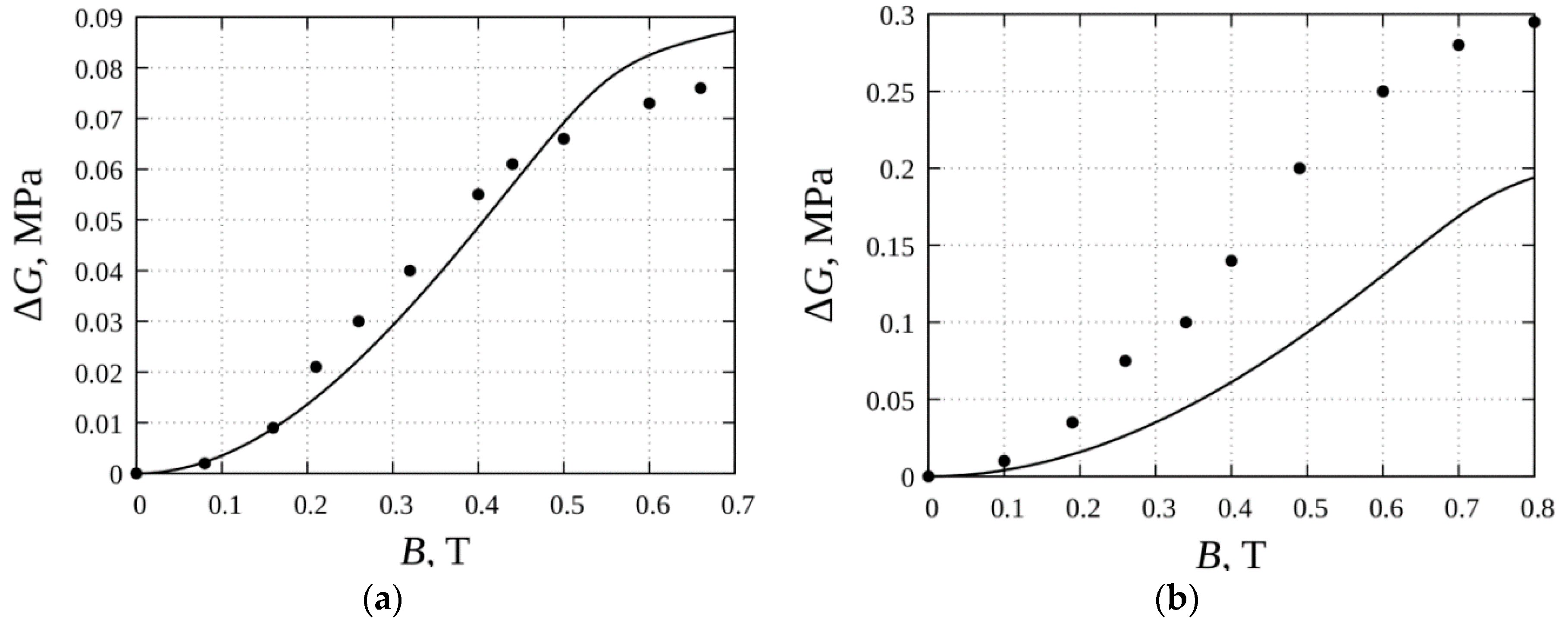
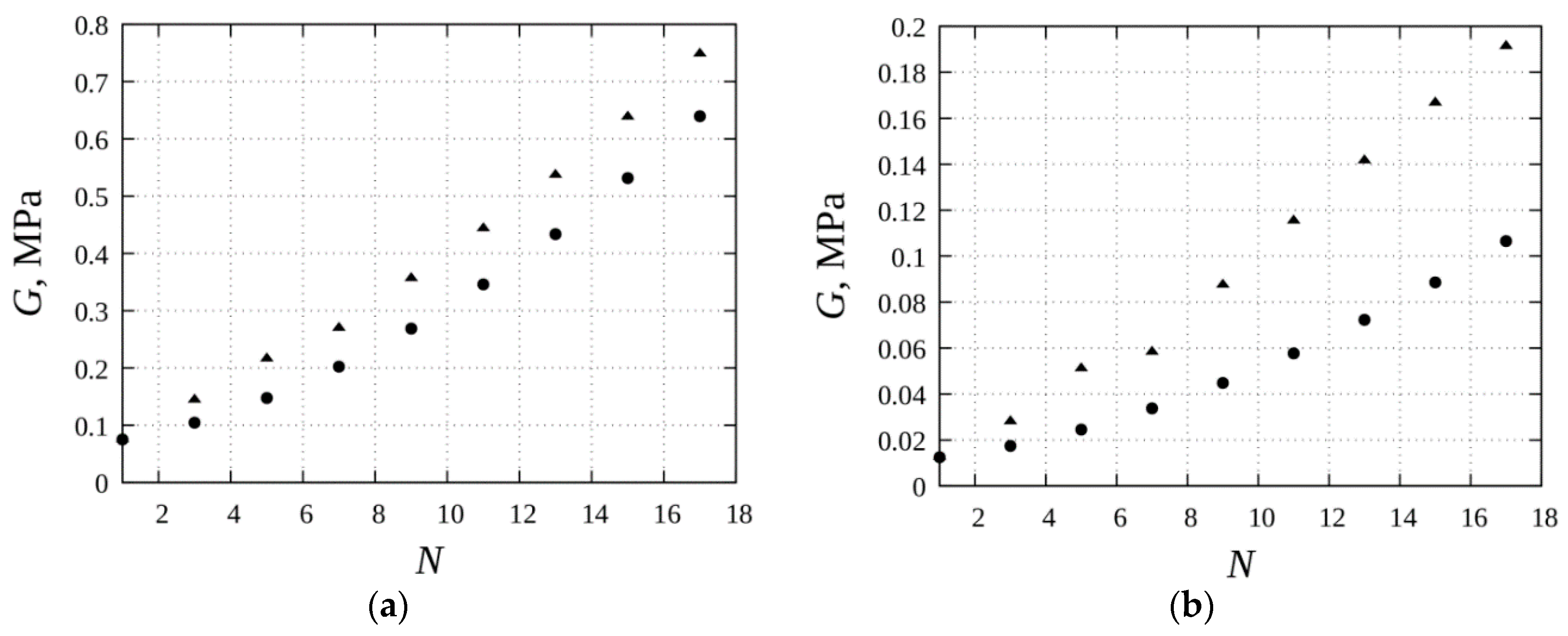
3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Bose, H.; Rabindranath, R.; Ehrlich, J. Soft magnetorheological elastomers as new actuators for valves. J. Intell. Mater. Syst. Struct. 2012, 23, 989–994. [Google Scholar] [CrossRef]
- Filipcsei, G.; Csetneki, I.; Szilagyi, A.; Zrınyi, M. Magnetic Field-Responsive Smart Polymer Composites. Adv. Polym. Sci. 2007, 206, 137–189. [Google Scholar] [CrossRef]
- Boczkowska, A.; Awietjan, S. Tuning active magnetorheological elastomers for damping applications. Mater. Sci. Forum 2010, 636–637, 766–771. [Google Scholar] [CrossRef]
- Dyke, S.; Spencer, B.; Sain, M.; Carlson, J. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater. Struct. 1996, 5, 565–575. [Google Scholar] [CrossRef] [Green Version]
- Occhiuzzi, A.; Spizzuoco, M.; Serino, G. Experimental analysis of magnetorheological dampers for structural control. Smart Mater. Struct. 2003, 12, 703–711. [Google Scholar] [CrossRef]
- Carmona, F.; Mouney, C. Temperature-dependent resistivity and conduction mechanism in carbon particle-filled polymers. J. Mater. Sci. 1992, 27, 1322–1326. [Google Scholar] [CrossRef]
- Feller, J.; Linossier, I.; Grohens, Y. Conductive polymer composites: Comparative study of poly(ester)-short carbon fibres and poly(epoxy)-short carbon fibres mechanical and electrical properties. Mater. Lett. 2002, 57, 64–71. [Google Scholar] [CrossRef]
- Bañobre-López, M.; Piñeiro-Redondo, Y.; de Santis, R.; Gloria, A.; Ambrosio, L.; Tampieri, A.; Tampieri, A.; Dediu, V.; Rivas, J. Poly(caprolactone) based magnetic scaffolds for bone tissue engineering. J. Appl. Phys. 2011, 109, 07B313. [Google Scholar] [CrossRef]
- Bock, N.; Riminucci, A.; Dionigi, C.; Russo, A.; Tampieri, A.; Landi, E.; Goranov, V.A.; Marcacci, M.; Dediu, V. A novel route in bone tissue engineering: Magnetic biomimetic scaffolds. Acta Biomater. 2010, 6, 786–796. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Metters, A. Hydrogels in controlled release formulations: Network design and mathematical modeling. Adv. Drug Deliv. Rev. 2006, 58, 1379–1408. [Google Scholar] [CrossRef] [PubMed]
- Langer, R. New methods of drug delivery. Science 1990, 249, 1527–1533. [Google Scholar] [CrossRef] [PubMed]
- Mitragotri, S.; Lahann, J. Physical approaches to biomaterial design. Nat. Mater. 2009, 8, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Choi, N.W.; Cabodi, M.; Held, B.; Gleghorn, J.P.; Bonassar, L.J.; Stroock, A.D. Microfluidic scaffolds for tissue engineering. Nat. Mater. 2007, 6, 908–915. [Google Scholar] [CrossRef] [PubMed]
- Kurlyandskaya, G.V.; Fernández, E.; Safronov, A.P.; Svalov, A.V.; Beketov, I.; Beitia, A.B.; García-Arribas, A.; Blyakhman, F.A. Giant magnetoimpedance biosensor for ferrogel detection: Model system to evaluate properties of natural tissue. Appl. Phys. Lett. 2015, 106, 193702. [Google Scholar] [CrossRef]
- Thevenot, J.; Oliveira, H.; Sandre, O.; Lecommandoux, S. Magnetic responsive polymer composite materials. Chem. Soc. Rev. 2013, 42, 7099–7116. [Google Scholar] [CrossRef] [PubMed]
- Hunt, N.C.; Grover, L.M. Cell encapsulation using biopolymer gels for regenerative medicine. Biotechnol. Lett. 2010, 32, 733–742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, B.; Mandal, M.; Upadhyay, A.; Chattopadhyay, P.; Karak, N. Bio-based hyperbranched polyurethane/Fe3O4 nanocomposites: Smart antibacterial biomaterials for biomedical devices and implants. Biomed. Mater. 2013, 8, 035003. [Google Scholar] [CrossRef] [PubMed]
- De Santis, R.; Gloria, A.; Russo, T.; d’Amora, U.; Zeppetelli, S.; Dionigi, C. A basic approach toward the development of nanocomposite magnetic scaffolds for advanced bone tissue engineering. J. Appl. Polym. Sci. 2011, 122, 3599–3605. [Google Scholar] [CrossRef]
- Gloria, A.; Russo, R.; d’Amora, U.; Zeppetelli, S.; d’Alessandro, T.; Sandri, M.; Bañobre-López, M.; Piñeiro-Redondo, Y.; Uhlarz, M.; Tampieri, A.; et al. Magnetic poly(1-caprolactone)/irondoped hydroxyapatite nanocomposite substrates for advanced bone tissue engineering. J. R. Soc. Interface 2013, 10, 20120833. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.H.; Liu, T.Y.; Tsai, C.H.; Chen, S.Y. Preparation and characterization of magnetic ferroscaffolds for tissue engineering. J. Magn. Magn. Mater. 2007, 310, 2871–2873. [Google Scholar] [CrossRef]
- Hu, H.; Jiang, W.; Lan, F.; Zeng, X.; Ma, S.; Wu, Y.; Gu, Z. Synergic effect of magnetic nanoparticles on the electrospun aligned superparamagnetic nanofibers as a potential tissue engineering scaffold. RSC Adv. 2013, 3, 879–886. [Google Scholar] [CrossRef]
- Lai, K.; Jiang, W.; Tang, J.Z.; Wu, Y.; He, B.; Wang, G.; Gu, Z. Superparamagnetic nano-composite scaffolds for promoting bone cell proliferation and defect reparation without a magnetic field. RSC Adv. 2012, 2, 13007–13017. [Google Scholar] [CrossRef]
- Li, Y.; Huang, G.; Zhang, X.; Li, B.; Chen, Y.; Lu, T.; Lu, T.J.; Xu, F. Magnetic Hydrogels and Their Potential Biomedical Applications. Adv. Funct. Mater. 2013, 23, 660–672. [Google Scholar] [CrossRef]
- Panseri, S.; Cunha, C.; Alessandro, T.; Sandri, M.; Giavaresi, G.; Marcacci, M.; Hung, C.T.; Tampieri, A. Intrinsically superparamagnetic Fe-hydroxyapatite nanoparticles positively influence osteoblast-like cell behavior. J. Nanobiotechnol. 2012, 10, 32. [Google Scholar] [CrossRef] [PubMed]
- Skaat, H.; Ziv-Polat, O.; Shahar, A.; Last, D.; Mardor, Y.; Margel, S. Magnetic Scaffolds Enriched with Bioactive Nanoparticles for Tissue Engineering. Adv. Healthc Mater. 2012, 1, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Tampieri, A.; Landi, E.; Valentini, F.; Sandri, M.; d’Alessandro, T.; Dediu, V.; Marcacci, M. A conceptually new type of bio-hybrid scaffold for bone regeneration. Nanotechnology 2011, 22, 015104. [Google Scholar] [CrossRef] [PubMed]
- Tampieri, A.; d’Alessandro, T.; Sandri, M.; Sprio, S.; Landi, E.; Bertinetti, L.; Panseri, S.; Pepponi, G.; Goettlicher, J.; Bañobre-López, M.; et al. Intrinsic magnetism and hyperthermia in bioactive Fe-doped hydroxyapatite. Acta Biomater. 2012, 8, 843–851. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.B.; Hu, H.; Xie, L.Q.; Lan, F.; Jiang, W.; Wu, Y.; Gu, Z.W. Magnetic responsive hydroxyapatite composite scaffolds construction for bone defect reparation. Int. J. Nanomed. 2012, 7, 3365–3378. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.B.; Hu, H.; Xie, L.Q.; Lan, F.; Wu, Y.; Gu, Z.W. Preparation and Properties of Supermagnetic Calcium Phosphate Composite Scaffold. J. Inorg. Mater. 2013, 28, 79–84. [Google Scholar] [CrossRef]
- Zhu, Y.; Shang, F.; Li, B.; Dong, Y.; Liu, Y.; Lohe, M.R.; Hanagatad, N.; Kaskel, S. Magnetic mesoporous bioactive glass scaffolds: Preparation, physicochemistry and biological properties. J. Mater. Chem. B 2013, 1, 1279–1288. [Google Scholar] [CrossRef]
- Ziv-Polat, O.; Skaat, H.; Shahar, A.; Margel, S. Novel magnetic fibrin hydrogel scaffolds containing thrombin and growth factors conjugated iron oxide nanoparticles for tissue engineering. Int. J. Nanomed. 2012, 7, 1259–1274. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.K.; Patel, K.D.; Lee, J.H.; Lee, E.J.; Kim, J.H.; Kim, T.H.; Kim, H.W. Potential of magnetic nanofiber scaffolds with mechanical and biological properties applicable for bone regeneration. PLoS ONE 2014, 9, e91584. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Lopez, M.T.; Scionti, G.; Oliveira, A.C.; Duran, J.D.G.; Campos, A.; Alaminos, M.; Rodriges, I.A. Generation and Characterization of Novel Magnetic Field-Responsive Biomaterials. PLoS ONE 2015, 10, e0133878. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nicodemus, G.D.; Bryant, S.J. Cell encapsulation in biodegradable hydrogels for tissue engineering applications. Tissue Eng. Part B 2008, 14, 149–165. [Google Scholar] [CrossRef] [PubMed]
- Ladet, S.; David, L.; Domard, A. Multi-membrane hydrogels. Nature 2008, 452, 76–79. [Google Scholar] [CrossRef] [PubMed]
- Caló, E.; Khutoryanskiy, V.V. Biomedical applications of hydrogels: A review of patents and commercial products. Eur. Polym. J. 2015, 65, 252–267. [Google Scholar] [CrossRef]
- Nair, L.S. (Ed.) Injectable Hydrogels for Regenerative Engineering; Imperial College Press: London, UK, 2016. [Google Scholar]
- Yun, H.M.; Ahn, S.J.; Park, K.R.; Kim, M.J.; Kim, J.J.; Jinc, G.Z.; Kim, H.W.; Kim, E.C. Magnetic nanocomposite scaffolds combined with static magnetic field in the stimulation of osteoblastic differentiation and bone formation. Biomaterials 2016, 85, 88–98. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Arco, L.; Rodriguez, I.A.; Carriel, V.; Bonhome-Espinosa, A.B.; Campos, F.; Kuzhir, P.; Duran, J.D.G.; Lopez-Lopez, M.T. Biocompatible magnetic core-shell nanocomposites for engineered magnetic tissues. Nanoscale 2016, 8, 8138–8150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopez-Lopez, M.T.; Rodriguez, I.A.; Rodriguez-Arco, L.; Carriel, V.; Bonhome-Espinosa, A.B.; Campos, F.; Zubarev, A.; Duran, J.D.G. Synthesis, characterization and in vivo evaluation of biocompatible ferrogels. J. Magn. Magn. Mater. 2017, 431, 110–114. [Google Scholar] [CrossRef]
- Bonhome-Espinosa, A.B.; Campos, F.; Rodriguez, I.A.; Carriel, V.; Marins, J.A.; Zubarev, A.; Duran, J.D.G.; Lopez-Lopez, M.T. Effect of particle concentration on the microstructural and macromechanical properties of biocompatible magnetic hydrogels. Soft Matter 2017, 13, 2928–2941. [Google Scholar] [CrossRef] [PubMed]
- Coquelle, E.; Bossis, G. Mullins effect in elastomers filled with particles aligned by a magnetic field. Int. J. Solids Struct. 2006, 43, 7659–7672. [Google Scholar] [CrossRef]
- Saxena, P.; Pelteret, J.P.; Steinmann, P. Modelling of iron-filled magneto-active polymers with a dispersed chain-like microstructure. Eur. J. Mech. A Solids 2015, 50, 132–151. [Google Scholar] [CrossRef]
- Jolly, M.R.; Carlson, J.D.; Muñoz, B.C.; Bullions, T.A. The Magnetoviscoelastic Response of Elastomer Composites Consisting of Ferrous Particles Embedded in a Polymer Matrix. J. Intell. Mater. Syst. Struct. 1996, 6, 613–622. [Google Scholar] [CrossRef]
- Danas, K.; Kankanala, S.V.; Triantafyllidis, N. Experiments and modeling of iron-particle-filled magnetorheological elastomers. J. Mech. Phys. Solids 2012, 60, 120–138. [Google Scholar] [CrossRef]
- Butter, K.; Bomans, P.H.H.; Frederik, P.M.; Vroege, G.J.; Philipse, A.P. Direct observation of dipolar chains in iron ferrofluids by cryogenic electron microscopy. Nat. Mater. 2003, 2, 88–91. [Google Scholar] [CrossRef] [PubMed]
- Klokkenburg, M.; Erne, B.H.; Meedldijk, J.D.; Wiedenmann, A.; Petukhov, A.V.; Dullens, R.P.A.; Philipse, A.P. In Situ Imaging of Field-Induced Hexagonal Columns in Magnetite Ferrofluids. Phys. Rev. Lett. 2006, 97, 185702. [Google Scholar] [CrossRef] [PubMed]
- Safronov, A.P.; Terziyan, T.V.; Istomina, A.S.; Beketov, I.V. Swelling and contraction of ferrogels based on polyacrylamide in a magnetic field. Polym. Sci. Ser. A 2012, 54, 26–33. [Google Scholar] [CrossRef]
- Benkoski, J.J.; Deacon, R.M.; Land, H.B.; Baird, L.M.; Breidenich, J.L.; Srinivasan, R.; Clatterbaugh, G.V.; Keng, P.Y.; Pyun, J. Dipolar assembly of ferromagnetic nanoparticles into magnetically driven artificial cilia. Soft Matter 2010, 6, 602–609. [Google Scholar] [CrossRef]
- Cheng, G.; Romero, D.; Fraser, G.T.; Hight Walker, A.R. Magnetic-field-induced assemblies of cobalt nanoparticles. Langmuir 2005, 21, 12055–12059. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Lopez, M.T.; Iskakova, L.Y.; Zubarev, A.Y. To the theory of shear elastic properties of magnetic gels. Physica A 2017, 486, 908–914. [Google Scholar] [CrossRef]
- Lopez-Lopez, M.T.; Borin, D.Y.; Zubarev, A.Y. Shear elasticity of isotropic magnetic gels. Phys. Rev. E 2017, 96, 022605. [Google Scholar] [CrossRef] [PubMed]
- Böse, H.; Röder, R. Magnetorheological Elastomers with High Variability of Their Mechanical Properties. J. Phys. Conf. Ser. 2009, 149, 012090. [Google Scholar] [CrossRef]
- Zubarev, A.Y.; Iskakova, L.Y.; Lopez-Lopez, M.T. Towards a theory of mechanical properties of ferrogels. Effect of chain-like aggregates. Physica A 2016, 455, 98–103. [Google Scholar] [CrossRef]
- Zubarev, A.Y.; Chirikov, D.N.; Borin, D.Y.; Stepanov, G.V. Hysteresis of the magnetic properties of soft magnetic gels. Soft Matter 2016, 12, 6473–6480. [Google Scholar] [CrossRef] [PubMed]
- Coquelle, E.; Bossis, G.; Szabo, D.; Giulieri, F. Micromechanical analysis of an elastomer filled with particles organized in chain-like structure. J. Mater. Sci. 2006, 41, 5941–5953. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Field; Butterworth-Heinemann: Oxford, UK, 1975; ISBN 978-0-7506-2768-9. [Google Scholar]
- Biller, A.M.; Stolbov, O.V.; Raikher, Y.L. Mesoscopic magnetomechanical hysteresis in a magnetorheological elastomer. Phys. Rev. E 2015, 92, 023202. [Google Scholar] [CrossRef] [PubMed]
- Bozorth, R. Ferromagnetism; Wiley: New York, NY, USA, 1993; ISBN1 13 978-0780310322. ISBN2 10 0780310322. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon Press: New York, NY, USA, 1960; ISBN 978-0-08-009105-1. [Google Scholar]
- Chirikov, D.N.; Fedotov, S.P.; Iskakova, L.Y.; Zubarev, A.Y. Viscoelastic properties of ferrofluids. Phys. Rev. E 2010, 82, 051495. [Google Scholar] [CrossRef] [PubMed]
- Pokrovskii, V.N. Statistical Mechanics of Dilute Suspensions; Nauka: Moscow, Russia, 1978. (In Russian) [Google Scholar]
- Bossis, G.; Lancon, P.; Meunier, A.; Iskakova, L.; Kostenko, V.; Zubarev, A. Kinetics of internal structures growth in magnetic suspensions. Physica A 2013, 392, 1567–1576. [Google Scholar] [CrossRef] [Green Version]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; University Press: Oxford, UK; New York, NY, USA, 1986; ISBN 0 19 852033 6. [Google Scholar]
- Larson, R.G. The Structure and Rheology of Complex Fluids; Oxford University Press: New York, NY, USA, 1999; ISBN 0-19-512197-X. [Google Scholar]
- Van Berkum, S.; Dee, J.T.; Philipse, A.P.; Erne, B.H. Frequency-Dependent Magnetic Susceptibility of Magnetite and Cobalt Ferrite Nanoparticles Embedded in PAA Hydrogel. Int. J. Mol. Sci. 2013, 14, 10162–10177. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weeber, R.; Hermes, M.; Schmidt, A.M.; Holm, C. Polymer architecture of magnetic gels: A review. J. Phys. Condens. Matter 2018, 30, 063002. [Google Scholar] [CrossRef] [PubMed]
| Volume Concentration of the Particles | Experimental [45] Shear Modulus of the Composite without a Magnetic Field (MPa) | Theoretical Shear Modulus of the Composite without a Magnetic Field (MPa) | Estimated Number of Particles N in the Chain |
|---|---|---|---|
| 10% (V/V) iron | 0.26 | 0.27 | 9 |
| 20% (V/V) iron | 0.74 | 0.81 | 13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borin, D.; Chirikov, D.; Zubarev, A. Shear Elasticity of Magnetic Gels with Internal Structures. Sensors 2018, 18, 2054. https://doi.org/10.3390/s18072054
Borin D, Chirikov D, Zubarev A. Shear Elasticity of Magnetic Gels with Internal Structures. Sensors. 2018; 18(7):2054. https://doi.org/10.3390/s18072054
Chicago/Turabian StyleBorin, Dmitry, Dmitri Chirikov, and Andrey Zubarev. 2018. "Shear Elasticity of Magnetic Gels with Internal Structures" Sensors 18, no. 7: 2054. https://doi.org/10.3390/s18072054
APA StyleBorin, D., Chirikov, D., & Zubarev, A. (2018). Shear Elasticity of Magnetic Gels with Internal Structures. Sensors, 18(7), 2054. https://doi.org/10.3390/s18072054





