Visual Information Fusion through Bayesian Inference for Adaptive Probability-Oriented Feature Matching
Abstract
1. Introduction
- The probability framework considers the 3D global reference system, instead of a 2D image frame representation.
- A 3D probability distribution is computed and projected onto the next image, associated to the next pose of the robot, by means of a filter-motion prediction stage. Such probability projection represents relevant areas on the image, where matching detection is more probable.
- The matching process is performed in a single batch, using the entire set of feature points associated with the probability areas projected on the image, instead of a multi-scaled matching, computed feature by feature.
- The information metric permits modulating the probability values for the probability areas, instead of simply representing a set of less precise coefficients for weighting the former multi-scaled matching.
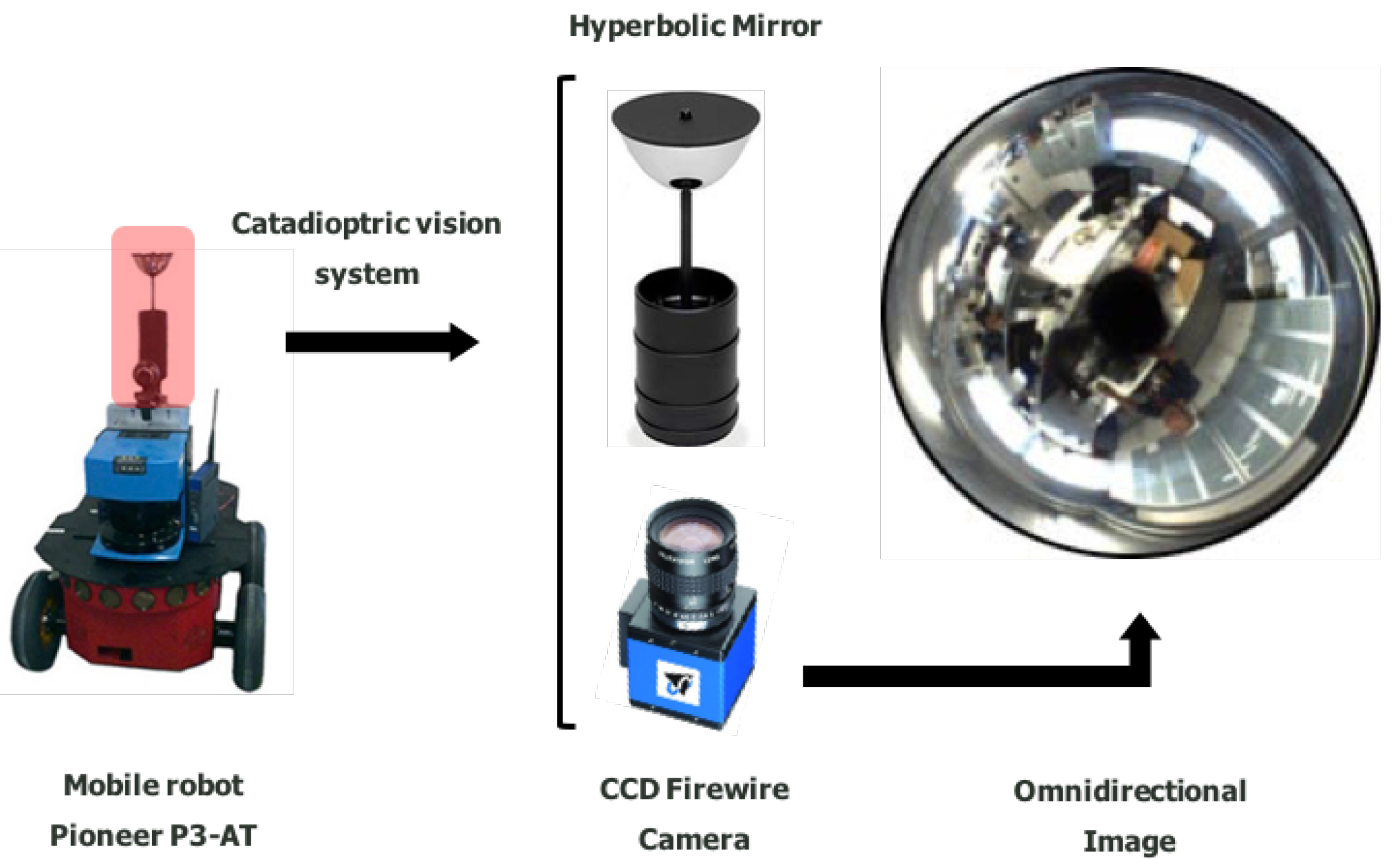
2. Vision System
3. Omnidirectional Visual Localization
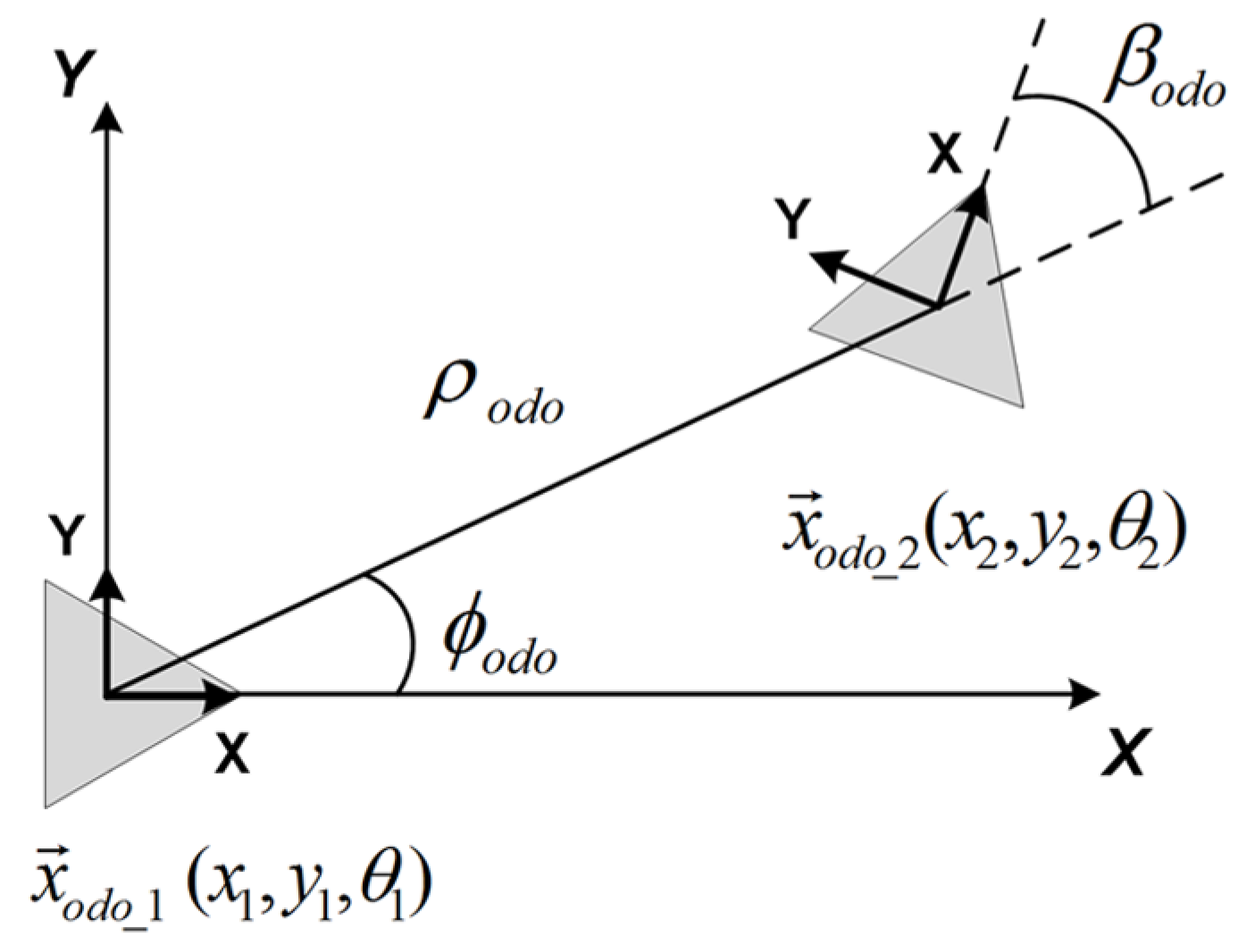
3.1. Angular Motion Recovery
3.2. Scale Estimation
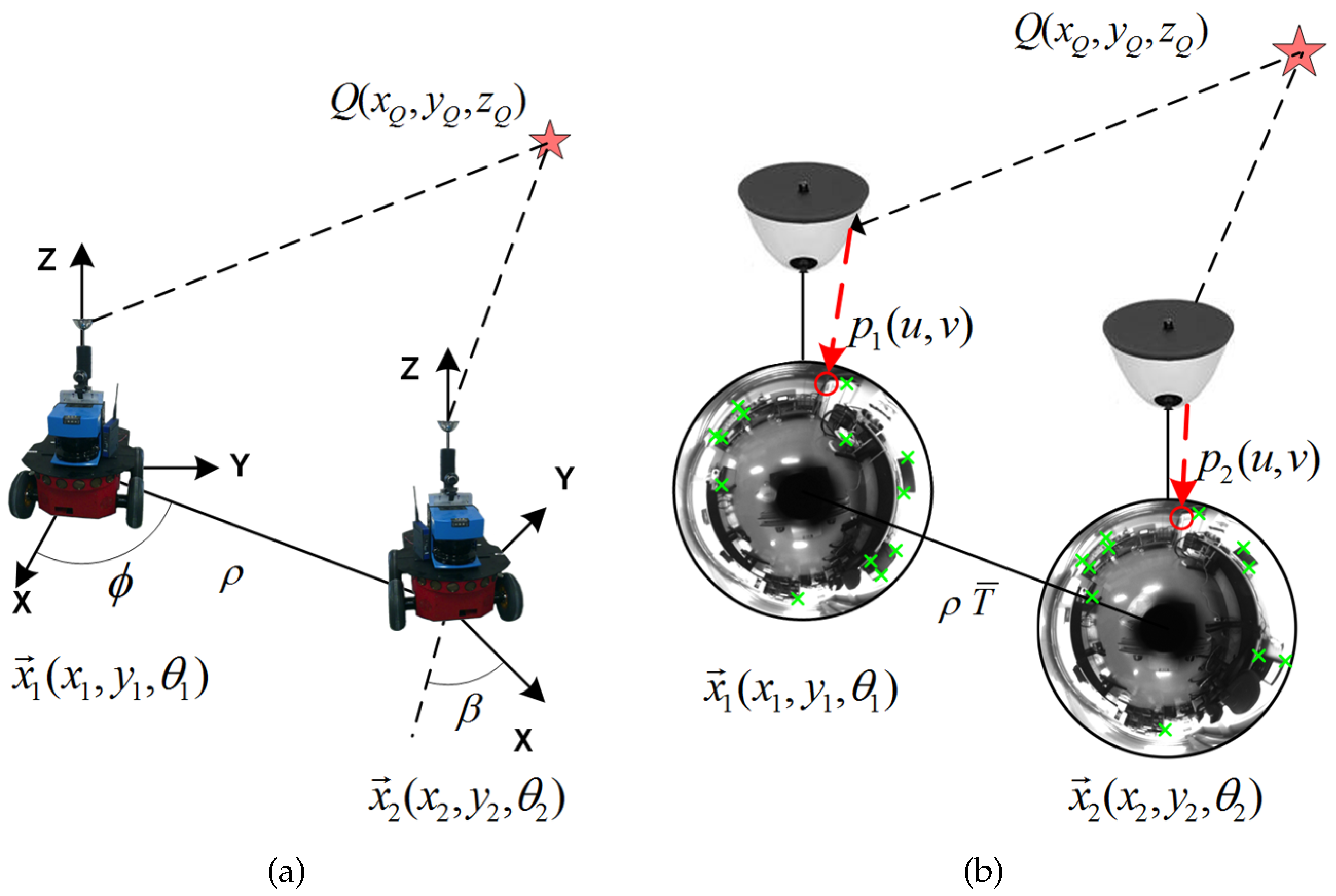
3.3. Notation Definitions
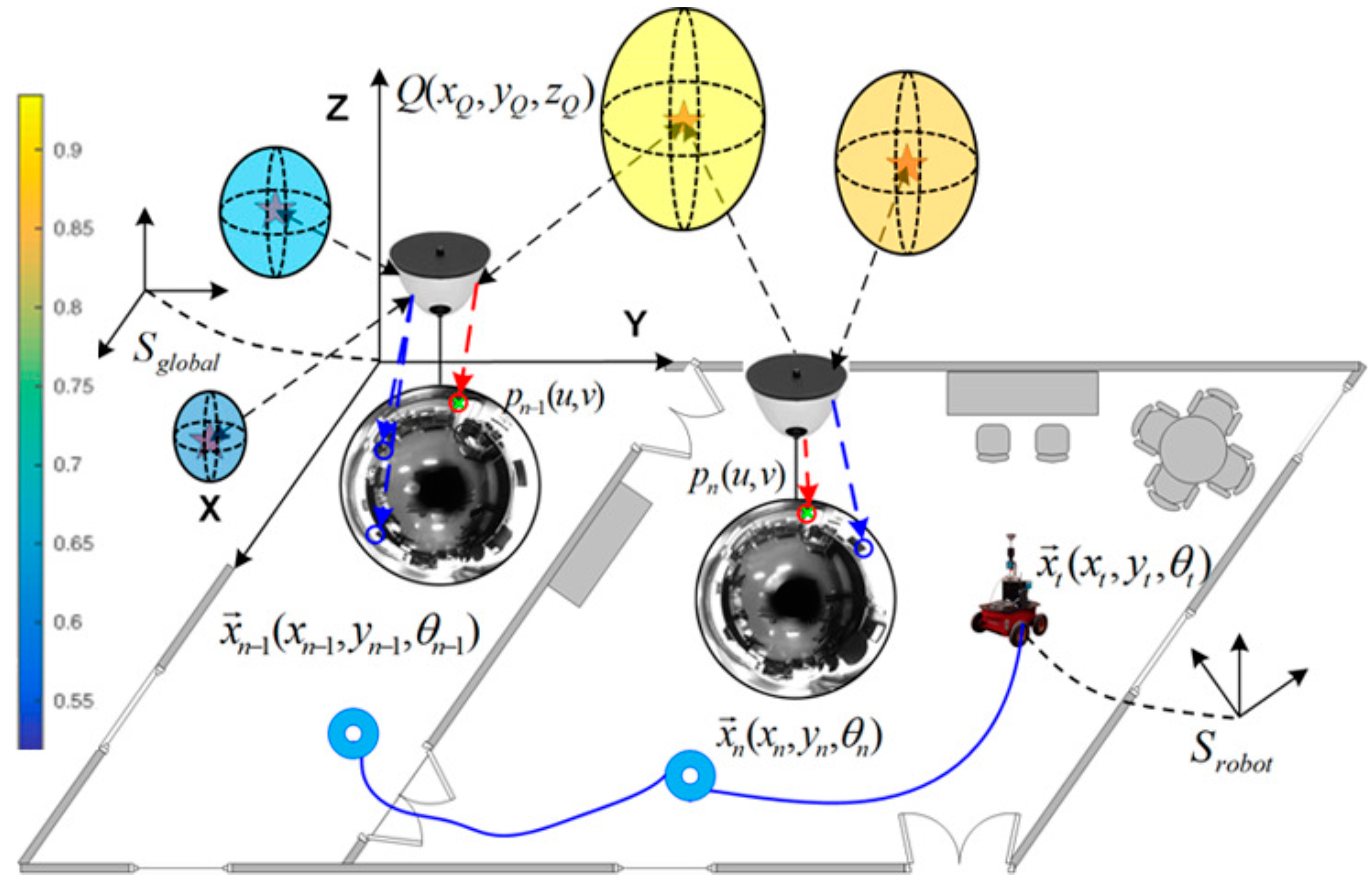
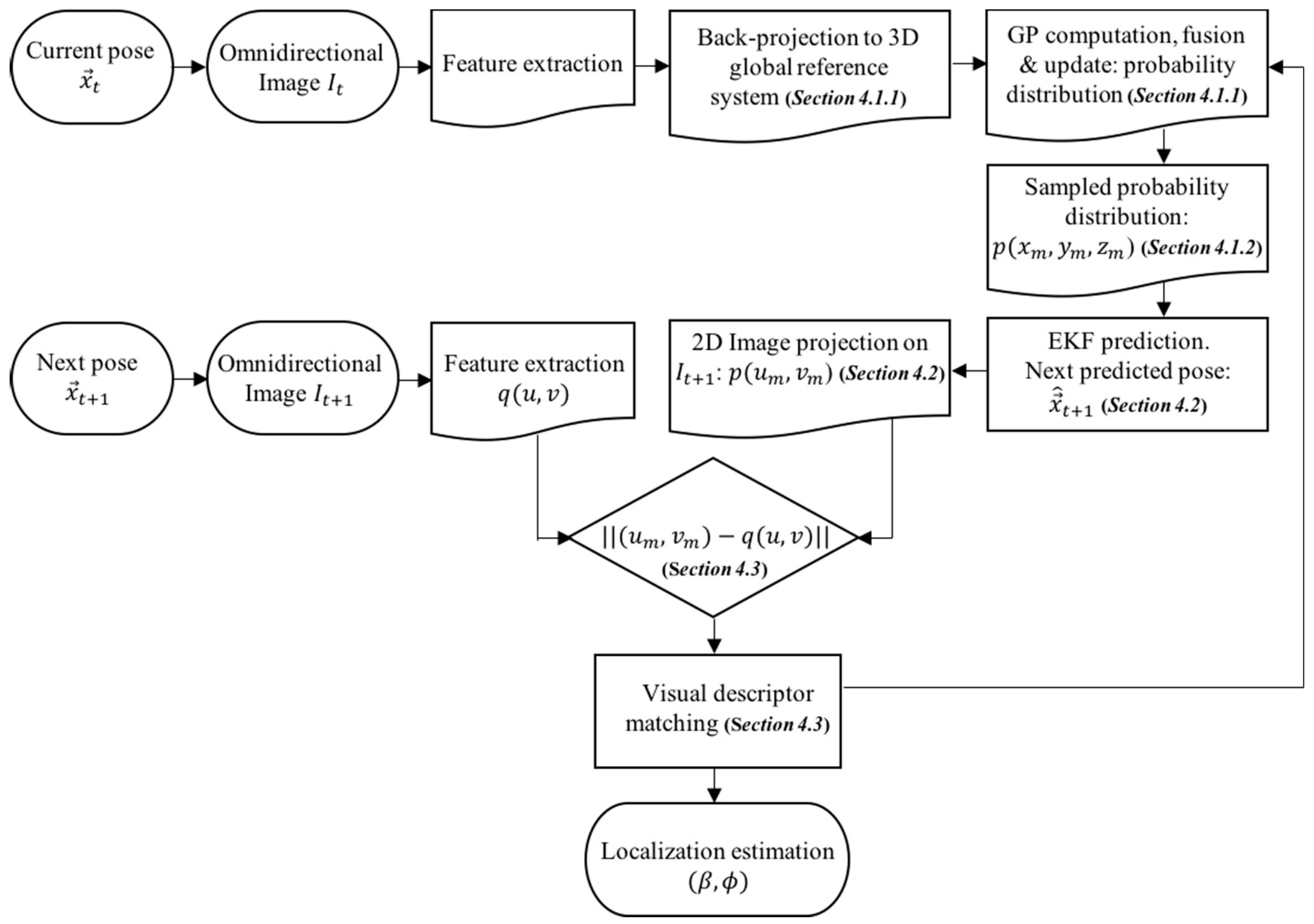
4. Visual Information Fusion
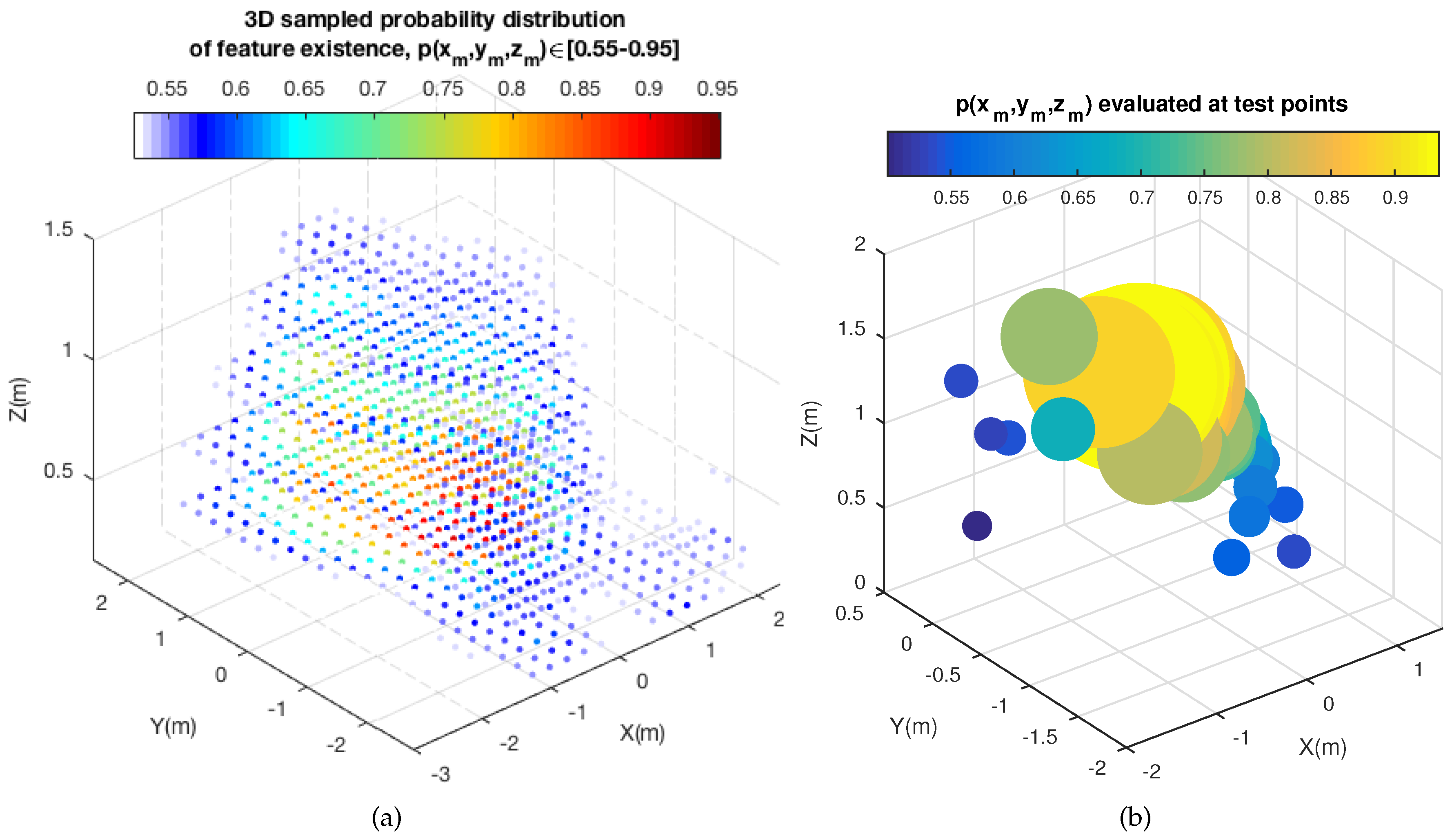
4.1. 3D Probability Distribution of Feature Existence: GP Computation and 3D Probability Sampling
4.1.1. GP Computation
4.1.2. 3D Probability Sampling
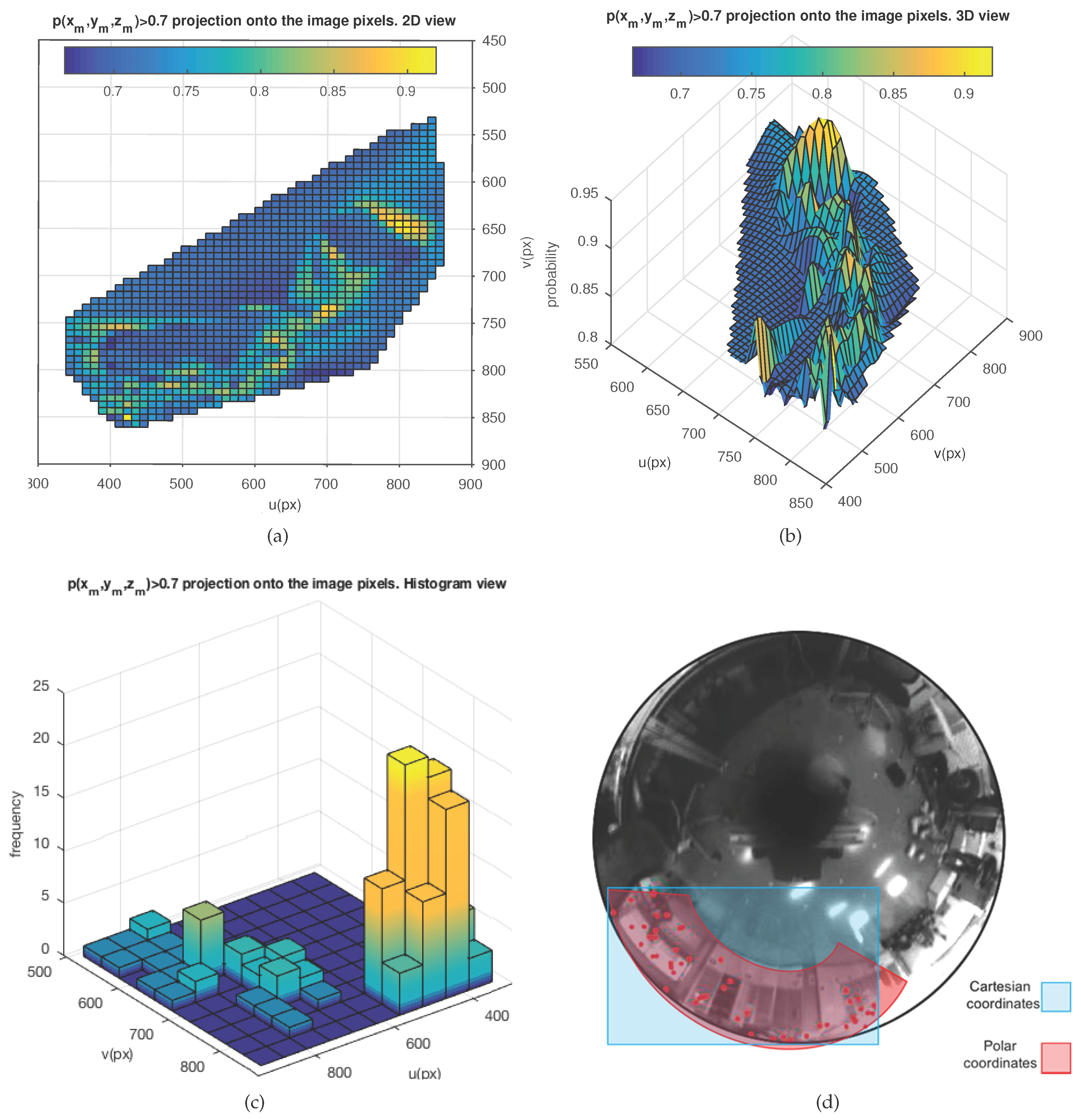
4.2. Motion Prediction and 2D Image Projection
4.3. Probability-Oriented Feature Matching
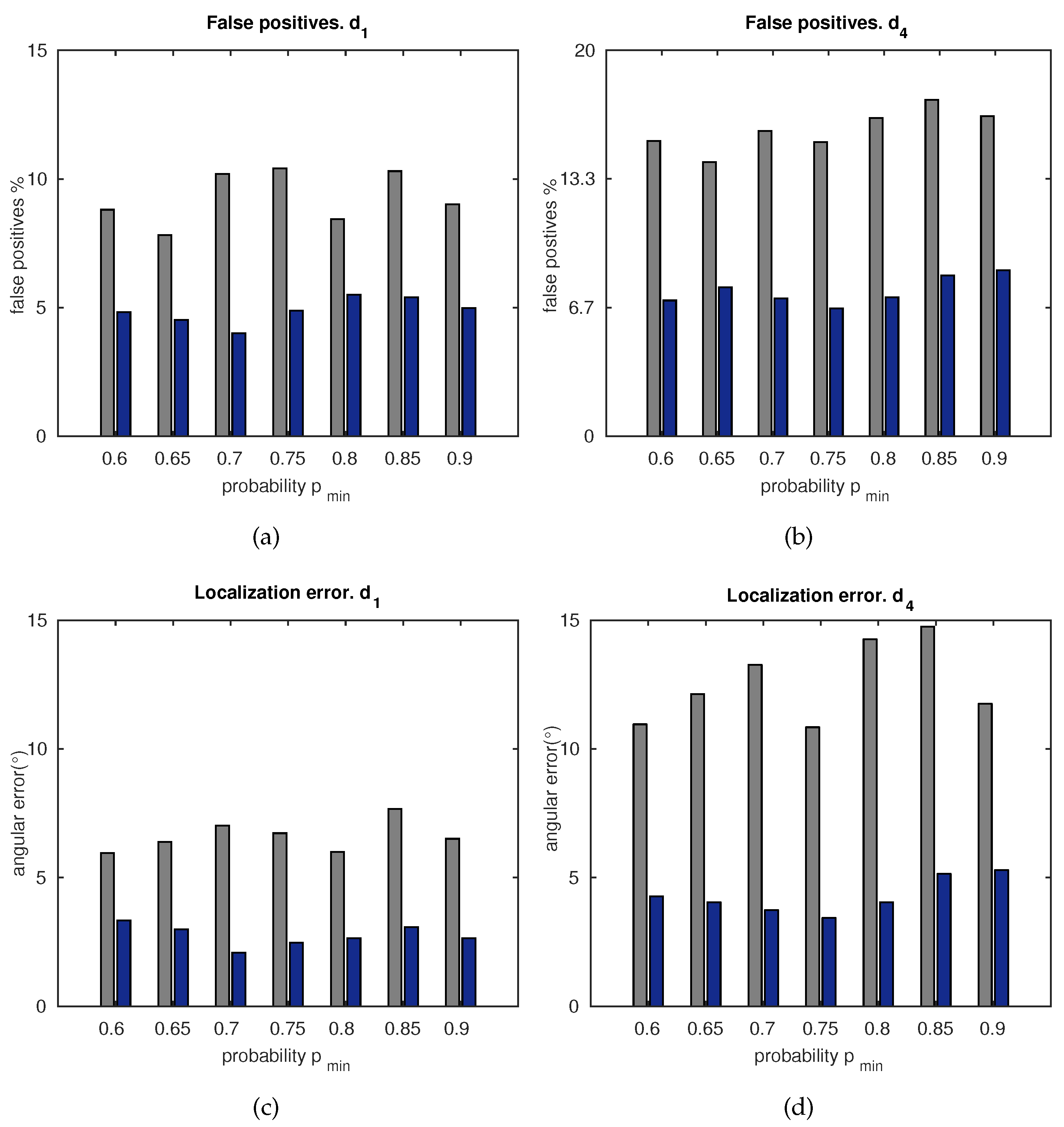
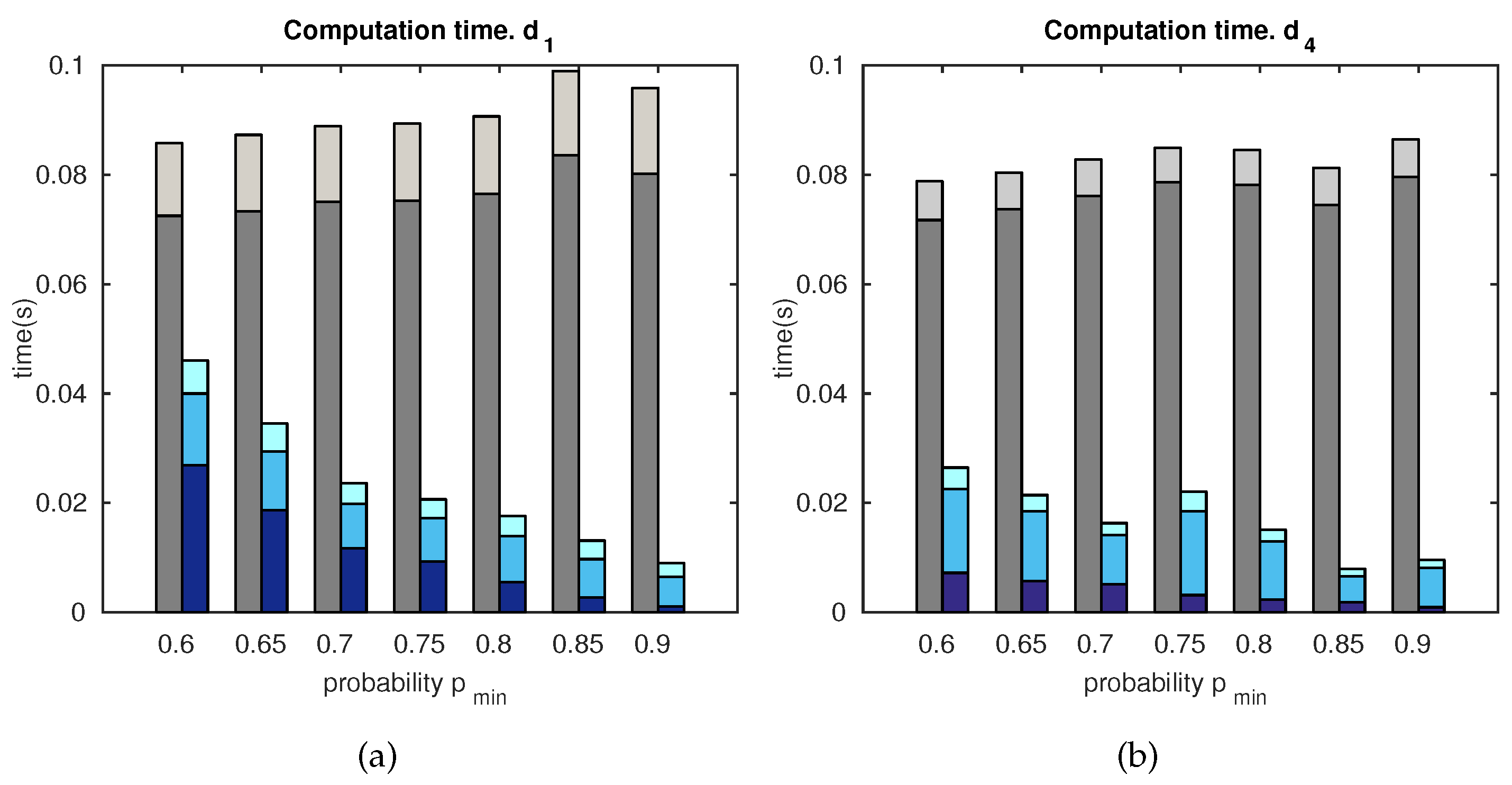
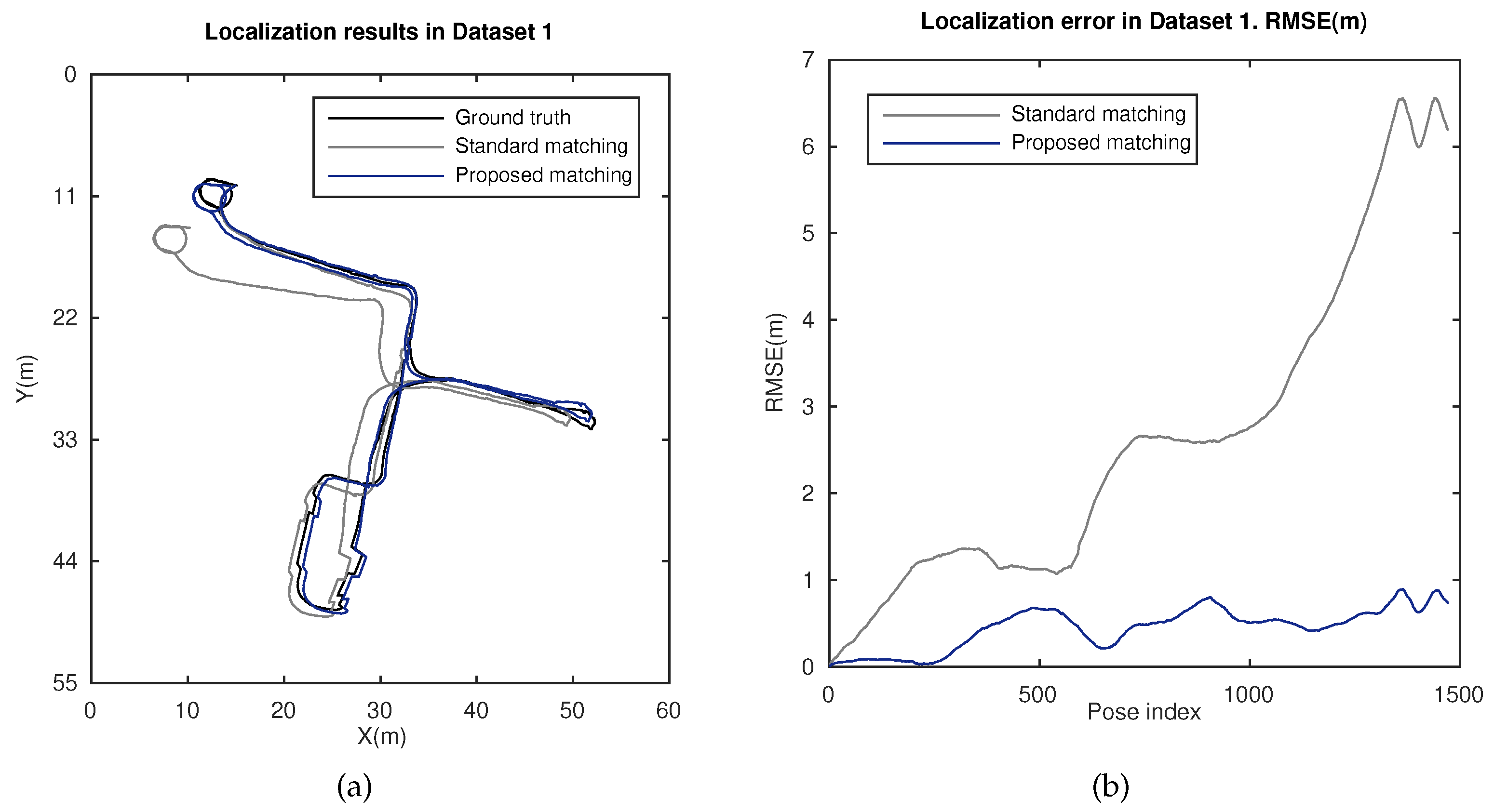
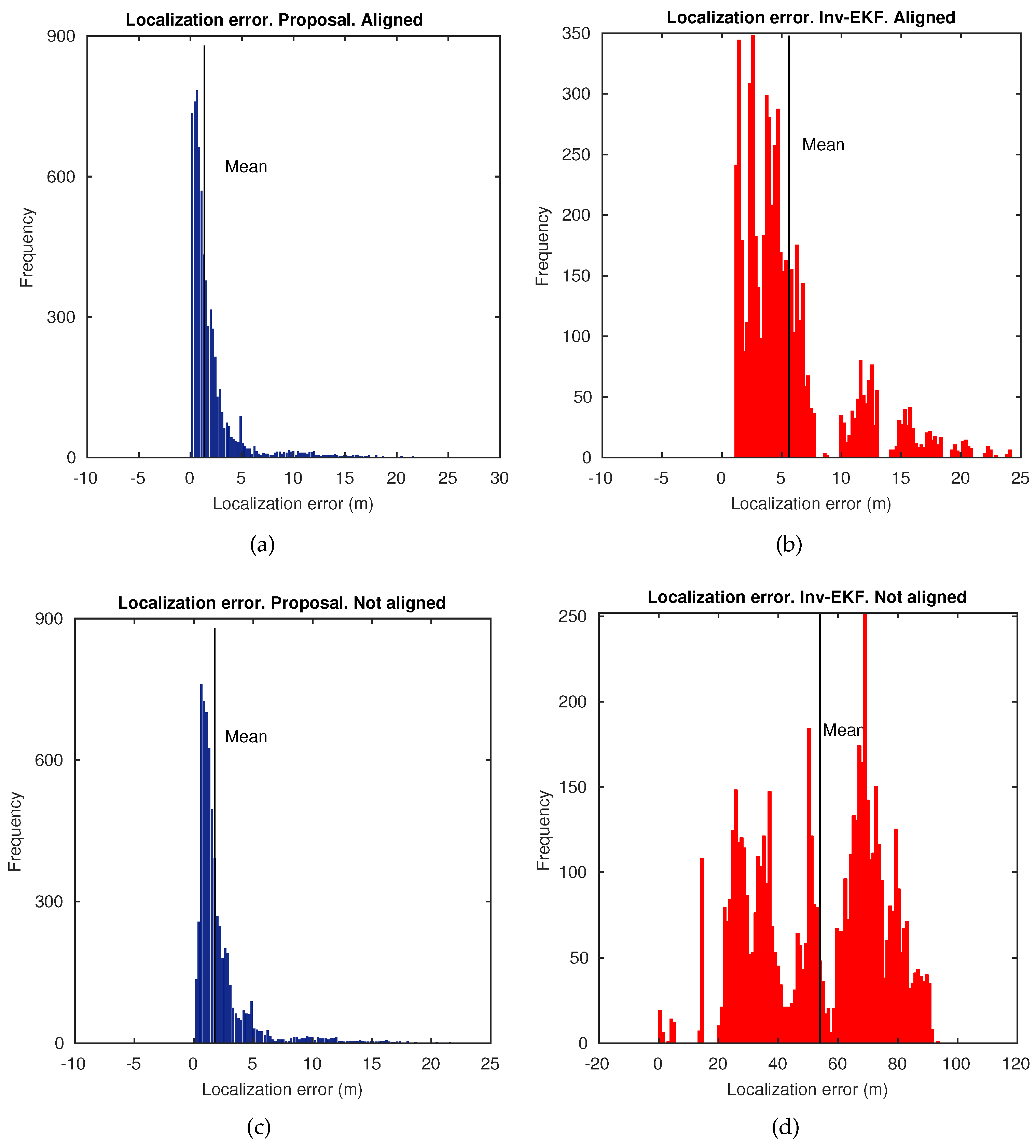
5. Results
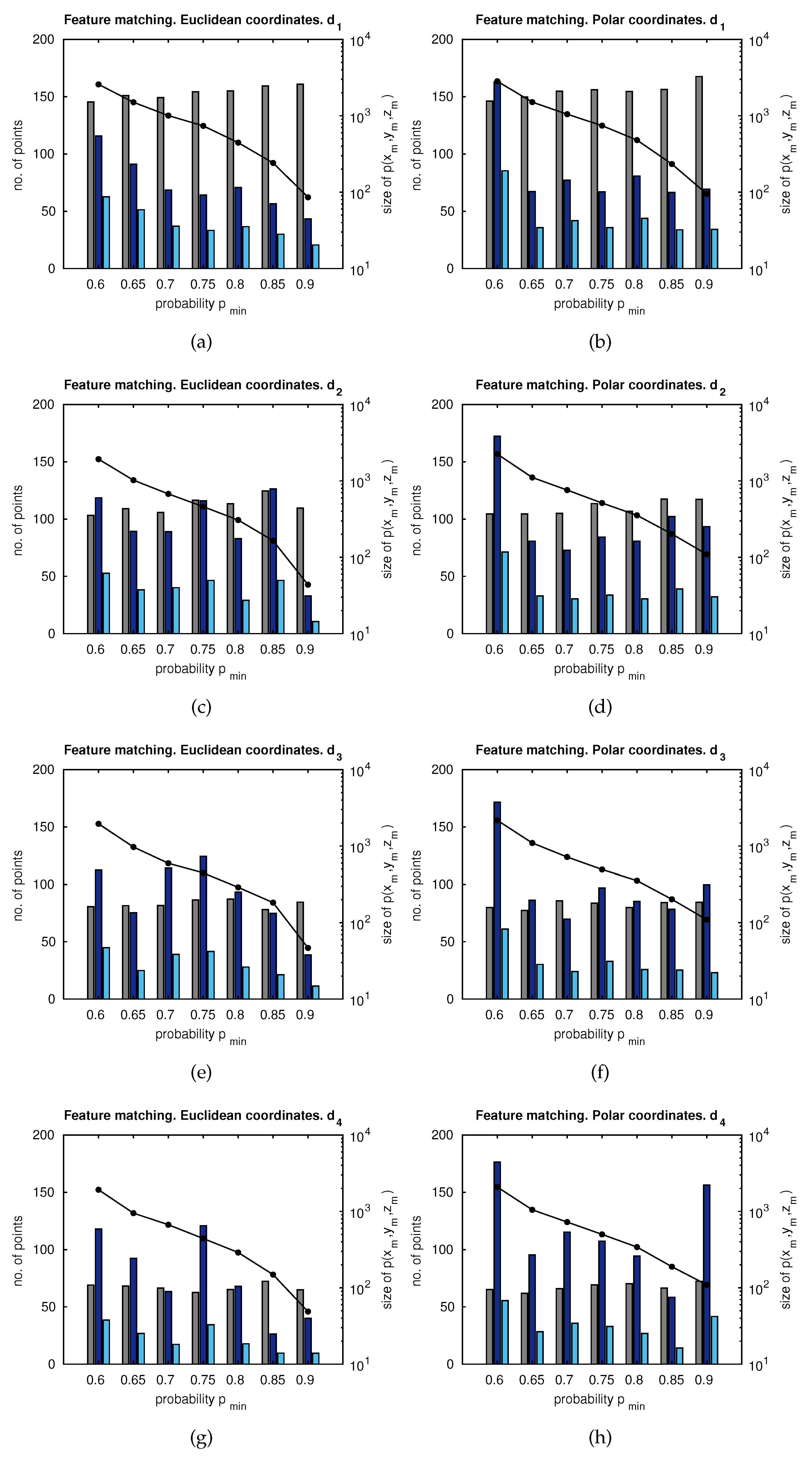
5.1. Matching Results
5.1.1. Number of Feature Matches
5.1.2. Accuracy
5.1.3. Computation Time
- (a)
- feature matching;
- (b)
- matching candidates;
- (c)
- final localization estimation.
5.2. Localization Results
6. Discussion
- Adaptive probability-oriented feature matching.
- Stable amount and accurate matches provided, in contrast to standard techniques.
- Efficient approach to work in real time.
- Robust final localization estimate in large and challenging scenarios.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CCD | charge-coupled device |
| EKF | extended Kalman filter |
| GP | Gaussian process |
| GPS | global positioning system |
| KL | Kullback–Leibler divergence |
| MLE | maximum likelihood estimator |
| SURF | speeded-up robust features |
| SVD | singular value decomposition |
| RMSE | root mean square error |
References
- Chen, L.C.; Hoang, D.C.; Lin, H.I.; Nguyen, T.H. Innovative Methodology for Multi-View Point Cloud Registration in Robotic 3D Object Scanning and Reconstruction. Appl. Sci. 2016, 6, 132. [Google Scholar] [CrossRef]
- Rodriguez-Cielos, R.; Galan-Garcia, J.L.; Padilla-Dominguez, Y.; Rodriguez-Cielos, P.; Bello-Patricio, A.B.; Lopez-Medina, J.A. LiDARgrammetry: A New Method for Generating Synthetic Stereoscopic Products from Digital Elevation Models. Appl. Sci. 2017, 7, 906. [Google Scholar] [CrossRef]
- Scaramuzza, D.; Fraundorfer, F. Visual Odometry [Tutorial]. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Payá, L.; Gil, A.; Reinoso, O. A State-of-the-Art Review on Mapping and Localization of Mobile Robots Using Omnidirectional Vision Sensors. J. Sens. 2017, 2017, 3497650. [Google Scholar] [CrossRef]
- Scaramuzza, D.; Fraundorfer, F.; Siegwart, R. Real-Time Monocular Visual Odometry for On-Road Vehicles with 1-Point RANSAC. In Proceedings of the IEEE International Conference on Robotics & Automation (ICRA), Kobe, Japan, 12–17 May 2009; pp. 4293–4299. [Google Scholar]
- Civera, J.; Grasa, O.G.; Davison, A.J.; Montiel, J.M.M. 1-point RANSAC for EKF-based Structure from Motion. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 3498–3504. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Chow, J.C.; Lichti, D.D.; Hol, J.D.; Bellusci, G.; Luinge, H. IMU and Multiple RGB-D Camera Fusion for Assisting Indoor Stop-and-Go 3D Terrestrial Laser Scanning. Robotics 2014, 3, 247–280. [Google Scholar] [CrossRef]
- Munguia, R.; Urzua, S.; Bolea, Y.; Grau, A. Vision-Based SLAM System for Unmanned Aerial Vehicles. Sensors 2016, 16, 372. [Google Scholar] [CrossRef] [PubMed]
- López, E.; García, S.; Barea, R.; Bergasa, L.M.; Molinos, E.J.; Arroyo, R.; Romera, E.; Pardo, S. A Multi-Sensorial Simultaneous Localization and Mapping (SLAM) System for Low-Cost Micro Aerial Vehicles in GPS-Denied Environments. Sensors 2017, 17, 802. [Google Scholar] [CrossRef] [PubMed]
- Davison, A.J.; Gonzalez Cid, Y.; Kita, N. Real-Time 3D SLAM with Wide-Angle Vision. In Proceedings of the 5th IFAC/EURON Symposium on Intelligent Autonomous Vehicles; Elsevier Ltd.: New York, NY, USA, 2004; pp. 117–124. [Google Scholar]
- Paya, L.; Reinoso, O.; Jimenez, L.M.; Julia, M. Estimating the position and orientation of a mobile robot with respect to a trajectory using omnidirectional imaging and global appearance. PLoS ONE 2017, 12, e0175938. [Google Scholar] [CrossRef] [PubMed]
- Fleer, D.; Moller, R. Comparing holistic and feature-based visual methods for estimating the relative pose of mobile robots. Robot. Auton. Syst. 2017, 89, 51–74. [Google Scholar] [CrossRef]
- Hu, F.; Zhu, Z.; Mejia, J.; Tang, H.; Zhang, J. Real-time indoor assistive localization with mobile omnidirectional vision and cloud GPU acceleration. AIMS Electron. Electr. Eng. 2017, 1, 74. [Google Scholar]
- Hu, F.; Zhu, Z.; Zhang, J. Mobile Panoramic Vision for Assisting the Blind via Indexing and Localization. In Computer Vision—ECCV 2014 Workshops; Agapito, L., Bronstein, M.M., Rother, C., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 600–614. [Google Scholar]
- Davison, A.J. Real-Time Simultaneous Localisation and Mapping with a Single Camera. In ICCV’03 Proceedings of the Ninth IEEE International Conference on Computer Vision; IEEE Computer Society: Washington, DC, USA, 2003; Volume 2, pp. 1403–1410. [Google Scholar]
- Karlsson, N.; di Bernardo, E.; Ostrowski, J.; Goncalves, L.; Pirjanian, P.; Munich, M.E. The vSLAM Algorithm for Robust Localization and Mapping. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 24–29. [Google Scholar]
- Chli, M.; Davison, A.J. Active matching for visual tracking. Robot. Auton. Syst. 2009, 57, 1173–1187. [Google Scholar] [CrossRef]
- Neira, J.; Tardós, J.D. Data association in stochastic mapping using the joint compatibility test. IEEE Trans. Robot. Autom. 2001, 17, 890–897. [Google Scholar] [CrossRef]
- Rasmussen, C.; Hager, G.D. Probabilistic data association methods for tracking complex visual objects. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 560–576. [Google Scholar] [CrossRef]
- Li, Y.; Li, S.; Song, Q.; Liu, H.; Meng, M.H. Fast and Robust Data Association Using Posterior Based Approximate Joint Compatibility Test. IEEE Trans. Ind. Inform. 2014, 10, 331–339. [Google Scholar] [CrossRef]
- Lowe, D. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Speeded Up Robust Features. Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Gerrits, M.; Bekaert, P. Local Stereo Matching with Segmentation-based Outlier Rejection. In Proceedings of the 3rd Canadian Conference on Computer and Robot Vision (CRV’06), Quebec City, QC, Canada, 7–9 June 2006; p. 66. [Google Scholar]
- Kitt, B.; Geiger, A.; Lategahn, H. Visual odometry based on stereo image sequences with RANSAC-based outlier rejection scheme. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, San Diego, CA, USA, 21–24 June 2010; pp. 486–492. [Google Scholar]
- Hasler, D.; Sbaiz, L.; Susstrunk, S.; Vetterli, M. Outlier modeling in image matching. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 301–315. [Google Scholar] [CrossRef]
- Liu, M.; Pradalier, C.; Siegwart, R. Visual Homing From Scale With an Uncalibrated Omnidirectional Camera. IEEE Trans. Robot. 2013, 29, 1353–1365. [Google Scholar] [CrossRef]
- Adam, A.; Rivlin, E.; Shimshoni, I. ROR: rejection of outliers by rotations. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 78–84. [Google Scholar] [CrossRef]
- Abduljabbar, Z.A.; Jin, H.; Ibrahim, A.; Hussien, Z.A.; Hussain, M.A.; Abbdal, S.H.; Zou, D. SEPIM: Secure and Efficient Private Image Matching. Appl. Sci. 2016, 6, 213. [Google Scholar] [CrossRef]
- Correal, R.; Pajares, G.; Ruz, J.J. A Matlab-Based Testbed for Integration, Evaluation and Comparison of Heterogeneous Stereo Vision Matching Algorithms. Robotics 2016, 5, 24. [Google Scholar] [CrossRef]
- Valiente, D.; Gil, A.; Payá, L.; Sebastián, J.M.; Reinoso, O. Robust Visual Localization with Dynamic Uncertainty Management in Omnidirectional SLAM. Appl. Sci. 2017, 7, 1294. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning Series; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006; pp. 1–266. [Google Scholar]
- Ghaffari Jadidi, M.; Valls Miro, J.; Dissanayake, G. Gaussian processes autonomous mapping and exploration for range-sensing mobile robots. Auton. Robots 2018, 42, 273–290. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Scaramuzza, D.; Martinelli, A.; Siegwart, R. A Toolbox for Easily Calibrating Omnidirectional Cameras. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 5695–5701. [Google Scholar]
- Longuet-Higgins, H.C. A computer algorithm for reconstructing a scene from two projections. Nature 1985, 293, 133–135. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Civera, J.; Davison, A.J.; Martínez Montiel, J.M. Inverse Depth Parametrization for Monocular SLAM. IEEE Trans. Robot. 2008, 24, 932–945. [Google Scholar] [CrossRef]
- Valiente, D.; Gil, A.; Reinoso, O.; Julia, M.; Holloway, M. Improved Omnidirectional Odometry for a View-Based Mapping Approach. Sensors 2017, 17, 325. [Google Scholar] [CrossRef] [PubMed]
- McLachlan, G. Discriminant Analysis and Statistical Pattern Recognition; Wiley Series in Probability an Statistics; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Kulback, S.; Leiber, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- ARVC: Automation, Robotics and Computer Vision Research Group. Miguel Hernandez University. Omnidirectional Image Dataset at Innova Building. Available online: http://arvc.umh.es/db/images/innova_trajectory/ (accessed on 20 March 2018).
- The Rawseeds Project: Public Multisensor Benchmarking Dataset. Available online: http://www.rawseeds.org (accessed on 20 March 2018).
- Civera, J.; Grasa, O.G.; Davison, A.J.; Montiel, J.M.M. 1-Point RANSAC for extended Kalman filtering: Application to real-time structure from motion and visual odometry. J. Field Robot. 2010, 27, 609–631. [Google Scholar] [CrossRef]
- Fontana, G.; Matteucci, M.; Sorrenti, D.G. Rawseeds: Building a Benchmarking Toolkit for Autonomous Robotics. In Methods and Experimental Techniques in Computer Engineering; Springer International Publishing: Cham, Switzerland, 2014; pp. 55–68. [Google Scholar]
- Quigley, M.; Gerkey, B.; Conley, K.; Faust, J.; Foote, T.; Leibs, J.; Berger, E.; Wheeler, R.; Ng, A. ROS: An open-source Robot Operating System. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Workshop on Open Source Robotics, Kobe, Japan, 12–17 May 2009. [Google Scholar]




| Filter-Based SLAM Stages | ||
|---|---|---|
| Stage | Expression | Terms |
| Prediction | : relates the odometer’s control input and the current state | |
| : odometer’s control input, initial prior | ||
| : relates the observation and the current state | ||
| : uncertainty covariance | ||
| : input noise covariance | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valiente, D.; Payá, L.; Jiménez, L.M.; Sebastián, J.M.; Reinoso, Ó. Visual Information Fusion through Bayesian Inference for Adaptive Probability-Oriented Feature Matching. Sensors 2018, 18, 2041. https://doi.org/10.3390/s18072041
Valiente D, Payá L, Jiménez LM, Sebastián JM, Reinoso Ó. Visual Information Fusion through Bayesian Inference for Adaptive Probability-Oriented Feature Matching. Sensors. 2018; 18(7):2041. https://doi.org/10.3390/s18072041
Chicago/Turabian StyleValiente, David, Luis Payá, Luis M. Jiménez, Jose M. Sebastián, and Óscar Reinoso. 2018. "Visual Information Fusion through Bayesian Inference for Adaptive Probability-Oriented Feature Matching" Sensors 18, no. 7: 2041. https://doi.org/10.3390/s18072041
APA StyleValiente, D., Payá, L., Jiménez, L. M., Sebastián, J. M., & Reinoso, Ó. (2018). Visual Information Fusion through Bayesian Inference for Adaptive Probability-Oriented Feature Matching. Sensors, 18(7), 2041. https://doi.org/10.3390/s18072041








