Reliability Evaluation and Robust Design of a Sensor in an Entire Roller-Embedded Shapemeter
Abstract
:1. Introduction
2. Application Background
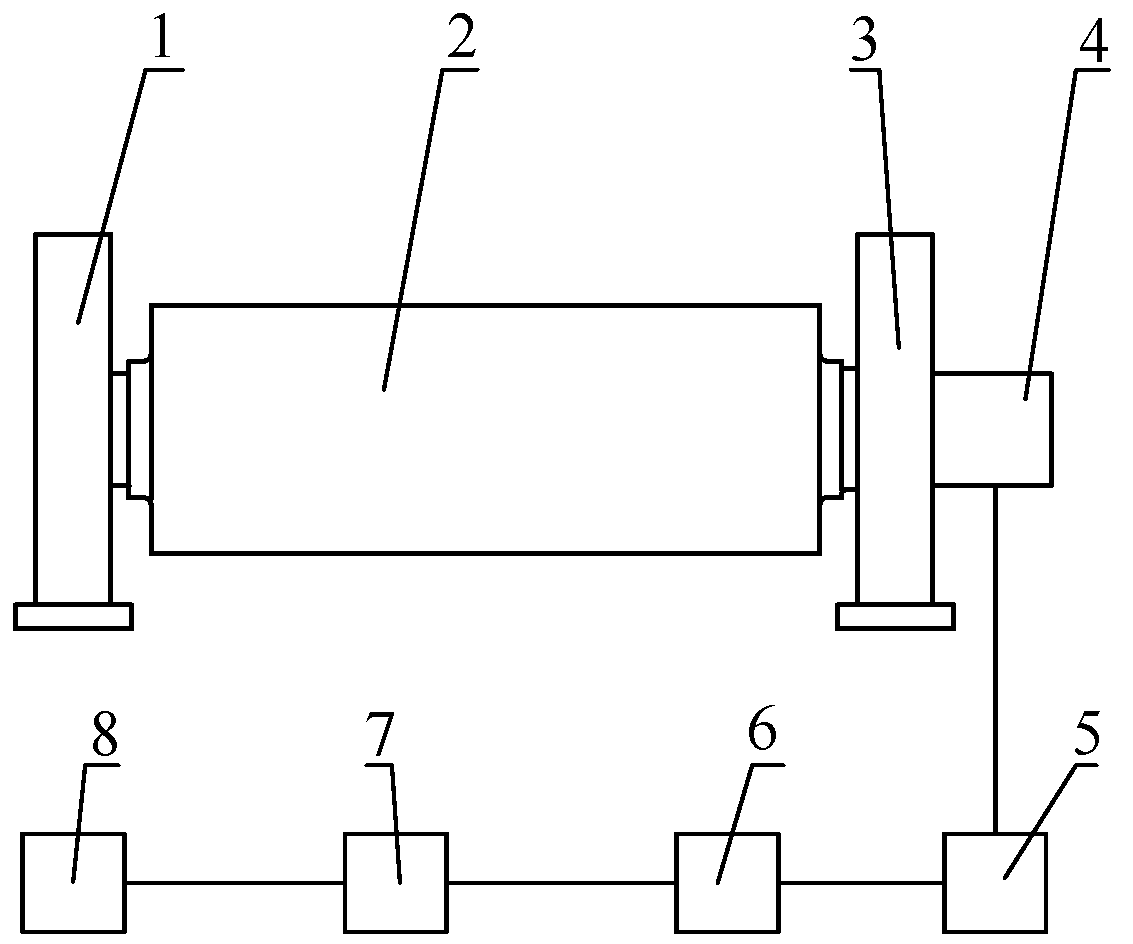
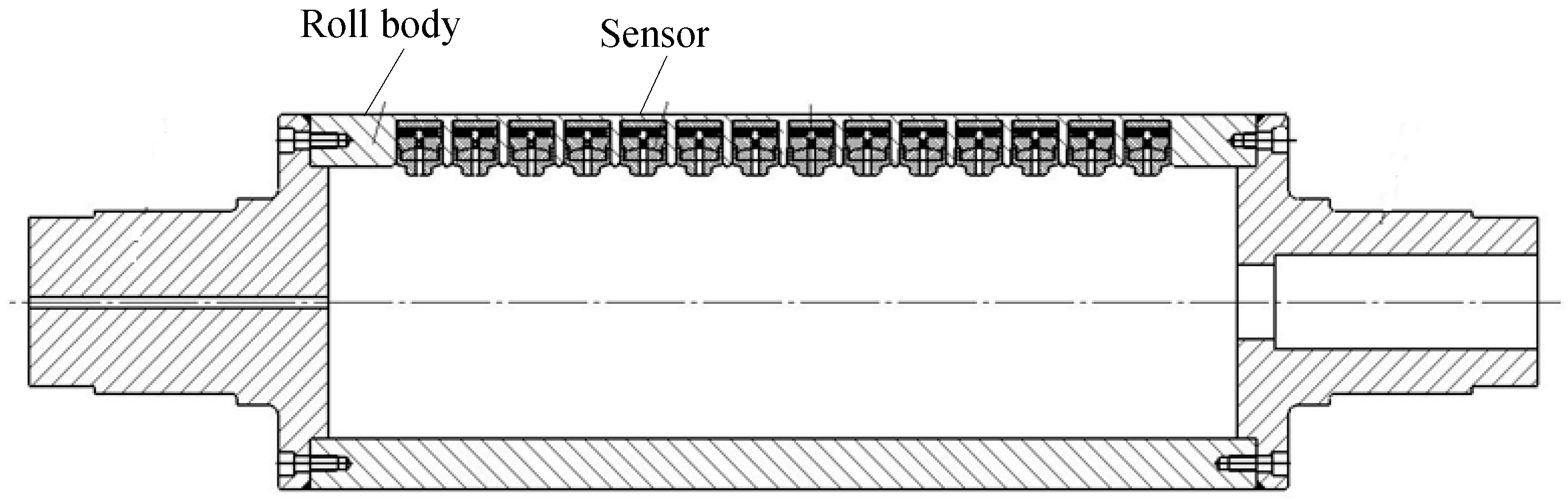
2.1. Composition of the Entire Roller-Embedded Shapemeter
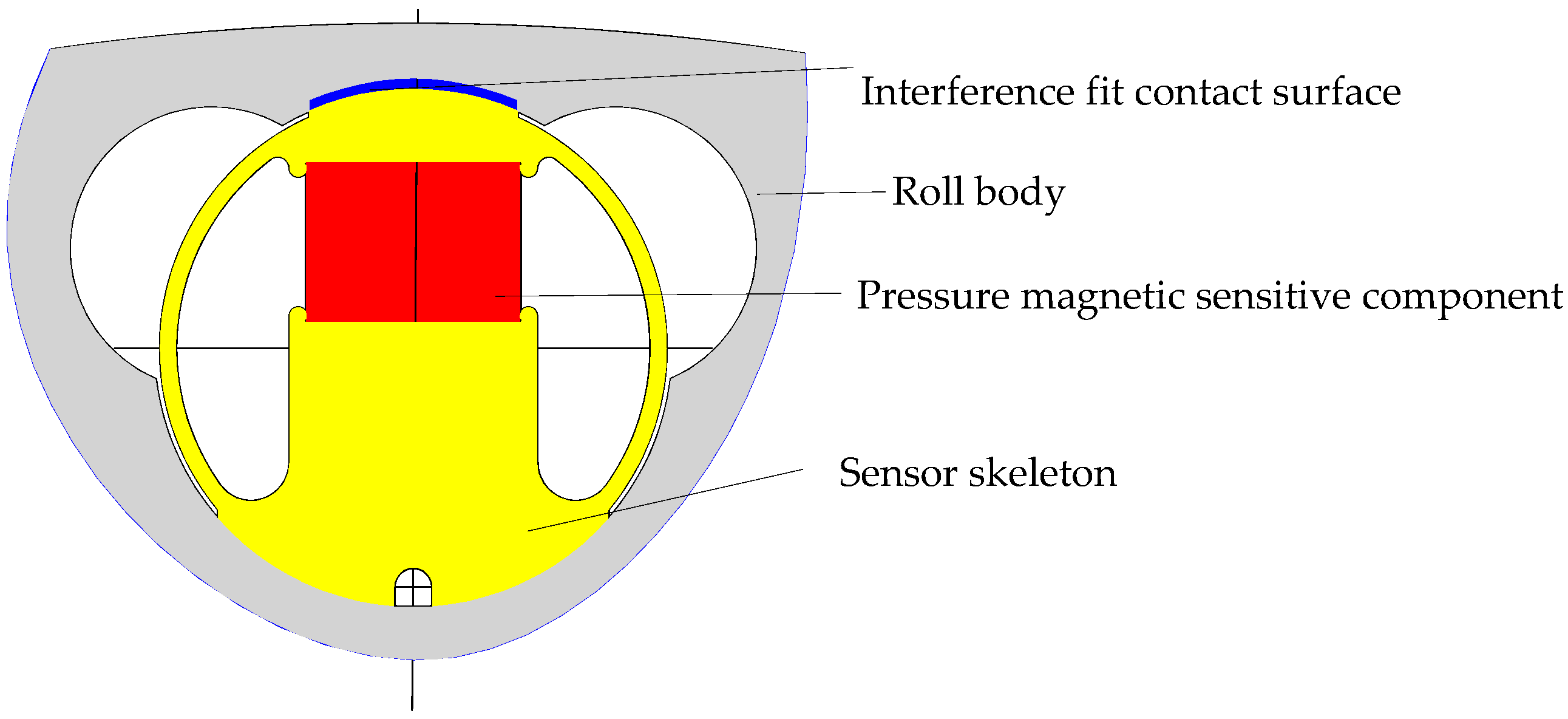
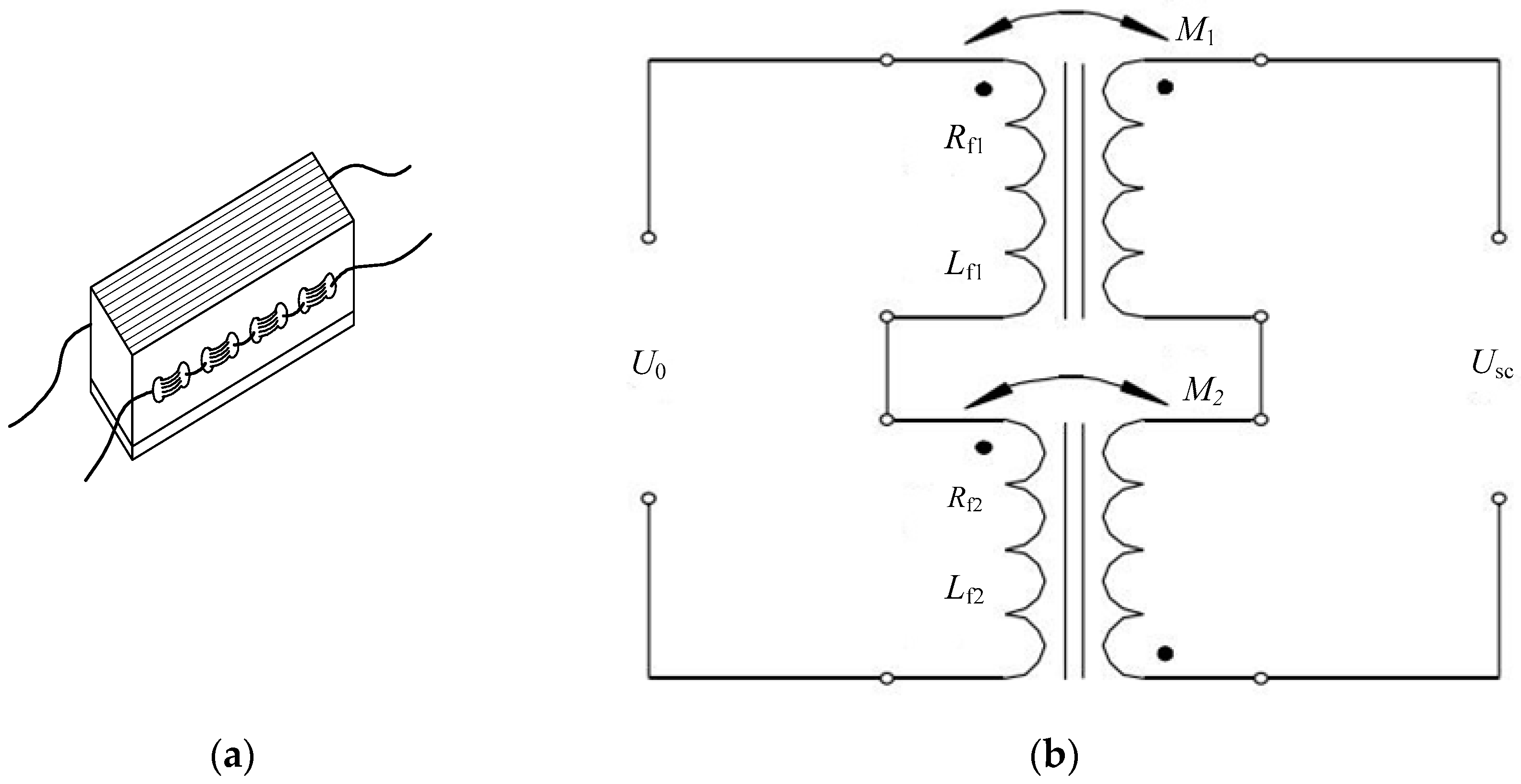
2.2. Composition of the Pressure Magnetic Sensitive Component
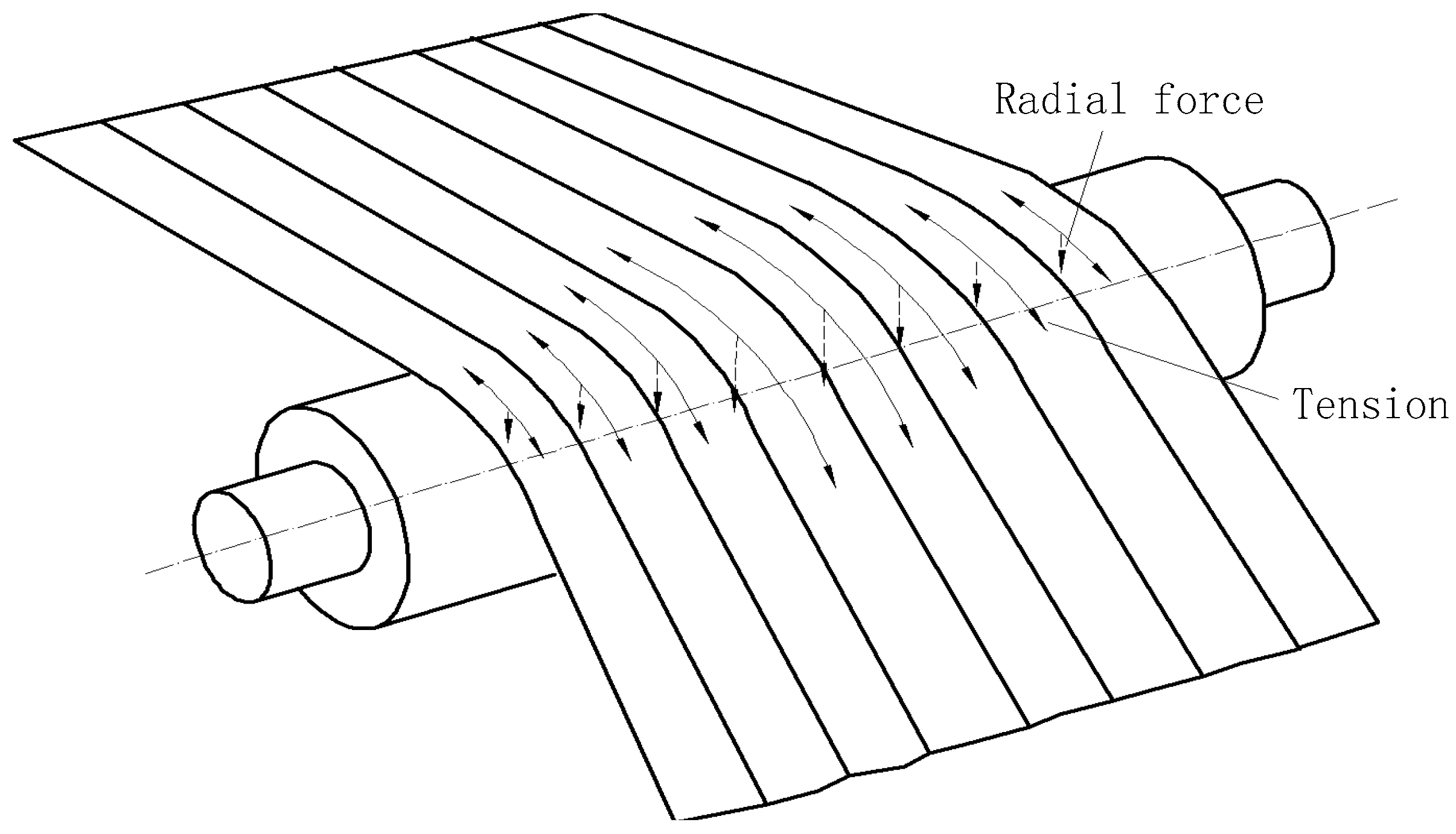
2.3. Strip Shape Detection Principle
2.4. Problem Introduction and Research Significance
3. Sensor Size Parameters Design Model
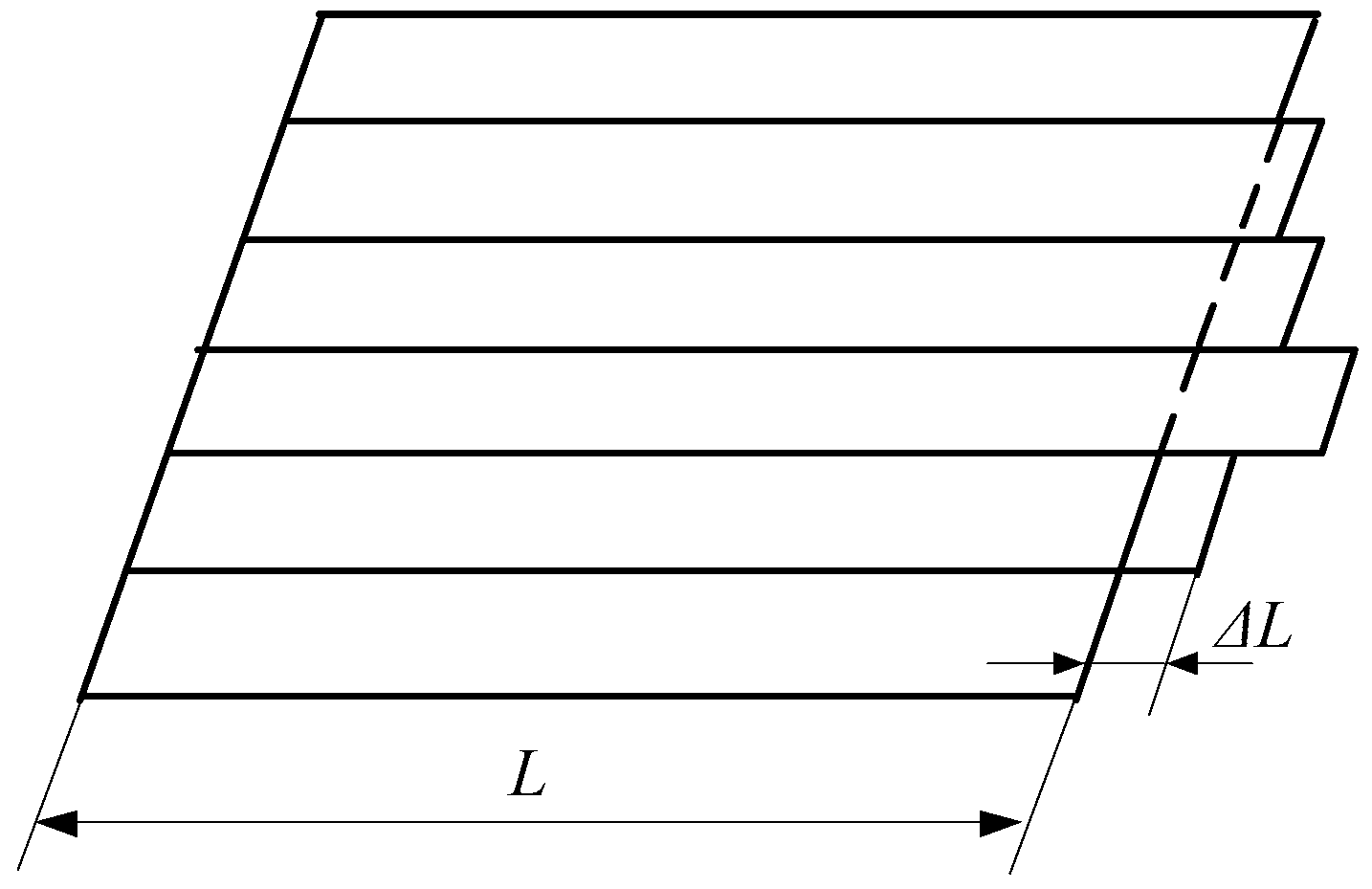
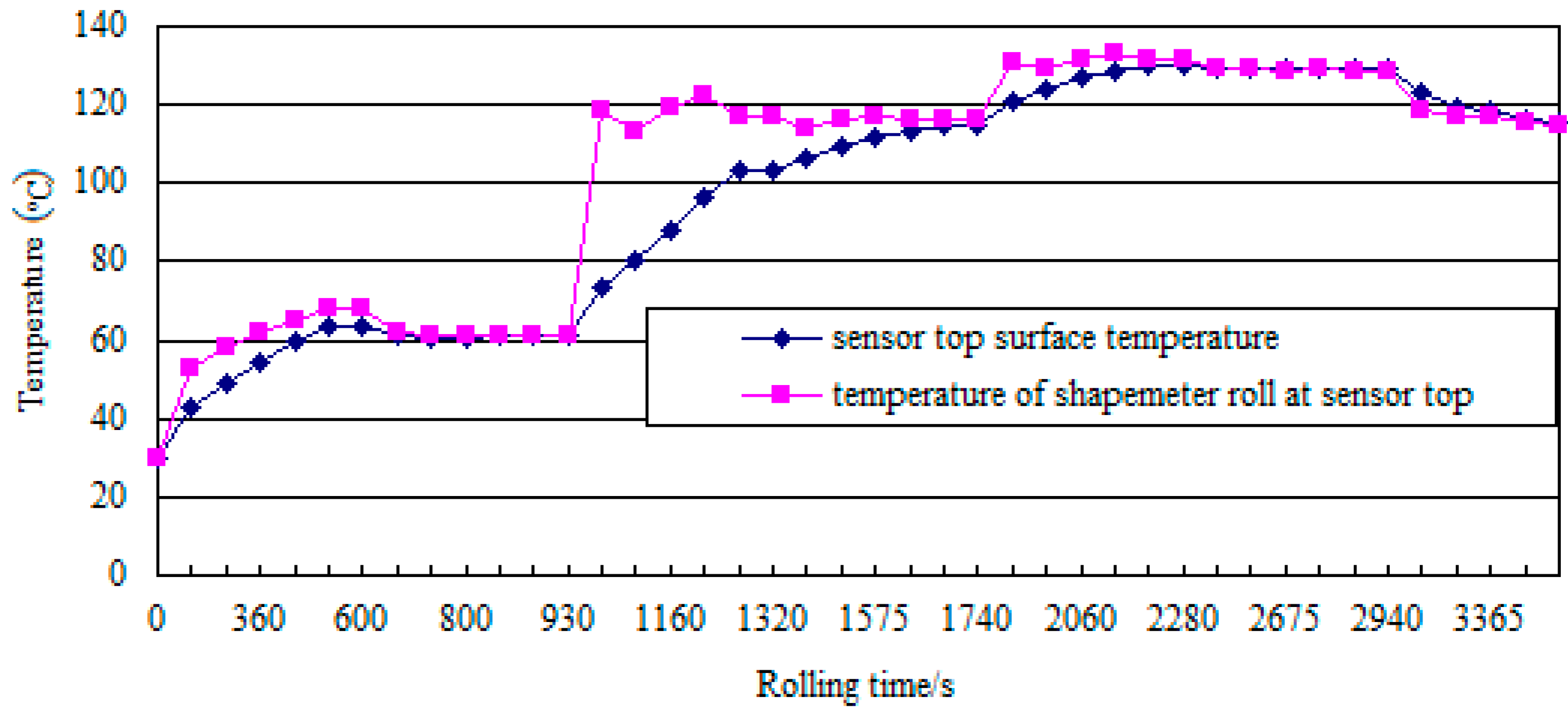
3.1. The Transient of Interference at the Sensor Top Surface
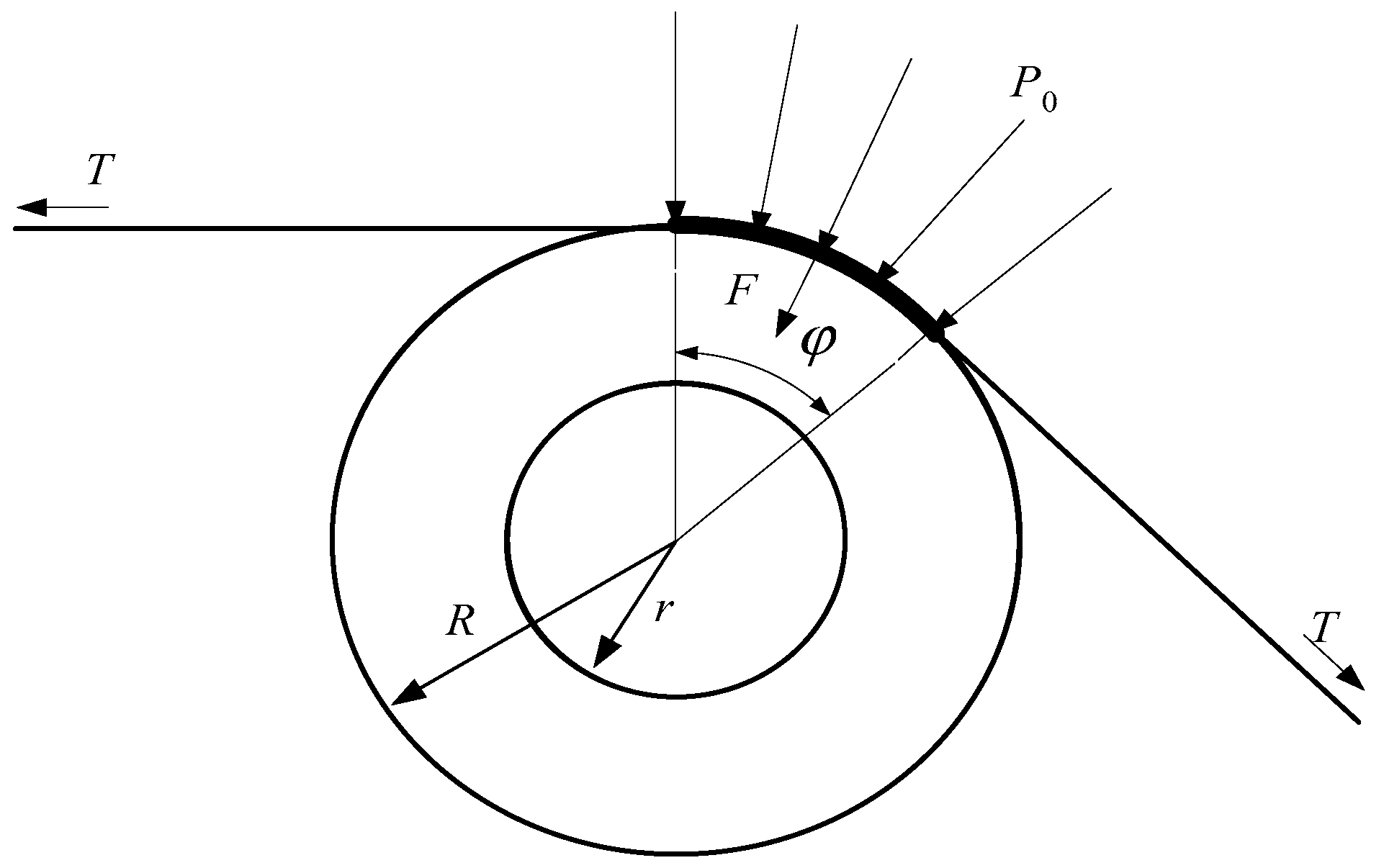
3.2. The Distance between the Sensor Top Surface and the Roll Outer Surface
4. Sensor Reliability Evaluation Model
4.1. Rolling Parameters
4.2. Limit State Function of Sensor Reliability
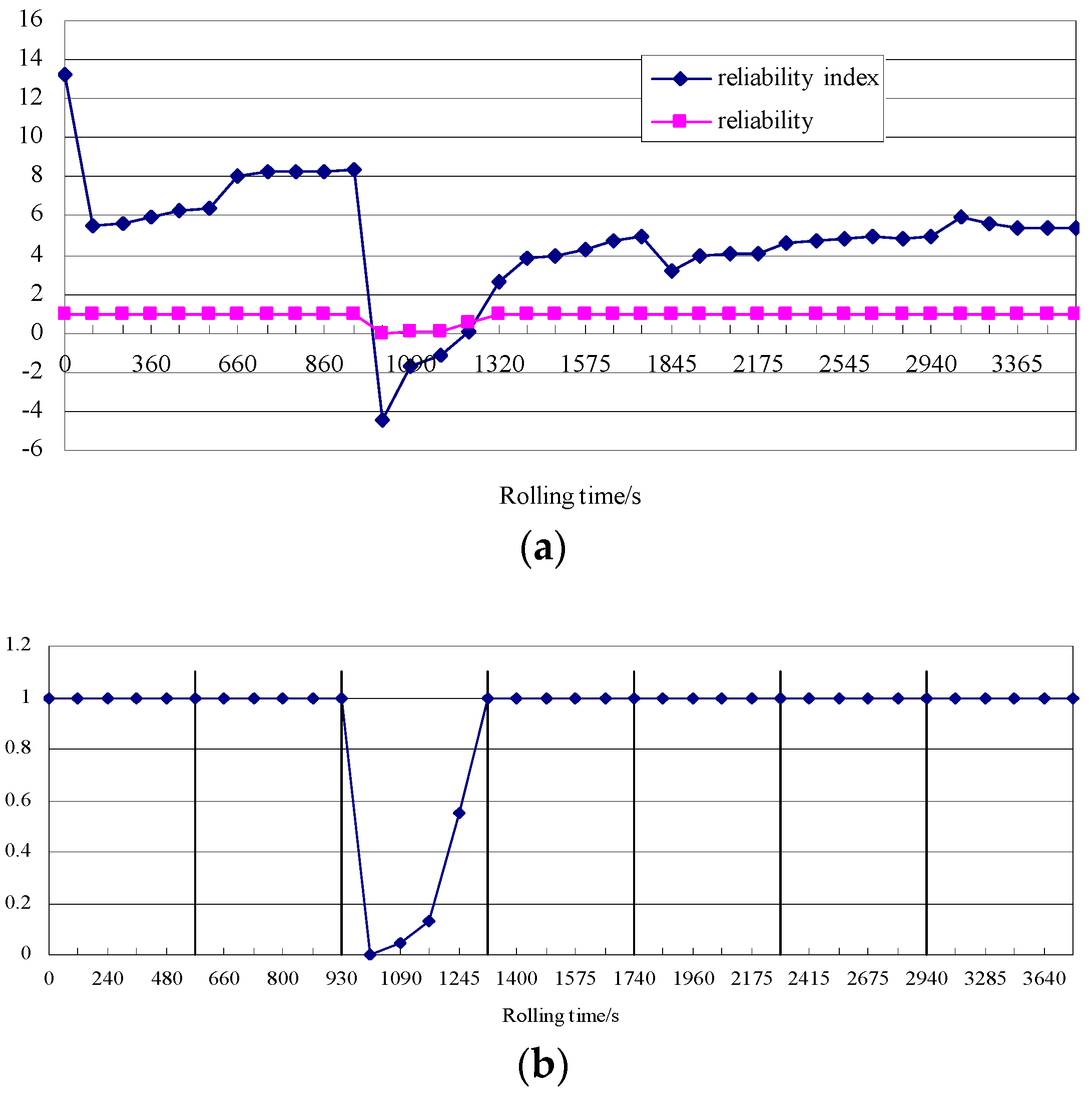
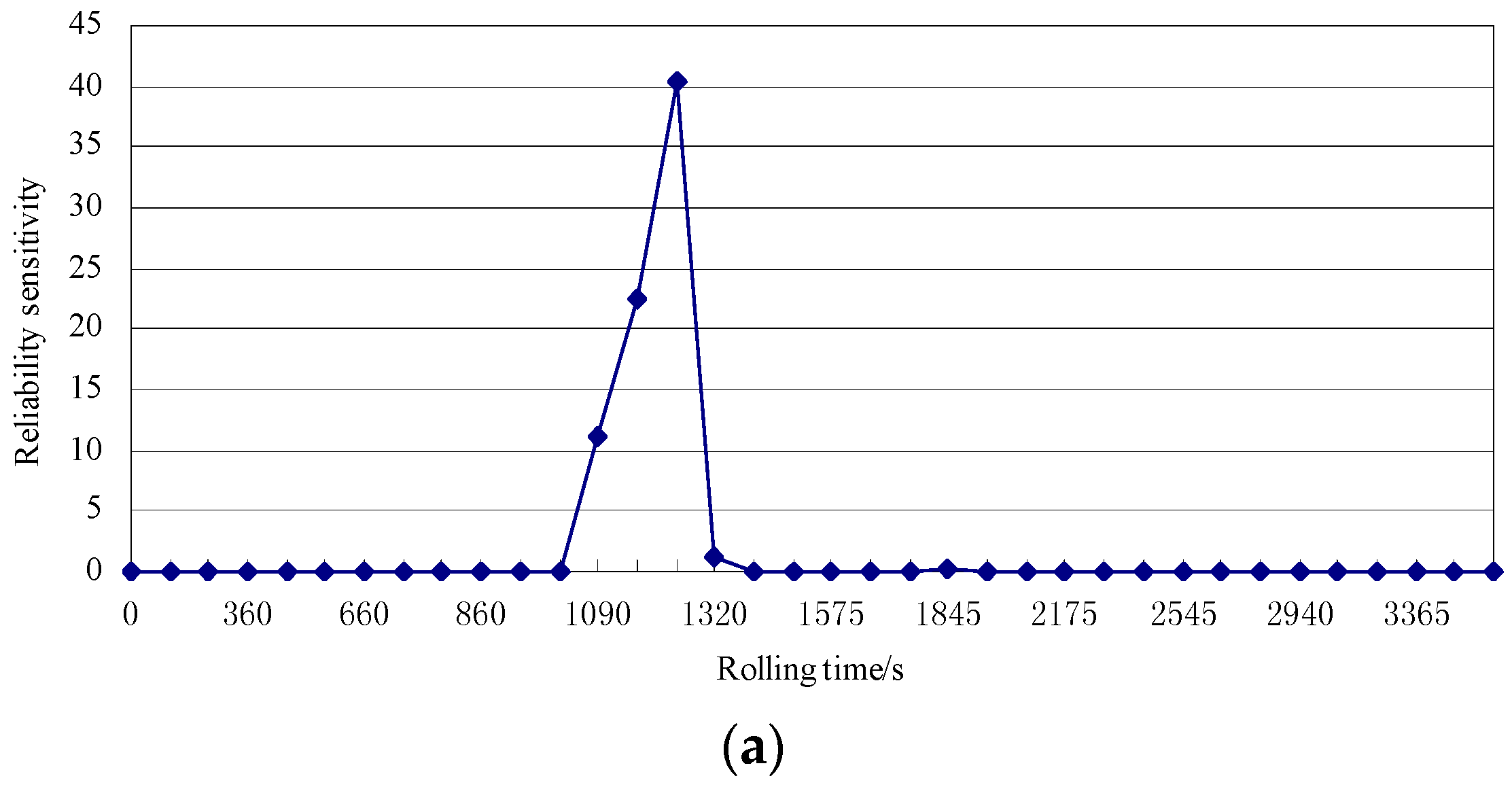
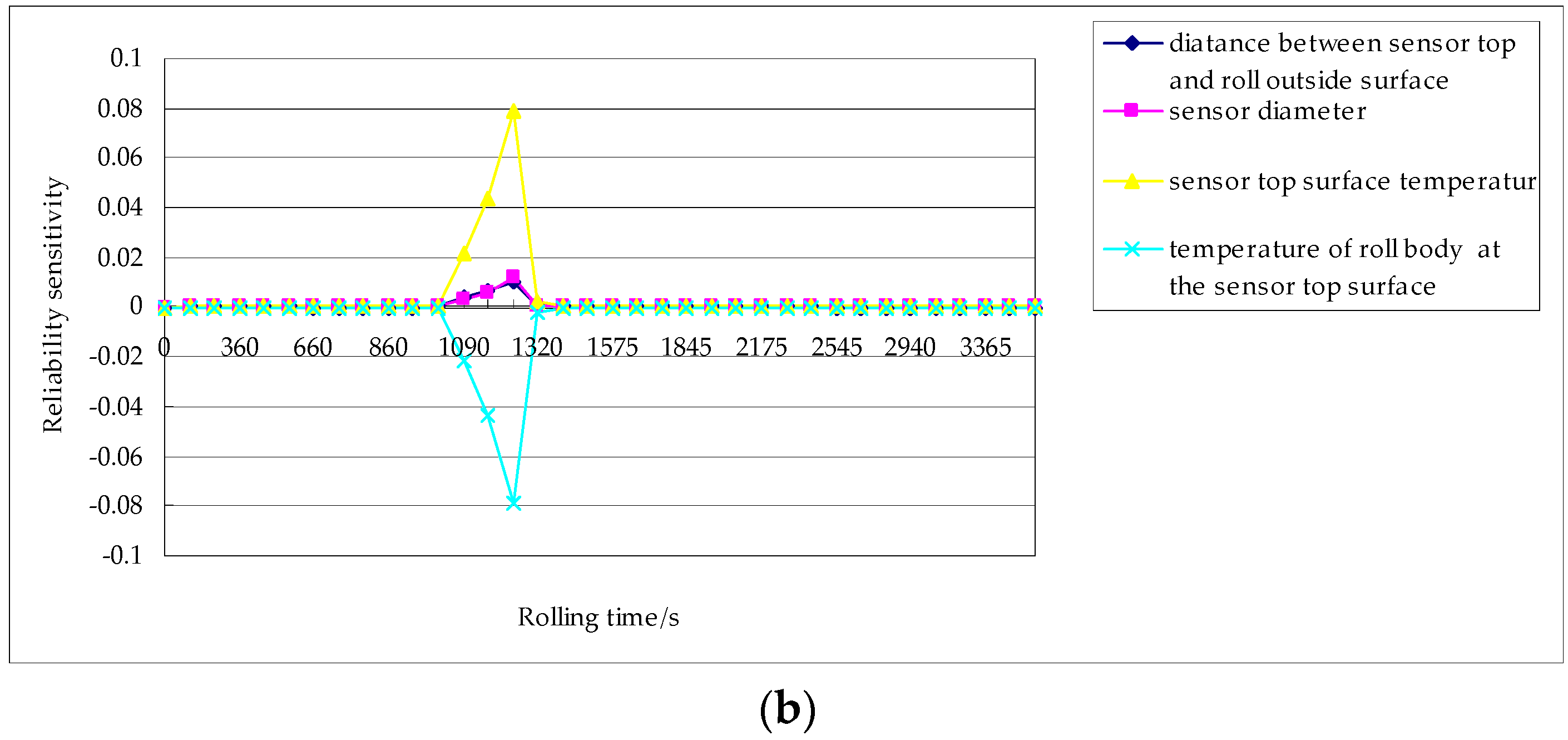
4.3. Result Analysis and Discussion
5. Reliability Robust Design Model of the Sensor
5.1. Mathematical Model of the Reliability Robust Design of the Sensor
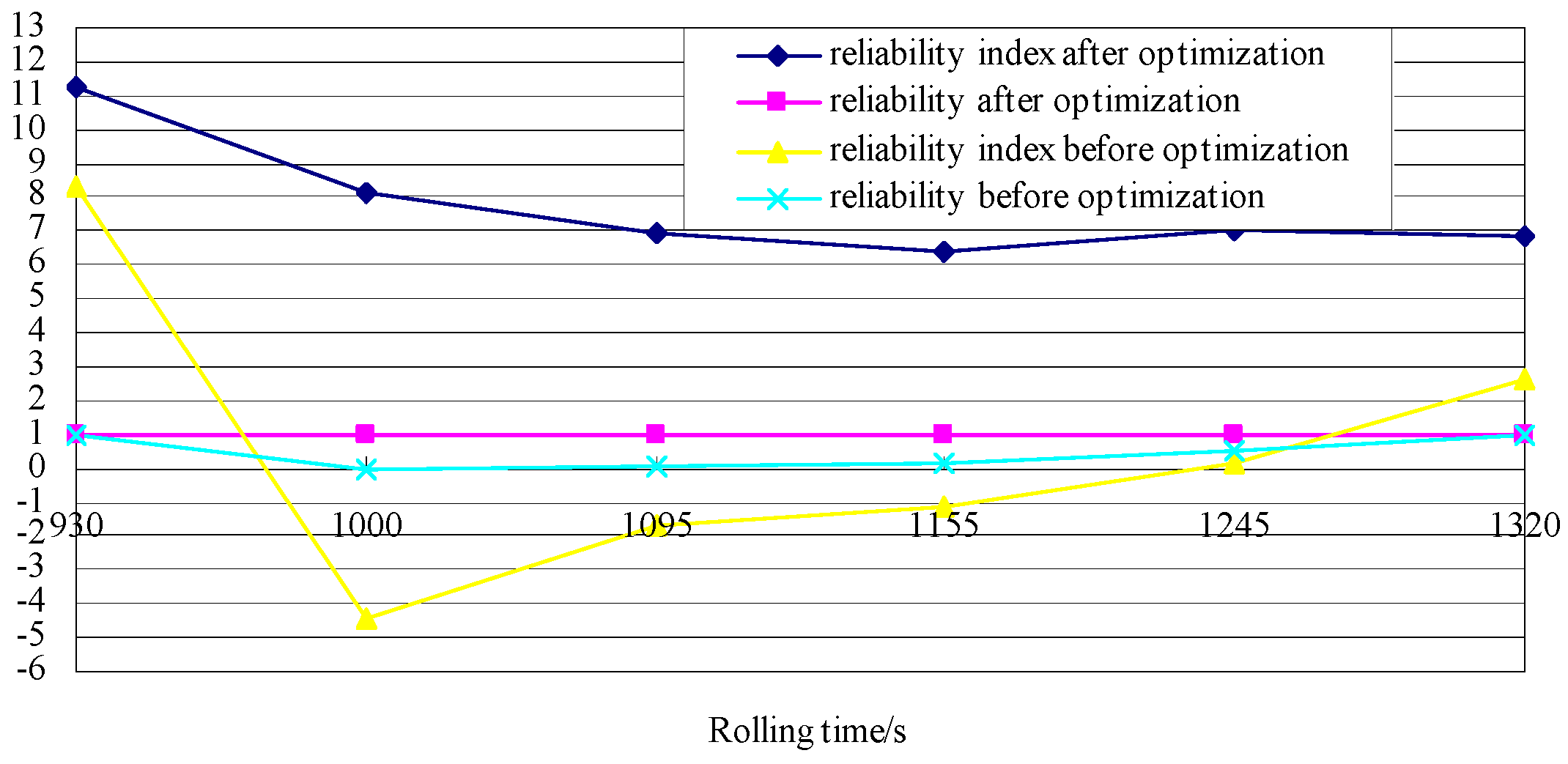
5.2. Analysis of the Optimal Result
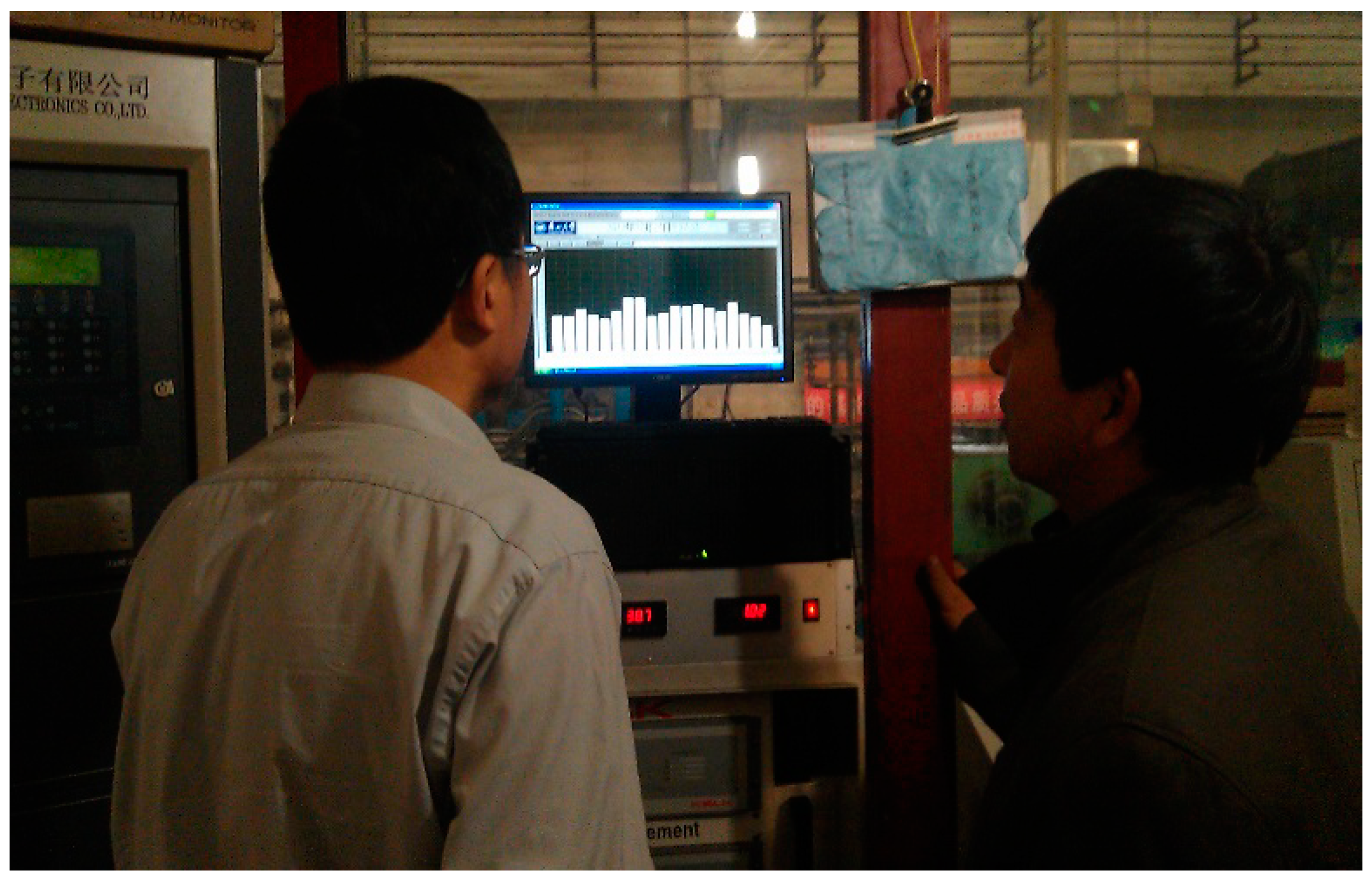
6. Test Verification
6.1. Manufacture and Installation of the Shapemeter Roll
6.2. Test Process
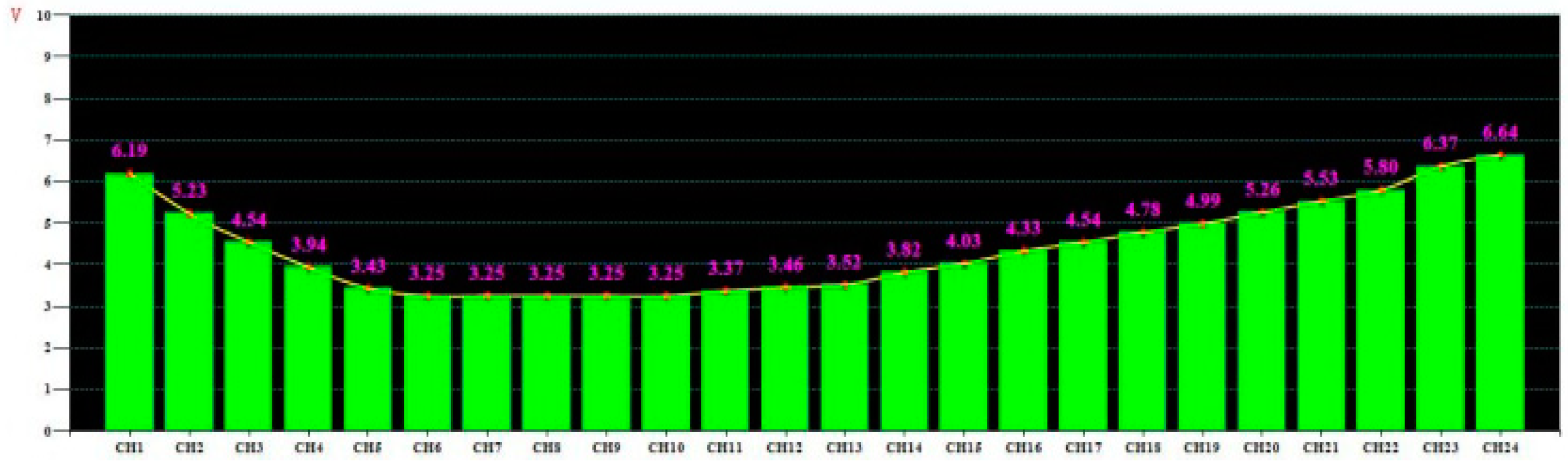
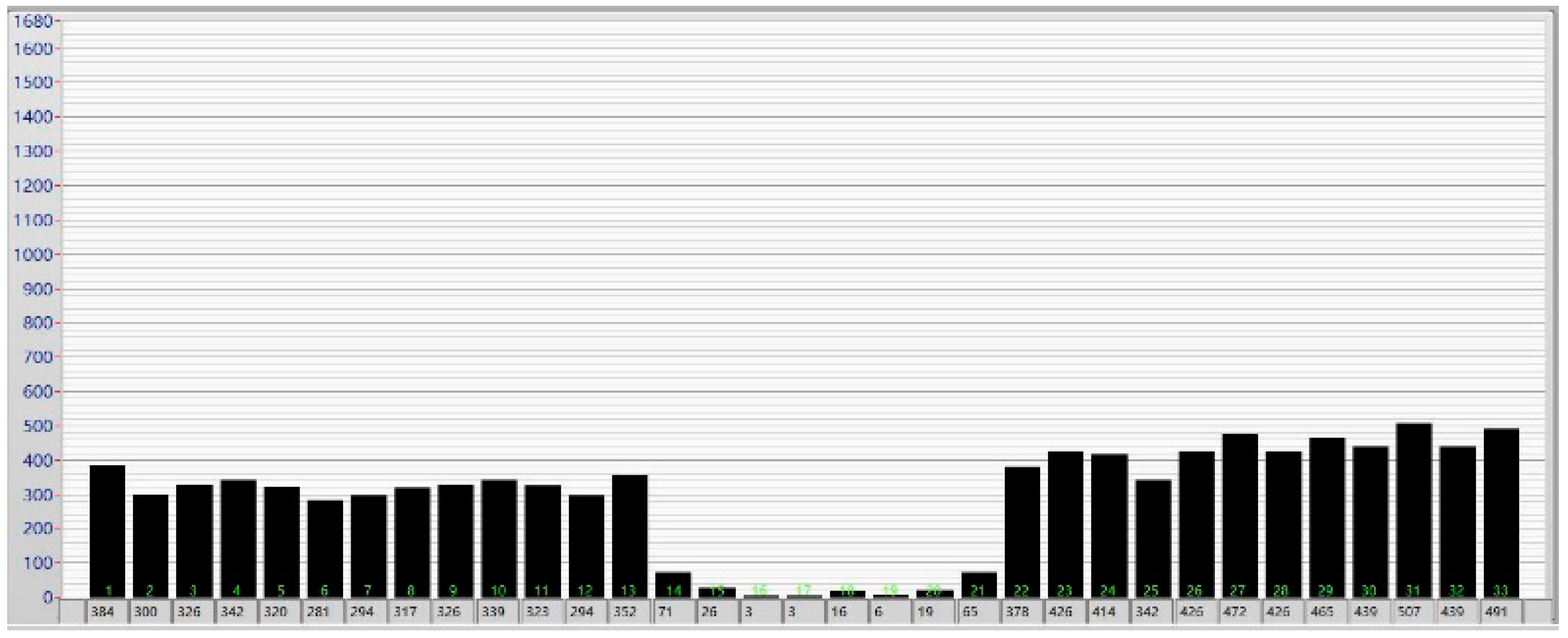
6.3. Test Result Analysis
7. Conclusions
- An interference of the sensor top surface is established based on the temperature change and the large tensile force of the strip in the working process. To ensure that the work pressure of the sensor lies within the linear range of the sensor characteristic curve, the distance between the sensor top surface and the roll outer surface is formulated, and the optimum value is obtained.
- Interference fit surface contact is ensured, by establishing a reliability evaluation model of the sensor. Considering the randomness of design variables, the reliability index and reliability of the sensor are evaluated via the random perturbation method. The reliability sensitivity of the design variables is also determined. The minimum value of the reliability (i.e., approximately zero) occurs in the third rolling pass, and the reliability is almost one in the other rolling passes. Moreover, the maximum reliability sensitivity is realized at the initial interference. Compared with the initial interference, the other design variables exhibit smaller reliability sensitivity, and hence, the (initial) interference is selected for reliability robust optimal design.
- A reliability robust optimal design model of initial interference is developed, based on constraints that the total pressure and reliability of the sensor must meet the allowable pressure and allowable reliability, respectively. The optimization results reveal a sensor reliability of approximately one for each rolling pass and that the sensor can work normally, at an initial interference of 0.06 mm.
- A new shapemeter roll, with an initial interference value of 0.06 mm, is fabricated and tested in a 1050 reversible cold rolling mill. The test results revealed that the sensor could work normally and the shape detection signal was continuous and complete in each rolling pass. More importantly, the intermittence of the shape detection signal was eliminated, further validating the correctness of the theoretical analysis performed in this work.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| z | The residual stress |
| Front tension stress | |
| Average front tension stress | |
| The total strip tension | |
| Residual pressure detected by the sensor | |
| Strip width | |
| Average value of the radial pressure detected by the sensors | |
| Strip thickness | |
| e | Width of special hole on the sensor top surface |
| R | Radius of the shapemeter roll |
| c | Contact width between the sensor top surface and the roll body |
| b | Axial length of the sensor |
| f | Distance between the sensor top surface and the roll outer surface |
| Sensor elastic modulus | |
| Shapemeter roll elastic modulus | |
| n | Number of sensors in the axial direction of the roll body |
| Poisson’s ratio of the roll body | |
| a | Sensor diameter |
| Temperature of the roll body at the top of the sensor in the rolling pass | |
| Temperature of the top surface of the sensor in the rolling pass | |
| Thermal expansion coefficient of the sensor | |
| Thermal expansion coefficient of the shapemeter roll | |
| Poisson's ratio of the sensor | |
| Initial interference at the top surface of the sensor | |
| The pressure that the strip applies to the sensor | |
| Initial pre-pressure of the sensor | |
| The maximum allowable pressure of the sensor | |
| The minimum allowable pressure of the sensor | |
| Xd | The definite part of the random variable |
| Xp | Random part of the random variable |
| ε | A small parameter |
| β | The reliability index |
| Re | The corresponding reliability |
| Φ | The standard normal distribution function |
| Thermal deformation difference between the contact surfaces | |
| Reliability sensitivity of the initial interference | |
| Weighting factor | |
| Optimal point of the single objective functions | |
| Optimal point of the single objective functions |
References
- Yu, B.; Liu, H.; Yang, L.; Peng, Y.; Li, Z. A new type of contact shape meter and its industry application. In Proceedings of the International Conference on Measuring Technology and Macaronis Automation (ICMTMA 2009), Zhangjiajie, China, 11–12 April 2009; Volume 4, pp. 1058–1061. [Google Scholar]
- Wu, H.; Liu, H. Influence of Cold-rolled Strip Temperature on the Interference Fit of Entire Roller Embedded Shapemeter Roll. J. Adv. Mater. Res. 2014, 941, 2293–2297. [Google Scholar] [CrossRef]
- Wu, H.; Liu, H.; Yu, B.; Yang, L. Influence of Cold Rolled Strip Temperature on Tnterference Fit Surfaces of Entire Roller Embedded Shapemeter Roll. Iron Steel 2016, 51, 55–59. [Google Scholar]
- Yang, L.; Yu, B.; Yu, H.; Du, C. Online Shape Dynamic Wrapping Angle Compensation Model of Cold Strip. J. Iron Steel Res. Int. 2011, 18, 28–32. [Google Scholar] [CrossRef]
- Yang, L.; Yu, B.; Yu, H.; Du, C. Quantitative Evaluation Method of Shape Indicator for Cold-rolled Strip. J. Iron Steel Res. Int. 2014, 21, 983–989. [Google Scholar] [CrossRef]
- Yang, L.; Yu, B.; Ding, D.; Liu, H. Industrial Shape Detecting System of Cold Rolling Strip. J. Cent. South Univ. 2012, 19, 994–1001. [Google Scholar] [CrossRef]
- Wu, H.; Liu, H.; Yu, B.; Yang, L. Transient Temperature Field and Stress Field Analysis of Entire Roller Embedded Shapemeter Roll. Iron Steel 2014, 49, 47–51. [Google Scholar]
- Wu, H.; Liu, H.; Yu, B.; Yang, L. Determination of the Value of Interference Fit on Entire Roller Embedded Shapemeter Roll. J. Cent. South Univ. 2014, 21, 4503–4508. [Google Scholar] [CrossRef]
- Wu, H.; Liu, H.; Wang, K. Thermal reliability research on entire roller-embedded shapemeter roll. Int. J. Adv. Manuf. Technol. 2018, 94, 3189–3198. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y. Reliability Design and Sensitivity Analysis of Cylindrical Worm Pairs. Mech. Mach. Theory 2014, 82, 218–230. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Z. Reliability-Based Sensitivity Analysis of Vehicle Components with Non-Normal Distribution Parameters. Int. J. Automot. Technol. 2009, 10, 181–194. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Li, H.; Lü, C. Dynamic Reliability Sensitivity of Cemented Carbide Cutting Tool. Chin. J. Mech. Eng. 2014, 27, 79–85. [Google Scholar] [CrossRef]
- Hu, Z.; Mahadevan, S.; Du, X. Uncertainty Quantification of Time-Dependent Reliability Analysis in the Presence of Parametric Uncertainty. J. Risk Uncertain. Eng. Syst. 2016, 2, 031005. [Google Scholar] [CrossRef]
- Zhang, J.; Du, X. Time-dependent Reliability Analysis for Function Generation Mechanisms with Random Joint Clearances. Mech. Mach. Theory 2015, 92, 184–199. [Google Scholar] [CrossRef]
- Chen, F.; Chen, S. Probabilistic Assessment of Vehicle Safety under Various Driving Conditions: A Reliability Approach. Procedia Soc. Behav. Sci. 2013, 96, 2414–2424. [Google Scholar] [CrossRef]
- Pommer, C.; Sinapius, M. Sensor Design Optimization for Ultrasonic Spectroscopy Cure Monitoring. Sensors 2018, 18. [Google Scholar] [CrossRef] [PubMed]
- Shao, S.; Liu, D.; Niu, Y.; O’Donnell, K.; Sengupta, D.; Park, S. A Study on the Thermo-mechanical Reliability Risks of Through-Silicon-Vias in Sensor Applications. Sensors 2017, 17, 322. [Google Scholar] [CrossRef] [PubMed]
- James, H. Heat Transfer Handbook; McGraw-Hill Education Press: New York, NY, USA, 1998; pp. 4–16. [Google Scholar]
- Volle, F.; Gradeck, M.; Maillet, D. Inverse Heat Conduction Applied to the Measurement of Heat Fluxes on a Rotating Cylinder: Comparison between an Analytical and a Numerical Technique. J. Heat Transf. 2008, 130, 081302. [Google Scholar] [CrossRef]
- Yiannopoulos, A.C.; Anifantis, N.K.; Dimarogonas, A.D. Thermal Stress Optimization in Metal Rolling. J. Therm. Stress. 2010, 40, 560–590. [Google Scholar] [CrossRef]
- Yang, X.W.; Zhu, J.C.; Lai, Z.H.; Yong, L.I.U.; Dong, H.E.; Nong, Z.S. Finite element analysis of quenching temperature field, residual stress and distortion in A357 aluminum alloy large complicated thin-wall workpieces. Trans. Nonferrous Met. Soc. China 2013, 23, 1751–1760. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Y. Reliability-based Robust Design of Cylindrical Gear Pairs with Non-normal Random Parameters. In Proceedings of the International Symposium on Reliability Engineering and Risk Management 2010 (ISRERM2010), Shanghai, China, 23–26 September 2010. [Google Scholar]


| Rolling Pass | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Export strip temperature (°C) | 87 | 127 | 130 | 146 | 135 | 151 | 115 |
| Reduction ratio (%) | 27.57 | 29.71 | 30.89 | 31.76 | 31.03 | 30.00 | 28.57 |
| Rolling time (s) | 0–600 | 600–930 | 930–1320 | 1320–1740 | 1740–2280 | 2280–2940 | 2940–3710 |
| Rolling speed (m·s−1) | 3 | 4.8 | 7.9 | 10 | 10.8 | 11.2 | 11.3 |
| Parameter | Thermal Conductivity (W·m−1·K−1) | Specific Heat Capacity (J·kg−1·K−1) | Density (kg·m−3) | Coefficient of Thermal Expansion (10−5 K−1) | Young’s Modulus (1011 Pa) | Poisson’s Ratio | Coefficient of Friction |
|---|---|---|---|---|---|---|---|
| Roll body | 50 | 480 | 7800 | 1.3 | 2 | 0.3 | 0.2 |
| Sensor | 50 | 480 | 7800 | 1.3 | 2 | 0.3 | 0.2 |
| Rolling Pass | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Temperature of the strip in contact with the shapemeter roll (°C) | 87 | 62 | 130 | 120 | 135 | 125 | 115 |
| Shapemeter roll outer surface temperature at the end of each rolling pass (°C) | 71 | 62 | 122 | 120 | 135 | 130 | 115 |
| Rolling Pass | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Equivalent heat transfer coefficient of the roll outer surface (10−6 W·m−2·K−1) | 350 | 350 | 1667 | 1500 | 1700 | 1500 | 1400 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Cui, G.; Zhang, D.; Liu, H. Reliability Evaluation and Robust Design of a Sensor in an Entire Roller-Embedded Shapemeter. Sensors 2018, 18, 1988. https://doi.org/10.3390/s18071988
Wu H, Cui G, Zhang D, Liu H. Reliability Evaluation and Robust Design of a Sensor in an Entire Roller-Embedded Shapemeter. Sensors. 2018; 18(7):1988. https://doi.org/10.3390/s18071988
Chicago/Turabian StyleWu, Haimiao, Guohua Cui, Dan Zhang, and Hongmin Liu. 2018. "Reliability Evaluation and Robust Design of a Sensor in an Entire Roller-Embedded Shapemeter" Sensors 18, no. 7: 1988. https://doi.org/10.3390/s18071988
APA StyleWu, H., Cui, G., Zhang, D., & Liu, H. (2018). Reliability Evaluation and Robust Design of a Sensor in an Entire Roller-Embedded Shapemeter. Sensors, 18(7), 1988. https://doi.org/10.3390/s18071988





