GNSS Code Multipath Mitigation by Cascading Measurement Monitoring Techniques
Abstract
1. Introduction
2. Background on Weighted Least-Squares Adjustment and Dilution of Precision (DOP)
2.1. Weighted Least-Squares Adjustment for a Pseudorange-Based Positioning
2.2. Measurement Geometry and DOP
3. Measurement Monitoring Techniques for Multipath Mitigation
3.1. Multipath Error Estimation and Measurement Correction
- Code-Minus-Carrier (CMC) for multipath estimation and correction
3.2. Stochastic Model of Measurements and Weighting Approach
- Carrier-to-Noise-density ratio (C/N0) metric for stochastic modeling
3.3. Multipath Detection for Excluding or De-Weighing Affected Measurements
- C/N0 as a single-frequency monitoring metric for detection
- Differential C/N0 (DC/N0)-based monitoring metric for detection
- Geometry-free (GF) monitoring metric for detection
4. Detection, Exclusion and De-Weighting Strategies
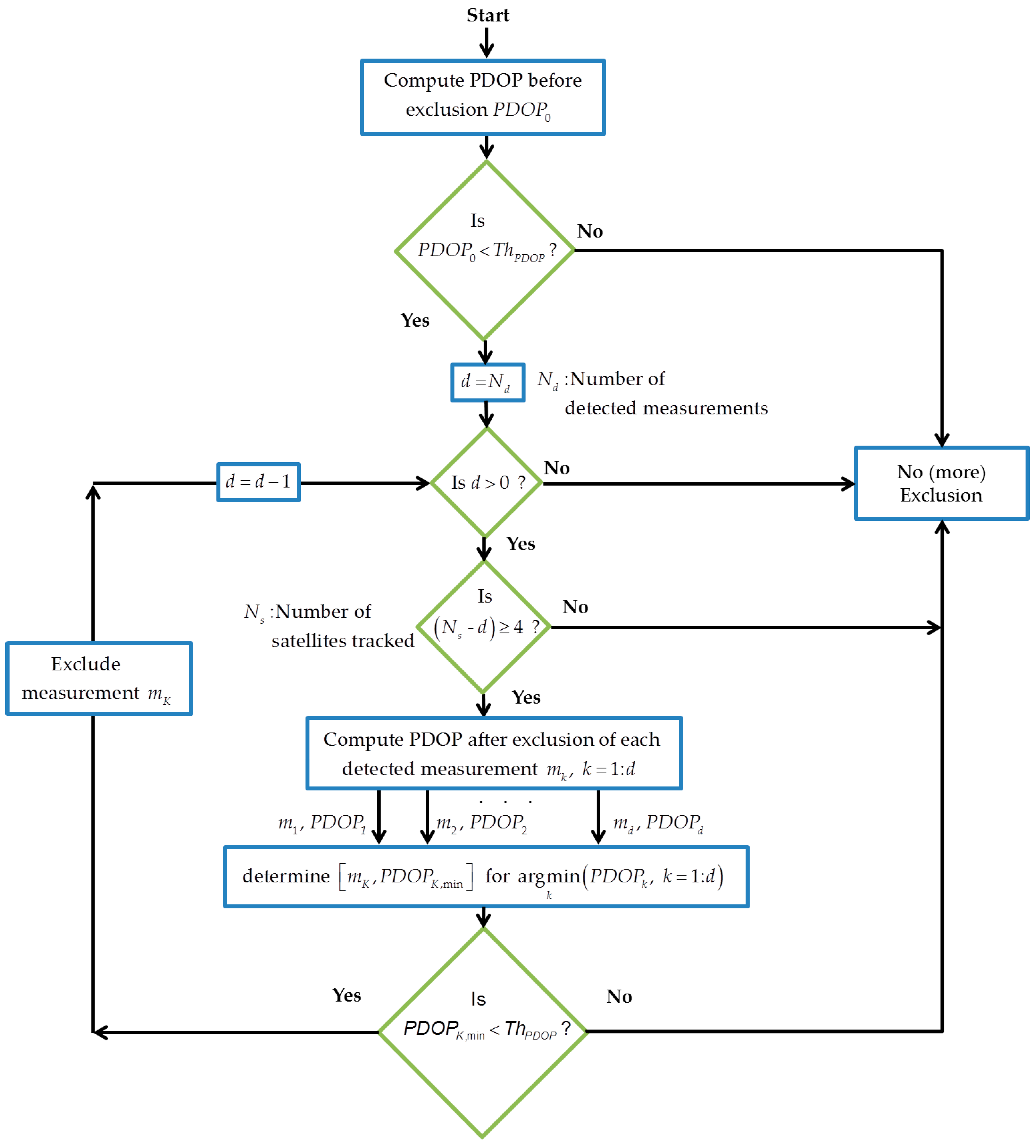
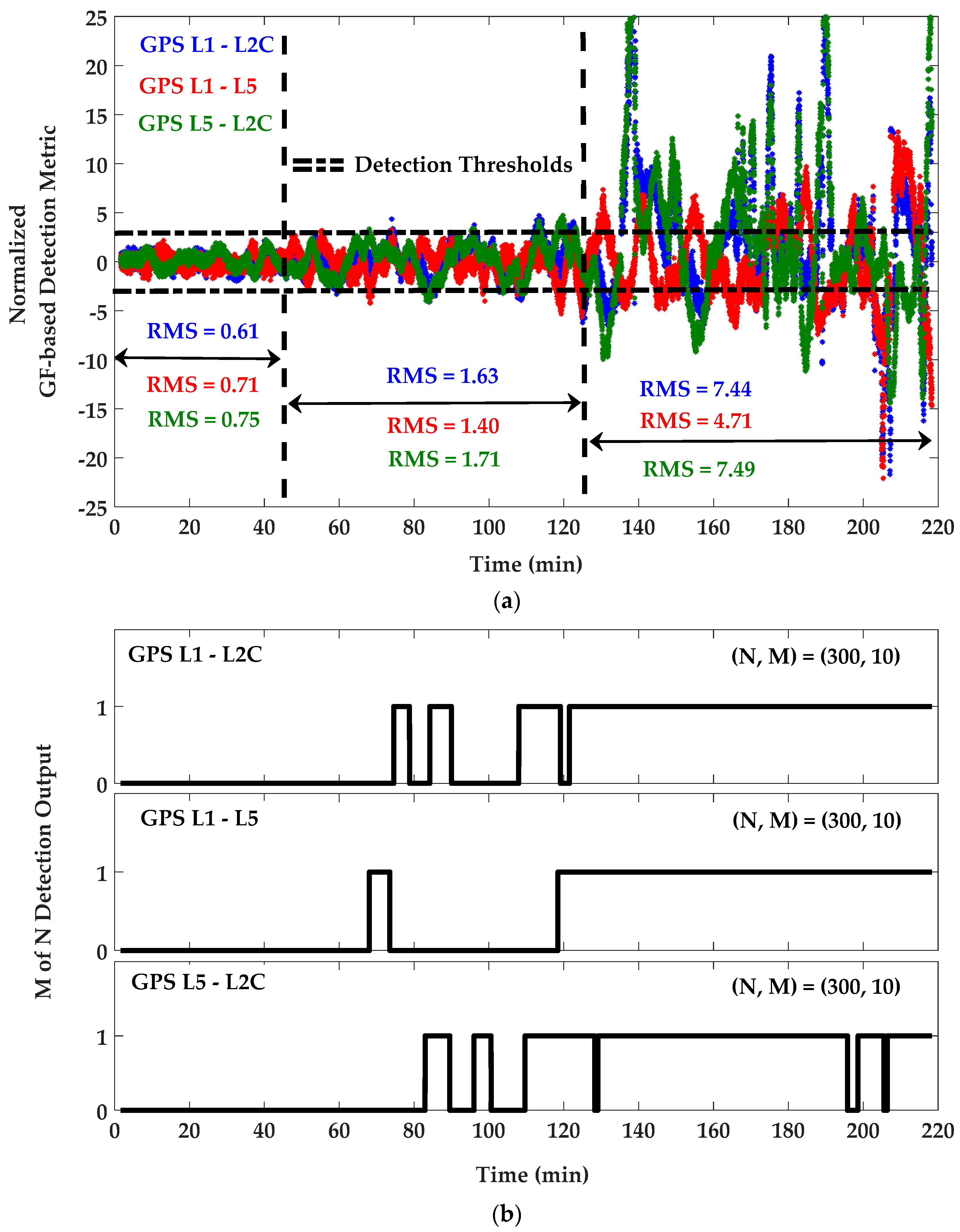
4.1. Detection Strategy
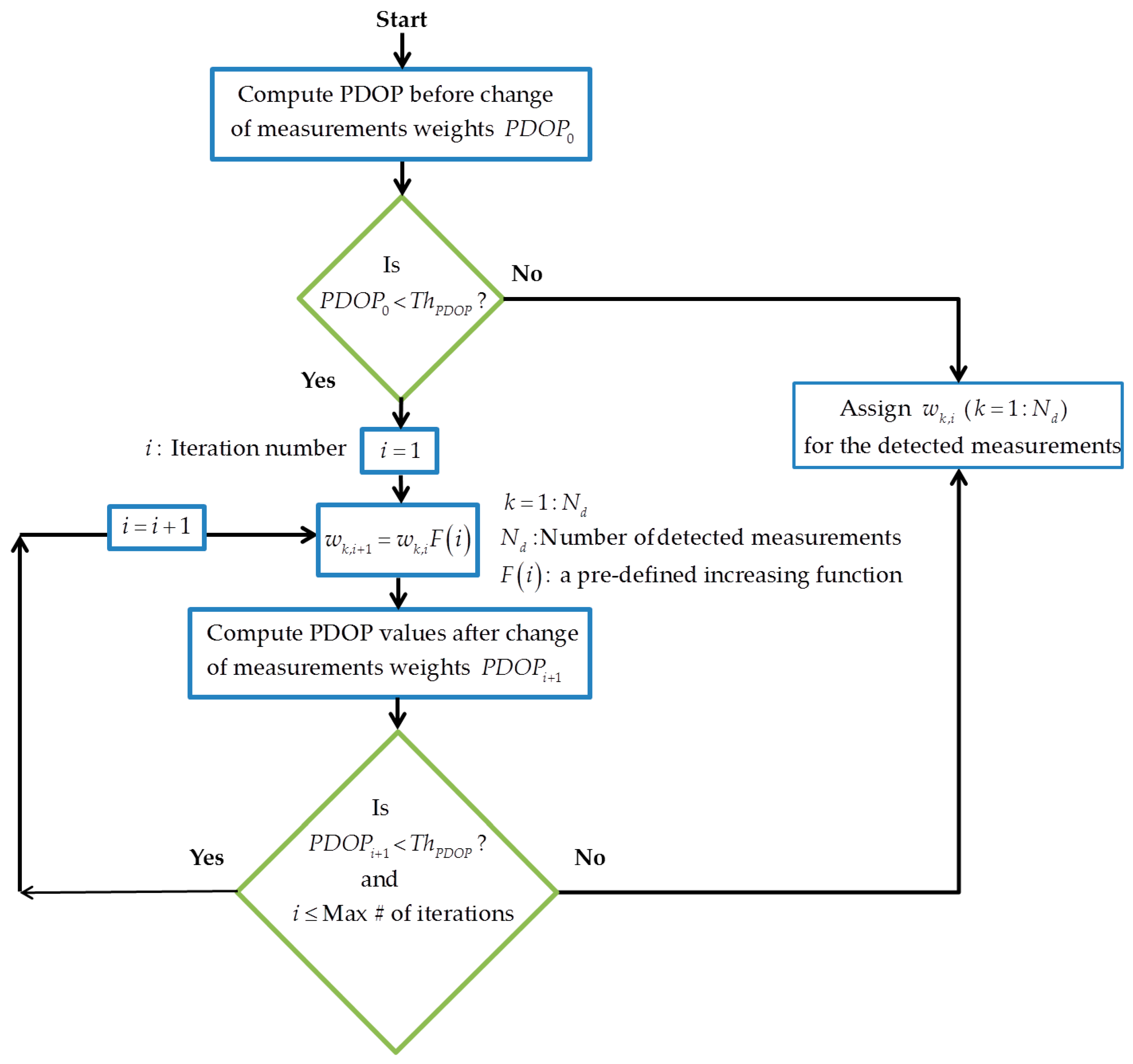
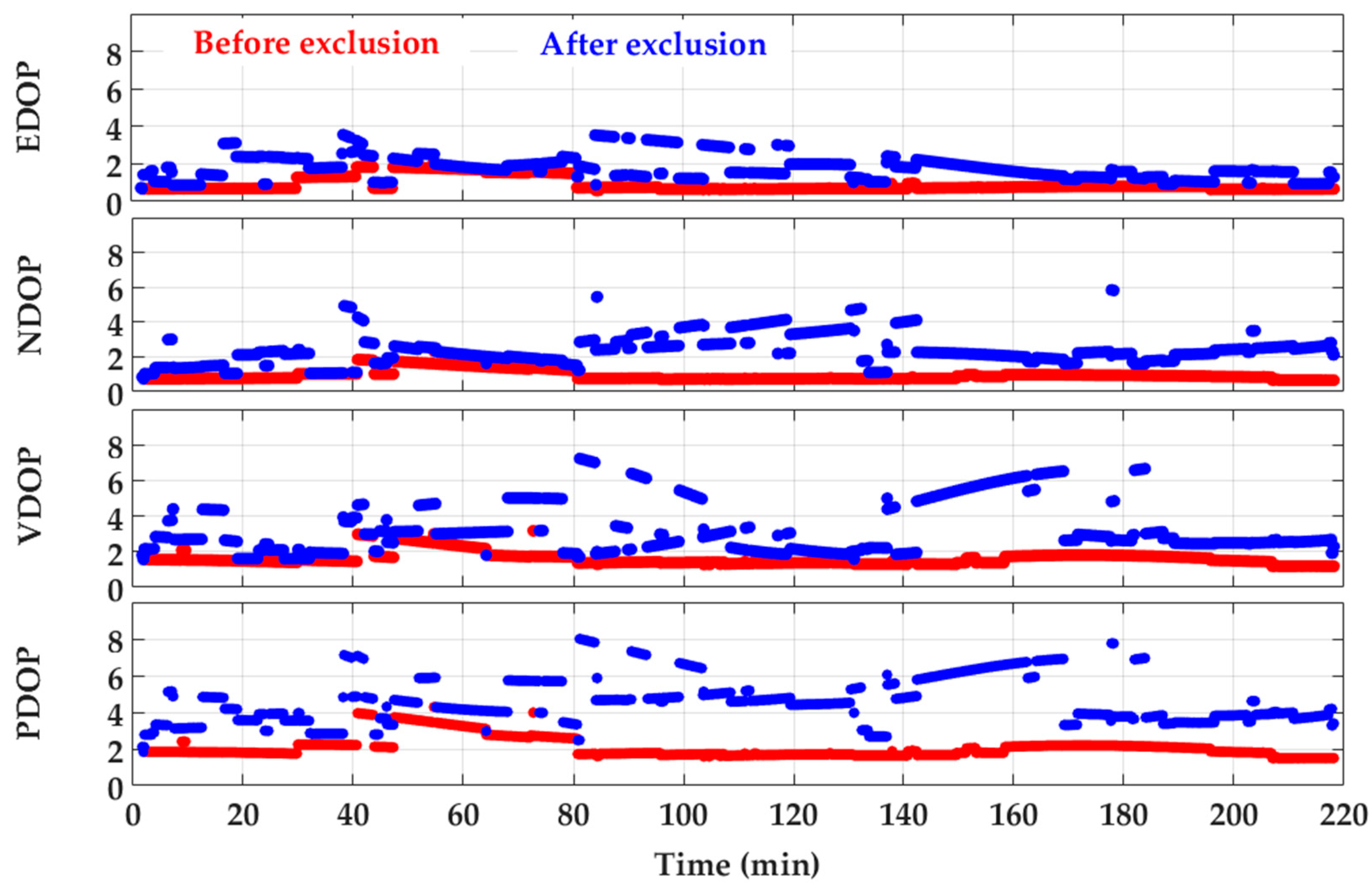
4.2. Exclusion and De-Weighting of Affected Measurements
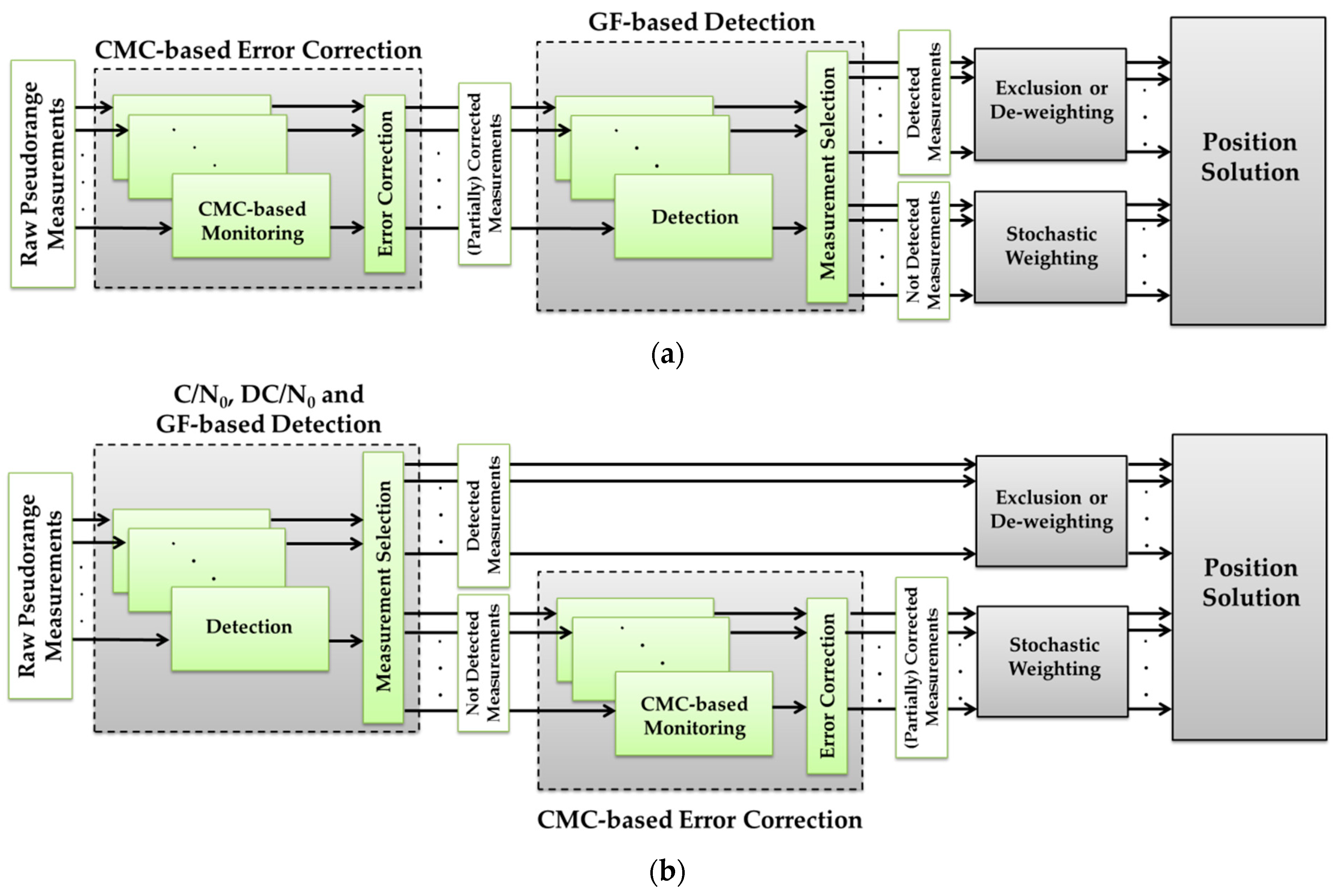
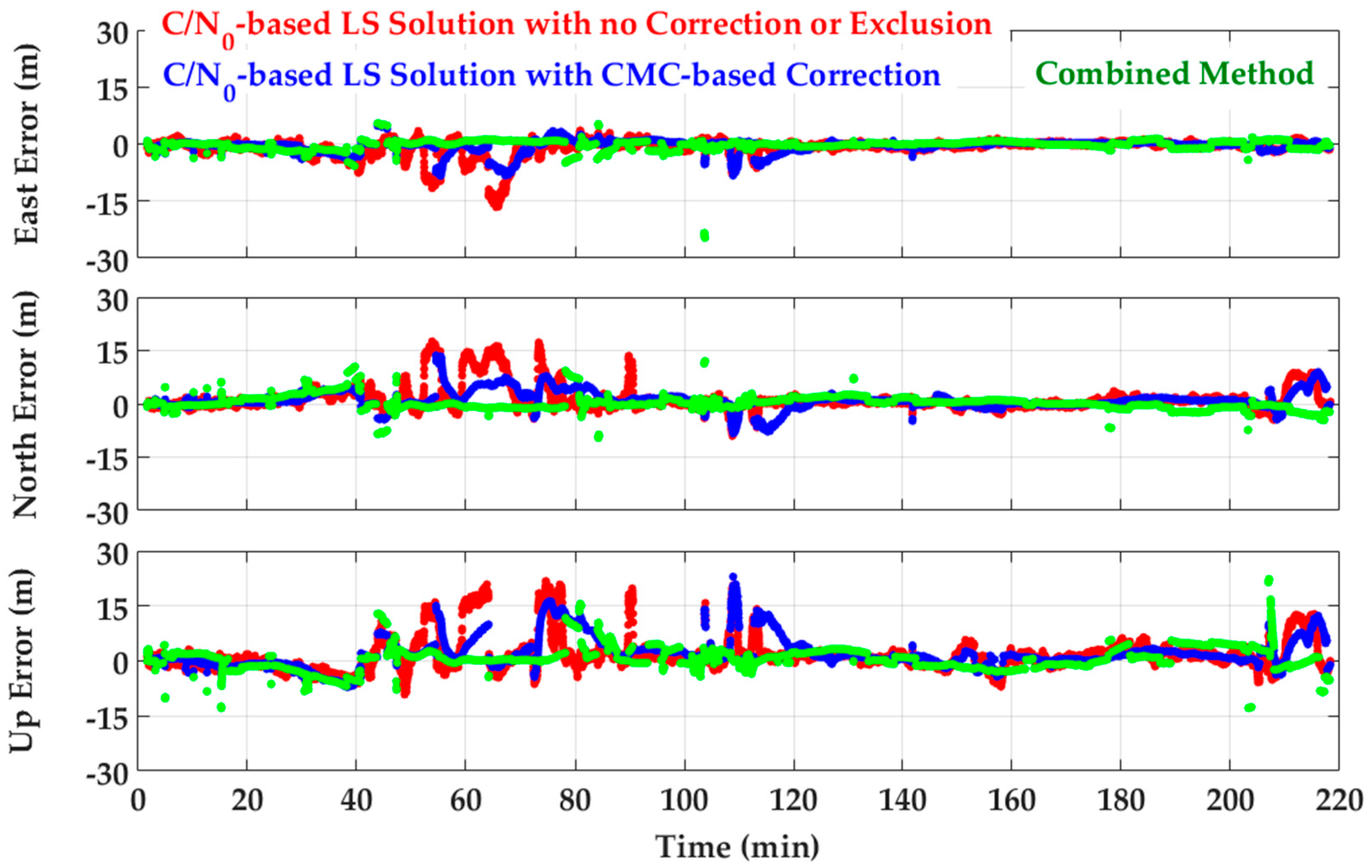
5. Combination of Monitoring Techniques for a Reliable Multipath Mitigation
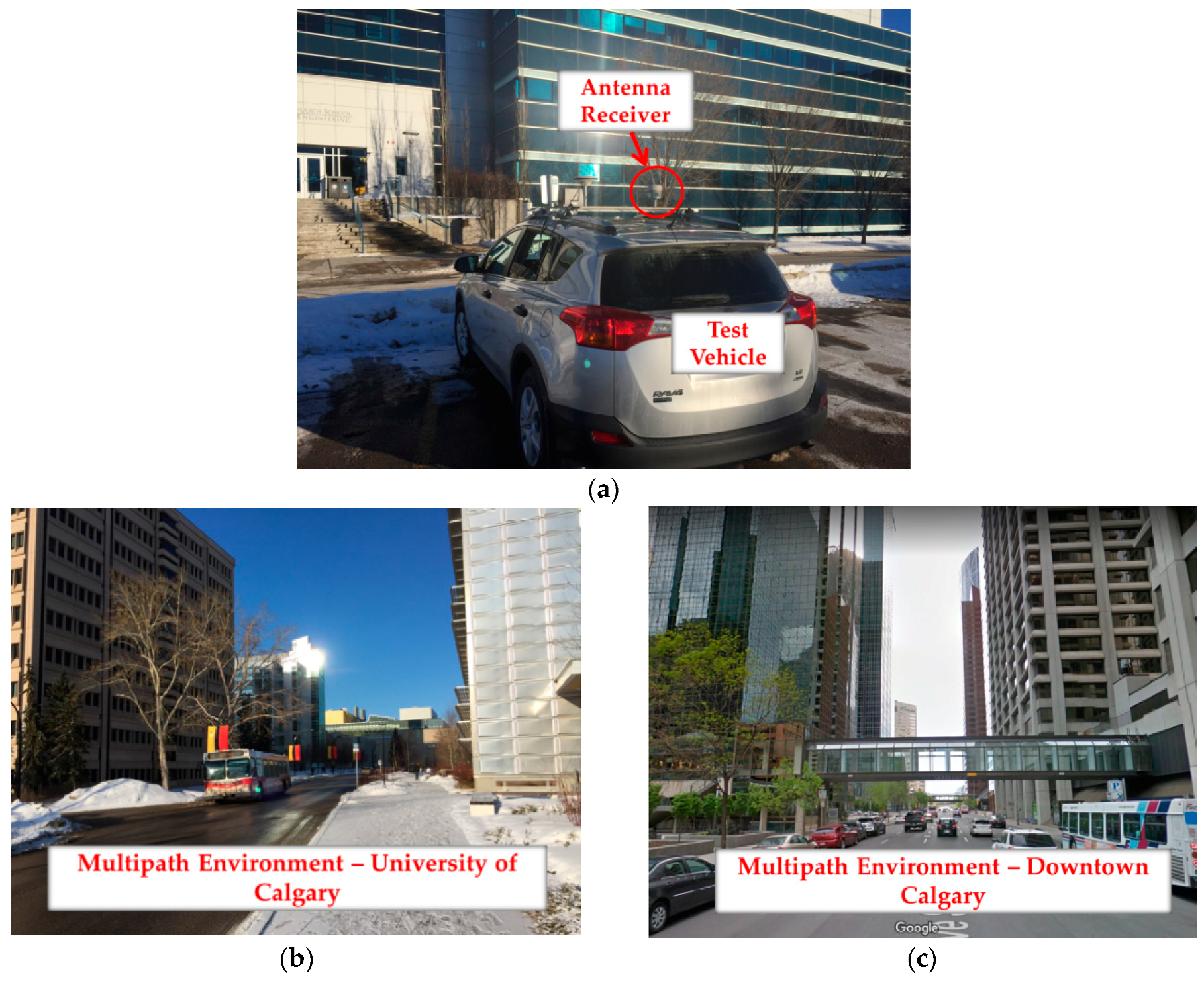
6. Field Data Analysis
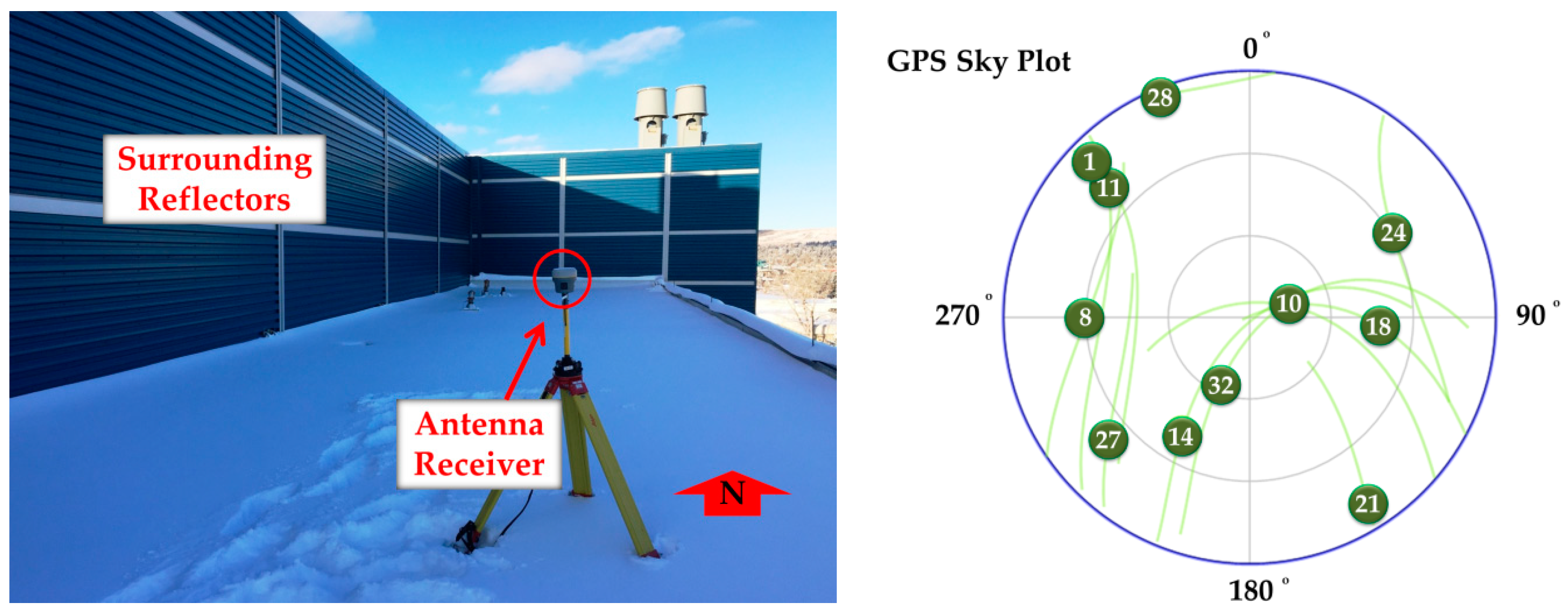
6.1. Static Test
6.1.1. Monitoring Results
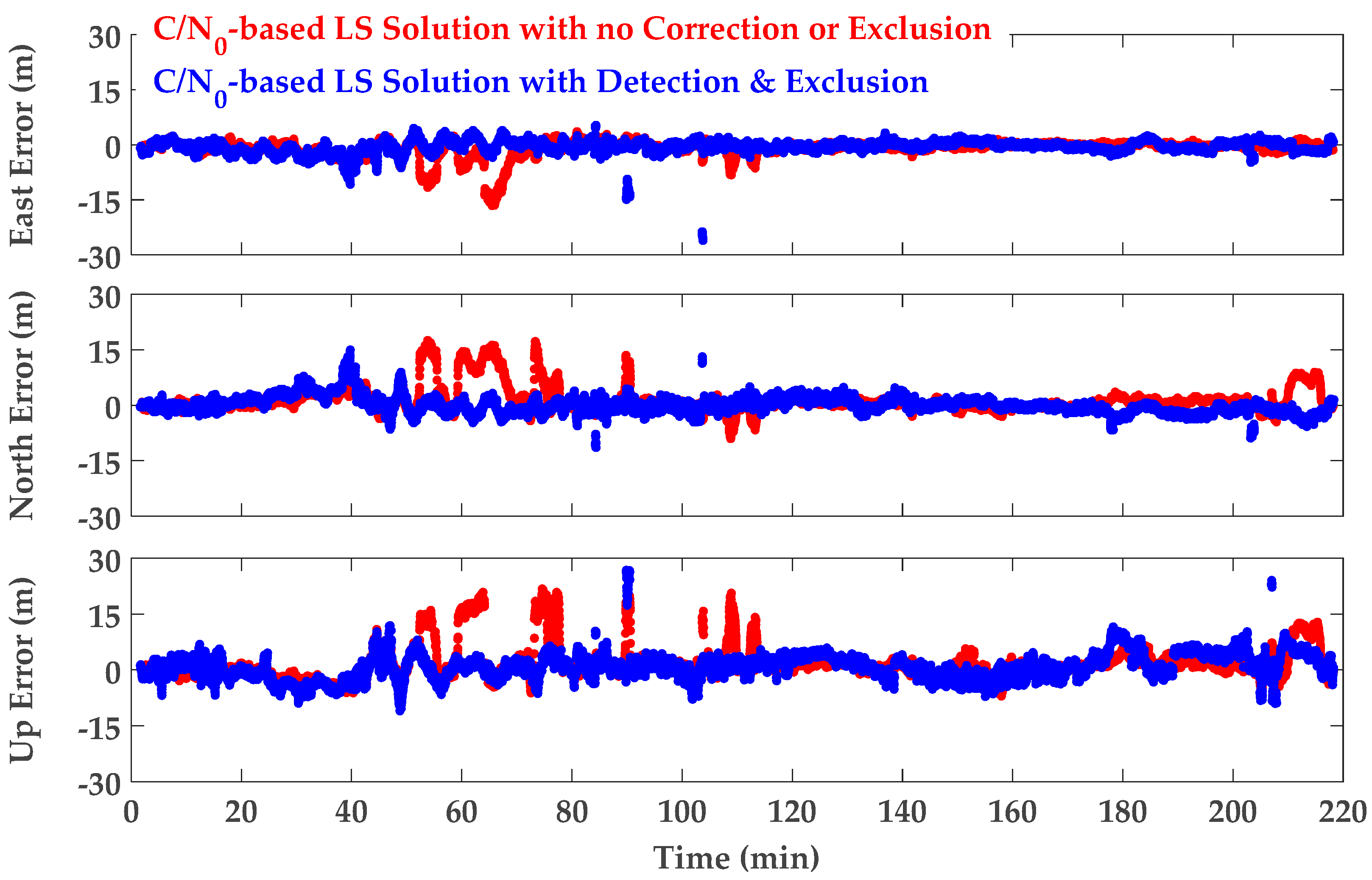
6.1.2. Position Results
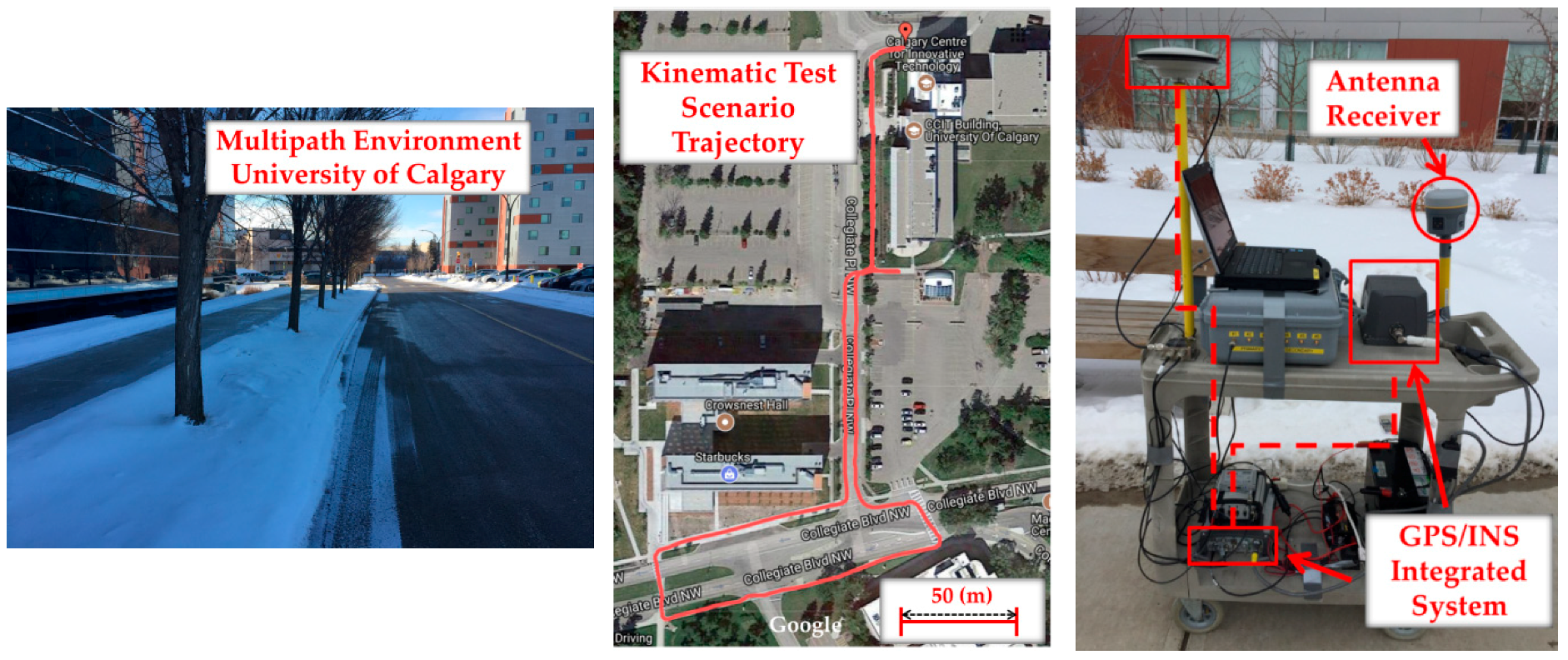
6.2. Pedestrian Kinematic Test
6.3. Land Vehicle Test
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Simple and Cumulative Moving Average
Appendix B: CMC-Based Error Correction as Carrier-Smoothing of Code Pseudoranges
References
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS Principles and Applications, 2nd ed.; Artch House: Norwood, MA, USA, 2006; ISBN 158-053-894-890. [Google Scholar]
- Bhuiyan, M.Z.H.; Lohan, E.S. Multipath Mitigation Techniques for Satellite-Based Positioning Applications. In Global Navigation Satellite Systems: Signal, Theory and Applications; Jin, S., Ed.; InTech: Rijeka, Croatia, 2012; pp. 405–426. [Google Scholar]
- Jafarnia-Jahromi, A.; Broumandan, A.; Nielsen, J.; Lachapelle, G. Pre-Despreading authenticity verification for GPS L1 C/A signals. Navigation 2014, 61, 1–11. [Google Scholar] [CrossRef]
- Joerger, M.; Pervan, B. Fault detection and exclusion using solution separation and chi–squared ARAIM. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 726–742. [Google Scholar] [CrossRef]
- Berardo, M.; Lo Presti, L. On the use of a signal quality index applying at tracking stage level to assist the RAIM system of a GNSS receiver. Sensors 2016, 16, 1029. [Google Scholar] [CrossRef] [PubMed]
- Pirsiavash, A.; Broumandan, A.; Lachapelle, G. Characterization of signal quality monitoring techniques for multipath detection in GNSS applications. Sensors 2017, 17, 1579. [Google Scholar] [CrossRef] [PubMed]
- Braasch, M.S. Isolation of GPS multipath and receiver tracking errors. J. Inst. Navig. 1994, 41, 415–435. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2006. [Google Scholar]
- Jiang, Y.; Milner, C.; Macabiau, C. Code carrier divergence monitoring for dual-frequency GBAS. GPS Solut. 2017, 21, 769–781. [Google Scholar] [CrossRef]
- Hilla, S.; Cline, M. Evaluating pseudorange multipath effects at stations in the national CORS network. GPS Solut. 2004, 7, 253–267. [Google Scholar] [CrossRef]
- Beitler, A.; Tollkuhn, A.; Giustiniano, D.; Plattner, B. CMCD: Multipath Detection for Mobile GNSS Receivers. In Proceedings of the International Technical Meeting of The Institute of Navigation, Dana Point, CA, USA, 26–28 January 2015; pp. 455–464. [Google Scholar]
- Kim, D.; Langley, R.B. The Multipath Divergence Problem in GPS Carrier-Smoothed Code Pseudorange. In Proceedings of the 47th Annual Conference of the Canadian Aeronautics and Space Institute, Ottawa, ON, Canada, 30 April–3 May 2000; pp. 161–163. [Google Scholar]
- Petovello, M.; Lo Presti, L.; Visintin, M. Can you list all the properties of the carrier-smoothing filter? Inside GNSS 2015, 10, 32–37. [Google Scholar]
- Ugazio, S.; Visintin, M. Optimizing Carrier Smoothing Parameters Considering a Cycle Slip Probabilistic Model. In Proceedings of the 2016 IEEE Metrology for Aerospace (MetroAeroSpace), Florence, Italy, 22–23 June 2016; pp. 473–478. [Google Scholar]
- Luo, X. Observation Weighting Using Signal Quality Measures. In GPS Stochastic Modelling: Signal Quality Measures and ARMA Processes; Springer Theses; Springer: Berlin/Heidelberg, Germany, 2013; pp. 137–162. [Google Scholar]
- Dach, R.; Hugentobler, U.; Fridez, P.; Meindl, M. Bernese GPS Software Version 5.0; Astronomical Institute, University of Bern: Bern, Switzerland, 2007. [Google Scholar]
- Hartinger, H.; Brunner, F.K. Variances of GPS phase observations: The SIGMA–ɛ model. GPS Solut. 1999, 2, 35–43. [Google Scholar] [CrossRef]
- Brunner, F.K.; Hartinger, H.; Troyer, L. GPS signal diffraction modelling: The stochastic SIGMA–Δ model. J. Geodesy 1999, 73, 259–267. [Google Scholar] [CrossRef]
- Wieser, A.; Brunner, F.K. An extended weight model for GPS phase observations. Earth Planets Space 2000, 52, 777–782. [Google Scholar] [CrossRef]
- Kuusniemi, H.; Wieser, A.; Lachapelle, G.; Takala, J. User-level reliability monitoring in urban personal satellite-navigation. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1305–1318. [Google Scholar] [CrossRef]
- Kuusniemi, H. User-Level Reliability and Quality Monitoring in Satellite-Based Personal Navigation. Ph.D. Thesis, Tampere University of Technology, Tampere, Finland, 2005. [Google Scholar]
- Wieser, A.; Gaggl, M.; Hartinger, H. Improved Positioning Accuracy with High Sensitivity GNSS Receivers and SNR Aided Integrity Monitoring of Pseudo-Range Observations. In Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005; pp. 1545–1554. [Google Scholar]
- Groves, P.D.; Jiang, Z. Height aiding, C/N0 weighting and consistency checking for GNSS NLOS and multipath mitigation in urban areas. J. Navig. 2013, 66, 653–669. [Google Scholar] [CrossRef]
- Pirsiavash, A.; Broumandan, A.; Lachapelle, G. Performance Evaluation of Signal Quality Monitoring Techniques for GNSS Multipath Detection and Mitigation. In Proceedings of the International Technical Symposium on Navigation and Timing (ITSNT), ENAC, Toulouse, France, 14–17 November 2017; 10p. [Google Scholar]
- Hsu, L.T.; Gu, Y.; Kamijo, S. NLOS correction/exclusion for GNSS measurement using RAIM and city building models. Sensors 2015, 15, 17329–17349. [Google Scholar] [CrossRef] [PubMed]
- Zair, S.; Hegarat-Mascle, S.L.; Seignez, E. Outlier detection in GNSS pseudo-range/Doppler measurements for robust localization. Sensors 2016, 16, 580. [Google Scholar] [CrossRef] [PubMed]
- Leick, A. GPS Satellite Surveying, 3rd ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Braasch, M.S.; Van Dierendonck, A.J. GPS receiver architectures and measurements. Proc. IEEE 1999, 87, 48–64. [Google Scholar] [CrossRef]
- Groves, P.D.; Jiang, Z.; Rudi, M.; Strode, P. A portfolio approach to NLOS and multipath mitigation in dense urban areas. In Proceedings of the 26th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013; pp. 3231–3247. [Google Scholar]
- Strode, P.R.; Groves, P.D. GNSS multipath detection using three-frequency signal-to-noise measurements. GPS Solut. 2016, 20, 399–412. [Google Scholar] [CrossRef]
- Koch, K.R. Parameter Estimation and Hypothesis Testing in Linear Models, 2nd ed.; Springer-Verlag: Berlin, Germany, 1999. [Google Scholar]
- Ray, J.K. Mitigation of GPS Code and Carrier Phase Multipath Effects Using a Multi–Antenna System. Ph.D. Thesis, Report, Department of Geomatics Engineering, University of Calgary, Calgary, AB, Canada, 2000. [Google Scholar]
- Abraham, D.A. Analysis and Design of Sliding m-of-n Detectors; Technical Report No. 2011-01; CausaSci LLC: Ellicott City, MD, USA, 2011. [Google Scholar]
- Langley, R.B. Dilution of precision. GPS World 1999, 10, 52–59. [Google Scholar]
- Pirsiavash, A.; Broumandan, A.; Lachapelle, G.; O’Keefe, K. Galileo E1/E5 Measurement Monitoring—Theory, Testing and Analysis. In Proceedings of the European Navigation Conference (ENC) 2018, Gothenburg, Sweden, 14–17 May 2018; 12p. [Google Scholar]
- Lachapelle, G.; Kielland, P.; Casey, M. GPS for Marine Navigation and Hydrography. Int. Hydrogr. Rev. 1992, 69, 43–69. [Google Scholar]
- Dunn, M.J. Global Positioning Systems Directorate, Systems Engineering & Integration, Interface Specification (IS-GPS-200), NAVSTAR GPS Space Segment/Navigation User Segment Interfaces; GPS Directorate (IRN-IS-200H): Los Angeles, CA, USA, 2014. [Google Scholar]
- Dunn, M.J. Global Positioning Systems Directorate, Systems Engineering & Integration, Interface Specification (IS-GPS-705), NAVSTAR GPS Space Segment/User Segment L5 Interfaces; GPS Directorate (IS-GPS-705D): Los Angeles, CA, USA, 2014. [Google Scholar]
- Falletti, E.; Pini, M.; Lo Presti, L. Are carrier-to-noise algorithms equivalent in all situations? Inside GNSS 2010, 2010, 20–27. [Google Scholar]
- Goad, C.; Goodman, L. A Modified Hopfield Tropospheric Refraction Correction Model. In Proceedings of the Fall Annual Meeting American Geophysical Union, San Francisco, CA, USA, December 1974. [Google Scholar]
- Parkingson, B.W.; Spilker, J.J. Global Positioning System: Theory and Applications; American Institute of Aeronautics and Astronautics Inc.: Washington, DC, USA, 1996; Volume 1. [Google Scholar]
- Smith, S. Digital Signal Processing: A Practical Guide for Engineers and Scientists; Newnes-Elsevier Science: Burlington, MA, USA, 2003. [Google Scholar]
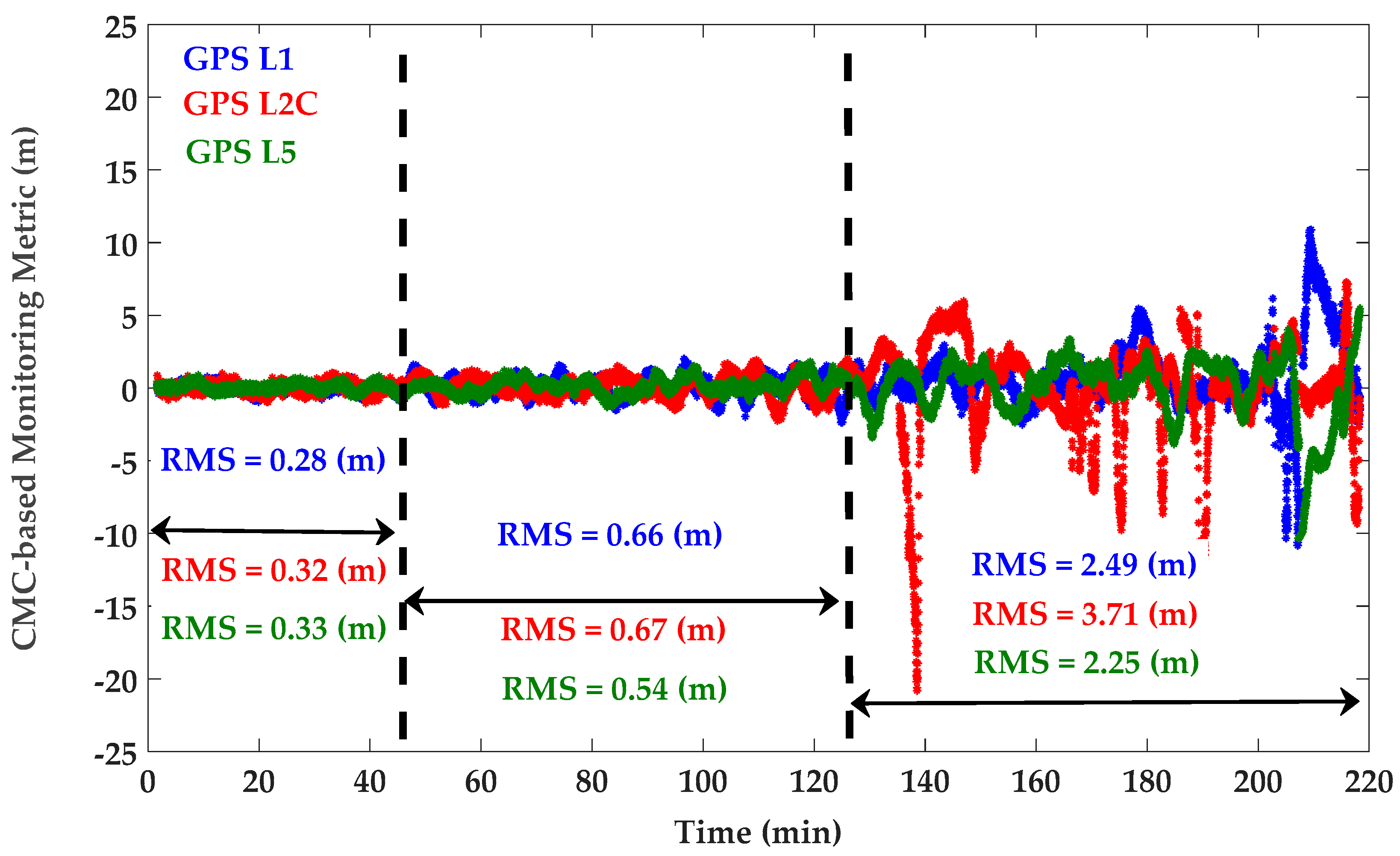
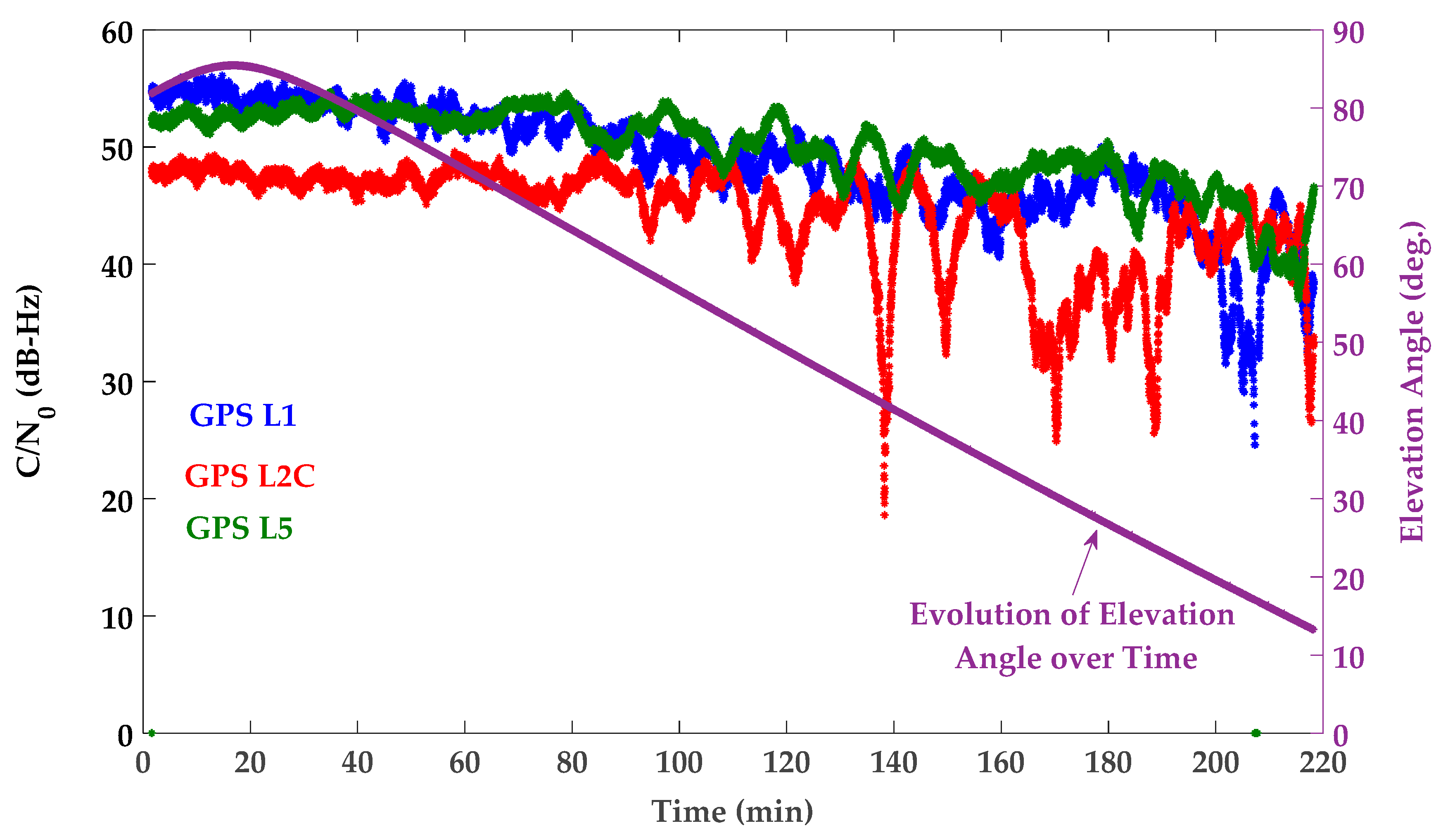
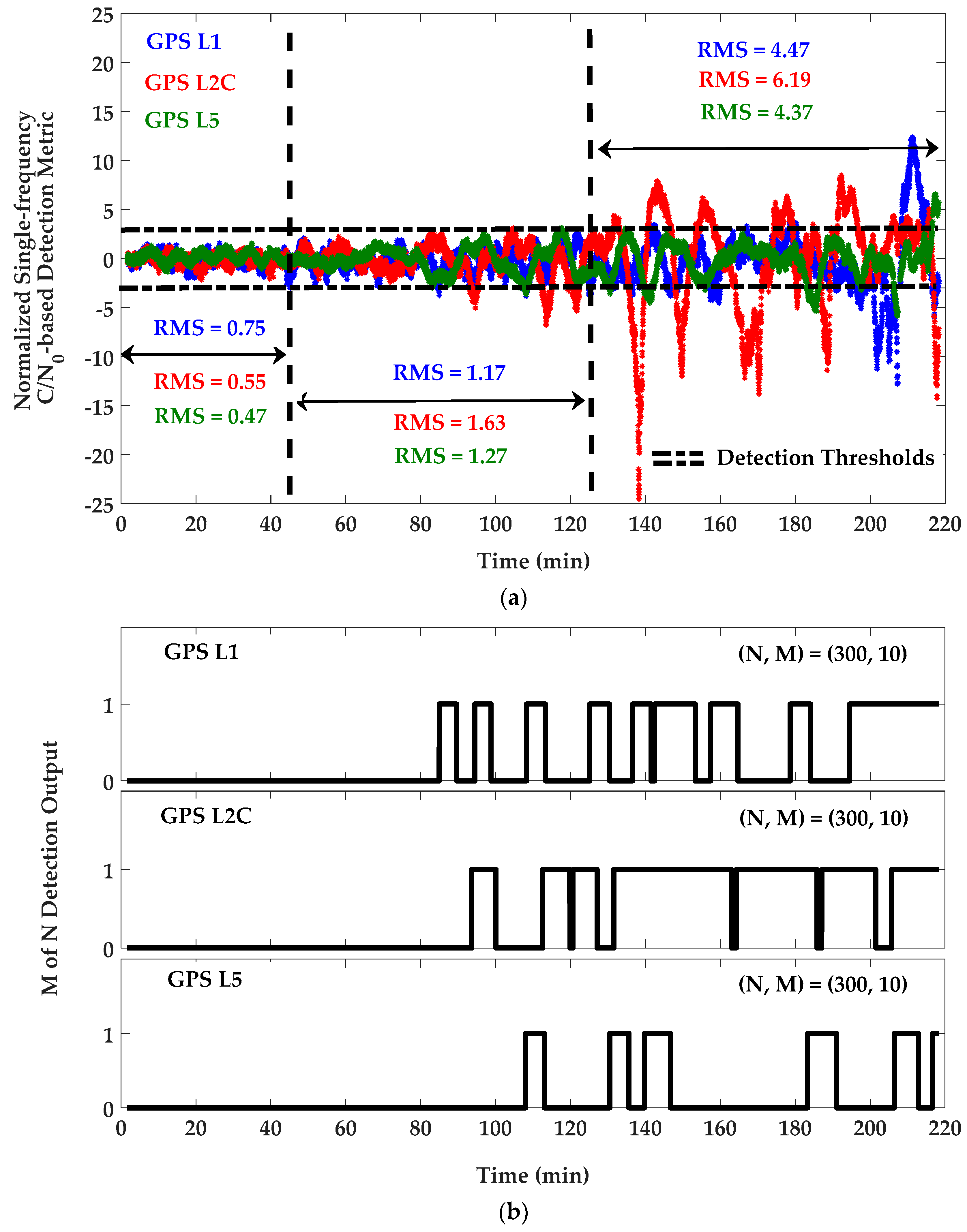
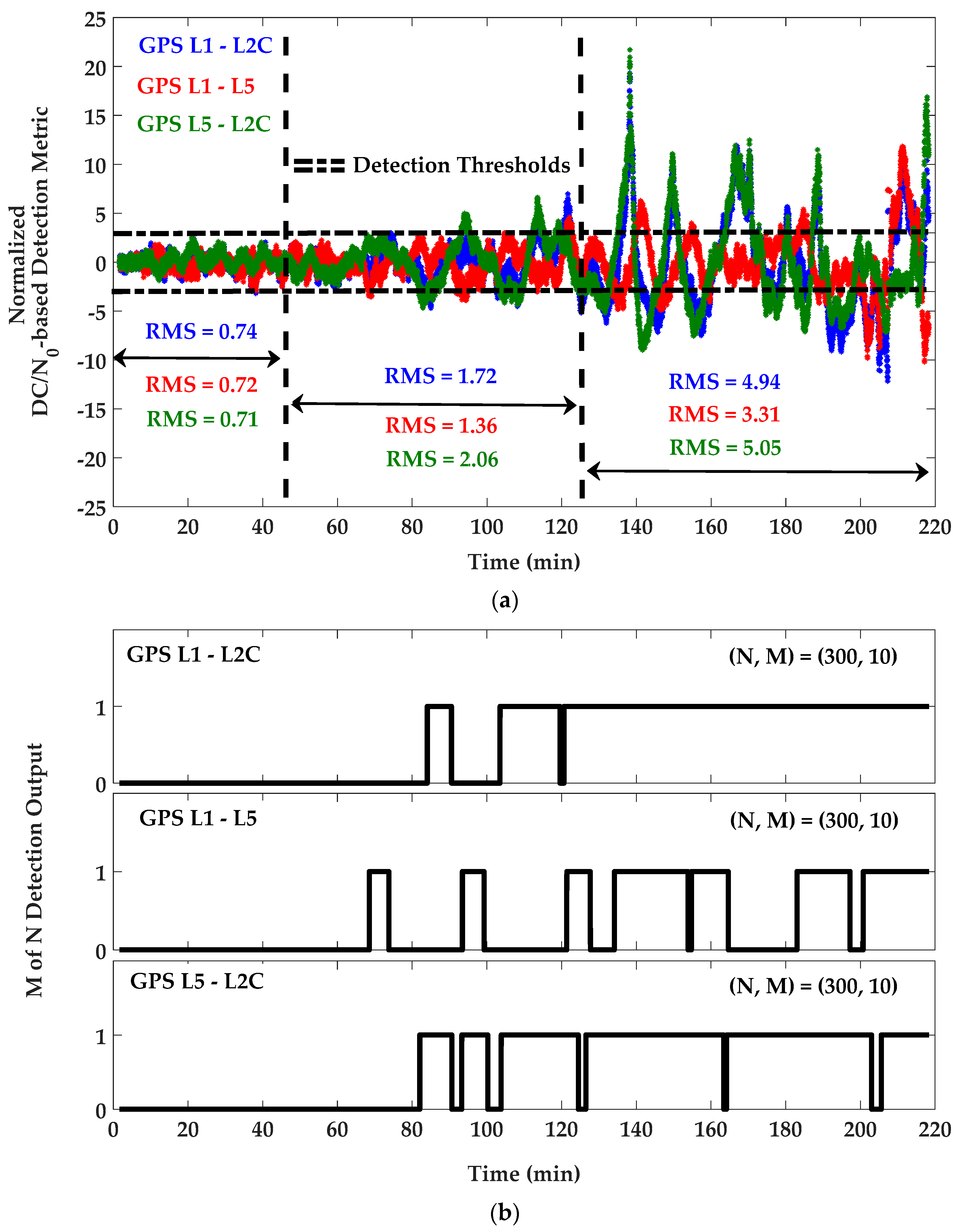
| Signal | Positioning Approach | East Mean (m) | North Mean (m) | Height Mean (m) | East RMS (m) | North RMS (m) | Height RMS (m) |
|---|---|---|---|---|---|---|---|
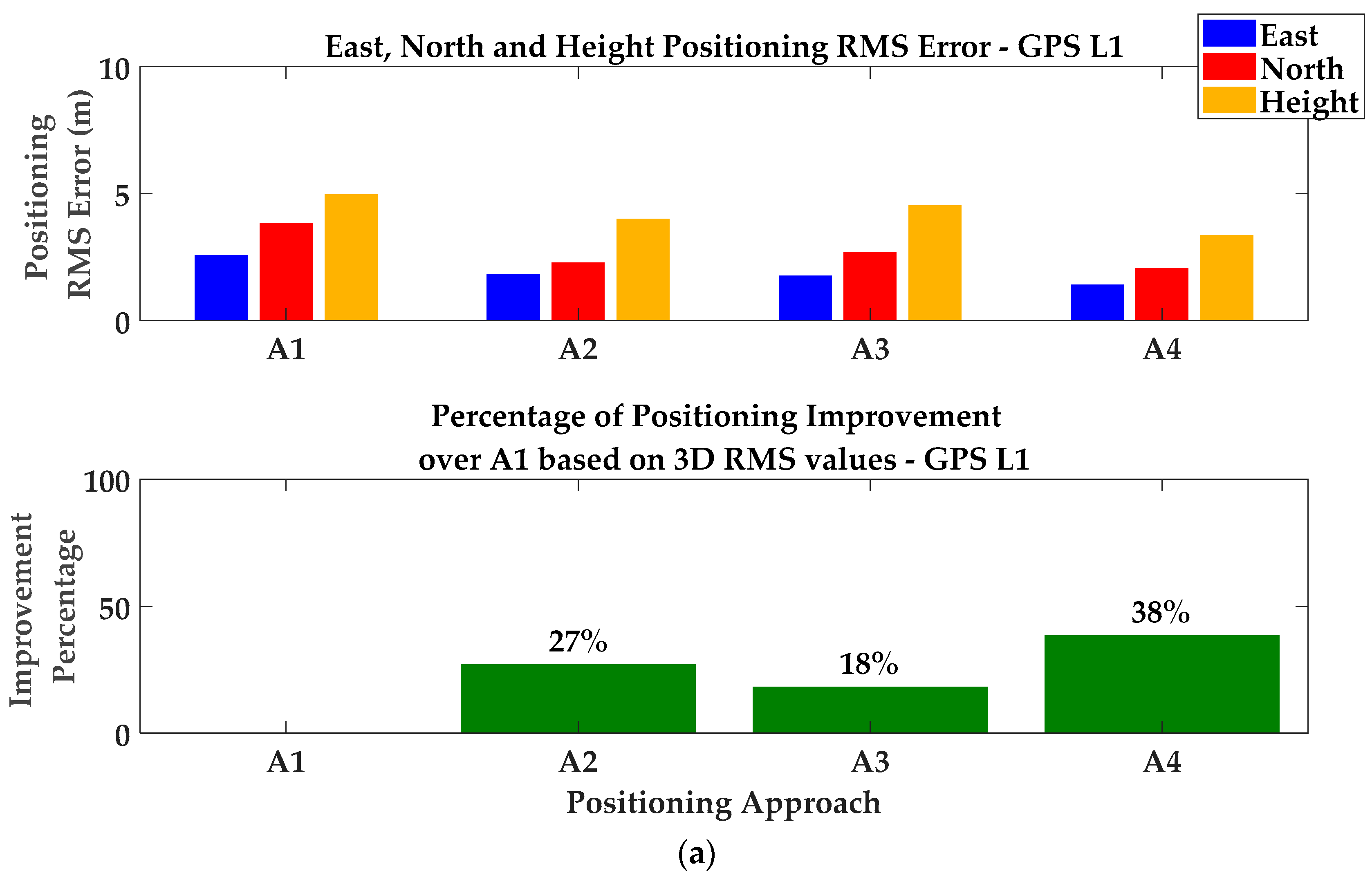
| GPS L1 C/A | A1 | −0.95 | 1.49 | 1.76 | 2.56 | 3.81 | 4.95 |
| A2 | −0.54 | −0.03 | 0.92 | 1.81 | 2.27 | 3.98 | |
| A3 | −0.49 | 1.07 | 2.02 | 1.75 | 2.67 | 4.52 | |
| A4 | −0.06 | 0.36 | 0.02 | 1.40 | 2.05 | 3.34 | |
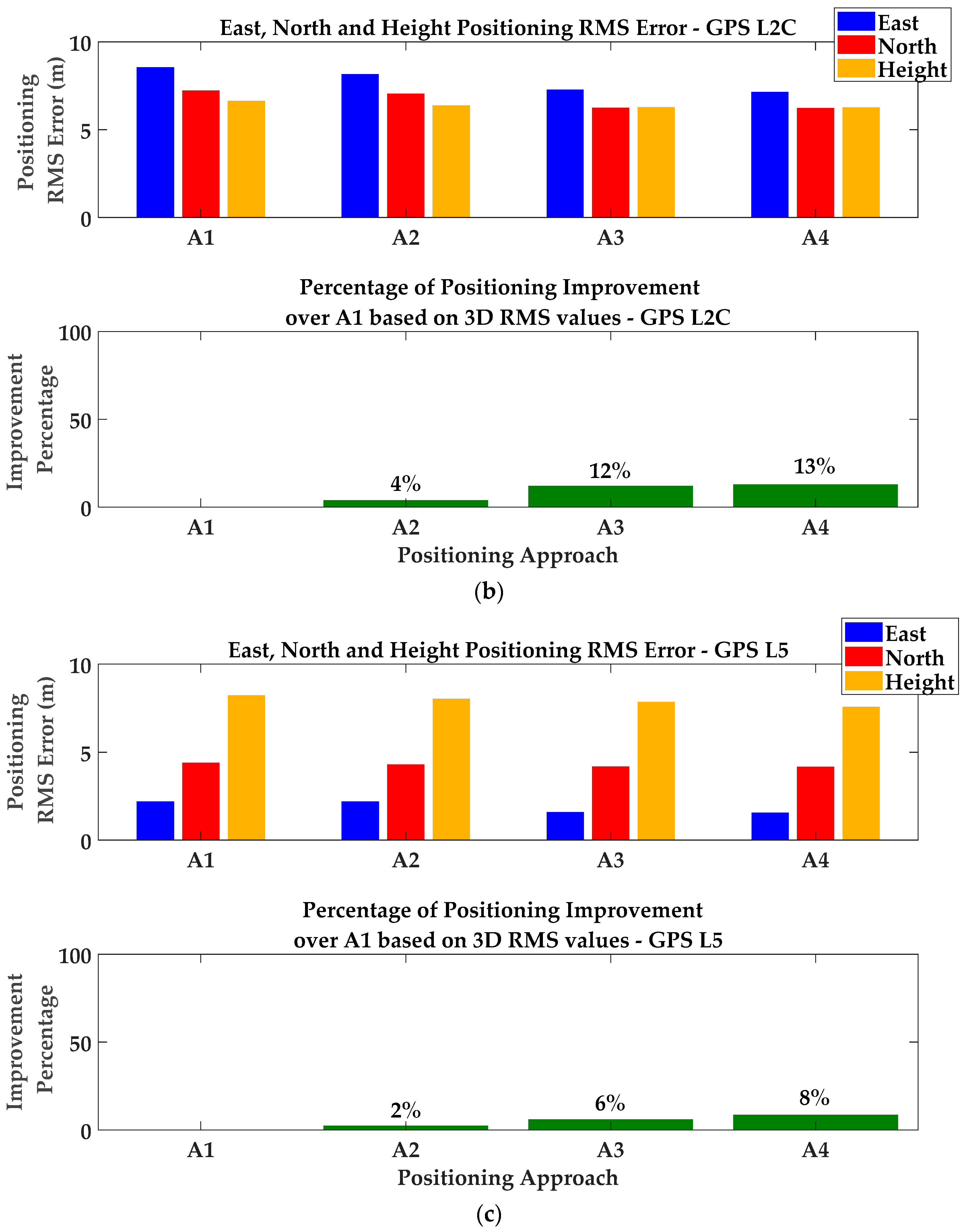
| GPS L2C M + L | A1 | −2.56 | 1.65 | 1.83 | 8.54 | 7.22 | 6.63 |
| A2 | −1.81 | −0.25 | 2.82 | 8.15 | 7.04 | 6.37 | |
| A3 | −2.38 | 1.56 | 1.80 | 7.27 | 6.24 | 6.26 | |
| A4 | −1.47 | −0.09 | 0.03 | 7.14 | 6.22 | 6.25 | |
| GPS L5 I + Q | A1 | −0.14 | −1.77 | 4.95 | 2.18 | 4.38 | 8.21 |
| A2 | −0.18 | −1.77 | 4.76 | 2.18 | 4.29 | 8.01 | |
| A3 | 0.01 | −2.27 | 5.16 | 1.57 | 4.18 | 7.83 | |
| A4 | 0.03 | −1.89 | 4.86 | 1.54 | 4.15 | 7.55 |
| Signal | Positioning Approach | East Mean (m) | North Mean (m) | Height Mean (m) | East RMS (m) | North RMS (m) | Height RMS (m) |
|---|---|---|---|---|---|---|---|
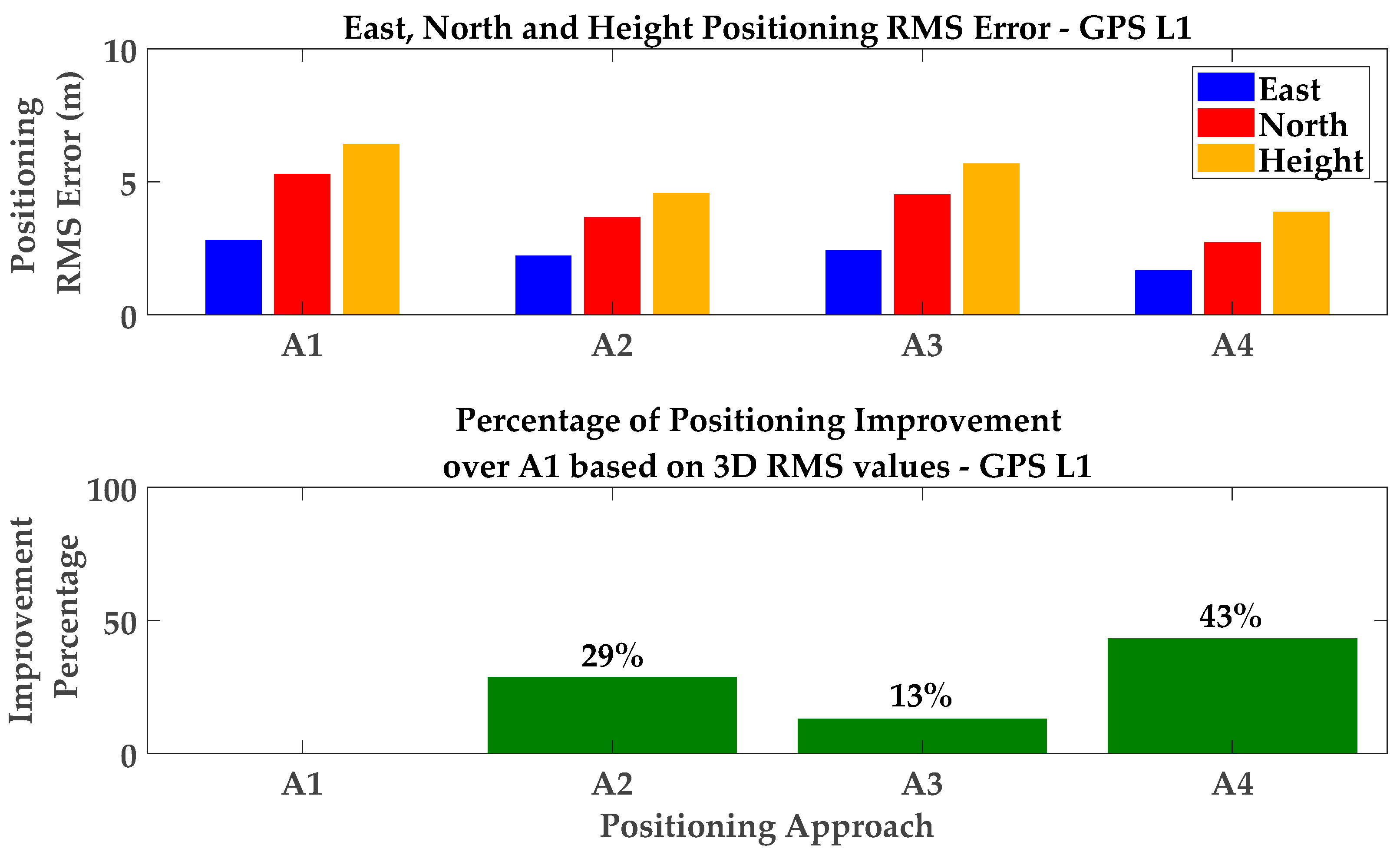
| GPS L1 C/A | A1 | −0.55 | −1.15 | 3.49 | 2.79 | 5.27 | 6.40 |
| A2 | −0.94 | −0.75 | 1.75 | 2.20 | 3.66 | 4.56 | |
| A3 | −0.38 | −0.82 | 3.06 | 2.40 | 4.50 | 5.67 | |
| A4 | −0.69 | −0.44 | 1.21 | 1.65 | 2.70 | 3.85 |
| Signal | Positioning Approach | East Mean (m) | North Mean (m) | Height Mean (m) | East RMS (m) | North RMS (m) | Height RMS (m) |
|---|---|---|---|---|---|---|---|
| Low Multipath Area | A1 | −1.10 | −0.05 | 1.38 | 1.26 | 0.49 | 1.49 |
| A2 | −1.09 | −0.13 | 1.31 | 1.27 | 0.52 | 1.48 | |
| A3 | −1.08 | −0.03 | 1.32 | 1.25 | 0.46 | 1.44 | |
| A4 | −1.07 | −0.11 | 1.29 | 1.25 | 0.49 | 1.45 | |
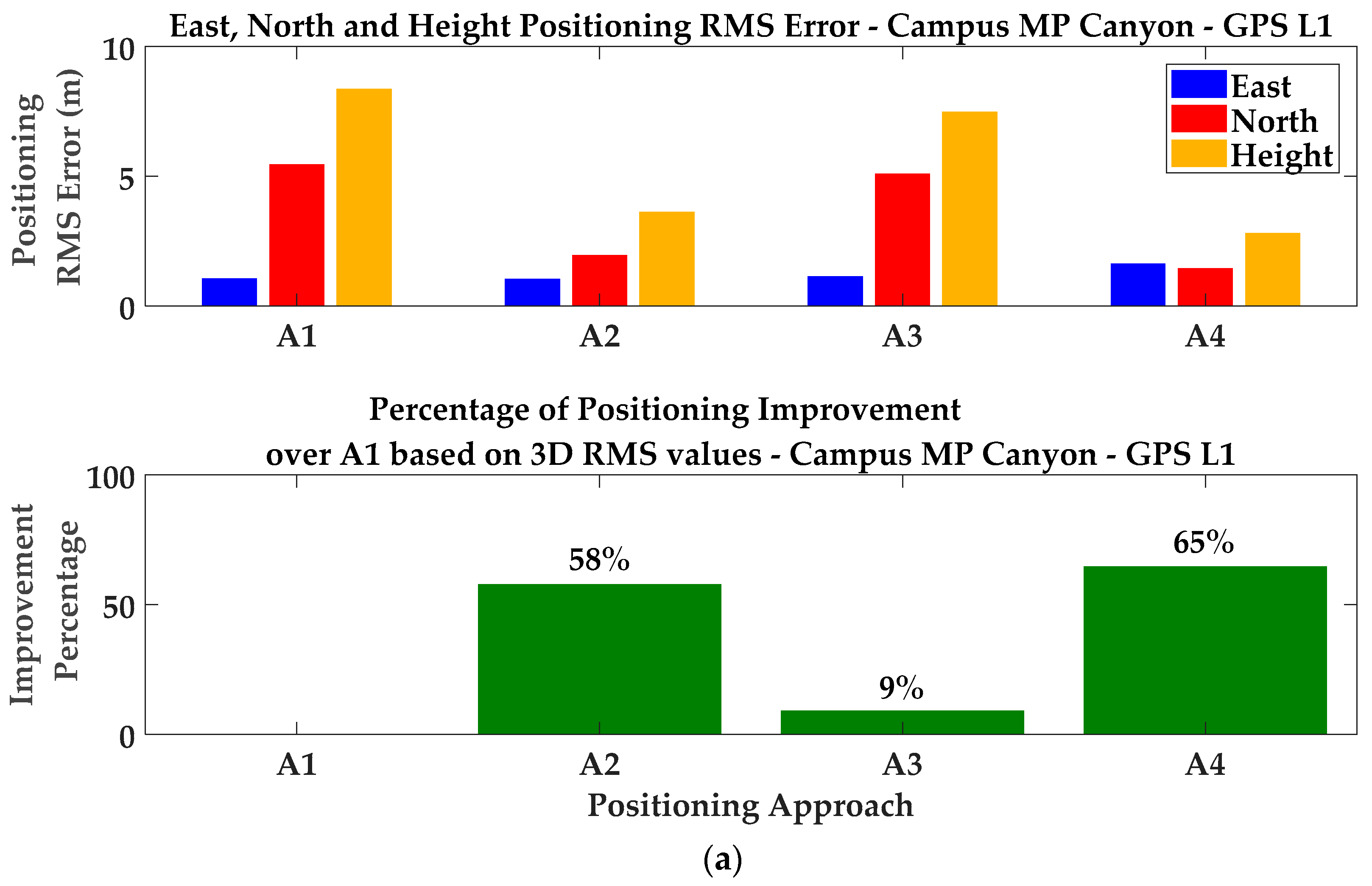
| Campus MP Canyon | A1 | −0.07 | 1.82 | 4.49 | 1.05 | 5.44 | 8.35 |
| A2 | 0.05 | 0.42 | 2.67 | 1.03 | 1.95 | 3.62 | |
| A3 | 0.62 | 2.13 | 3.68 | 1.14 | 5.09 | 7.48 | |
| A4 | 0.36 | 0.68 | 1.73 | 1.63 | 1.44 | 2.80 | |
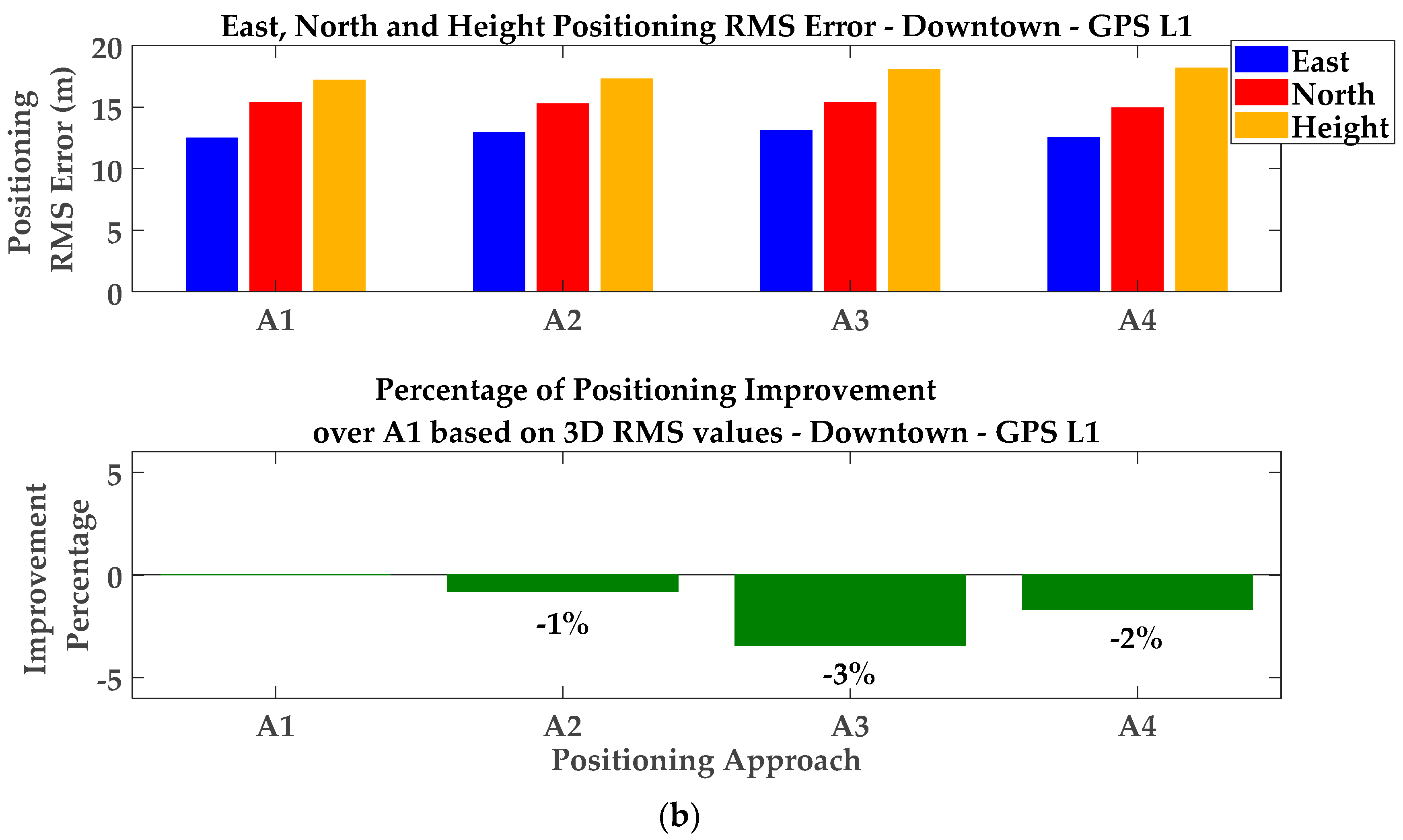
| Downtown Area | A1 | −0.11 | 2.08 | 3.29 | 12.50 | 15.38 | 17.19 |
| A2 | 0.35 | 2.38 | 3.58 | 12.95 | 15.27 | 17.29 | |
| A3 | −0.15 | 2.06 | 3.35 | 13.12 | 15.41 | 18.09 | |
| A4 | 0.38 | 2.37 | 3.57 | 12.55 | 14.95 | 18.19 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirsiavash, A.; Broumandan, A.; Lachapelle, G.; O’Keefe, K. GNSS Code Multipath Mitigation by Cascading Measurement Monitoring Techniques. Sensors 2018, 18, 1967. https://doi.org/10.3390/s18061967
Pirsiavash A, Broumandan A, Lachapelle G, O’Keefe K. GNSS Code Multipath Mitigation by Cascading Measurement Monitoring Techniques. Sensors. 2018; 18(6):1967. https://doi.org/10.3390/s18061967
Chicago/Turabian StylePirsiavash, Ali, Ali Broumandan, Gérard Lachapelle, and Kyle O’Keefe. 2018. "GNSS Code Multipath Mitigation by Cascading Measurement Monitoring Techniques" Sensors 18, no. 6: 1967. https://doi.org/10.3390/s18061967
APA StylePirsiavash, A., Broumandan, A., Lachapelle, G., & O’Keefe, K. (2018). GNSS Code Multipath Mitigation by Cascading Measurement Monitoring Techniques. Sensors, 18(6), 1967. https://doi.org/10.3390/s18061967





