Adaptive Maximum Correntropy Gaussian Filter Based on Variational Bayes
Abstract
1. Introduction
2. Gaussian Filter Based on the Maximum Correntropy Criterion
2.1. Correntropy
2.2. Maximum Correntropy Gaussian Filter
3. Variation Beysian Maximum Correntropy Gaussian Filter
- Step 1:
- Predict:
- Step 2:
- Update:For , iterate the following equations:End For. In addition, set , , and .
4. Experimental Results
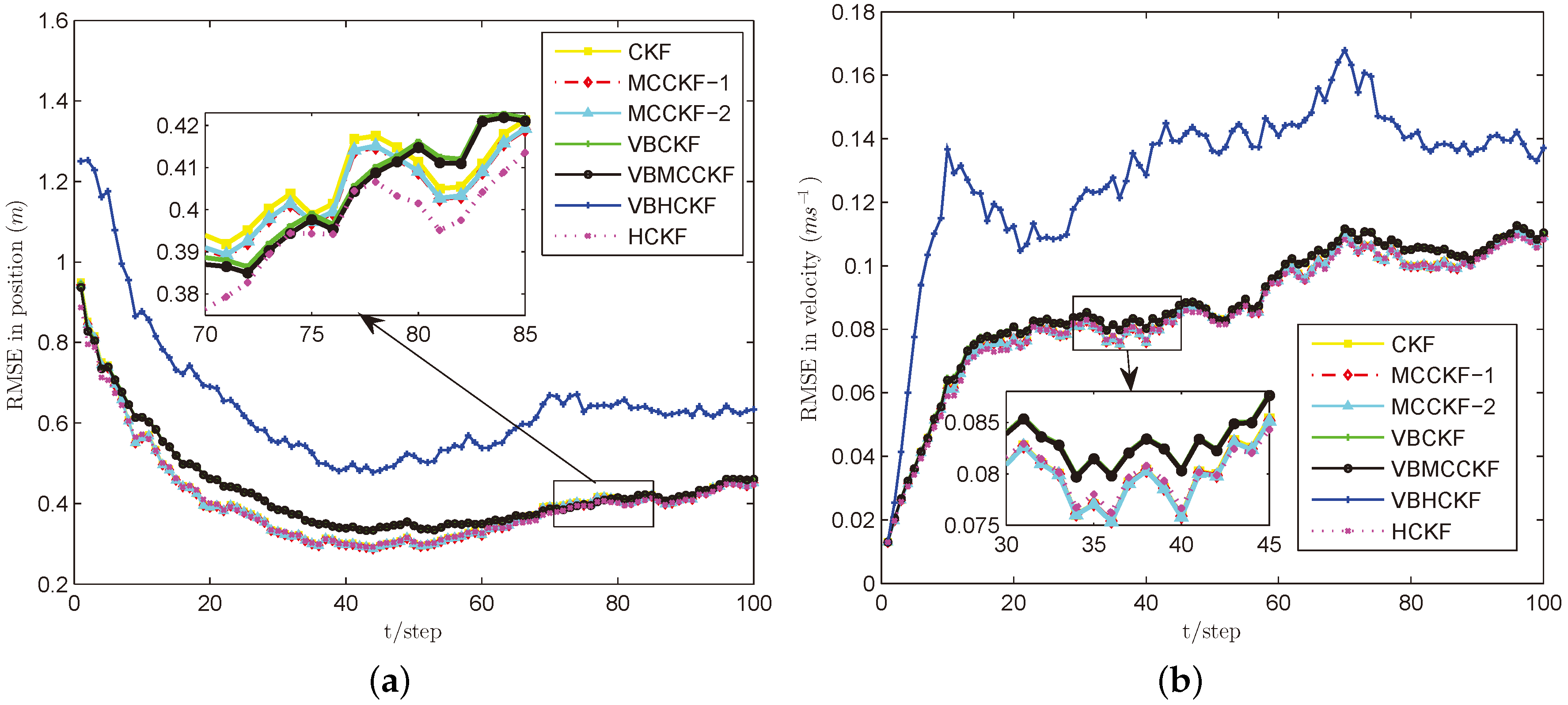
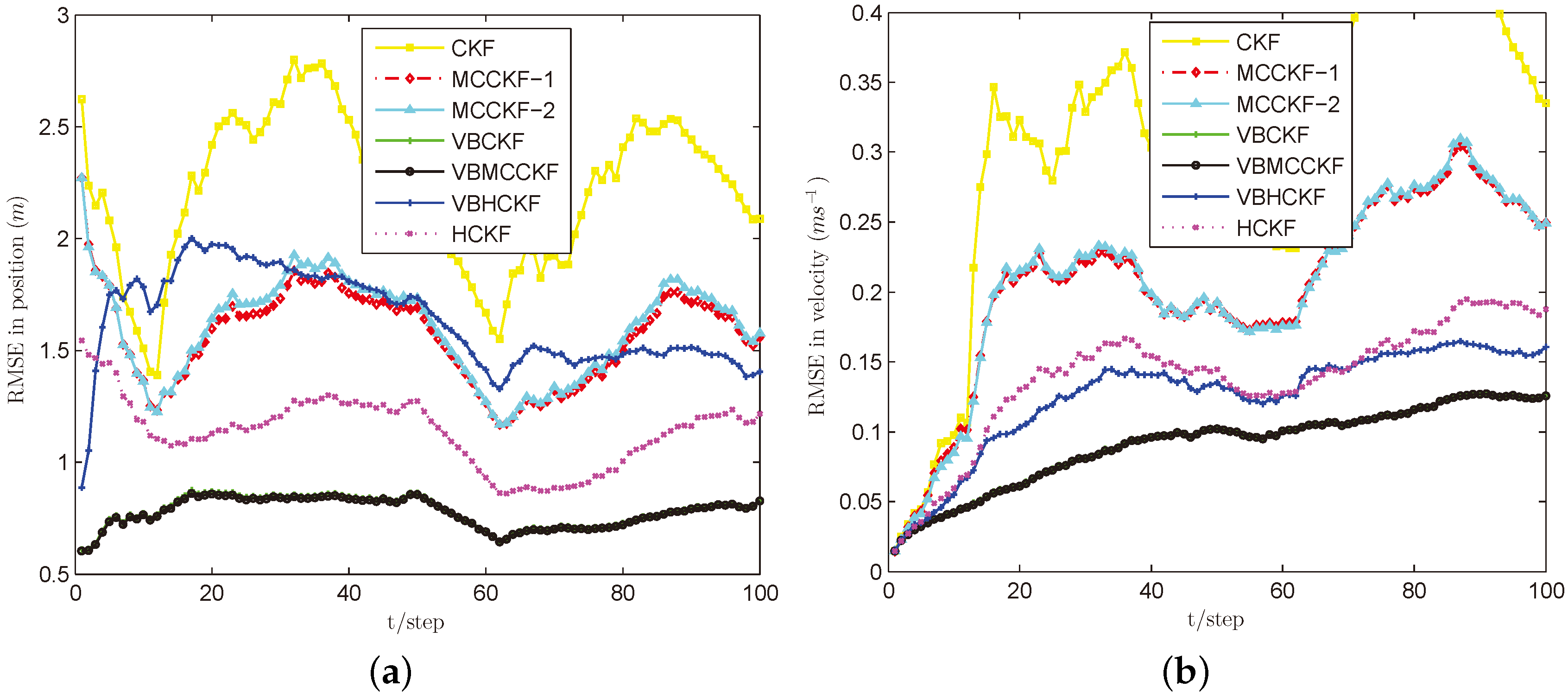
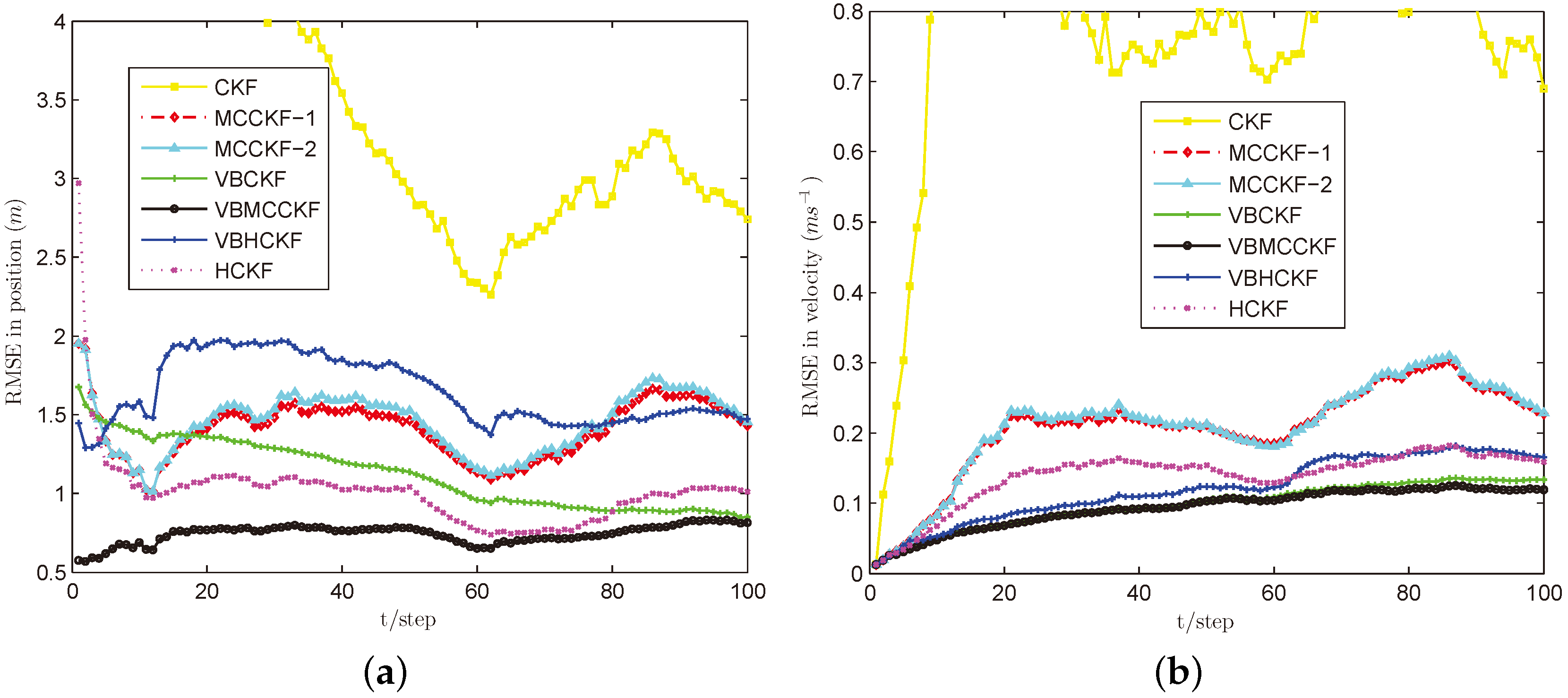
4.1. Simulation Results of the Target Tracking Model
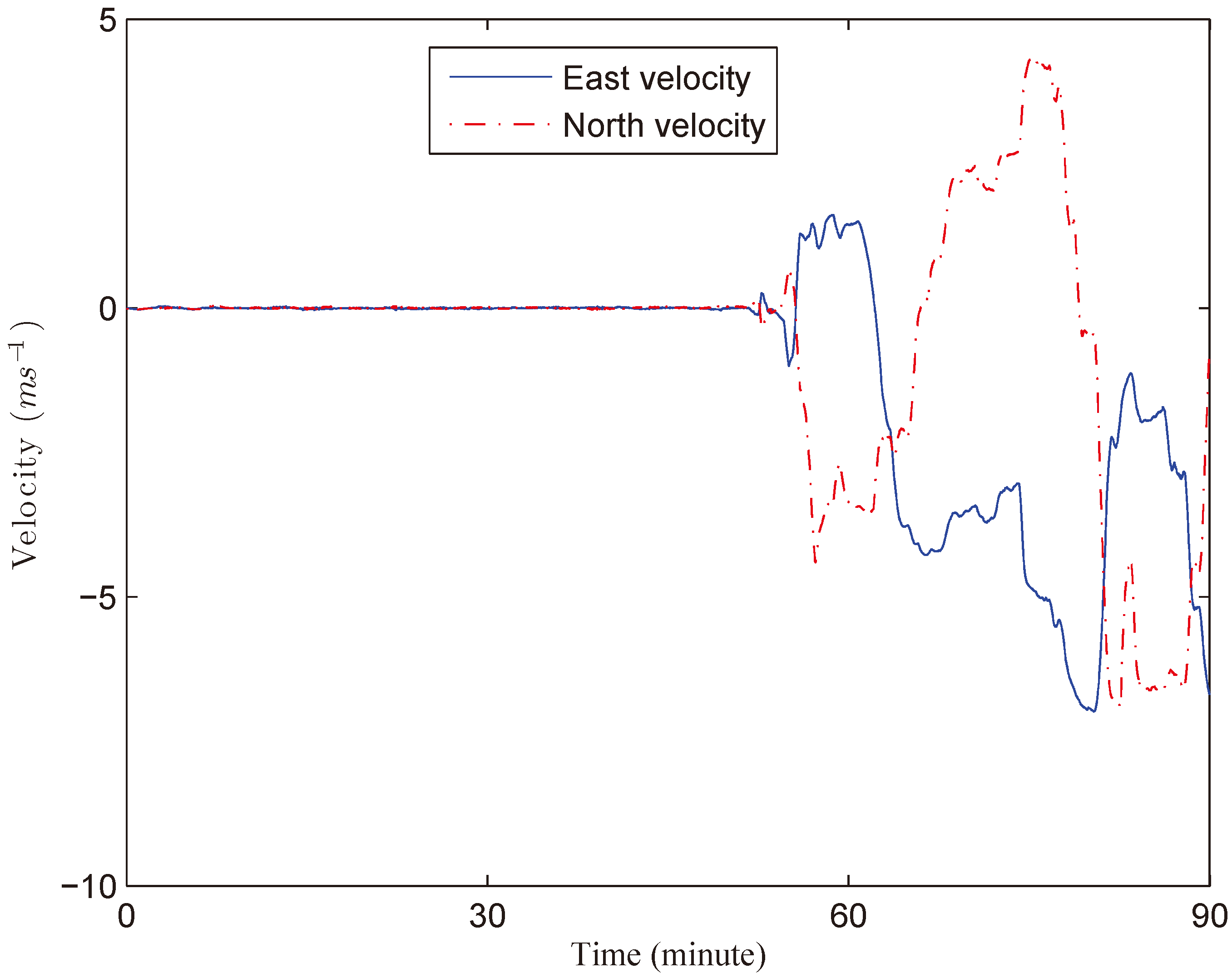
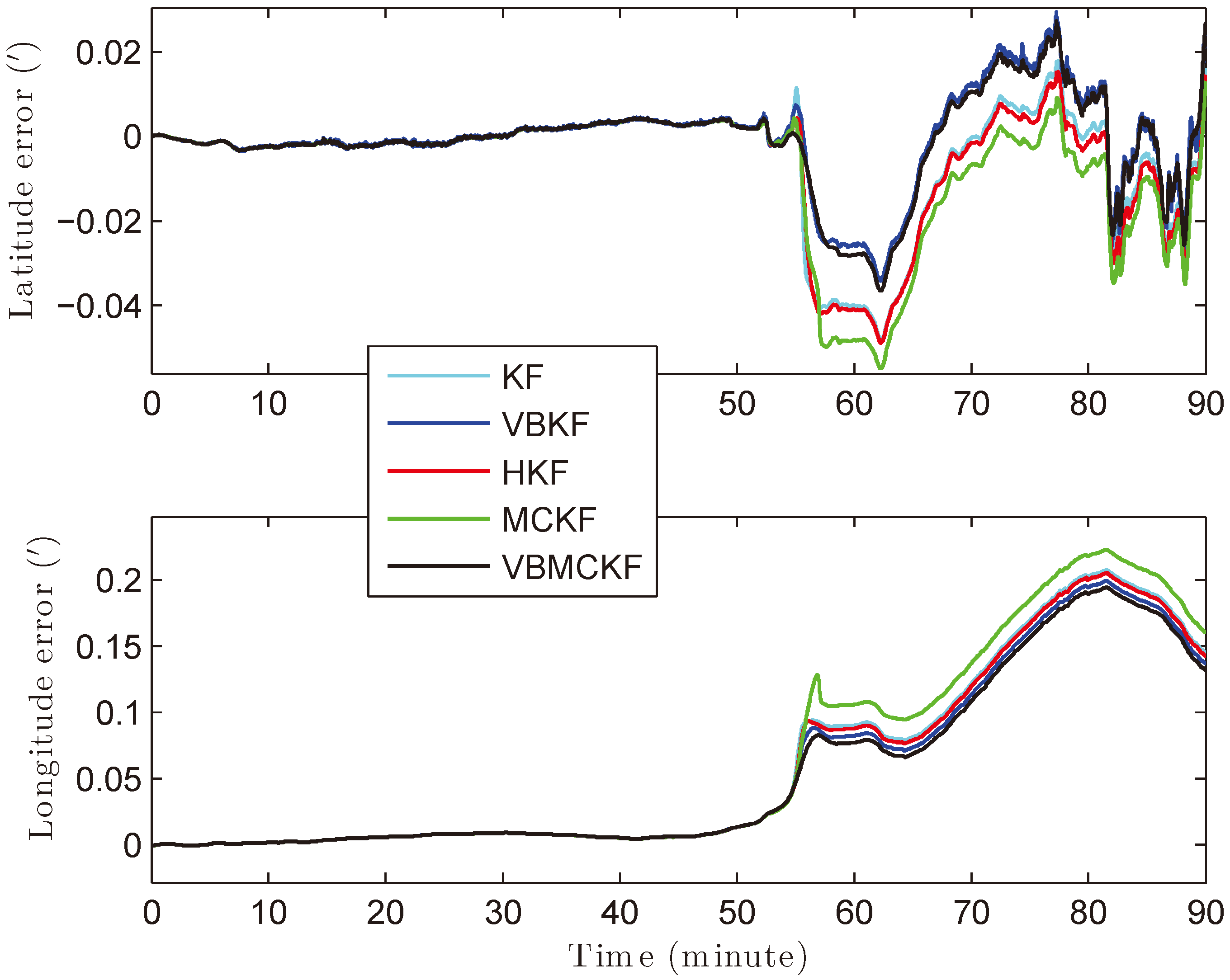
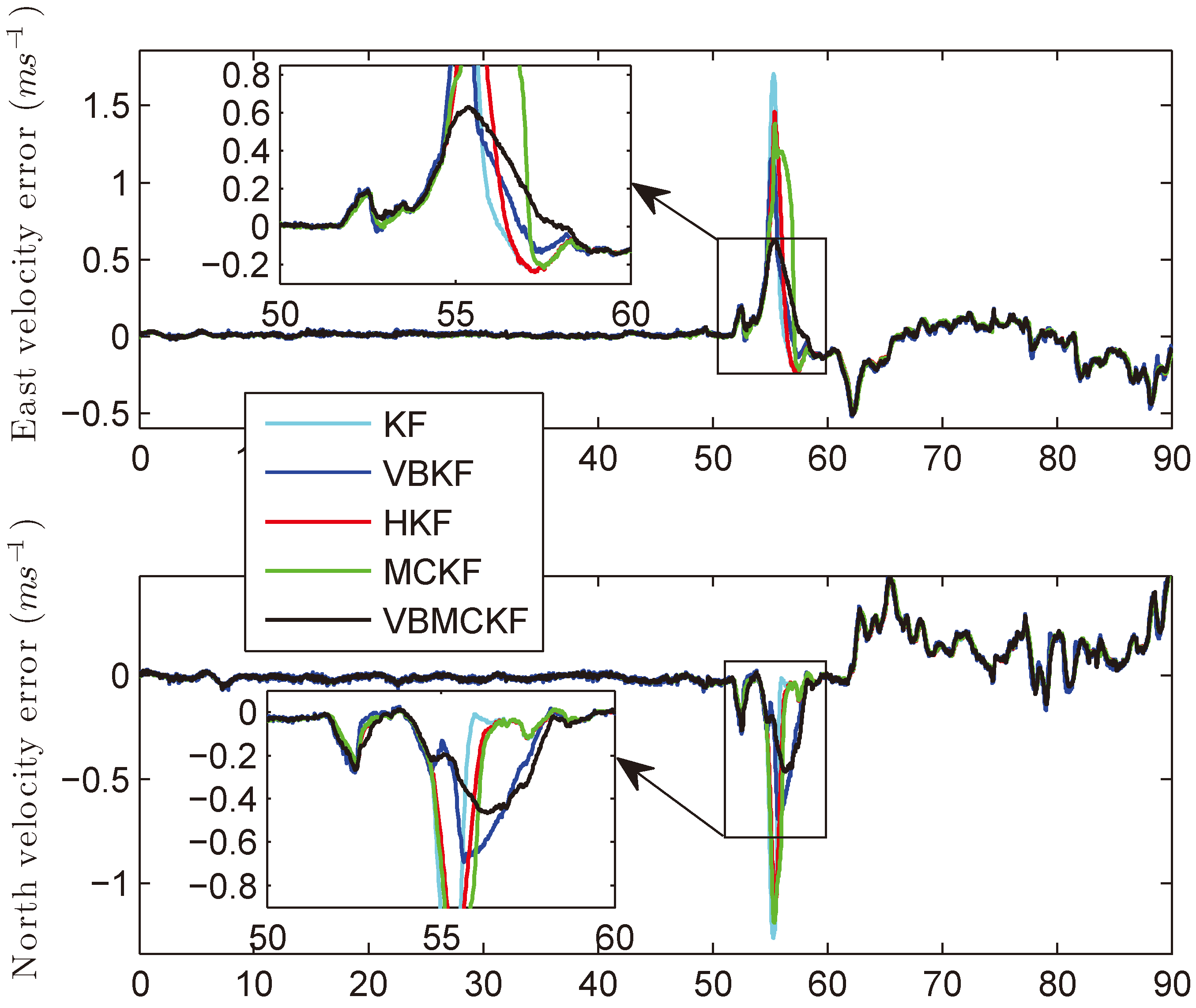
4.2. Field Results of Integrated Navigation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Auger, F.; Hilairet, M.; Guerrero, J.M.; Monmasson, E.; Orlowska-Kowalska, T.; Katsura, S. Industrial Applications of the Kalman Filter: A Review. IEEE Trans. Ind. Electron. 2013, 60, 5458–5471. [Google Scholar] [CrossRef]
- Wang, G.; Li, N.; Zhang, Y. An Event based Multi-sensor Fusion Algorithm with Deadzone Like Measurements. Inf. Fusion 2018, 42, 111–118. [Google Scholar] [CrossRef]
- Wang, G.; Li, N.; Zhang, Y. Diffusion Distributed Kalman Filter over Sensor Networks without Exchanging Raw Measurements. Signal Process. 2017, 132, 1–7. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Xu, B.; Wu, Z.; Chambers, J. A New Outlier-Robust Student’s t Based Gaussian Approximate Filter for Cooperative Localization. IEEE ASME Trans. Mechatron. 2017, 22, 2380–2386. [Google Scholar] [CrossRef]
- Reif, K.; Günther, S.; Yaz, E.; Unbehauen, R. Stochastic Stability of the Discrete-time Extended Kalman Filter. IEEE Trans. Autom. Control 1999, 44, 714–728. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented Filtering and Nonlinear Estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- N Rgaard, M.; Poulsen, N.K.; Ravn, O. New Developments in State Estimation for Nonlinear Systems. Automatica 2000, 36, 1627–1638. [Google Scholar] [CrossRef]
- Särkkä, S.; Hartikainen, J. Non-linear Noise Adaptive Kalman Filtering via Variational Bayes. In Proceedings of the 2013 IEEE International Workshop on Machine Learning for Signal Processing, Southampton, UK, 14 November 2013; pp. 1–6. [Google Scholar]
- Huang, Y.; Zhang, Y.; Wang, X.; Zhao, L. Gaussian Filter for Nonlinear Systems with Correlated Noises at the Same Epoch. Automatica 2015, 60, 122–126. [Google Scholar] [CrossRef]
- Wang, G.; Li, N.; Zhang, Y. Hybrid Consensus Sigma Point Approximation Nonlinear Filter Using Statistical Linearization. Trans. Inst. Meas. Control 2018, 40, 2517–2525. [Google Scholar] [CrossRef]
- Shmaliy, Y.S.; Zhao, S.; Ahn, C.K. Unbiased Finite Impulse Response Filtering: An Iterative Alternative to Kalman Filtering Ignoring Noise and Initial Conditions. IEEE Control Syst. Mag. 2017, 37, 70–89. [Google Scholar] [CrossRef]
- Zhao, S.; Shmaliy, Y.S.; Shi, P.; Ahn, C.K. Fusion Kalman/UFIR Filter for State Estimation with Uncertain Parameters and Noise Statistics. IEEE Trans. Ind. Electron. 2017, 64, 3075–3083. [Google Scholar] [CrossRef]
- Kotecha, J.H.; Djuric, P.M. Gaussian Particle Filtering. IEEE Trans. Signal Process. 2003, 51, 2592–2601. [Google Scholar] [CrossRef]
- Pak, J.M.; Ahn, C.K.; Shmaliy, Y.S.; Lim, M.T. Improving Reliability of Particle Filter-Based Localization in Wireless Sensor Networks via Hybrid Particle/FIR Filtering. IEEE Trans. Ind. Inform. 2015, 11, 1089–1098. [Google Scholar] [CrossRef]
- Alspach, D.; Sorenson, H. Nonlinear Bayesian Estimation Using Gaussian Sum Approximations. IEEE Trans. Autom. Control 1972, 17, 439–448. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of Maneuvering Target Tracking. Part V. Multiple-model Methods. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1255–1321. [Google Scholar]
- Chang, L.; Hu, B.; Chang, G.; Li, A. Multiple Outliers Suppression Derivative-Free Filter Based on Unscented Transformation. J. Guid. Control Dyn. 2012, 35, 1902–1907. [Google Scholar] [CrossRef]
- Karlgaard, C.D. Nonlinear Regression Huber-Kalman Filtering and Fixed-Interval Smoothing. J. Guid. Control Dyn. 2014, 38, 322–330. [Google Scholar] [CrossRef]
- Wu, H.; Chen, S.; Yang, B.; Chen, K. Robust Derivative-Free Cubature Kalman Filter for Bearings-Only Tracking. J. Guid. Control Dyn. 2016, 39, 1866–1871. [Google Scholar] [CrossRef]
- Hur, H.; Ahn, H.S. Discrete-Time H∞ Filtering for Mobile Robot Localization Using Wireless Sensor Network. IEEE Sens. J. 2013, 13, 245–252. [Google Scholar] [CrossRef]
- Graham, M.C.; How, J.P.; Gustafson, D.E. Robust State Estimation with Sparse Outliers. J. Guid. Control Dyn. 2015, 38, 1229–1240. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, W.; Sun, S.; Li, L. Robust Information Filter Based on Maximum Correntropy Criterion. J. Guid. Control Dyn. 2016, 39, 1126–1131. [Google Scholar] [CrossRef]
- Chen, B.; Liu, X.; Zhao, H.; Principe, J.C. Maximum Correntropy Kalman Filter. Automatica 2017, 76, 70–77. [Google Scholar] [CrossRef]
- Liu, X.; Qu, H.; Zhao, J.; Yue, P.; Wang, M. Maximum Correntropy Unscented Kalman Filter for Spacecraft Relative State Estimation. Sensors 2016, 16, 1530. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Chen, B.D.; Xu, B.; Wu, Z.Z.; Honeine, P. Maximum Correntropy Unscented Filter. Int. J. Syst. Sci. 2017, 48, 1607–1615. [Google Scholar] [CrossRef]
- Liu, X.; Qu, H.; Zhao, J.; Chen, B. Extended Kalman Filter under Maximum Correntropy Criterion. In Proceedings of the 2016 International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; pp. 1733–1737. [Google Scholar]
- Wang, G.; Li, N.; Zhang, Y. Maximum Correntropy Unscented Kalman and Information Filters for Non-Gaussian Measurement Noise. J. Frankl. Inst. 2017, 354, 8659–8677. [Google Scholar] [CrossRef]
- Narasimhappa, M.; Rangababu, P.; Sabat, S.L.; Nayak, J. A modified Sage–Husa Adaptive Kalman Filter for Denoising Fiber Optic Gyroscope Signal. In Proceedings of the 2012 Annual IEEE India Conference, Kochi, India, 7–9 December 2012; pp. 1266–1271. [Google Scholar]
- Wang, Y.; Sun, S.; Li, L. Adaptively Robust Unscented Kalman Filter for Tracking a Maneuvering Vehicle. J. Guid. Control Dyn. 2014, 37, 1696–1701. [Google Scholar] [CrossRef]
- Li, K.; Chang, L.; Hu, B. A Variational Bayesian-Based Unscented Kalman Filter with Both Adaptivity and Robustness. IEEE Sens. J. 2016, 16, 6966–6976. [Google Scholar] [CrossRef]
- Sarkka, S.; Nummenmaa, A. Recursive Noise Adaptive Kalman Filtering by Variational Bayesian Approximations. IEEE Trans. Autom. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Mbalawata, I.S.; Särkkä, S.; Vihola, M.; Haario, H. Adaptive Metropolis Algorithm using Variational Bayesian Adaptive Kalman Filter. Comput. Stat. Data Anal. 2015, 83, 101–115. [Google Scholar] [CrossRef]
- Gao, W.; Li, J.; Zhou, G.; Li, Q. Adaptive Kalman Filtering with Recursive Noise Estimator for Integrated SINS/DVL Systems. J. Navig. 2015, 68, 142–161. [Google Scholar] [CrossRef]
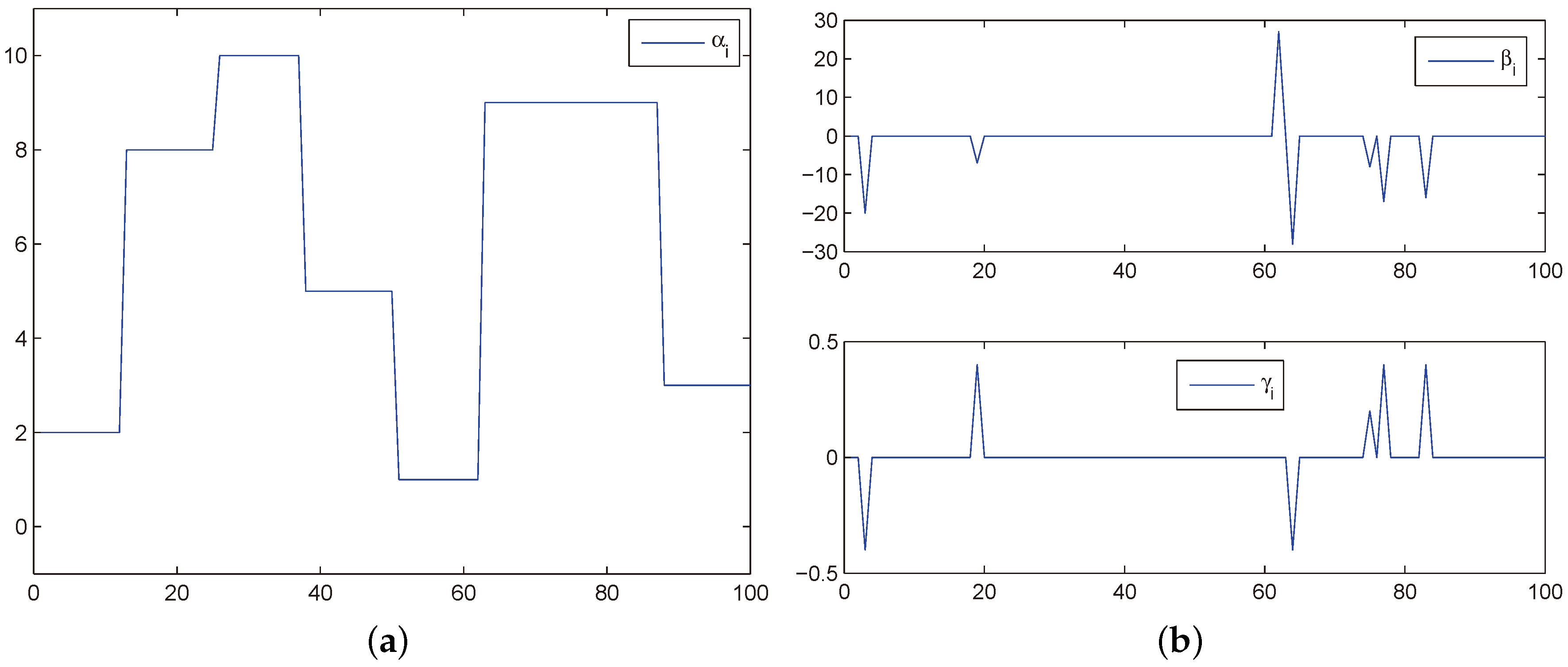

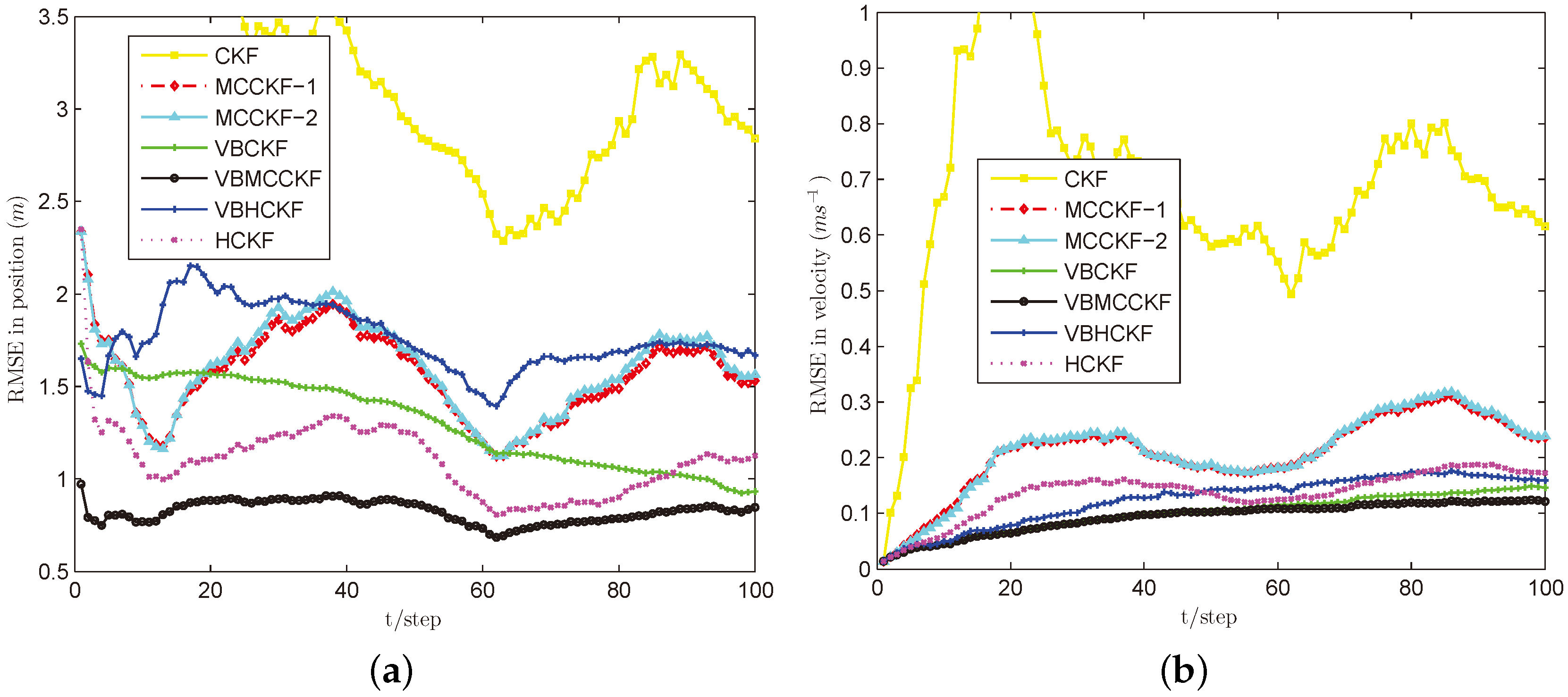
| Algorithms | Case A | Case B | Case C | Case D | Case E | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pos. | Vel. | Pos. | Vel. | Pos. | Vel. | Pos. | Vel. | Pos. | Vel. | |
| CKF | 0.4097 | 0.0855 | 2.2930 | 0.3121 | 2.2050 | 0.3053 | 3.7720 | 0.7809 | 3.2960 | 0.6923 |
| MCCKF-1 | 0.4077 | 0.0854 | 1.4960 | 0.1959 | 1.5680 | 0.2052 | 1.4090 | 0.2077 | 1.5680 | 0.2100 |
| MCCKF-2 | 0.4079 | 0.0853 | 1.5280 | 0.1989 | 1.5990 | 0.2058 | 1.4500 | 0.2098 | 1.6010 | 0.2114 |
| HCKF | 0.4045 | 0.0847 | 1.0990 | 0.1304 | 1.1360 | 0.1390 | 1.0100 | 0.1384 | 1.1030 | 0.1365 |
| VBHCKF | 0.6500 | 0.1296 | 1.7180 | 0.1185 | 1.6360 | 0.1260 | 1.6460 | 0.1207 | 1.7590 | 0.1251 |
| VBCKF | 0.4362 | 0.0880 | 0.8761 | 0.0845 | 0.7828 | 0.0914 | 1.1240 | 0.0977 | 1.3100 | 0.1000 |
| VBMCCKF | 0.4350 | 0.0878 | 0.8633 | 0.0843 | 0.7752 | 0.0909 | 0.7424 | 0.0933 | 0.8236 | 0.0931 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Gao, Z.; Zhang, Y.; Ma, B. Adaptive Maximum Correntropy Gaussian Filter Based on Variational Bayes. Sensors 2018, 18, 1960. https://doi.org/10.3390/s18061960
Wang G, Gao Z, Zhang Y, Ma B. Adaptive Maximum Correntropy Gaussian Filter Based on Variational Bayes. Sensors. 2018; 18(6):1960. https://doi.org/10.3390/s18061960
Chicago/Turabian StyleWang, Guoqing, Zhongxing Gao, Yonggang Zhang, and Bin Ma. 2018. "Adaptive Maximum Correntropy Gaussian Filter Based on Variational Bayes" Sensors 18, no. 6: 1960. https://doi.org/10.3390/s18061960
APA StyleWang, G., Gao, Z., Zhang, Y., & Ma, B. (2018). Adaptive Maximum Correntropy Gaussian Filter Based on Variational Bayes. Sensors, 18(6), 1960. https://doi.org/10.3390/s18061960







