Joint Cache Content Placement and Task Offloading in C-RAN Enabled by Multi-Layer MEC
Abstract
1. Introduction
- We design a Joint Cache content placement and task Offloading Solution, named JCOS, to solve those two problems of CMM-CRAN. With JCOS, UE tasks in CMM-CRAN are easier to obtain the frequently requested content through cache, and the computation tasks can be handled by the best fit edge cloud guaranteeing the benefits of both mobile users and the network. Therefore, JCOS could effectively save UE task latency, energy cost and fronthaul capacity, then improve the performance of CMM-CRAN.
- JCOS utilizes the well known GS method to come up a Cache Content Placement Algorithm(CCPA) to solve the many-to-many matching problem on cache placement. CCPA considers the storage capacity of each RRH, the fronthaul and RF link capacities, and the content popularity to solve the matching problem.
- JCOS also applies the PE game theory coupled with a use of a AHP as the method to solve the MMCK problem on user task offloading. The PE method works out the offloading choices based on a series of comparisons of cloud selection utilities. A cloud selection utility is associated to cloud capacity constraint, fronthaul constraint, and RF constraint.
- The CCPA on cache and PE method on dynamic task offloading work jointly in JCOS to have acceptable complexity, stability and salability.
2. Model and Problem Formulation
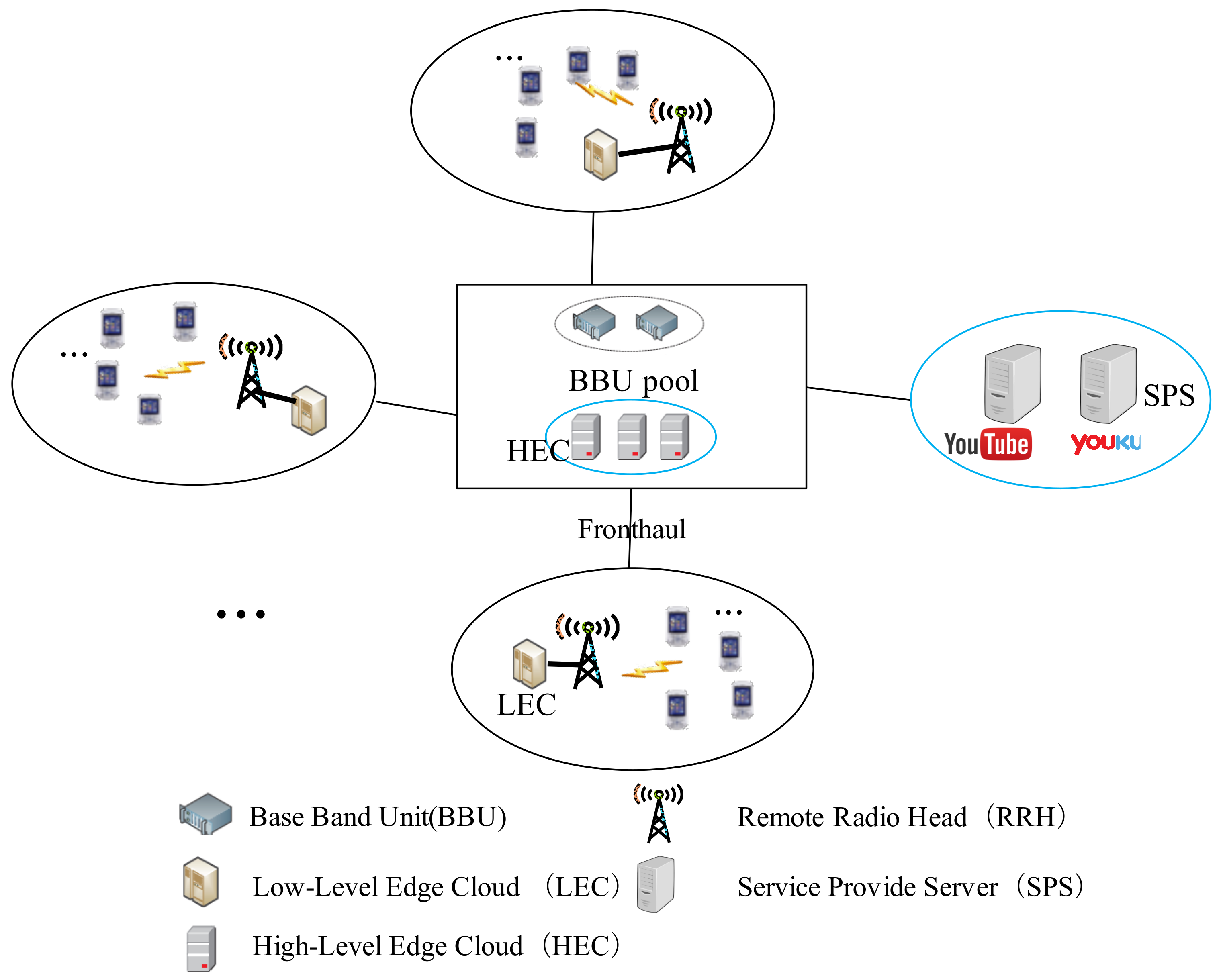
2.1. CMM-CRAN Model
2.2. Problem Formulation
2.2.1. UE Task, Latency and Energy Cost
2.2.2. Formulate the Cache and Task Offloading Problems
- 1.
- is contained inandis contained in;
- 2.
- for all v in;
- 3.
- for all j in;
- 4.
- j is inif and only if v is in;
3. Solutions
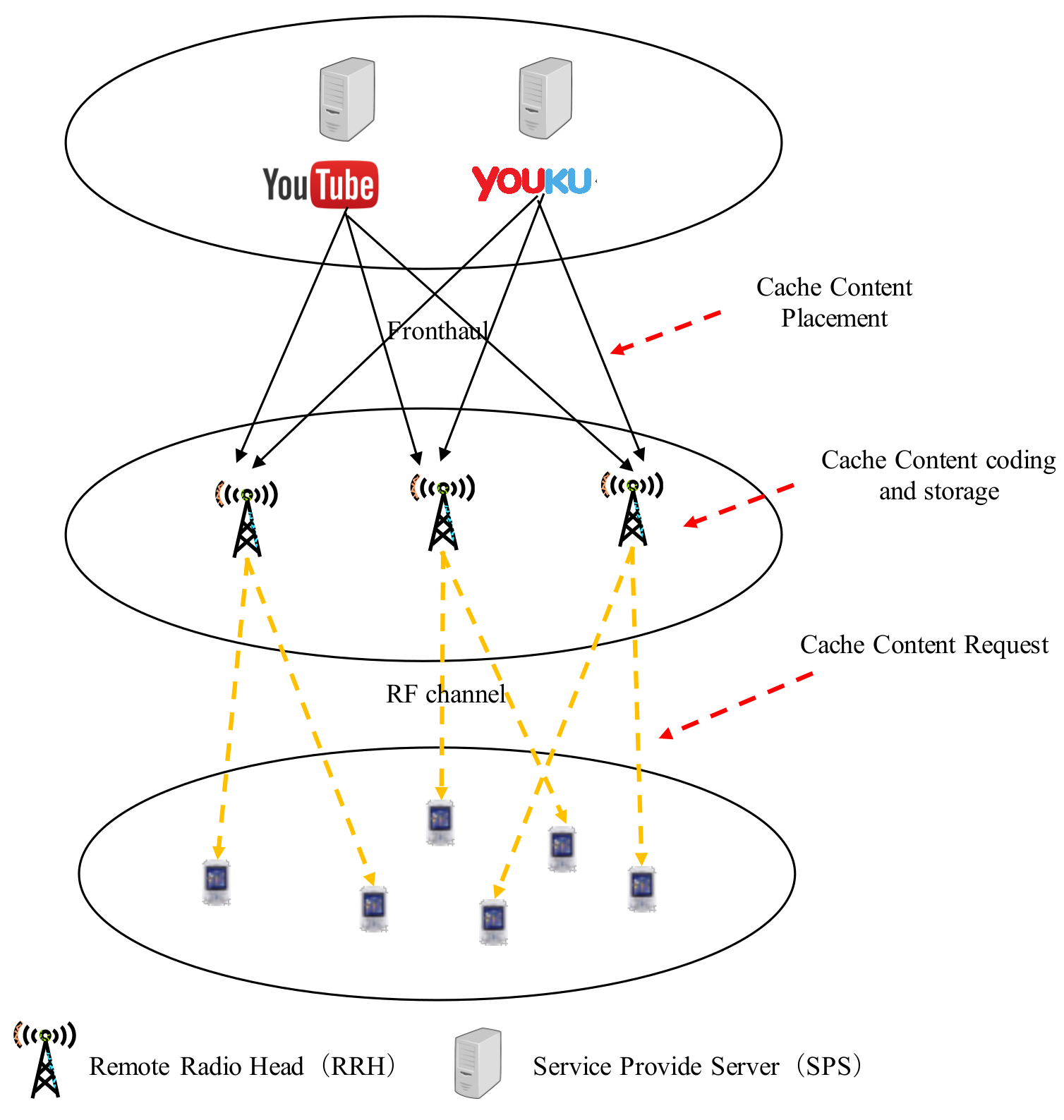
3.1. Cache Content Placement Algorithm
3.1.1. Preferences of RRHs and Contents
3.1.2. Algorithm Design
| Algorithm 1: Cache Content Placement Algorithm. |
 |
3.2. PE Method on User Task Offloading
3.2.1. Population Evolution Game
3.2.2. Calculate Cloud Selection Utility by AHP
3.3. Joint Solution on Cache Content Placement and User Task Offloading
| Algorithm 2: Joint Solution on Cache Content Placement and User Task Offloading. |
 |
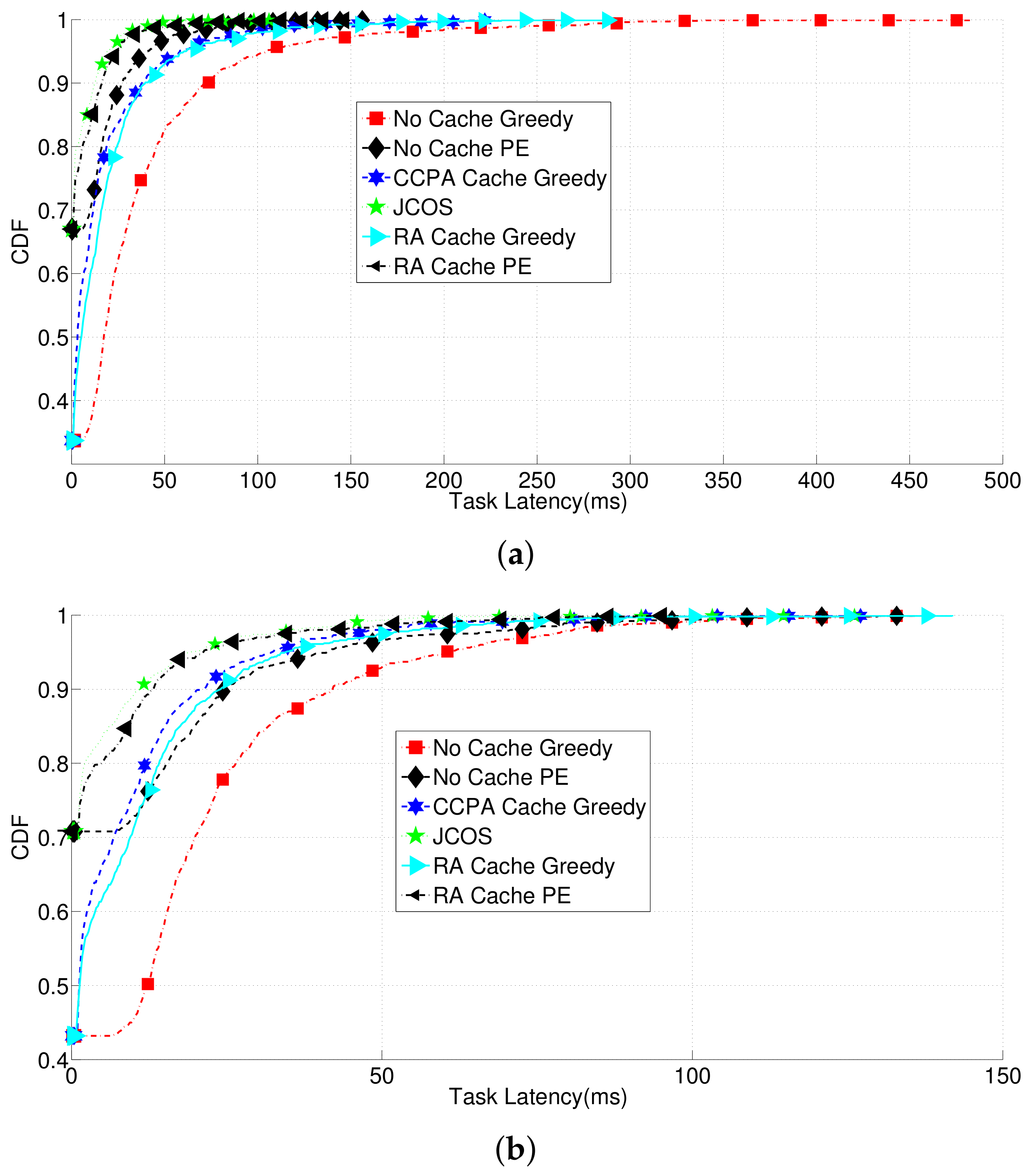
4. Simulation and Analysis
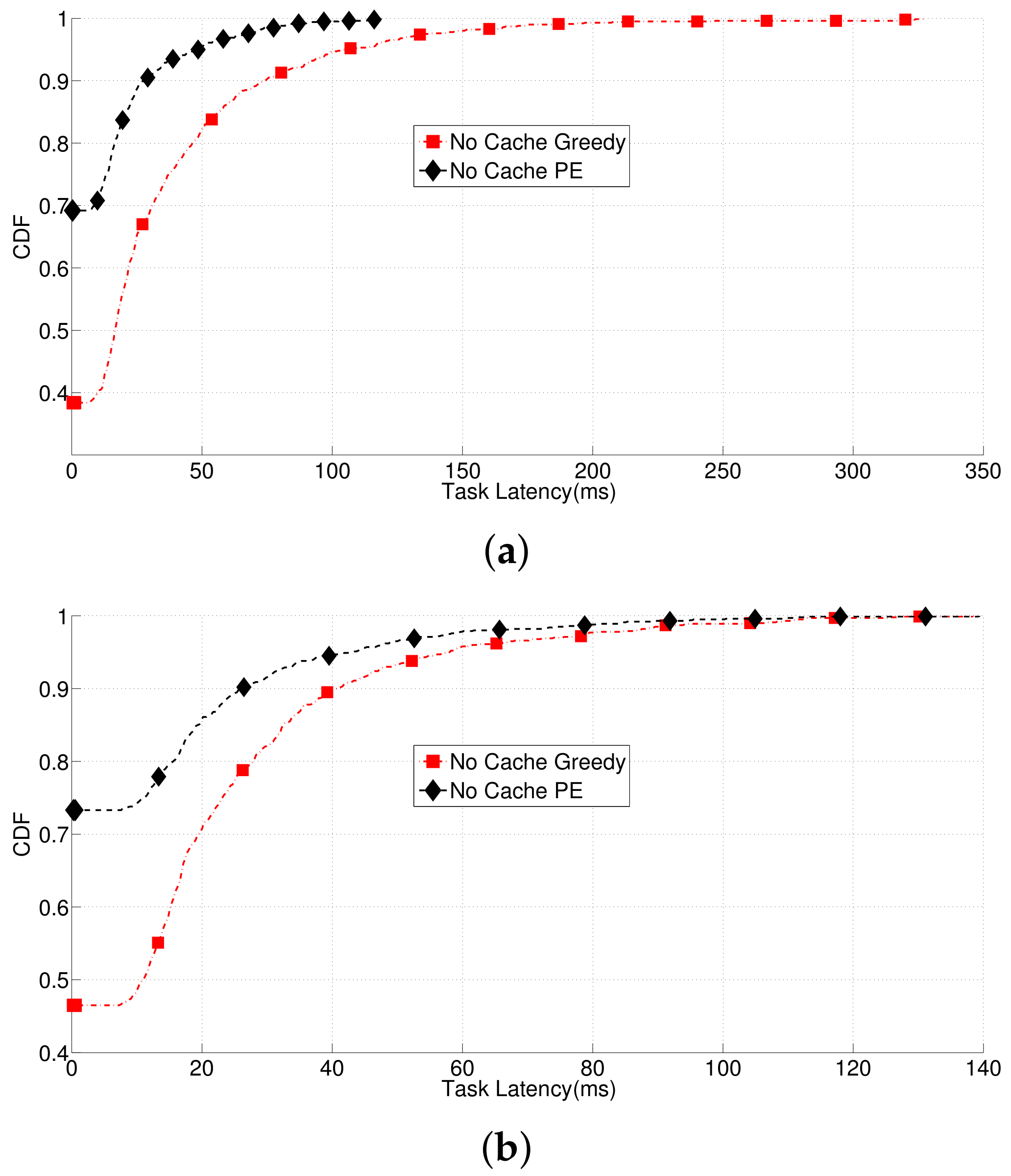
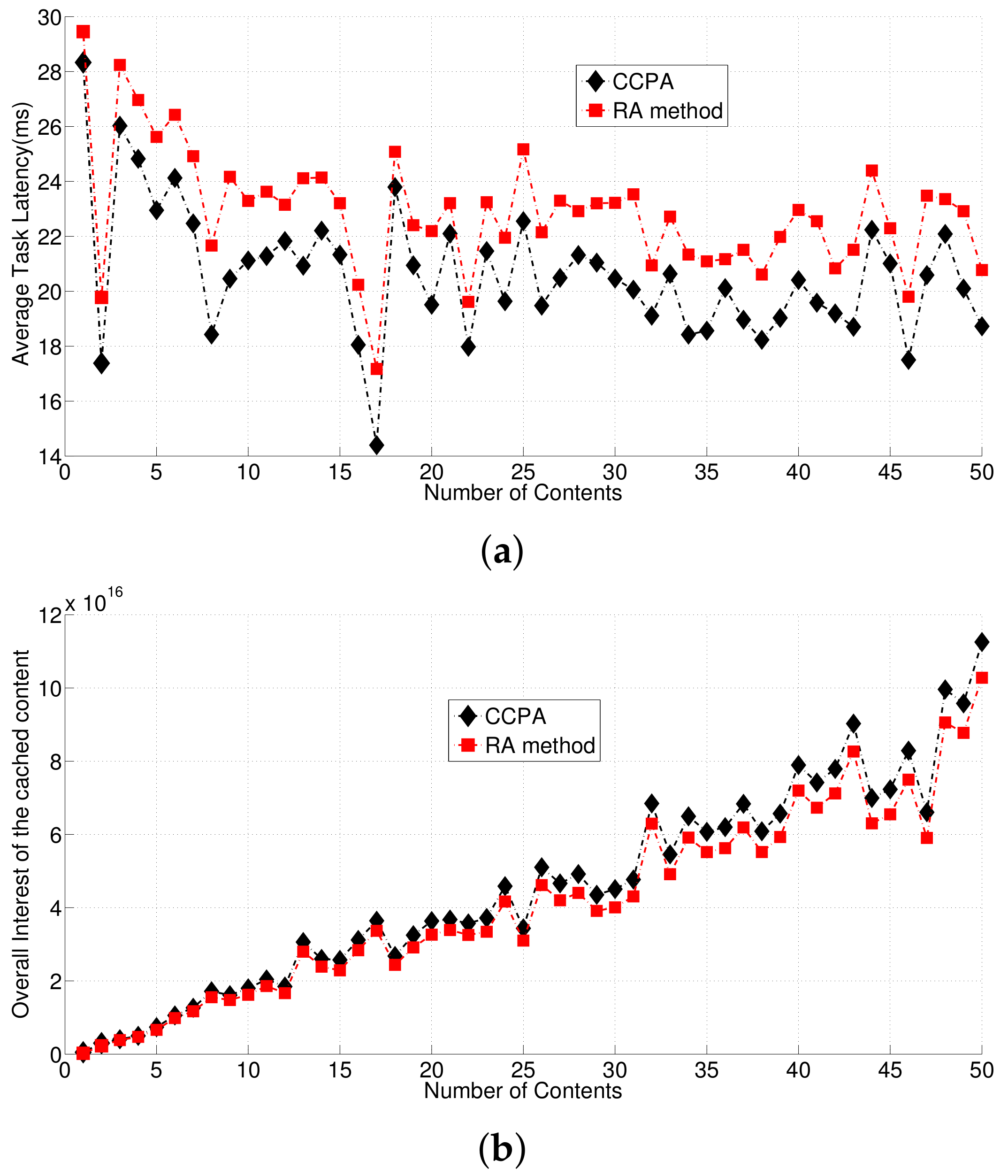
4.1. Simulation Outputs
4.2. Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Cloud Radio Access Network | C-RAN |
| Cache and Multi-layer MEC enabled C-RAN | CMM-CRAN |
| Remote Radio Head | RRH |
| Proportional Fairness | PF |
| Population Evolution | PE |
| User Equipment | UE |
| Fog computing-based RAN | F-RAN |
| High-level Edge Cloud | HEC |
| Cache Content Placement Algorithm | CCPA |
| Radio Block | RB |
| Multi-Dimension Multiple-Choice Knapsack | MMCK |
| Cumulative Distribution Function | CDF |
| Mobile Edge Computing | MEC |
| Service Provide Server | SPS |
| Joint Cache content placement and task Offloading Solution | JCOS |
| Gale-Shaply | GS |
| Analytic Hierarchy Process | AHP |
| Base Band Unit | BBU |
| Maximum Distance Separable | MDS |
| Low-level Edge Cloud | LEC |
| Signal to Interference plus Noise Ratio | SINR |
| Computation Block | CB |
| Random Access | RA |
| Orthogonal Frequency Division Multiplexing | OFDM |
References
- C-RAN The Road Towards Green RAN. China Mobile Research Institute, White Paper v 3.0, December 2013. Available online: http://labs.chinamobile.com/cran/wp-content/uploads/2014/06/20140613-C-RAN-WP-3.0.pdf (accessed on 12 August 2016).
- Mobile Edge Computing Introductory Technical White Paper (PDF). 2014-09-01. Retrieved 2015-10-26. Available online: etsi.org (accessed on 10 December 2017).
- Tran, T.X.; Hajisami, A.; Pandey, P.; Pompili, D. Collaborative Mobile Edge Computing in 5G Networks: New Paradigms, Scenarios, and Challenges. IEEE Commun. Mag. 2017, 55, 54–61. [Google Scholar] [CrossRef]
- China Mobile Research Institute. Toward 5G C-RAN: Requirements, Architecture and Challenges. While Paper, v1.0. 2016. Available online: http://labs.chinamobile.com/cran/wp-content/uploads/2016/11/WP-Toward-5G-C-RAN-Requirements-Architecture-and-Challenges-v1.0.pdf (accessed on 12 December 2017).
- Wang, X.; Leng, S.; Yang, K. Social-Aware Edge Caching in Fog Radio Access Networks. IEEE Access 2017, 5, 8492–8501. [Google Scholar] [CrossRef]
- Peng, M.; Yan, S.; Zhang, K.; Wang, C. Fog-computing-based radio access networks: Issues and challenges. IEEE Netw. 2016, 30, 46–53. [Google Scholar] [CrossRef]
- Shih, Y.Y.; Chung, W.H.; Pang, A.C.; Chiu, T.C.; Wei, H.Y. Enabling Low-Latency Applications in Fog-Radio Access Networks. IEEE Netw. 2017, 31, 52–58. [Google Scholar] [CrossRef]
- Bonomi, F.; Milito, R.; Zhu, J.; Addepalli, S. Fog computing and its role in the Internet of Things. In Proceedings of the 1st Edition of the MCC Workshop on Mobile Cloud Computing, Helsinki, Finland, 17 August 2012; pp. 13–16. [Google Scholar]
- Lien, S.Y.; Hung, S.C.; Hsu, H.; Chen, K.C. Collaborative radio access of heterogeneous cloud radio access networks and edge computing networks. In Proceedings of the 2016 IEEE International Conference on Communications Workshops (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 193–199. [Google Scholar]
- Mei, H.; Wang, K.; Yang, K. Multi-Layer Cloud-RAN With Cooperative Resource Allocations for Low-Latency Computing and Communication Services. IEEE Access 2017, 5, 19023–19032. [Google Scholar] [CrossRef]
- Wang, K.; Yang, K.; Magurawalage, C. Joint energy minimization and resource allocation in C-RAN with mobile cloud. IEEE Trans. Cloud Comput. 2016. [Google Scholar] [CrossRef]
- Wang, K.; Yang, K.; Wang, X.; Magurawalage, C. Cost-effective resource allocation in C-RAN with mobile cloud. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Zhao, P.; Tian, H.; Qin, C.; Nie, G. Energy-Saving Offloading by Jointly Allocating Radio and Computational Resources for Mobile Edge Computing. IEEE Access 2017, 5, 11255–11268. [Google Scholar] [CrossRef]
- Li, T.; Magurawalage, C.S.; Wang, K.; Xu, K.; Yang, K.; Wang, H. On Efficient Offloading Control in Cloud Radio Access Network with Mobile Edge Computing. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; pp. 2258–2263. [Google Scholar]
- Zhang, K.; Mao, Y.; Leng, S.; Zhao, Q.; Li, L.; Peng, X.; Pan, L.; Maharjan, S.; Zhang, Y. Energy-Efficient Offloading for Mobile Edge Computing in 5G Heterogeneous Networks. IEEE Access 2016, 4, 5896–5907. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, K.; Xuan, D.; Yang, K. Optimal Task Allocation In Near-Far Computing Enhanced C-RAN for Wireless Big Data Processing. IEEE Wirel. Commun. 2017. [Google Scholar] [CrossRef]
- Liao, J.; Wong, K.K.; Zhang, Y.; Zheng, Z.; Yang, K. Coding, Multicast, and Cooperation for Cache-Enabled Heterogeneous Small Cell Networks. IEEE Trans. Wirel. Commun. 2017, 16, 6838–6853. [Google Scholar] [CrossRef]
- Cao, Y.; Tao, M.; Xu, F.; Liu, K. Fundamental Storage-Latency Tradeoff in Cache-Aided MIMO Interference Networks. IEEE Trans. Wirel. Commun. 2017, 16, 5061–5076. [Google Scholar] [CrossRef]
- Zhou, B.; Cui, Y.; Tao, M. Optimal Dynamic Multicast Scheduling for Cache-Enabled Content-Centric Wireless Networks. IEEE Trans. Wirel. Commun. 2017, 65, 2956–2970. [Google Scholar] [CrossRef]
- Xu, X.; Tao, M. Modeling, Analysis, and Optimization of Coded Caching in Small-Cell Networks. IEEE Trans. Wirel. Commun. 2017, 65, 3415–3428. [Google Scholar]
- Hamidouche, K.; Saad, W.; Debbah, M. Many-to-many matching games for proactive social-caching in wireless small cell networks. In Proceedings of the 12th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt), Hammamet, Tunisia, 13 January 2014; pp. 569–574. [Google Scholar]
- Sun, Z.; Yin, C.; Yue, G. Reduced-complexity proportional fair scheduling for ofdma systems. In Proceedings of the International Conference on Communications, Circuits and Systems, Guilin, China, 25–28 June 2006. [Google Scholar]
- Mei, H.; Bigham, J.; Jiang, P.; Bodanese, E. Distributed Dynamic Frequency Allocation in Fractional Frequency Reused Relay Based Cellular Networks. IEEE Trans. Wirel. Commun. 2013, 61, 1327–1336. [Google Scholar]
- Gale, D.; Shapley, L. College admissions and the stability of marriage. Am. Math. Mon. 1962, 69, 9–15. [Google Scholar] [CrossRef]
- Roth, A. Stability and polarization of interests in job matching. Econometrica 1984, 52, 47–57. [Google Scholar] [CrossRef]
- Niyato, D.; Hossain, E. Dynamics of Network Selection in Heterogeneous Wireless Networks: An Evolutionary Game Approach. IEEE Trans. Veh. Technol. 2009, 58, 2008–2017. [Google Scholar] [CrossRef]
- Osborne, M.J. An Introduction to Game Theory; Oxford University Press: London, UK, 2003. [Google Scholar]
- Shah, I.A.; Jan, S.; Khan, I.; Qamar, S. An Overview of Game Theory and its Applications in Communication Networks. Available online: www.ijmse.org/Volume3/Issue4/paper2.pdf (accessed on 7 April 2018).
- Pervaiz, H.; Mei, H.; Bigham, J.; Jiang, P. Enhanced cooperation in heterogeneous wireless networks using coverage adjustment. In Proceedings of the 6th International Wireless Communications and Mobile Computing Conference, Caen, France, 28 June–2 July 2010; pp. 241–245. [Google Scholar]
- Fischer, S.; Vocking, B. Evolutionary game theory with applications to adaptive routing. In Proceedings of the ECCS, Paris, France, 17 November 2005; pp. 104–109. [Google Scholar]
- Hammerstein, P.; Selten, R. Game theory and evolutionary biology. In Handbook of Game Theory; Aumann, R.J., Hart, S., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1994; Volume 2, pp. 929–993. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw Hill International: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
| Elements | UEs’ Sensitivenesses to Each Element | |||
|---|---|---|---|---|
| Voice | Data-Process | Stream | Multi-Media | |
| Cloud Capacity | 2(low) | 8(high) | 5(medium) | 9(high) |
| Fh Constraint | 8(high) | 1(low) | 6(medium) | 8(high) |
| RF Constraint | 9(high) | 3(low) | 4(medium) | 7(high) |
| Parameter | Value |
|---|---|
| Number of RRH: J | 20 |
| Number of UEs in a RRH: | |
| Number of contents: V | |
| Capacity of a LEC: | |
| Capacity of HEC: | |
| CPU requirement of voice task | |
| CPU requirement of data process task | 30 ∼ 50 |
| CPU requirement of data stream task | |
| CPU requirement of multi-media task | |
| Sensitivity for sensitized element | |
| Sensitivity for medium-sensitized element | |
| Sensitivity for non-sensitized element | |
| Cache capacity of each RRH | |
| Size of a content | |
| Data rate of Fronthaul per RRH | 100 Mbs ∼ 200 Mbs |
| Data rate of a RF link | |
| The interest of a UE to a content: | |
| Maximal allowed task latency: | 200 ms |
| Maximal allowed energy cost of each user task: | 5 J |
| Maximal step of the PE procedure: | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, H.; Wang, K.; Yang, K. Joint Cache Content Placement and Task Offloading in C-RAN Enabled by Multi-Layer MEC. Sensors 2018, 18, 1826. https://doi.org/10.3390/s18061826
Mei H, Wang K, Yang K. Joint Cache Content Placement and Task Offloading in C-RAN Enabled by Multi-Layer MEC. Sensors. 2018; 18(6):1826. https://doi.org/10.3390/s18061826
Chicago/Turabian StyleMei, Haibo, Kezhi Wang, and Kun Yang. 2018. "Joint Cache Content Placement and Task Offloading in C-RAN Enabled by Multi-Layer MEC" Sensors 18, no. 6: 1826. https://doi.org/10.3390/s18061826
APA StyleMei, H., Wang, K., & Yang, K. (2018). Joint Cache Content Placement and Task Offloading in C-RAN Enabled by Multi-Layer MEC. Sensors, 18(6), 1826. https://doi.org/10.3390/s18061826





