Real-Time Monitoring for BDS Signal-In-Space Anomalies Using Ground Observation Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. BDS Ground SIS Monitoring Method
- Combining cleanly BDS ephemeris based on real-time raw data from tracking network.
- The SIS UREs of all the satellites are calculated by the selected tracking stations’ observations.
- The mean value and the standard deviation of the SIS UREs of each satellite observed by each station are calculated, as the prior information.
- The threshold of the SIS UREs is calculated using Equation (1) based on a given confidence level and the prior information obtained in step 3.where is the mean value of the SIS UREs, is the standard deviation of the SIS UREs, and is the quantile of the corresponding confidence . In this step, we assume that the SIS UREs obey a Gaussian distribution.
2.2. Data Source
2.3. Combined Real-Time Broadcast Ephemeris
- Broadcast ephemeris from a number of tracking stations are simultaneously received and added into the set O. Ensure that each satellite can be observed by a number of tracking stations (generally more than three tracking stations) at the same time.
- For each navigation message e in O, if there is already a navigation message f in the set P (its database of different robust parameters) having the same robust parameters as e, then add the fragile parameters of e into f ’s database; otherwise, add e into P.
- For each navigation message f in P, apply majority vote to each fragile parameter (except the Transmission Time of Message (TTOM)) according to f’s database, and record the number of stations that report f.
2.4. Computation of SIS UREs
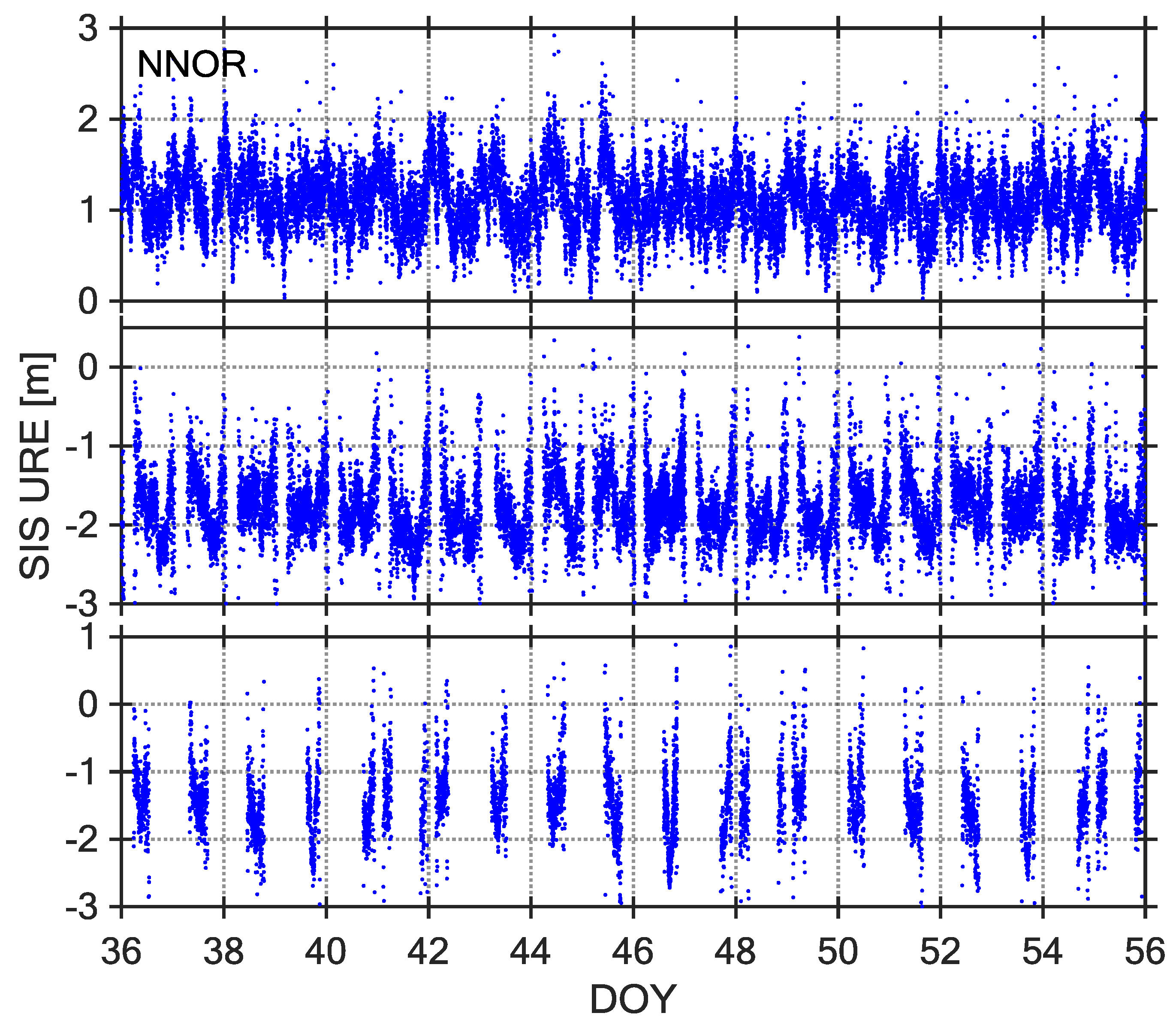
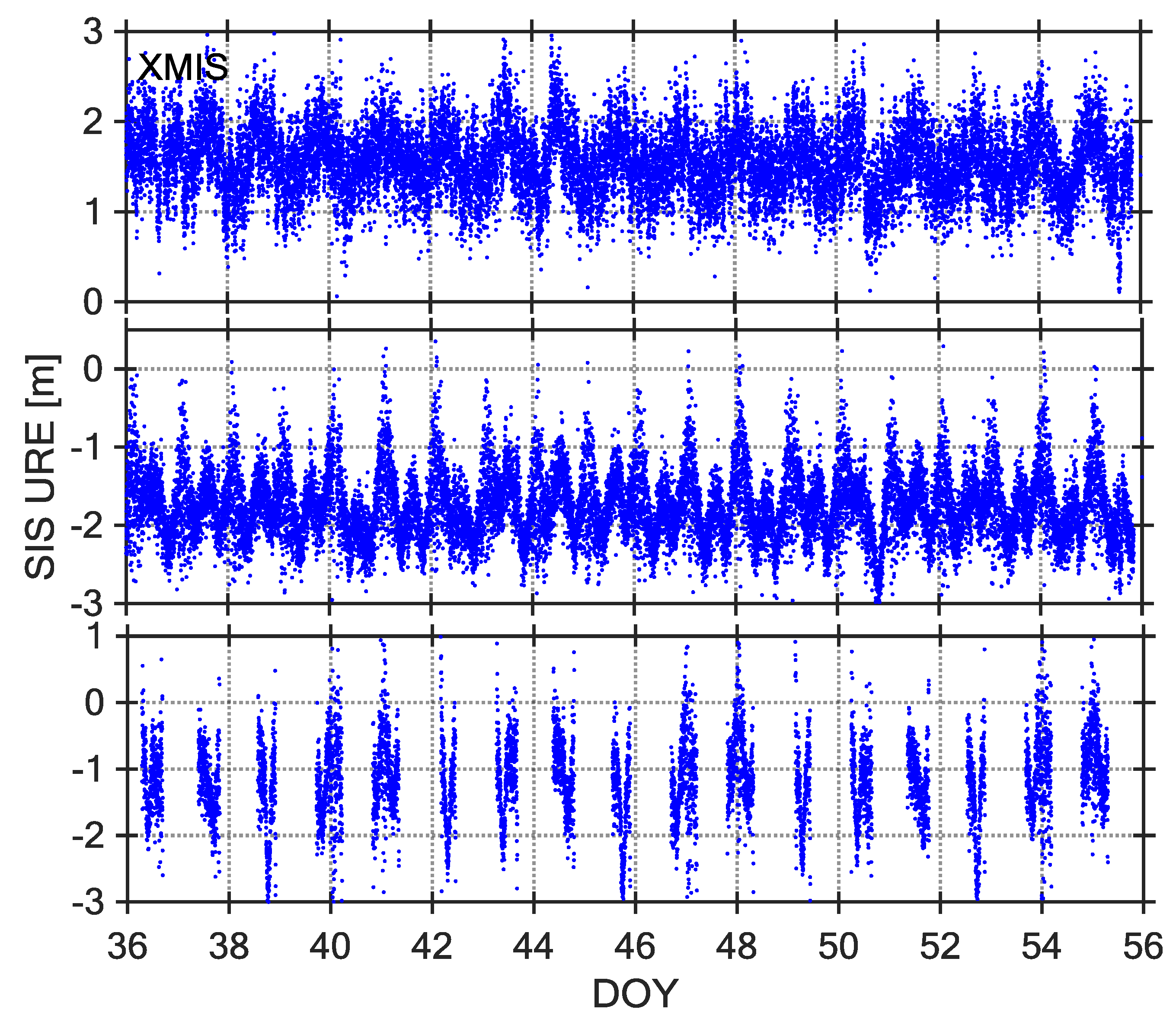
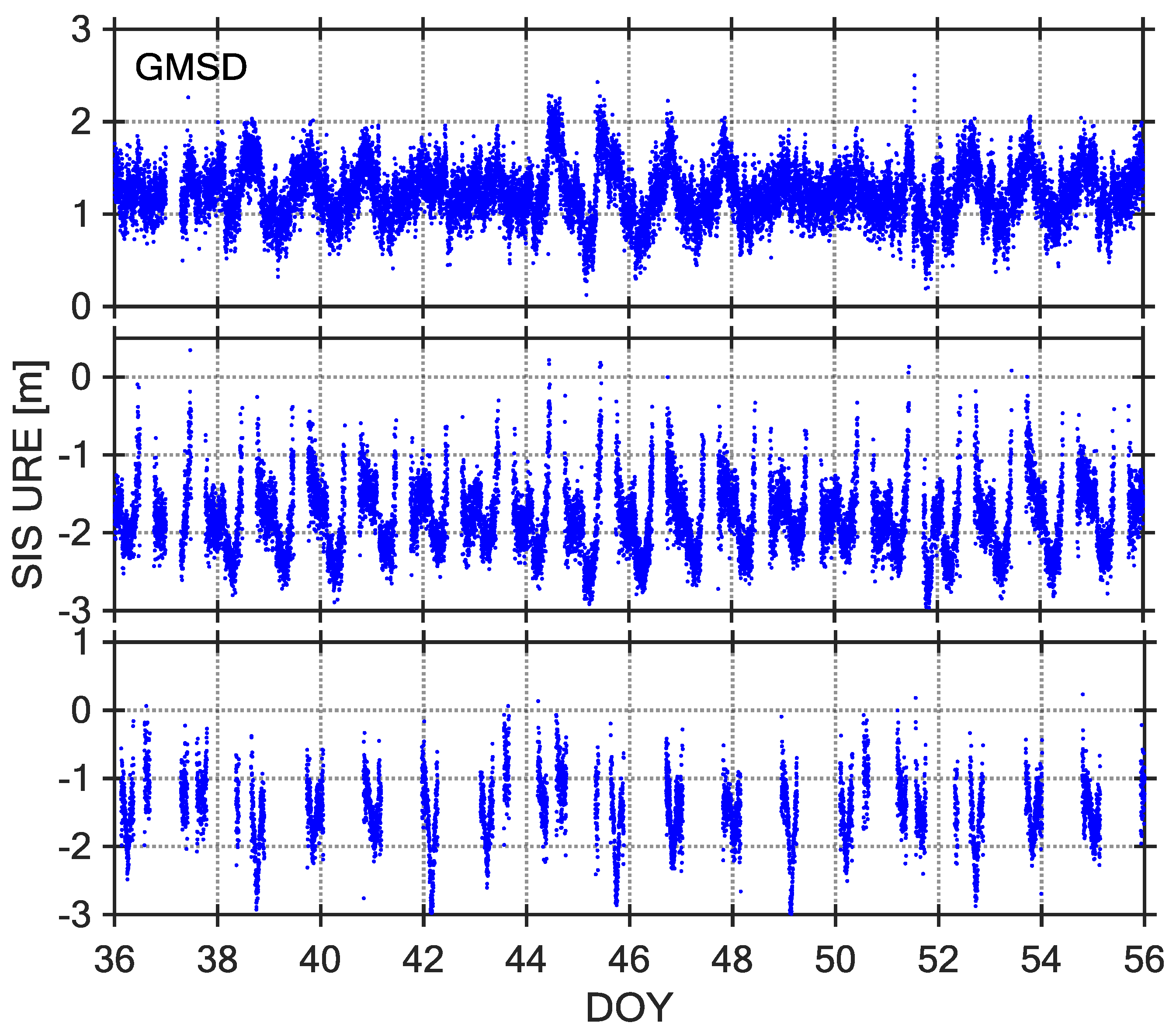
3. BDS SIS URE Analysis and Discussion
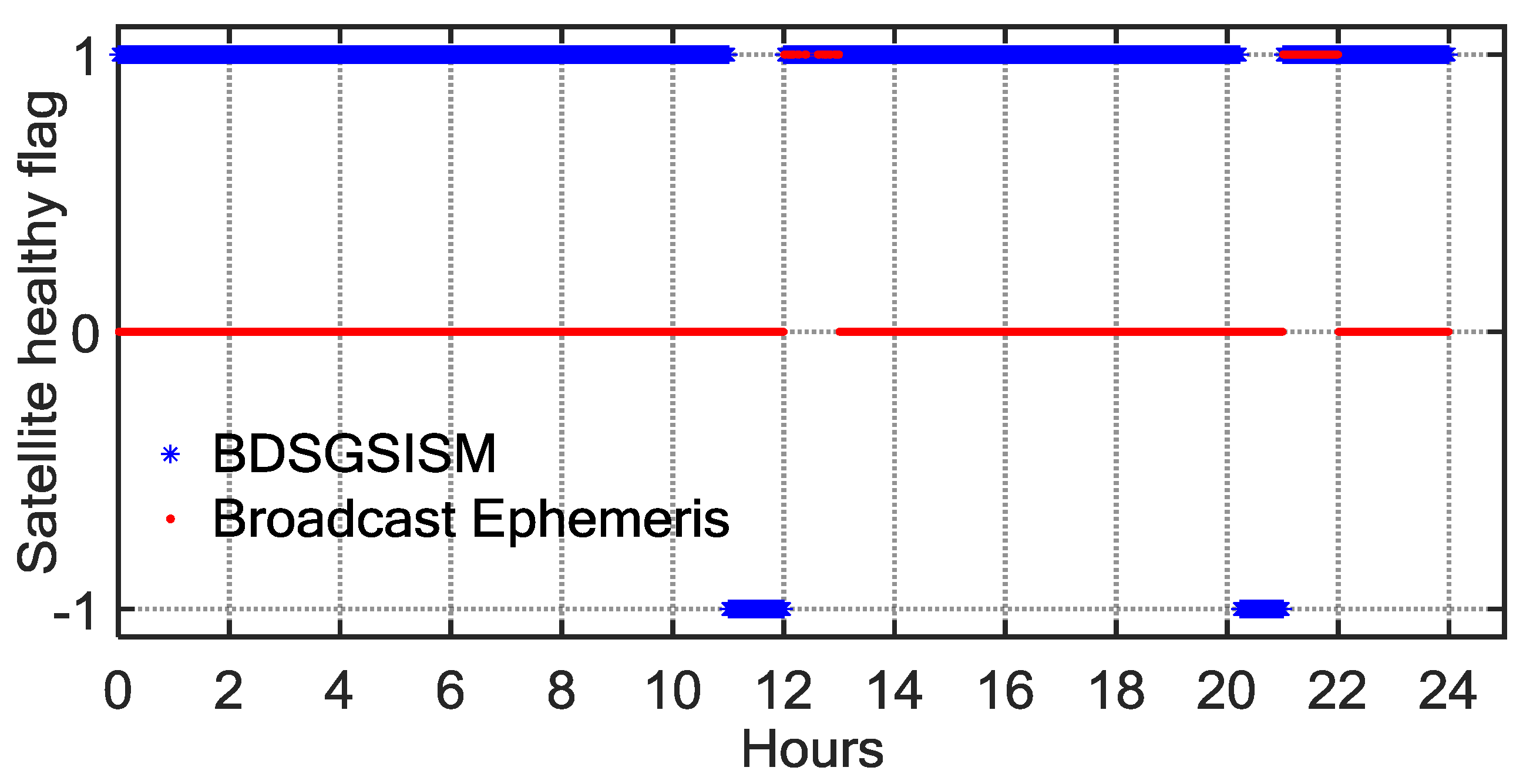
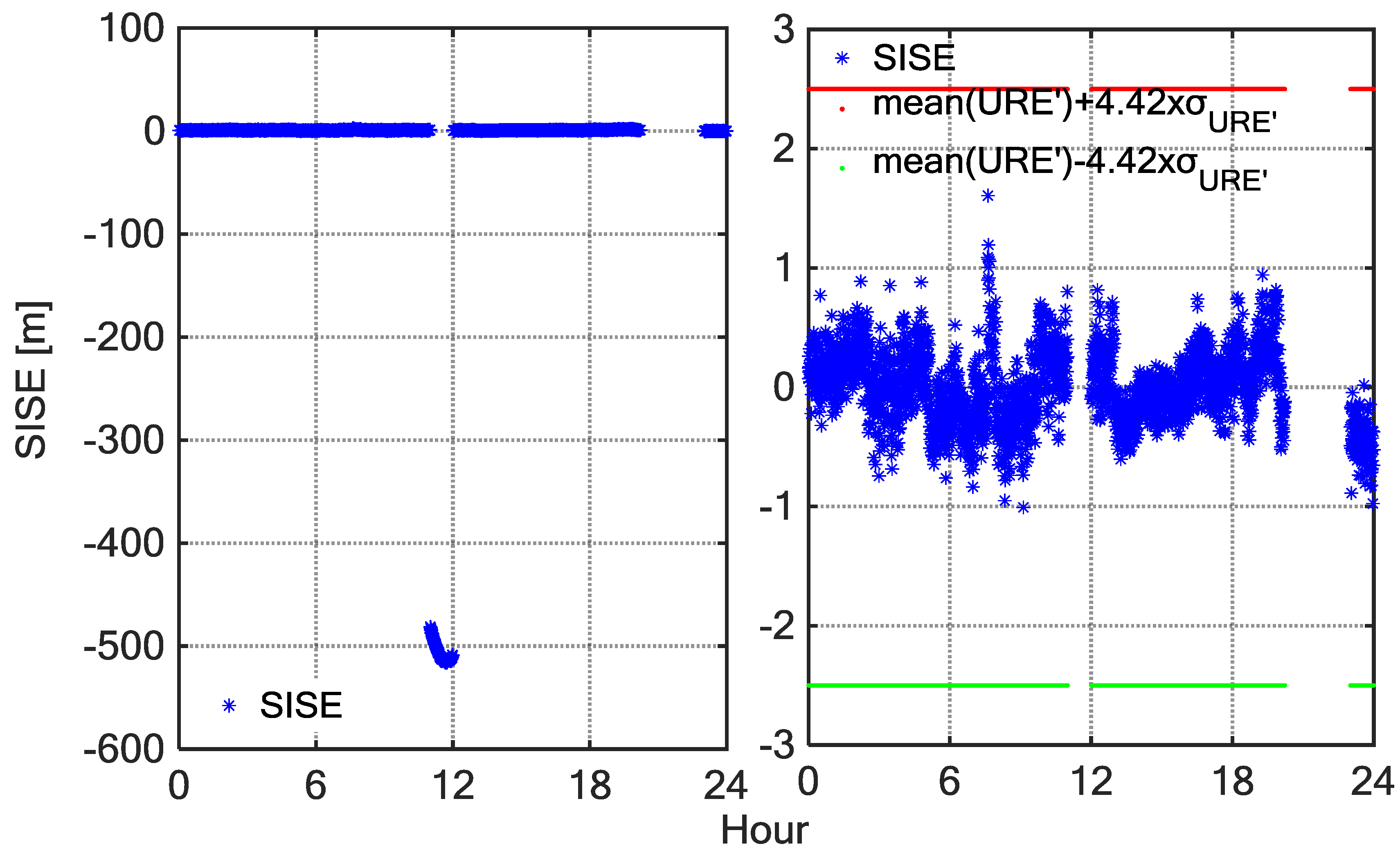
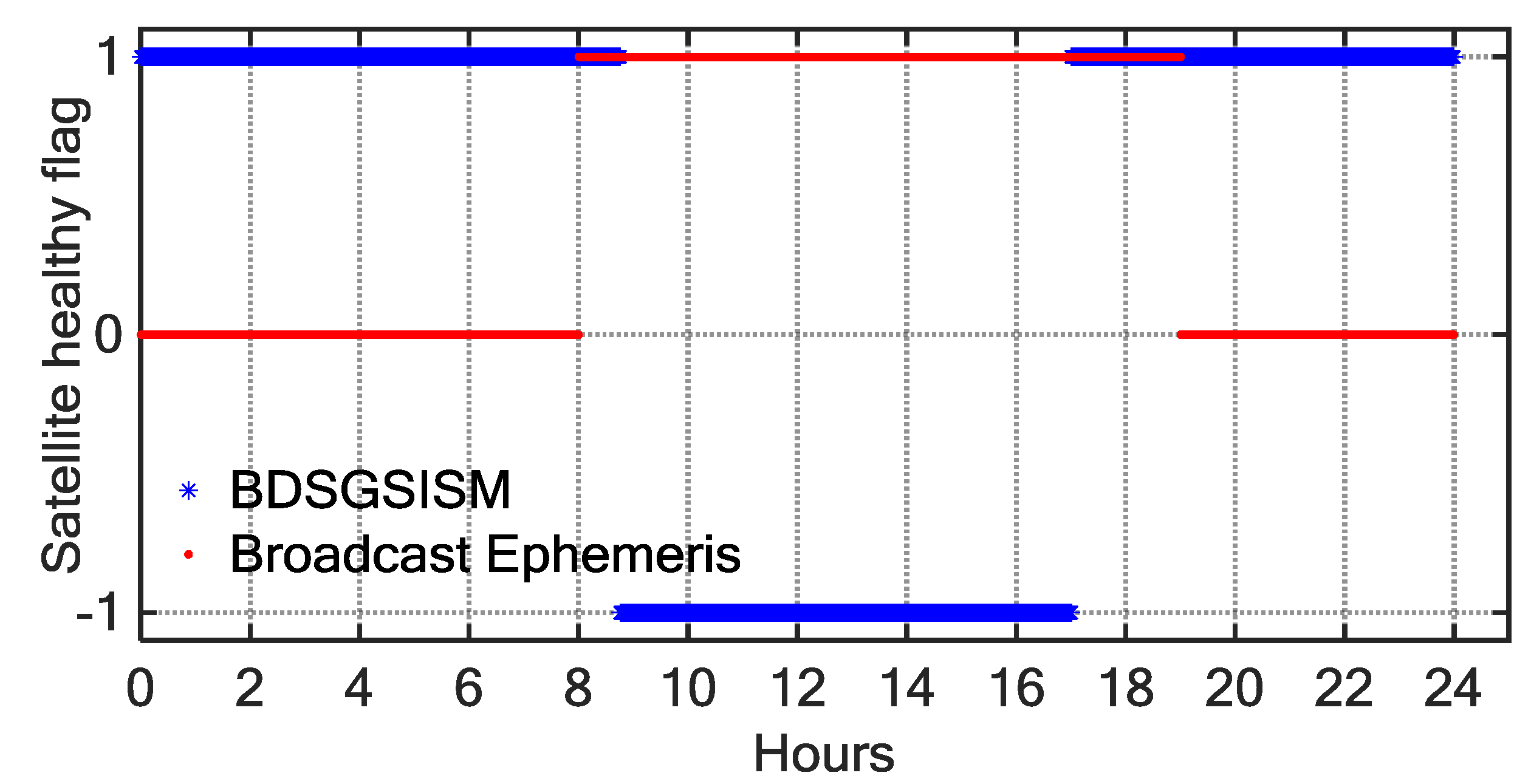
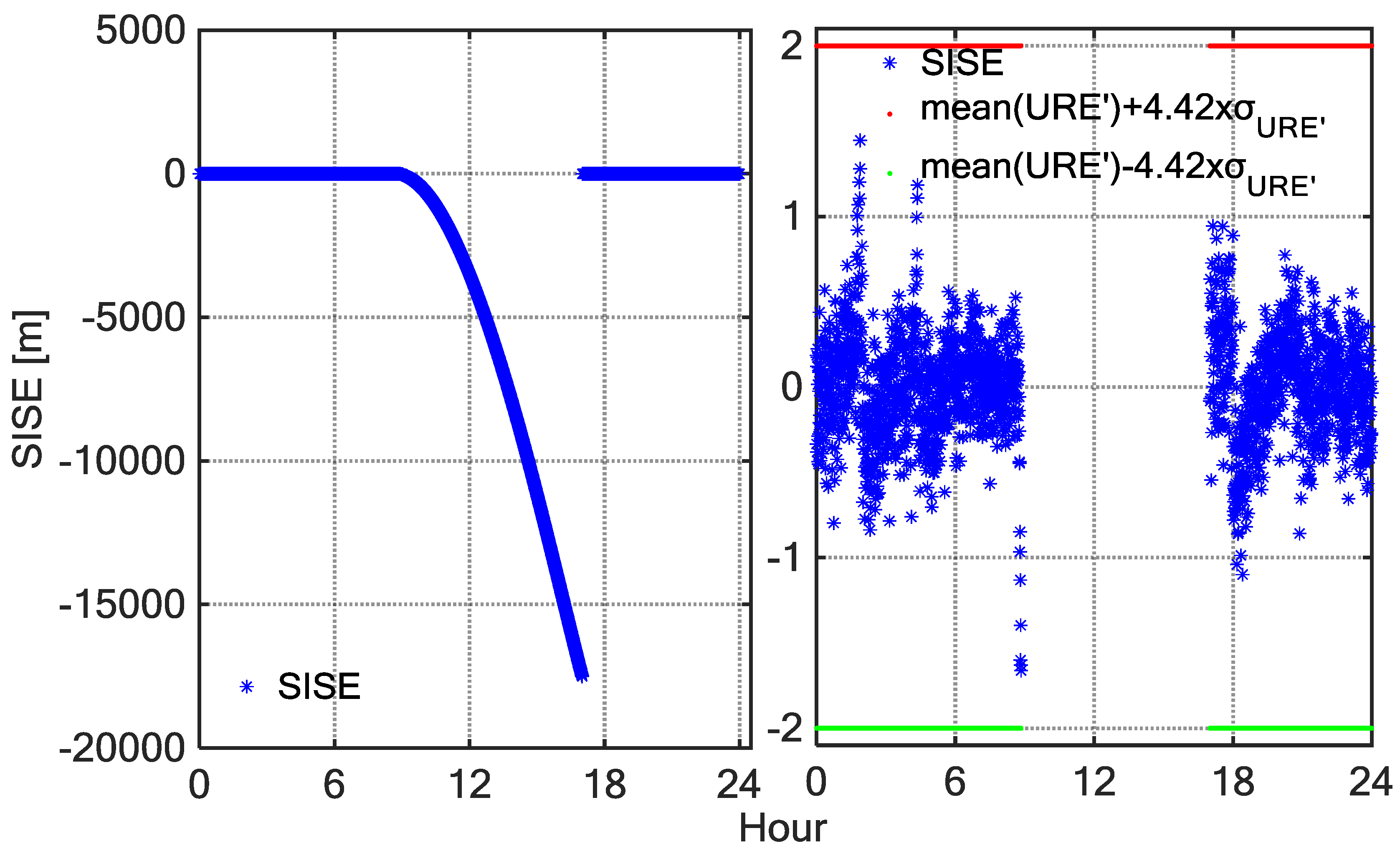
4. Case Studies of BDS SIS Anomalies
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- CSNO. Beidou Navigation Satellite System Signal in Space Interface Control Document, Open Service Signal (Version 2.0); China Satellite Navigation Office (CSNO): Beijing, China, 2013. [Google Scholar]
- Han, C.; Yang, Y.; Cai, Z. Beidou navigation satellite system and its time scales. Metrologia 2011, 48, S213. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, Q.L.; Hu, Z.G.; Liu, J.N. Precise relative positioning using real tracking data from compass geo and igso satellites. GPS Solut. 2013, 17, 103–119. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Shen, J.; Dai, X. Preliminary assessment of the navigation and positioning performance of beidou regional navigation satellite system. Sci. China-Earth Sci. 2014, 57, 144–152. [Google Scholar] [CrossRef]
- Cohenour, C.; Graas, F.V. GPS orbit and clock error distributions. Navigation 2011, 58, 17–28. [Google Scholar] [CrossRef]
- Heng, L.; Gao, G.X.; Walter, T.; Enge, P. Automated verification of potential GPS signal-in-space anomalies using ground observation data. In Proceedings of the IEEE/ION PLANS 2012, Myrtle Beach, SC, USA, 24–26 April 2012; pp. 1111–1118. [Google Scholar]
- Chen, L.; Jiao, W.; Huang, X.; Geng, C.; Ai, L.; Lu, L.; Hu, Z. Study on signal-in-space errors calculation method and statistical characterization of beidou navigation satellite system. In Lecture Notes in Electrical Engineering, Proceedings of the China Satellite Navigation Conference (CSNC), Wuhan, China, 15–17 May 2013; Springer: Berlin, Germany, 2013; Volume 243, pp. 423–434. [Google Scholar]
- Shi, C.; Zheng, F.; Lou, Y.; Gu, S.; Zhang, W.; Dai, X.; Li, X.; Guo, H.; Gong, X.; Shi, C. National bds augmentation service system (nbass) of China: Progress and assessment. Remote Sens. 2017, 9, 837. [Google Scholar]
- Liu, S.A.; Jia, X.L.; Ma, Z.X. The analysis of GNSS SIS accuracy. In Proceedings of the China Satellite Navigation Conference, Xi’an, China, 13–15 May 2015; Sun, J., Liu, J., Fan, S., Lu, X., Eds.; Springer: New York, NY, USA, 2015; Volume 340, pp. 375–386. [Google Scholar]
- Wu, T.; Peck, S. An analysis of satellite integrity monitoring improvement for was. In Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2002), Portland, OR, USA, 24–27 September 2002; pp. 756–765. [Google Scholar]
- DiLellio, J.A. GPS Navigation System with Integrity and Reliability Monitoring Channels. US Patent 7400292, 15 July 2008. [Google Scholar]
- Gao, G.X.; Tang, H.C.; Blanch, J.; Lee, J.; Walter, T.; Enge, P. Methodology and case studies of signal-in-space error calculation top-down meets bottom-up. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (Ion Gnss 2009), Savannah, GA, USA, 22–25 September 2009; pp. 2824–2831. [Google Scholar]
- Heng, L.; Gao, G.X.; Walter, T.; Enge, P.; Inst, N. GPS ephemeris error screening and results for 2006–2009. In Proceedings of the 2010 International Technical Meeting of the Institute of Navigation—ITM 2010, San Diego, CA, USA, 25–27 January 2010; pp. 1014–1022. [Google Scholar]
- Lee, Y.C. Ground monitoring schemes for GPS integrity channel. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 481–489. [Google Scholar] [CrossRef]
- Jan, S.S.; Tao, A.L. The open service signal in space navigation data comparison of the global positioning system and the beidou navigation satellite system. Sensors 2014, 14, 15182–15202. [Google Scholar] [CrossRef] [PubMed]
- Heng, L.; Gao, G.X.; Walter, T.; Enge, P. GPS signal-in-space integrity performance evolution in the last decade. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2932–2946. [Google Scholar] [CrossRef]
- Dins, A.; Ping, Y.; Schipper, B. Statistical characterization of beidou and GPS sis errors in the Asian region. In Proceedings of the 2015 IEEE/AIAA 34th, Digital Avionics Systems Conference, New York, NY, USA, 13–18 September 2015. [Google Scholar]
- CNSO. Beidou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B2A (Version 1.0); China Satellite Navigation Office: Beijing, China, 2017. [Google Scholar]
- Ye, F.; Yuan, Y.; Tan, B.; Ou, J. A robust method to detect beidou navigation satellite system orbit maneuvering/anomalies and its applications to precise orbit determination. Sensors 2017, 17, 1129. [Google Scholar] [CrossRef] [PubMed]
- Saastamoinen, J.; Richard, J.R. Simultaneous drying and pyrolysis of solid fuel particles. Combust. Flame 1996, 106, 288–300. [Google Scholar] [CrossRef]
- Schmid, R.; Rothacher, M.; Thaller, D.; Steigenberger, P. Absolute phase center corrections of satellite and receiver antennas. GPS Solut. 2005, 9, 283–293. [Google Scholar] [CrossRef]
- Shively, C.A. A gaussian mixture model for error distributions used in assessing raim performance. In Proceedings of the 2012 International Technical Meeting of the Institute of Navigation, Newport Beach, CA, USA, 30–31 January 2012; pp. 1590–1602. [Google Scholar]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Hugentobler, U.; Teunissen, P.; Nakamura, S. Initial assessment of the compass/beidou-2 regional navigation satellite system. GPS Solut. 2013, 17, 211–222. [Google Scholar] [CrossRef]
- Wanninger, L.; Beer, S. Beidou satellite-induced code pseudorange Variations: Diagnosis and therapy. GPS Solut. 2015, 19, 639–648. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Broadcast versus precise Ephemerides: A multi-gnss perspective. GPS Solut. 2015, 19, 321–333. [Google Scholar] [CrossRef]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of multipath effect in gnss short baseline positioning by the multipath hemispherical map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Panicciari, T.; Soliman, M.A.; Moura, G. Evaluation of a gnss receiver performance in different multipath environments with a novel real-time multipath simulation system. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS + 2017), Portland, OR, USA, 25–29 September 2017; pp. 427–435. [Google Scholar]
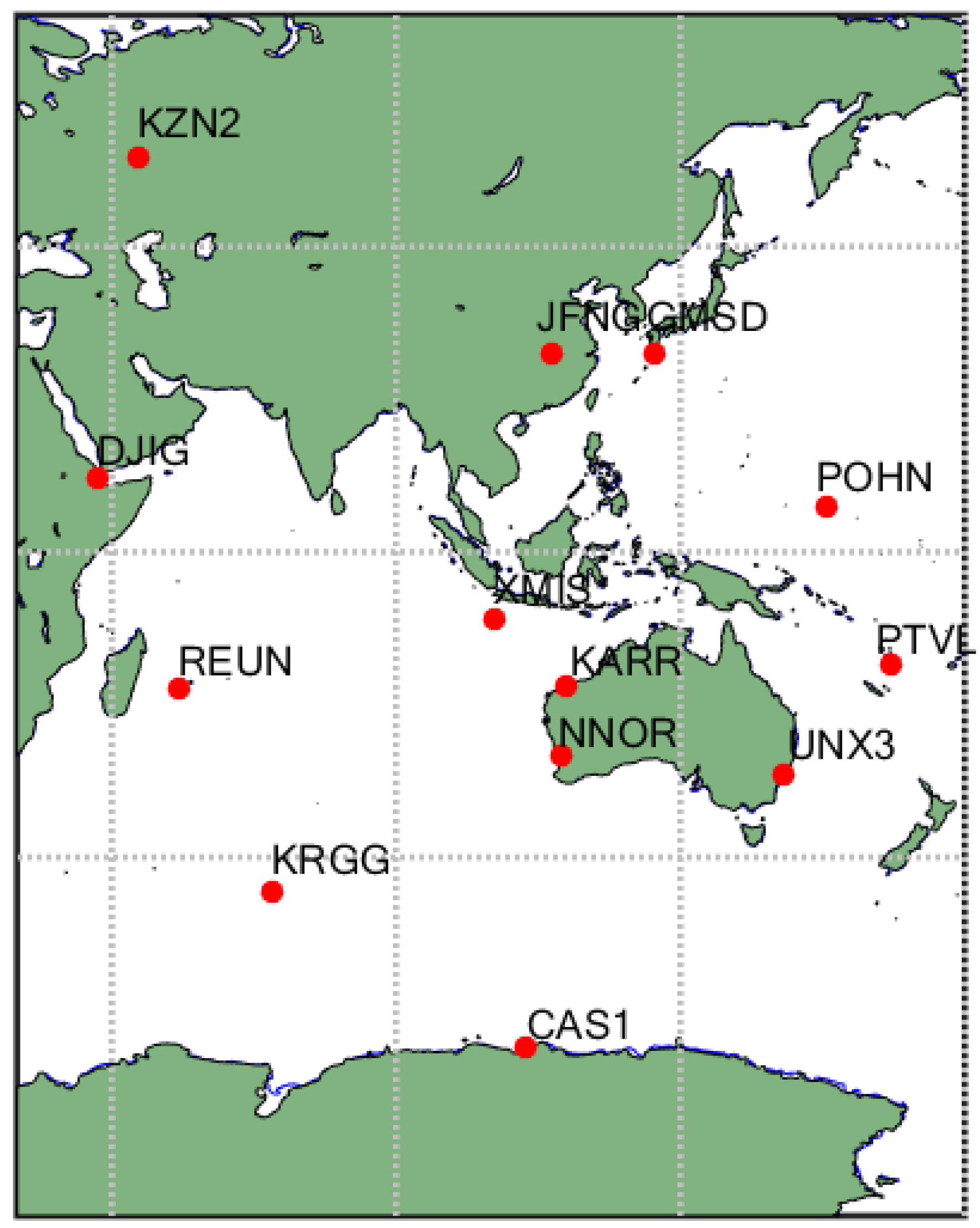

| Tracking Stations | Receiver Type | Antenna Type | PRN of Tracking |
|---|---|---|---|
| CAS1 | Trimble NETR9 | LEIAR25.R3 | C01 C03 C06 C07 C08 C09 C10 C11 C12 C14 |
| DJIG | Trimble NETR9 | TRM59800.00 | C02 C03 C05 C06 C07 C08 C09 C10 C11 C12 C14 |
| GMSD | Trimble NETR9 | TRM59800.00 | C01 C02 C03 C04 C06 C07 C08 C09 C10 C11 C12 C14 |
| KARR | Trimble NETR9 | TRM59800.00 | C01 C03 C04 C05 C06 C07 C08 C09 C10 C11 C12 C14 |
| KRGG | Leica GR10 | LEIAR25.R4 | C02 C03 C05 C06 C07 C08 C09 C10 C11 C12 C14 |
| KZN2 | Trimble NETR9 | TRM59800.00 | C02 C05 C06 C07 C08 C09 C10 C11 C12 C14 |
| JFNG | Trimble NETR9 | TRM59800.00 | C01 C02 C03 C04 C05 C06 C07 C08 C09 C10 C11 C12 C14 |
| NNOR | SEPT POLARX4 | SEPCHOKE_MC | C01 C02 C03 C04 C05 C06 C07 C08 C09 C10 C11 C12 C14 |
| POHN | Trimble NETR9 | TRM59800.00 | C01 C03 C04 C06 C07 C08 C09 C10 C11 C12 C14 |
| PTVL | Trimble NETR | TRM59800.00 | C01 C03 C04 C06 C07 C08 C09 C10 C11 C12 C14 |
| REUN | Trimble NETR9 | TRM55971.00 | C02 C03 C05 C06 C07 C08 C09 C10 C11 C12 C14 |
| UNX3 | SEPT ASTERX3 | LEIAR25.R3 | C01 C03 C04 C06 C07 C08 C09 C10 C11 C12 C14 |
| XMIS | Trimble NETR9 | TRM59800.00 | C01 C03 C04 C05 C06 C07 C08 C09 C10 C11 C12 C14 |
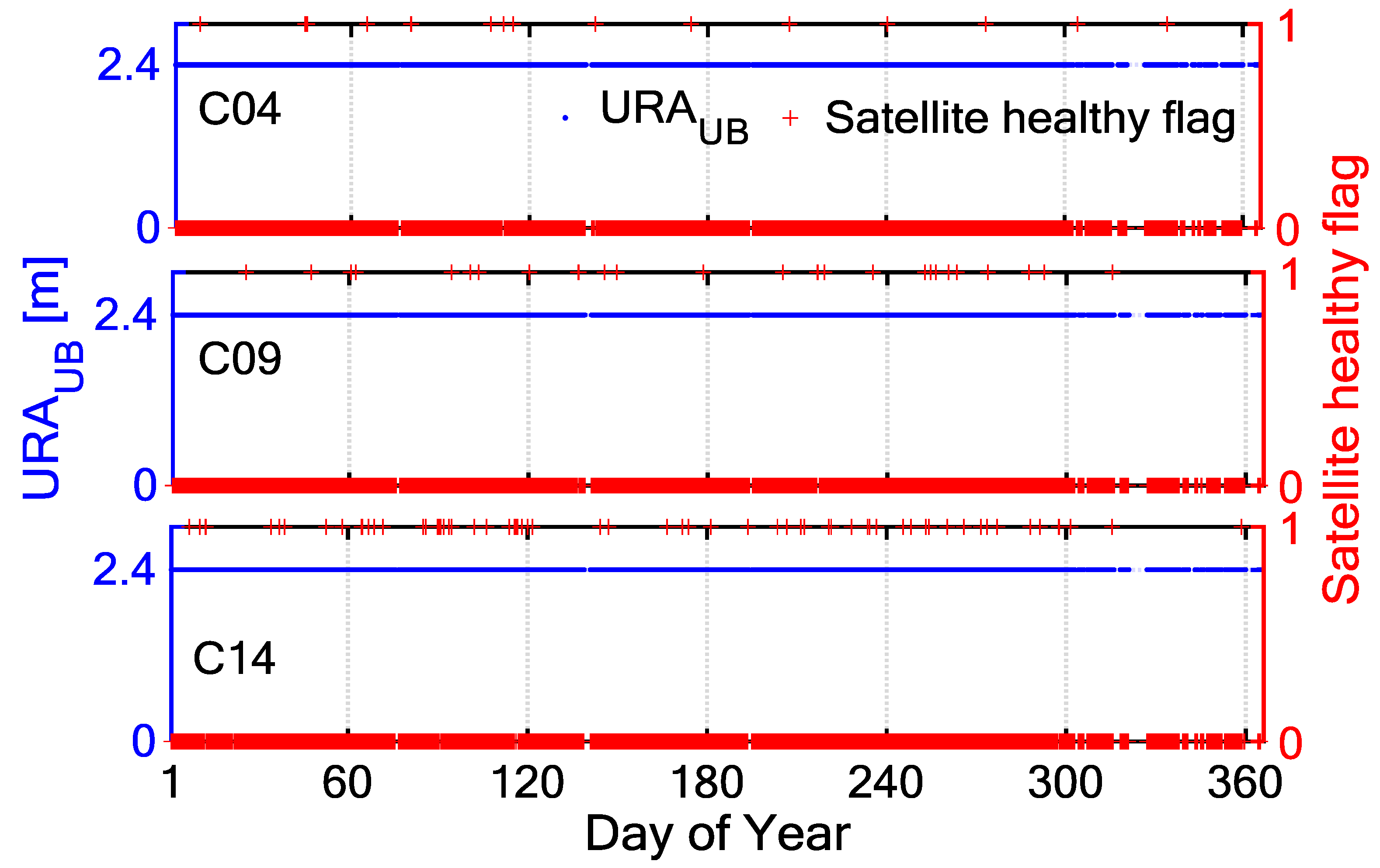
| Station | Frequency | C04 | C09 | C14 | |||
|---|---|---|---|---|---|---|---|
| Mean/m | STD/m | Mean/m | STD/m | Mean/m | STD/m | ||
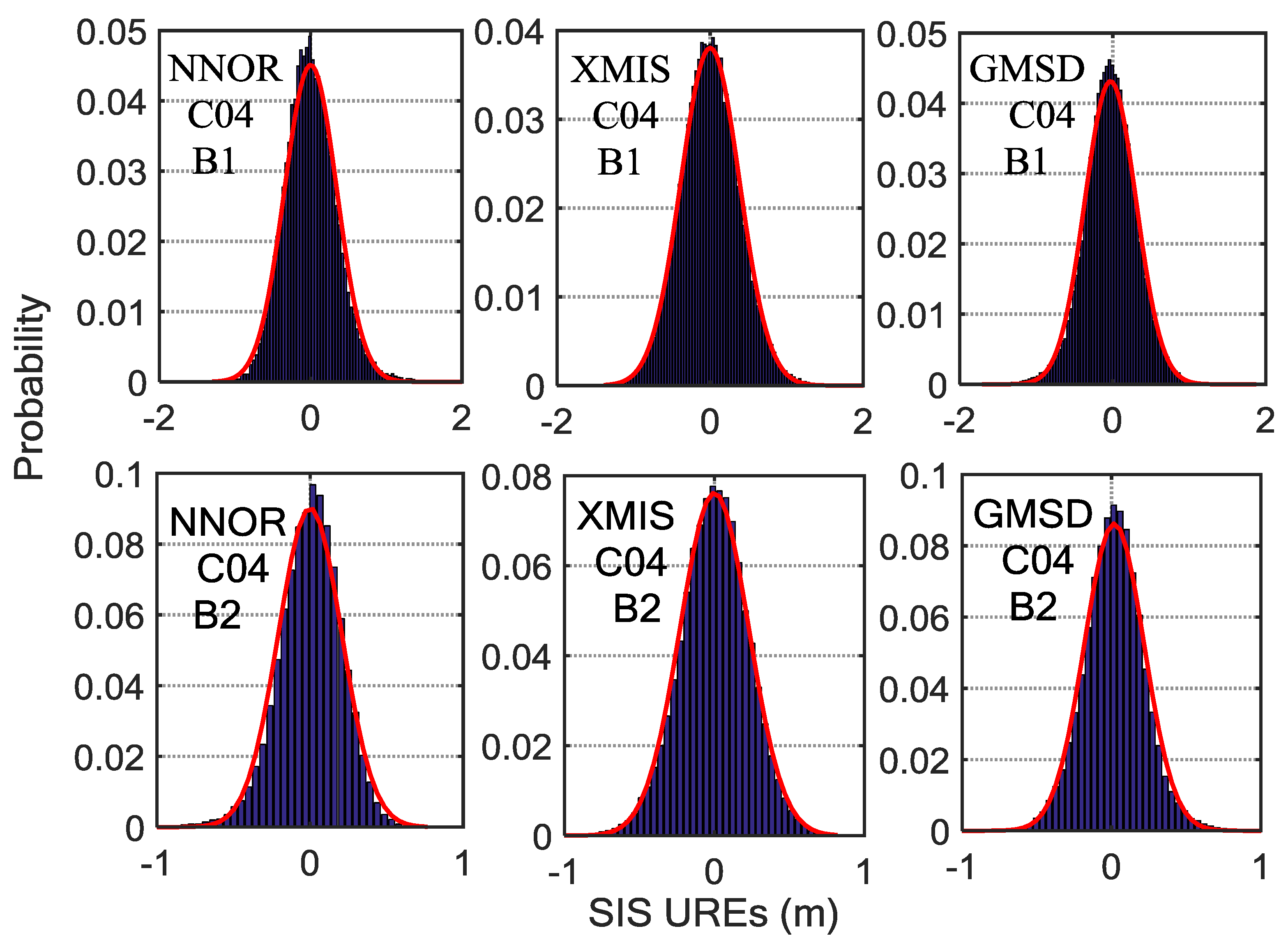
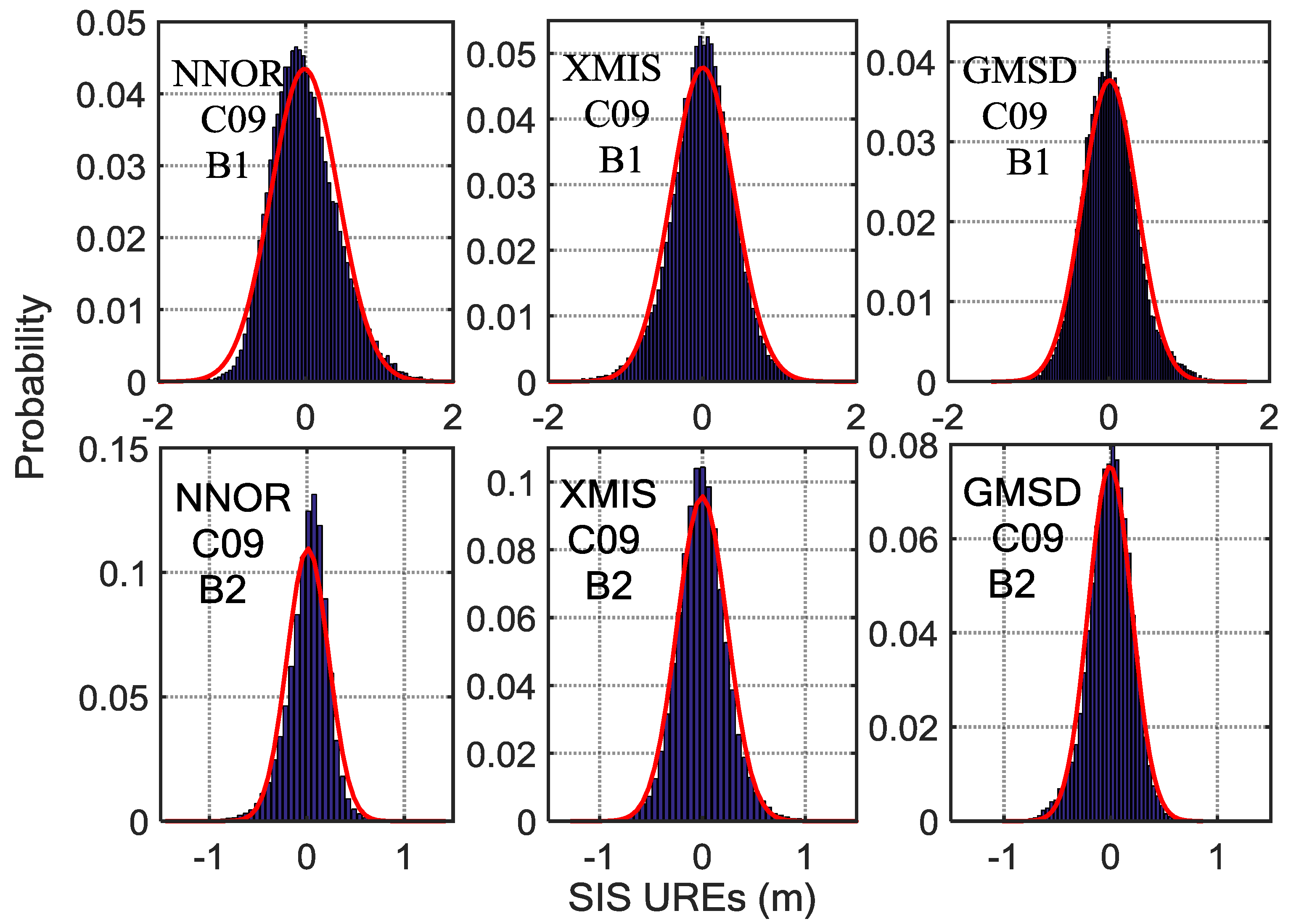
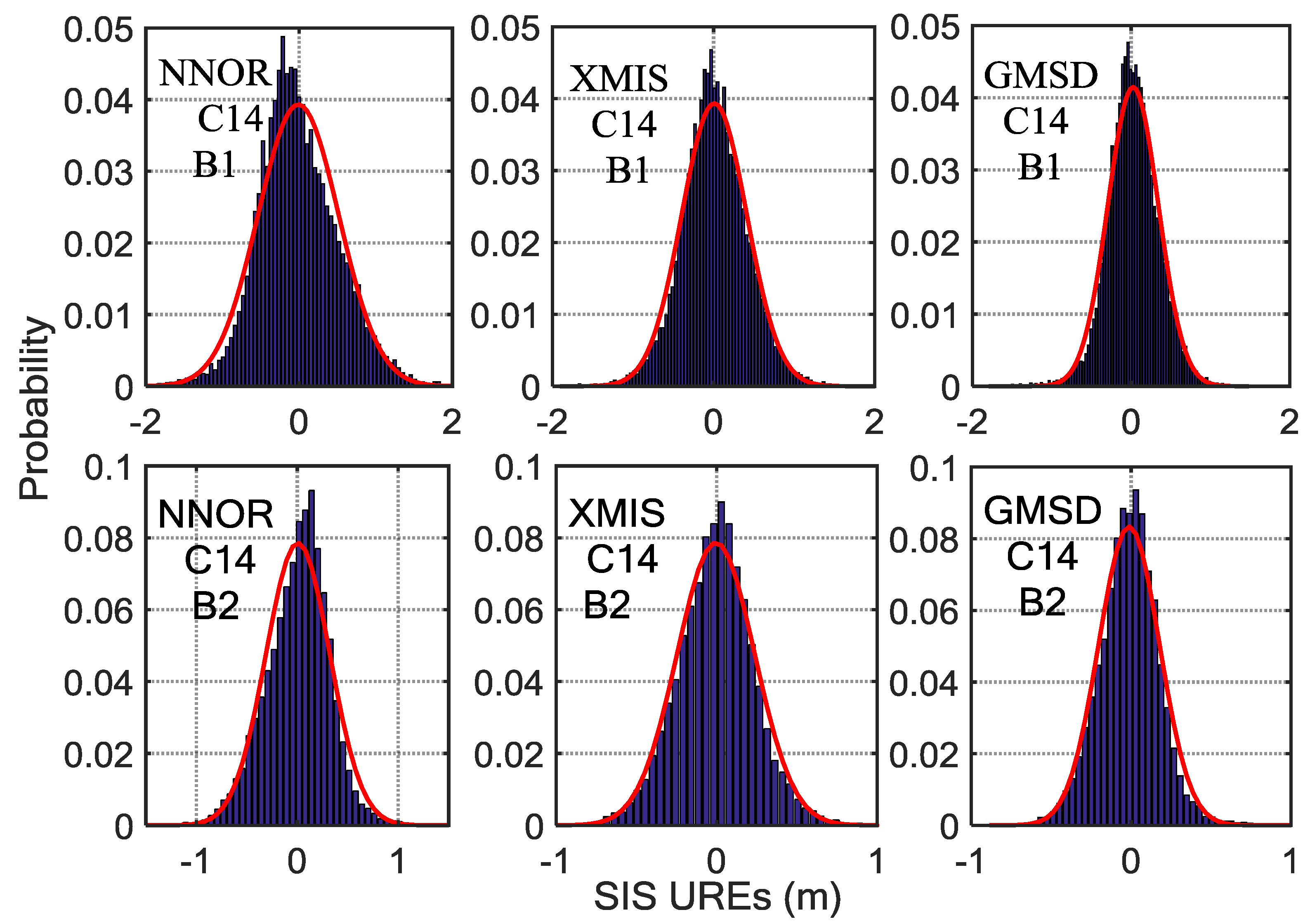
| NNOR | B1 | 0 | 0.35 | −0.02 | 0.46 | −0.01 | 0.53 |
| B2 | 0 | 0.21 | 0.01 | 0.21 | 0.01 | 0.32 | |
| XMIS | B1 | 0 | 0.38 | 0 | 0.41 | 0.01 | 0.40 |
| B2 | 0 | 0.23 | 0 | 0.24 | 0 | 0.24 | |
| GMSD | B1 | 0.05 | 0.33 | 0 | 0.37 | 0.02 | 0.32 |
| B2 | 0.06 | 0.20 | 0 | 0.21 | −0.01 | 0.19 | |
| Satellite | PRN | Date | Start Time | Duration (Minutes) |
|---|---|---|---|---|
| G04 | C04 | 6 November 2015 | 07:29 | 32 |
| I01 | C06 | 7 November 2015 | 03:23 | 41 |
| I02 | C07 | 7 November 2015 | 11:17 | 50 |
| M03 | C11 | 8 November 2015 | 15:15 | 44 |
| G06 | C02 | 11 November 2015 | 04:08 | 51 |
| G03 | C03 | 11 November 2015 | 07:40 | 21 |
| G04 | C04 | 14 November 2015 | 02:29 | 93 |
| I05 | C10 | 14 November 2015 | 12:00 | 20 |
| I02 | C07 | 14 November 2015 | 15:30 | 47 |
| M03 | C11 | 14 November 2015 | 17:55 | 365 |
| M03 | C11 | 15 November 2015 | 00:01 | 180 |
| G06 | C02 | 15 November 2015 | 05:18 | 42 |
| G06 | C02 | 19 November 2015 | 06:10 | 51 |
| G06 | C02 | 21 November 2015 | 07:07 | 53 |
| G06 | C02 | 27 November 2015 | 01:44 | 29 |
| G06 | C02 | 1 December 2015 | 00:25 | 81 |
| I01 | C06 | 2 December 2015 | 01:42 | 112 |
| G06 | C02 | 7 December 2015 | 20:08 | 52 |
| G03 | C03 | 8 December 2015 | 07:59 | 61 |
| G04 | C04 | 8 December 2015 | 21:23 | 38 |
| G06 | C02 | 9 December 2015 | 19:57 | 63 |
| I01 | C06 | 11 December 2015 | 06:40 | 62 |
| I02 | C07 | 11 December 2015 | 09:02 | 84 |
| G06 | C02 | 12 December 2015 | 11:00 | 120 |
| G06 | C02 | 13 December 2015 | 01:50 | 28 |
| G04 | C04 | 14 December 2015 | 08:27 | 32 |
| G06 | C02 | 15 December 2015 | 07:12 | 48 |
| M04 | C12 | 15 December 2015 | 07:38 | 25 |
| G06 | C02 | 16 December 2015 | 06:33 | 31 |
| G05 | C05 | 18 December 2015 | 04:15 | 43 |
| G06 | C02 | 20 December 2015 | 10:53 | 29 |
| I01 | C06 | 23 December 2015 | 04:44 | 32 |
| M04 | C12 | 23 December 2015 | 07:10 | 23 |
| I02 | C07 | 25 December 2015 | 12:45 | 29 |
| G06 | C02 | 27 December 2015 | 05:23 | 25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Wang, H.; Wang, Z.; Yuan, Y. Real-Time Monitoring for BDS Signal-In-Space Anomalies Using Ground Observation Data. Sensors 2018, 18, 1816. https://doi.org/10.3390/s18061816
Jiang H, Wang H, Wang Z, Yuan Y. Real-Time Monitoring for BDS Signal-In-Space Anomalies Using Ground Observation Data. Sensors. 2018; 18(6):1816. https://doi.org/10.3390/s18061816
Chicago/Turabian StyleJiang, Hu, Haitao Wang, Zemin Wang, and Yunbin Yuan. 2018. "Real-Time Monitoring for BDS Signal-In-Space Anomalies Using Ground Observation Data" Sensors 18, no. 6: 1816. https://doi.org/10.3390/s18061816
APA StyleJiang, H., Wang, H., Wang, Z., & Yuan, Y. (2018). Real-Time Monitoring for BDS Signal-In-Space Anomalies Using Ground Observation Data. Sensors, 18(6), 1816. https://doi.org/10.3390/s18061816






