Two-Dimensional Direction-of-Arrival Fast Estimation of Multiple Signals with Matrix Completion Theory in Coprime Planar Array
Abstract
:1. Introduction
2. System Model
3. The Proposed Algorithm
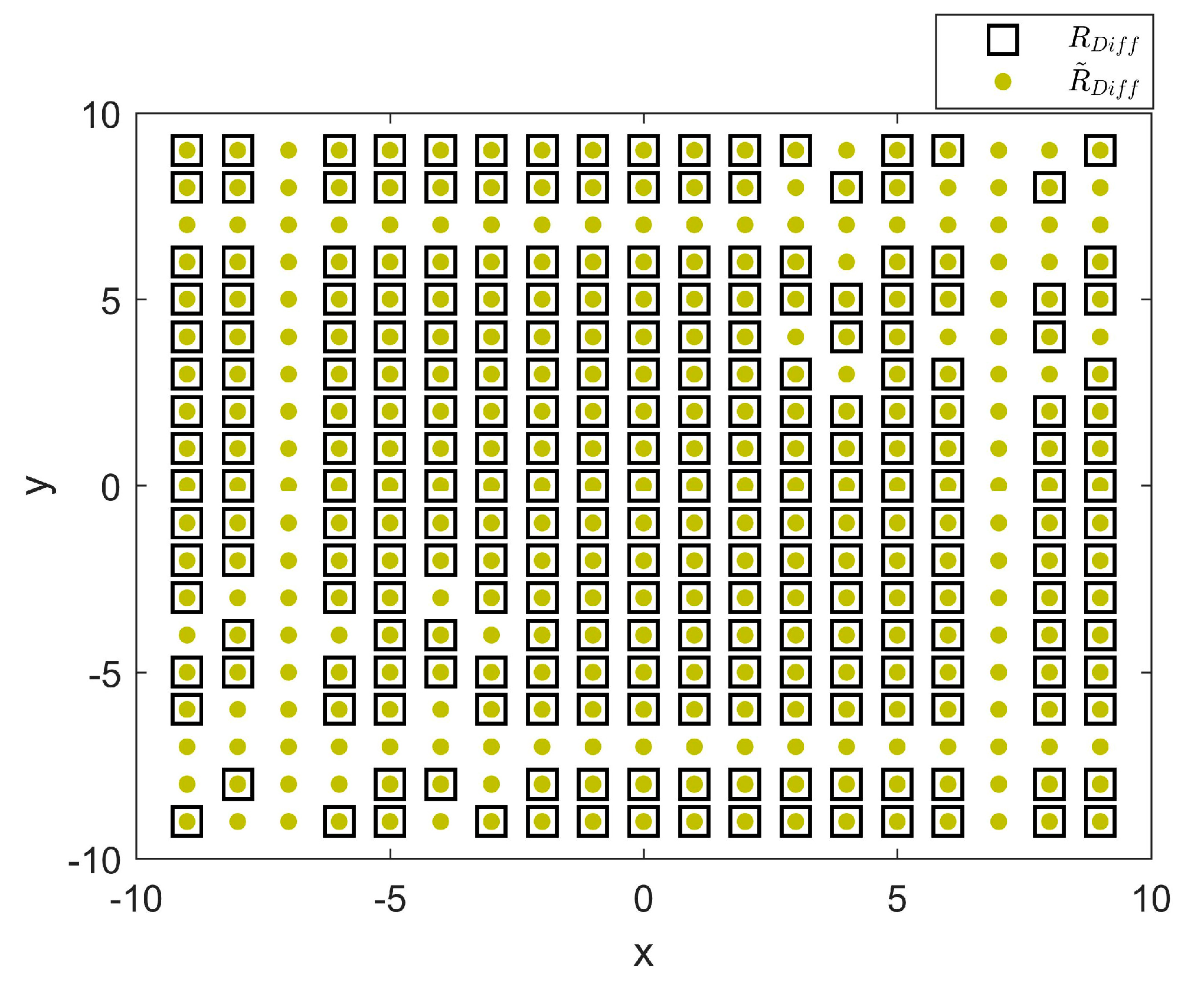
3.1. Reconstructing the Covariance Matrix of the Virtual Array
3.2. Matrix Completion Theory
- Step 1:
- Choose appropriate values of and then initialize ;
- Step 2:
- Calculate the on the th iteration;
- Step 3:
- Update ;
- Step 4:
- If , let and return to step 2. If not, define .
3.3. Unitary-ESPRIT Algorithm
3.4. Algorithm Steps Conclusion
- Step 1:
- Calculate the received signals’ covariance matrix .
- Step 2:
- Given , estimate the covariance matrix of the virtual uniform array combined with the array structure.
- Step 3:
- Apply the matrix completion theory to estimate the zero-location elements of and obtain .
- Step 4:
- Use the Unitary-ESPRIT algorithm to solve for the estimated DOA values .
4. Computational Complexity and Freedom Degree Analysis
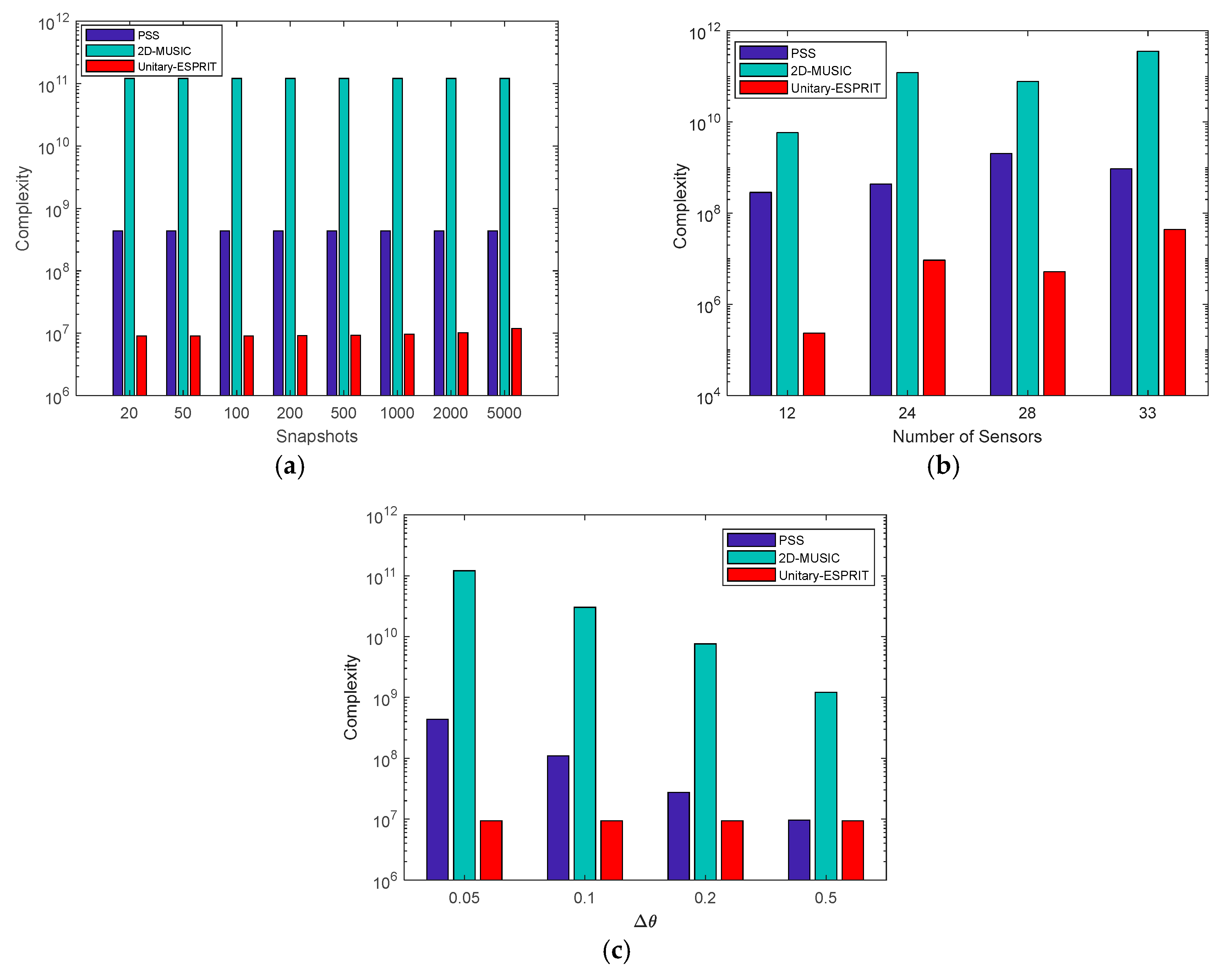
4.1. Complexity Analysis
4.2. Freedom Degree Analysis
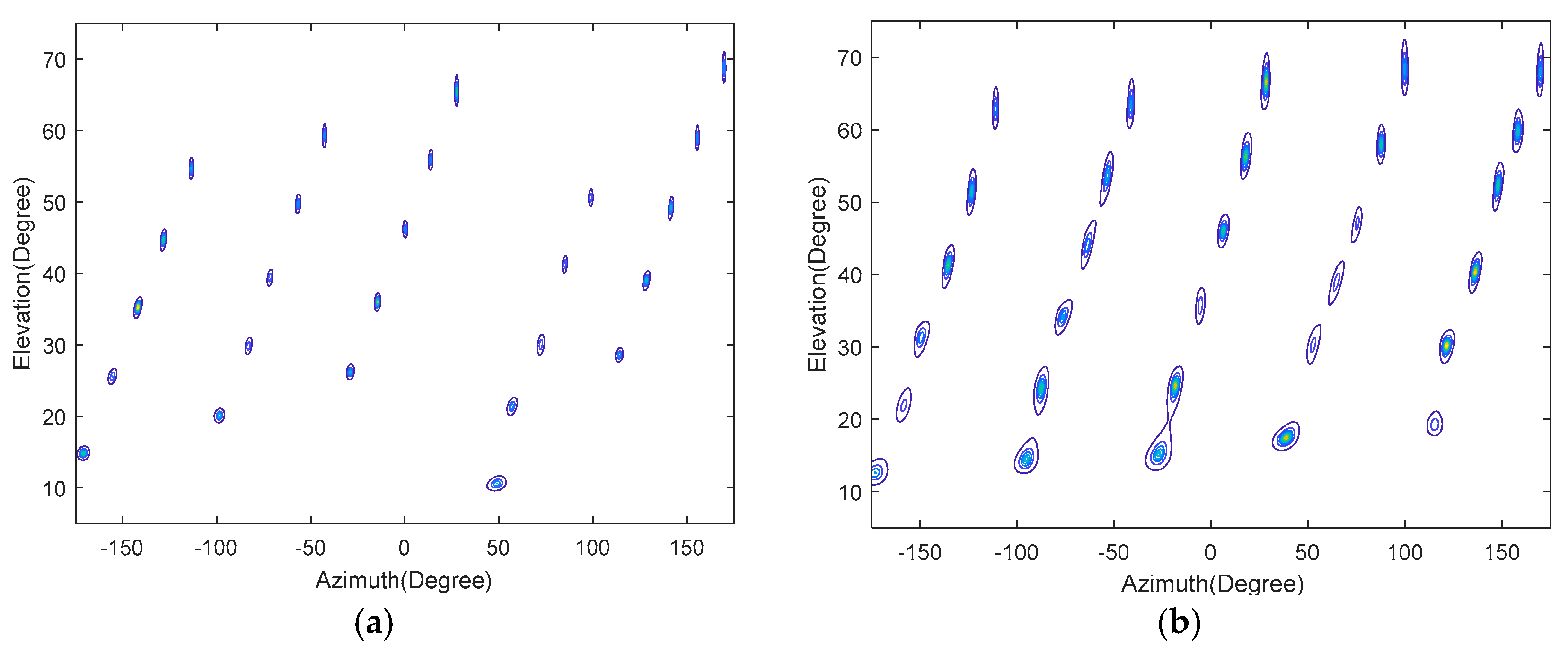
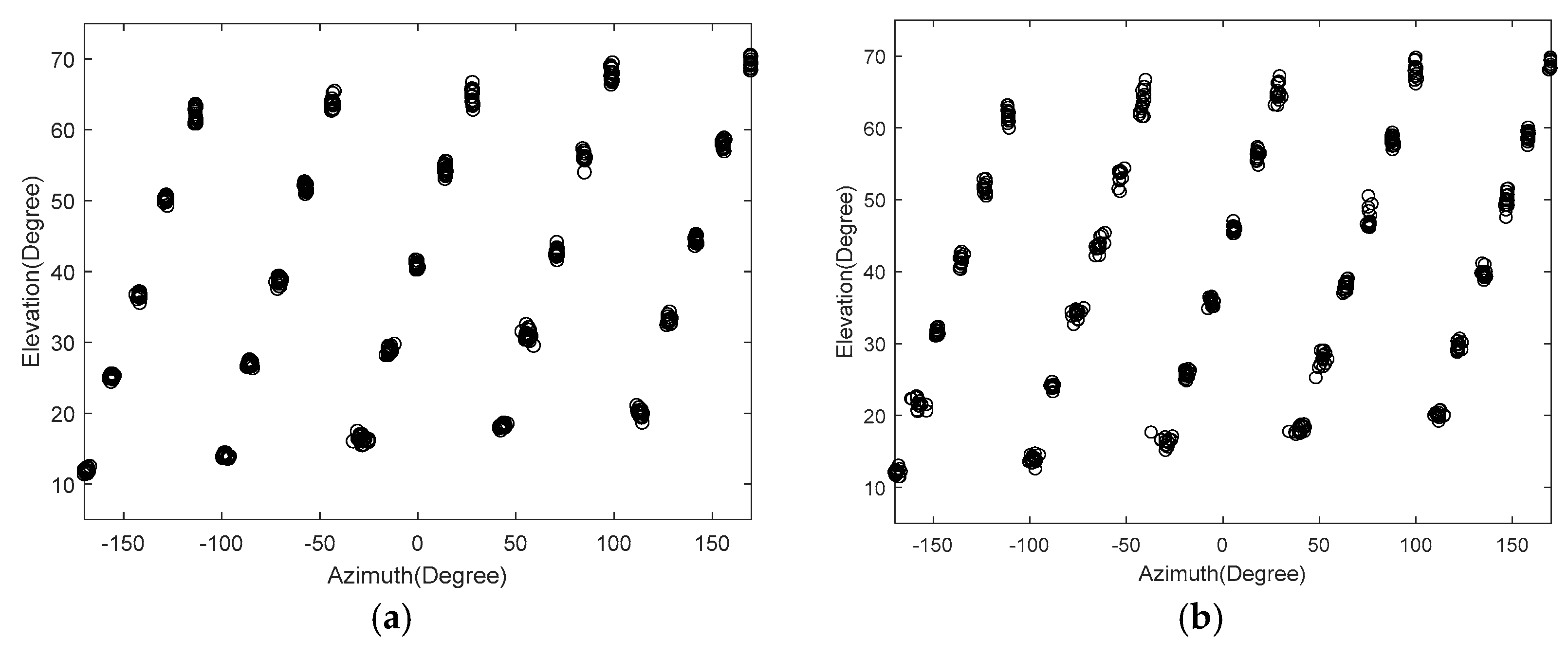
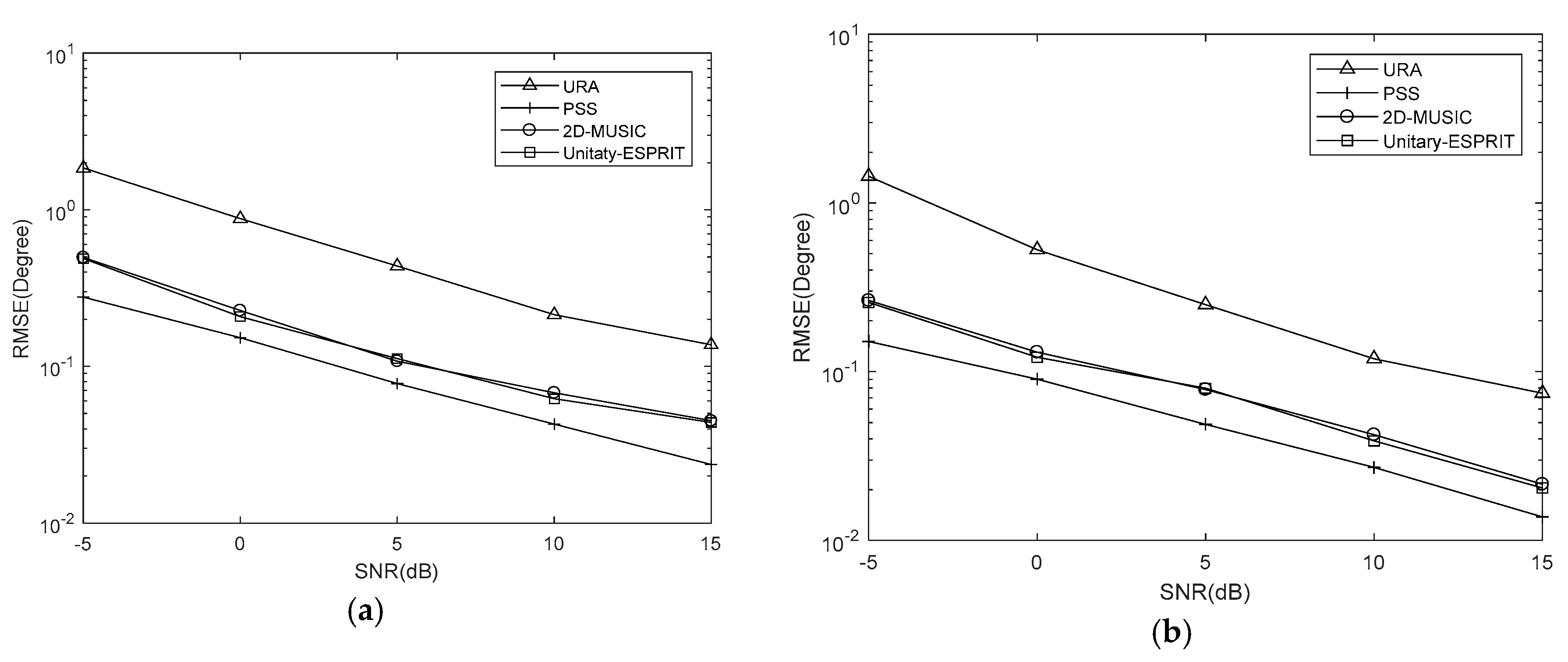
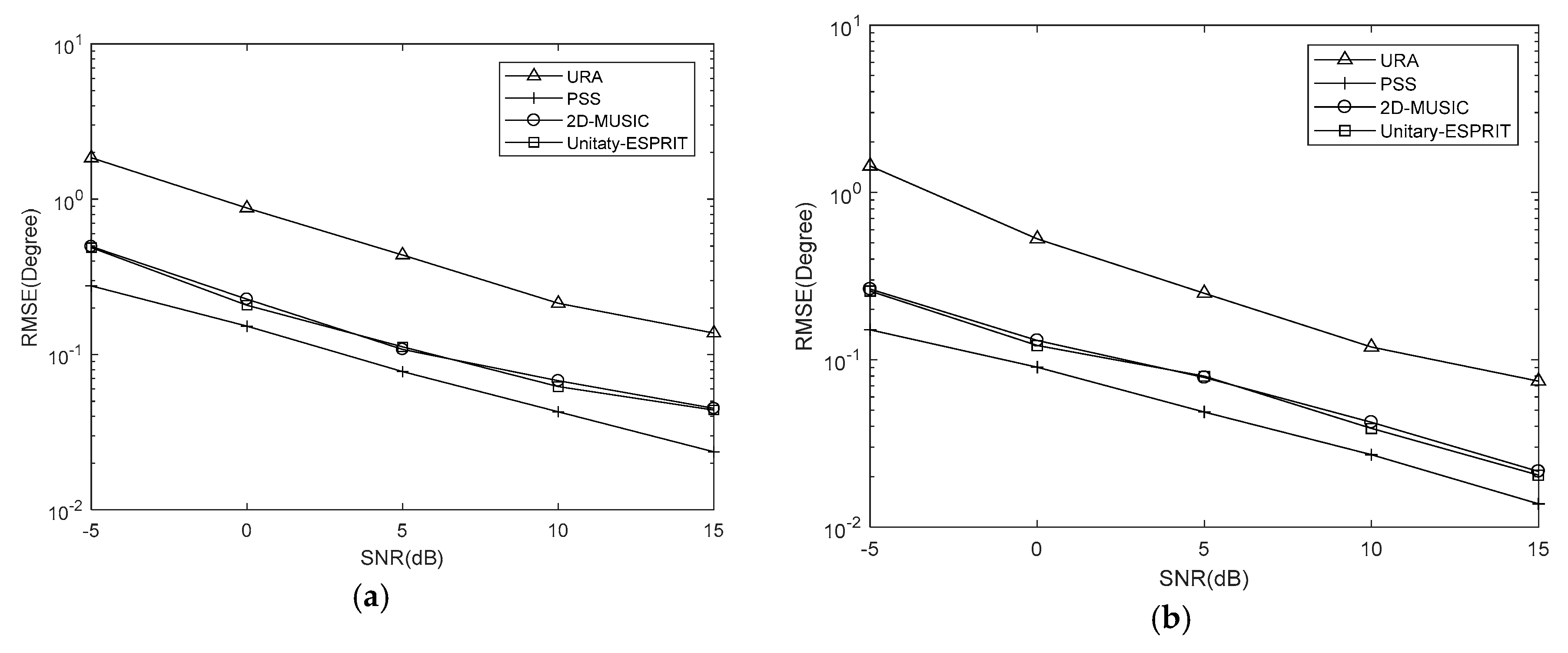
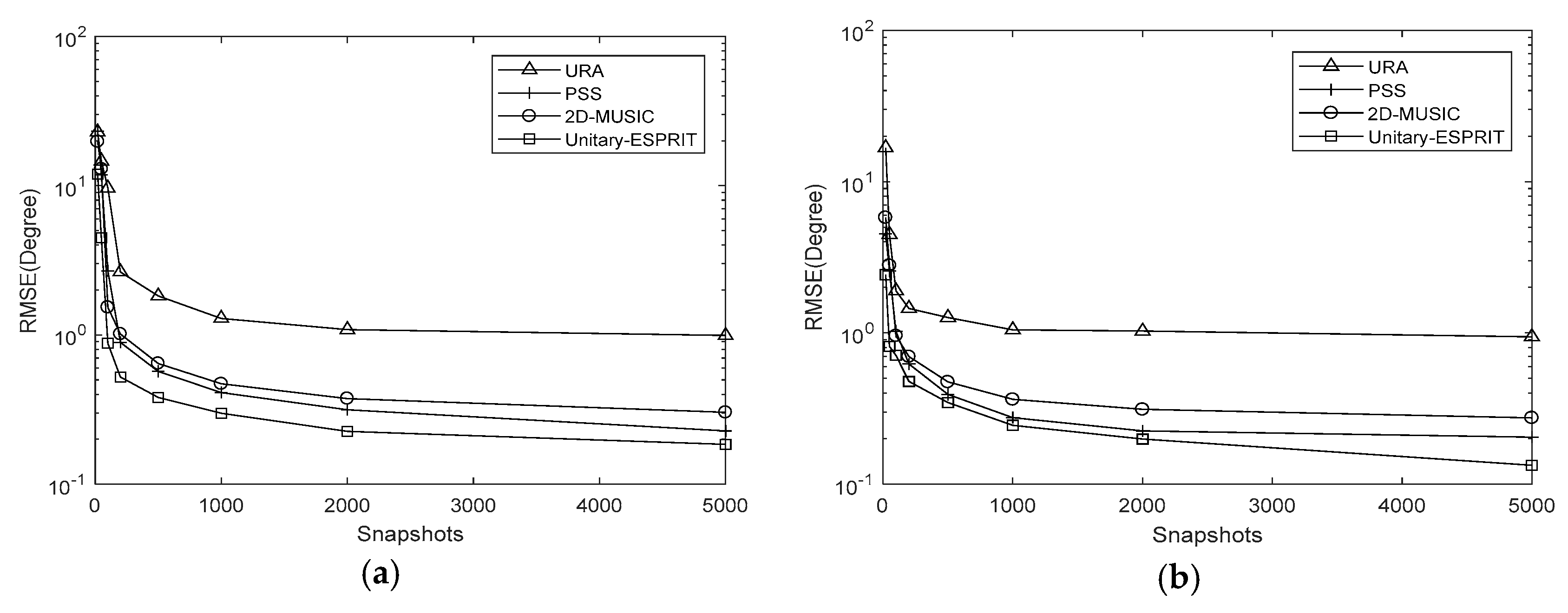
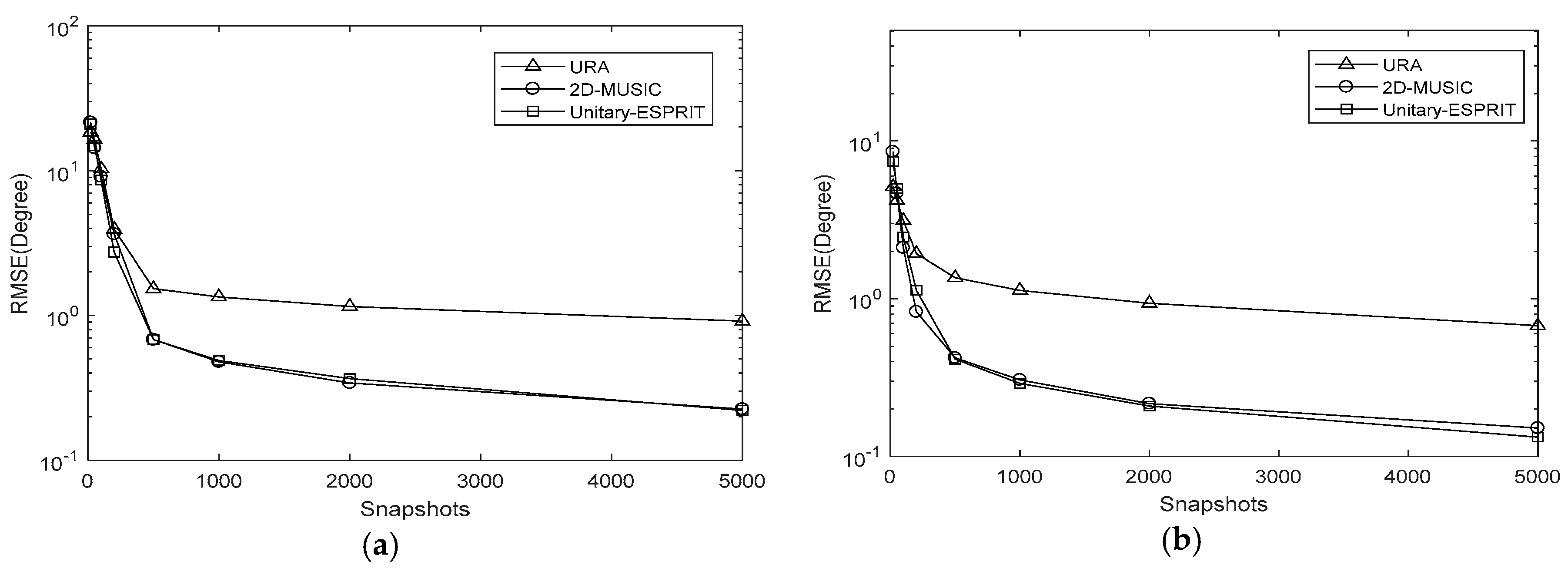
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wei, X.; Liu, Z.; Ding, X.; Fan, M. Super-Resolution Reconstruction of Radar Tomographic Image Based on Image Decomposition. IEEE Geosci. Remote Sens. Lett. 2013, 11, 607–611. [Google Scholar]
- Wang, Y.L.; Ma, S.L.; Liang, G.L.; Fan, Z. Chirp Spread Spectrum of Orthogonal Frequency Division Multiplexing Underwater Acoustic Communication System Based on Multi-path Diversity Receive. Acta Phys. Sin. 2014, 63. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Lu, Z.; Wang, Z. Super-resolution Sparse MIMO-OFDM Channel Estimation Based on Spatial and Temporal Correlations. IEEE Commun. Lett. 2014, 18, 1266–1269. [Google Scholar] [CrossRef]
- Ye, Z.; Dai, J.; Xu, X.; Wu, X. DOA Estimation for Uniform Linear Array with Mutual Coupling. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 280–288. [Google Scholar]
- Heidenreich, P.; Zoubir, A.M.; Rubsamen, M. Joint 2-D DOA Estimation and Phase Calibration for Uniform Rectangular Arrays. IEEE Trans. Signal Process. 2012, 60, 4683–4693. [Google Scholar] [CrossRef]
- Han, H.; Zhao, P.J. A Two-dimensional direction finding estimation with L-shape uniform linear arrays. In Proceedings of the International Symposium on Instrumentation and Measurement, Sensor Network and Automation, Toronto, ON, Canada, 23–24 December 2013; IEEE: Piscataway, NJ, USA, 2014; pp. 779–782. [Google Scholar]
- Pal, P.; Vaidyanathan, P.P. Coprime sampling and the music algorithm. In Proceedings of the 2011 IEEE Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop, Sedona, AZ, USA, 4–7 January 2011; pp. 289–294. [Google Scholar]
- Zhang, D.; Zhang, Y.; Zheng, G.; Feng, C.; Tang, J. Improved DOA Estimation Algorithm for Co-prime Linear Arrays Using Root-MUSIC Algorithm. Electron. Lett. 2017, 53, 1277–1279. [Google Scholar] [CrossRef]
- Zhou, C.; Zhou, J. Direction-of-Arrival Estimation with Coarray ESPRIT for Coprime Array. Sensors 2017, 17. [Google Scholar] [CrossRef]
- Byun, B.G.; Yoo, D.S. Improved Direction of Arrival Estimation Based on Coprime Array and Propagator Method by Noise Power Spectral Density Estimation. J. Adv. Nav. Tech. 2016, 20, 367–373. [Google Scholar] [CrossRef]
- Dai, Z.-L.; Cui, W.-J.; Ba, B.; Zhang, Y.-K. Two-dimensional Direction-of-arrival Estimation of Coherently Distributed Noncircular Signals via Symmetric Shift Invariance. Acta Phys. Sin. 2017, 66, 220701. [Google Scholar] [CrossRef]
- Ba, B.; Liu, G.-C.; Li, T.; Lin, Y.-C.; Wang, Y. Joint for Time of Arrival and Direction of Arrival Estimation Algorithm Based on the Subspace of Extended Hadamard Product. Acta Phys. Sin. 2015, 64, 078403. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing with Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse Sensing With Co-Prime Samplers and Arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, F.; Lan, P.; Ding, G.; Zhang, X. Two-Dimensional Direction-of-Arrival Estimation for Co-Prime Planar Arrays: A Partial Spectral Search Approach. IEEE Sens. J. 2016, 16, 5660–5670. [Google Scholar] [CrossRef]
- Liu, S.; Yang, L.; Li, D.; Cao, H. Subspace Extension Algorithm for 2D DOA Estimation with L-shaped Sparse Array. Multidimens. Syst. Signal Process. 2017, 28, 315–327. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Two-dimensional DOA estimation using parallel coprime subarrays. In Proceedings of the 2016 IEEE Sensor Array and Multichannel Signal Processing Workshop, Rio de Janerio, Brazil, 10–13 July 2016. [Google Scholar]
- Pillai, S.; Haber, F. Statistical Analysis of a High Resolution Spatial Spectrum Estimator Utilizing an Augmented Covariance Matrix. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1517–1523. [Google Scholar] [CrossRef]
- Chen, T.; Guo, M.; Guo, L. A Direct Coarray Interpolation Approach for Direction Finding. Sensors 2017, 17, 2149. [Google Scholar] [CrossRef] [PubMed]
- Guo, M.; Chen, T.; Wang, B. An Improved DOA Estimation Approach Using Coarray Interpolation and Matrix Denoising. Sensors 2017, 17, 1140. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.X.; Zhang, M.; Wang, K.R. An Underdetermined DOA Estimation Approach in Coprime Array Based on Matrix Completion. J. Sichuan Univ. Eng. Sci. Ed. 2017, 49, 156–163. [Google Scholar]
- Cai, J.F.; Candes, E.J.; Shen, Z.W. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J. Optim. 2010, 4, 1956–1982. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. A Grid-Less Approach to Underdetermined Direction of Arrival Estimation via Low Rank Matrix Denoising. IEEE Signal Process. Lett. 2014, 21, 737–741. [Google Scholar] [CrossRef]
- Sun, F.; Wu, Q.; Lan, P.; Ding, G.; Chen, L. Real-Valued DOA Estimation with Unknown Number of Sources via Reweighted Nuclear Norm Minimization. Signal Process. 2018, 148, 48–55. [Google Scholar] [CrossRef]
- Chen, Y.M.; Lee, J.H.; Yeh, C.C. Two-dimensional Angle-of-arrival Estimation for Uniform Planar Arrays with Sensor Position Errors. IEE Proc. F Radar Signal Process. 1993, 140, 37–42. [Google Scholar] [CrossRef]
- Haardt, M.; Nossek, J.A. Unitary ESPRIT: How to Obtain Increased Estimation Accuracy with a Reduced Computational Burden. IEEE Trans. Signal Process. 1995, 43, 1232–1242. [Google Scholar] [CrossRef]
- Zoltowski, M.D.; Haardt, M.; Mathews, C.P. Closed-form 2-D Angle Estimation with Rectangular Arrays in Element Space or Beamspace via Unitary ESPRIT. IEEE Trans. Signal Process. 1996, 44, 316–328. [Google Scholar] [CrossRef]




| Algorithms | Complexity |
|---|---|
| Unitary-ESPRIT | |
| 2D-MUSIC | |
| PSS |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Zhang, Y.; Ba, B.; Wang, D.; Li, X. Two-Dimensional Direction-of-Arrival Fast Estimation of Multiple Signals with Matrix Completion Theory in Coprime Planar Array. Sensors 2018, 18, 1741. https://doi.org/10.3390/s18061741
Xu H, Zhang Y, Ba B, Wang D, Li X. Two-Dimensional Direction-of-Arrival Fast Estimation of Multiple Signals with Matrix Completion Theory in Coprime Planar Array. Sensors. 2018; 18(6):1741. https://doi.org/10.3390/s18061741
Chicago/Turabian StyleXu, Haiyun, Yankui Zhang, Bin Ba, Daming Wang, and Xiangzhi Li. 2018. "Two-Dimensional Direction-of-Arrival Fast Estimation of Multiple Signals with Matrix Completion Theory in Coprime Planar Array" Sensors 18, no. 6: 1741. https://doi.org/10.3390/s18061741
APA StyleXu, H., Zhang, Y., Ba, B., Wang, D., & Li, X. (2018). Two-Dimensional Direction-of-Arrival Fast Estimation of Multiple Signals with Matrix Completion Theory in Coprime Planar Array. Sensors, 18(6), 1741. https://doi.org/10.3390/s18061741





