Numerical Simulation of a Novel Sensing Approach Based on Abnormal Blocking by Periodic Grating Strips near the Silicon Wire Waveguide
Abstract
:1. Introduction
2. The Effect of Abnormal Guided Wave Blocking
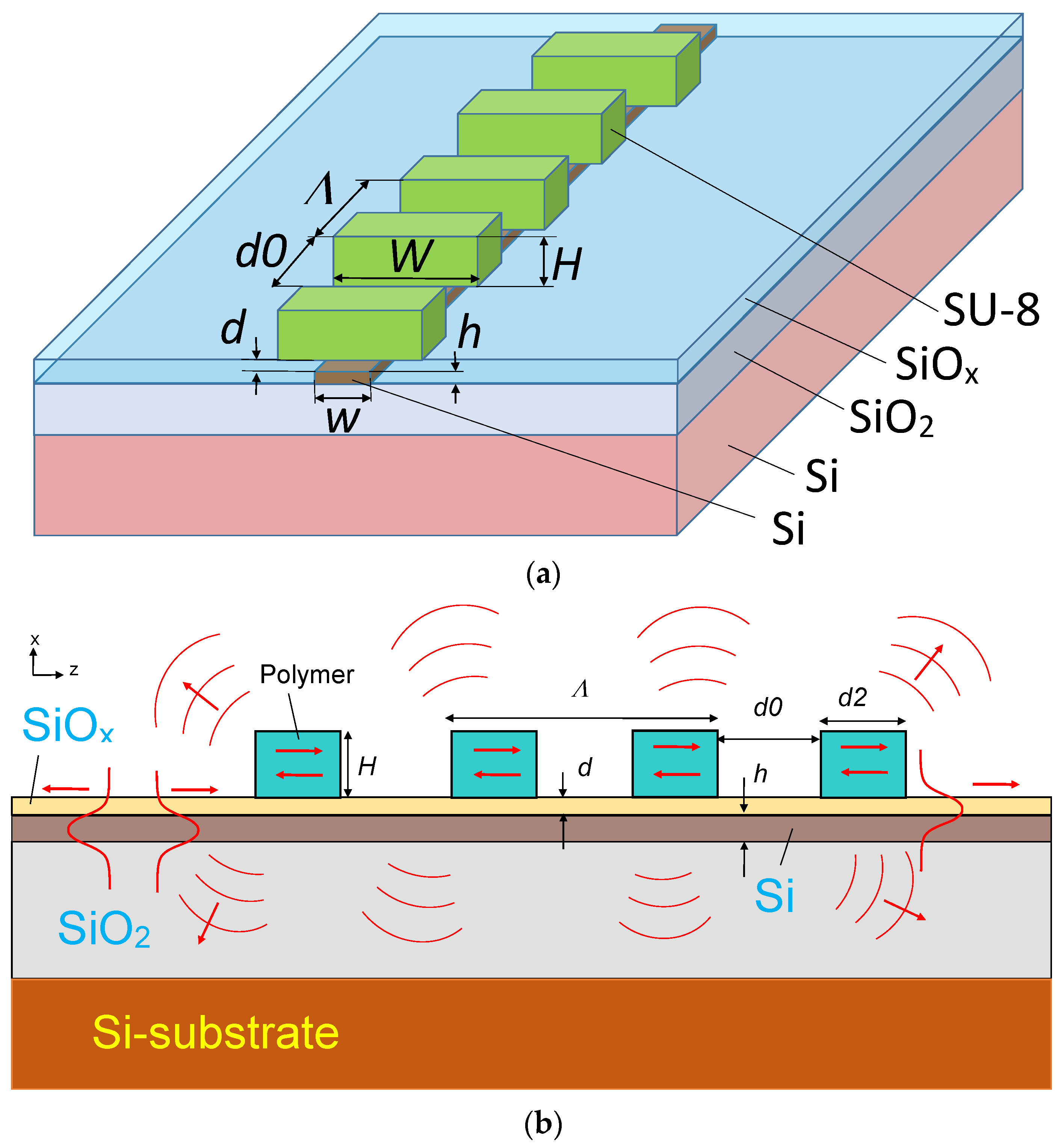
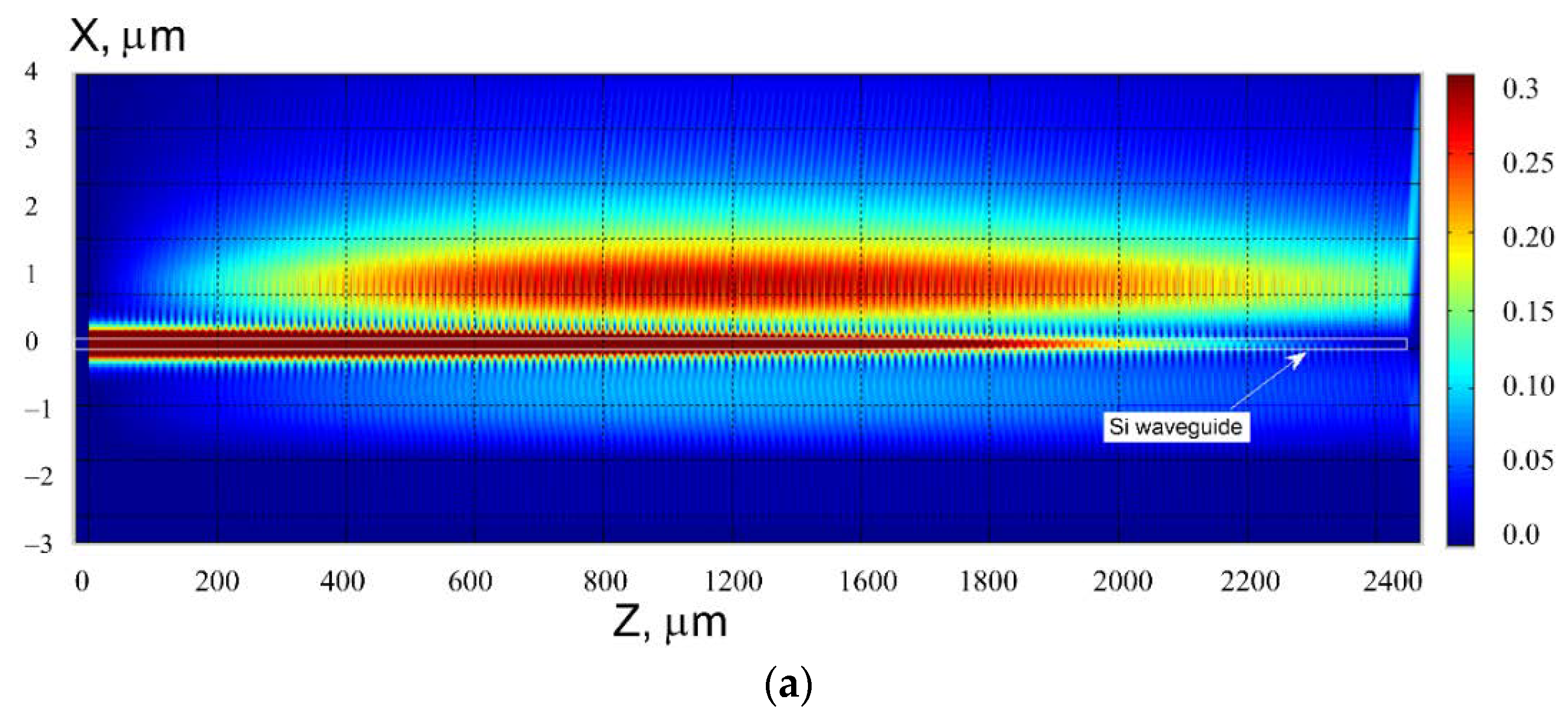
2.1. Genreral Description of the Abnormal Blocking in the Guided Wave Structure with the Segmented Grating
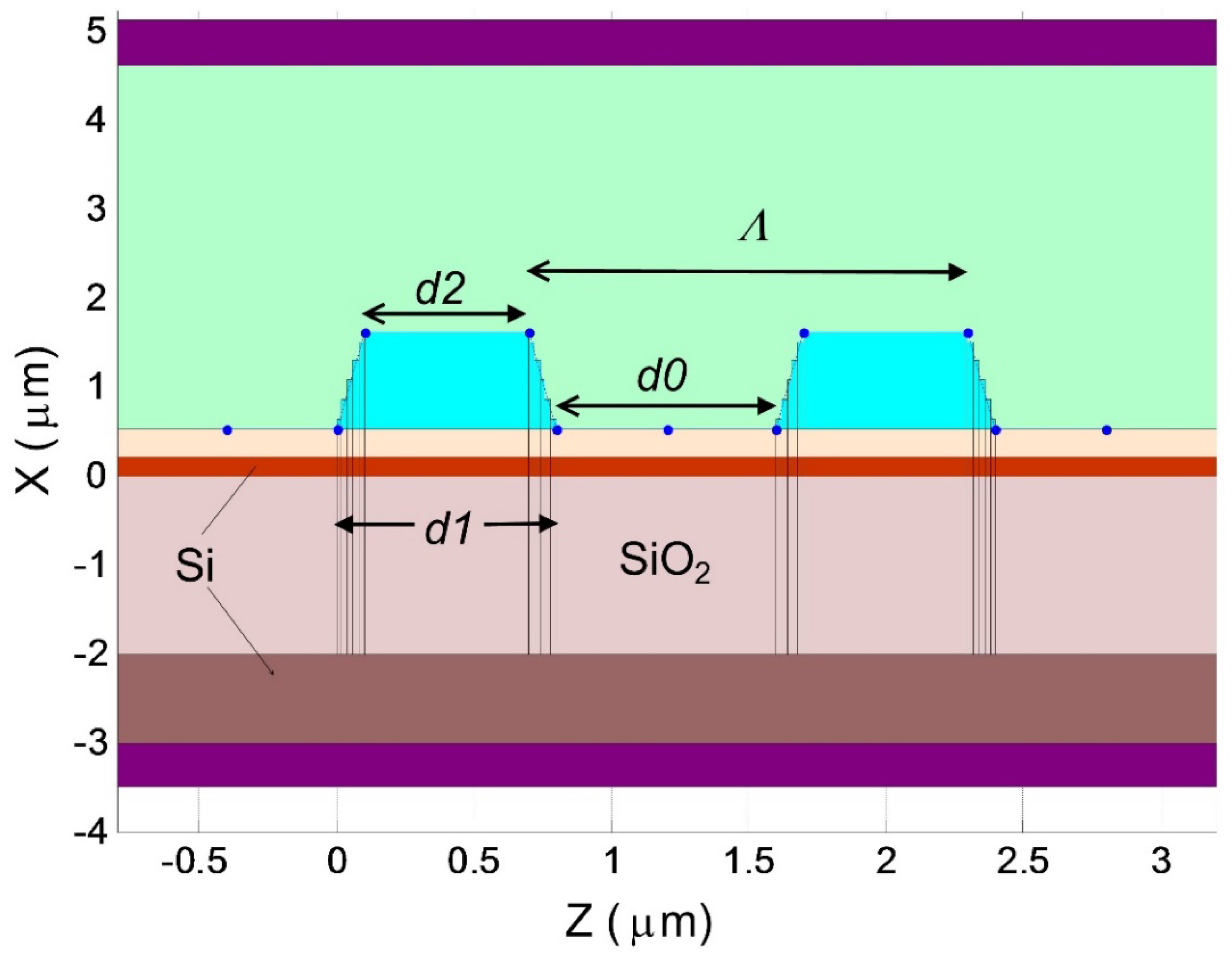
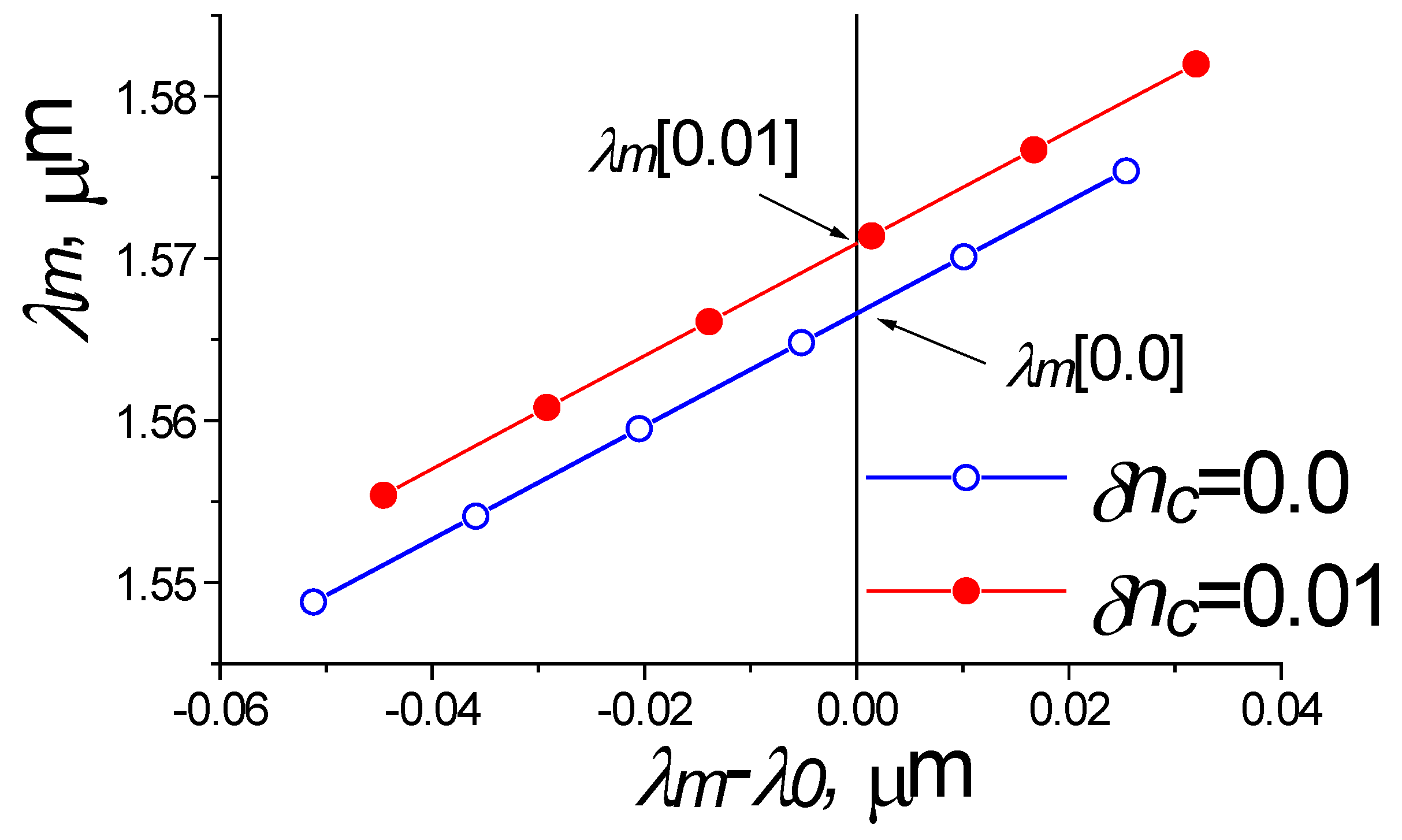
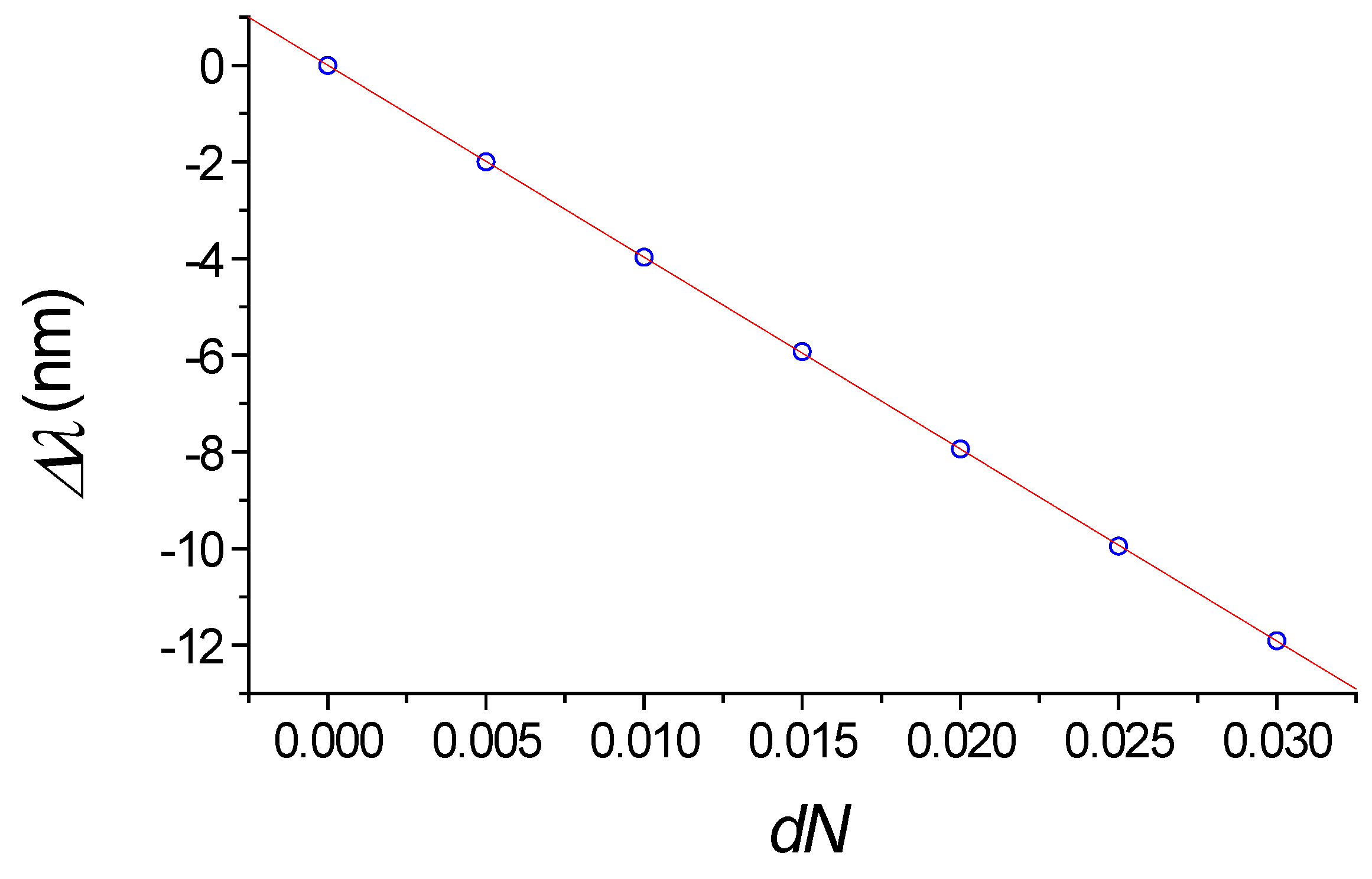
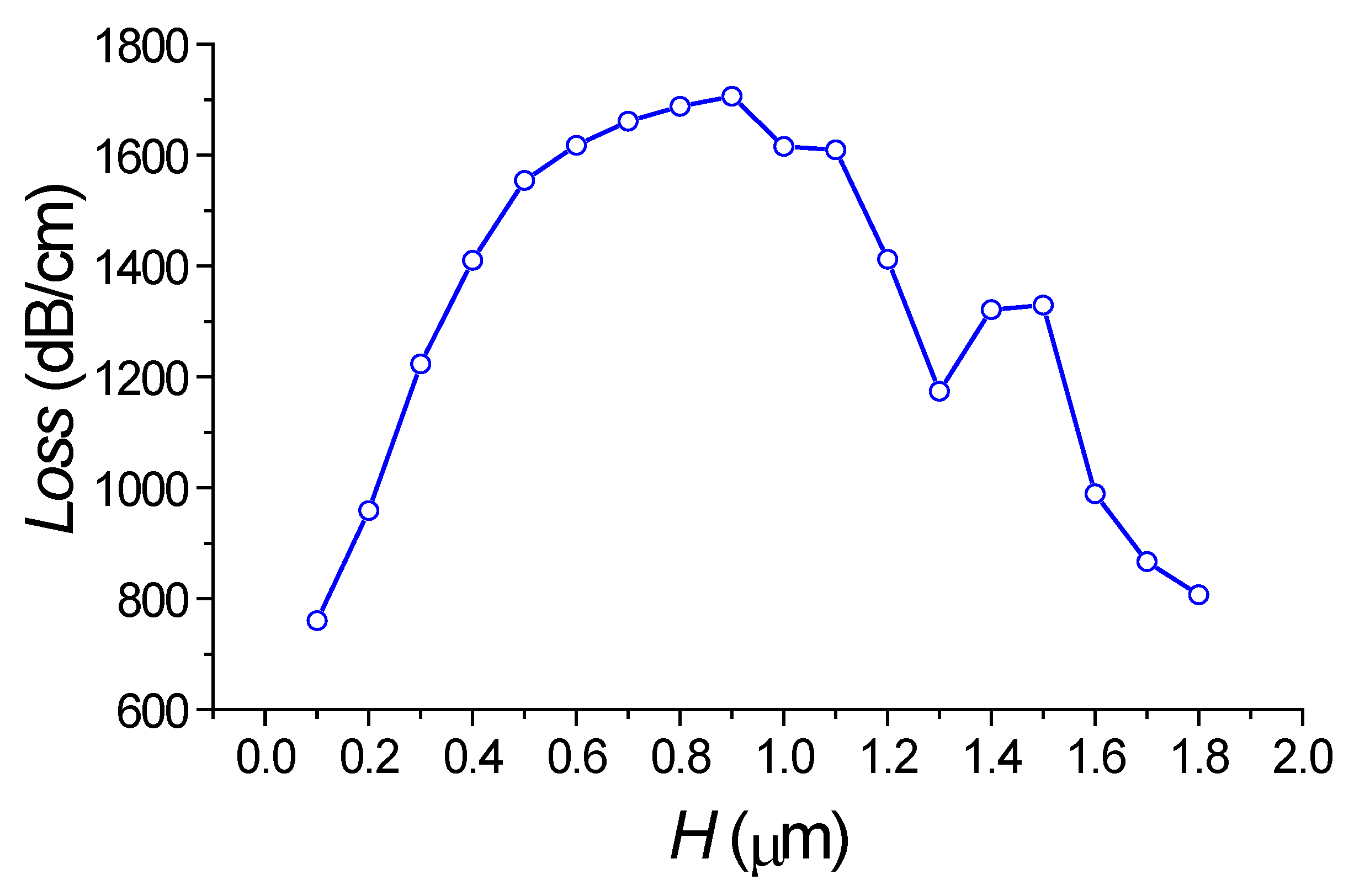
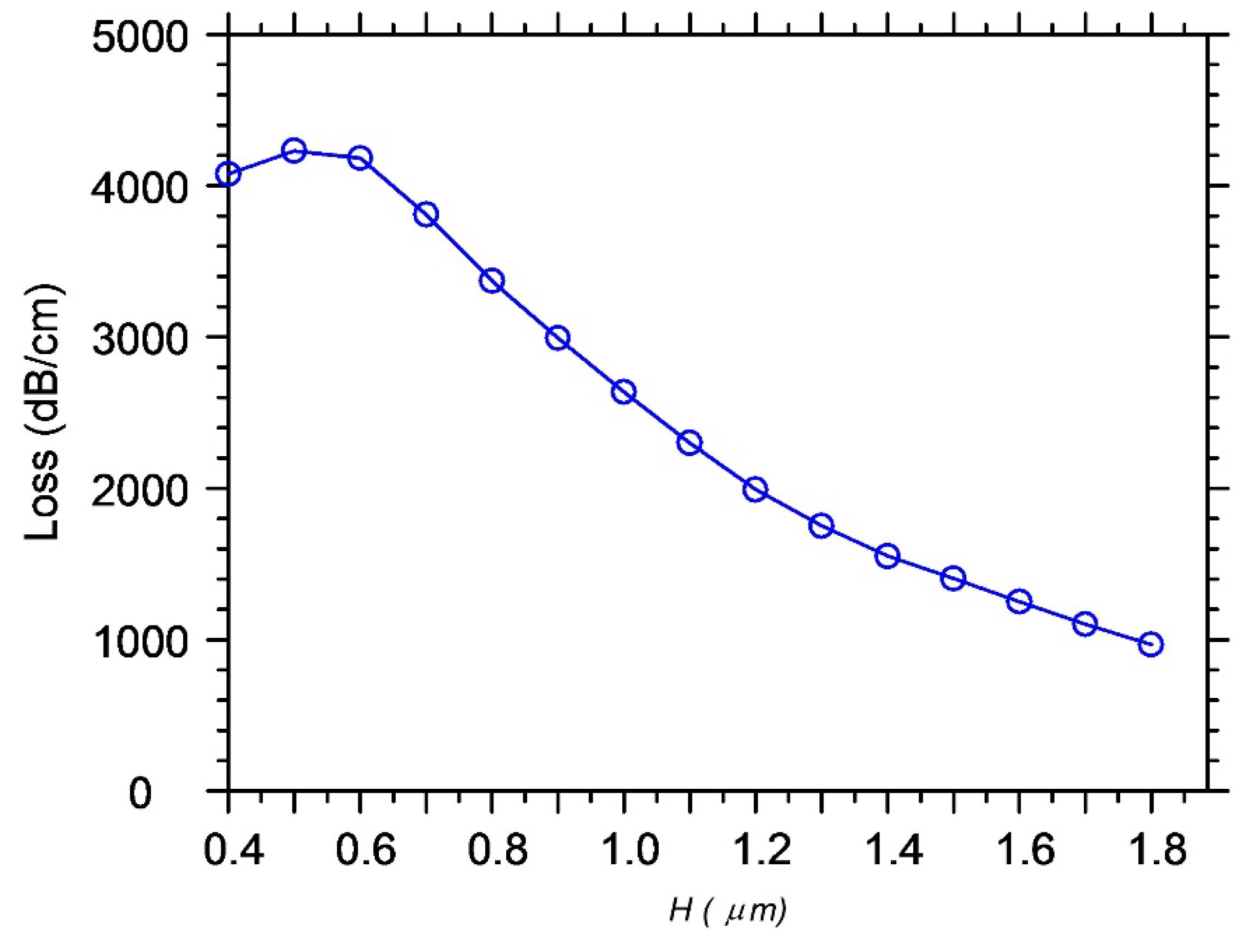
2.2. Not-Vertical Etching Profile
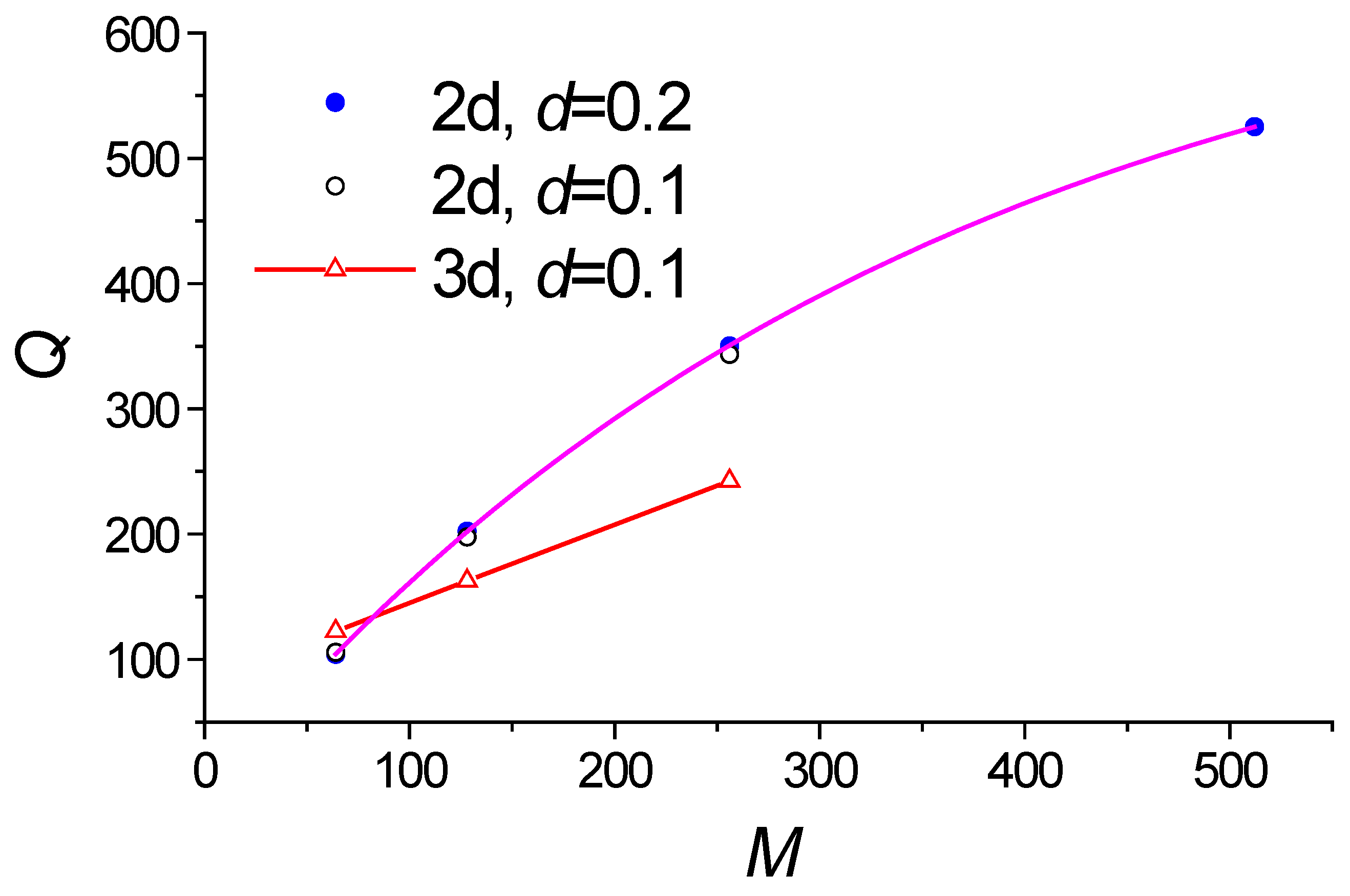
2.3. Effective Index Method and Implementation of 2D FDTD
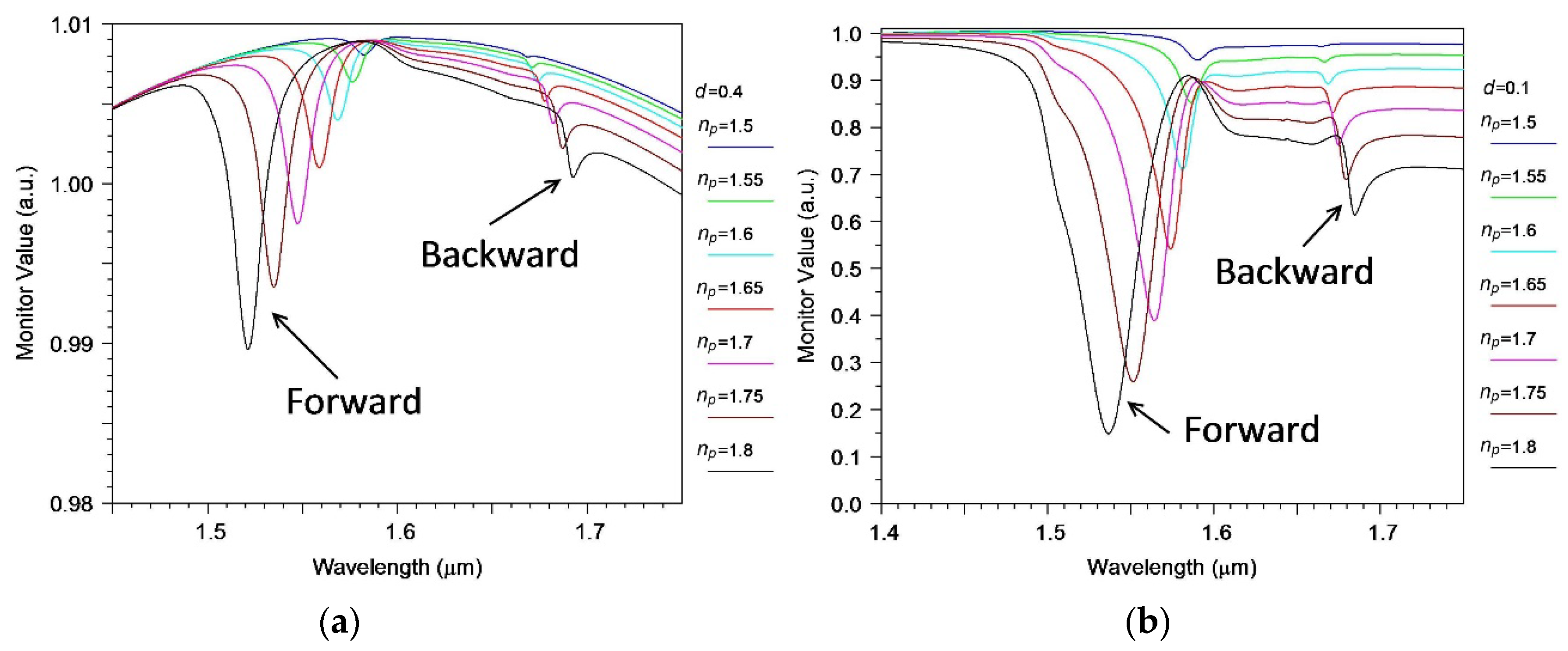
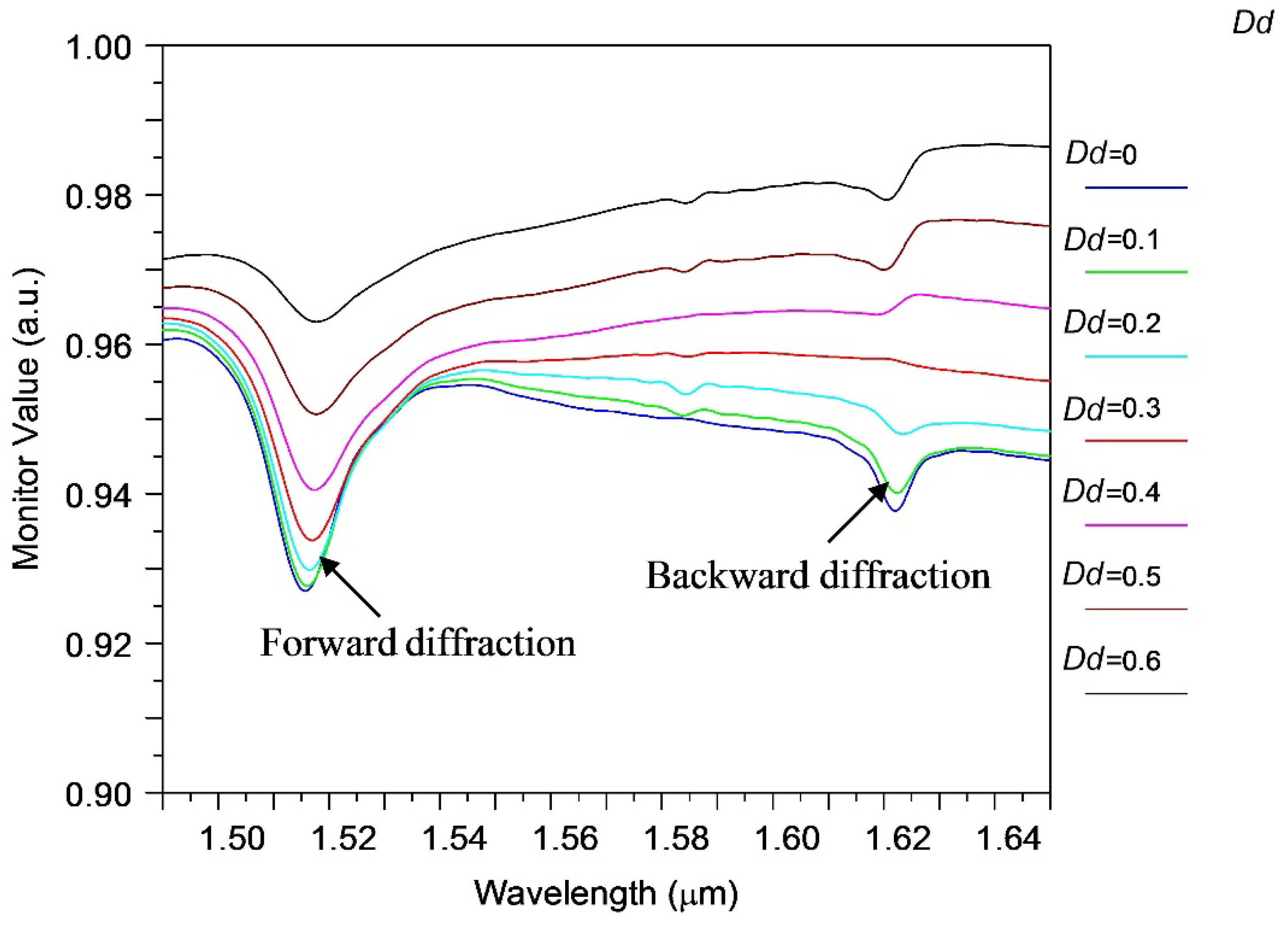
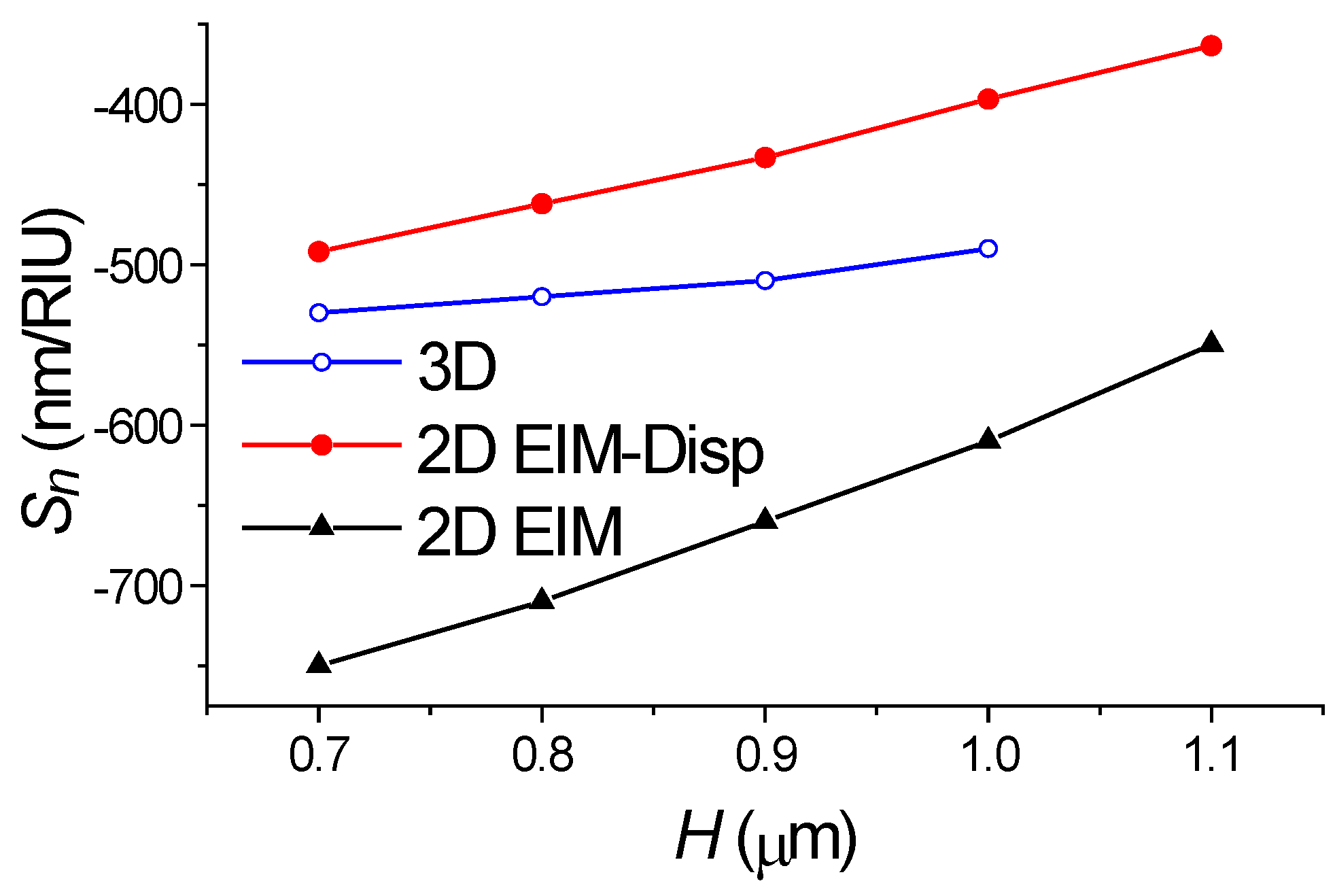
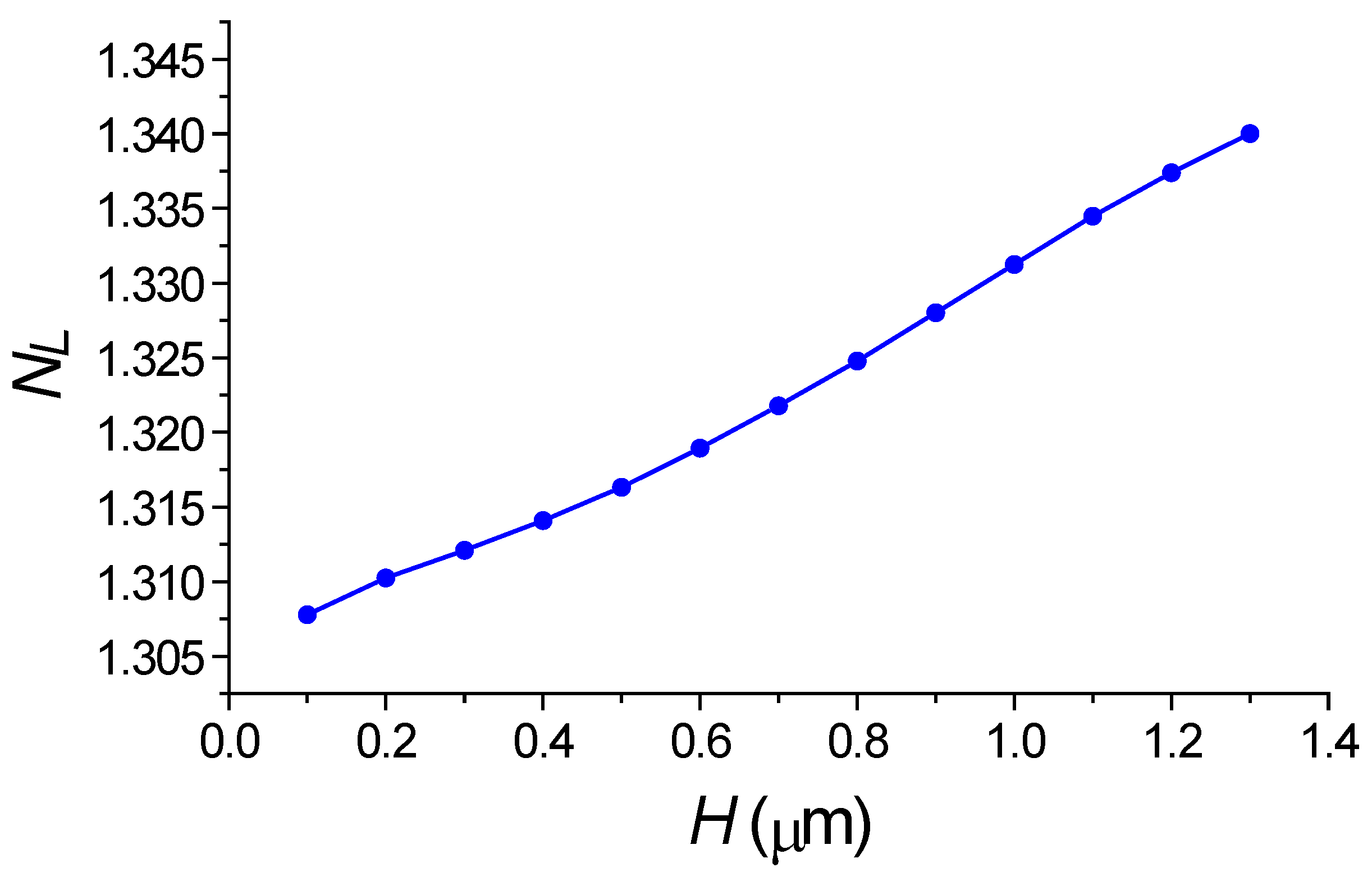
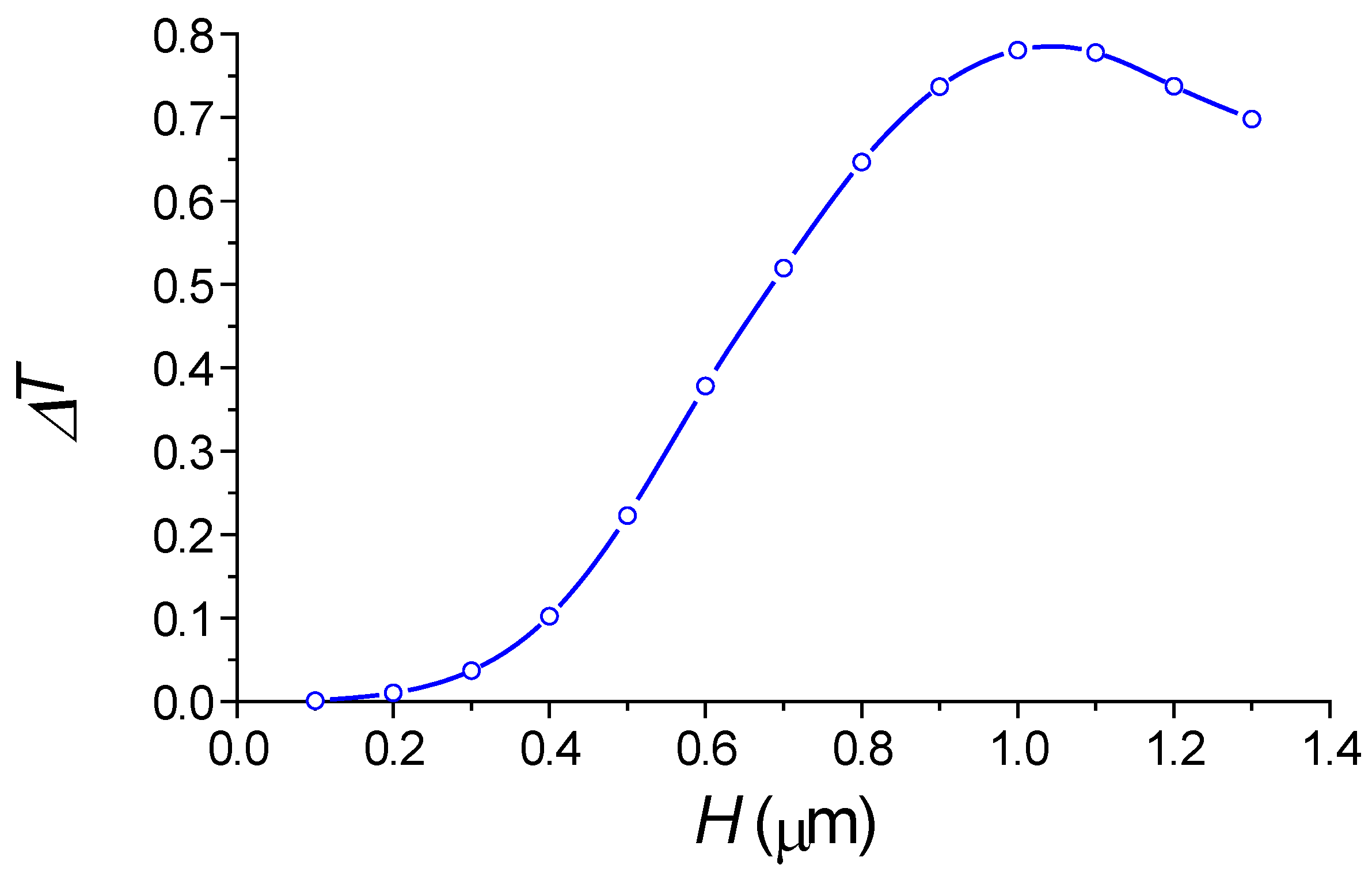
2.4. The Refractometric Sensitivity of the Silicon Wire with the Segmented Grating
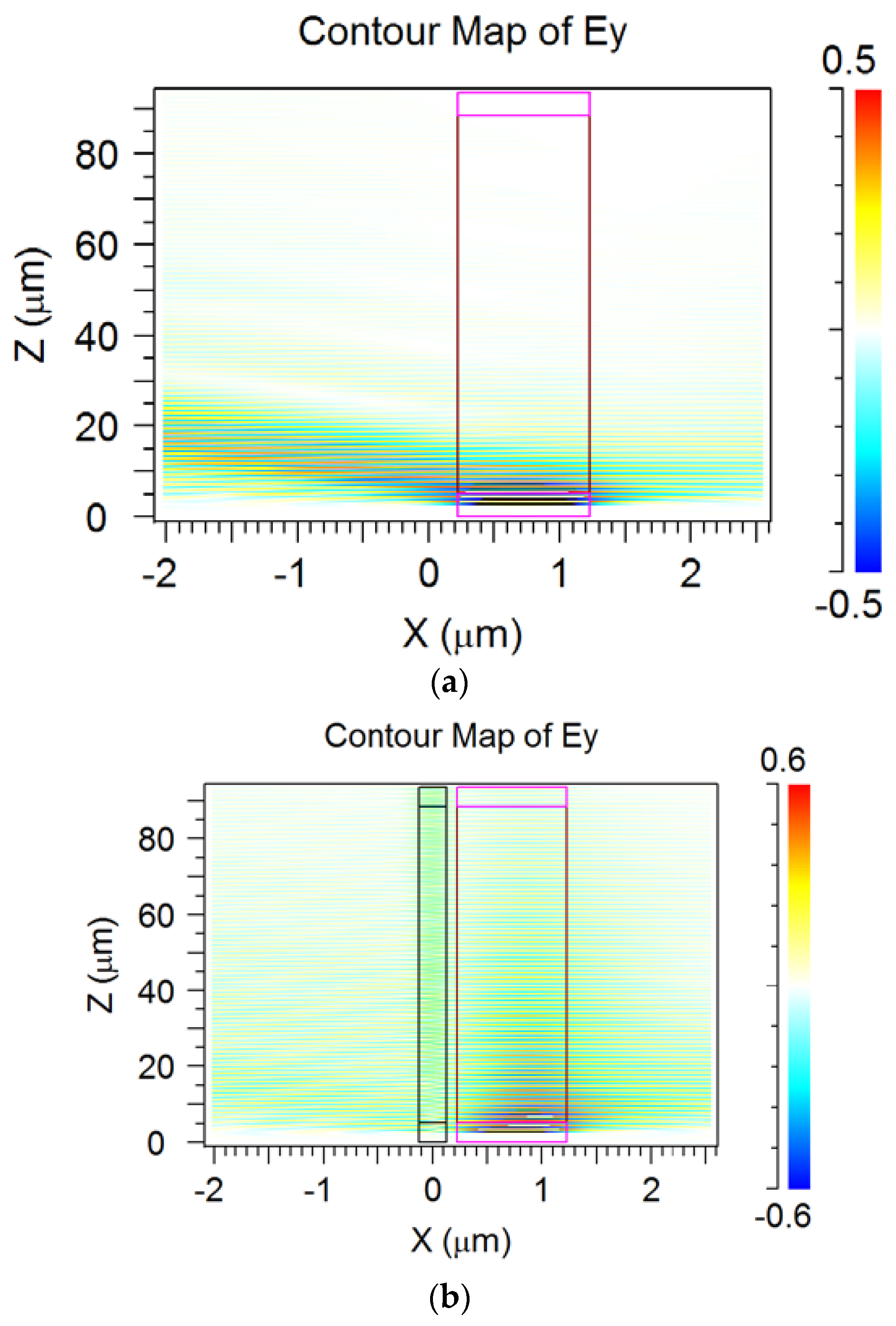
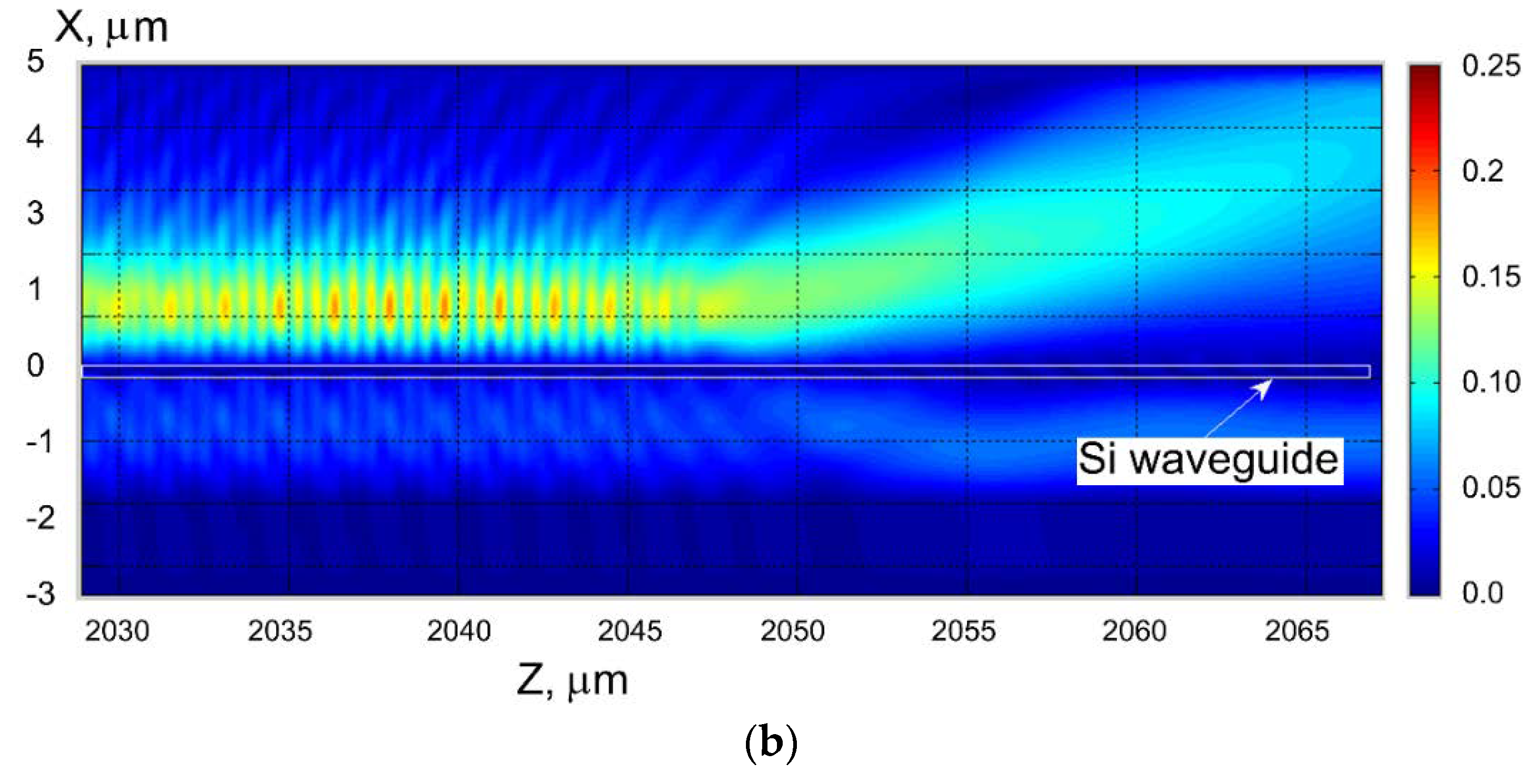
2.5. The Physical Nature of the Virtual Leaky Wave in Segmented Grating Structure in the Vicinity of the Silicon Wire Waveguide
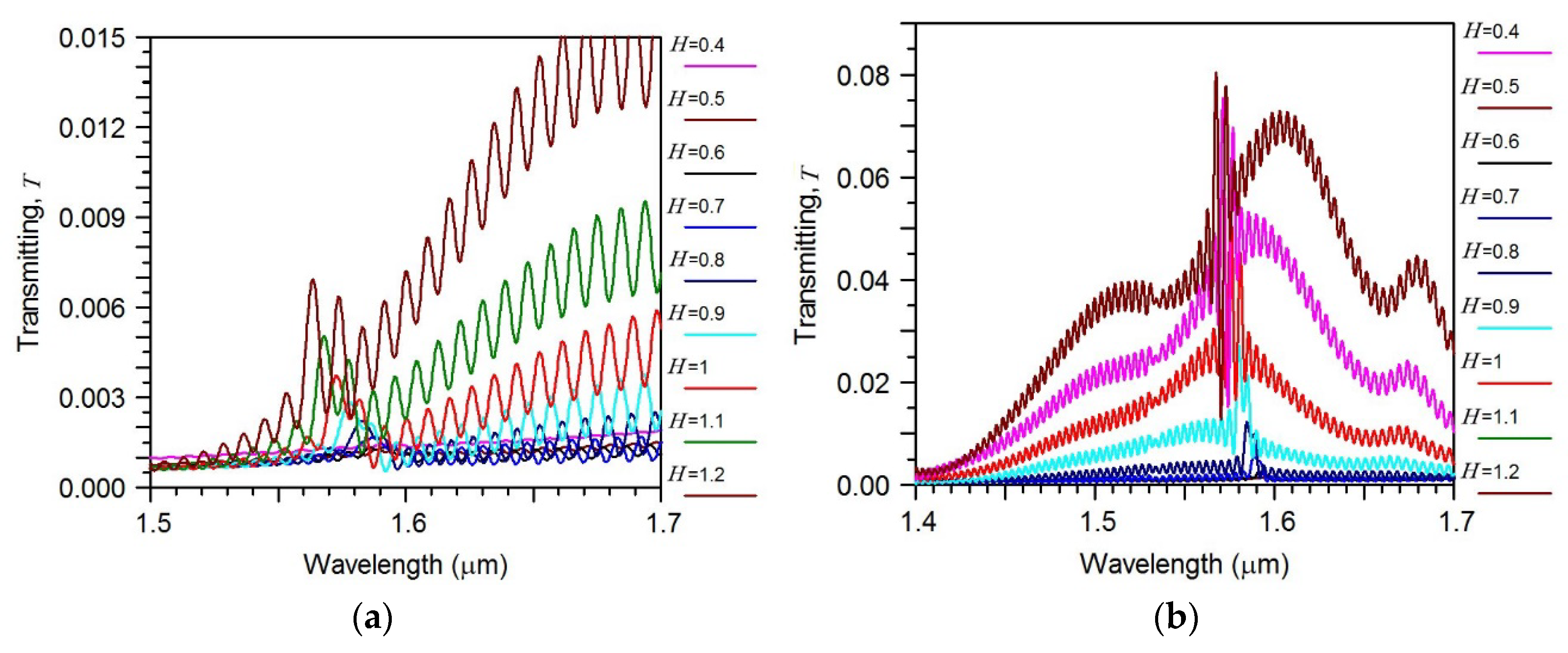
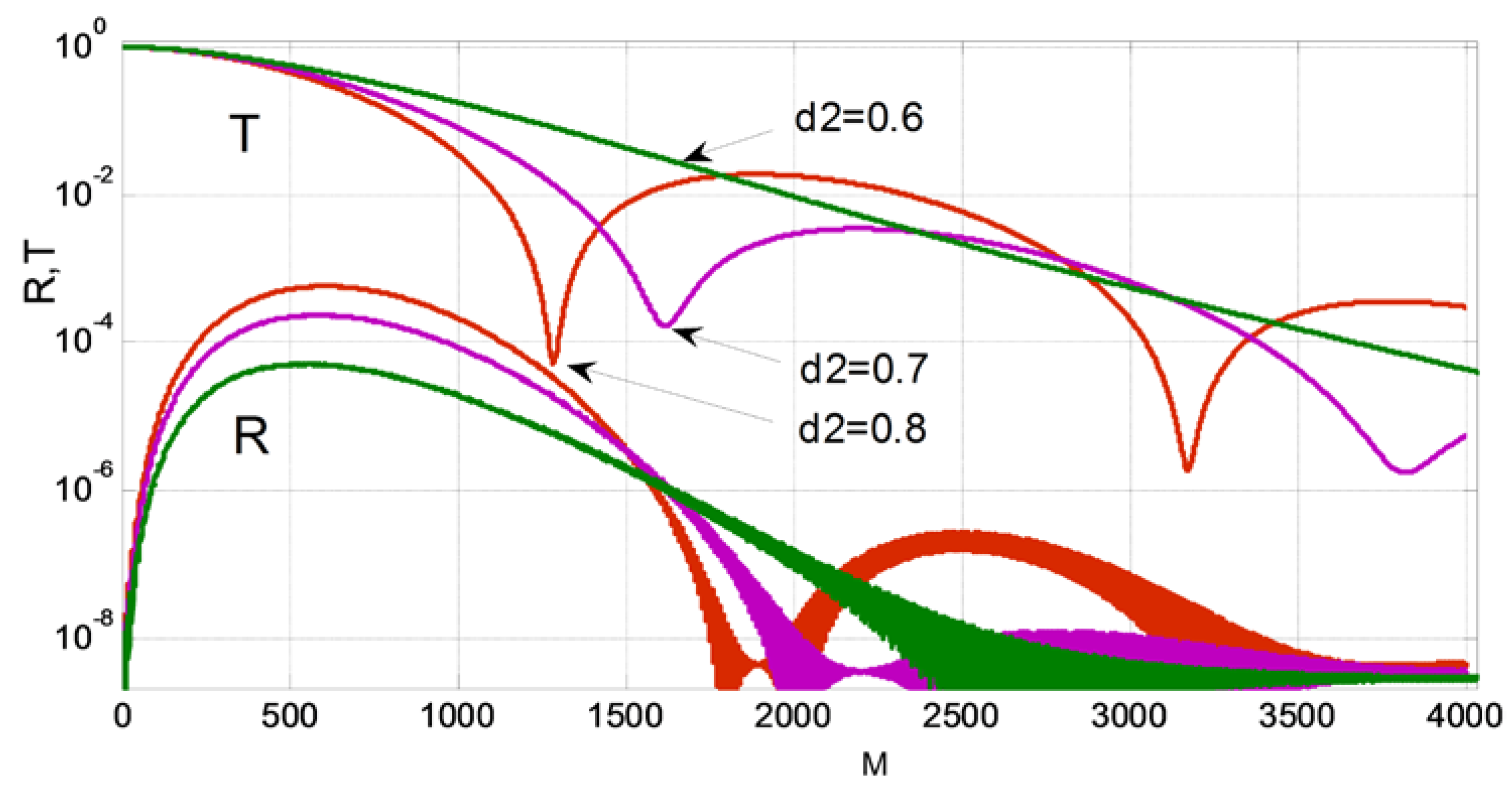
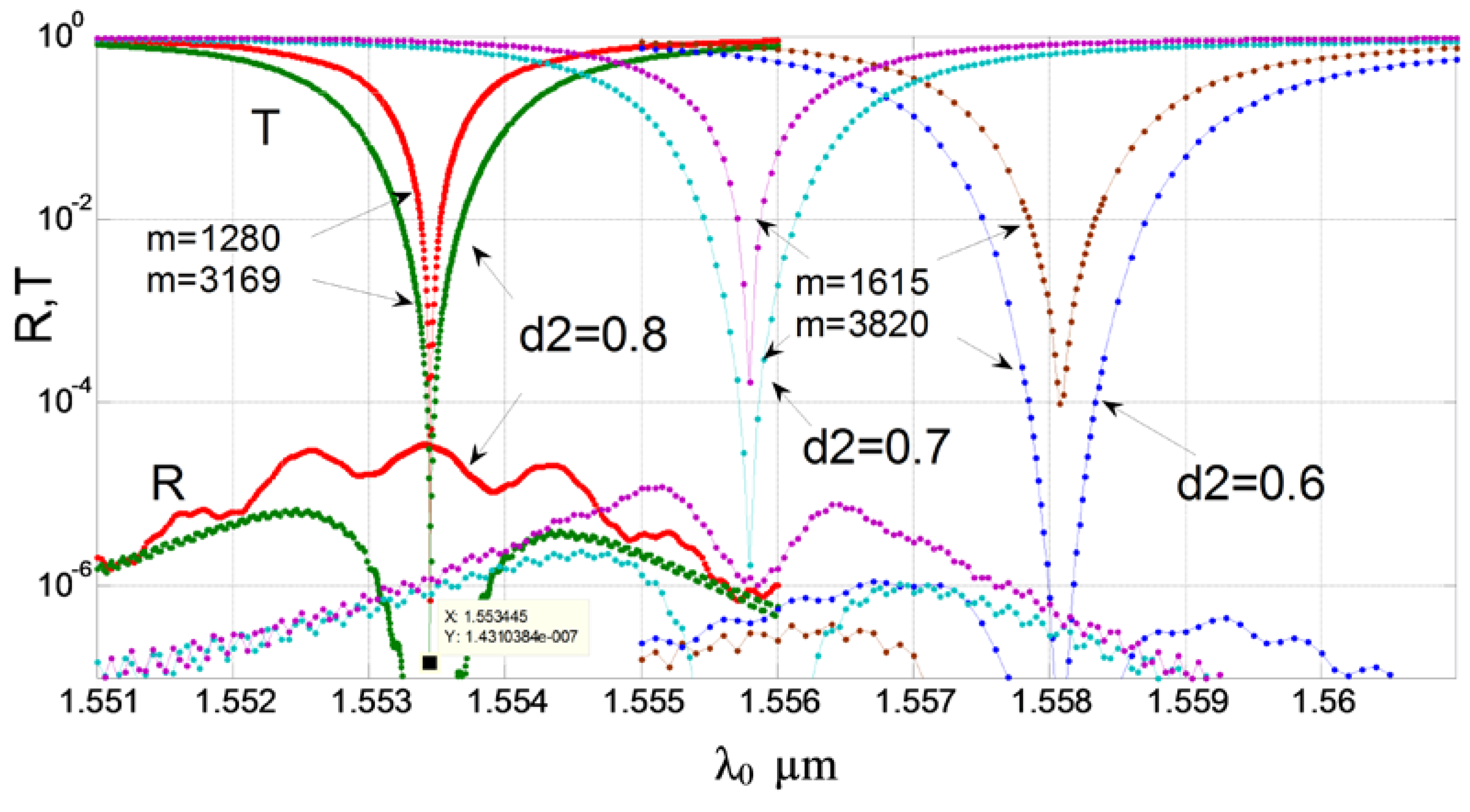
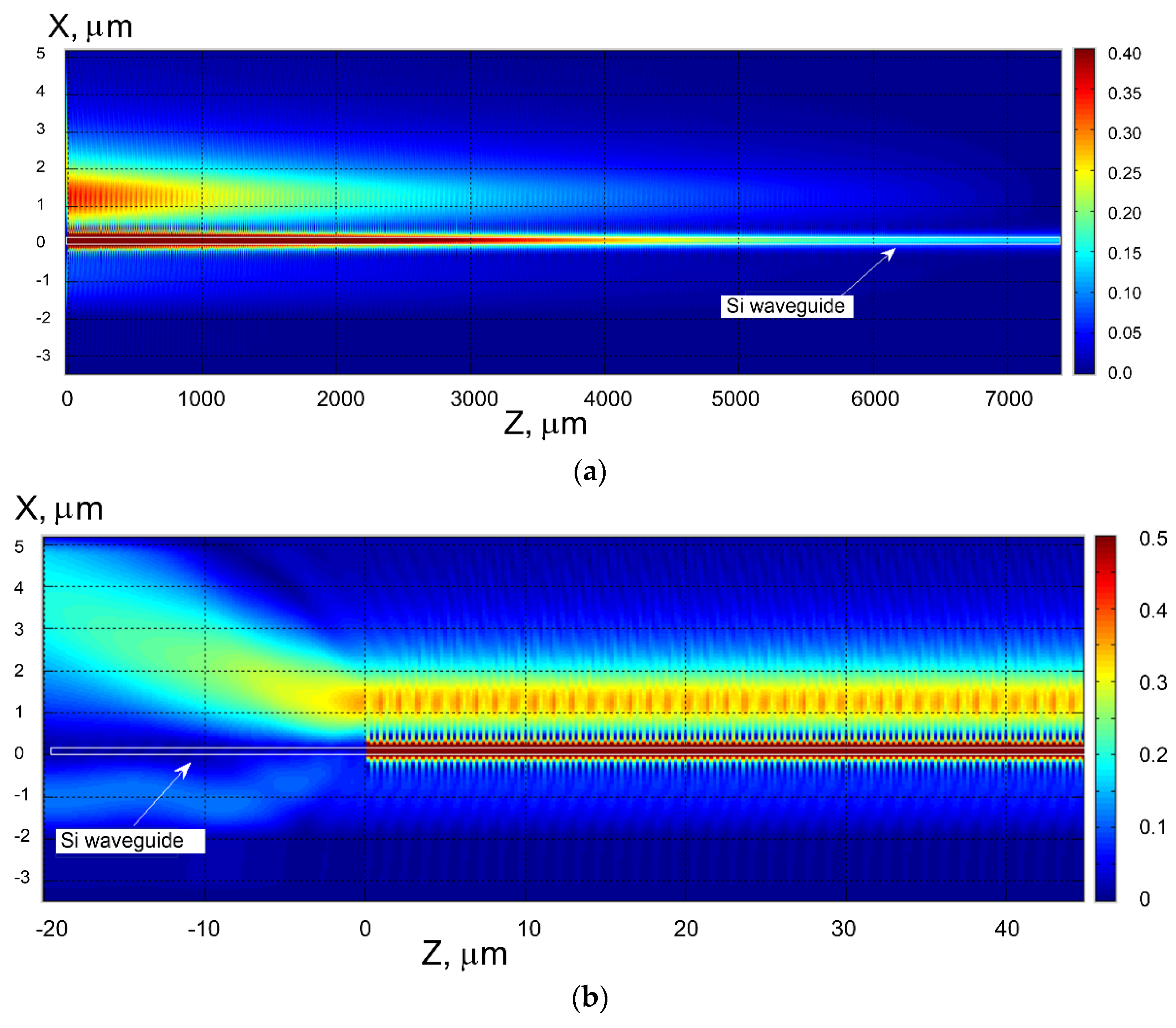
2.6. The Notch Filter Effect in the Silicon Wire Coupled with the Long Grating Structure
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Marcuse, D. Directional couplers made of nonidentical asymmetric slabs. Part II: Grating-assisted couplers. J. Lightw. Technol. 1987, LT-5, 268–273. [Google Scholar] [CrossRef]
- Zhang, S.H.; Tamir, T. Grating-assisted couplers with broadband characteristics. Opt. Lett. 1997, 22, 1159–1161. [Google Scholar] [CrossRef] [PubMed]
- Passaro, V.M.N. Optimal design of grating-assisted directional couplers. J. Lightw. Technol. 2000, 18, 973–984. [Google Scholar] [CrossRef]
- Taillaert, D.; Bienstman, P.; Baets, R. Compact efficient broadband grating coupler for silicon-on-insulator waveguides. Opt. Lett. 2004, 29, 2749–2751. [Google Scholar] [CrossRef] [PubMed]
- Doylend, J.K.; Knights, A.P. Design and Simulation of an Integrated Fiber-to-Chip Coupler for Silicon-on-Insulator Waveguides. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1363–1370. [Google Scholar] [CrossRef]
- Kwon, M.-S.; Shin, S.-Y. Tunable Notch Filter Using a Thermooptic Long-Period Grating. J. Lightw. Technol. 2004, 22, 1968–1975. [Google Scholar] [CrossRef]
- Helfert, S.F.; Pregla, R. Efficient Analysis of Periodic Structures. J. Lightw. Technol. 1998, 16, 1694–1702. [Google Scholar] [CrossRef]
- Alferness, R.C.; Koch, T.L.; Buhl, L.L.; Storz, F.; Heismann, F.; Martyak, M.J.R. Grating-assisted InGaAsP/InP vertical codirectional coupler filter. Appl. Phys. Lett. 1989, 55, 2011–2013. [Google Scholar] [CrossRef]
- Shi, W.; Wang, X.; Lin, C.; Yun, H.; Liu, Y.; Baehr-Jones, T.; Hochberg, M.; Jaeger, N.A.F.; Chrostowski, L. Silicon photonic grating-assisted, contra-directional couplers. Opt. Express 2013, 21, 3633–3650. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Genrich, G.; Keil, N.; Grote, N. Widely tunable grating-assisted heterogeneous silicon nitride/polymer waveguide coupler. Opt. Lett. 2014, 39, 162–165. [Google Scholar] [CrossRef] [PubMed]
- Tsarev, A.V. New wide strip and grating loaded quasi-single-mode waveguide on SOI. Opt. Express 2009, 17, 13095–13101. [Google Scholar] [CrossRef] [PubMed]
- Kolosovskii, E.A.; Tsarev, A.V. Abnormal blocking of a guided mode propagating in a silicon optical waveguide with periodic tunnel coupling. Quantum Electron. 2017, 47, 58–64. [Google Scholar] [CrossRef]
- Roelkens, G.; Dumon, P.; Bogaerts, W.; Van Thourhout, D.; Baets, R. Efficient silicon-on-insulator fiber coupler fabricate during 248-nm-deep UV lithography. IEEE Photonics Technol. Lett. 2005, 17, 2613–2615. [Google Scholar] [CrossRef]
- Rsoft FullWave by SYNOPSYS. Photonic Design Software. Available online: https://www.synopsys.com/optical-solutions/rsoft.html (accessed on 18 January 2018).
- Dell’Olio, F.; Passaro, V.M.N. Optical sensing by optimized silicon slot waveguides. Opt. Express 2007, 15, 4977–4993. [Google Scholar] [CrossRef] [PubMed]
- Claes, T.; Molera, J.G.; De Vos, K.; Schacht, E.; Baets, R.; Bienstman, P. Label-free biosensing with a slot-waveguide-based ring resonator in silicon on insulator. IEEE Photon. J. 2009, 1, 197–204. [Google Scholar] [CrossRef]
- Schmidt, S.; Flueckiger, J.; Wu, W.; Grist, S.M.; Talebi Fard, S.; Donzella, V.; Khumwan, P.; Thompson, E.R.; Wang, Q.; Kulik, P.; et al. Improving the performance of silicon photonic rings, disks, and Bragg gratings for use in label-free biosensing. In Proceedings of the Biosensing and Nanomedicine VII, San Diego, CA, USA, 17–20 August 2014. [Google Scholar]
- Flueckiger, J.; Schmidt, S.V.; Donzella Sherwali, A.; Ratner, D.M.; Chrostowski, L.; Cheung, K.C. Sub-wavelength grating for enhanced ring resonator biosensor. Opt. Express 2016, 24, 15672–15686. [Google Scholar] [CrossRef] [PubMed]
- Chiang, K.S. Dual effective-index method for the analysis of rectangular dielectric waveguides. Appl. Opt. 1986, 25, 2169–2174. [Google Scholar] [CrossRef] [PubMed]
- Tsarev, A. Modified effective index method to fit the phase and group index of 3D photonic wire waveguide. Opt. Lett. 2013, 38, 293–295. [Google Scholar] [CrossRef] [PubMed]
- O’Faolain, L.; Tsarev, A. Experimental demonstration of original optical filter based on multiply coupled waveguides. Opt. Lett. 2014, 39, 3627–3629. [Google Scholar] [CrossRef] [PubMed]
- De Vos, K.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-on-insulator microring resonator for sensitive and label-free biosensing. Opt. Express 2007, 15, 7610–7615. [Google Scholar] [CrossRef] [PubMed]
- MathWorks. Available online: www.mathworks.com (accessed on 1 January 2015).
- Rogge, U.; Pregla, R. Method of lines for the analysis of strip-loaded optical waveguides. Opt. Soc. Am. B 1991, 8, 459–463. [Google Scholar] [CrossRef]
- Scarmozzino, R.; Gopinath, A.; Pregla, R.; Helfert, S. Numerical techniques for modeling guided-wave photonic devices. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 150–161. [Google Scholar] [CrossRef]
- Jamid, H.A.; Akram, M.N. Analysis of Deep Waveguide Gratings: An Efficient Cascading and Doubling Algorithm in the Method of Lines Framework. J. Lightw. Technol. 2002, 20, 1204–1209. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsarev, A.; Kolosovsky, E.; De Leonardis, F.; Passaro, V.M.N. Numerical Simulation of a Novel Sensing Approach Based on Abnormal Blocking by Periodic Grating Strips near the Silicon Wire Waveguide. Sensors 2018, 18, 1707. https://doi.org/10.3390/s18061707
Tsarev A, Kolosovsky E, De Leonardis F, Passaro VMN. Numerical Simulation of a Novel Sensing Approach Based on Abnormal Blocking by Periodic Grating Strips near the Silicon Wire Waveguide. Sensors. 2018; 18(6):1707. https://doi.org/10.3390/s18061707
Chicago/Turabian StyleTsarev, Andrei, Eugeny Kolosovsky, Francesco De Leonardis, and Vittorio M. N. Passaro. 2018. "Numerical Simulation of a Novel Sensing Approach Based on Abnormal Blocking by Periodic Grating Strips near the Silicon Wire Waveguide" Sensors 18, no. 6: 1707. https://doi.org/10.3390/s18061707
APA StyleTsarev, A., Kolosovsky, E., De Leonardis, F., & Passaro, V. M. N. (2018). Numerical Simulation of a Novel Sensing Approach Based on Abnormal Blocking by Periodic Grating Strips near the Silicon Wire Waveguide. Sensors, 18(6), 1707. https://doi.org/10.3390/s18061707







