Development and Performance Evaluation of Image-Based Robotic Waxing System for Detailing Automobiles
Abstract
1. Introduction
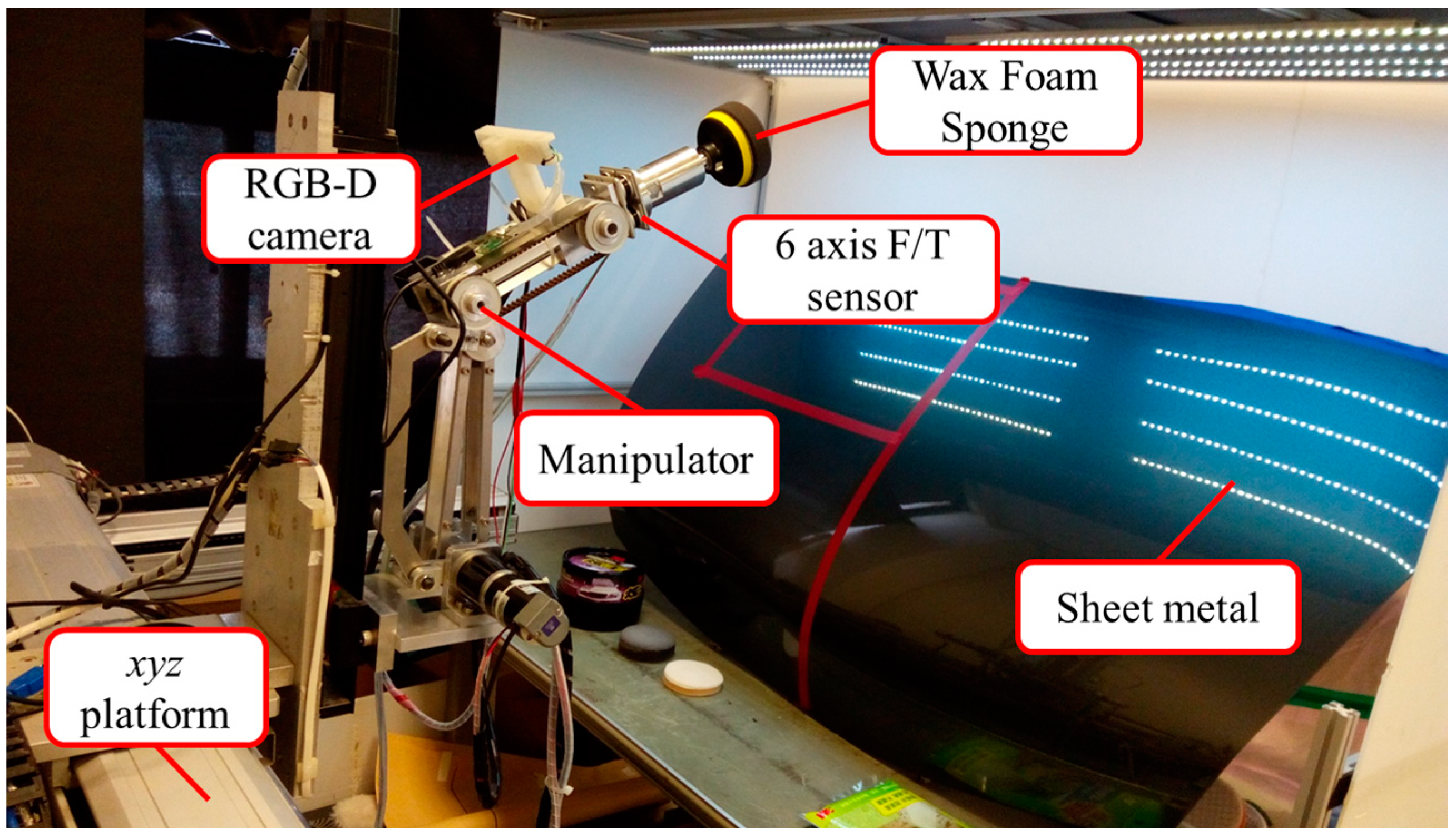
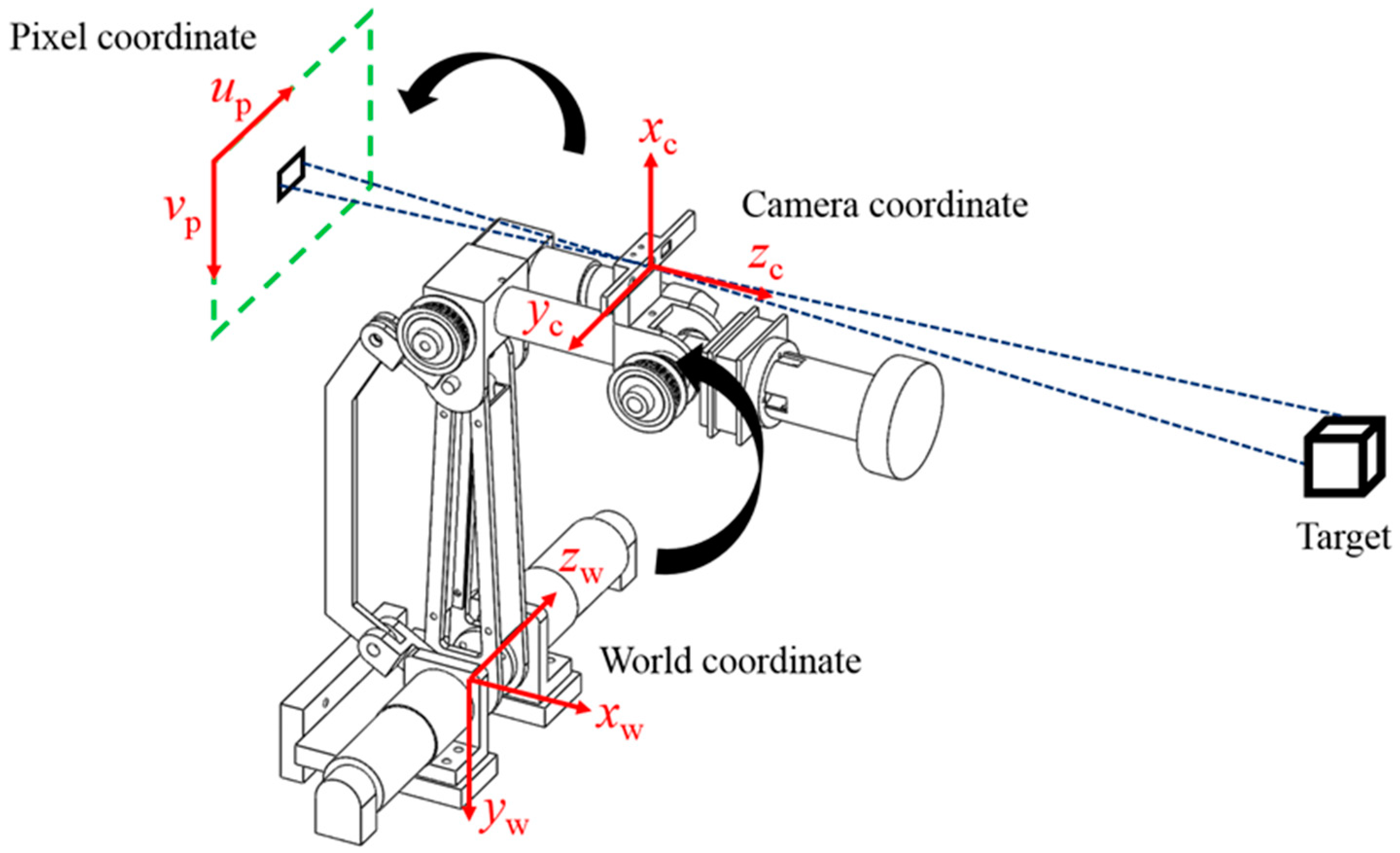
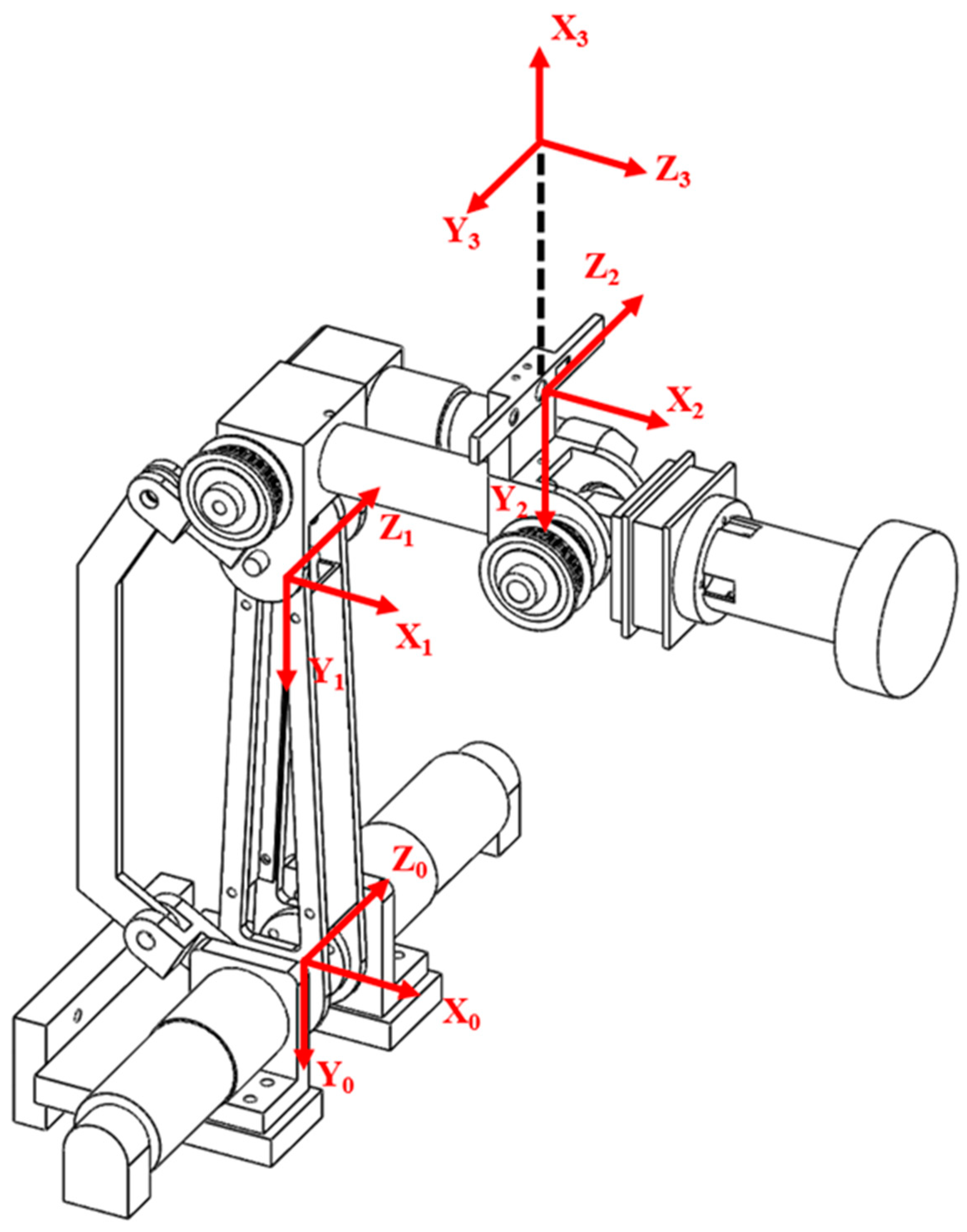
2. System Description
3. Stereo Vision and Path Planning
3.1. Image Processing
3.2. Stereo Vision
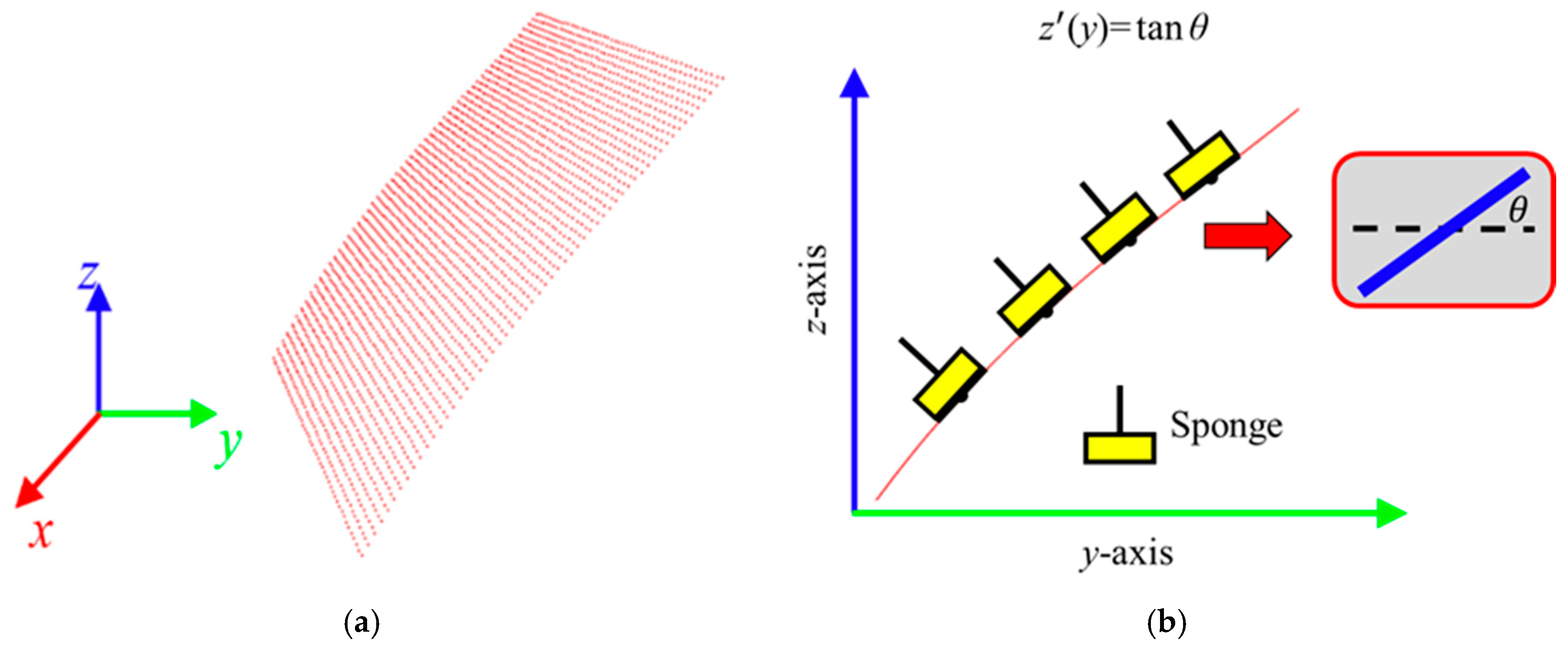
3.3. Planning of Waxing Path
4. Force Control of Robotic Arm
5. Image Based Performance Evaluation
5.1. Selection of External Light Source
5.2. Waxing Assessment Criteria
5.2.1. Image Preprocessing
5.2.2. Establishment of Image Assessment Criteria
6. Experiments and Performance Analysis
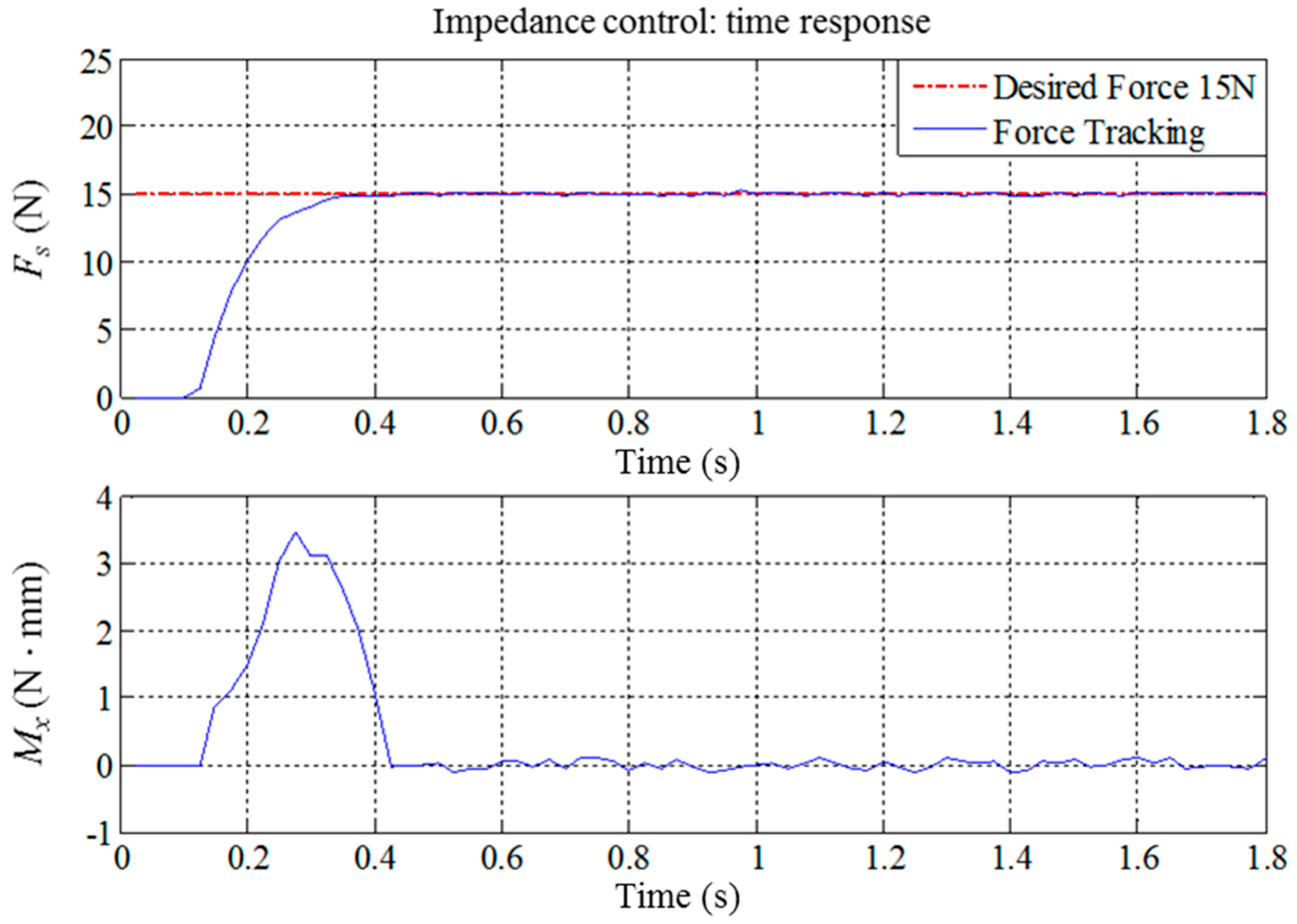
6.1. Analysis of Force Tracking Performance
6.2. Examination of Waxing Parameters
6.2.1. Experiment Conditions and Parameter Settings
6.2.2. Discussion of Waxing Results
6.3. Waxing Parameter Optimization
6.3.1. Problem Formulation
6.3.2. Optimization Results and Verification
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kumar, S. Theories of musculoskeletal injury causation. Ergonomics 2001, 44, 17–47. [Google Scholar] [CrossRef] [PubMed]
- Wagner, H.R. Apparatus for Washing and Waxing Cars. U.S. Patent 3447505, 3 June 1969. [Google Scholar]
- Falls, J.W. Automatic Car Waxer. U.S. Patent 5076202, 31 December 1991. [Google Scholar]
- Hung, V. Car Waxing Machine with Driving Handle. U.S. Patent 6725491, 27 April 2004. [Google Scholar]
- Wu, X.; Wu, X.; Guo, H. Combination Automobile Detailing Machine. U.S. Patent 11518864, 11 September 2006. [Google Scholar]
- Ning, F.; Cong, W.; Wang, H.; Hu, Y.; Hu, Z.; Pei, Z. Surface grinding of CFRP composites with rotary ultrasonic machining: A mechanistic model on cutting force in the feed direction. Int. J. Adv. Manuf. Technol. 2017, 92, 1217–1229. [Google Scholar] [CrossRef]
- Sallinen, M.; Heikkila, T.; Sirvio, M. Robotic Deburring System of Foundry Castings Based on Flexible Workobject Localization; SPIE: Boston, MA, USA, 2001; pp. 476–487. [Google Scholar]
- Hsu, F.Y.; Fu, L.C. Intelligent robot deburring using adaptive fuzzy hybrid position/force control. IEEE Trans. Robot. Autom. 2000, 16, 325–335. [Google Scholar] [CrossRef]
- Mohsin, I.; He, K.; Cai, J.; Chen, H.; Du, R. Robotic polishing with force controlled end effector and multi-step path planning. In Proceedings of the IEEE International Conference on Information and Automation, Macau, China, 18–20 July 2017; pp. 344–348. [Google Scholar]
- Chen, F.; Hao, S.; Miao, X.; Yin, S.; Huang, S. Numerical and experimental study on low-pressure abrasive flow polishing of rectangular microgroove. Powder Technol. 2018, 327, 215–222. [Google Scholar] [CrossRef]
- Han, G.; Sun, M. Compound control of the robotic polishing process basing on the assistant electromagnetic field. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Changchun, China, 9–12 August 2009; pp. 1551–1555. [Google Scholar]
- Sharma, K.; Shirwalkar, V.; Das, A.P.; Pal, P.K. Robotic polishing of pilger-die. In Proceedings of the Conference on Advances in Robotics, Goa, India, 2–4 July 2015. [Google Scholar]
- Jamisola, R.; Ang, M.H.; Oetomo, D.; Khatib, O.; Ming, T.; Lim, S.Y. The operational space formulation implementation to aircraft canopy polishing using a mobile manipulator. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; pp. 400–405. [Google Scholar]
- Zhang, D.; Yun, C.; Song, D.; Lan, X.; Wu, X. Design and application for robotic polishing system. In Proceedings of the IEEE International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 26–28 June 2010; pp. 2470–2474. [Google Scholar]
- Guvenc, L.; Srinivasan, K. Force controller design and evaluation for robot-assisted die and mould polishing. Mech. Syst. Signal. Process. 1995, 9, 31–49. [Google Scholar] [CrossRef]
- Lu, Y.Y.; Dong, J.H. The study of force control with artificial intelligence in ceramic grinding process. In Proceedings of the IEEE International Symposium on Intelligence Information Processing and Trusted Computing, Huanggang, China, 28–29 October 2010; pp. 208–211. [Google Scholar]
- Liu, H.; Wan, Y.; Zeng, Z.; Xu, L.; Zhao, H.; Fang, K. Freeform surface grinding and polishing by CCOS based on industrial robot. In Proceedings of the International Symposium on Advanced Optical Manufacturing and Testing Technologies, Suzhou, China, 26–29 April 2016. [Google Scholar]
- Zhao, T.; Shi, Y.; Lin, X.; Duan, J.; Sun, P.; Zhang, J. Surface roughness prediction and parameters optimization in grinding and polishing process for IBR of aero-engine. Int. J. Adv. Manuf. Technol. 2014, 74, 653–663. [Google Scholar] [CrossRef]
- Akafuah, N.K.; Poozesh, S.; Salaimeh, A.; Patrick, G.; Lawler, K.; Saito, K. Evolution of the automotive body coating process—A review. Coatings 2016, 6, 24. [Google Scholar] [CrossRef]
- Placido, F.; Birney, R.; Kavanagh, J. Investigation of automotive detailing products by ellipsometry and contact angle analysis. Acta Phys. Pol. A 2009, 116, 712–714. [Google Scholar] [CrossRef]
- Gomez, O.; Perales, E.; Chorro, E.; Burgos, F.J.; Viqueira, V.; Vilaseca, M.; Martinez-Verdu, F.M.; Pujol, J. Visual and instrumental assessments of color differences in automotive coatings. Color Res. Appl. 2016, 41, 384–391. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Alirezaee, S.; Amirfattahi, R.; Sadri, S. Detection of steel defect using the image processing algorithms. In Proceedings of the IEEE International Multitopic Conference, Karachi, Pakistan, 23–24 December 2008; pp. 125–127. [Google Scholar]
- Besari, A.R.A.; Zamri, R.; Rahman, K.A.A.; Palil, M.D.M.; Prabuwono, A.S. Surface defect characterization in polishing process using contour dispersion. In Proceedings of the IEEE International Conference on Soft Computing and Pattern Recognition, Malacca, Malaysia, 4–7 December 2009; pp. 707–710. [Google Scholar]
- Samtaş, G. Measurement and evaluation of surface roughness based on optic system using image processing and artificial neural network. Int. J. Adv. Manuf. Technol. 2014, 73, 353–364. [Google Scholar] [CrossRef]
- Khoo, S.W.; Karuppanan, S.; Tan, C.S. A review of surface deformation and strain measurement using two-dimensional digital image correlation. Metrol. Meas. Syst. 2016, 23, 461–480. [Google Scholar] [CrossRef]
- Simunovic, G.; Svalina, I.; Simunovic, K.; Saric, T.; Havrlisan, S.; Vukelic, D. Surface roughness assessing based on digital image features. Adv. Prod. Eng. Manag. 2016, 11, 93–140. [Google Scholar] [CrossRef][Green Version]
- Liu, E.; Liu, J.; Gao, R.; Yi, H.; Wang, W.; Suo, X. Designing indices to measure surface roughness based on the color distribution statistical matrix (CDSM). Tribol. Int. 2018, 122, 96–107. [Google Scholar] [CrossRef]
- Besari, A.R.A.; Prabuwono, A.S.; Zamri, R.; Palil, M.D.M. Computer vision approach for robotic polishing application using artificial neural networks. In Proceedings of the IEEE Student Conference on Research and Development, Kuala Lumpur, Malaysia, 13–14 December 2010; pp. 281–286. [Google Scholar]
- Luh, J.Y.S.; Lin, C.S. Optimum path planning for mechanical manipulators. J. Dyn. Syst. Meas. Control 1981, 103, 142–151. [Google Scholar] [CrossRef]
- Tsai, L.W. Robot Analysis: The Mechanics of Serial and Parallel Manipulators; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Jung, S.; Hsia, T.C.; Bonitz, R.G. Force tracking impedance control of robot manipulators under unknown environment. IEEE Trans. Control Syst. Technol. 2004, 12, 474–483. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef] [PubMed]
- Ballard, D.H. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognit. 1981, 13, 111–122. [Google Scholar] [CrossRef]
- Norman, S.N. Control Systems Engineering; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Luenberger, D.G.; Te, Y. Linear and Nonlinear Programming; Springer: New York, NY, USA, 2008. [Google Scholar]






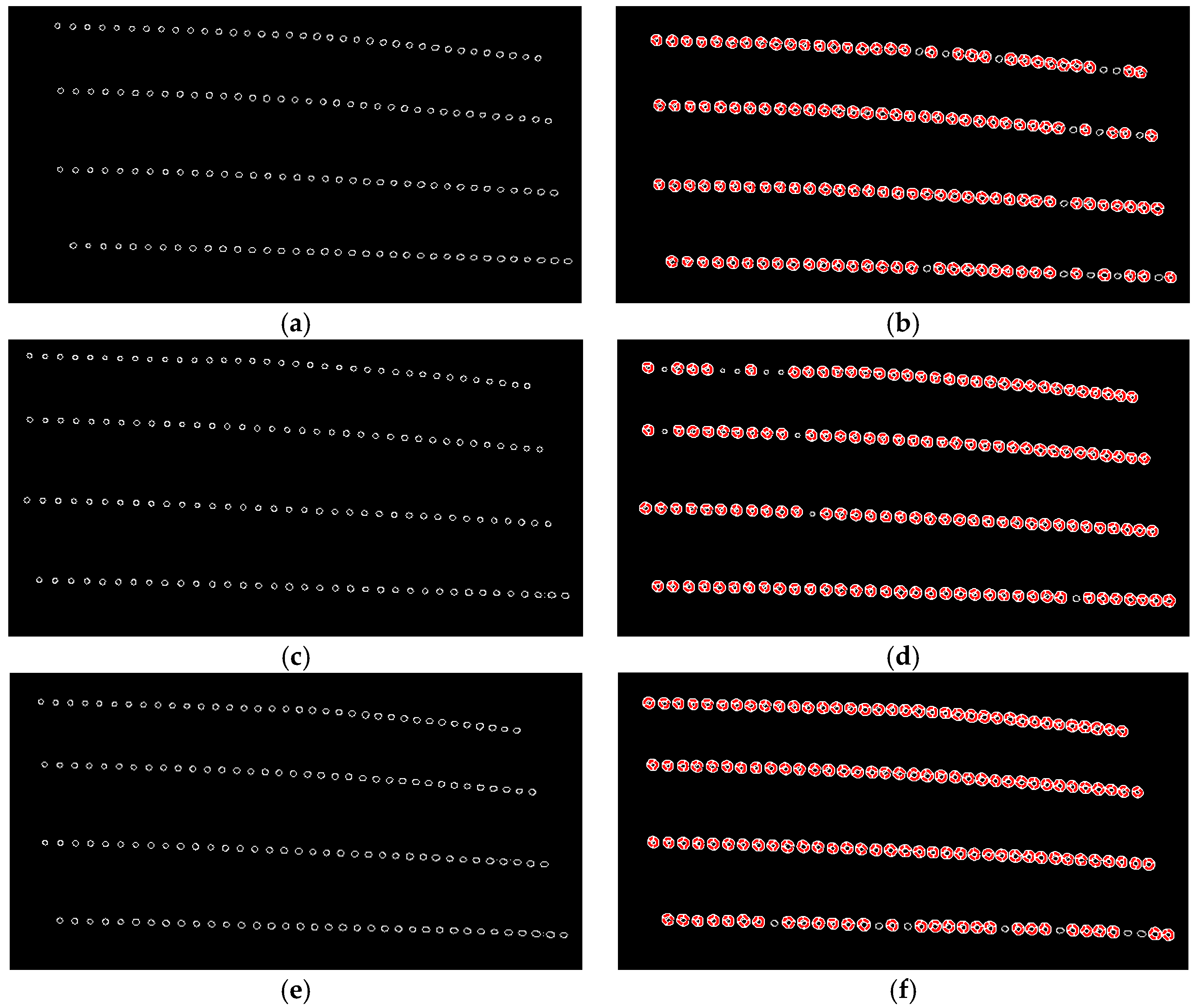


| # of Path | Path Function (after Cubic Curve Fitting) |
|---|---|
| Path 1 | |
| Path 2 | |
| Path 3 | |
| Path 4 | |
| Path 5 | |
| Path 6 |
| Samples in Different Range () | |||
|---|---|---|---|
| Camera View (θ) | Total Samples | ||
| 15° | 144 | 96 samples | 130 samples |
| 30° | 144 | 98 samples | 135 samples |
| 45° | 144 | 97 samples | 137 samples |
| Estimation of Radius | Criterion Definition |
|---|---|
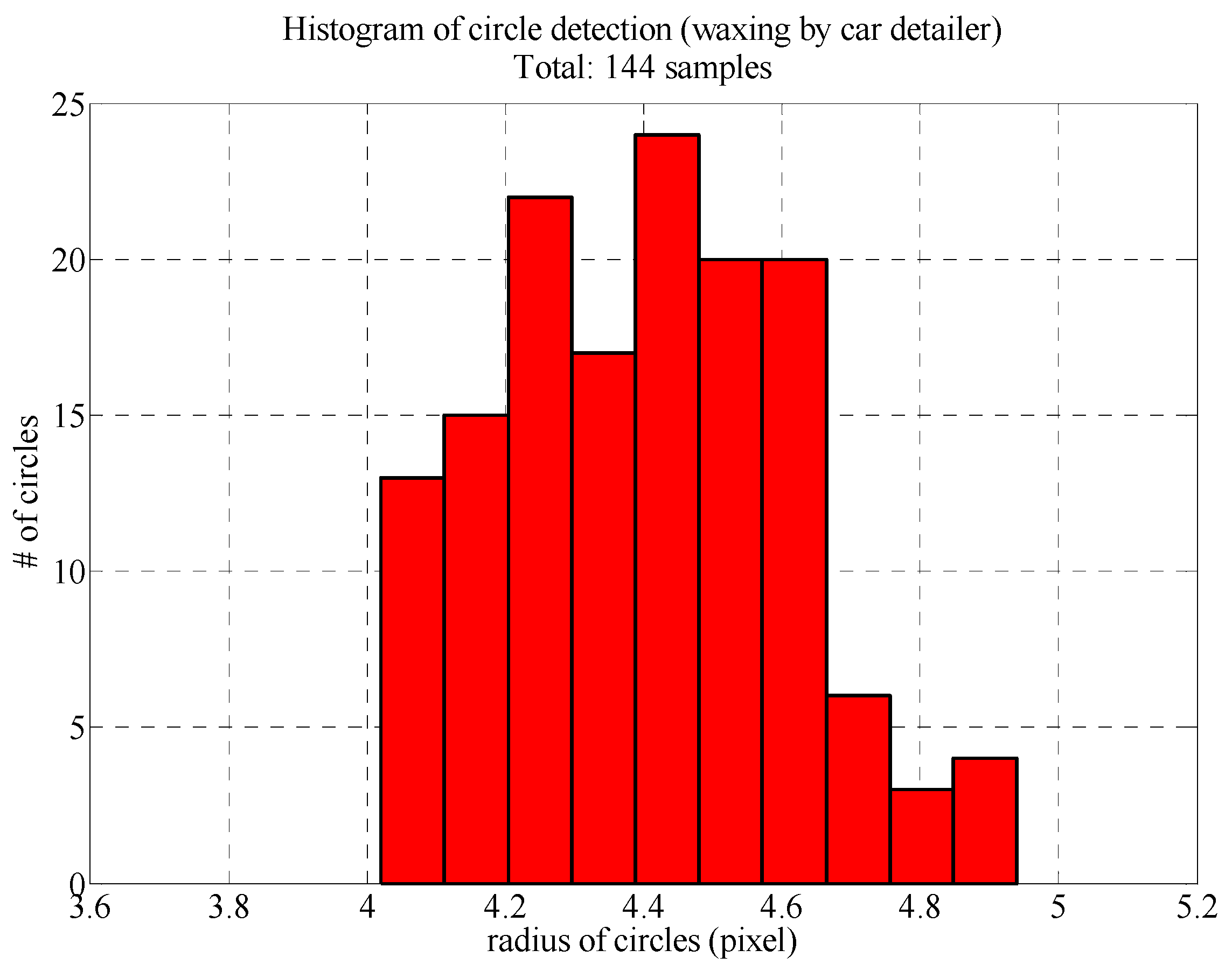
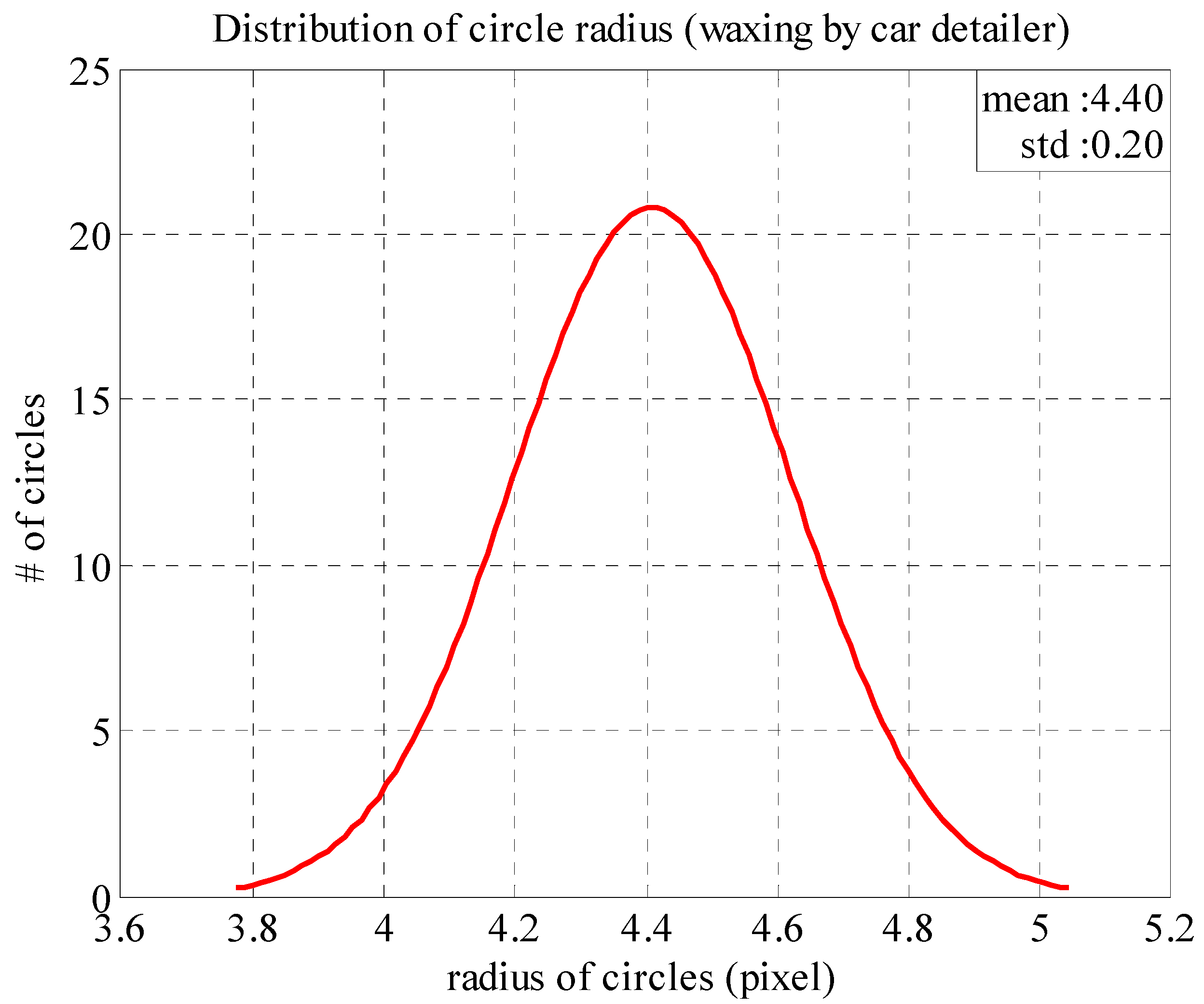
| Mean value () | 4.4 pixel |
| Standard deviation (σ) | 0.2 pixel |
| Range of circle radius | |
| Average result from Table 2 | 134 samples |
| Threshold | 10 samples |
| Waxing Motor Specifications | Waxing Force (From 10 to 19 N) | Dwell Time | Executing Time for all Paths (Approx.) |
|---|---|---|---|
| 24 V—850 rpm (30 N-m) | 10 N | 0.1 s/pt 0.2 s/pt 0.3 s/pt 0.4 s/pt | 5~6 min 10~11 min 15~16 min 20~21 min |
| 13 N | |||
| 15 N | |||
| 17 N | |||
| 19 N |
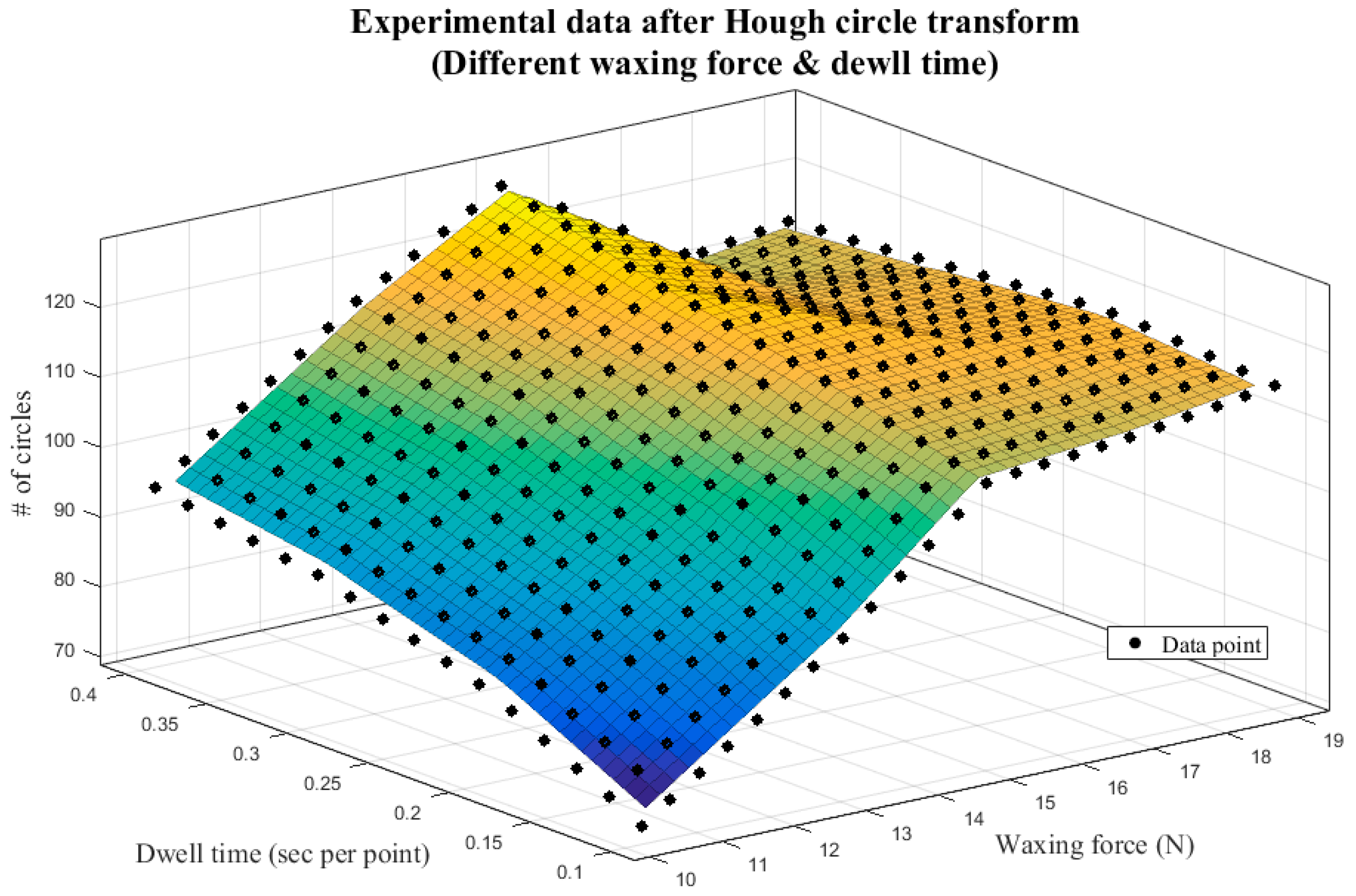
| Waxing Force | Dwell Time | Executing Time | Estimated Result (Total: 144 Samples) |
|---|---|---|---|
| 10 N | 0.1 s/pt | 5 min 28 s | 70 samples |
| 0.2 s/pt | 10 min 35 s | 82 samples | |
| 0.3 s/pt | 15 min 24 s | 89 samples | |
| 0.4 s/pt | 20 min 19 s | 93 samples | |
| 13 N | 0.1 s/pt | 5 min 36 s | 92 samples |
| 0.2 s/pt | 10 min 21 s | 102 samples | |
| 0.3 s/pt | 15 min 18 s | 110 samples | |
| 0.4 s/pt | 20 min 30 s | 115 samples | |
| 15 N | 0.1 s/pt | 5 min 23 s | 110 samples |
| 0.2 s/pt | 10 min 29 s | 116 samples | |
| 0.3 s/pt | 15 min 34 s | 121 samples | |
| 0.4 s/pt | 20 min 36 s | 127 samples | |
| 17 N | 0.1 s/pt | 5 min 31 s | 112 samples |
| 0.2 s/pt | 10 min 33 s | 117 samples | |
| 0.3 s/pt | 15 min 29 s | 115 samples | |
| 0.4 s/pt | 20 min 24 s | 110 samples | |
| 19 N | 0.1 s/pt | 5 min 36 s | 115 samples |
| 0.2 s/pt | 10 min 21 s | 117 samples | |
| 0.3 s/pt | 15 min 18 s | 115 samples | |
| 0.4 s/pt | 20 min 30 s | 113 samples |
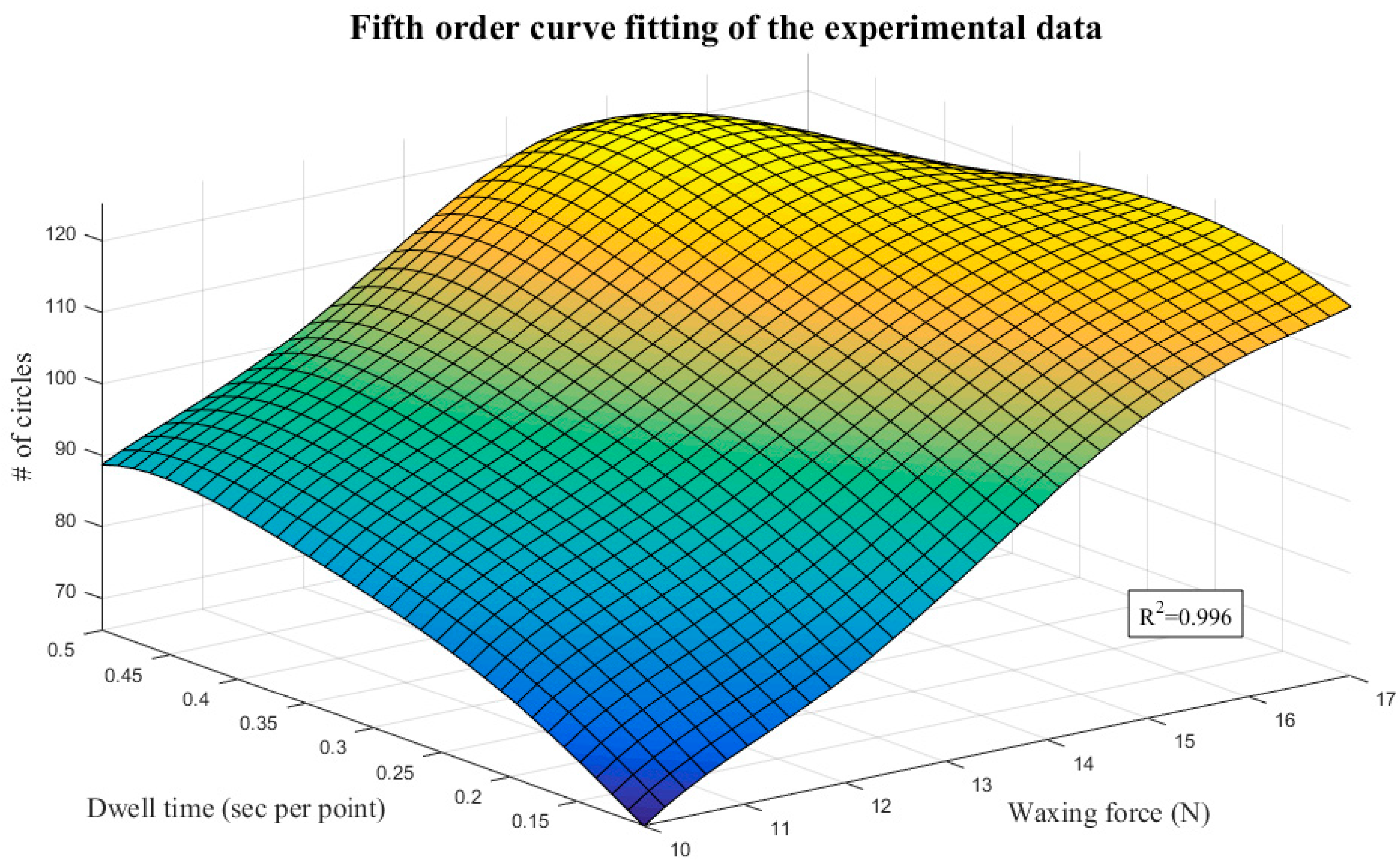
| p00 | −7917 | p21 | −76.58 | p04 | 18140 |
| p10 | 3081 | p12 | −1923 | p50 | 0.01935 |
| p01 | −3663 | p03 | −8127 | p41 | −0.008048 |
| p20 | −471.6 | p40 | −1.324 | p32 | −4.448 |
| p11 | 915.7 | p31 | 2.224 | p23 | 12.24 |
| p02 | 9295 | p22 | 159.7 | p14 | −255.9 |
| p30 | 35.63 | p13 | −83.42 | p05 | −11600 |
| Optimization Parameters of the Waxing System | Lower and Upper Bounds |
|---|---|
| Force (N) | From 10 N to 17 N |
| Dwell time (s/pt) | From 0.1 s/pt to 0.5 s/pt |
| Executing Time | Estimated Result (Total: 144 Samples) | |
|---|---|---|
| Car detailer | About 15 min | 134 samples |
| The waxing system | 25 min 16 s | 130 samples |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-Y.; Hsu, B.-C. Development and Performance Evaluation of Image-Based Robotic Waxing System for Detailing Automobiles. Sensors 2018, 18, 1548. https://doi.org/10.3390/s18051548
Lin C-Y, Hsu B-C. Development and Performance Evaluation of Image-Based Robotic Waxing System for Detailing Automobiles. Sensors. 2018; 18(5):1548. https://doi.org/10.3390/s18051548
Chicago/Turabian StyleLin, Chi-Ying, and Bing-Cheng Hsu. 2018. "Development and Performance Evaluation of Image-Based Robotic Waxing System for Detailing Automobiles" Sensors 18, no. 5: 1548. https://doi.org/10.3390/s18051548
APA StyleLin, C.-Y., & Hsu, B.-C. (2018). Development and Performance Evaluation of Image-Based Robotic Waxing System for Detailing Automobiles. Sensors, 18(5), 1548. https://doi.org/10.3390/s18051548





